Mesoscale modeling of multi-protein-DNA assemblies: the role of the catabolic activator protein in Lac-repressor-mediated looping

Abstract

DNA looping plays a key role in the regulation of the lac operon in Escherichia coli. The presence of a tightly bent loop (between sequentially distant sites of Lac repressor protein binding) purportedly hinders the binding of RNA polymerase and subsequent transcription of the genetic message. The unexpectedly favorable binding interaction of this protein-DNA assembly with the catabolic activator protein (CAP), a protein that also bends DNA and paradoxically facilitates the binding of RNA polymerase, stimulated extension of our base-pair level theory of DNA elasticity to the treatment of DNA loops formed in the presence of several proteins. Here we describe in detail a procedure to determine the structures and free energies of multi-protein-DNA assemblies and illustrate the predicted effects of CAP binding on the configurations of the wild-type 92-bp Lac repressor-mediated O3-O1 DNA loop. We show that the DNA loop adopts an antiparallel orientation in the most likely structure and that this loop accounts for the published experimental observation that, when CAP is bound to the loop, one of the arms of LacR binds to an alternative site that is displaced from the original site by 5 bp.

Introduction

Understanding the biological functions of macromolecules and their assemblies requires detailed knowledge of their three-dimensional structures. The experimental methods that are used to elucidate biomolecular structure provide data that represent a compromise between the size of the object studied and the amount of detail obtained, e.g., low-resolution electron microscopic images of large multi-component systems sacrifice the precise atomic information found in the high-resolution X-ray structures of small molecules. Computational methods help to overcome this limitation by combining the available experimental data with models that reflect well-known biophysical properties of the molecular systems.

This paper describes the computational approach that we have developed for determining the structures and free energies of multi-protein-DNA assemblies. Our method assumes that the DNA deforms in such an assembly, with the protein components providing spatial constraints on DNA, either by distorting the DNA double-helical structure at the binding site or by placing restrictions on the locations of the ends of an otherwise free DNA segment. Thus, correct determination of the configuration and energy of the constrained DNA leads to a model that provides a very good approximation of the actual structure of the assembly.

We make use of a base-pair level theory of DNA elasticity [1] and an efficient algorithm for calculating the configuration of protein-constrained DNA. One of the important advantages of this procedure is that the DNA and protein molecules are represented as elastic bodies and, consequently, that their deformations can be described using a relatively small number of variables. Such an approach makes the modeling of assemblies with tens of thousands of atoms both computationally feasible and efficient.

We developed this methodology in order to gain deeper understanding of the large protein-DNA assemblies formed during transcription, the first step in the expression of genes, and the communication of the many molecular species involved in the regulation of this process. The transcription of most genes reflects the interplay of activator or repressor proteins that bind in the vicinity of the transcription start site, i.e., the precise location on DNA where RNA polymerase (RNAP), the enzyme that copies the information encoded in DNA into RNA, first binds. The mechanisms of control range from the simple competition of repressors with RNAP for overlapping binding sites on DNA to the recruitment of RNAP by activators near the transcription start site and the so-called “action at a distance” [2] of activators/repressors and RNAP from binding sites separated by hundreds of base pairs (100–500 bp). The DNA in the latter case forms loops, which bring sequentially distant sites close together. The classic example of transcription regulation in which DNA looping plays an important role is the E. coli lac operon, the system of proteins and the DNA sequences responsible for the expression of the enzymes used by the bacterium in lactose metabolism. A 5-bp change in the separation of the nucleotide sites where proteins bind alters the looping ability of DNA and can completely disrupt the regulatory function of the operon [3].

Here we continue our investigation of the DNA loops formed by the binding of the tetrameric Lac repressor (LacR) protein to its recognition sequences within the lac operon. The primary site of attachment of LacR to DNA, called O1, lies 401 and 92 bp away from two secondary sites, respectively called O2 and O3. The LacR complex can adopt either a rigid V-shaped structure, or a flexible extended arrangement with dimeric domains connected by a flexible hinge. The DNA can associate with LacR in one of several possible looping modes, depending upon the orientation of the bound nucleotide sequence with respect to the protein. Our earlier work [4] predicts that LacR adopts the extended form when bound to the O3-O1 loop in vitro. The sequence of the wild-type O3-O1 loop of the lac operon contains a binding site for another E. coli protein, the catabolite activator protein (CAP), also called the cAMP receptor protein, located 11 bp away from the O3 LacR recognition site [5]. Other weaker sites of CAP binding within the lac operon do not appear to play a role in transcription activation [6]. Much attention has been given to the question of whether LacR, a repressor of Lac genes, and CAP, an activator of those genes, can bind simultaneously to DNA in the so-called promoter region preceding (downstream of) the transcription start site. Hudson and Fried [7] concluded from enzyme-cutting patterns of DNA that CAP binding places no restrictions on the binding of LacR to the O1 site but precludes binding to the O3 site. They subsequently found [8] that simultaneous binding of CAP and LacR to the O3 site is possible at high concentrations of LacR but that the sequence covered by LacR, the so-called footprint, is shifted approximately 5–6 bp upstream. Balaeff et al. [9] recently constructed a model of the LacR-CAP-DNA loop complex in one of the possible looping modes using the V-shaped LacR structure and an ideal elastic-rod representation of DNA. A 6–8 bp upstream relocation of the O3 site lowers the computed energy of their modeled DNA loop.

Here we determine the configurations and deformational free energies of LacR-CAP-DNA loop complexes using our sequence-dependent treatment of DNA. We take into account all DNA looping modes, the precise structural changes in DNA induced by the binding of LacR and CAP, the possibility of opening LacR, and the binding interactions of LacR with DNA. We find that, in the vicinity of the O3 binding site, there is an alternative LacR binding site, which we call O3*, that preserves nearly all of the observed hydrogen-bonding interactions of DNA with LacR in the complex with the O1 site [10]. When CAP is bound to the loop and LacR to O3*, one of the antiparallel loop types becomes very favorable in terms of its free energy. We propose that this structure is the LacR-mediated loop found by Fried and Hudson [8] in the presence of CAP.

Methods

Sequence-dependent DNA elasticity

The mechanical properties of DNA influence its role in the cell [11]. High-resolution structural studies show that both the intrinsic structure and the elastic properties depend on sequence. Some base-pair steps, i.e., neighboring base pairs, act as natural wedges that change the direction of the helical axis; others are sites of under- or overtwisting relative to the average twist of ca. 36°. The positioning of local bends in phase with the double-helical structure gives the DNA intrinsic curvature [12]–[14], and the positioning of the local stiffness in phase with the helical repeat leads to bending anisotropy [15]. The six rigid-body motions describing the relative rotation and displacement of neighboring base pairs, depicted in Fig. 1, can be strongly coupled [16]. The untwisting of adjacent residues frequently induces an increase in roll, the parameter that describes the component of bending with predominant influence on the widths of the major and minor grooves. Untwisting can also induce a decrease in slide, the parameter describing the motion of a base-pair plane along its long axis.

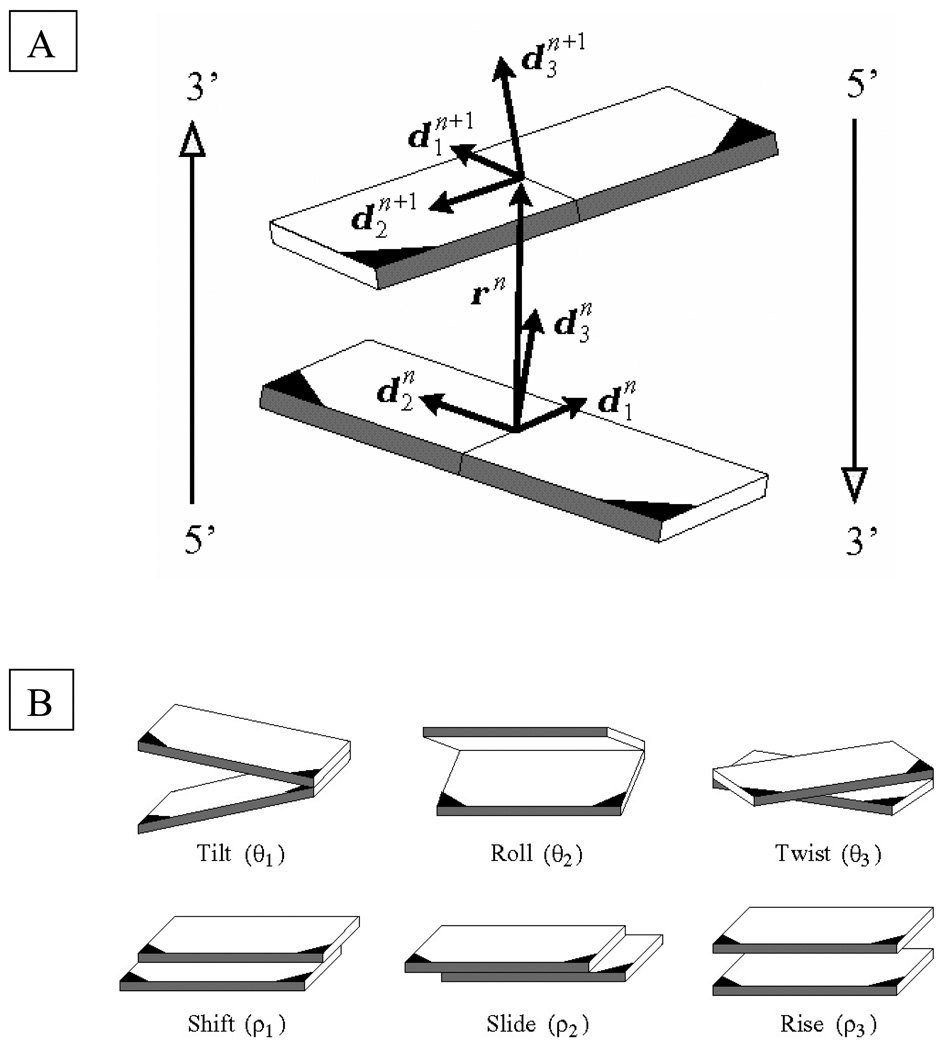
Fig. 1.

(A) Model of a base-pair step showing the vector rⁿ = xⁿ⁺¹ − xⁿ that connects the origins of successive residues and the orthonormal frames $({\mathbf{d}}_1^n,{\mathbf{d}}_2^n,{\mathbf{d}}_3^n),({\mathbf{d}}_1^{n+1},{\mathbf{d}}_2^{n+1},{\mathbf{d}}_3^{n+1})$ on the base pairs. Each base is covalently bonded at the darkened corner to one of the two sugar-phosphate chains. The minor-groove edges of base pairs are shaded in gray, and the antiparallel 5′-3′ directions of the complementary strands are denoted by the arrows at the edges.

(B) Schematic representation of kinematical variables describing the relative orientation and displacement of base pairs in a step. Images illustrate positive values of the designated variables with respect to the leading strand, denoted in (A) by the arrow on the left.

The elastic theory used here captures these deformational features of DNA and also accounts for the dependence of the mechanical properties on nucleotide sequence [1], [17]. The DNA configuration is specified by giving, for each base pair, numbered by index n, its location xⁿ in space and its orientation described by an embedded orthonormal frame $({\mathbf{d}}_1^n,{\mathbf{d}}_2^n,{\mathbf{d}}_3^n)$. The relative orientation and position of the base pair and its predecessor are specified by six kinematical variables ${\xi }_i^n=({\theta }_1^n,{\theta }_2^n,{\theta }_3^n,{\rho }_1^n,{\rho }_2^n,{\rho }_3^n)$, termed, respectively, tilt, roll, twist, shift, slide, and rise (see Fig. 1 for representative images and the Appendix for a convenient definition of the kinematical variables) [18].

Let us write $\mathrm{\Xi }={\{{\xi }_i^n\}}_{i=1‥6}^{n=1‥N-1}$ for the configuration of a DNA segment of length N. The elastic energy Ψ = Ψ(Ξ) is taken to be the sum of the base-pair step energies ψⁿ, each of which is a quadratic function of the corresponding variables ${\xi }_i^n$, i.e.,

$$\mathrm{\Psi }={\displaystyle \sum _{n=1}^{N-1}{\psi }^n},{\psi }^n=\frac{1}{2}{\displaystyle \sum _{i=1}^3{\displaystyle \sum _{j=1}^3{F}_{ij}^{\text{XY}}}\mathrm{\Delta }{\xi }_i^n\mathrm{\Delta }{\xi }_j^n;}$$ (1)

here XY is the nucleotide sequence (in the direction of the coding strand) of the n^th base-pair step, $\mathrm{\Delta }{\xi }_i^n={\xi }_i^n-{\overline{\xi }}_i^{\text{XY}}$ are the deviations of variables from their intrinsic values ${\overline{\xi }}_i^{\text{XY}},\text{and}{F}_{ij}^{\text{XY}}$ are the elastic moduli. We use empirical estimates of intrinsic values and moduli deduced from the averages and fluctuations of base-pair step parameters in high-resolution DNA-protein complexes [16] and normalized so that the persistence length of mixed-sequence DNA matches observed values (~500Å) [19].

Electrostatic energy of DNA

We account for the polyelectrolyte nature of DNA by adding to the total energy the contribution resulting from the repulsion between negatively charged phosphate groups on the DNA backbone. The electrostatic energy Φ is a sum of pairwise interactions, adjusted for counterion condensation and screening effects due to ionic environment. For simplicity it is convenient to merge the two charges associated with each base pair into a single charge of twice the magnitude located at the centroid of the base pair, in which case the energy Φ becomes:

$$\mathrm{\Phi }=\frac{{(2\delta )}^2}{4\pi \epsilon }{\displaystyle \sum _{m=1}^{N-2}{\displaystyle \sum _{n=m+2}^N\frac{\text{exp}(-\kappa |{\mathbf{r}}^{mn}|)}{|{\mathbf{r}}^{mn}|}}},$$ (2)

where r^mn = x^m – xⁿ is the position vector connecting the centers of base pairs m and n, δ is the net effective charge of the base pair, taken to be 0.48e⁻ or 7.7 × 10⁻²⁰ Coulombs assuming 76% charge neutralization by condensed cations [20], ε is the permittivity of water at 300 K, and κ is the Debye screening parameter, which, for monovalent salt such as NaCl, depends on the molar salt concentration c as $\kappa =0.329\sqrt{c}{\AA }^{-1}$. The merging of charges reduces the amount of computer time needed to evaluate Φ and introduces, in our experience, only small error to the resulting configurations [unpublished results]. The sum in (2) does not include the electrostatic interaction of nearest neighbors, because we assume that such an interaction is already accounted for in the local elastic terms in (1). Thus, equation (2) represents only nonlocal (i.e., long-range) effects.

Constraints on DNA configurations

The binding of proteins imposes several types of constraints on DNA in macromolecular complexes.

(A) Intrinsic structure

The binding of a protein to DNA between base pairs n₁ and n₂, alters the intrinsic values ${\overline{\xi }}_i^n$ and moduli $F_{ij}^n,n_1\le n<n_2,i,j=1\dots 6$, of the contacted base-pair steps. Good estimates of these quantities can be found from analysis of available high-resolution structures of the protein-DNA complex of interest [21]. If no such structures exist, one can approximate the configuration of the bound complex with a related structure or a so-called homology model [22]. We generally assume that the configuration of protein-bound DNA is identical to the configuration of the crystal structure, and that that configuration is rigid and unaffected by the deformation of adjacent DNA, i.e., ${\xi }_i^n,n_1\le n\le n_2,i=1\dots 6$ will be held fixed for each bound protein.

(B) Rigid end conditions

Some proteins bind two DNA sites simultaneously and impose spatial constraints, i.e., end conditions, on the DNA segment between the binding sites. Such proteins, if rigid, will impose constraints on the relative position and orientation of the bound DNA segments. If the bound DNA is also rigid, a relation between two base pairs, one from each bound segment, is sufficient to describe the constraint:

$${\mathbf{d}}_i^m·{\mathbf{d}}_j^n=D_{ij}^{mn},{\mathbf{d}}_i^m·({\mathbf{x}}^n-{\mathbf{x}}^m)=r_{ij}^{mn}.$$ (3)

(C) Semi-rigid end conditions

In some circumstances, the protein can deform via one or several degrees of freedom α_k, k = 1,…,K. In such cases the relative position and orientation of the bound DNA segments are functions of the degrees of freedom:

$${\mathbf{d}}_i^m\cdot {\mathbf{d}}_j^n=g_{ij}^{mn}(\{{\alpha }_k\}),{\mathbf{d}}_i^m\cdot ({\mathbf{x}}^n-{\mathbf{x}}^m)=h_i^{mn}(\{{\alpha }_k\}).$$ (4)

(D) Cyclization

Ring closure imposes special configurational constraints on a DNA segment. Such constraints can be accounted for by introducing an additional, hypothetical (N+1) base pair and then requiring that the position and orientation of such a base pair are identical to the position and orientation of the first base pair:

$${\mathbf{x}}^1={\mathbf{x}}^{N+1},{\mathbf{d}}_i^1={\mathbf{d}}_i^{N+1}.$$ (5)

(E) Linking number

A circular DNA or a DNA closed by binding to a protein at two or more sites is subject to the topological constraint of fixed linking number. The linking number of circular DNA is an integer that represents how many times the two strands of the molecule are intertwined [23],[24]. For closed DNA, the linking number cannot be changed unless one of the strands of DNA is severed. The linking number of a DNA segment bound to a protein at two ends, however, can be changed. The linking number is defined in this case by introducing a virtual closure for each strand and can be changed by dissociation of the protein from the DNA.

The linking number Lk(Ξ) of two piecewise linear curves ${\{{\mathbf{x}}^n+\epsilon {\mathbf{d}}_2^n\}}_{n=1}^N\text{and}{\{{\mathbf{x}}^n-\epsilon {\mathbf{d}}_2^n\}}_{n=1}^N$ representing the DNA strands can be computed using the results of [25]. An important consequence of Lk(Ξ) being an integer invariant is that it does not change when the configuration Ξ is perturbed infinitesimally. Therefore it does not contribute to the Lagrangian (see below) and serves primarily to classify computed equilibrium configurations.

We denote the above collection of constraints (A)–(E) imposed on the configuration Ξ of the DNA under consideration as:

$$C_j(\mathrm{\Xi })=0j=1,\dots ,M.$$ (6)

(F) Soft end conditions

There are proteins that bind to DNA in two places but contain a flexible polypeptide tether between the DNA binding subunits. Such proteins do not impose a rigid constraint on the relative location and orientation of the bound DNA, but rather provide an additional contribution to the total energy of the system:

$$\mathrm{\Theta }=\mathrm{\Theta }(\mathrm{\Xi }).$$ (7)

For example, for polypeptide linkers one may take the energy derived from the radial distribution function Θ(Ξ) = −kT ln p(r(Ξ)), where p(r) = cπr² exp(−a(r − b)²) (see [26]) and r(Ξ) is the distance between anchoring points on subunits bound to DNA with configuration Ξ. This added energy Θ can also be used to take account of conservative applied external forces, as in single-molecule manipulation experiments.[27]

(G) DNA-DNA steric hindrance

Although the total energy contains an electrostatic term that penalizes configurations in which two parts of the same DNA molecule come into close proximity, it does not, by itself, prevent overlap of computed configurations. Thus, one must include constraints of steric hindrance to insure that no points in two distinct DNA base pairs occupy the same position in space. There are, in fact, two situations that must be avoided: (a) cases in which the DNA is bent to such a degree that two neighboring base pairs intersect and (b) cases in which two DNA segments come together in such a way that sequentially distant base pairs intersect. For a DNA represented as a tube with a continuous axial curve, a convenient way to enforce both constraints at once is to restrict the global curvature of the tube [28]. That method is not appropriate for the discrete model because of the possibility of shearing deformations. Instead we use a simple and efficient approximation to enforce the two constraints. Specifically, we treat each base-pair n as a disc of diameter d = 20 Å centered at xⁿ with normal ${\mathbf{d}}_3^n$ and require (a) that for each n the discs Dⁿ and Dⁿ⁺¹ do not intersect and (b) that the centers of Dⁿ and Dⁿ⁺¹ are separated more than d for any m, n such that | m − n | > πd /(2 < ρ̅₃ >) (where < ρ̅₃ > = 3.4 Å is the average rise in undeformed DNA). Both constraints (a) and (b) can be represented as inequalities

$$E_k(\mathrm{\Xi })\le 0k=1,\dots ,K.$$ (8)

(H) Protein-DNA steric hindrance

In addition to constraining the steric interactions of DNA with itself, the DNA must be prevented from sterically interfering with the bound proteins and the bound proteins from interfering with one another. These additional constraints can be implemented by introducing a surface for each bound protein and requiring that no sphere Sⁿ intersects any protein surface and no two protein surfaces intersect each other. It should be noted that the detailed features of protein surfaces can greatly increase the number of equilibrium configurations of the assembly and therefore, in the interest of computational efficiency, the proteins can be roughly approximated by appropriate ideal geometrical bodies, such as ellipsoids. The resulting constraints will again have the form (8).

Classical mechanics

We are concerned with two goals: (i) computing the locally stable configurational states of the constrained DNA, and (ii) describing the likelihood of occurrence of each of the states in a thermally excited environment. We omit consideration of the dynamics of DNA or the rates of transitions between configurational states.

Statistical mechanics tells us that the most likely configuration of DNA is the one for which the total energy E of the DNA,

$$E(\mathrm{\Xi })=\mathrm{\Psi }(\mathrm{\Xi })+\mathrm{\Phi }(\mathrm{\Xi })+\mathrm{\Theta }(\mathrm{\Xi }),$$ (9)

i.e., the sum of the elastic energy Ψ, the electrostatic energy Φ, and the total energy of deformable proteins and applied loading Θ, is minimized subject to the imposed constraints (6) and (8). Such a configuration is clearly one for which the first variation in E vanishes for any perturbation. Following the standard approach to nonlinear constrained optimization [29] we introduce the Lagrangian L(Ξ,Γ,Λ) with Lagrange multiplier constants $\mathrm{\Gamma }={\{F_j\}}_{j=1}^M\text{and}\mathrm{\Lambda }={\{G_j\}}_{j=1}^{N^2}$ follows:

$$L(\mathrm{\Xi },\mathrm{\Gamma },\mathrm{\Lambda })=E(\mathrm{\Xi })+{\displaystyle \sum _{j=1}^M{F}_j{C}_j(\mathrm{\Xi })}+{\displaystyle \sum _{j=1}^K{G}_j{E}_j(\mathrm{\Xi })}.$$ (10)

A necessary condition for a configuration Ξ* obeying constraints (6) and (8) to be in equilibrium is that there are multipliers Γ* and Λ* ≥ 0 such that Ξ* obeys the Kuhn-Tucker equations [30]:

$${\mathrm{\nabla }}_{\mathrm{\Xi }}L({\mathrm{\Xi }}^{*},{\mathrm{\Gamma }}^{*},{\mathrm{\Lambda }}^{*})={\mathrm{\nabla }}_{\mathrm{\Xi }}E({\mathrm{\Xi }}^{*})+{\displaystyle \sum _{j=1}^M{F}_j^{*}{\mathrm{\nabla }}_{\mathrm{\Xi }}{C}_j({\mathrm{\Xi }}^{*})+{\displaystyle \sum _{k=1}^K{G}_k^{*}{\mathrm{\nabla }}_{\mathrm{\Xi }}{E}_k({\mathrm{\Xi }}^{*})=0,}}$$ (11a)

$$C_j({\mathrm{\Xi }}^{*})=0,j=1,\dots ,M,$$ (11b)

$$G_k^{*}{E}_k({\mathrm{\Xi }}^{*})=0,k=1,\dots ,K.$$ (11c)

Note that the variational equation in (11) expresses the laws of balance of forces and moments acting on the n^th base pair [1]:

$${\mathbf{f}}^n-{\mathbf{f}}^{n-1}={\mathbf{g}}^n,{\mathbf{m}}^n-{\mathbf{m}}^{n-1}={\mathbf{f}}^n\times {\mathbf{r}}^n+{\mathbf{n}}^{n}n=2,\dots ,N,$$ (12)

where fⁿ and mⁿ are the force and moment exerted on the n^th base pair by the (n+1)^th base pair, and gⁿ and nⁿ are the external force and moment acting on the n^th base pair, which result from the electrostatic interaction or arise as Lagrange multipliers corresponding to constraints (6) and (8). Our assumption about the charges centralized in the base pairs implies (see [31]) that if Θ = 0 and self-contact is absent, then nⁿ = 0 and

$${\mathbf{g}}^n=\frac{{(2\delta )}^2}{4\pi \epsilon }{\displaystyle \sum _{m=1}^{N-2}{\displaystyle \sum _{n=m+2}^N\frac{-(1+\kappa |{\mathbf{r}}^{mn}|)\text{exp}(-\kappa |{\mathbf{r}}^{mn}|)}{|{\mathbf{r}}^{mn}{|}^3}}}{\mathbf{r}}^{mn}.$$ (13)

As shown in [1], equations (1) and (12) imply that

$${\mathbf{f}}^n\cdot {\mathbf{d}}_i^n={\displaystyle \sum _{j=1}^3{Q}_{ij}^n}\frac{\partial {\psi }^n}{\partial {\rho }_j^n}={\displaystyle \sum _{j=1}^3{\displaystyle \sum _{k=1}^3{Q}_{ij}^n}}{F}_{(j+3)k}^{\text{XY}}\mathrm{\Delta }{\xi }_k^n,$$ (14)

$${\mathbf{m}}^n\cdot {\mathbf{d}}_i^n={\displaystyle \sum _{j=1}^3{\mathrm{\Gamma }}_{ij}^n}({\displaystyle \sum _{s=1}^3{F}_{js}^{\text{XY}}}\mathrm{\Delta }{\xi }_s^n+{\displaystyle \sum _{k=1}^3{\displaystyle \sum _{l=1}^3{}_j\mathrm{\Lambda }_{\mathit{\text{kl}}}^n{\rho }_l^n{\displaystyle \sum _{s=1}^3{F}_{{(j+3)}_s}^{\text{XY}}}\mathrm{\Delta }{\mathrm{\xi }}_s^n}}),$$ (15)

where the matrices $Q_{ij}^n,{\mathrm{\Gamma }}_{ij}^n,\text{and}{}_j\mathrm{\Lambda }_{\mathit{\text{kl}}}^n$ (not to be confused with the Lagrange multipliers introduced above) depend on $({\xi }_i^n)$ as shown in the Appendix.

A solution Ξ* of equations (11) (or, equivalently, equations (11b),(11c),(12)–(15)) is in equilibrium in the sense that the first variation of the total energy vanishes for all perturbations. Such a solution is not necessarily the configuration globally minimizing E, but can be any metastable or unstable equilibrium configuration corresponding to the set of constraints. The stability of an equilibrium configuration Ξ* can be verified by checking that the constrained Hessian,

$${\mathrm{\nabla }}_{\mathrm{\Xi }}^{2}L({\mathrm{\Xi }}^{*},{\mathrm{\Gamma }}^{*},{\mathrm{\Lambda }}^{*})={\mathrm{\nabla }}_{\mathrm{\Xi }}^{2}E({\mathrm{\Xi }}^{*})+{\displaystyle \sum _{j=1}^M{F}_j^{*}{\mathrm{\nabla }}_{\mathrm{\Xi }}^2{C}_j({\mathrm{\Xi }}^{*})}+{\displaystyle \sum _{k=1}^K{G}_k^{*}{\mathrm{\nabla }}_{\mathrm{\Xi }}^2{E}_k({\mathrm{\Xi }}^{*})},$$ (16)

obeys ${\mathrm{\nabla }}_{\mathrm{\Xi }}^{2}L({\mathrm{\Xi }}^{*},{\mathrm{\Gamma }}^{*},{\mathrm{\Lambda }}^{*})[\mathrm{X},\mathrm{X}]>0$ for all normalized perturbations X such that

$$\begin{array}{cc}{\mathrm{\nabla }}_{\mathrm{\Xi }}{C}_j({\mathrm{\Xi }}^{*})[\mathrm{X}]=0\hfill & j=1,\dots ,M,\hfill \\ G_k^{*}{\mathrm{\nabla }}_{\mathrm{\Xi }}{E}_k({\mathrm{\Xi }}^{*})[\mathrm{X}]=0,\hfill & k=1,\dots ,K.\hfill \end{array}$$ (17)

Equilibrium configurations for which the Hessian is not positive definite are saddle points on the energy surface and can be used to characterize transition points (mountain passes) between locally stable configurations.

Statistical mechanics of the assembly

Each configuration Ξ* that locally minimizes the energy E is a possible state of the system. The probability of occurrence of a state Ξ* is proportional to the integral

$$Z({\mathrm{\Xi }}^{*})={\displaystyle \underset{B({\mathrm{\Xi }}^{*})}{\int }\text{exp}(-E(\mathrm{\Xi })/kT)J(\mathrm{\Xi })d\mathrm{\Xi },}$$ (18)

where B(Ξ*) is the basin of attraction of Ξ*, defined as the set of configurations Ξ obeying constraints (6) and (8) from which there is a downhill path to Ξ* but not to any other local minimum of the system. The Jacobian J is included in the probability measure because of the non-canonical choice of independent variables [32]. If Ξ* is a sufficiently deep minimum, one can approximate the integral in (18) by another in which (i) the integration domain is extended from B(Ξ*) to the entire set of configurations that obey the constraints, and (ii) the energy function is replaced (and its definition extended to points not in B(Ξ*)) by a quadratic expansion about Ξ*:¹

$$\begin{array}{cc}Z({\mathrm{\Xi }}^{*})\hfill & \cong {\displaystyle \underset{C_j(\mathrm{\Xi })=0}{\int }\text{exp}(-E(\mathrm{\Xi })/kT+\text{ln}J(\mathrm{\Xi }))d\mathrm{\Xi }}\hfill \\ \hfill & \cong \text{exp}(-E({\mathrm{\Xi }}^{*})/kT)J({\mathrm{\Xi }}^{*}){\displaystyle \underset{\underset{G_k^{*}{\mathrm{\nabla }}_{\mathrm{\Xi }}{E}_k({\mathrm{\Xi }}^{*})[\mathrm{X}]=0}{{\mathrm{\nabla }}_{\mathrm{\Xi }}{C}_j({\mathrm{\Xi }}^{*})[\mathrm{X}]=0}}{\int }\text{exp}(-\frac{A[\mathrm{X},\mathrm{X}]}{2kT})d\mathrm{X}’}\hfill \end{array}$$ (19)

where the quadratic functional A has the form:

$$A={\mathrm{\nabla }}_{\mathrm{\Xi }}^{2}L({\mathrm{\Xi }}^{*},{\mathrm{\Gamma }}^{*},{\mathrm{\Lambda }}^{*})-2kT{\mathrm{\nabla }}_{\mathrm{\Xi }}^2\text{ln}J({\mathrm{\Xi }}^{*}).$$ (20)

The error of this approximation depends on the depth of the potential well corresponding to the minimum, the size of B(Ξ*) , and the departure of L from a quadratic function. Therefore it is difficult to asses this error a priori except for very special cases. The presence of constraints in the integration domain can be treated by using a reduced set of perturbations Y that belong to the joint nullspace of the linear operators ∇_ΞC_j (Ξ*) and $G_k^{*}{\mathrm{\nabla }}_{\mathrm{\Xi }}{E}_k({\mathrm{\Xi }}^{*})$ (see next section).

If multiple equilibrium states ${\mathrm{\Xi }}_1^{*},{\mathrm{\Xi }}_2^{*},\dots ,{\mathrm{\Xi }}_K^{*}$ are present for given constraints (6) and (8), the probability of each such state is computed as:

$$P({\mathrm{\Xi }}_j^{*})=Z({\mathrm{\Xi }}_j^{*})/{\displaystyle {\sum }_{i=1}^{K}Z({\mathrm{\Xi }}_i^{*})j=1,\dots ,K}.$$ (21)

The aforementioned method can be used to calculate many cases of interest, such as (i) the free energies of multiple states of a single topoisomer, or (ii) the free energies of topoisomers, by relaxing the constraint of fixed Lk while keeping the constraint of closure.

The free energy G_DNA of a state Ξ* is given by:

$$G_{\text{DNA}}=-kT\text{ln}Z({\mathrm{\Xi }}^{*}).$$ (22)

The looping free energy difference ΔG_DNA can be estimated as the difference between G_DNA and the free energy G_free of a state with the closure conditions (B), (C) and (D) relaxed. The energy ΔG_DNA describes only the contribution from DNA deformation and does not include the protein-DNA binding energies, which must be added in order to assess the probability of loop formation under experimental conditions. Nonetheless, ΔG_DNA can be used to compare the probability of formation of distinct states (loop types) in which the number, type, and location of bound proteins are the same.

Although the method above has been applied to computations of looping and ring-closure probability, the possible errors associated with comparing the closed and open states have not been thoroughly examined. Thus for the computation of closure probabilities and the cyclization factor it is better to use a Monte-Carlo procedure [34] which can yield such quantities efficiently and with high precision.

Computational procedure

The (equations (11) represent a system of non-polynomial algebraic equations in the variables $\mathrm{\Xi }={\{{\mathrm{\xi }}_i^n\}}_{i=1‥6}^{n=1‥N-1}$. If the only contribution to the energy E is the elastic energy Ψ (as was the case in [1] and [17]) then the equations form a weakly coupled system that can be solved for base pairs 1,2,…, N consecutively in terms of the moments and forces applied to the first base pair, in a way similar to solving an initial value problem for an ordinary differential equation. In the general case, the Hessian matrix for the system is full. A solution Ξ* can be found by solving the system of algebraic equations (11) numerically using, for example, the Levenberg-Marquardt procedure starting from an appropriate initial configuration. Multiple solutions can be found by randomizing starting configurations for the algorithm.

A more convenient approach is to use a continuation method with one of the constraints depending on a homotopy parameter 0 ≤ λ ≤1 in such a way that λ = 0 corresponds to constraints giving a known solution, e.g., the stress-free state, and λ = 1 corresponds to the constraints for which a solution is sought. One commonly employed situation is that in which various topoisomers are found by relaxing the constraint of fixed angle ϕ between d₁ vectors at the two ends of DNA. Knowing the solution for one topoisomer, one can compute another topoisomer by varying ϕ over the interval [0,2π]. Other variable parameters may be the length N, various matrix elements in (3) and (4), or the diameter d.

Once an equilibrium configuration Ξ* is found, its stability is verified by computing the constrained Hessian (16). If Ξ* is stable then its partition function Z can be computed approximately using (19) and (20): the quadratic functional A in (20) and the orthogonal basis B for the joint nullspace of ∇_ΞC_j(Ξ*) (with j = 1,…,M) and $G_k^{*}{\mathrm{\nabla }}_{\mathrm{\Xi }}{E}_k({\mathrm{\Xi }}^{*})$ (with k = 1,…,K) is computed, and the integral in (20) is converted to a standard multivariate Gauss integral and evaluated explicitly as:

$${\displaystyle \int \text{exp}(-\frac{{\mathrm{y}}^{\mathrm{T}}{B}^{T}AB\mathrm{y}}{2kT})}d{\mathrm{y}}_1\dots d{\mathrm{y}}_M=\sqrt{\frac{{(2\pi )}^M}{\text{det}(B^{T}AB)}.}$$ (23)

In all computations full use is made of symbolic algebra software (Maple 10 by Maplesoft) and automatic differentiation [35].

Proteins

Lac repressor

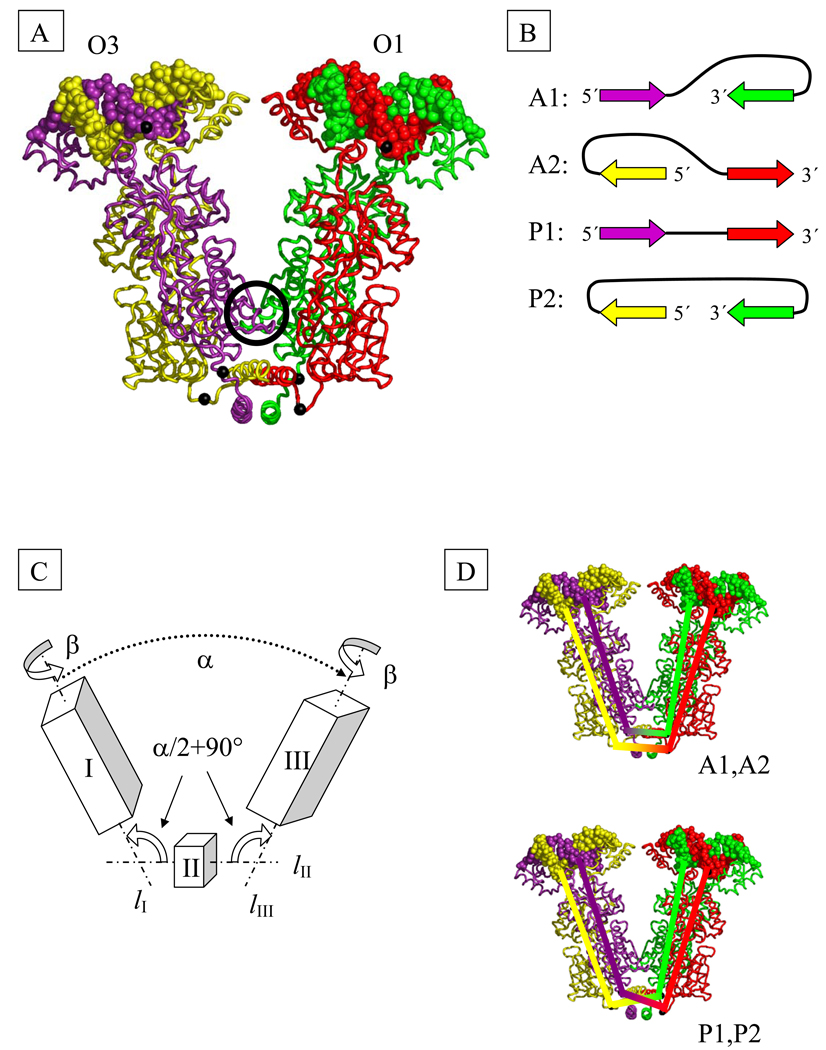
Each arm of the LacR tetramer (represented schematically by boxes I and III in Fig. 2C) contains two polypeptide chains. A four-helix bundle tetramerization domain, located at the base of the “V” (represented by cube II in Fig. 2C), holds the two halves of the complex in place. A small contact interface between the dimeric fragments (located in the circle in Fig. 2A) further stabilizes the complex. Disruption of that contact interface is expected to promote the opening of the V-shaped structure. Electron microscopic images of freeze-etched samples of LacR [36] show extended forms that are presumably obtained by opening the “V” to the extent that the tetramerization domain occupies the middle of the assembly and the DNA binding sites lie at opposite ends of the complex.² As in [4] we treat the opening of the tetramer as a concerted motion of three rigid domains—I, II, and III—about two hinges (Fig. 2C). For simplicity we assume that the two hinge angles i.e., the angle between l_I and l_II and that between l_II and l_III, shown in Fig. 2C, are identical and hence equal to one half of the total angle of opening α. Additional flexibility is provided by allowing the rotation of domains I and III about axes l_I and l_III by equal amounts β, where −90° ≤ β ≤ 90°. For the V-shaped configuration found in the crystal α = 34° and β = 33°. We assume that LacR can exist in two states: (i) the aforementioned V-shaped arrangement [38],[39] or (ii) a flexible state with two degrees of freedom, α and β. The free-energy penalty for opening LacR, G_LacR, has been estimated [4] to be between 1.8 kT and 3.8 kT.³

Fig. 2.

(A) Model of the structure of the tetrameric Lac repressor protein (LacR) in complex with O1 and O3 operator segments, obtained by composition of available X-ray data (see Methods). The black spheres on protein represent the C^α atoms of Gln 335 and those on DNA the P atoms of the central base pairs. Color-coding denotes the protein monomers and DNA chains in closest contact at the highlighted P atoms. The black circle marks the dimer contact interface found in the crystal structure.

(B) DNA loop types. The color-coded arrows depict the 5′-3′ directions of the sequence strand on LacR in the four possible orientations of DNA on the tetramer. The colors correspond to those of the associated DNA and protein chains in part (A).

(C) Schematic representation of LacR opening. The rigid domains I (residues 1–332 of chains A and B and the DNA bound to these chains) and III (corresponding residues of chains C and D and the bound DNA) are connected to domain II (residues 340–354 of chains A, B, C, D) by two hinges. The axes of rotational symmetry of the three domains are l_I, l_II, and l_III. Chains (A–D) correspond respectively to proteins shown in (A) in violet, yellow, green, and red.

(D) Schematic representation of the closures of DNA strands used in the computation of linking number. The top closure is appropriate for antiparallel loops and the bottom for parallel and extended loops.

For our calculations we assign to the protein-bound segments of DNA a three-dimensional structure that is in accord with currently available crystallographic data. Because the crystal structure of the LacR tetramer with one dimer bound to the O3 sequence and the other to O1 has not been determined, we employ a model built by superposing the 2.6-Å resolution structure [40] of the LacR dimer complexed with the O_sym operator (PDB_id: 1EFA) and the 2.7-Å structure [39] of the LacR tetramer lacking DNA-binding headpieces (PDB_id: 1LBI). We assume that the bound O3 operator adopts the same structure as the bound O1 operator and the complex is symmetric.

The DNA operators can be oriented in one of two ways with respect to each protein dimer, with the 5′-3′ direction of the coding strand pointing inside or outside the V-shaped reference state (Fig. 2B). The combination of possible DNA orientations for each dimer gives rise to four possible DNA looping modes for the repressor assembly (eight possible modes if the V-shaped complex is asymmetric [41].) Following the notation of Geanacopoulos et al. [42] and our earlier work [4], we denote these modes A1, A2, P1, P2, where the A and P refer, respectively, to antiparallel and parallel orientations of operators (see Fig. 2B). Because the core regions of the protein monomers are congruent, there appears to be no a priori preference for a given orientation of DNA on the protein.

For the computation of the linking number, Lk, we introduce virtual closures of the two DNA strands through the tetramer assembly (see Fig. 2D). Each of these closures originates at the phosphorus atom on one of the DNA strands attached to the central base pair of the O3 operator, passes through the Gln 335 C^α atom of the LacR chain that makes direct contact with the 5′-end of the strand [10], continues through a second Gln 335 C^α atom in the other half of the protein assembly, and terminates at the corresponding phosphorus atom on the O1 operator in such a way that the linked phosphorus atoms lie on the same DNA strand.

Catabolite activator protein

The catabolite activator protein (CAP) is a dimeric protein, with each subunit containing a ligand-binding domain and a DNA-binding domain. The affinity of CAP for its DNA binding site increases upon binding two cAMP molecules, yielding an apparent equilibrium constant of 4.1×10⁷ M⁻¹ [43]. Upon binding DNA, CAP kinks the double-helical structure sharply at two sites, producing a global bend of 80°±12° [5],[44]. The base-pair step parameters used here to model the 20-bp CAP binding site found between the O3 or O3* and O1 operator sites on DNA correspond to those in the crystal complex of CAP with the consensus binding sequence [5] (PDB_id: 1CGP).

Results

The above procedure underlies our earlier analyses of (i) the sequence-dependent configurations of closed DNA minicircles [1], [17], (ii) the looping of DNA mediated by LacR [4], and (iii) the determination of the structures of open and closed complexes of RNAP and CAP [6]. Here we report an additional application of our method, extending the analysis of DNA looping mediated by the LacR to cases in which CAP is present.

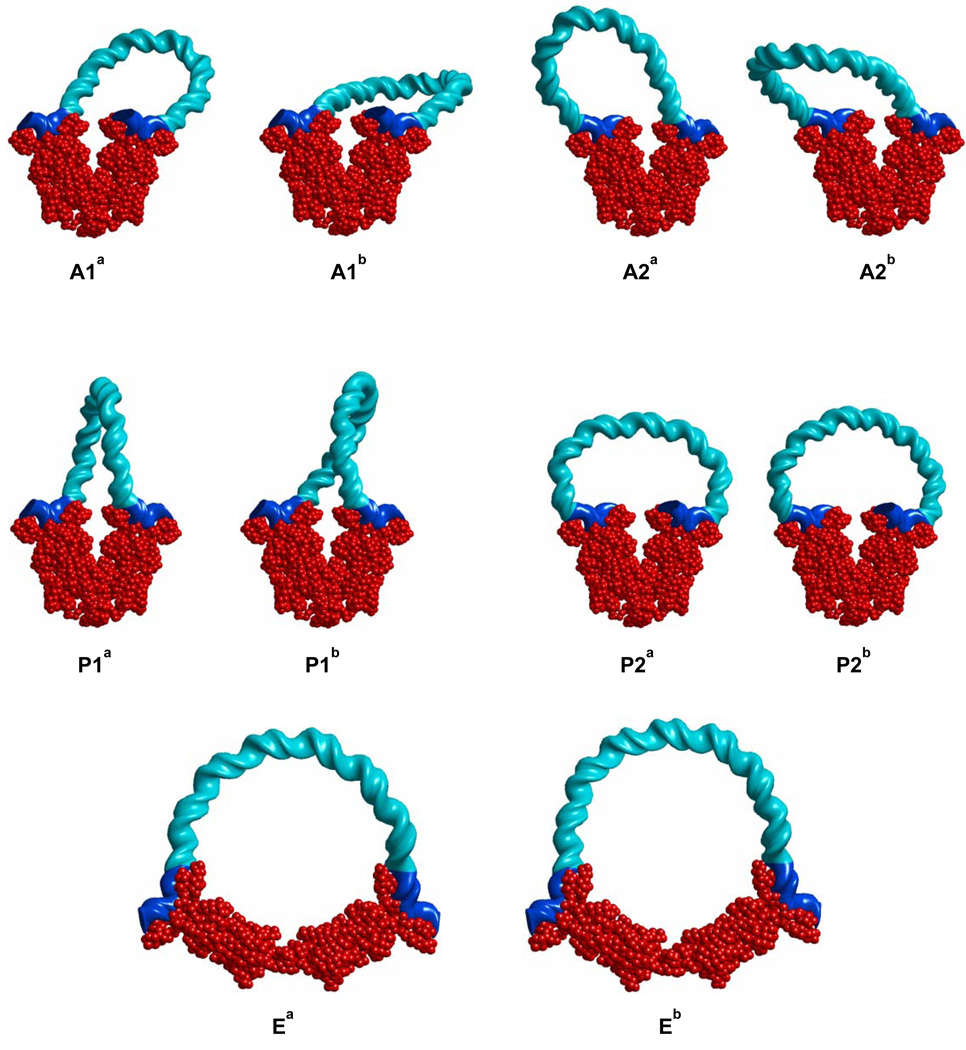
Figure 3 illustrates representative minimum-energy configurations of the wild-type O3–O1 loop mediated by LacR for various combinations of looping mode, linking number, and LacR conformation. The configurations shown for each looping mode are the two most probable topoisomers. Each of these configurations minimizes the energy of DNA looping at fixed linking number Lk for the given choice of anchoring conditions on the protein.⁴ Configurations E^a and E^b (previously called P1^E) optimize LacR-opening geometry. The calculated values of ΔG_DNA and other characteristics of the configurations are listed in Table 1.⁵ As shown previously [4], the elastic contribution dominates the energies of the preferred configurations, and the E^b loop with flexible LacR has the lowest total free energy. Thus, the E^b loop is predicted to be the most likely arrangements of the DNA-LacR complex in vitro.⁶

Fig. 3.

Representative minimum-energy configurations of LacR-mediated O3-O1 loops with DNA shown in aqua, LacR in red, and operator sites in blue. Geometric and energetic properties of the loops are given in Table 1.

Table 1.

Calculated energy (in kT) and configurational parameters for O3-O1 LacR-mediated DNA loops.^†

Loop	α	β	Lk	Ψ	Φ	GLacR	GDNA	ΔGDNA
A1a	34	33	9	32.1	71.9	–	117.7	36.5
A1b	34	33	10	39.1	70.0	–	122.7	41.4
A2a	34	33	8	33.1	71.6	–	118.0	36.7
A2b	34	33	9	41.6	70.3	–	125.3	44.1
P1a	34	33	9	38.8	73.0	–	123.4	42.2
P1b	34	33	10	62.5	71.3	–	145.4	64.1
P2a	34	33	9	71.3	73.4	–	145.4	77.4
P2b	34	33	10	45.7	70.8	–	130.4	49.1
Ea			8	41.2	70.0	2.8±1	127.2±1	45.9±1
Eb			9	23.1	68.3	2.8±1	107.4±1	26.1±1
Free	–	–	–	0	68.2	–	81.2

^†Loops denoted by labels in Figure 3; LacR deformation angles (α,β) and closed pathway used to calculate Lk defined in Figure 2; Ψ: elastic energy; Φ: electrostatic energy at 10 mM salt; G_LacR: free energy of LacR opening; G_DNA: free energy of LacR-mediated loop at room temperature under the given ionic conditions. ΔG_DNA free energy difference between loop and “free” DNA with bound LacR dimers. “Free” refers to the unconstrained linear DNA chain of the same wild-type (O3-O1) sequence: GGCAGTGAGCGCAACGCAATTAATGTGAGTTAGCTCACTCATTAGGCACCCCAGGCTTTACACTTTATGCTTCCGGCTCGTATGTTGTGTGGAATTGTGAGCGGATAACAATT. Here the O3 and O1 sequences are shown in boldface.

Complexes with CAP

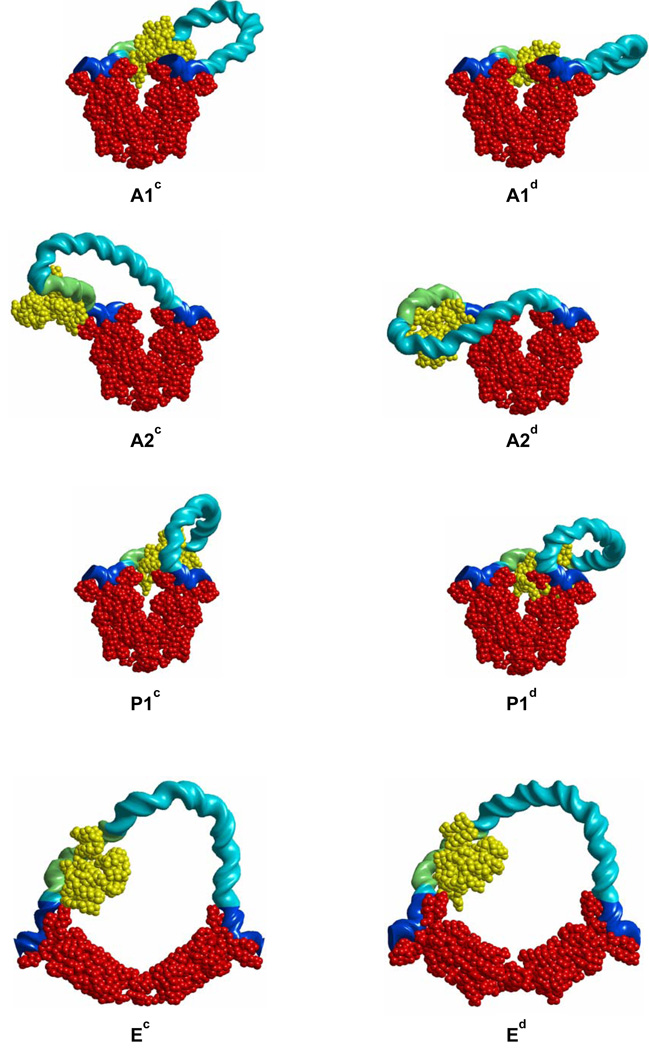
In principle, there is no steric hindrance preventing the simultaneous binding of CAP to its DNA recognition site and LacR to the O3 site on the E. coli lac operon. Representative configurations and free energies of the O3-O1 loops with bound CAP are reported, respectively, in Figure 4 and Table 2. The free energies ΔG_DNA of CAP-bound DNA loops anchored to the V-shaped LacR structure exceed, by at least 5kT, those of the corresponding CAP-free structures. The outer surface of CAP (i.e., the surface antipodal to the DNA binding site) makes unfavorable steric contacts with LacR or DNA in some configurations (A1^c, A1^d, A2^d, P1^c, and P1^d) and the bending of the activator protein is ~180° out of phase with the bending of the LacR-mediated loop in others (A2^c and A2^d). The E^d configuration is much lower in free energy than all other configurations and minimizes ΔG_DNA with a value comparable to that of the E^b loop formed in the absence of CAP.

Fig. 4.

Representative minimum-energy configurations of LacR-mediated O3-O1 loops with bound CAP shown in yellow and other components color-coded as in Figure 3. Geometric and energetic properties of the loops are given in Table 2.

Table 2.

Calculated energy (in kT) and configurational parameters for O3-O1 LacR-mediated DNA loops with bound CAP.^†

Loop	α	β	Lk	Ψ	Φ	GLacR	GDNA	ΔGDNA
A1c	34	33	9	38.2	71.2	–	121.9	42.2
A1d	34	33	10	50.1	70.0	–	132.1	52.4
A2c	34	33	8	76.5	73.7	–	162.6	82.9
A2d	34	33	9	80.6	73.6	–	167.0	87.3
P1c	34	33	9	44.5	72.9	–	128.2	48.5
P1d	34	33	10	82.8	73.9	–	167.7	88.0
Ec	110	18	8	35.6	68.9	2.8±1	120.1±1	40.4±1
Ed	108	−50	9	24.3	67.2	2.8±1	105.9±1	26.2±1
Free	–	–	–	0	67.0	–	79.7

^†Loops denoted by labels in Figure 4; α, β, Lk, Ψ, Φ, G_LacR, G_DNA are as in Table 1. ΔG_DNA: free energy difference between loop and “free” DNA with bound CAP and LacR dimers. Sequence: GGCAGTGAGCGCAACGCAATTAATGTGAGTTAGCTCACTCATTAGGCACCCCAGGCTTTACACTTTATGCTTCCGGCTCGTATGTTGTGTGGAATTGTGAGCGGATAACAATT. Here the O3 and O1 sequences are shown in boldface and the CAP binding site is underlined.

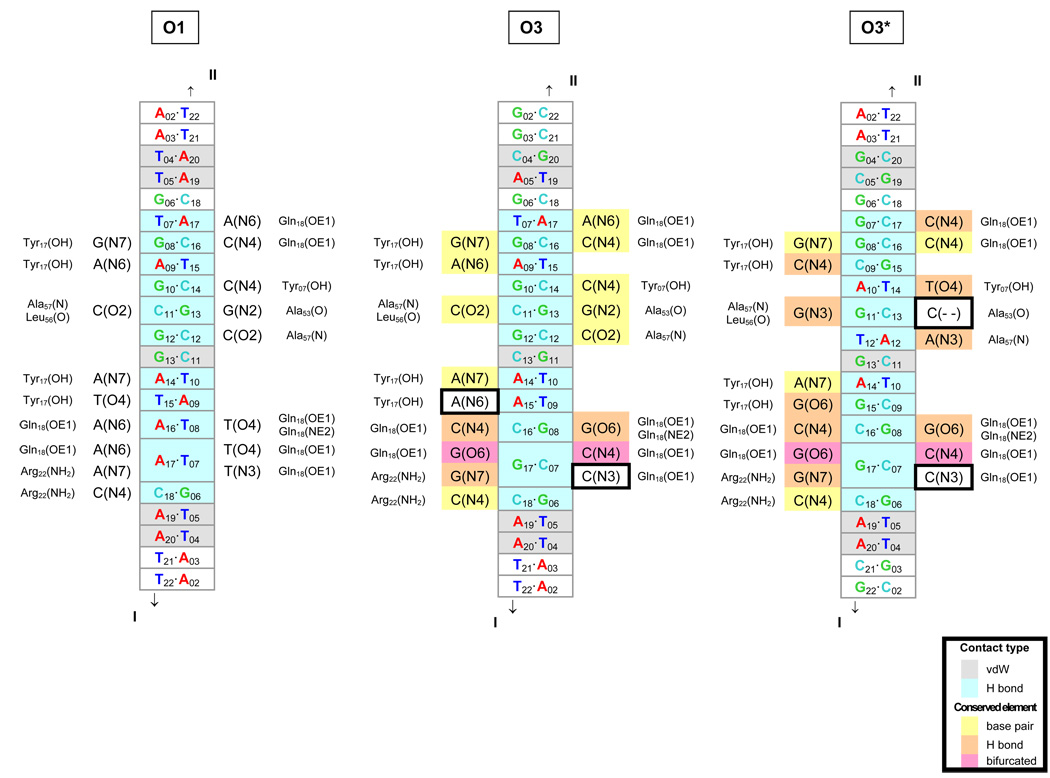
Exploration of the DNA sequence in the vicinity of the O3 site reveals an additional putative LacR binding site 5 bp upstream of O3, GCGGGCAGTGAGCGCAA, which shares structural similarities with the O1 site. As shown in Fig. 5, all but two of the unique hydrogen-bonding contacts between protein and DNA atoms would be preserved if the LacR were to associate with the modified sequence, here termed O3*, in the same way that it binds the natural O1 operator in solution [10]. Although the putative binding site aligns poorly against the nucleotides that comprise O1 (only 5 of 19 base pairs are identical), the base-pair modifications at the key sites are conservative in the sense that the substitutions preserve the positioning of key elements in DNA recognized by protein [48] e.g., the O4 hydrogen-bond acceptor on T is replaced by O6 on G and the N6 hydrogen-bond donor on A is replaced by N4 on C in the six T.A→G.C modifications. Moreover, two thirds of the close contacts of LacR and DNA (≤ 3.4 Å) are nonspecific in that they involve sugar and base atoms.

Fig. 5.

Diagrams of comparative molecular interactions of the LacR headpiece with the O1, O3, and O3* operators. Strand I is the leading strand of each recognition site, i.e., the sequences listed in Table 1–Table 2 for O1 and O3 and in Table 3 for O3*, and Strand II is the complement. The O1 interactions are as found in solution [10]; the O3 and O3* interactions are putative. DNA base pairs in close contact (interatomic distances of 3.4 Å or less) with protein residues in the O1 complex are denoted in gray (van der Waals’ interactions) and aqua (hydrogen bonds) in the center of each diagram. The contacted atoms of the bases are indicated on each side of the center column, together with the corresponding protein residues on the outside. The base pair contacts in O3 and O3* that are identical to those in O1 are highlighted in yellow, and the contacts that preserve hydrogen bonding are denoted in orange. The bifurcated hydrogen bonding (at position 17) that accommodates all base-pair combinations is shown in pink. Comparison of the three sites shows that most of the hydrogen-bonding elements are conserved upon substitution of the O3 or O3* sequence—a direct consequence of the isosteric character of the Watson-Crick base pairs, the pseudo-symmetric positioning of hydrogen-bond donor atoms in the DNA minor groove [48], the equivalent positioning of major-groove atoms in conservatively substituted (G↔T and A↔C) bases [48], and the dual hydrogen-bonding (donor or acceptor) capabilities of selected amino acids. The two potential hydrogen-bonding elements not conserved upon substitution of the O3 or O3* sequences are outlined by boxes.

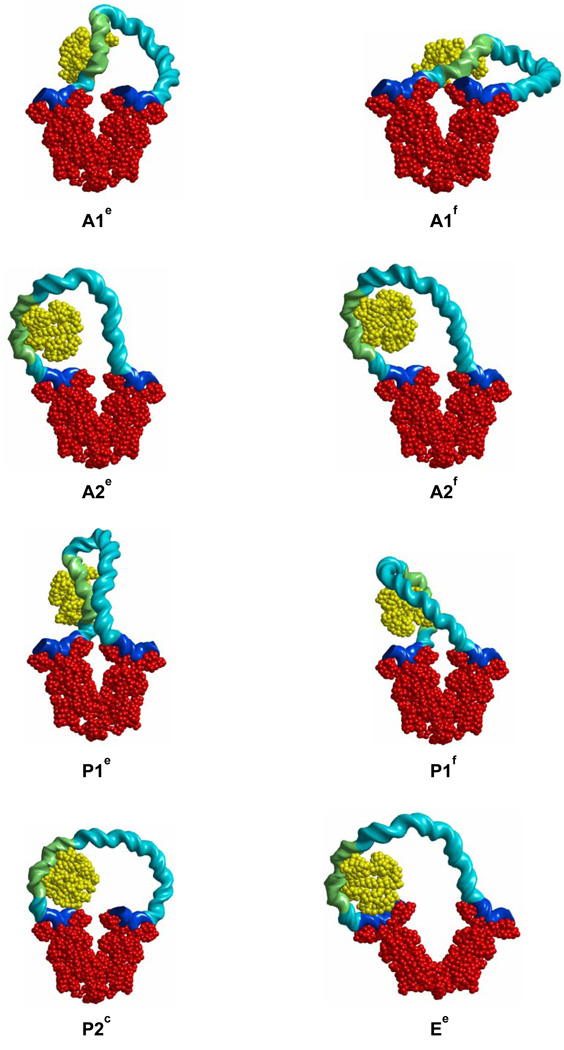
Representative configurations of LacR-CAP-DNA loop topoisomers with LacR bound at the putative O3* site are shown in Figure 6, and the computed free energies are given in Table 3. The free energies of all topoisomers are generally larger than those for the O3-O1 loops without CAP, with the singular exception of the A2^f loop, for which ΔG_DNA equals 24.0 kT at 10 mM monovalent salt. This number is lower than ΔG_DNA for the open E^e loop, making it the most likely CAP-bound O3*-O1 loop, and is even lower than the free energy of E^d, the most optimal CAP-bound O3-O1 loop. Direct comparison of ΔG_DNA for the A2^f and E^d loops, however, is precluded because G_O3*, the binding energy of LacR to the O3* site, is not known. The CAP-induced bend is naturally positioned near the locus of highest curvature in the A2^f loop, thereby absorbing the cost of bending DNA. The same happens, but to a lesser degree, in the A2^e, P2^c, and E^e loops. The P1^e and P1^f loops resemble the U and O CAP-bound loops reported by Balaeff et al. [9] in which LacR is bound 7 bp upstream of the O3 site (a location different from O3*). The energies of the P1^e and P1^f loops found here, with LacR bound at O3*, substantially exceed that of A2^f, or, for that matter, the P2^c loop.

Fig. 6.

Representative minimum-energy configurations of LacR-mediated O3*-O1 loops with bound CAP and LacR positioned at the alternate O3* binding site. Geometric and energetic properties of the loops are given in Table 3 and the molecular color-coding in Figure 3 and Figure 4.

Table 3.

Calculated energy (in kT) and configurational parameters for O3*-O1 LacR-mediated DNA loops with bound CAP.^†

Loop	α	β	Lk	Ψ	Φ	GLacR	GDNA	ΔGDNA
A1e	34	33	9	65.6	76.2	–	154.4	70.2
A1f	34	33	10	48.4	72.6	–	133.6	49.4
A2e	34	33	8	65.2	74.9	–	153.0	68.8
A2f	34	33	9	23.0	72.8	–	108.1	23.9
P1e	34	33	9	90.6	80.6	–	183.2	99.0
P1f	34	33	10	54.8	75.7	–	142.5	58.3
P2c	34	33	10	35.4	73.9	–	122.4	38.2
Ee	61	2	9	54.4	73.7	2.8±1	144.0±1	59.8±1
Free	–	–	–	0	70.5	–	84.2

^†Loops denoted by labels in Figure 6; α, β, Lk, Ψ, Φ, G_LacR, G_DNA are as in Table 1. “Free” refers to the unbound, linear DNA chain of the (O3*-O1) sequence: AAGCGGGCAGTGAGCGCAACGCAATTAATGTGAGTTAGCTCACTCATTAGGCACCCCAGGCTTTACACTTTATGCTTCCGGCTCGTATGTTGTGTGGAATTGTGAGCGGATAACAATT. Here the O3* and O1 sequences are shown in boldface and the CAP binding site is underlined.

Discussion

The general procedure described here for computing equilibrium configurations of protein-DNA assemblies and estimating their free energies takes into account the sequence-dependence of DNA deformability and various types of constraints on such configurations, including conformational changes induced by binding proteins, flexibility of protein-bound DNA, restrictions on contacts between sequentially distant DNA segments, closure constraints, electrostatic forces, and the constraint of fixed linking number. The advantage in using a discrete, as opposed to a continuum, model for DNA is that the protein-induced changes in intrinsic structure and deformability, found in high-resolution structures, are represented exactly. Although we employ a quadratic energy function for DNA deformation, the formalism developed here can be easily extended to more general energy functions, provided they remain additive; in that case only equations (13) and (14) would be affected. The procedure is computationally efficient: a single configuration and its free energy can be determined within a few minutes on a standard desktop PC computer (Dell Optiplex GX270, with 3GHz Pentium 4, running Matlab 6). We have verified that the main conclusions reported in this paper would be valid even if the DNA were assumed to be ideally elastic, i.e., homogeneous, isotropic, intrinsically straight, and with no coupling. Such assumptions, however, do not simplify the computation and hence there is no reason to make them here.

The application of this procedure to the analysis of DNA looping mediated by the Lac repressor protein is an important first step for obtaining a dynamical picture of the interactions of LacR, CAP, RNAP, and DNA that will add to current understanding of the regulation of the lac operon in vivo. The proposed configuration of the LacR-CAP-DNA loop, shown as A2^f in Fig. 6, in which LacR binds to the alternative site O3*, agrees with the experimental evidence [8] showing a 5-bp upstream shift of the LacR binding site upon CAP binding. Although the O3* site has not yet been confirmed experimentally, it is likely that if LacR binds to the sequence, it does so only in the presence of CAP. The strong CAP-induced bending deformation of DNA contributes to the stability of the A2^f loop by mimicking the site of highest curvature. This looping mode also brings the DNA surrounding the CAP recognition sequence into close contact with positively charged residues on the sides of CAP (Lys26, Lys166, His199, and Lys201; possibly, Lys22 and Lys44) that may provide additional stabilizing energy [49]. These sites appear to be responsible for the CAP-induced bending of DNA observed in time-resolved fluorescence measurements [44].

In addition, we find that the E^d loop (the extended form of the P1 loop), in which LacR is bound to the O3 site, is energetically comparable to the optimum O3*-bound A2^f loop. As is clear from Fig. 2B, the O1 operator is oriented in the same direction on LacR in the A2 and P1 (E^d) looping modes, but O3 is oriented differently. Thus, interconversion between the A2^f form and the open E^d configuration would entail reorientation of O3 with respect to LacR, as well as the shift of binding site. Such configurational transitions may occur in solution. Final determination of the likely configurations of LacR-mediated DNA loops in the presence of CAP requires further experimental work.

In summary, we predict that the presence of CAP completely alters the distribution of LacR-mediated loop types. The binding of CAP also appears to increase the apparent affinity of LacR to DNA by lowering the loop-formation energy. In other words, the looped structure induces a mechanical coupling that gives rise to a binding cooperativity between CAP and LacR that cannot be accounted for by traditional mechanisms because these proteins are not in direct contact. The structure and precise placement of CAP and other proteins on DNA undoubtedly play important roles in determining both the configurations and the populations of DNA loops formed in the cell and detected in gene expression studies. Our predictions can be tested experimentally in several ways: (i) the presence of the A2^f loop can be detected by measuring the cutting enhancement of DNAse I in footprinting experiments, a method we have described previously,[4] and (ii) the existence of the alternative binding site can be tested by binding affinity experiments.

Appendix

In the interest of making this paper self-contained we here review the parametrization ξ₁ = (θ₁, θ₂ θ₃, ρ₁, ρ₂, ρ₃) and the matrices Q_ij, Γ_ij, and _jΛ_kl used to describe DNA structure in our computations. For simplicity, the superscript n denoting the base-pair number has been omitted from these terms. If we let $D_{ij}={\mathbf{d}}_i^n\cdot {\mathbf{d}}_j^{n+1}$ be the matrix of coordinates of the frame ${\mathbf{d}}_j^{n+1}$ with respect to the frame ${\mathbf{d}}_i^n$, then D = TBT, where T and B are defined as

$$\begin{array}{c}\hfill T=[\begin{array}{ccc}\hfill \text{cos}({\theta }_3/2)\hfill & \hfill -\text{sin}({\theta }_3/2)\hfill & 0\\ \hfill \text{sin}({\theta }_3/2)\hfill & \hfill \text{cos}({\theta }_3/2)\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill 0\hfill & \hfill 1\hfill \end{array}],N={\kappa }^{-1}[\begin{array}{ccc}\hfill {\theta }_2\hfill & \hfill -{\theta }_1\hfill & \hfill 0\hfill \\ \hfill {\theta }_1\hfill & \hfill {\theta }_2\hfill & \hfill 0\hfill \\ 0& \hfill 0\hfill & \hfill 1\hfill \end{array}],K=[\begin{array}{ccc}\hfill \text{cos}\kappa \hfill & \hfill 0\hfill & \text{sin}\kappa \\ \hfill 0\hfill & \hfill 1\hfill & \hfill 0\hfill \\ \hfill -\text{sin}\kappa \hfill & \hfill 0\hfill & \hfill \text{cos}\kappa \hfill \end{array}],\hfill \\ \hfill B=N^{T}KN={\kappa }^{-2}[\begin{array}{ccc}\hfill {\theta }_1^2+{\theta }_2^2\text{cos}\kappa \hfill & \hfill {\theta }_1{\theta }_2(1-\text{cos}\kappa )\hfill & \hfill {\theta }_2\kappa \text{sin}\kappa \hfill \\ \hfill {\theta }_1{\theta }_2(1-\text{cos}\kappa )\hfill & \hfill {\theta }_1^2\text{cos}\kappa +{\theta }_2^2\hfill & \hfill -{\theta }_1\kappa \text{sin}\kappa \hfill \\ \hfill -{\theta }_2\kappa \text{sin}\kappa \hfill & \hfill {\theta }_1\kappa \text{sin}\kappa \hfill & \hfill {\kappa }^2\text{cos}\kappa \hfill \end{array}],\hfill \end{array}$$

with $\kappa =\sqrt{{\theta }_1^2+{\theta }_2^2}$. Thus κ is the overall bending angle and θ₁, θ₂ describe the bending direction. If we let $r_i={\mathbf{d}}_i^n\cdot ({\mathbf{x}}^{n+1}-{\mathbf{x}}^n)$ be the vector of components of the displacement vector with respect to the frame ${\mathbf{d}}_i^n$, we can then define ρ = Q^Tr where $Q=T\sqrt{B}$. (Incidentally, the matrix $\sqrt{B}$ has the same form as B except sin κ and cos κ are replaced by sin(κ / 2) and cos(κ / 2)). Finally,

$$\mathrm{\Gamma }=[\begin{array}{ccc}-\frac{{\theta }_1\text{sin}\zeta }{\kappa }+\frac{{\theta }_2\text{cos}\zeta }{2\text{tan}(\kappa /2)}\hfill & -\frac{{\theta }_2\text{sin}\zeta }{\kappa }-\frac{{\theta }_1\text{cos}\zeta }{2\text{tan}(\kappa /2)}\hfill & \text{tan}(\kappa /2)\text{cos}\zeta \hfill \\ \frac{{\theta }_1\text{cos}\zeta }{\kappa }+\frac{{\theta }_2\text{sin}\zeta }{2\text{tan}(\kappa /2)}\hfill & \frac{{\theta }_2\text{cos}\zeta }{\kappa }+\frac{{\theta }_1\text{sin}\zeta }{2\text{tan}(\kappa /2)}\hfill & \text{tan}(\kappa /2)\text{sin}\zeta \hfill \\ \hfill -{\theta }_2/2\hfill & \hfill {\theta }_1/2\hfill & \hfill 1\hfill \end{array}],$$

where ζ =θ₃ / 2 − γ, sin γ = θ₁/κ, cos γ = θ₂ / κ, and for each j the matrix _jΛ is a skew matrix with the following components:

$$\begin{array}{ccc}{}_1\mathrm{\Lambda }_{12}=\frac{{\theta }_2(1-\text{cos}(\kappa /2))}{{\kappa }^2},\hfill & {}_1\mathrm{\Lambda }_{13}=\frac{{\theta }_1{\theta }_2(2\text{sin}(\kappa /2)-\kappa )}{2{\kappa }^3},\hfill & {}_1\mathrm{\Lambda }_{23}=\frac{1}{2}+\frac{{\theta }_2^2(2\text{sin}(\kappa /2)-\kappa )}{2{\kappa }^3}\hfill \\ {}_2\mathrm{\Lambda }_{12}=\frac{{\theta }_1(\text{cos}(\kappa /2)-1)}{{\kappa }^2},\hfill & {}_2\mathrm{\Lambda }_{13}=\frac{{\theta }_1^2(\kappa -2\text{sin}(\kappa /2))}{2{\kappa }^3}-\frac{1}{2},\hfill & \hfill {}_3\mathrm{\Lambda }_{23}=\frac{{\theta }_1{\theta }_2(\kappa -2\text{sin}(\kappa /2))}{2{\kappa }^3}\\ {}_3\mathrm{\Lambda }_{12}=\frac{\text{cos}(\kappa /2)}{2},\hfill & {}_3\mathrm{\Lambda }_{13}=\frac{{\theta }_1\text{sin}(\kappa /2)}{2\kappa },\hfill & {}_3\mathrm{\Lambda }_{23}=\frac{{\theta }_2\text{sin}(\kappa /2)}{2\kappa }\hfill \end{array}$$

Using the formulae of [32] one can show that the Jacobian J in (18)–(20) is given by:

$$J(\mathrm{\Xi })={\displaystyle \prod _{i=1}^N\text{cos}({\kappa }^n)={\displaystyle \prod _{i=1}^N\text{cos}(\sqrt{{({\theta }_1^n)}^2+{({\theta }_2^n)}^2})}}={\displaystyle \prod _{i=1}^N\text{cos}(\sqrt{{({\xi }_1^n)}^2+{({\xi }_2^n)}^2})}$$

Other parametrizations of the discrete DNA model have been proposed (see the review [50]) but only the one introduced in [18] and described here has the property that θ₃ is independent of θ₁, θ₂ in the following sense: consider a configuration in which the centers xⁿ and the normal vectors ${\mathbf{d}}_3^n$ all lie in a plane P, and the configuration can be described by the set ${\{{\theta }_1^n,{\theta }_2^n,{\theta }_3^n,{\rho }_1^n,{\rho }_2^n,{\rho }_3^n\}}_{n=1}^N$. Now suppose that the structure is deformed in such a way that xⁿ and ${\mathbf{d}}_3^n$ still lie in P and the angle between ${\mathbf{d}}_1^n$ and the plane P is held fixed. The parametrization described above guarantees that the new configuration will have ${\{{\theta }_3^n\}}_{n=1}^N$ identical to those of the old configuration. This property is important for separating the twisting and bending energy contributions to the DNA energy and is not true for any other parametrization defined in the literature.