Multisample aCGH Data Analysis via Total Variation and Spectral Regularization

Abstract

DNA copy number variation (CNV) accounts for a large proportion of genetic variation. One commonly used approach to detecting CNVs is array-based comparative genomic hybridization (aCGH). Although many methods have been proposed to analyze aCGH data, it is not clear how to combine information from multiple samples to improve CNV detection. In this paper, we propose to use a matrix to approximate the multisample aCGH data and minimize the total variation of each sample as well as the nuclear norm of the whole matrix. In this way, we can make use of the smoothness property of each sample and the correlation among multiple samples simultaneously in a convex optimization framework. We also developed an efficient and scalable algorithm to handle large-scale data. Experiments demonstrate that the proposed method outperforms the state-of-the-art techniques under a wide range of scenarios and it is capable of processing large data sets with millions of probes.

1 Introduction

Genetic diseases are caused by a variety of possible alterations in DNA sequences. Traditionally, it was believed that DNA sequences between any two unrelated human individuals are about 99.9 percent identical and the small difference is mainly attributed to single nucleotides polymorphism (SNP). However, recent studies revealed another type of genetic alternation named copy number variation (CNV), which covers more than 12 percent of the human genome [1]. A CNV is defined as a gain or loss in copies of a DNA segment [2]. CNVs can alter gene expression in cells and potentially cause genetic diseases. For instance, it was reported that individuals who carried a lower copy number of gene CCL3L1 than population average were significantly more vulnerable to HIV/acquired immunodeficiency syndrome (AIDS) [3].

One major approach to detecting CNVs is to use array-based comparative genomic hybridization (aCGH) [4]. In a typical aCGH experiment, DNA segments are extracted from test and reference samples and labeled with two different dyes. The labeled DNA segments are hybridized to a microarray spotted with DNA probes. The ratio of fluorescence intensity between the test DNA and the reference DNA ideally represents the relative copy number of the test genome compared to the reference genome. The aCGH data is generally in the form of log₂-ratio. A value greater than zero indicates a gain in the copy number while a value less than zero indicates a loss.

The main goal of analyzing aCGH data is to recover true CNV signals from noisy measurements. Due to measurement noise in aCGH experiments, it is difficult to identify CNVs by simply thresholding the raw log₂-ratios [4]. Traditional methods include break point detection [5], [6], [7], signal smoothing [8], [9], [10], hidden Markov models [11], [12], and variational models [13], [14], among others. Please refer to [15], [16] for a review and comprehensive comparison.

All above-mentioned methods process aCGH profiles from individuals separately. Recently, more efforts are focused on analyzing aCGH data from multiple samples simultaneously. The additional information from a group of samples proved to be useful in analysis. For example, some researchers proposed to use multisample information to normalize the data and remove the reference bias in aCGH profiles [17], [18], [19]. Some aimed to detect recurrent CNVs within multiple samples [20], [21], [22], [23], but these methods rarely considered the CNVs shared by subgroups. Zhang et al. [24], [25] tried to find simultaneous change-points using chi-square statistics and correlation analysis across samples, respectively. Picard et al. [19] extended the dynamic programming method for single aCGH profile segmentation to the multisample case. Recently, Nowak et al. [26] proposed a matrix factorization-based model to explore common CNV patterns among multiple samples. We will discuss this method in detail and compare it to our method in Section 3.

In this paper, we aim to address the problem of identifying CNVs from multisample aCGH data. The main contributions are summarized as follows:

1. We propose a novel framework to denoise multisample aCGH data, which uses both the smoothness property along each sample and the correlation among multiple samples.

2. The problem is formulated as convex optimization and an efficient algorithm is developed to solve the problem exactly.

3. The model naturally handles missing values that usually exist in raw aCGH data.

4. The relationship between our model and other closely related models is discussed.

The MATLAB code of our algorithm is publicly available at http://bioinformatics.ust.hk/tvsp/tvsp.html.

2 Method

2.1 Problem Statement

Let D ∈ ℝ^m×n represent an aCGH data set obtained from multiple samples, where m is the number of probes/genes and n is the number of samples. Each entry (i, j) records the log₂-ratio at probe i of sample j and the value of (i, j) is denoted by D_ij. The jth column D_j corresponds to an aCGH profile from sample j. We propose to use the following model to describe a given data set

$$D=B+\epsilon .$$ (1)

B ∈ ℝ^m×n denotes true CNV signals and ε ∈ ℝ^m×n is measurement noise. Our goal is to recover B from D.

2.2 Formulation

To make the decomposition in (1) possible, we need some knowledge about the properties of B. Our analysis is based on two assumptions:

• For each sample, the copy numbers at contiguous chromosome positions should be identical except for abrupt changes between different segments, i.e., the signal should be piecewise constant.

• For a set of related samples, the CNV signals are likely to share similar patterns or linearly correlated with each other.

The first assumption is generally required in most methods for aCGH data analysis [15], while the second assumption is the basic motivation for researchers to analyze aCGH data from multiple samples simultaneously.

Based on the above two assumptions, we propose to estimate B by minimizing the following energy¹

$$\underset{B}{\text{min}}\frac{1}{2}{\Vert D-B\Vert }_F^2+\alpha {\Vert B\Vert }_{*}+\gamma \sum _{j=1}^n{\Vert B_j\Vert }_{TV}.$$ (2)

Here, we regularize B with the nuclear norm to encode the message that CNV signals from multiple samples should be correlated with each other as much as possible. Recently, the nuclear norm minimization has proven to be an effective method to reconstruct a low-rank matrix [28]. As mentioned in [29], the nuclear norm is not only a convex surrogate of the rank operator but also a good regularization method, which usually achieves better prediction accuracy for model building. The last term in (2) minimizes the total variation of each sample, which encourages each column of B to be piecewise constant.

There usually exist missing values in real aCGH data sets. Suppose Ω is the set of observed entries. To handle missing values, we modify the formulation in (2) to be

$$\underset{B}{\text{min}}\frac{1}{2}{\Vert {𝒫}_{\mathrm{\Omega }}(D-B)\Vert }_F^2+\alpha {\Vert B\Vert }_{*}+\gamma \sum _{j=1}^n{\Vert B_j\Vert }_{TV},$$ (3)

where 𝒫_Ω(·) represents the projection to the linear space of matrices whose nonzero entries are restricted in Ω

$${𝒫}_{\mathrm{\Omega }}(X)(i,j)=\{\begin{array}{cc}{X}_{ij},\hfill & \text{if}(i,j)\in \mathrm{\Omega },\hfill \\ 0,\hfill & \text{if}(i,j)\notin \mathrm{\Omega }.\hfill \end{array}$$ (4)

The first term in (3) means that only the observed entries inside Ω is used for model fitting. By this formulation, we can recover the signal and complete the missing values at the same time.

Both (2) and (3) are convex programming. In Section 2.3, we provide efficient algorithms to solve them with guaranteed optimal solutions.

2.3 Algorithms

To solve (3), we first try to solve (2), which is a special case of (3), with Ω being all entries in the matrix.

The optimization in (2) is convex [30], which can be solved using modern convex optimization software like CVX and SeDumi if the problem size is small. However, these generic methods are not scalable to solve large problems. Here, we provide an efficient algorithm to solve (2) exactly based on singular value thresholding (SVT) [31] and the Alternating Direction Method of Multipliers (ADMMs) [32].

First, we introduce a variable Z with the same size of B to separate the nonsmooth terms in (2)

$$\underset{B,Z}{\text{min}}\frac{1}{2}{\Vert D-B\Vert }_F^2+\alpha {\Vert B\Vert }_{*}+\gamma \sum _{j=1}^n{\Vert Z_j\Vert }_{TV},\mathrm{s}.\mathrm{t}.B=Z.$$ (5)

Obviously, the problems in (5) and (2) have the same solution.

We follow the standard procedure of ADMM to solve (5). The augmented Lagrangian of (5) reads

$$ℒ(B,Z,Y)=\frac{1}{2}{\Vert D-B\Vert }_F^2+\alpha {\Vert B\Vert }_{*}+\gamma \sum _{j=1}^n{\Vert Z_j\Vert }_{TV}+\langle Y,B-Z\rangle +\frac{\rho }{2}{\Vert B-Z\Vert }_F^2,$$ (6)

where Y is the dual variable, 〈·, ·〉 means the inner product and ρ is a positive number controlling the step length of updating variables. Then, the following steps are iterated until convergence

$$B^{k+1}=\text{arg}\underset{B}{\text{min}}ℒ(B,Z^k,Y^k),$$ (7)

$$Z^{k+1}=\text{arg}\underset{Z}{\text{min}}ℒ(B^{k+1},Z,Y^k),$$ (8)

$$Y^{k+1}=Y^k+\rho (B^{k+1}-Z^{k+1}).$$ (9)

It can be proved that the sequence of B^k generated by the above iterations will converge to the global optimal solution of (5) [32].

Next, we give the solution to each step in ADMM iterations. The B-step in (7) can be written as

$$\underset{B}{\text{min}}\frac{1}{2}{\Vert D-B\Vert }_F^2+\alpha {\Vert B\Vert }_{*}+\langle Y^k,B-Z^k\rangle +\frac{\rho }{2}{\Vert B-Z^k\Vert }_F^2=\underset{B}{\text{min}}\frac{1+\rho }{2}{\Vert \frac{D+\rho (Z^k-\frac{1}{\rho }{Y}^k)}{1+\rho }-B\Vert }_F^2+\alpha {\Vert B\Vert }_{*},$$ (10)

which has the following closed-form solution [31]

$$B^{k+1}={\mathbf{S}}_{\frac{\alpha }{1+\rho }}\left(\frac{D+\rho (Z^k-\frac{1}{\rho }{Y}^k)}{1+\rho }\right),$$ (11)

where S_λ(·) means the SVT operator

$${\mathbf{S}}_{\lambda }(X)=U{\mathrm{\Sigma }}_{\lambda }{V}^T,$$ (12)

Σ_λ = diag[(d₁ − λ)₊, …, (d_r − λ)₊], UΣV^T is the SVD of X, Σ = diag[d₁, …, d_r] and t₊ = max(t, 0).

The Z-step in (8) can be written as

$$\underset{Z}{\text{min}}\gamma \sum _{j=1}^n{\Vert \nabla Z_j\Vert }_1+\langle Y^k,B^{k+1}-Z\rangle +\frac{\rho }{2}{\Vert B^{k+1}-Z\Vert }_F^2=\underset{Z}{\text{min}}\frac{\rho }{2}{\Vert B^{k+1}+\frac{1}{\rho }{Y}^k-Z\Vert }_F^2+\gamma \sum _{j=1}^n{\Vert Z_j\Vert }_{TV}.$$ (13)

Obviously, this minimization can be operated for each column separately

$$Z_j^{k+1}=\text{arg}\underset{\mathbf{x}}{\text{min}}\frac{\rho }{2}{\Vert B_j^{k+1}+\frac{1}{\rho }{Y}_j^k-\mathbf{x}\Vert }_2^2+\gamma {\Vert \mathbf{x}\Vert }_{TV}.$$ (14)

The minimization in (14) is the fused lasso signal approximation (FLSA) problem, which can be solved efficiently [33] using existing algorithms.

The overall algorithm to solve (2) is summarized in Algorithm 1. The optimality of the solution can be guaranteed [32]. Please refer to [32] for detailed description on selection of coefficient ρ and the criterion of convergence.

Algorithm 1.

The algorithm to solve (2)

1.	Input: D
2.	Initialize: B̂ = 0, Z = 0 and Y = 0
3.	repeat
4.	$\mathrm{B̂}\leftarrow {\text{arg min}}_{\mathrm{B̂}}\frac{1}{2}{\Vert \frac{D+\rho (Z^k-\frac{1}{\rho }{Y}^k)}{1+\rho }-\mathrm{B̂}\Vert }_F^2+\frac{\alpha }{1+\rho }{\Vert \mathrm{B̂}\Vert }_{*}$
5.	for j = 1 to n do
6.	$Z_j\leftarrow {\text{arg min}}_{\mathbf{x}}\frac{1}{2}{\Vert {\mathrm{B̂}}_j+\frac{1}{\rho }{Y}_j-\mathbf{x}\Vert }_2^2+\frac{\gamma }{\rho }{\Vert \mathbf{x}\Vert }_{TV}$
7.	end for
8.	Y ← Y + ρ(B̂ − Z)
9.	until convergence
10.	Output: B̂.

Next, we give the algorithm to solve the extended model in (3). First, we define ${\pi }_{\alpha }^{\gamma }(D)$ to be the solution of (2) with given D and fixed α and γ. To solve (3), we first rewrite it as

$$\underset{B}{\text{min}}\frac{1}{2}{\Vert {𝒫}_{\mathrm{\Omega }}(D)+{𝒫}_{{\mathrm{\Omega }}^{\perp }}(B)-B\Vert }_F^2+\alpha {\Vert B\Vert }_{*}+\gamma \sum _{j=1}^n{\Vert B_j\Vert }_{TV},$$ (15)

where Ω^⊥ is the complementary set of Ω. Comparing (15) with (2), we propose to solve the extended model by iteratively updating B using

$$B^{k+1}={\pi }_{\alpha }^{\gamma }({𝒫}_{\mathrm{\Omega }}(D)+{𝒫}_{{\mathrm{\Omega }}^{\perp }}(B^k)).$$ (16)

Theorem 1. The sequence B^k generated by (16) converges to a limit B^∞ that solves the problem in (3).

The proof of Theorem 1 is given in the supplementary document, which can be found on the Computer Society Digital Library at http://doi.ieeecomputersociety.org/10.1109/TCBB.2012.166, and the algorithm to solve (3) is summarized in Algorithm 2.

Algorithm 2.

The algorithm to solve (3)

1.	Input: D, the set of observed entries Ω
2.	Initialize: B̂ = 0
3.	repeat
4.	$\mathrm{B̂}\leftarrow {\pi }_{\alpha }^{\gamma }({𝒫}_{\mathrm{\Omega }}(D)+{𝒫}_{{\mathrm{\Omega }}^{\perp }}(\mathrm{B̂}))$
5.	until convergence
6.	Output: B̂.

2.4 Parameter Tuning

We have two parameters in our model: α controls the nuclear norm of B̂ and γ controls the total variation of each B̂_j. Here, we propose to choose the parameters by formulating the problem as a matrix completion problem [29] and use the prediction error to guide the parameter selection.

Let Ω₀ be the observed entries in matrix D. We further divide Ω₀ into a training set Ω₁ and a testing set Ω₂. Ω₁ ⋃ Ω₂ = Ω₀ and |Ω₁|/|Ω₀| = 50%.² First, we use entries in Ω₁ to fit the model by solving

$$\underset{B}{\text{min}}\frac{1}{2}{\Vert {𝒫}_{{\mathrm{\Omega }}_1}(D-B)\Vert }_F^2+\alpha {\Vert B\Vert }_{*}+\gamma \sum _{j=1}^n{\Vert B_j\Vert }_{TV},$$ (17)

and denote the solution by B̂(α, γ). Then, we evaluate the prediction error over the testing set Ω₂

$$\mathit{\text{Err}}(\alpha ,\gamma )=\frac{1}{2}{\Vert {𝒫}_{{\mathrm{\Omega }}_2}(D-\mathrm{B̂}(\alpha ,\gamma ))\Vert }_F.$$ (18)

The problem in (17) is solved multiple times for a grid of (α, γ) values. Finally, we choose (α̂, γ̂) that gives the minimum prediction error as the final parameters, and we run Algorithm 1 again with full observation in Ω₀.

In implementation, since the 2D searching of parameters is computationally expensive, we first search for γ̂ by fixing α = 0 and then search for α̂ by fixing γ = γ̂. We let α = c_αα_max and γ = c_γγ_max, where α_max and γ_max are fixed upper bounds for α and γ, respectively. c_α and c_γ are coefficients selected from {0.1, 0.2, …, 1}. In all experiments, we choose ${\alpha }_{\mathit{\text{max}}}=0.2\sqrt{m}\mathrm{\sigma ̂}$ and γ_max = 2σ̂ empirically. σ̂ is the standard deviation of noise in the data set, which can be estimated robustly by the median absolute deviation [34].

Please refer to the online supplemental document for the experiments on stability and effectiveness of our parameter selection method.

2.5 Estimation of FDR

After processing the aCGH data, we use a threshold T to determine whether (i, j) is an abberation or not by comparing |B̂_ij| with T. The false discovery rate (FDR) [35] is usually used for statistical assessment of detection accuracy, which is defined as

$$\mathrm{F}\mathrm{D}\mathrm{R}(T)=\frac{|{𝒩}_T|}{|{𝒜}_T|},$$ (19)

where 𝒜_T = {(i, j) : |B_ij| > T} is the set of declared abberations and 𝒩_T is the set of false abberations. To estimate the FDR for a given T, |𝒩_T| needs to be calculated, which is unknown in real experiments. However, it can be roughly approximated by the number of abberations picked from the null data. Since there is no reference data in practice, the null data is usually generated by permutation [10], [26]. More specifically, during the kth permutation, we randomly permute the probe locations for each sample and form a null data set D̅^(k). Then, we apply our algorithm on D̅^(k) and produce an approximated matrix B̅^(k). Hence, ${\mathrm{𝒩̅}}_T^{(k)}=\{(i,j):|{\mathrm{B̅}}_{ij}^{(k)}|>T\}$ gives an estimate to the number of false detections. To reduce bias, we run K times of permutation, and the FDR for threshold T is estimated by

$$\widehat{\mathrm{F}\mathrm{D}\mathrm{R}}(T)=\frac{\frac{1}{K}{\sum }_{k=1}^K|{\mathrm{𝒩̅}}_T^{(k)}|}{|{𝒜}_T|}.$$ (20)

3 Relation to Other Methods

In this section, we discuss the relationship between our method and two closely related methods for aCGH data analysis.

The first method is fused lasso for signal approximation (FLSA) [10]. Briefly, they process each sample separately. If D_j represents the aCGH profile of sample j, FLSA tries to find a sparse and piecewise-constant vector B_j to approximate D_j by solving

$$\underset{B_j}{\text{min}}{\Vert D_j-B_j\Vert }_2^2+{\lambda }_1{\Vert B_j\Vert }_1+{\lambda }_2{\Vert B_j\Vert }_{TV}.$$ (21)

Comparing (21) and (2), we can find that our model differs from FLSA by replacing the ℓ₁-norm of individual columns with the nuclear norm of the whole matrix. The nuclear norm regularization prefers that the detected CNVs are shared by as many samples as possible. The utilization of information among multiple samples can improve the accuracy of detection.

Another closely related method is named the Fused Lasso Latent Feature Model (FLLat) proposed by Nowak et al. [26]. In this model, each aCGH profile is modeled as a linear combination of some latent features D = UV + ε, where D ∈ ℝ^m×n is the input data set, U ∈ ℝ^m×J is the feature matrix with each column representing a latent feature, V ∈ ℝ^J×n is the weight matrix, ε denotes noise and J is the predefined number of features. U and V are estimated by solving

$$\underset{U,V}{\text{min}}{\Vert D-UV\Vert }_F^2+{\lambda }_1\sum _{j=1}^J{\Vert U_j\Vert }_1+{\lambda }_2\sum _{j=1}^J{\Vert U_j\Vert }_{TV},\mathrm{s}.\mathrm{t}.{\Vert V_j\Vert }_2\le 1.$$ (22)

Essentially, the underlying assumptions of our method and FLLat are identical. On the one hand, we can notice that rank(UV) = J, which means that FLLat will output a low-rank matrix if J is relatively small. On the other hand, the smoothness constraint on latent features is equivalent to the smoothness constraint on each profile, which is just a linear combination of the features. However, there are differences between our method and FLLat:

1. Convex versus nonconvex. The formulation in (2) is convex. Hence, a global optimal solution can be guaranteed. While the formulation of FLLat can be solved efficiently, its solution depends on initialization and may get stuck at local optimum.

2. Nuclear norm versus rank operator. Comparison between the nuclear norm used in our model and the rank operator used in FLLat is analogous to comparison of the ℓ₁-norm versus the ℓ₀-norm used in regression problems [28]. To see this, let B̂ be the matrix to be estimated and w = [σ₁, …, σ_r]^T be the vector of singular values of B̂. Then, in this paper, ‖B̂‖_* or ‖w‖₁ is minimized, while in FLLat rank(B̂) or ‖w‖₀ is fixed to be J. For regression problems, it has been stated that the ℓ₁-norm achieves better consistency of feature selection [36]. Similarly, for matrix learning, the nuclear norm regularization usually performs more stably [29], while the hard constraint on the matrix rank used in FLLat may be too aggressive in selecting the singular vectors (i.e., latent features in FLLat).

4 Results

4.1 Synthesized Data

Synthesized data is generated to test the proposed method. For each data set, 50 samples of aCGH profiles with a length of 500 probes are generated. The intensity at probe i of sample j is given by D_ij = B_ij + ε_ij, where B_ij is true signal intensity and ε_ij is noise. We set B_ij = 1 if (i, j) is located in an abberation segment and B_ij = 0 otherwise. ε_ij ∈ 𝒩(0, σ) and the signal-to-noise ratio (SNR) is defined as 1/σ. Two types of abberation segments are added. The first type is unshared segment that is independently added to each sample at random locations. The second type is shared segment that presents at the same location for multiple samples. The shared percentage is defined as the ratio between the number of shared abberation segments and the total number of abberation segments. The length of segments L is selected from {10, 20, 30, 40, 50}. For each L, 50 segments are added to 50 samples. If the shared percentage is p, we randomly choose p × n samples to add a segment with length L to each of them at the same probe location. Then, we add a segment with the same length to each of the other (1 − p) × n samples at random probe locations. Fig. 1 gives illustrative examples. With the shared percentage increasing, the common patterns becomes more and more visible. The results produced by Algorithm 1 are given in the last row. Compared to the raw input in the middle row, random noise is suppressed while the CNV signal is maintained.

Fig. 1.

Examples of synthesized data. Top: data without noise; Middle: data with noise (SNR = 2); Bottom: signals recovered by Algorithm 1. The columns from left to right correspond to various shared percentages.

The pattern of shared abberations could be more complex than what has been synthesized in our simulation. For example, six possible scenarios of recurrent regions are described in the work by Rueda and Diaz-Uriarte [37]. Our simulation only covers the first two. In practice, our method can be applied to all scenarios since the patterns in these scenarios all admit our assumptions: The abberation region covers a set of contiguous probes and affects a group or a subgroup of samples, regardless of the type of the abberation and whether a region overlaps another or not.

4.2 Performance Comparison

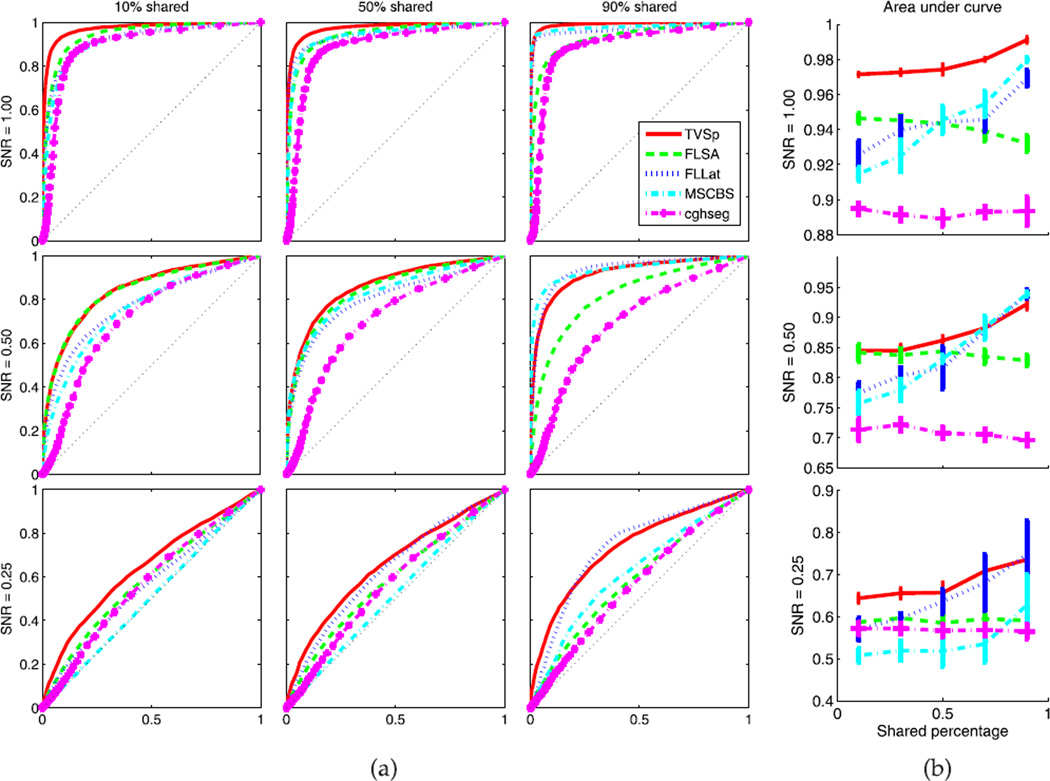
We compare our method with FLSA [10], FLLat [26], MSCBS [24], and cghseg [19] on synthesized data sets. The R packages of all methods are downloaded and the default parameter settings are applied. Fig. 2a plots the receiver operating characteristic (ROC) curves under different cases. A ROC curve deviating more from the diagonal line generally indicates better performance. To better display, we also plot the area under curve (AUC), as shown in Fig. 2b.

Fig. 2.

Performance comparison of our method (abbr. TV-Sp), FLSA [10], FLLat [26], MSCBS [24], and cghseg [19] (a) The ROC curves of different methods on synthesized data sets with various shared percentages and SNRs. The y-axis and x-axis of each plot represent the true positive rate and the false positive rate, respectively. (b) The AUC versus the shared percentage. The bar length means the standard deviation.

Our model consistently outperforms FLSA, especially for large shared percentages. This demonstrates that utilization of multisample information via the nuclear norm regularization can increase the power of detecting common abberations among multiple samples. FLLat performs extremely well when the shared percentage is high, since the data structure almost meets its underlying model. However, when the shared percentage gets lower, the performance of FLLat drops dramatically. This is due to the fact that the hard constraint on the matrix rank used in FLLat is not flexible enough when the low-rank assumption is not rigorously satisfied, which was discussed in Section 3. Also, the variance of AUC for FLLat is relatively large due to its nonconvex formulation. Instead, the nuclear norm regularization and the convex formulation of our method performs consistently well under various cases. Compared with other two alternative methods MSCBS and cghseg, our method also shows better performance.

4.3 FDR Estimation

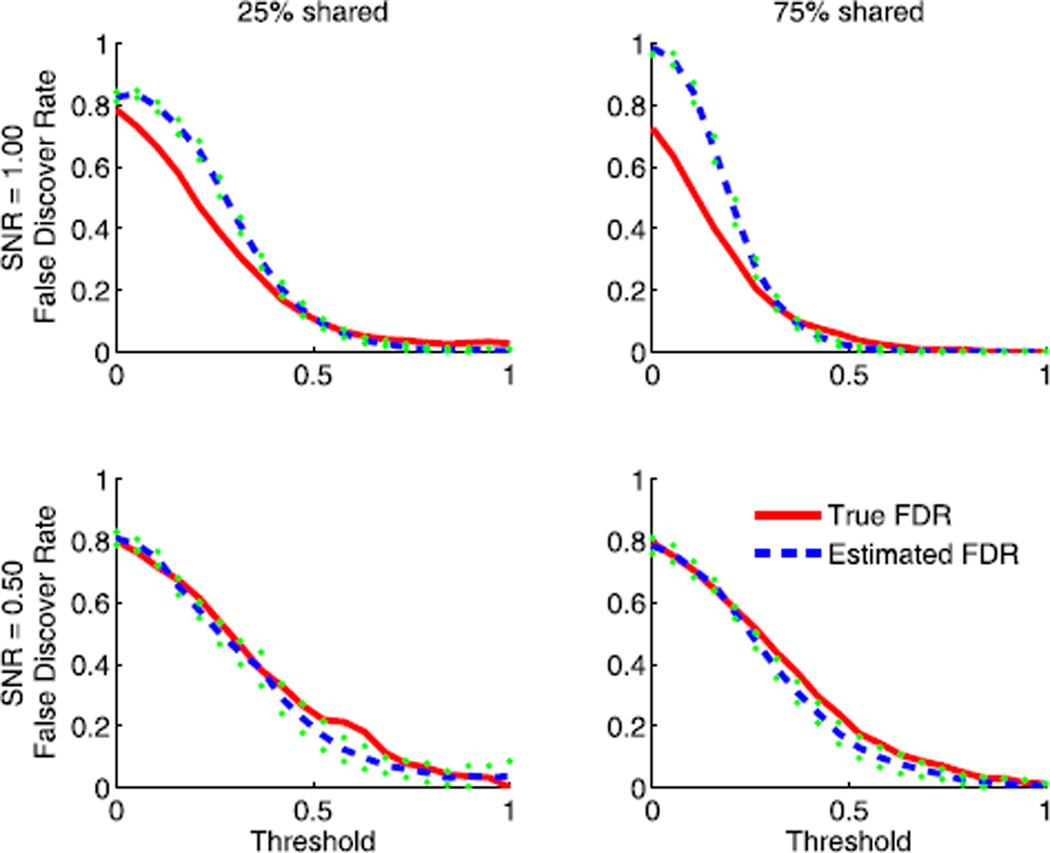
To verify the reliability of FDR estimation introduced in Section 2.5, we compare the estimated FDR with its true value on synthesized data sets. As shown in Fig. 3, the FDR is overestimated when the value is large, while it is approximated well when the value is small. Generally, the FDR should be controlled under 0.2, where our estimation is fairly accurate.

Fig. 3.

The comparison between the estimated false discovery rate and the true FDR on synthesized data sets.

4.4 Application on Breast Cancer Data

We apply our method on two independent breast cancer data sets. The first one is from Pollack et al. [38], which consists of aCGH profiles over 6,691 mapped human genes for 44 locally advanced primary breast tumors. The other one is from Chin et al. [39], which includes aCGH profiles over 2,149 DNA clones for 141 primary breast tumors.

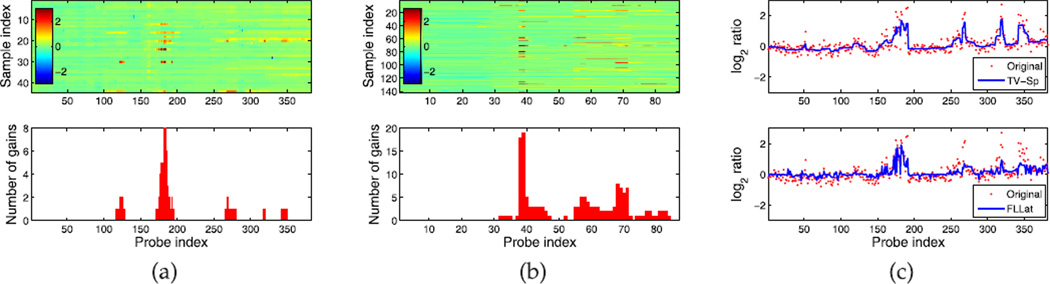
The results for chromosome 17 are presented in Fig. 4. The recovered matrices are displayed using the heat map and the bar plot at the bottom shows the number of gains summed over all samples for each probe with a threshold equal to 1. The high-amplification regions discovered from the two data sets, i.e., probes 178–184 from Pollack et al. and probes 38–39 from Chin et al., coincide with each other regarding their locations on the chromosome. Several genes that have been verified to be functionally important to breast cancer are located within this region [39], such as the transcription regulation protein PPARBP, the receptor tyrosine kinase ERBB2 and the adaptor protein GRB7. Fig. 4c shows the log₂-ratio of a selected sample from Pollack et al. before and after processing. Compared with FLLat, our method gives a more smooth profile while keeping more candidate signals unsuppressed, e.g., the amplifications around probe 321, which were also reported by [38] with high-elevated mRNA levels.

Fig. 4.

(a) The results of applying our method to the data set from Pollack et al. [38]. From top to bottom are the 2D images of recovered signals and the number of detected gains along the chromosome. (b) The results on the data set from Chin et al. [39]. (c) The 1D profile of a selected sample of the data set from Pollack et al. Our result is shown in the top panel. The FLLat result is shown in the bottom panel.

Further downstream analysis can be carried out on our results, e.g., identifying disease-related CNVs by existing tools such as CanPredict [40] or using gene expression data [41].

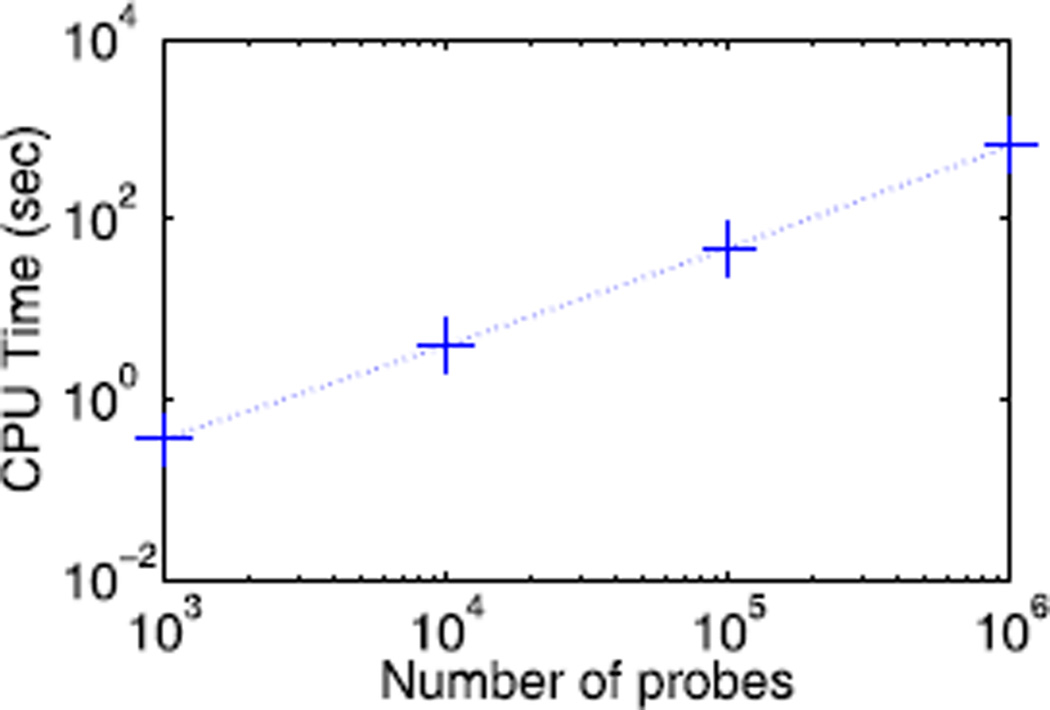
4.5 Computational Time

The time cost of our algorithm is mainly from the singular value decomposition (SVD) and FLSA computed in each iteration. For a matrix X ∈ ℝ^m×n, the complexity of SVD is 𝒪(mn²) if n ≪ m. For a vector x ∈ ℝ^m, the complexity of current FLSA algorithms is 𝒪(m) empirically [33]. Overall, the complexity of our algorithm is 𝒪(mn²) for limited iterations. Fig. 5 shows the real CPU time of our algorithm to solve synthesized problems with different numbers of probes. Here, parameter α and γ are fixed. The algorithm is run on a desktop PC with a 3.4-GHz Intel i7 CPU and 8-GB RAM. As we can see, the computational time increases almost linearly over the number of probes. In aCGH experiments, the number of probes is always much larger than the number of samples, and our algorithm shows great scalability to process large data sets, e.g., the data from the next generation of microarrays. Specifically, the computational time is 516 s for (m, n) = (10⁶, 50), while those of FLLat and FLSA are 1,932 and 39 s, respectively.

Fig. 5.

Time cost versus number of probes on synthesized data sets. The number of samples is 50.

5 Conclusion

In this paper, we propose a convex formulation for analyzing multisample aCGH data. There are two major advantages to formulate the problem as convex optimization. First, the global optimal solution is guaranteed, which makes the method perform stable in various problems. Second, a very efficient and scalable algorithm can be developed based on modern convex optimization techniques. Moreover, we explain the relationship between our model and two closely related models. The experiments demonstrate that our method is competitive to the state-of-the-art approaches and more robust under various cases.