Correcting for the Ewald Sphere in High-Resolution Single-Particle Reconstructions

Abstract

To avoid the challenges of crystallization and the size limitations of NMR, it has long been hoped that single-particle cryo-electron microscopy (cryo-EM) would eventually yield atomically interpretable reconstructions. For the most favorable class of specimens (large icosahedral viruses), one of the key obstacles is curvature of the Ewald sphere, which leads to a breakdown of the Projection Theorem used by conventional three-dimensional (3D) reconstruction programs. Here, we review the basic problem and our implementation of the “paraboloid” reconstruction method, which overcomes the limitation by averaging information from images recorded from different points of view.

1. Introduction

X-ray crystallography and nuclear magnetic resonance (NMR) spectroscopy were the first techniques to reveal the atomic structures of biological macromolecules. Electron crystallography then followed, first on “two-dimensional” (2D) crystals (crystals one unit cell thick) (Henderson et al., 1990; Kuhlbrandt et al., 1994) and then on helical (tubular) crystals (Unwin, 2005). To avoid the challenges of crystallization and the size limitations of NMR, it has long been hoped that single-particle cryo-electron microscopy (cryo-EM) would eventually also produce atomically interpretable maps. Steady progress toward this goal has been made, led by reconstructions of large icosahedral viruses, whose 60-fold symmetry, size, and rigid architecture all facilitate precise image alignment (Chapter 7, Vol. 482). Eventually, such efforts will be hampered by the fact that conventional methods assume that EM images are true projections, but in fact they are not: the information delivered by the microscope is actually a mixture of information belonging to a curved surface within the 3D Fourier transform (FT) of the specimen called the Ewald sphere. The mixing occurs when the complex electron wave functions are measured by the CCD or film to produce real images. The severity of the problem increases with specimen thickness, resolution, and electron wavelength.

A method for recovering the full, complex electron wavefunction from focal series was proposed by Schiske (1968). Further discussion then followed through 1990, when the method was reproposed using a different, more intuitive approach (Van Dyck and Op de Beeck, 1990). Saxton, who referred to this class of approaches as the “paraboloid method,” later showed it to be equivalent to the original (Saxton, 1994). More recently, the problem was discussed in the context of 3D reconstruction by DeRosier, who outlined four basic strategies to recover all the unique Fourier coefficients by merging focal pairs, images at different tilt angles, or images of ordered (crystalline or helical) objects in reciprocal space (DeRosier, 2000). A different idea for addressing the problem in real space was proposed by Jensen and Kornberg (2000), followed by additional analyses and suggestions by Wan et al. (2004). Wolf et al. (2006) implemented a version of the paraboloid method in the popular FREALIGN package (Grigorieff, 2007). Simultaneously with the Wolf work, we implemented an iterative version of the same basic method we called Prec (for Paraboloid reconstruction) (Leong, 2009) in three major single particle reconstruction software packages: Bsoft (Heymann, 2001), EMAN (Ludtke et al., 1999), and IMIRS (Liang et al., 2002). The Bsoft and EMAN versions use Cartesian-coordinate systems, while the IMIRS version uses cylindrical coordinates to exploit the advantages of Fourier–Bessel transforms (Klug et al., 1958) (Chapter 5, Vol. 482).

2. The Ewald Curvature Problem and Symbols Used

To introduce needed symbols, we will follow DeRosier’s derivation of the effects of the Ewald sphere curvature closely (DeRosier, 2000), except that here all Fourier coefficients F are complex and amplitude contrast is included explicitly. Beginning first with the effect of a sample on an incident electron wave and its weak-phase approximation,

$$\frac{A_{\text{t}}(x)}{A_0}={\text{e}}^{-(\alpha +\text{i}\beta )\rho (x)}\approx 1-(\alpha +\text{i}\beta )\rho (x)$$ (14.1)

where A_t(x) is the transmitted wave, A₀ is the incoming wave, α is the amplitude contrast value, $\beta =\sqrt{1-{\alpha }^2}$is the phase contrast value (Erickson and Klug, 1971), ρ(x) is the density of the sample, and i is an imaginary number with magnitude 1; the diffracted wave F(X) takes the form

$$F(X)=\text{FT}[1-(\alpha +\text{i}\beta )\rho (x)]=\delta (X)-(\alpha +\text{i}\beta )F_{\rho }(X)$$ (14.2)

where F_ρ(X) is the FT of our sample density.

Considering the sum of a single, symmetric pair of diffracted beams represented by Fourier coefficients F_L and F_R on an Ewald sphere (Fig. 14.1), whose additional path length through the lens with respect to the unscattered beam adds an additional phase shift of e^iχ, we have:

$$F(X)=\delta (X)-(\alpha +\text{i}\beta )F_{\text{L}}{\text{e}}^{\text{i}\chi }\delta (X+X_{\text{a}})-(\alpha +\text{i}\beta )F_{\text{R}}{\text{e}}^{\text{i}\chi }\delta (X-X_{\text{a}})$$ (14.3)

where χ is the wave aberration function at X_a and is defined as

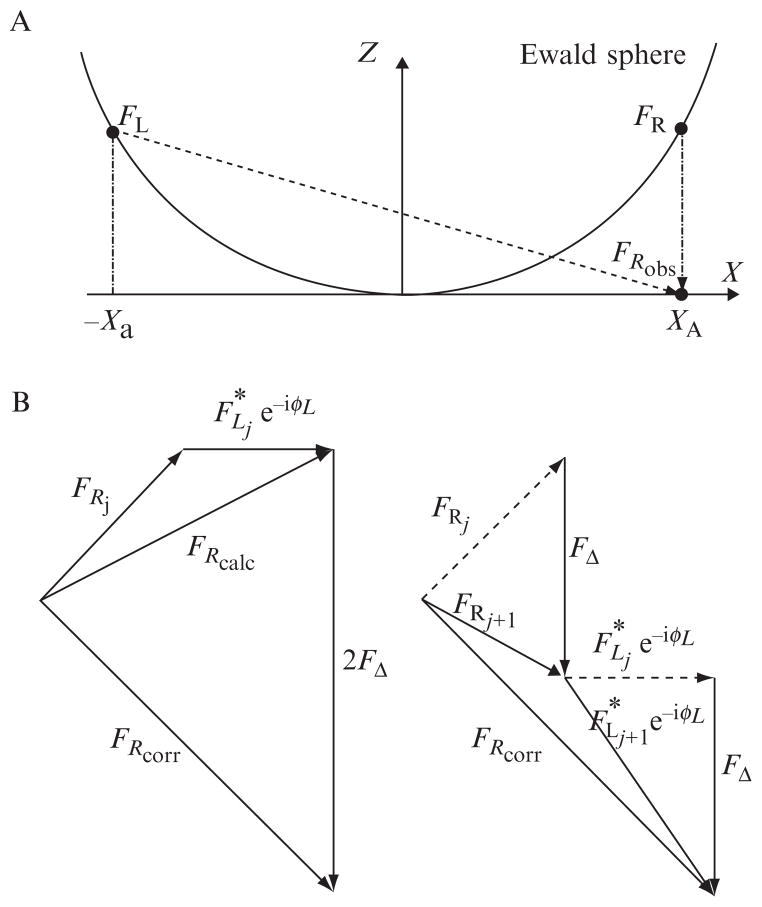
Figure 14.1.

The Ewald sphere and Prec algorithm. (A) Fourier coefficients in the transforms of electron microscope images (F_Robs) are actually combinations of coefficients (F_L and F_R) that lie on a spherical surface through the 3D transform of the specimen called the Ewald sphere. (B) Prec iteratively recovers the independent values of these coefficients by comparing CTF-corrected observations (F_Rcorr) with the calculated sum (F_Rcalc) that would have been expected from the right (F_Rj) and left (F_Lj) terms of some previous reconstruction, with appropriate phase factors e^iφ_L = (α + iβ)²e^i2χ. Half the difference (F_Δ) is then added to F_Rj and F_Lj to produce the next iteration (F_{Rj + 1} and F_{Lj + 1}).

$$\chi (s)=\frac{\pi }{2}{C}_{\text{s}}{\lambda }^3{s}^4-\pi \mathrm{\Delta }f\lambda s^2$$ (14.4)

in which λ is the electron wavelength, s is the spatial frequency, C_s is the spherical aberration coefficient, and Δf is the defocus.

The interference of these beams will produce a single complex fringe with a periodicity of 1/X_a whose amplitude, σ(x), will be

$$\sigma (x)={\text{FT}}^{-1}[F(X)]=1-(\alpha +\text{i}\beta )F_{\text{L}}{\text{e}}^{\text{i}\chi }{\text{e}}^{-2\pi \text{i}x{X}_{\text{a}}}-(\alpha +\text{i}\beta )F_{\text{R}}{\text{e}}^{\text{i}\chi }{\text{e}}^{2\pi \text{i}x{X}_{\text{a}}}$$ (14.5)

The intensity of the wave is recorded as our image

$${\mid \sigma (x)\mid }^2\approx 1-\left[(\alpha +\text{i}\beta )F_{\text{L}}{\text{e}}^{\text{i}\chi }+(\alpha -\text{i}\beta )F_{\text{R}}^{\ast }{\text{e}}^{-\text{i}\chi }\right]{\text{e}}^{-2\pi \text{i}x{X}_{\text{a}}}-\left[(\alpha +\text{i}\beta )F_{\text{R}}{\text{e}}^{\text{i}\chi }+(\alpha -\text{i}\beta )F_{\text{L}}^{\ast }{\text{e}}^{-\text{i}\chi }\right]{\text{e}}^{2\pi \text{i}x{X}_{\text{a}}}$$ (14.6)

where the F² terms can be ignored due to the weak-phase approximation.

The FT of our image F_obs(X) is then

$$F_{\text{obs}}(X)=\delta (X)-\left[(\alpha +\text{i}\beta )F_{\text{L}}{\text{e}}^{\text{i}\chi }+(\alpha -\text{i}\beta )F_{\text{R}}^{\ast }{\text{e}}^{-\text{i}\chi }\right]\delta (X+X_{\text{a}})-\left[(\alpha -\text{i}\beta )F_{\text{L}}^{\ast }{\text{e}}^{-\text{i}\chi }+(\alpha +\text{i}\beta )F_{\text{R}}{\text{e}}^{\text{i}\chi }\right]\delta (X-X_{\text{a}})$$ (14.7)

We see that F_Robs, the observed Fourier value on the right side at X = X_a, is

$$F_{R_{\text{obs}}}=-F_{\text{L}}^{\ast }(\alpha -\text{i}\beta ){\text{e}}^{-\text{i}\chi }-F_{\text{R}}(\alpha +\text{i}\beta ){\text{e}}^{\text{i}\chi }$$ (14.8)

Because of the curvature of the Ewald sphere, F_L and F_R are not a Friedel pair (i.e., not complex conjugates), but rather independent Fourier coefficients, mixed by the process of image formation. Thus, conventional methods, which treat F_Robs as if it were the sum of a Friedel pair F_L and F_R, do progressively worse as F_L and F_R diverge at higher resolutions.

3. The Paraboloid Method in the Context of 3D Reconstruction

The original Fourier coefficients can be recovered by averaging information from multiple images, which each contain different combinations of the unique coefficients. First, images are corrected for the contrast transfer function (CTF). This is performed by multiplying each term F_obs by −(α − iβ)e^−iχ. Unlike conventional CTF corrections, where values around CTF zeros are discarded, here there is no such requirement, since this “complex” CTF-correction (cCTF) is a multiplication by a factor of magnitude 1 rather than a division by a number potentially close to zero. Thus, F_Rcorr, the cCTF-corrected coefficient on the right side, is

$$F_{R_{\text{corr}}}=-F_{R_{\text{obs}}}(\alpha -\text{i}\beta ){\text{e}}^{-\text{i}\chi }=F_{\text{R}}+F_{\text{L}}^{\ast }{(\alpha -\text{i}\beta )}^2{\text{e}}^{-\text{i}2\chi }$$ (14.9)

Because each F_Rcorr is the sum of the correct F_R and a phase-shifted, complex-conjugated F_L, at this point it becomes clear how by averaging F_Rcorr from a number of different images, each measuring the same F_R but different F_L’s, the F_R’s will add coherently but the sum of F_L’s will diminish in comparison. At low resolution, however, where F_L^* ≈ F_R,

$$F_{R_{\text{obs}}}\approx -F_{\text{R}}(\alpha -\text{i}\beta ){\text{e}}^{-\text{i}\chi }-F_{\text{R}}(\alpha +\text{i}\beta ){\text{e}}^{\text{i}\chi }=-2F_{\text{R}}(\alpha cos\chi -\beta sin\chi )$$ (14.10)

The cCTF-correction then leads to wrong values

$$F_{R_{\text{corr}}}=F_{\text{R}}+F_{\text{R}}{(\alpha -\text{i}\beta )}^2{\text{e}}^{-\text{i}2\chi }$$ (14.11)

since χ does not vary quickly, causing the second terms to also add coherently and introduce a significant error. Thus at low resolution, it is better to use the simpler, real CTF correction (rCTF), where F_obs is divided by the factor − 2(α cos χ − β sin χ). A practical transition point can be found as the spatial frequency at which the cCTF-corrected and the rCTF-corrected reconstructions match best.

After CTF-correcting the raw images, the paraboloid method places the F_corr values in their correct position in Fourier space on the Ewald sphere:

$$F_{R_{\text{PM}}}=\frac{1}{N}\sum _k^N{F}_{R_{\text{corr}}^k}=\frac{1}{N}\sum _k^N{F}_{R_k}+\frac{1}{N}\sum _k^N{F}_{L_k}^{\ast }{(\alpha -\text{i}\beta )}^2{\text{e}}^{-\text{i}2{\chi }_k}$$ (14.12)

$$F_{L_{\text{PM}}}=\frac{1}{N}\sum _k^N{F}_{L_{\text{corr}}^k}=\frac{1}{N}\sum _k^N{F}_{L_k}+\frac{1}{N}\sum _k^N{F}_{R_k}^{\ast }{(\alpha -\text{i}\beta )}^2{\text{e}}^{-\text{i}2{\chi }_k}$$ (14.13)

where N is the total number of images (indexed by k) which contribute to each point.

4. The Prec Algorithm

In essence, the paraboloid method therefore “splits” the observed values F_obs into estimates of F_R and F_L by averaging information from a set of images. Once initial estimates are obtained, they can be refined through iteration, since knowledge of any particular coefficient will affect how all the sums it is involved in should be split. In Prec’s iterative refinement loop, each F_obs of each image is compared to the expected (“calculated”) value F_Rcalc that is obtained by combining Ewald sphere-related Fourier coefficients from a previous reconstruction:

$$F_{R_{\text{calc}}}=F_{R_j}+F_{L_j}^{\ast }{(\alpha -\text{i}\beta )}^2{\text{e}}^{-\text{i}2\chi }$$ (14.14)

where the index j represents the jth iteration of the reconstruction. The difference between the CTF-corrected observed value for image k and this calculated value is stored as the “error” 2F_Δk:

$$F_{R_{\text{corr}}^k}-F_{R_{\text{calc}}^k}=2F_{{\mathrm{\Delta }}_k}$$ (14.15)

Half of these errors are then added as a refinement to the Fourier component on the right:

$$F_{R_{j+1}}=F_{R_j}+\frac{1}{N}\sum _k^N{F}_{{\mathrm{\Delta }}_k}$$ (14.16)

The correction can also be immediately added to the left side:

$$F_{L_{j+1}}^{\ast }{(\alpha -\text{i}\beta )}^2{\text{e}}^{-\text{i}2\chi }=F_{L_j}^{\ast }{(\alpha -\text{i}\beta )}^2{\text{e}}^{-\text{i}2\chi }+F_{\mathrm{\Delta }}$$ (14.17)

which after rotation, complex conjugation and summation of corrections simplifies to:

$$F_{L_{j+1}}=F_{L_j}+\frac{1}{N}\sum _k^N{F}_{{\mathrm{\Delta }}_k}^{\ast }{(\alpha -\text{i}\beta )}^2{\text{e}}^{-\text{i}2{\chi }_k}$$ (14.18)

To begin the process, in the first iteration the “reconstruction” to be refined can simply be a set of zeroes. Then the calculated value, F_Rcalc, is also zero and thus the correction applied to the left and right Fourier components (F_R0 and F_L0) are just the values called for by the paraboloid method, scaled by a simple factor of $\frac{1}{2}$:

$$F_{R_{\text{corr}}^k}=2F_{{\mathrm{\Delta }}_k}$$ (14.19)

$$F_{R_0}=\frac{1}{N}\sum _k^N{F}_{{\mathrm{\Delta }}_k}=\frac{1}{N}\sum _k^N\frac{1}{2}{F}_{R_{\text{corr}}^k}=\frac{1}{2}{F}_{R_{\text{PM}}}$$ (14.20)

$$\begin{array}{l}{F}_{L_0}=\frac{1}{N}\sum _k^N{F}_{{\mathrm{\Delta }}_k}^{\ast }{(\alpha -\text{i}\beta )}^2{\text{e}}^{-\text{i}2{\chi }_k}=\frac{1}{N}\sum _k^N\frac{1}{2}{F}_{R_{\text{corr}}^k}^{\ast }{(\alpha -\text{i}\beta )}^2{\text{e}}^{-\text{i}2{\chi }_k}\\ =\frac{1}{N}\sum _k^N\frac{1}{2}{F}_{L_{\text{corr}}^k}=\frac{1}{2}{F}_{L_{PM}}\end{array}$$ (14.21)

Subsequent iterations refine that estimate. Take, for example, any Fourier coefficient F_R0 and the contributions to it:

$$F_{R_0}=\frac{1}{N}\sum _k^N{F}_{R_k}+\frac{1}{N}\sum _k^N{F}_{L_k}^{\ast }{(\alpha -\text{i}\beta )}^2{\text{e}}^{-\text{i}2{\chi }_k}$$ (14.22)

where N is the number of images that measured F_R.

This can be recast as

$$F_{R_0}\approx {\overline{F}}_{\text{R}}+\epsilon$$ (14.23)

where F̄_R is the average F_Rk and ε is the residual error which consists of the average of the F_Lk (α − iβ)²e ^{− i2χ_k} terms, which is a random walk with step size of approximately $\overline{\mid F_{L_k}\mid }$. Thus, after the first refinement cycle, the residual error falls off as $~\frac{1}{\sqrt{N}}$.

5. Implementation of the Prec Algorithm

Three versions of Prec have been implemented, one each in the software packages Bsoft, IMIRS, and EMAN, which each have all the functionality required to produce high-resolution reconstructions from raw cryo-EM images. While the mathematical theory is as described above, key differences exist in how the interpolations are handled in the different coordinate systems. Bsoft and EMAN use a Cartesian-coordinate system. Starting with raw cryo-EM images, the Bsoft and EMAN implementations of Prec begin by calculating the images’ 2D FTs, multiplying them by the cCTF, and then calculating the “z-” coordinate (height up the Ewald sphere) for each Fourier coefficient. Taking into account the projection direction, the coefficients from the image are then added to the nearest corresponding lattice points of the “reconstruction” 3D FT with appropriate phase factors. In the Bsoft version, the standard interpolation procedure with weight w = 1 − d (where d is distance in pixels from the measurement to the 3D lattice point) is used. In the EMAN version, any of its various built-in interpolation procedures can be used. After all the data are added to the “reconstruction” 3D FT, each amplitude is divided by the total weight of all the measurements that contributed, and a density map is produced through an inverse 3D FT. Refinement cycles, as implemented in Bsoft, loop through each coefficient of each corrected image transform. The expected value is calculated by summing the coefficients at the nearest corresponding lattice points of the 3D FT of the current reconstruction with appropriate phase factors and complex conjugation. Half the difference between this expected value and the (CTF-corrected) observed value is added to each contributing coefficient.

A different version of Prec was implemented within IMIRS. IMIRS uses a cylindrical coordinate system for the reconstruction process, where the 3D reconstruction and its FT are expressed as expansions of cylinder functions, as proposed by Klug et al. (1958). We follow the notation used by Crowther et al. (1970). The 2D FTs of the raw images are calculated and multiplied by the cCTF as before. The 3D FT of the object is represented in cylindrical coordinates, Z, R, and Φ. The Ewald sphere of measurements recorded in each image will in general intersect each ring of coordinates in two places. For each intersection of an image Ewald sphere and a ring of the 3D FT, a Fourier coefficient for that location is estimated from the pixels of the FT of the image through bilinear interpolation. Once all the estimates on a particular ring have been calculated, all of them are used to determine then cylindrical expansion terms, G_n(R,Z) through a least squares fit which differs from the conventional IMIRS reconstruction in that the magnitude of the cCTF term is 1 and therefore is not a factor in the weighting of terms. A Fourier–Bessel transform is used next to obtain the g_n(r,Z) terms, which are then used to generate the density map.

Because in this case, the F_L that pairs with each F_R of a randomly spaced intersection of an image Ewald sphere and a Fourier ring does not generally fall upon any ring, a 3D nearest neighbor interpolation was required to estimate its value. Our tests suggested that the losses due to this less accurate nearest neighbor interpolation outweighed the gains obtained by iteration, so that iteration of the cylindrical-coordinate-based version of Prec is not recommended. Similarly for the Cartesian-coordinate-based versions of Prec, iterations beyond the first refinement cycle are also not recommended as successive refinements yield minimal gains (see Eq. (14.23)).

6. Tests on Simulated Data

All three implementations of Prec have been tested on both simulated and experimental data. As an example, a large number of images of the moderate-sized (~300-Å diameter) Foot and Mouth Virus (FMV) (Fry et al., 1993) were simulated with different methodologies, voltages, and signal-to-noise ratios. A complete pdb was generated using the VIPERdb (Shepherd et al., 2006) and then its density was sampled to produce a reference volume using a modified version of bgex of the Bsoft package. “Ewald projection” images were simulated by simply summing Fourier coefficients on Ewald spheres using Eq. (14.8) and a complete 1D Whittaker–Shannon interpolation (Shannon, 1949; Whittaker, 1915) in the Z direction, followed by an inverse 2D FT. Six data sets of 5000 images each, with acceleration voltages of 15, 25, 50, 100, 200, and 300 kV, respectively, were calculated. FMV reconstructions were then calculated from each data set using the conventional reconstruction programs in Bsoft, IMIRS, and EMAN, which do not correct for curvature of the Ewald sphere. The resolution of each reconstruction was measured by its correlation with the original reference density map in Fourier shells (FSC) and confirmed visually (Fig. 14.2, Bsoft results only). The large number of images ensured that Fourier space was well sampled. The expected increase in resolution as a function of voltage demonstrated the Ewald sphere curvature problem. Analogous reconstructions of the 15 kV data set were then performed with Bsoft, IMIRS, and EMAN implementations of Prec. All three programs completely overcame the effects of Ewald sphere curvature (Fig. 14.2, again Bsoft results only). Similarly successful tests have been performed with more accurate sets of simulated images generated using the multislice algorithm (Cowley and Moodie, 1957), with different signal-to-noise ratios, and a larger virus model (the 754-Å diameter Reovirus; Reinisch et al., 2000).

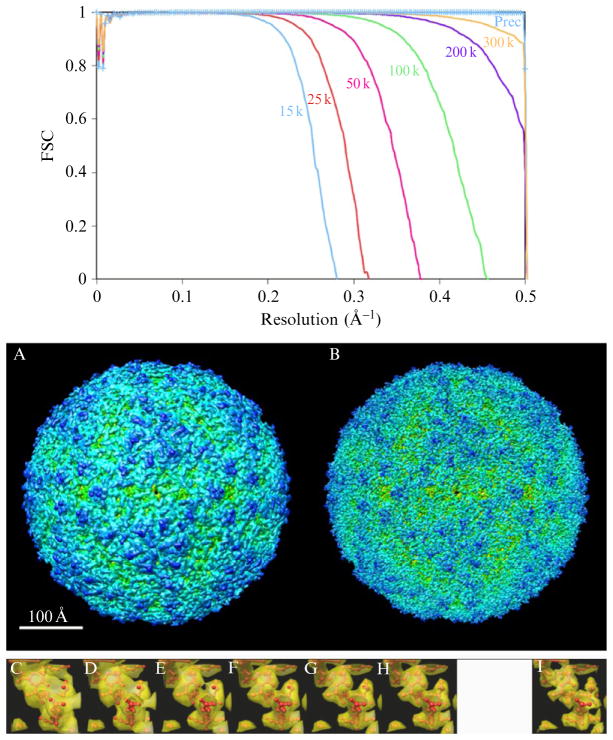
Figure 14.2.

Prec overcomes the curvature problem in Ewald projections. (Top) FSC curves for conventional Bsoft reconstructions of the Foot and Mouth Virus from 5000 “Ewald projection” images simulated with the voltages shown, plus a reconstruction from the 15 kV images calculated by the Prec program, which completely corrects for the curvature problem. (A and B) Isosurface renderings of the conventional and Prec 15 kV reconstructions, respectively. (C–H) Transparent isosurfaces of a single α-helix from the 15, 25, 50, 100, 200, and 300 kV reconstructions, respectively, surrounding the atomic model used to simulate the images. (I) The same helix from the Prec 15 kV reconstruction. FSC curves were calculated with bresolve (Heymann, 2001) and isosurfaces were rendered with Chimera (Pettersen et al., 2004).

7. Application to Experimental Reconstructions

To what extent current experimental reconstructions of icosahedral viruses suffer from uncorrected Ewald sphere curvature remains unclear. While previous analyses (DeRosier, 2000; Jensen and Kornberg, 2000) suggest that Ewald curvature should already be one of the principal resolution limitations in the most recent, highest resolution (<4 Å) reconstructions, actual reconstructions from simulated images of Reovirus showed that the Ewald curvature did not become severely limiting until ~2.5 Å resolution, and an improvement of an experimental reconstruction through curvature correction has yet to be reported (Leong, 2009). Nevertheless as the size of reconstructed viruses, the number and quality of images that are included in reconstructions, and the precision to which those images can be mutually aligned continue to increase, Ewald curvature correction will eventually become critical.

The Bsoft and IMIRS versions of Prec can be downloaded from www.jensenlab.caltech.edu. The EMAN implementation can be obtained from jiang.bio.purdue.edu.