Empirical likelihood-based tests for stochastic ordering

Abstract

This paper develops an empirical likelihood approach to testing for the presence of stochastic ordering among univariate distributions based on independent random samples from each distribution. The proposed test statistic is formed by integrating a localized empirical likelihood statistic with respect to the empirical distribution of the pooled sample. The asymptotic null distribution of this test statistic is found to have a simple distribution-free representation in terms of standard Brownian bridge processes. The approach is used to compare the lengths of rule of Roman Emperors over various historical periods, including the “decline and fall” phase of the empire. In a simulation study, the power of the proposed test is found to improve substantially upon that of a competing test due to El Barmi and Mukerjee.

1. Introduction

Comparing random variables in terms of their distributions can provide an understanding of underlying causal mechanisms and risks. In addition, knowledge of an ordering of distributions can be useful for increasing the efficiency of estimation procedures, as is well documented in the literature on order restricted inference; see, for example, the comprehensive monograph of Silvapulle and Sen [20]. There are many types of ordering for the comparison of univariate distributions. These include, with increasing generality, likelihood ratio ordering, uniform stochastic ordering (equivalent to hazard rate ordering), stochastic ordering, and increasing convex ordering (of interest in economics and actuarial science); see Shaked and Shanthikumar [19] for an overview.

The aim of this paper is to develop an empirical likelihood approach to testing for the presence of the classical type of stochastic ordering. Such ordering often arises in the biomedical sciences and reliability engineering, for example, with lifetime distributions of human populations exposed to higher risk, or of engineering systems under greater stress. The notion of stochastic ordering is due to Lehmann [11] who defined a random variable X₁ to be stochastically larger than a random variable X₂ if F₁ (x) ≤ F₂ (x) for all x (with strict inequality for some x), where F₁ and F₂ are the corresponding cdfs; we write this as F₁ ≻ F₂. For a stochastic ordering of k distributions, we write F₁ ≻ F₂ ≻ ⋯ ≻ F_k if F_j (x) ≤ F_j+1 (x) for all x and j = 1, …, k − 1, with strict inequality for some x and some j.

There is an extensive literature on the problem of testing for equality of two distributions against the alternative that they are stochastically ordered. Lee and Wolf [10] proposed a Mann–Whitney–Wilcoxon-type test. Robertson and Wright [17] studied the corresponding likelihood test (LRT) in the one- and two-sample cases when the distributions are discrete. They showed that the limiting distributions are chi-bar square. Their results indicate that, in the two-sample case, the LRT is not asymptotically distribution free. They also obtained the least favorable distribution in this case. Other tests are discussed in Dykstra, Madsen and Fairbanks [3], Franck [7] and Mau [12]. For more than two populations, Wang [21] discussed the LRT in the multinomial case; El Barmi and Johnson [5] showed that the limiting distribution of his test statistic is of chi-bar square type and gave the expression of the weighting values. Also in the k-sample case (k ≥ 2), El Barmi and Mukerjee [6] provided an asymptotically distribution-free test based on the sequential testing procedure originally introduced by Hogg [8]. This test is applicable in both the multinomial and the continuous cases, with or without censoring. Recently, Baringhaus and Grübel [1] introduced a nonparametric two-sample test for the more general hypothesis of increasing convex ordering; their test is not asymptotically distribution-free, however, and requires the critical values to be obtained via a bootstrap procedure.

The contribution of the present paper is to provide empirical likelihood based k-sample tests for alternatives that are stochastically ordered. The empirical likelihood (EL) method was originally introduced by Owen [15,16] for the purpose of finding confidence regions for parameters defined by general classes of estimating equations. It combines the flexibility of nonparametric methods with the efficiency of likelihood-ratio-based inference. Inference based on EL has many attractive properties: estimation of variance is typically not required, the range of the parameter space is automatically respected and confidence regions have greater accuracy than those based on the Wald approach. Einmahl and McKeague [4] developed a localized version of EL, to allow nonparametric hypothesis testing, and showed via simulation studies that it outperforms (in terms of power) the corresponding Cramér–von Mises statistics for a variety of classical testing problems. Their approach is restricted to omnibus alternatives, whereas ordered alternatives are often more useful because they can provide a more direct interpretation of the result of the test.

The development of the proposed test statistic and results on its asymptotic null distribution are given in Section 2. First we consider the special case of testing whether a distribution function is stochastically larger than a specified distribution function, based on a single sample. Once the theory has been developed in this one-sample case, it is relatively straightforward to extend the approach to the general k-sample setting in which all the distribution functions are unknown. Section 3 presents the results of a simulation study in which we find that the proposed test has superior power to the test of El Barmi and Mukerjee [6], which is the only previous test to have been developed for ordered alternatives in this setting. Section 3 also contains an application of the proposed test to a comparison of the lengths of rule of Roman Emperors over various historical periods. Some concluding remarks are given in Section 4. Proofs of the main results are collected in Section 5.

2. Empirical likelihood approach

2.1. Stochastic ordering relative to a specified distribution

Suppose we are given a random sample X₁, X₂, …, X_n from the cdf F, and we want to test the null hypothesis H₀: F = F₀ versus H₁: F ≻ F₀, where F₀ is a specified cdf.

Adapting the approach of Einmahl and McKeague [4] to the present setting, we first need to consider testing the “local” null hypothesis $H_0^x:F(x)=F_0(x)$ versus the alternative $H_1^x:F(x)<F_0(x)$, where x is fixed. The empirical likelihood procedure in this case rejects $H_0^x$ for small values of

$$R(x)=\frac{\sup \{L(F):F(x)=F_0(x)\}}{\sup \{L(F):F(x)\le F_0(x)\}},$$ (1)

where the suprema are over cdfs F that are supported by the data points, L(F) is the nonparametric likelihood function and, by convention, sup Ø = 0 and 0/0 = 1. For F having point mass p_i at X_i, define the new parameters θ_i = p_i/ϕ and ψ_i = p_i/(1 − ϕ), where 0 < ϕ = F(x) < 1. In terms of this new parameterization, with F̂ denoting the empirical cdf, we need to maximize

$$L(F)=\prod _{i=1}^n{p}_i=\left\{\prod _{i:X_i\le x}{\theta }_i\right\}\left\{\prod _{i:X_i>x}{\psi }_i\right\}{\varphi }^{n\widehat{F}(x)}{[1-\varphi ]}^{n(1-\widehat{F}(x))},$$ (2)

subject to the constraint

$$\sum _{i:X_i\le x}{\theta }_i=\sum _{i:X_i>x}{\psi }_i=1,$$

with either ϕ = F₀(x) under $H_0^x$, or ϕ < F₀ (x) under $H_1^x$. Note that the three terms in the right-hand side of (2) can be maximized separately. As the constraints for the first two terms of (2) are the same for both the numerator and the denominator of (1), these terms cancel and make no contribution to R(x). The third term of (2) is maximized by ϕ = F₀(x) under $H_0^x$, or ϕ = F₀(x) ∧ F̂(x) under $H_1^x$. Consequently,

$$R(x)=\{\begin{array}{ll}1,& \mathrm{if}\widehat{F}(x)>F_0(x),\\ {\left[\frac{F_0(x)}{\widehat{F}(x)}\right]}^{n\widehat{F}(x)}{\left[\frac{1-F_0(x)}{1-\widehat{F}(x)}\right]}^{n(1-\widehat{F}(x))},& \mathrm{if}\widehat{F}(x)\le F_0(x),\end{array}$$

with the convention that any term raised to a zero power is set to 1. Using a second-order Taylor expansion of log(1 + y) about y = 0, it can be shown (see the proof of the theorem below) that, for a given x, such that 0 < F₀(x) < 1, under $H_0^x$,

$$\begin{array}{lll}-2\log R(x)& =& n{(\widehat{F}(x)-F_0(x))}^2\left[\frac{1}{\widehat{F}(x)}+\frac{1}{1-\widehat{F}(x)}\right]I[0<\widehat{F}(x)\le F_0(x)]+{\mathrm{o}}_p(1)\\ & \stackrel{d}{\to }& Z^{2}I(Z\ge 0),\end{array}$$

using the CLT and the continuous mapping theorem, where Z ~ N(0, 1). That is, the asymptotic null distribution of −2 log R(x) is chi-bar square.

To test H₀ against H₁, we introduce the integral-type test statistic

$$T_n=-2{\mathit{\int }}_{-\infty }^{\infty }\log (R(x))\mathrm{d}{F}_0(x).$$

Here the range of integration is actually restricted to the interval [X₍₁₎, X_(n)], where X₍₁₎ and X_(n) are the smallest and largest order statistics in the sample, because the integrand vanishes outside this interval. The following result gives the asymptotic null distribution of T_n.

Theorem 1

If F₀ is continuous, then under H₀,

$$T_n\stackrel{d}{\to }{\mathit{\int }}_0^1\frac{B^2(t)}{t(1-t)}I(B(t)\ge 0)\mathrm{d}t,$$

where B is a standard Brownian bridge.

Remark 1

An alternative test statistic is obtained by integrating with respect to the empirical cdf (instead of F₀),

$$T_n^{\ast }=-2{\mathit{\int }}_{-\infty }^{\infty }\log (R(x))\mathrm{d}\widehat{F}(x).$$

It can be shown using a martingale argument (see Section 5), that $T_n^{\ast }$ has the same asymptotic null distribution as T_n.

2.2. Stochastic ordering among k distributions

Suppose now that we are given a random sample of size n_j from the cdf F_j, for j = 1, …, k, the k samples are independent and we want to test the null hypothesis H₀: F₁ = ⋯ = F_k versus H₁: F₁ ≻ ⋯ ≻ F_k. We assume that the proportion w_j = n_j/n of observations in the jth sample remains fixed as the total sample size n → ∞, with 0 < w_j < 1 for all j = 1, …, k.

Adapting the approach of Section 2.1, we now consider the localized empirical likelihood function

$$R(x)=\frac{\sup \{{\prod }_{j=1}^{k}L(F_j):F_j(x)=F_{j+1}(x),j=1,\dots ,k-1\}}{\sup \{{\prod }_{j=1}^{k}L(F_j):F_j(x)\le F_{j+1}(x),j=1,\dots ,k-1\}},$$ (3)

where, in each supremum, F_j is supported by the observations in the j th sample. Applying the same parameterization used in (2), separately for each F_j, and making the same cancelation in the numerator and denominator, it suffices to maximize

$$\prod _{j=1}^k{\varphi }_j^{n_j{\widehat{F}}_j(x)}{[1-{\varphi }_j]}^{n_j(1-{\widehat{F}}_j(x))}$$ (4)

subject to the constraint 0 < ϕ₁ = ⋯ = ϕ_k < 1, or 0 < ϕ₁ ≤ ⋯ ≤ ϕ_k < 1, depending on whether it is the numerator or the denominator of (3). Here F̂_j is the empirical cdf based on the jth sample. Under the first of these constraints, (4) is maximized by ϕ_j = F̂(x), where F̂ is the empirical cdf of the pooled sample. Under the second constraint, this is the classical bioassay problem, as discussed in Robertson et al. [18], page 32, and it follows that (4) is maximized by

$${\varphi }_j=E_{\mathbf{w}}{(\widehat{\mathit{\varphi }}\mid I)}_j\equiv {\stackrel{\sim }{F}}_j(x),$$

where E_w(ϕ̂∣I) is the weighted least squares projection of ϕ̂ = (F̂₁(x), …, F̂_k(x))^T onto I = {z ∈ ℝ^k: z₁ ≤ z₂ ≤ ⋯ ≤ z_k}, with weights w_j. In passing, we mention that several algorithms have been developed for computing this projection, including the pool-adjacent-violators algorithm, see Robertson et al. [18]. We now have

$$R(x)=\prod _{j=1}^k{\left[\frac{\widehat{F}(x)}{{\stackrel{\sim }{F}}_j(x)}\right]}^{n_j{\widehat{F}}_j(x)}{\left[\frac{1-\widehat{F}(x)}{1-{\stackrel{\sim }{F}}_j(x)}\right]}^{n_j(1-{\widehat{F}}_j(x))}$$ (5)

under the convention that any term raised to a zero power is set to 1.

To test H₀ against H₁, we propose the test statistic

$$T_n=-2{\mathit{\int }}_{-\infty }^{\infty }\log R(x)\mathrm{d}\widehat{F}(x).$$ (6)

The following theorem gives the asymptotic null distribution of T_n.

Theorem 2

Under H₀ and assuming that the common distribution function F is continuous,

$$T_n\stackrel{d}{\to }\sum _{j=1}^k{w}_j{\mathit{\int }}_0^1\frac{{(E_{\mathbf{w}}{\left[\mathbf{B}(t)|I\right]}_j-\overline{B}(t))}^2}{t(1-t)}\mathrm{d}t,$$ (7)

where $\mathbf{B}={(B_1/\sqrt{w_1},B_2/\sqrt{w_2},\dots ,B_k/\sqrt{w_k})}^T$, the processes B₁, B₂, …, B_k are independent standard Brownian bridges, and $\overline{B}={\sum }_{j=1}^k{\sqrt{w}}_j{B}_j$.

Remark 2

For the two-sample case, it can be shown that the limiting distribution in the above result coincides with that in the one-sample case (Theorem 1); the equivalence arises from the fact that $B=\sqrt{w_2}{B}_1-\sqrt{w_1}{B}_2$ is a standard Brownian bridge. Moreover, when testing against the unrestricted alternative F₁ ≠ F₂, the limiting distribution of the corresponding test statistic (see Einmahl and McKeague [4], Theorem 2a) is the same apart from the presence of the indicator I (B(t) ≥ 0) in the integrand.

3. Numerical examples

In this section we discuss some numerical examples illustrating the proposed test for a comparison of two or more distributions developed in Section 2.2.

To implement the proposed test we first need to obtain critical values for T_n. The null distribution of T_n is not tractable, even asymptotically, but it is asymptotically distribution free. We use simulation to approximate selected critical values as provided in Table 1. These critical values are based on 100 000 data sets distributed as N(0, 1), with sample sizes of n_i = 100, i = 1, …, k, in each case. The (Fortran) program used to compute the critical values in Table 1 is available online in the supplemental files.

Table 1.

Selected critical points of T_n

k	Significance level α
	0.01	0.05	0.10
2	3.185	1.821	1.288
3	4.128	2.613	1.943
4	4.663	3.107	2.404
5	5.144	3.470	2.701

3.1. Simulation study

Here we present the results of a simulation study designed to compare the performance of T_n with the test statistic S_n of El Barmi and Mukerjee [6], which is defined as the maximum of a sequence of (one-sided) two-sample Kolmogorov–Smirnov test statistics. As far as we know, S_n is the only previously developed test statistic when k ≥ 3.

Tables 2 and 3 give the results for a variety of distributions and sample sizes, for k = 2 and k = 3, respectively. In each case, 10 000 data sets were used to approximate the power at a nominal level of α = 0.05, with critical values for T_n taken from Table 1; critical values for S_n are obtained from its asymptotic distribution, which is available in a closed form. In all cases, T_n has greater power than S_n and has better agreement with the nominal level of the test.

Table 2.

Power comparison of tests for stochastic ordering of k = 2 distributions at level α = 0.05

Distributions		n1 = 50, n2 = 30		n1 = 30, n2 = 50		n1 = 50, n2 = 50
F1	F2	Tn	Sn	Tn	Sn	Tn	Sn
Uni(0, 1)	Uni(0, 1)	0.064	0.038	0.051	0.045	0.051	0.036
Uni(0, 1.1)	Uni(0, 1)	0.143	0.104	0.162	0.111	0.199	0.125
Uni(0, 2)	Uni(0, 1)	0.911	0.816	0.912	0.818	0.908	0.815
Uni(0.1, 1.1)	Uni(0, 1)	0.377	0.244	0.357	0.246	0.468	0.287
Exp(1)	Exp(1)	0.063	0.037	0.048	0.041	0.047	0.036
Exp(1)	Exp(1.1)	0.123	0.076	0.091	0.068	0.108	0.076
Exp(1)	Exp(2)	0.782	0.716	0.813	0.718	0.909	0.815
0.1 + Exp(1)	Exp(1)	0.207	0.118	0.137	0.105	0.195	0.127
N(0, 1)	N(0, 1)	0.063	0.037	0.049	0.040	0.051	0.036
N(0.1, 1)	N(0, 1)	0.132	0.081	0.100	0.079	0.122	0.079
N(0.5, 1)	N(0, 1)	0.646	0.530	0.690	0.540	0.771	0.628
N(1, 1)	N(0, 1)	0.992	0.975	0.991	0.975	0.993	0.976

Table 3.

Power comparison of tests for stochastic ordering of k = 3 distributions at level α = 0.05

Distributions			n1 = n2 = n3 = 30		n1 = n2 = n3 = 50
F1	F2	F3	Tn	Sn	Tn	Sn
Uni(0, 1)	Uni(0, 1)	Uni(0, 1)	0.038	0.033	0.045	0.039
Uni(0, 1.1)	Uni(0, 1)	Uni(0, 1)	0.455	0.370	0.740	0.647
Uni(0, 1.1)	Uni(0, 1.1)	Uni(0, 1)	0.389	0.319	0.651	0.633
Uni(0.1, 1.1)	Uni(0, 1)	Uni(0, 1)	0.948	0.884	0.999	0.885
Exp(1)	Exp(1)	Exp(1)	0.041	0.019	0.049	0.045
Exp(1)	Exp(1)	Exp(1.1)	0.076	0.033	0.098	0.067
Exp(1)	Exp(1.1)	Exp(1.1)	0.067	0.029	0.098	0.073
Exp(1)	Exp(1.1)	Exp(1.2)	0.116	0.046	0.171	0.109
Exp(1)	Exp(1.25)	Exp(1.5)	0.313	0.121	0.507	0.321
N(0, 1)	N(0, 1)	N(0, 1)	0.042	0.035	0.049	0.035
N(0.1, 1)	N(0, 1)	N(0, 1)	0.272	0.183	0.423	0.292
N(0.1, 1)	N(0.1, 1)	N(0, 1)	0.246	0.151	0.393	0.249
N(0.5, 1)	N(0.25, 1)	N(0, 1)	1.000	0.993	1.000	1.000

3.2. Lengths of rule of Roman Emperors

A recent article of Khmaladze, Brownrigg and Haywood [9] reached the interesting conclusion that the lengths of rule of Roman Emperors were exponentially distributed, implying that their reigns ceased unexpectedly (“brittle power”). It is also of interest to examine whether there were changes in the distribution of rule lengths, especially during the “decline and fall” phase of the empire. We use the list of n = 70 Roman Emperors from Augustus to Theodossius, covering 27 BC to 395 AD. Our analysis is based on the chronology of Parkin (see Khmaladze et al. [9] for further details). The (Fortran) programs used for the two analyzes are available online in the supplemental files.

First we consider whether there is an effect on duration of rule due to the Crisis of the Third Century (235–284 AD), when the Roman Empire nearly collapsed under the pressure of civil war (among other things!). Figure 1 shows the empirical survival function of durations of rule for the Principate (27 BC–235 AD), which was the relatively stable period preceding the Crisis, compared with the period after 235 AD; the sample sizes are n₁ = 29 and n₂ = 41, respectively. The two distributions appear to be exponential, and the likelihood ratio test of stochastic ordering under this assumption has p-value 0.195; the corresponding unrestricted likelihood-ratio test has p-value 0.390. Applying our proposed test (with k = 2) to assess whether the duration of rule is stochastically shorter after the Principate, we obtain T_n = 0.3161 with a p-value of 0.424. This compares with a p-value of 0.575 based on S_n.

Figure 1.

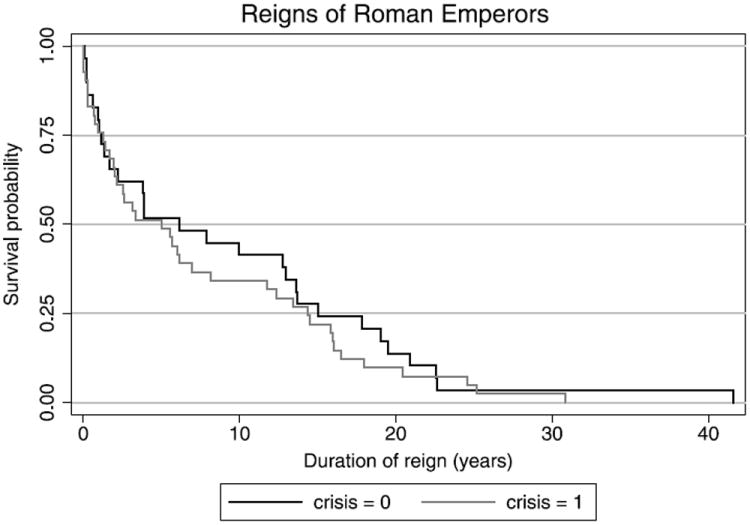
Empirical survival functions of durations of rule of the first 70 Roman Emperors before 235 AD (crisis = 0), and after 235 AD (crisis = 1).

The period 285–395 AD forms part of what is known as the Dominate, the despotic later phase of the empire. Inspection of Figure 2 suggests that the exponential hypothesis is not tenable for each separate period, so our nonparametric approach is more reasonable. The plot also suggests that the rule lengths are stochastically ordered as Dominate ≻ Principate ≻ Crisis. Applying our approach to formally test this hypothesis, we find that T_n has a p-value of 0.0002, compared with a p-value of 0.0017 for S_n. Under the assumption of exponential distributions, the likelihood ratio test has p-value less than 0.0007.

Figure 2.

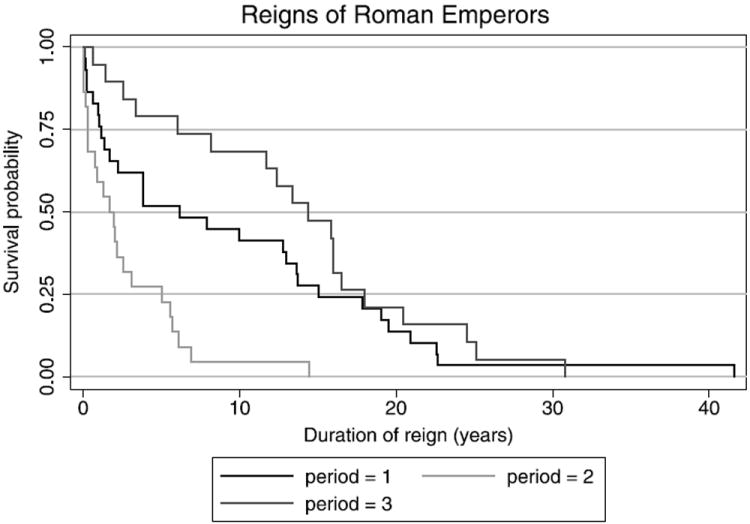
Empirical survival functions of durations of rule during the Principate, 27 BC–235 AD (period = 1), the Crisis, 235–284 AD (period = 2) and the Dominate, 284–395 AD (period = 3).

4. Discussion

In this paper we have developed a novel empirical likelihood approach to the important problem of nonparametrically testing for the presence of stochastic ordering based on k independent samples. The proposed tests are computationally efficient to implement, and could be used with massive data sets because they do not rely on the bootstrap or any other simulation technique, and they reduce to a local test for an ordering of binomial probabilities, which only requires a single sweep through the pooled data in the k groups.

Various extensions of the proposed tests are possible. In change-point problems, for example, it is of interest to test whether there is a sudden change in the distribution of a sequence of independent random variables X₁, …, X_n. Einmahl and McKeague [4] developed an EL-based change-point test for the presence of an (unknown) change-point τ ∈ {2, …, n} such that

$$X_1,\dots ,X_{\tau -1}~F_1\mathrm{and}{X}_{\tau },\dots ,X_n~F_2.$$

They only considered the unrestricted alternative F₁ ≠ F₂, but it is also of interest to consider the ordered alternative F₁ ≻ F₂. This can be done by extending the two-sample case to allow the sample sizes to depend on an additional local parameter, namely t ∈ [1/n, 1), with n₁ = ⌊nt⌋ and n₂ = n − ⌊nt⌋. The resulting test statistic has a limiting distribution of the same form as in Theorem 2 of Einmahl and McKeague [4], involving the integral of a four-sided tied-down Wiener process W₀(t, y), except that the integrand now includes the indicator I (W₀(t, y) ≥ 0).

Our approach also naturally extends to non-monotonic alternatives, namely to testing whether F₁, F₂, …, F_k are isotonic with respect to a quasi-order on {1, 2, …, k}. A relation ≲ on {1, 2, …, k} is a quasi-order if it is reflexive and transitive (and a partial order if, in addition, it is antisymmetric). We say that F₁, F₂, …, F_k are isotonic with respect to ≲ if F_i ≻ F_j whenever i ≲ j. Examples of such ordered alternatives include F₁ ≻ F_i, i = 2, …, k (tree ordering) and F₁ ≻ F₂ ≻ ⋯ ≻ F_i0 ≺ F_i0+1 ≺ ⋯ ≺ F_k, where i₀ is known (umbrella ordering). The localized empirical likelihood (3) extends naturally to such ordered alternatives, the only difference being that in ϕ_j = E_w(ϕ̂∣I)_j the set I is now the isotonic cone corresponding to ≲. For exampls, in the case of tree ordering, the cone becomes I = {z ∈ ℝ^k: z₁ ≤ z_i, i = 2, …, k}. The ϕ_j can be computed using quadratic programming or algorithms described in Robertson, Wright and Dykstra [18], one of the most general being the lower-sets algorithm. The limiting distribution of the resulting test statistic is obtained by taking I in (7) as the isotonic cone corresponding to ≲.

An important and challenging problem for future research in this area would be to develop EL-based tests for stochastic ordering based on censored data. EL methods are well developed for the comparison of survival functions from right-censored data, see McKeague and Zhao [13, 14], but these methods only apply to omnibus alternatives. The complication in extending the present tests to right-censored data arises because the EL ratio would then no longer have such an explicit form as in (5), and Lagrange multipliers would be involved. This extension is beyond the scope of the present paper.

5. Proofs

Proof of Theorem 1

For 0 < ε < 1, let x_ε, y_ε be real numbers such that F₀(x_ε) = 1 − F₀(y_ε) = ε/2. Then decompose the test statistic as T_n = T_1n + T_2n, where

$$T_{1n}=-2{\mathit{\int }}_{x_{\epsilon }}^{y_{\epsilon }}\log (R(x))\mathrm{d}{F}_0(x)$$

and

$$T_{2n}=-2{\mathit{\int }}_{{[x_{\epsilon },y_{\epsilon }]}^c}\log (R(x))\mathrm{d}{F}_0(x).$$

By appealing to Theorem 4.2 of Billingsley [2], note that, to complete the proof of the theorem, it suffices to show that for fixed ε,

$$T_{1n}\stackrel{d}{\to }{\mathit{\int }}_{\epsilon /2}^{1-\epsilon /2}\frac{B^2(t)}{t(1-t)}I(B(t)\ge 0)\mathrm{d}t$$ (8)

as n → ∞, and, for each δ > 0, that lim sup_n→∞ P (|T_2n| ≥ δ) → 0 as ε → 0.

First consider T_1n. Using the inequality | log(1 + y) − y + y²/2| ≤ |y|³/3 when |y| ≤ 1/2, the Glivenko–Cantelli theorem and Donsker’s theorem, we have

$$\begin{array}{l}\underset{n\to \infty }{\mathrm{lim\; sup}}\underset{x\in [x_{\epsilon },y_{\epsilon }]}{\sup }\left|\log \left(R(x)\right)+\frac{n}{2}{\left(\widehat{F}(x)-F_0(x)\right)}^2\left[\frac{1}{\widehat{F}(x)}+\frac{1}{1-\widehat{F}(x)}\right]I[\widehat{F}(x)\le F_0(x)]\right|\\ \le \underset{n\to \infty }{\mathrm{lim\; sup}}\underset{x\in [x_{\epsilon },y_{\epsilon }]}{\sup }\frac{n}{3}{|\widehat{F}(x)-F_0(x)|}^3\left[\frac{1}{\widehat{F}(x)}+\frac{1}{1-\widehat{F}(x)}\right]=0,\end{array}$$

almost surely. Then, noting that F̂(x) = Γ̂ (F₀(x)), where Γ̂ is the empirical cdf of V_i = F₀(X_i) ~ U (0, 1), i = 1, …, n, and changing variables in the integration to t = F₀(x), it follows that

$$\begin{array}{lll}{T}_{1n}& =& {\mathit{\int }}_{\epsilon /2}^{1-\epsilon /2}n{(\widehat{\mathrm{\Gamma }}(t)-t)}^2\left[\frac{1}{\widehat{\mathrm{\Gamma }}(t)}+\frac{1}{1-\widehat{\mathrm{\Gamma }}(t)}\right]I[\sqrt{n}(\widehat{\mathrm{\Gamma }}(t)-t)\le 0]\mathrm{d}t+{\mathrm{o}}_p(1)\\ & =& {\mathit{\int }}_{\epsilon /2}^{1-\epsilon /2}\frac{\widehat{U}{(t)}^2}{t(1-t)}I[\widehat{U}(t)\le 0]\mathrm{d}t+{\mathrm{o}}_p(1),\end{array}$$ (9)

where $\widehat{U}(t)=\sqrt{n}(\widehat{\mathrm{\Gamma }}(t)-t)$ is the uniform empirical process. Note that (for any fixed 0 < ε < 1) the functional

$$\begin{array}{ll}f\mapsto {\mathit{\int }}_{\epsilon /2}^{1-\epsilon /2}\frac{f{(t)}^2}{t(1-t)}I(f(t)\le 0)\mathrm{d}t,& f\in D[0,1],\end{array}$$

is continuous when the Skorohod space D[0, 1] is equipped with the uniform norm. By Donsker’s theorem, Û converges weakly to B in D[0, 1], so applying the continuous mapping theorem to the leading term in (9) establishes (8).

Finally we need to verify the claim concerning T_2n. This follows immediately from a corresponding result in Einmahl and McKeague [4], who considered the test of the null hypothesis F = F₀ versus the (omnibus) alternative F ≠ F₀, with the same integral-type test statistic as T_n except that the integrand does not vanish when F̂(x) > F₀(x). This completes the proof.

Proof for Remark 1

The asymptotic distribution of $T_n^{\ast }$ can be obtained following the same steps as the proof of Theorem 1, except that the leading term in T_1n now becomes

$${\mathit{\int }}_{\epsilon /2}^{1-\epsilon /2}\frac{\widehat{U}{(t)}^2}{t(1-t)}I[\widehat{U}(t)\le 0]\mathrm{d}\widehat{\mathrm{\Gamma }}(t)={\mathit{\int }}_{\epsilon /2}^{1-\epsilon /2}V(t-)\mathrm{d}\widehat{\mathrm{\Gamma }}(t)+{\mathrm{o}}_p(1),$$

where

$$V(t)=\frac{\widehat{U}{(t)}^2}{t(1-t)}I[\widehat{U}(t)\le 0,\epsilon /2<t\le 1-\epsilon /2].$$

Note that

$$M(t)=\widehat{\mathrm{\Gamma }}(t)-{\mathit{\int }}_0^t[1-\widehat{\mathrm{\Gamma }}(s-)]{(1-s)}^{-1}\mathrm{d}s$$

is a martingale wrt to the natural filtration defined by Γ̂, and its predictable quadratic variation process is $\langle M\rangle (t)=n^{-1}{\mathit{\int }}_0^t[1-\widehat{\mathrm{\Gamma }}(s-)]{(1-s)}^{-1}\mathrm{d}s$. Also note that V (t−) is a predictable process because it is adapted and left-continuous. Write

$$\begin{array}{l}{\mathit{\int }}_{\epsilon /2}^{1-\epsilon /2}V(t-)\mathrm{d}\widehat{\mathrm{\Gamma }}(t)\\ ={\mathit{\int }}_{\epsilon /2}^{1-\epsilon /2}V(t-)\mathrm{d}M(t)+{\mathit{\int }}_{\epsilon /2}^{1-\epsilon /2}V(t-)[1-\widehat{\mathrm{\Gamma }}(t-)]{(1-t)}^{-1}\mathrm{d}t.\end{array}$$

Using a basic property of martingale integrals, the second moment of the first term above is

$$E{\mathit{\int }}_{\epsilon /2}^{1-\epsilon /2}V{(t-)}^2\mathrm{d}\langle M\rangle (t)=\mathrm{O}(1/n),$$

so this term tends in probability to zero. The second term in the above display can be handled in the same way as the main term T_1n in the proof of Theorem 1, and has the same limit distribution.

Proof of Theorem 2

The proof is similar to the proof of Theorem 1, so we only indicate the main steps. Using the Taylor expansion of log(1 + y), as before, and the (uniform) consistency of F̃_j as an estimator of F_j = F (see, e.g., El Barmi and Mukerjee [6], page 253), for each fixed x, such that 0 < t = F (x) < 1, we have

$$\begin{array}{lll}-2\log R(x)& =& \sum _{j=1}^k{n}_j{({\stackrel{\sim }{F}}_j(x)-\widehat{F}(x))}^2\left[\frac{1}{{\stackrel{\sim }{F}}_j(x)}+\frac{1}{1-{\stackrel{\sim }{F}}_j(x)}\right]+{\mathrm{o}}_p(1)\\ & =& \sum _{j=1}^k{w}_j\frac{{[\sqrt{n}({\stackrel{\sim }{F}}_j(x)-F(x))-\sqrt{n}(\widehat{F}(x)-F(x))]}^2}{F(x)(1-F\left(x\right))}+{\mathrm{o}}_p(1)\\ & =& \sum _{j=1}^k{w}_j\frac{{(E_{\mathbf{w}}{[\widehat{\mathbf{U}}(t)\mid I]}_j-\overline{U}(t))}^2}{t(1-t)}+{\mathrm{o}}_p(1)\\ & \stackrel{d}{\to }& \sum _{j=1}^k{w}_j\frac{{(E_{\mathbf{w}}{[\mathbf{B}(t)\mid I]}_j-\overline{B}(t))}^2}{t(1-t)},\end{array}$$

where $\widehat{\mathbf{U}}={({\widehat{U}}_1/\sqrt{w_1},{\widehat{U}}_2/\sqrt{w_2},\dots ,{\widehat{U}}_k/\sqrt{w_k})}^T$, ${\widehat{U}}_j(t)=\sqrt{n_j}({\widehat{F}}_j(x)-F(x))$ are independent uniform empirical processes, and $\overline{U}={\sum }_{j=1}^k{\sqrt{w}}_j{\widehat{U}}_j$. Donsker’s theorem and the continuous mapping theorem have been used as before, but we have also used the fact that E_w(·∣I) is a continuous function on ℝ^k.