Automatic Segmentation and Quantitative Analysis of the Articular Cartilages From Magnetic Resonance Images of the Knee

Abstract

In this paper, we present a segmentation scheme that automatically and accurately segments all the cartilages from magnetic resonance (MR) images of nonpathological knees. Our scheme involves the automatic segmentation of the bones using a three-dimensional active shape model, the extraction of the expected bone-cartilage interface (BCI), and cartilage segmentation from the BCI using a deformable model that utilizes localization, patient specific tissue estimation and a model of the thickness variation. The accuracy of this scheme was experimentally validated using leave one out experiments on a database of fat suppressed spoiled gradient recall MR images. The scheme was compared to three state of the art approaches, tissue classification, a modified semi-automatic watershed algorithm and nonrigid registration (B-spline based free form deformation). Our scheme obtained an average Dice similarity coefficient (DSC) of (0.83, 0.83, 0.85) for the (patellar, tibial, femoral) cartilages, while (0.82, 0.81, 0.86) was obtained with a tissue classifier and (0.73, 0.79, 0.76) was obtained with nonrigid registration. The average DSC obtained for all the cartilages using a semi-automatic watershed algorithm (0.90) was slightly higher than our approach (0.89), however unlike this approach we segment each cartilage as a separate object. The effectiveness of our approach for quantitative analysis was evaluated using volume and thickness measures with a median volume difference error of (5.92, 4.65, 5.69) and absolute Laplacian thickness difference of (0.13, 0.24, 0.12) mm.

I. INTRODUCTION

QUANTITATIVE analysis of healthy cartilage joints can improve our understanding of cartilage morphology and physiology. In particular, by examining the influence of demographics [1], [2] and monitoring physiological effects [3]. This allows the factors that influence normal cartilage variation to be determined, which is an important prerequisite to improving our understanding of cartilage diseases like osteoarthritis (OA) and allowing the development and refinement of cartilage-dedicated therapeutic strategies and surgical treatments.

Magnetic resonance (MR) imaging is the most promising imaging modality to detect structural changes in cartilage tissue, as it provides direct and noninvasive images of the whole knee joint, including the cartilage tissue [4]. Obtaining accurate and reproducible quantitative cartilage measures from MR images is still an open problem and has been the focus of significant research. In the literature several measures are commonly used, including volume, thickness, surface area, and curvature [5]–[7]. These measures require the cartilages to be segmented, a task whose accuracy significantly influences the error and precision of the quantitative analysis. Unfortunately due to the structure and morphology of the cartilages as well as the nature of MR acquisition, obtaining accurate segmentations can be problematic.

As MR could allow more accurate monitoring of cartilage-dedicated therapeutic strategies and surgical treatments, a significant amount of research has been focused on improving the automation, accuracy and precision of the quantitative analysis by improving: the MR sequence, the segmentation process, and the quantitative measures. The rest of this section provides a brief overview of all these areas, however this paper only examines two: automatic cartilage segmentation and quantitative analysis.

A. MR Imaging for Cartilage Assessment

The cartilages consist of several layers, each with different water and protein content and varying collagen fibre orientation. Acquired MR images of the cartilages often exhibit varying signal due to these natural changes in local tissue properties and from various MR artifacts (susceptibility, magic angle, and partial volume effects).

The MR sequence that is most commonly used for cartilage quantification is fat suppressed (FS)T₁-weighted spoiled gradient recall (SPGR) [6], [8]. It provides good spatial resolution, contrast-to-noise ratio (CNR) and signal-to-noise ratio (SNR). Fat suppression potentially increases the dynamic range of signal acquisition and removes the chemical shift artifact. In FS SPGR the boundary between the bone and the cartilage [i.e., the bone-cartilage interface (BCI)] is particularly well delineated. However, low contrast between the cartilage-meniscus and cartilage-synovial fluid interfaces, often cause poor delineation of cartilage defects [9].

In recent years, several cartilage-specific sequences have been developed that exhibit less imaging artifacts, improved CNR, SNR, and often permit higher resolutions [9]–[11]. Two promising modalities are water-selective excitation double echo in the steady state (weDESS) [10] and multiecho data image combination (MEDIC) [12]. In this paper, we use T₁ weighted FS SPGR images, weDESS, and MEDIC MR images.

B. Prior Work on Segmentation of Cartilages

To perform quantitative analysis requires the cartilages to be segmented. Due to the small changes that are required to be detected this must be performed with a high level of accuracy and precision. Difficulties in non pathological knees are due to the thin variable morphology of the cartilages, variable intensity homogeneity, MR artifacts, and low contrast areas in the joint surface.

C. Semi-Automatic Cartilage Segmentation

In clinical studies, due to the lack of accurate and robust automated algorithms, fully manual or 2-D slice by slice semi-automated segmentation approaches are usually used [8]. This is time consuming and requires trained operators (often three months of training [13]), who interact with the algorithm on a slice by slice basis: initializing, correcting and validating the segmentation. When rigorous procedures are used, these approaches can take several hours per knee [13]. Semi-automatic segmentation approaches previously used include region growing [14], active contours [5], B-spline snakes [6], [11], and live-wires [15]. In longitudinal studies, significantly improved follow up segmentation times have been achieved by assuming the bones only undergo rigid changes and utilizing edge detection and thresholding on the propagated baseline cartilage segmentations [13].

D. Automatic Cartilage Segmentation

In recent years, there have been several interesting approaches which allow automated segmentation of the cartilages; Folkesson used an approximate nearest neighbor framework to perform tissue classification on various derived image features and the absolute position [16], Grau used a modified watershed metric which utilized prior information [17] and Glocker used a statistical atlas in a registration scheme to segment the patellar cartilage by deforming the atlas so that the conditional posterior of the atlas density is maximized with respect to the image [18].

Folkesson's approach was validated on a large database of low field (0.18 T) non-FS T₁ weighted MR images acquired from healthy and OA subjects, with a segmentation accuracy for the tibial (Sens. 0.868±0.077, Spec. 1.00±0.01, DSC 0.810±0.06) and feromal (Sens. 0.803 ± 0.116, Spec. 0.999 ± 0.03, DSC 0.770±0.08) cartilages. Glocker's segmentation accuracy for the patellar cartilage (Sens. 0.941, Spec. 0.999, DSC 0.840) was obtained from a reasonably large database of T₂ weighted MRs acquired from healthy subjects. Grau segmented cartilage tissue from a small database of healthy subjects, and is the most accurate approach that has been reported (Sens. 0.900 ± 0.03, Spec. 0.999 ± 0.00, DSC 0.895 ± 0.01), however, it is semi-automatic, requiring around 10 min of user seeding and it can only segment the individual cartilages as a single object.

E. Bone Segmentation, BCI Extraction, and Cartilage Segmentation

As direct cartilage segmentation is difficult, several approaches have been presented which first segment the bone and use this segmentation as a basis for cartilage segmentation and analysis [19]–[21]. Bone segmentation of FS SPGR images is nontrivial because the adipose (fat) tissue, background, and tendons all have essentially the same intensity distribution with poor delineation at these interfaces (see Fig. 1).

Fig. 1.

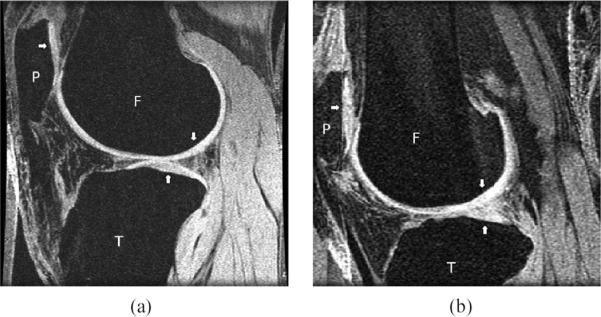
Labelled (P—Patella, T—Tibia, F—Femur, with arrows pointing towards Articular cartilage tissue) Sagittal fat suppressed SPGR MR images of the knee: (a) case 2 (1.5T, 60/7 (T_R/T_E), 40° flip angle, 512×512 matrix, 120 mm FOV) (b) case 20 (1.5 T, 60/5, 40° flip angle, 256×256, 120 mm FOV). The cartilage displays high signal intensity, while bone, tendons, and adipose tissue have low signal intensity.

An early work by Kapur (on non-FS MRIs), used a model-based approach that utilized the geometric relation of the cartilage to the underlying bone to obtained cartilage segmentations with a mean distance error of 1.25 pixels [19]. Tamez-Pena [20] used image fusion and multispectral classifier segmentation to augment the different discrimination provided by two different sequences (FS T₁ weighted and non-FS T₂ weighted 3-D gradient recall echo acquisitions). This approach required the acquisition of two MRs, with around 5 min of manual merging to obtain accurate bone segmentations, while the cartilages required a further 30 min of interactive correction. If only a single FS image is acquired, the bone segmentation takes four times longer as there is not “enough information to separate the bone tissue from surrounding fatty tissue and the background.”

An almost fully automatic approach based on graph searching has been used on eight isotropic MR images of the ankle [21]. In this approach the bones were presegmented using a level set based algorithm with a deformable shape and texture model driven by deformations produced using cubic B-spline based free form deformation. The bone segmentation is then converted into a mesh surface which is used to build a local graph from which the two (bone and cartilage) surfaces are extracted simultaneously using two separate cost functions. This approach obtains good results for the ankle and only requires a simple manual initialization of seed points for the bone segmentation.

F. Prior Work on Quantitative Analysis

Quantitative analysis has been the focus of significant research, with measures of volume, thickness, surface area and curvature investigated [5]–[7], [22]. Volume (and area) measurements usually involve the direct numerical integration of the voxels (or triangles) attributed to each segmented cartilage. As the acquired images are usually highly anisotropic, resampling using shape based interpolation (SBI) is often performed in preprocessing [23]. Surface area and curvature measurements are commonly performed by fitting B-spline [7] and m-rep surfaces [24]. Thickness measurements can be defined in numerous ways and require a unique association between two points and some definition of the distance between them. Definitions previously used in the literature include normal vectors from the BCI [5], Euclidean distance [6], offset map differences [22], and Laplacian distance [25].

G. Outline and Aims

In this paper, we present a model based scheme that is designed to segment all the bones and cartilages in the knee. Our approach is compared to three state of the art approaches, a tissue classification scheme inspired by Folkesson [16], a modified semi-automatic watershed algorithm [17] and non-rigid registration (NRR, B-spline based free form deformation [26]). These approaches were trained and validated against expert manual segmentations of a heterogeneous database of FS SPGR MR images. Validation of the obtained quantitative measures was performed using volume and thickness.

II. MATERIALS AND METHODS

A. MR Image Acquisition

We used an anonymised database of 20 healthy volunteers who were not known to have OA or knee pain. They were imaged using a FS SPGR MR sequence (Fig. 1). Demographic information was not available, however no exclusion criteria based on age or gender was used. Each of the acquired images were manually segmented by an expert using 3-D Slicer [27], resulting in labeled images of the patella, tibia, and femoral bones and cartilages.

The MR images were acquired using three different sets of parameters. Several parameters were common, with all images acquired in the sagittal plane with a field of view (FOV) 120 mm, slice thickness 1.5 mm, and repetition time (T_R) 60 ms. A flip angle of 40° was used on all cases except case 7 which used 30°. Six scans were acquired at 3 T with in-plane spacing 0.23 × 0.23 mm and echo time (T_E)7 ms. A birdcage coil was used for 5 of these scans (cases 1, 6, 14, 15, 16) and a head coil was used on case 3. Fourteen scans were acquired at 1.5T using two different extremity array coils. A G.E. coil was used for five of the scans with image matrix with in-plane spacing 0.46 × 0.46 mm, T_E5 ms used for four cases (cases 17, 18, 19, 20), while case 7 was acquired with in-plane spacing 0.23 × 0.23 mm, T_E3.2 ms, and flip angle 30°. A MEDRAD coil was used for the other nine images with in-plane spacing 0.23 × 0.23 mm, T_E 7 ms (cases 2, 5, 8, 10, 12, 13), and 12 ms (cases 4, 9, 11).

To investigate the consistency of the segmentation algorithm against partial volume and repositioning effects, we were kindly provided the MR image and manual segmentations used in [17]. This single patient was scanned four times with a FS SPGR sequence (in-plane spacing 0.23 × 0.23 and slice thickness 1.5 mm) with Scan 1 taken before “a half-voxel shift was applied and Scan 2 was acquired. After moving the volunteer out of the scanner for 20 min and repositioning the knee, Scans 3 and 4 were acquired, again with a half-voxel shift applied after Scan 3.” To further consider the consistency of the segmentation algorithm, we obtained several weDESS (T_E = 8.6 ms, T_R = 25 ms, 0.41 × 0.41 mm, and slice thickness 1.5 mm) and MEDIC (T_E = 22 ms, T_R = 44 ms, 0.41 × 0.41 or 0.3 × 0.3 mm and slice thickness 1.5 mm) MR sequences. These images were acquired from three young volunteers (ages 27, 30, and 46) on a 1.5 T Siemens scanner.

B. Validation Methodology

All the experiments presented were performed using a leave one out approach. The cartilage segmentations automatically obtained were compared to the expert binary manual segmentations using sensitivity = T_P/(T_P + F_N), specificity = T_N/(T_N + F_P) and Dice similarity coefficient (DSC) = 2T_P/(2T_P+F_P+F_N) where T_P is true positive, T_N is true negative, F_P is false positive, and F_N false negative count for the voxels. The sensitivity is the “true positive fraction” and specificity the “true negative fraction,” while DSC is a spatial overlap index [28].

C. Quantitative Analysis

In this paper, we used volume and thickness quantitative measures to compare the segmentation results from our scheme to those obtained with manual segmentations. These measures were performed on isotropically resampled segmentations (SBI [23]). The volume measurements were performed by direct numerical integration of the voxels attributed to each segmented cartilage. To allow direct comparisons, all volumes were calculated with the voxelized segmentations.

The thickness was evaluated using two different approaches. The first approach defines the thickness as the distance from the outer cartilage surface to the BCI calculated from the voxelization using a 3-D exact Euclidean distance transform (EEDT) [29]. For this, a 3-D EEDT is calculated from the outer cartilage interface to the BCI. This transform is not a bijective mapping, and reflects the shortest distance between points on the interfaces. Similar types of approaches are commonly used in the cartilage quantitative analysis literature [6].

The second approach uses Laplace's equation to define the thickness [25], [30]. For this, the top (other tissues) and bottom (BCI) surfaces are set to fixed potentials, which meet around the edges of the cartilages. The Laplace equation is then solved in the cartilage volume to obtain a scalar field which divides the cartilage into a set of equipotential sublayers. The length of streamlines that connect pairs of points on the inner and outer interfaces are used to define the cartilage thickness. The advantage of this approach is that the thickness obtained is a bijective mapping, so each outer cartilage point maps to a unique BCI point.

D. Segmentation Approaches

Our segmentation scheme is based on using a segmentation hierarchy, where easier objects are segmented first to aid the initialization and provide constraints on the segmentation of harder objects. In the knee there is a strong spatial relationship between the bones and cartilages. Our fully automatic scheme utilizes this relationship to perform cartilage segmentation from the BCI. This interface is determined adaptively using image information and prior knowledge from training. The scheme consists of using a bone statistical shape model, augmented with cartilage thickness statistics, to obtain a coupled but elastic bone-cartilage model. Using this model, the three main bones in the knee joint (femur, tibia, and patella) are segmented after which the BCI is extracted and used to initialize and constrain the segmentation of the articular cartilages. The statistical shape model creation, bone segmentation and initial BCI extraction have previously been presented in [31] with the focus of this paper being on the cartilage segmentation.

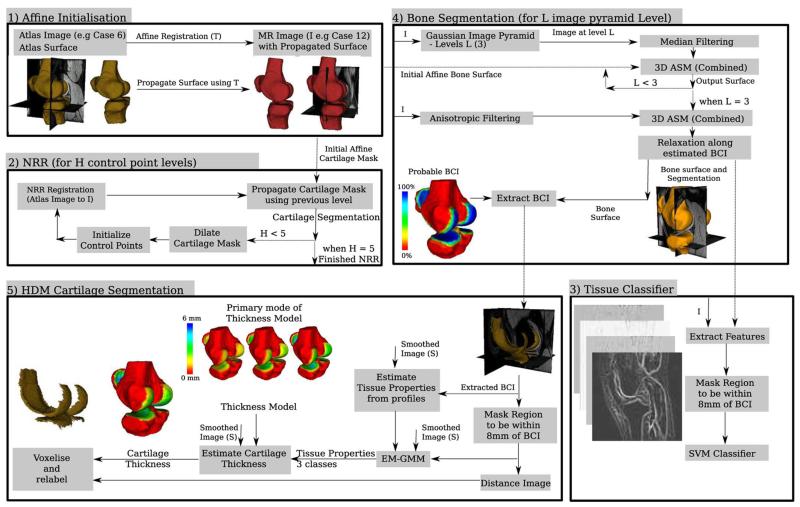
A schematic of our approach and the affine registration, non-rigid registration (NRR, B-spline based free form deformation [26]) and the tissue classification scheme are presented in Fig. 2.

Fig. 2.

Flow diagram of the different segmentation schemes used to automatically segment the bones, extract the BCIs and segment the cartilages. The surface rendering results presented are of case 12 with case 6 used as the atlas.

1) Affine Registration

A global transformation T_g between case i; i = 1,2,…,N and the atlas is estimated by an affine transformation determined from correspondences between very similar areas in both images using a block matching strategy. This procedure has previously been described in [32] for use in the registration of anatomical sections. The atlas case used in this work was simply another labeled MR case which had been manually segmented.

2) Nonrigid Registration (NRR)

NRR uses local transformations to match the case i; i = 1,2,… and the atlas and has been used previously to segment the patellar cartilage [18]. There are many NRR approaches; in this paper we use the free form deformation approach first proposed by Rueckert (see [26] for full details). In this approach, a mesh of B-spline control points is used to parameterize the deformation field, which is optimized using a gradient descent search with normalized mutual information (NMI) used as a similarity measure. To reduce the computational cost a five-level hierarchical multiresolution approach is used to perform the segmentation propagation, with control point spacing 20 mm, 10 mm, 5 mm, 2.5 mm, and 1 mm. The computational load is further reduced to approximately 18 h by using dilated masks (20, 15, 10, 10, and 5 radius kernel) to restrict the set of active control points.

3) Tissue Classification

The tissue classification approach was inspired by the work of Folkesson [16] and used to segment each individual cartilage compartment. Differences to Folkesson's work include the use of a support vector machine [33], [34] for training and classification, a reduced set of features and instead of using absolute cartilage position, we use the Euclidean distance from each bone. The full set of features we use are the normalized image, the Euclidean distance from each of the presegmented bones, then using three different scales (σ = 0.5, 1.0, and 2.0 mm) we generate recursive Gaussian images, with first- and second-order derivatives in (x, y, and z) and the three eigenvalues of the Hessian image. Unlike Folkesson, we did not use the third-order derivatives, structure tensor or the eigenvectors of the Hessian image. Both the automatic and expert manual segmentations were used as presegmentations of the bones. Training was performed in two different ways; leave one out was performed using the consensus [35] of the automatic bone segmentations, while five training sets each of nine images were used with the manual bone segmentations. The computational load of the classification was approximately 5–10 min per cartilage, and was performed in a localized region within 8 mm of the BCI using a three-level image classification pyramid.

4) Our Approach: Bone Segmentation and Extraction of Initial Bone Cartilage Interface

In FS SPGR images, both the bones and cartilages have interfaces with other tissues which are poorly delineated. The FS in the SPGR sequence removes most of the signal from the bone, which primarily consists of fat, and increases the dynamic range of the cartilage tissue, which primarily consists of water. As a result, the bones are similar in appearance to the background, tendons, and other fat tissue, with little contrast between these tissues. However, the interface between the bone and cartilage is very well delineated, moreover, the intensity distribution of the voxels in MR images that belong to the bone can be modeled by a Gaussian distribution. To handle missing boundaries or poorly delineated objects, the use of active shape models [36] has proved to be successful in many applications.

The bone segmentation approach used in this work is presented in [31] and is based on using 3-D active shape models (ASMs), built from a training set of triangulated surface representation of each of the bones in the knee. Prior knowledge about the probability of having cartilage tissue and its thickness was also embedded in the ASM and was used to estimate the location of the BCI.

Initialization of the 3-D ASM was provided by an affine registration of an atlas (another labeled MR case with surface) to the case. After segmenting the bones, the points in the ASM with a probability of more than 90% of having cartilage are extracted and treated as the initial estimate of the BCI. This is then refined in the following way.

• a)
  Model the cartilage tissue parameters by a Gaussian distribution.

  • Extract tissue samples along a 4 mm 1-D profile normal to the BCI (samples extracted at twice the in-plane resolution using cubic B-spline interpolation).
• b)
  Consider points with at least two neighbors on the BCI (via triangulation).

  • If a point has 25% of its extracted samples with intensity above the estimated cartilage tissue mean then add it to the BCI.
• c)Converge if the number of points on the BCI unchanged else Goto b).

5) Our Approach: Cartilage Segmentation

The cartilage segmentation algorithm further refines the bone segmentation, BCI extraction and estimated thickness profile. Localized estimates of tissue properties and classification is incorporated, while the BCI and thickness maps (Euclidean distance) from the training database are used to build a principal component model of thickness variation for the points on the BCI. The number of modes used was constrained to account for 90% of the variation in the training data. These are combined and used in a 3-D active surface model approach to segment the cartilages.

The first stage of the cartilage segmentation process refines the estimate of the tissue properties used in the BCI extraction and generates a distance image for each of the bones. This is achieved by first creating a binary mask of voxels that are above and within 8 mm of the BCI. Using this mask a localized estimate of the tissue properties is obtained using an expectation maximization Gaussian mixture model [three classes, initialized using previous estimate of bones, cartilage and other (tissue between bone and cartilage intensities)]. Once the tissue properties have been estimated, a probability image for cartilage tissue is generated (Gaussian based with any value above the mean value assigned a probability of one). This information is then used as input to the cartilage segmentation algorithm, which operates as follows.

Until range is 0:

• a)
  For each point i on BCI find thickness t_i.

  • Extract profile along a 8 mm 1-D profile normal to the BCI (k samples extracted at twice the in-plane resolution using cubic B-spline interpolation).
  • Assume that the position j along the profile that maximizes the MR image gradient g and internal tissue probabilities (p) (F(g_j,p_j) = max(|δ_gj|/max(|δ_g|) + 1/kΣ_kp_j–_k) corresponds to the correct outer cartilage edge.
• b)Parameterize and reconstruct likely thickness using model of thickness variation (trained from normal patients).
• c)Enforce BCI boundary constraints.
• d)Set t_i to 0 for points that do not have internally more than 60% of samples with p ≥ 95%.
• e)Decrease capture range by reducing search range around t_i.

After convergence the coupled bone–cartilage model is voxelised and the distance map is used to relabel any overlapping voxels as the nearest cartilage interface. Similarly any voxels along the outer cartilage surface with intensity close to the bone are discarded. The computational time for the cartilage segmentation is approximately 15 min.

III. RESULTS

A. Segmentation Validation

The block matching strategy used to estimate the affine transformation between the patient image and the atlas qualitatively obtained robust results and provided a good estimate of the “global” affine deformation between the images. However, although it was sufficient to initialize subsequent approaches, it has only limited sensitivity and specificity for cartilage segmentation (see Table I). The use of NRR to perform cartilage segmentation propagation, obtained significantly improved results compared to it's affine initialization. However, the accuracy of the final NRR results were often closely related to the accuracy of the initial affine registration.

TABLE I.

Mean (Standard Deviation) of Validation Measures

Affine	Sensitivity	Specificity	DSC
- (Patellar)	0.450 (0.163)	0.998 (0.001)	0.422 (0.164)
- (Tibial)	0.460 (0.170)	0.998 (0.001)	0.473 (0.166)
- (Femoral)	0.418 (0.143)	0.994 (0.002)	0.427 (0.138)

Non-Rigid	Sensitivity	Specificity	DSC
After 10mm
- (Patellar)	0.506 (0.178)	0.998 (0.001)	0.479 (0.186)
- (Tibial)	0.652 (0.153)	0.999 (0.001)	0.671 (0.139)
- (Femoral)	0.664 (0.154)	0.997 (0.002)	0.682 (0.144)
After lmm
- (Patellar)	0.803(0.119)	0.999 (0.001)	0.732 (0.156)
- (Tibial)	0.781 (0.156)	0.999 (0.001)	0.785 (0.095)
- (Femoral)	0.795 (0.162)	0.997 (0.002)	0.758 (0.148)

Tissue Classifier	Sensitivity	Specificity	DSC
- (Patellar)	0.903 (0.126)	0.998 (0.001)	0.810 (0.116)
- (Tibial)	0.908 (0.093)	0.996 (0.001)	0.793 (0.068)
- (Femoral)	0.867 (0.120)	0.996 (0.001)	0.849 (0.075)
Leave one out (auto bone)
- (Patellar)	0.895 (0.040)	0.998 (0.001)	0.817 (0.105)
- (Tibial)	0.867 (0.067)	0.997 (0.001)	0.812 (0.050)
- (Femoral)	0.844 (0.147)	0.997 (0.001)	0.862 (0.040)

Our Approach	Sensitivity	Specificity	DSC
- (Patellar)	0.821 (0.135)	1.000 (0.000)	0.833 (0.135)
- (Tibial)	0.829 (0.207)	0.999 (0.000)	0.826 (0.083)
- (Femoral)	0.837 (0.162)	0.999 (0.000)	0.848 (0.076)

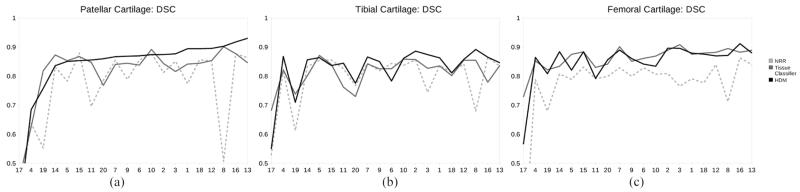
As can be seen in Table I and Fig. 3, our approach and the tissue classifier obtained significantly better DSC than NRR (significance was found using a paired t-test with p < 0.05 for the patellar and femoral, although only the HDM was found to be significant for the tibial). There was no statistical difference in DSC between our approach and the tissue classifier.

Fig. 3.

DSC results obtained for the (a) Patellar, (b) Tibial, and (c) Femoral cartilages with nonrigid registration (1 mm), tissue classification and our hybrid deformable model approach. The results are sorted based on patellar cartilage DSC of our approach.

The results obtained by our approach, NRR and the tissue classifier followed a similar trend across the cases (Fig. 3) varying mainly depending on the image quality. A qualitative illustration of the difference between our approach, manual segmentation and NRR is given in Fig. 4. The low resolution (cases 17–20) images were much noisier with less contrast between the cartilages and surrounding tissue. This was especially true for cases 17 and 19 where low contrast resulted in none or very poor delineation of the outer cartilage interfaces. None of the approaches investigated performed well on these images.

Fig. 4.

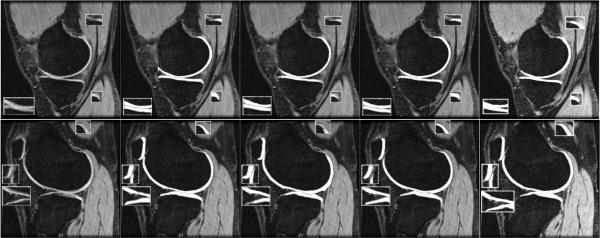
Overlayed segmentations (gray contour on patellar and tibial cartilages) for case 9 (case 15 as atlas, slices 16 and 48). From left to right: MR, Manual, NRR (DSC = 0.82,0.79,0.82), our approach (DSC = 0.87, 0.85, 0.86), and the texture classifier initialized using our bone segmentation (DSC = 0.84, 0.83, 0.87). Note: Areas of interest used 1.5 × zoom.

Qualitatively, the tissue classifier slightly outperformed our approach when segmenting the femoral cartilage, but our approach was slightly better at segmenting the patellar and tibial cartilages. One reason for this is that our model approach finds it more difficult to accurately model regions of high curvature without causing under-segmentation. For the tissue classifier, the synovial fluid and cruciate ligament regions and the cartilage–cartilage interfaces were found to be more difficult to segment correctly. Overall we found that the tissue classifier slightly oversegmented the cartilages, hence its higher specificity (higher true positive and lower false negatives), while our approach tended to under-segment (lower false positive).

Overall the primary cause of segmentation errors were regions affected by partial voluming and other signal decreases. This occurred primarily around the edges and thin regions of the cartilages, and was also observed in regions of high curvature (in slice thickness direction). In a few cases small errors were also observed between the femoral and tibial cartilages (e.g., Slice 48 in Fig. 4). Small errors were also observed at the femoral and patellar cartilage interface. The overall approach was quite robust to initialization (atlas choice) with failures in the cartilage segmentation only occurring in case 17 and the patellar of case 4, except when the previous bone segmentation had already failed (which occurred in 3.60% of the segmentations [31]).

We further validated this approach using the data of the fourth subject from [17]. This subject was scanned four times to evaluate the effect of partial voluming and repositioning, with the ground truth of each scan obtained using STAPLE on 10 manual segmentations performed by two experts (five times each). As can be seen in Table II, the values of sensitivity, specificity and DSC for the total cartilage (patellar, tibial and femoral) were similar, with the lower sensitivity and higher specificity of our approach indicating it slightly under-segments compared to the modified watershed algorithm. The primary advantage of our approach is that it does not require any user interaction and each cartilage is segmented and labeled separately, which is essential for quantitative analysis.

TABLE II.

Average (From 5 Segmentations) of the Total Cartilage (Patellar, Tibial and Femoral) Results Obtained Using Our Algorithm Compared to the Improved Watershed Approach of Grau [17]. Total Cartilage was Used as Grau's Approach Cannot Differentiate Between Different Cartilages

	Improved Watershed			Our approach
Scan	Sens.	Spec.	DSC	Sens.	Spec.	DSC
(1)	0.8965	0.9987	0.8988	0.8410	0.9993	0.8897
(2)	0.8649	0.9990	0.8907	0.8402	0.9994	0.8898
(3)	0.8763	0.9990	0.8984	0.8490	0.9992	0.8902
(4)	0.8905	0.9988	0.8978	0.8591	0.9992	0.8959

B. Quantitative Analysis

1) Volume

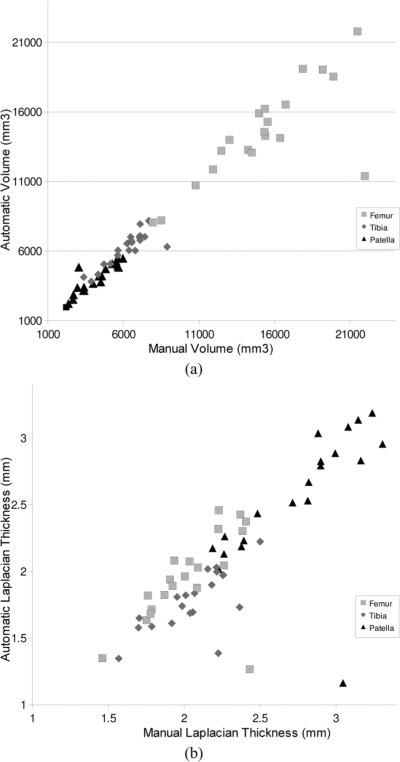
Fig. 5(a) presents a scatter graph of the volume calculated from the (manual, automatic) segmentations, which had an average volume of (4047, 3912), (6026, 6056), and (14703, 14463) mm³ and median absolute volume difference error of (5.92%, 4.45%, and 5.69%) for the patellar, tibial and femoral cartilages respectively (excluding case 17 which failed). The correlation between the volume measured from manual segmentation and the automatic algorithm using Pearsons was (0.89, 0.95, 0.97). Although the patellar results appear low, after removing the more problematic results of case 4, this increases to 0.97.

Fig. 5.

Scatter graph of the (a) volume and (b) average Laplacian thickness measured for the cartilages of each case using manual and automated segmentations.

2) Thickness

The difference in the distance images obtained using the Laplacian and EEDT definition of thickness is illustrated in Fig. 6, with the average thickness calculated by integrating the value of all the voxels on BCI. A scatter graph comparing the Laplacian thickness calculated from our algorithm and that of the manual segmentations is presented in Fig. 5(b). The Laplacian thickness measure was generally larger than the EEDT (which obtains the shortest 3-D distance) with a Pearson coefficient of (0.92, 0.86, 0.93) compared to (0.94, 0.92, 0.94) for (patellar, tibial, femoral), respectively. In Fig. 7, a volume rendering of the Laplacian thickness provides a qualitative illustration of the results obtained from both manual and our automated segmentations.

Fig. 6.

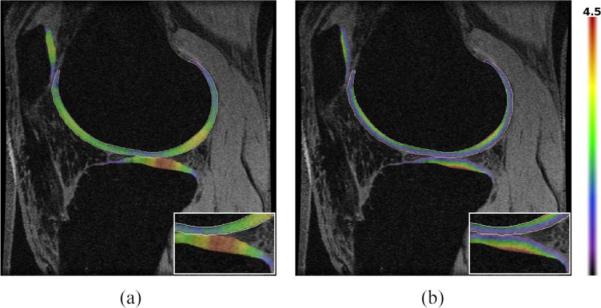
(a) Laplacian and (b) EEDT thickness map (mm) calculated from the automatic segmentation of case 3 overlayed on the MR slice, with the distance calculated on the BCI. Note: Area of interest used a 1.5 × zoom.

Fig. 7.

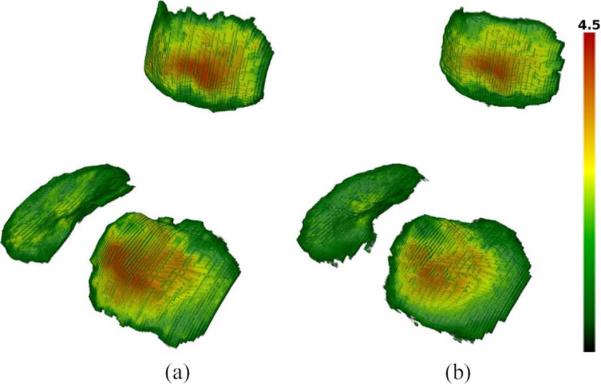
Volume rendering of the Laplacian thickness map (mm) obtained for the (patellar, tibial) cartilages of case 9 using (a) manual (2.38 ± 1.04, 2.17 ± 0.94 mm) and (b) automatic segmentations (2.25 ± 1.06, 1.85 ± 0.90 mm).

C. Reproducibility of Quantitative Analysis

To validate that our segmentation and quantitative analysis is consistent we calculated the quantitative measures for each of the four scans of the same patient. As can be seen in Table III the quantitative analysis measures are quite consistent between scans, with only one of the patellar segmentations exhibiting a large variation in volume. A general variation of about 5% in mean thickness was observed, with a significant amount of this variation observed between the repositioned “pairs” of scans, with scan 1 similar to 2 and 3 similar to 4.

TABLE III.

Cartilage Quantitative Analysis Using Volume and Mean (STD) (Maximum) Thickness for Each Scan of The Same Patient [17]

Scan		Volume (mm3)	Laplacian BCI (mm)	EEDT BCI (mm)
Patellar	(1)	2717	2.32 (0.94) (4.34)	2.16 (0.97) (4.22)
	(2)	2684	2.34 (0.96) (4.49)	2.17 (0.99) (4.25)
	(3)	3093	2.47 (0.88) (4.32)	2.13 (0.99) (4.09)
	(4)	2808	2.30 (0.95) (4.42)	2.12 (0.99) (4.12)
Tibial	(1)	4471	1.68 (0.83) (4.18)	1.58 (0.80) (3.96)
	(2)	4395	1.72 (0.80) (4.05)	1.62 (0.78) (3.98)
	(3)	4225	1.77 (0.82) (4.11)	1.67 (0.79) (3.99)
	(4)	4323	1.74 (0.86) (4.41)	1.63 (0.83) (4.15)
Femoral	(1)	10277	1.87 (0.69) (4.01)	1.80 (0.70) (3.96)
	(2)	10246	1.86 (0.69) (4.08)	1.78 (0.70) (4.05)
	(3)	10644	1.90 (0.69) (4.05)	1.82 (0.71) (3.99)
	(4)	10634	1.87 (0.69) (4.12)	1.79 (0.70) (4.15)

Although our scheme was designed for FS SPGR images, it can be applied to MRs that exhibit similar anatomical appearance (Fig. 8). This and the consistency of the quantitative analysis was further evaluated by scanning three volunteers (A to C) using weDESS and MEDIC MR sequences, with one volunteer (A) scanned twice (two weeks apart). The MEDIC scans for volunteer C and one of the scans for volunteer A were acquired with in-plane resolution 0.3 × 0.3 mm, all other scans were acquired with in-plane resolution 0.41 × 0.41 mm. All scans were automatically segmented and quantitative measures calculated (Table IV).

Fig. 8.

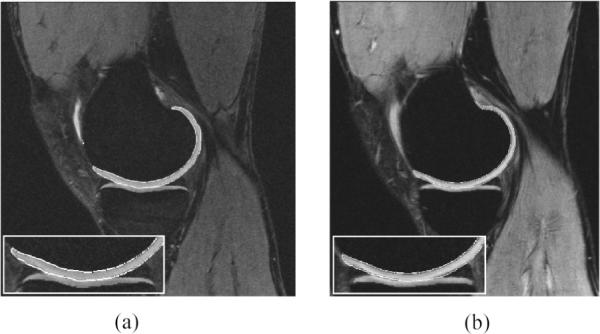
Automatic segmentation results for the (a) weDESS and (b) MEDIC MR images of volunteer B visualized at approximately the same anatomical location. Note: Areas of interest used 1.5 × zoom.

TABLE IV.

Cartilage Quantitative Analysis Using Volume and Mean (STD) Laplacian Thickness for Wedess and Medic Images of the Three Volunteers (A to C)

	weDESS		MEDIC
Scan	Volume	Laplacian	Volume	Laplacian
Patellar (Al)	4493	3.45 (1.48)	4734	3.67 (1.58)
Patellar (A2)	4679	3.54 (1.53)	4924	3.66 (1.62)
Patellar (B)	4182	3.45 (0.98)	3971	3.35 (1.00)
Patellar (C)	3031	2.57 (1.53)	3486	2.56 (1.49)
Tibial (Al)	4264	1.94 (0.68)	4909	2.23 (0.86)
Tibial (A2)	5023	2.12 (0.90)	5454	2.08 (0.98)
Tibial (B)	6473	2.35 (0.81)	5966	2.38 (0.74)
Tibial (C)	5759	2.04 (1.01)	4765	1.77 (0.97)
Femoral (Al)	13422	2.42 (0.89)	13490	2.52 (0.98)
Femoral (A2)	13219	2.44 (0.94)	13590	2.40 (0.93)
Femoral (B)	14929	2.61 (0.87)	13523	2.48 (0.88)
Femoral (C)	13947	2.28 (0.87)	12130	2.15 (0.89)

IV. CONCLUSION AND FUTURE WORK

Quantitative analysis of healthy cartilage joints allows a greater understanding of the natural variation, influence of demographics and physiological effects on cartilage morphology and physiology. In this paper we have presented a fully automatic segmentation scheme that obtains cartilage segmentation results for FS SPGR images of nonpathological knees that are comparable or superior to other published automatic algorithms. This is particularly true for the patellar and tibial cartilages, although, the tissue classifier was found to obtain slightly better results for the femoral cartilage. The decrease in accuracy of all algorithms on lower resolution images (with decreased SNR and CNR) indicate fully automated cartilage segmentation requires MR images with as high resolution, SNR and CNR as possible.

Our scheme is based on using a segmentation hierarchy where easier objects initialize and constrain the segmentation of harder objects. It uses trained information in the form of bone shape and cartilage thickness, with patient specific tissue properties used instead of trained appearance models as these varied too much between patients, position and scans. The advantage of our scheme over previous approaches is that we utilize a very good automatic segmentation of the bone to extract the BCIs, from which local appearance and edge information is used to perform the segmentation while being constrained by global tissue appearance and trained thickness constraints. This allows us to obtain highly accurate segmentations of each cartilage in the knee, where the average error is less than half the in-plane spacing. The use of the Laplacian thickness measure to perform quantitative measure was found to be precise, however, on the non pathological knees examined, it was not found to provide any advantages over other techniques. In the future we intend to investigate whether it may be more sensitive to pathological changes like lesions.

The primary limitation of this paper is that it has only been validated on nonpathological knees, and may require changes to adapt this to OA subjects. That being said, there is still significant clinical and research interest in the segmentation of healthy cartilage tissue. We also believe the use of a larger cohort with more specific demographic (age and sex), acquired at high field strength (3 T) with homogeneous MR parameters will further improve the segmentation results.