A Simple and Robust Method for Partially Matched Samples Using the P-Values Pooling Approach

Abstract

This paper focuses on statistical analyses in scenarios where some samples from the matched pairs design are missing, resulting in partially matched samples. Motivated by the idea of meta-analysis, we recast the partially matched samples as coming from two experimental designs, and propose a simple yet robust approach based on the weighted Z-test to integrate the p-values computed from these two designs. We show that the proposed approach achieves better operating characteristics in simulations and a case study, compared to existing methods for partially matched samples.

1. Introduction

The last few decades have seen a revolution of high-throughout technologies including microarrays and next generation sequencing instruments in genomics. These advancements have spurred rapid biomarker discovery and personalized medicine approach in multiple diseases, in particular cancer research. A common experimental design in profiling genetic and epigenetic markers includes collecting n tumor and matched normal tissues. Such tumor/matched normal sample is an example of matched pairs design and allows for the control of patient variability and unmeasured confounders. The matched normal samples can be adjacent normal tissues from the same patient, or tissues from normal patients matched by demographic attributes. Alternatively, matched pair designs can arise from comparison of two different treatments (or pre/post treatment) within the same subjects, e.g., profiling gene expression of cancer cell lines before and after drug treatment or in response to stimuli. In both cases, the inherent matching structure results in correlation between the matched pairs. For ease of exposition, we will use the tumor/matched normal example hereafter.

In an ideal case, one would expect a total of 2n samples. However in practice, circumstances such as RNA sample degradation, failed samples or insufficient resources could result in a subset of patients missing in either the tumor or matched normal biomarker profiles. In other words, n₁(< n) patients have both the tumor and matched normal profiles, whereas n₂ and n₃ patients have only tumor or normal samples, respectively. We call this partially matched samples.

A wide variety of softwares and bioinformatics tools are available for analyzing these high-throughput microarray or sequencing data. However, to our knowledge, commonly used softwares such as SAM (Tusher et al. [1]) do not deal with partially matched samples. The users are often left with the choice of either only analyzing the n₁ samples using paired-sample methods, or by treating n₁ + n₂ tumor and n₁ + n₃ normal as two independent samples. Both approaches are sub-optimal; in the paired-sample analysis, only a subset of data is utilized, whereas in the two-sample approach, the inherent patient matched pair correlation structure is ignored. Partially matched samples in microarray studies were considered in Kim et al. [2] where they proposed a modified t-statistic in microarray studies. Closely related approaches are the corrected Z-test by Looney and Jones [3] and maximum likelihood based tests by Lin and Stivers [4], Ekbohm [5] for comparing two normal means.

This paper focuses on statistical analysis strategies for partially matched samples. Our approach is motivated by high-throughput experiments such as microarrays and next generation sequencing which profile thousands of genomic biomarkers. Unlike Lin and Stivers [4], Ekbohm [5], Kim et al. [2], Looney and Jones [3] which were developed by assuming that the data can be approximated with a Gaussian distribution, we borrow the idea from meta-analysis framework and consider an alternative approach for analyzing partially matched sample based on p-values pooling (Hedges and Olkin [6]). In many circumstances, such an approach is more appealing and robust, which can be applied to both continuous and discrete data, as well as parametric and non-parametric statistical tests. In contrast, modified test statistics of Lin and Stivers [4], Ekbohm [5], Kim et al. [2], Looney and Jones [3] may not be valid for non-gaussian genomic data of small or moderate sizes where t- or Z-tests are not appropriate. In such cases, robust non-parametric approaches such as the Wilcoxon signed-rank or the Mann-Whitney may be more appropriate.

This paper is organized as follows. In Section 2, we briefly describe the different types of p-values pooling strategies. In Section 3, we design simulation studies to compare the different strategies for handling partially matched samples, followed by a case study of a publicly available microRNA expression data in colon adenocarcinoma (Schetter et al. [7]) in Section 4. We conclude with a discussion in Section 5.

2. Methods

Partially matched samples can be viewed as data generated from two experimental designs; (i) n₁ matched pairs or repeated measures, and (ii) independent groups with n₂ and n₃ per group, where both designs intend to estimate the same parameter. This observation allows us to recast the problem within a meta-analysis framework, where the goal is to combine the results across the two experiments. A vast literature in meta-analysis is available, and the two popular approaches are the p-value and effect size pooling. For our motivating example based on high-throughput genomic biomarkers profiling, the p-values pooling approach has several advantages over the effect size pooling. The p-values are more readily available as most of the popular bioinformatics tools for analyzing such data often report the p-values to reflect the statistical significance of each biomarker using either the repeated measures or independent groups analysis. In addition, the effect size combination methods require proper transformation and standardization into a common metric which is not straightforward for the two different research designs here (Morris and DeShon [8]) and have been shown to be more conservative (Marot et al. [9]).

Commonly used methods for p-values pooling in meta-analysis include the inverse normal and Fisher’s methods. A recent paper by Zaykin [10] provides an excellent overview of the different p-values pooling strategies in meta-analysis. The main idea of the p-values pooling approach is to transform each p-value to a random variable which follows a tractable sum (or weighted sum) distribution under the assumption that each p-value is uniformly distributed under the null hypothesis. For instance, Fisher’s method is based on the chi-squared distribution and uses the property that $-2{\sum }_{k=1}^K\log (\mathrm{p}­{\mathrm{value}}_k)~{\chi }_{2K}^2$. In contrast, the inverse normal approach is based on Φ⁻¹ (1 − p-value_k) ~ N (0, 1), where Φ is the standard Gaussian cumulative distribution function. Whitlock [11], Zaykin [10] showed that the weighted Z-test is advantageous over Fisher’s method for combining p-values, including its flexibility to be easily extended to more complicated scenarios such as correlated studies. In addition, Fisher’s method treats the large and small p-values asymmetrically which could potentially introduce bias and may not be desirable as pointed out in Whitlock [11].

Within the context of the partially matched samples problem, the weighted Z-test can be adapted as follows. Let p_1i be the p-value for biomarker i computed from the n₁ paired samples, and p_2i be the corresponding p-value computed from the independent groups with n₂ and n₃ samples per group. For instance, in microarray gene expression data, p_1i and p_2i can be computed from the paired sample and two sample t-tests, respectively or the SAM analysis with the “Paired” and “Two Class” option, respectively. The combined p-value by the weighted Z-test introduced by Liptak [12] is

$$p_{\mathit{ci}}=1-\mathrm{\Phi }\left(\frac{w_1{Z}_{1i}+w_2{Z}_{2i}}{\sqrt{w_1^2+w_2^2}}\right)$$ (1)

where Z_ai = Φ⁻¹ (1 − p_ai), a = 1, 2 and w_a’s are the corresponding weights. Several choices of weights have been proposed in the literature (Liptak [12], Zaykin [10]). In the absence of additional information, Liptak [12] suggested setting the weights to be the square root of the sample sizes. Won et al. [13] extended the weighted Z-test approach for combining p-values by showing that the optimal weights are given by the expected effect sizes. This method relies on a strong assumption as the information on the effect sizes is usually unavailable. Therefore, Zaykin [10] proposed a more feasible weighting by either the inverse of the estimated standard error or the square root of the sample sizes in practice.

Note that the p-values pooling is only meaningful if p_1i and p_2i are computed from one-sided hypothesis tests to avoid directional conflict. Two-sided combined p-values can be obtained with a slight modification (Zaykin [10]). Let p_1i and p_2i be the one-sided p-values for the same alternative (e.g., “greater”) hypothesis and p_ci be the combined one-sided p-value from equation (1). For instance, in the context of microarray gene expression, this corresponds to computing a one-sided p-value for either up-regulation or down-regulation. The two-sided p-value is then obtained via

$$p_{\mathit{ci}}^{\ast }=\{\begin{array}{ll}2p_{\mathit{ci}},& \mathrm{if}{p}_{\mathit{ci}}<1/2\\ 2(1-p_{\mathit{ci}}),& \mathrm{otherwise}\end{array}$$ (2)

(See Appendix for further justification).

Next, we describe the modified t-statistic of Kim et al. [2] and corrected Z-test of Looney and Jones [3]. The modified t-statistic t₃ of Kim et al. [2] takes the form

$$t_3=\frac{n_1\overline{D}+n_H(\overline{T}-\overline{N})}{\sqrt{n_1{S}_D^2+n_H^2(S_N^2/n_3+S_T^2/n_2)}}$$ (3)

where D̄ is the mean difference of the n₁ paired samples, T̄ and N̄ are the mean tumor and normal for the n₂ and n₃ unmatched samples, respectively. S_D, S_T and S_N are the corresponding sample standard deviations, and n_H is the harmonic mean of n₂ and n₃. The null distribution of t₃ is approximated with a standard Gaussian distribution. On the other hand, the corrected Z-test Z_corr of Looney and Jones [3] is based on a modified variance estimation of the standard Z-test by accounting for the correlation among the n₁ matched pairs,

$$Z_{\mathit{corr}}=\frac{{\overline{T}}^{\ast }-{\overline{N}}^{\ast }}{\sqrt{S_T^{\ast 2}/(n_1+n_2)+S_N^{\ast 2}/(n_1+n_3)-2n_1{S}_{T{N}_1}/(n_1+n_2)(n_1+n_3)}}$$ (4)

where T̄* and N̄* are the mean tumor and normal for the n₁ + n₂ and n₁ + n₃ matched and unmatched samples combined, respectively. $S_T^{\ast }$ and $S_N^{\ast }$ are the corresponding sample standard deviations, and S_TN1 is the sample covariance of the n₁ paired samples. Z_corr reduces to paired sample or two-sample Z-test when n₂ = n₃ = 0 or n₁ = 0, respectively.

In addition to the two approaches above, closely related approaches for dealing with partially matched samples include the work of Lin and Stivers [4] and Ekbohm [5]. The authors proposed several procedures based on a modified maximum likelihood estimator (MLE) and simple mean difference for testing the equality of two correlated means with incomplete data under the bivariate Gaussian assumption. The authors compared the performance of the procedures under both homo- and heteroscedasticity, and varying degrees of correlation between the responses. Here, we describe the maximum likelihood based tests as recommended by Ekbohm [5] which were shown to perform well when the correlation is medium or large, or unknown. The MLE based test statistic under heteroscedasticity was proposed by Lin and Stivers [4] and takes the form

$$Z_{\mathit{LS}}=\frac{\{f({\overline{T}}_1-\overline{T})-g({\overline{N}}_1-\overline{N})+\overline{T}-\overline{N}\}}{\sqrt{V_1}}$$ (5)

where

$$\begin{array}{lll}{V}_1& =& \frac{\{f^2/n_1+{(1-f)}^2/n_2\}{S}_{T_1}^2(n_1-1)+\{g^2/n_1+{(1-g)}^2/n_3\}{S}_{N_1}^2(n_1-1)-2\mathit{f\; g}{S}_{T{N}_1}(n_1-1)/n_1}{(n_1-1)}\\ f& =& n_1(n_1+n_3+n_2{S}_{T{N}_1}/S_{T_1}^2){\{(n_1+n_2)(n_1+n_3)-n_2{n}_3{r}^2\}}^{-1}\\ g& =& n_1(n_1+n_2+n_3{S}_{T{N}_1}/S_{N_1}^2){\{(n_1+n_2)(n_1+n_3)-n_2{n}_3{r}^2\}}^{-1}\\ r& =& S_{T{N}_1}/S_{T_1}{S}_{N_1}\end{array}$$

T̄₁ and N̄₁ are the mean tumor and normal for the n₁ paired samples. S_T1 and S_N1 are the corresponding sample standard deviations, respectively. Under the null hypothesis, Z_LS is approximately distributed as t with n₁ degrees of freedom.

On the other hand, when the variances of tumor and normal are equal, Ekbohm [5] suggested the following MLE based test statistic

$$Z_E=\frac{\{f^{\ast }({\overline{T}}_1-\overline{T})-g^{\ast }({\overline{N}}_1-\overline{N})+\overline{T}-\overline{N}\}}{\sqrt{V_1^{\ast }}}$$ (6)

where

$$\begin{array}{ccc}{V}_1^{\ast }& =& {\widehat{\sigma }}^2\left\{\frac{2n_1(1-r)+(n_2+n_3)(1-r^2)}{(n_1+n_2)(n_1+n_3)-n_2{n}_3{r}^2}\right\}\\ {\widehat{\sigma }}^2& =& \frac{S_{T_1}^2(n_1-1)+S_{N_1}^2(n_1-1)+(1+r^2)[S_T^2(n_2-1)+S_N^2(n_3-1)]}{2(n_1-1)+(1+r^2)(n_2+n_3-2)}\\ f^{\ast }& =& n_1(n_1+n_3+n_{2}r){\{(n_1+n_2)(n_1+n_3)-n_2{n}_3{r}^2\}}^{-1}\\ g^{\ast }& =& n_1(n_1+n_2+n_{3}r){\{(n_1+n_2)(n_1+n_3)-n_2{n}_3{r}^2\}}^{-1}\end{array}$$

Ekbohm [5] further showed that Z_E can be approximated by t distribution with n₁ degrees of freedom.

Nevertheless, as mentioned in Section 1, modified test statistics are usually not straightforward in cases where the Gaussian or t-distribution are not suitable. For instance, combining the non-parametric Wilcoxon signed-rank and the Mann-Whitney statistics for discrete or ranked data. In contrast, p-values pooling is easy to implement and can be applied regardless of the types of statistical tests chosen for the paired and independent samples. This enables users to select their preferred choice of analysis from the vast bionformatics tools developed for the matched and unmatched samples separately, followed by pooling the p-values of the two subsets of samples.

In the next section, we carry out some simulations to evaluate the performance of the different approaches. As our motivating example is based on high-throughput microarray data profiling multiple genes, our simulation setup evaluates the performance of the different strategies in terms of false discovery rate (FDR) control to account for multiple testings, instead of single test type I error rate and power approach of Lin and Stivers [4], Ekbohm [5], Looney and Jones [3].

3. Simulation

We generate n paired sample measurements (T_ij, N_ij) of a biomarker i for the tumor and matched normal groups from bivariate Gaussian, respectively, where,

$$\left(\begin{array}{c}{T}_{\mathit{ij}}\\ N_{\mathit{ij}}\end{array}\right)~N\left(\left(\begin{array}{c}{\mu }_T\\ {\mu }_N\end{array}\right),\left(\begin{array}{cc}{\sigma }_T^2& \rho {\sigma }_T{\sigma }_N\\ \rho {\sigma }_T{\sigma }_N& {\sigma }_N^2\end{array}\right)\right)$$

We consider n = 20, 50 and set μ_T = μ_N = 0, ρ = 0.2, 0.5, 0.7 to capture the different degrees of correlation between the paired samples. When ρ = 0, the tumor and normal group are independent. We also consider both the homo- and heteroscedastic cases, where ${\sigma }_T^2={\sigma }_N^2=1$ under homoscedasticity and ${\sigma }_T^2=2{\sigma }_N^2=2$ under heteroscedasticity. In addition, we vary n₁, n₂ and n₃ to represent the different combinations of missing matched samples. In an ideal case where all the data is observed, i.e., n pairs of tumor and matched normal observations, the proper statistical test is the paired sample t-test on all the 2n observations. We call this the oracle test. We compare the performance of the different methods for the partially matched samples, namely (i) modified t-statistic of Kim et al. [2], (ii) corrected Z-test of Looney and Jones [3], (iii) MLE based test of Ekbohm [5] under homoscedasticity, (iv) MLE based test of Lin and Stivers [4] under heteroscedasticity (v) paired t-test on the n₁ matched samples only, (vi) independent two-sample t-test on n₁ + n₂ and n₁ + n₃ observations in tumor and normal group, respectively by ignoring the inherent pairing structure, and (vii) the proposed weighted Z-test combination. We refer to methods (i)-(iv) collectively as the modified test statistics approaches. For the proposed weighted Z-test combination, we consider weighting by the (1) square root of samples sizes and (2) inverse of the estimated standard error under both the homo- (pooled estimate) and heteroscedasticity assumptions. We generate data for 1000 biomarkers and compare Lin’s concordance correlation coefficient, r_c (Lin [14]) of the estimated p-values of each method to the p-values from the oracle test. The aim is to assess the reliability and robustness of each method in dealing with incomplete data against the test performed on complete data. The whole setup is replicated by 1000 times. Figures 1 and 2 plot the average r_c of each method across different (n₁, n₂, n₃) and correlation ρ between the tumor and normal group under homoscedasticity and heteroscedasticity bivariate Gaussian simulation setup, respectively. A superior method will exhibit higher concordance with the oracle test. At low correlation, all the methods have comparable performance except for the paired t-test on the n₁ matched samples only. The MLE based tests have the best performance at high correlation structure under the heteroscedasticity simulation setup (Figure 2), and the proposed weighted Z-tests follow closely.

Figure 1.

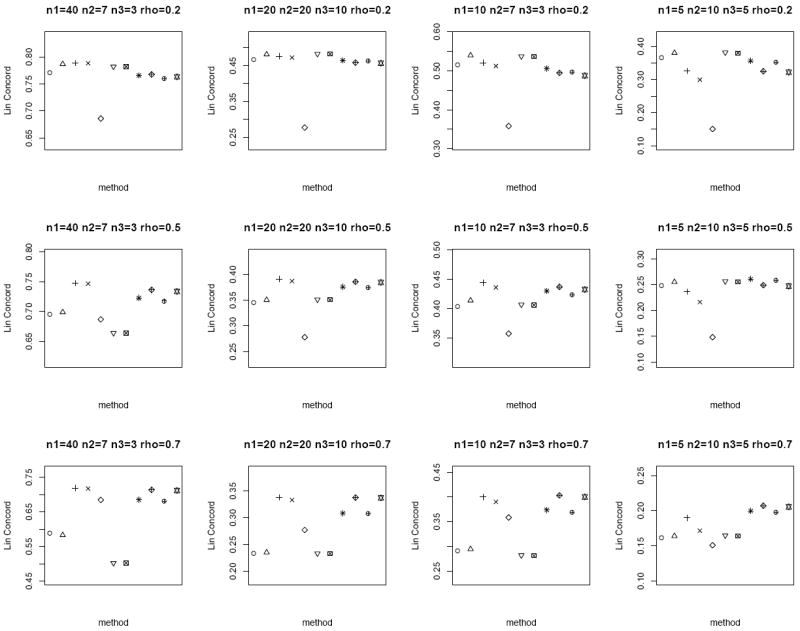
Average r_c of the different methods under the homoscedastic bivariate Gaussian simulation setup. Each panel corresponds to a different (n₁, n₂, n₃, ρ) combination. The plotting symbols (from left to right) correspond to ○:modified t-statistic, Δ:corrected Z-test, +:MLE based test of Ekbohm [5], ×:MLE based test of Lin and Stivers [4], ◇:paired t-test on the n₁ matched samples only, ▽:two-sample t-test on n₁ + n₂ and n₁ + n₃ observations under the homoscedasticity assumption, ⊠:two-sample t-test on n₁ + n₂ and n₁ + n₃ observations under the heteroscedasticity assumption, ✳:weighted Z-test using square root of sample sizes weighting under the homoscedasticity assumption, :weighted Z-test using inverse of estimated standard error weighting under the homoscedasticity assumption, ⊕:weighted Z-test using square root of sample sizes weighting under the heteroscedasticity assumption, ✡:weighted Z-test using inverse of estimated standard error weighting under the heteroscedasticity assumption. The estimated standard errors of average r_c are in the order of < 10⁻³.

Figure 2.

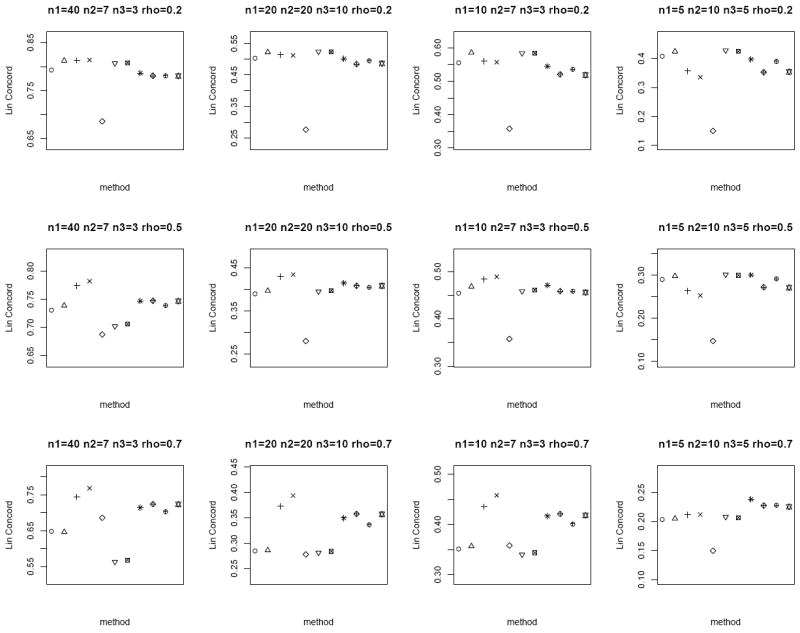
Average r_c of the different methods under the heteroscedastic bivariate Gaussian simulation setup. Each panel corresponds to a different (n₁, n₂, n₃, ρ) combination. The plotting symbols (from left to right) correspond to ○:modified t-statistic, Δ:corrected Z-test, +:MLE based test of Ekbohm [5], ×:MLE based test of Lin and Stivers [4], ◇:paired t-test on the n₁ matched samples only, ▽:two-sample t-test on n₁ + n₂ and n₁ + n₃ observations under the homoscedasticity assumption, ⊠:two-sample t-test on n₁ + n₂ and n₁ + n₃ observations under the heteroscedasticity assumption, ✳:weighted Z-test using square root of sample sizes weighting under the homoscedasticity assumption, :weighted Z-test using inverse of estimated standard error weighting under the homoscedasticity assumption, ⊕:weighted Z-test using square root of sample sizes weighting under the heteroscedasticity assumption, ✡:weighted Z-test using inverse of estimated standard error weighting under the heteroscedasticity assumption. The estimated standard errors of average r_c are in the order of < 10⁻³.

In the next scenario, we repeat the simulations by generating n paired measurements for 1000 biomarkers from bivariate Gaussian. We set a randomly selected 1% of the biomarkers to have true mean difference between the tumor and normal group, where μ_T ~ N (0, 1) and μ_N = 0. In addition, we randomly sample ρ ~ U (0, 1) and vary n₁, n₂, and n₃. For each method, the p-values are computed and further adjusted using the Benjamini and Hochberg [15] False Discovery Rate (FDR) control to account for multiple comparisons. Statistically significant differentially expressed biomarkers are declared at nominal FDR of 0.1. We evaluate the performance of the competing methods by the empirical FDR and False Non-discovery Rate (FNR). FNR is an analog of Type II error rate, and is loosely the proportion of true positive among the tests which are not declared to be statistically significant. In addition, we also compare the sensitivity and specificity of the lists of 1000 biomarkers ranked ordered by each method via the area under receiver operating characteristics curve (ROC). We expect the superior method to exhibit smaller FNR and larger ROC, in addition to controlling the FDR at 0.1. From Figure 3 (homoscedastic bivariate Gaussian) and Figure 4 (heteroscedastic bivariate Gaussian), the four methods based on modified test-statistics have inflated empirical FDR. The proposed weighted Z-tests using square root of sample size weighting show valid FDR control, i.e., their empirical FDR is bounded above by the nominal FDR. A slight inflation of FDR is observed in a few cases for weighting based on the inverse of the estimated standard errors. The two-sample approach by ignoring the inherent correlation between the two groups has larger FNR, and therefore is less powerful in general. Among the other methods which provide valid FDR control (excluding the oracle test), the weighted Z-test approach achieves the lowest FNR and highest ROC throughout.

Figure 3.

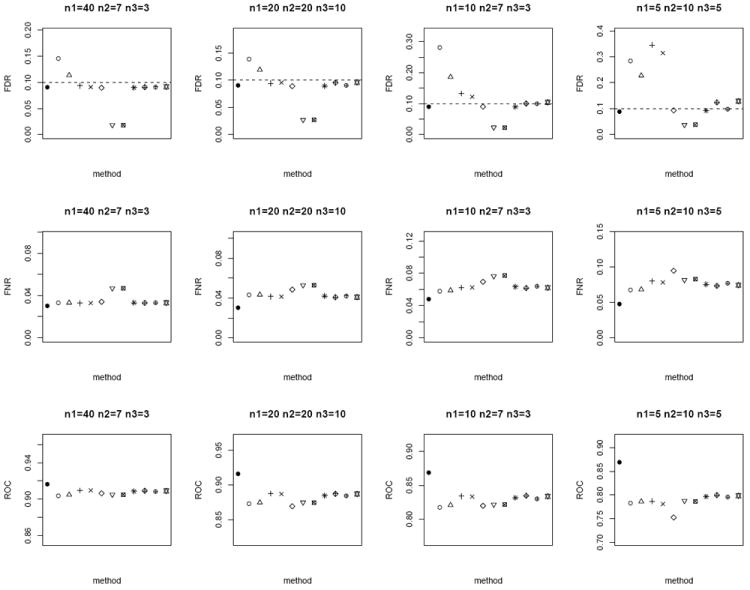
Average FDR (top row), FNR (middle row) and ROC (bottom row) of the different methods under the homoscedastic bivariate Gaussian simulation setup. Dotted horizontal lines in the top row correspond to the nominal FDR level of 0.1. Each panel corresponds to a different (n₁, n₂, n₃) combination. The plotting symbols (from left to right) correspond to ●:oracle test, ○:modified t-statistic, Δ:corrected Z-test, +:MLE based test of Ekbohm [5], ×:MLE based test of Lin and Stivers [4], ◇:paired t-test on the n₁ matched samples only, ▽:two-sample t-test on n₁ + n₂ and n₁ + n₃ observations under the homoscedasticity assumption, ⊠:two-sample t-test on n₁ + n₂ and n₁ + n₃ observations under the heteroscedasticity assumption, ✳:weighted Z-test using square root of sample sizes weighting under the homoscedasticity assumption, :weighted Z-test using inverse of estimated standard error weighting under the homoscedasticity assumption, ⊕:weighted Z-test using square root of sample sizes weighting under the heteroscedasticity assumption, ✡:weighted Z-test using inverse of estimated standard error weighting under the heteroscedasticity assumption. The estimated standard errors of all the statistical measurements (FDR, FNR, ROC) are in the order of < 10⁻³.

Figure 4.

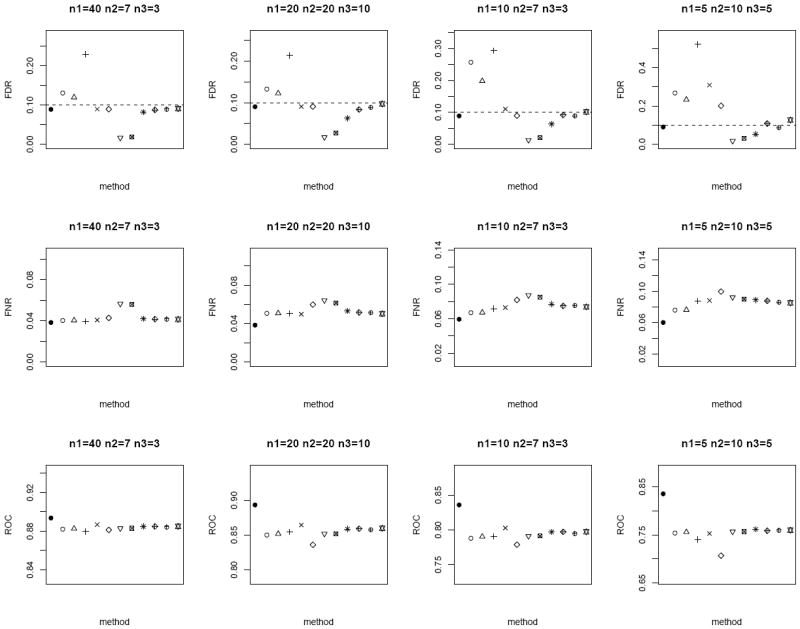
Average FDR (top row), FNR (middle row) and ROC (bottom row) of the different methods under the heteroscedastic bivariate Gaussian simulation setup. Dotted horizontal lines in the top row correspond to the nominal FDR level of 0.1. Each panel corresponds to a different (n₁, n₂, n₃) combination. The plotting symbols (from left to right) correspond to ●:oracle test, ○ :modified t-statistic, Δ:corrected Z-test, +:MLE based test of Ekbohm [5], ×:MLE based test of Lin and Stivers [4], ◇:paired t-test on the n₁ matched samples only, ▽:two-sample t-test on n₁ + n₂ and n₁ + n₃ observations under the homoscedasticity assumption, ⊠:two-sample t-test on n₁ + n₂ and n₁ + n₃ observations under the heteroscedasticity assumption, ✳:weighted Z-test using square root of sample sizes weighting under the homoscedasticity assumption, :weighted Z-test using inverse of estimated standard error weighting under the homoscedasticity assumption, ⊕:weighted Z-test using square root of sample sizes weighting under the heteroscedasticity assumption, ✡:weighted Z-test using inverse of estimated standard error weighting under the heteroscedasticity assumption. The estimated standard errors of all the statistical measurements (FDR, FNR, ROC) are in the order of < 10⁻³.

In the next scenario, we generate n paired sample measurements (T_ij, N_ij) for a biomarker i, i = 1,…, 1000 for the tumor and matched normal groups from bivariate Gamma as follows. Let X_ij, Y_ij, Z_ij be independent Gamma with shape parameters a_X, a_Y, a_Z and common scale parameter b. We set T_ij = X_ij + Z_ij and N_ij = Y_ij + Z_ij, where E(T_ij) = b(a_X + a_Z), E(N_ij) = b(a_Y + a_Z) and Cov(T_ij, N_ij) = b² a_Z. We set a_X = a_Y = 0.3, b = 2 and vary a_Z so that the correlation ρ(T_ij, N_ij) = 0.2, 0.5, 0.7, respectively, similar to the bivariate Gaussian setup above. We define the oracle test as the Wilcoxon signed-rank test on the difference T_ij − N_ij, and choose the Mann-Whitney test as the two-sample test by treating n₁ + n₂ tumor and n₁ + n₃ normal as independent groups. For the proposed weighted Z-test combination, we replace p_1i and p_2i with the p-values computed from the Wilcoxon signed-rank test on the difference T_ij − N_ij among the n₁ paired samples and the Mann-Whitney test on the independent groups with n₂ and n₃ samples per group, respectively. Similar to the bivariate Gaussian case above, we compare r_c of the computed p-values of the different methods to the p-values of the oracle test. Figure 5 shows that the weighted Z-test p-value pooling approach attains the largest r_c, compared to other methods. Given the skewed nature of the simulated data, the modified test statistics approaches (Lin and Stivers [4],Ekbohm [5],Kim et al. [2],Looney and Jones [3]) deviate from the oracle test to a larger extent.

Figure 5.

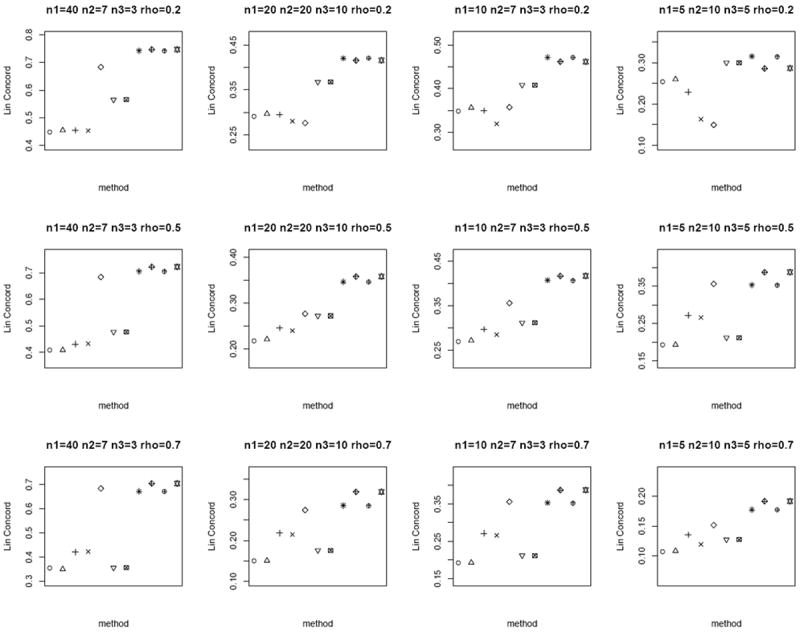
Average r_c of the different methods under the bivariate Gamma simulation setup. Each panel corresponds to a different (n₁, n₂, n₃, ρ) combination. The plotting symbols (from left to right) correspond to ○:modified t-statistic, Δ:corrected Z-test, +:MLE based test of Ekbohm [5], ×:MLE based test of Lin and Stivers [4], ◇:Wilcoxon signed-rank test on the n₁ matched samples only, ▽:Mann-Whitney test on n₁ + n₂ and n₁ + n₃ observations under the homoscedasticity assumption, ⊠:Mann-Whitney test on n₁ + n₂ and n₁ + n₃ observations under the heteroscedasticity assumption, ✳:weighted Z-test using square root of sample sizes weighting under the homoscedasticity assumption, :weighted Z-test using inverse of estimated standard error weighting under the homoscedasticity assumption, ⊕:weighted Z-test using square root of sample sizes weighting under the heteroscedasticity assumption, ✡:weighted Z-test using inverse of estimated standard error weighting under the heteroscedasticity assumption. Note that the results of the Mann-Whitney test and the weighted Z-test using square root of sample sizes weighting under heteroscedasticity are identical to their respective results under homoscedasticity (since the underlying assumption of the Mann-Whitney test is homoscedasticity). We keep these results in the plot for consistency and ease of comparison with earlier figures. The estimated standard errors of average r_c are in the order of < 10⁻³.

Similar to the bivariate Gaussian simulation setup, we also spike in 1% of biomarkers with true mean difference in the bivariate Gamma simulation, and compare the FDR, FNR and ROC of the different methods in Figure 6. Compared to the bivariate Gaussian case, the non-parametric Wilcoxon signed-rank test and Mann-Whitney tests yield larger FNR and smaller ROC overall. All the methods except for the modified t-statistic and MLE based test of Lin and Stivers [4] control the nominal FDR of 0.1 for n = 50. For n = 20, the modified test statistics approaches exhibit large degree of FDR inflation. In addition, our proposed weighted Z-test achieves the best performance overall (excluding the oracle test) with the smallest FNR (i.e., most powerful), as well as the largest ROC among the methods which control the FDR. These simulation results also suggest that weighting by the square root of sample size under the heteroscedascticity assumption is robust and performs well in various scenarios.

Figure 6.

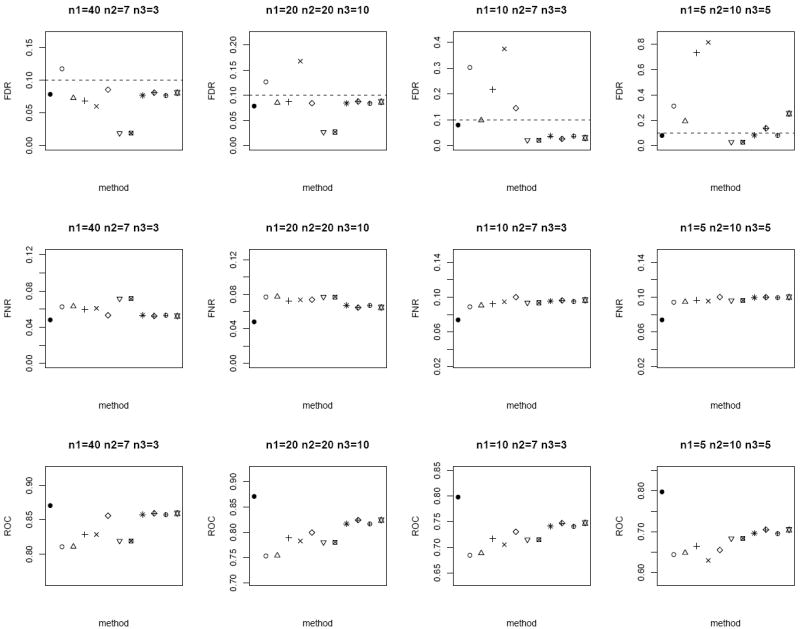
Average FDR (top row), FNR (middle row) and ROC (bottom row) of the different methods under the bivariate Gamma simulation setup. Dotted horizontal lines in the top row correspond to the nominal FDR level of 0.1. Each panel corresponds to a different (n₁, n₂, n₃) combination. The plotting symbols (from left to right) correspond to ●:oracle test, ○:modified t-statistic, Δ:corrected Z-test, +:MLE based test of Ekbohm [5], ×:MLE based test of Lin and Stivers [4], ◇:Wilcoxon signed-rank test on the n₁ matched samples only, ▽:Mann-Whitney test on n₁ + n₂ and n₁ + n₃ observations under the homoscedasticity assumption, ⊠:Mann-Whitney test on n₁ + n₂ and n₁ + n₃ observations under the heteroscedasticity assumption, ✳:weighted Z-test using square root of sample sizes weighting under the homoscedasticity assumption, :weighted Z-test using inverse of estimated standard error weighting under the homoscedasticity assumption, ⊕:weighted Z-test using square root of sample sizes weighting under the heteroscedasticity assumption, ✡:weighted Z-test using inverse of estimated standard error weighting under the heteroscedasticity assumption. Note that the results of the Mann-Whitney test and the weighted Z-test using square root of sample sizes weighting under heteroscedasticity are identical to their respective results under homoscedasticity (since the underlying assumption of the Mann-Whitney test is homoscedasticity). We keep these results in the plot for consistency and ease of comparison with earlier figures. The estimated standard errors of all the statistical measurements (FDR, FNR, ROC) are in the order of < 10⁻³.

4. Case Study

In this section, we compare the different methods using a publicly available microRNA expression data of Schetter et al. [7] which aimed to identify differentially expressed microRNAs in colon adenocarcinoma. The loess normalized dataset is downloaded from the Gene Expresion Omnibus (accession number GSE7828). After further preprocessing to remove probes with more than 20% missing values as outlined in Schetter et al. [7], as well as control probes, we have a total of 229 microRNAs in 84 colon adenocarcinomas and 84 matching non-tumorous tissue. n₁ out of 84 matched pairs are randomly selected to be the observed complete matched samples. For the remaining 84 − n₁ pairs, half are set to be missing in the colon adenocarcinomas (n₂), and the other half to be missing in non-tumorous tissue samples (n₃). We vary n₁ between 5 to 70 to capture the high to low degree of missingness in matching samples. The random subsampling is repeated 1000 times for each n₁.

In an ideal case where all the 84 matched pairs are observed, we apply the paired sample t-test similar to Schetter et al. [7] and refer to this as the oracle test. Similar to the simulation studies in Section 3, we compute the average Lin’s concordance correlation coefficient r_c for the seven competing methods, namely (i) modified t-statistic of Kim et al. [2], (ii) corrected Z-test of Looney and Jones [3], (iii) MLE based test of Ekbohm [5] under homoscedasticity, (iv) MLE based test of Lin and Stivers [4] under heteroscedasticity (v) paired t-test on the n₁ matched samples only, (vi) independent two-sample t-test on n₁ + n₂ and n₁ + n₃ observations in colon adenocarcinomas and non-tumorous tissue group, respectively by ignoring the inherent pairing structure, and (vii) the proposed weighted Z-test using square root of sample sizes weighting under heteroscedasticity. The results are summarized in Table 1(A). Since the ground truth of differentially expressed microRNAs is unknown in the real data, we create a gold standard set by selecting the microRNAs identified by the oracle test at FDR of 0.1 to be the true positive set. We compare the empirical FDR and FNR of the different methods in Table 1(B) and 1(C), respectively. The modified test statistics approaches and the weighted Z-test achieve comparable performance under the Gaussian assumption, and exhibit inflated FDR (MLE based tests) for the extreme case where n₁ = 5.

Table 1.

(A) Lin’s concordance correlation coefficient, r_c, (B) empirical FDR and (C) empirical FNR of each method compared to the oracle test under the Gaussian assumption averaged over 1000 replications. The standard error of the estimate (×10⁻³) is given in the parentheses. Paired sample t-test on the complete 84 matched pairs is used as the oracle test.

(A) Lin’s concordance correlation coefficient, rc
n1	Modified t	Corrected Z	MLEE	MLELS	Paired only	Two-sample	Weighted Z
5	0.375 (3.36)	0.375 (3.37)	0.346 (3.46)	0.334 (3.41)	0.092 (3.45)	0.37 (3.28)	0.381 (3.36)
10	0.409 (3.37)	0.41 (3.33)	0.423 (3.51)	0.418 (3.53)	0.181 (3.98)	0.401 (3.2)	0.426 (3.42)
20	0.479 (3.53)	0.482 (3.47)	0.526 (3.58)	0.524 (3.59)	0.347 (4.55)	0.463 (3.23)	0.51 (3.6)
30	0.564 (3.06)	0.568 (2.99)	0.621 (3.2)	0.619 (3.22)	0.481 (4.33)	0.536 (2.69)	0.598 (3.14)
40	0.642 (2.77)	0.646 (2.65)	0.702 (2.76)	0.701 (2.77)	0.599 (3.88)	0.603 (2.3)	0.675 (2.78)
50	0.731 (2.28)	0.734 (2.2)	0.788 (2.26)	0.788 (2.25)	0.714 (3.22)	0.676 (1.85)	0.765 (2.23)
60	0.822 (1.72)	0.824 (1.64)	0.866 (1.57)	0.866 (1.56)	0.821 (2.25)	0.751 (1.38)	0.851 (1.61)
70	0.898 (1.07)	0.898 (1.07)	0.926 (0.93)	0.926 (0.93)	0.901 (1.37)	0.811 (0.93)	0.919 (0.94)
(B) FDR
n1	Modified t	Corrected Z	MLEE	MLELS	Paired only	Two-sample	Weighted Z
5	0.09 (3.24)	0.088 (3.18)	0.36 (10.59)	0.283 (7.42)	0.356 (13.78)	0.059 (2.75)	0.073 (3)
10	0.094 (3.12)	0.09 (3.07)	0.088 (4.2)	0.103 (3.7)	0.161 (8.76)	0.05 (2.73)	0.078 (2.95)
20	0.092 (2.73)	0.088 (2.71)	0.07 (2.32)	0.081 (2.44)	0.076 (3.91)	0.033 (1.93)	0.08 (2.48)
30	0.09 (2.24)	0.087 (2.19)	0.076 (2.11)	0.081 (2.14)	0.07 (2.67)	0.021 (1.42)	0.083 (2.12)
40	0.092 (2.12)	0.086 (2.09)	0.083 (1.98)	0.084 (2.02)	0.078 (2.37)	0.013 (1.06)	0.089 (1.96)
50	0.085 (1.81)	0.081 (1.78)	0.076 (1.77)	0.075 (1.76)	0.073 (2.05)	0.006 (0.66)	0.078 (1.72)
60	0.081 (1.53)	0.078 (1.5)	0.071 (1.55)	0.068 (1.58)	0.069 (1.76)	0.003 (0.42)	0.07 (1.51)
70	0.079 (1.41)	0.077 (1.39)	0.068 (1.49)	0.065 (1.49)	0.067 (1.64)	0.002 (0.22)	0.064 (1.41)
(C) FNR
n1	Modified t	Corrected Z	MLEE	MLELS	Paired only	Two-sample	Weighted Z
5	0.33 (0.99)	0.33 (0.98)	0.379 (0.39)	0.363 (0.83)	0.384 (0.07)	0.345 (0.86)	0.338 (0.96)
10	0.314 (1.06)	0.314 (1.05)	0.358 (0.98)	0.34 (1.18)	0.381 (0.29)	0.342 (0.89)	0.32 (1.08)
20	0.283 (1.16)	0.283 (1.16)	0.29 (1.54)	0.282 (1.57)	0.357 (1.08)	0.333 (0.96)	0.28 (1.3)
30	0.247 (1.27)	0.246 (1.23)	0.235 (1.56)	0.23 (1.54)	0.31 (1.63)	0.328 (0.95)	0.239 (1.38)
40	0.202 (1.16)	0.202 (1.13)	0.18 (1.28)	0.179 (1.31)	0.24 (1.72)	0.316 (0.95)	0.19 (1.21)
50	0.16 (1.05)	0.161 (1.01)	0.139 (1.02)	0.14 (1.02)	0.178 (1.31)	0.304 (0.89)	0.149 (1.01)
60	0.113 (0.92)	0.112 (0.89)	0.099 (0.9)	0.102 (0.94)	0.126 (1.08)	0.289 (0.81)	0.108 (0.9)
70	0.072 (0.79)	0.071 (0.79)	0.064 (0.81)	0.066 (0.83)	0.08 (0.95)	0.272 (0.69)	0.071 (0.82)

We repeat the analysis by treating the non-parametric Wilcoxon signed-rank test on all the 84 matched pairs as the oracle test, and replace (i) the paired t-test on the n₁ matched samples only with the Wilcoxon signed-rank test, (ii) independent two-sample t-test on n₁ + n₂ and n₁ + n₃ observations in colon adenocarcinomas and non-tumorous tissue group with the Mann-Whitney test, and similarly for the proposed weighted Z-test combination as in the simulation. The average Lin’s concordance correlation coefficient, empirical FDR and FNR are given in Table 2(A), 2(B) and 2(C), respectively. The modified test statistics approaches exhibit inflated FDR, whereas the proposed weighted Z-test achieves the minimum FNR among the other methods which have valid FDR control.

Table 2.

(A) Lin’s concordance correlation coefficient, r_c, (B) empirical FDR and (C) empirical FNR each method compared to the oracle test under non Gaussian assumption averaged over 1000 replications. The standard error of the estimate (×10⁻³) is given in the parentheses. Wilcoxon signed-rank test on the complete 84 matched pairs is used as the oracle test. No microRNA is detected using the paired only test for n₁ = 5, and thus the empirical FDR is set as NA.

Lin’s concordance correlation coefficient, rc
n1	Modified t	Corrected Z	MLEE	MLELS	Paired only	Two-sample	Weighted Z
5	0.376 (3.32)	0.376 (3.33)	0.351 (3.41)	0.335 (3.38)	0.084 (3.08)	0.375 (3.18)	0.38 (3.21)
10	0.408 (3.3)	0.409 (3.28)	0.426 (3.44)	0.42 (3.47)	0.181 (3.78)	0.407 (3.16)	0.429 (3.36)
20	0.475 (3.45)	0.478 (3.41)	0.525 (3.42)	0.522 (3.43)	0.353 (4.48)	0.47 (3.13)	0.519 (3.46)
30	0.55 (2.93)	0.556 (2.92)	0.606 (3.02)	0.604 (3.05)	0.489 (4.23)	0.54 (2.58)	0.605 (3.02)
40	0.62 (2.69)	0.627 (2.66)	0.676 (2.71)	0.675 (2.73)	0.611 (3.85)	0.604 (2.18)	0.685 (2.72)
50	0.695 (2.21)	0.699 (2.21)	0.747 (2.18)	0.747 (2.18)	0.727 (3.22)	0.666 (1.73)	0.774 (2.2)
60	0.773 (1.7)	0.775 (1.71)	0.811 (1.54)	0.81 (1.54)	0.834 (2.14)	0.728 (1.22)	0.861 (1.49)
70	0.835 (1.27)	0.835 (1.31)	0.858 (1.1)	0.858 (1.11)	0.91 (1.19)	0.776 (0.83)	0.924 (0.82)
FDR
n1	Modified t	Corrected Z	MLEE	MLELS	Paired only	Two-sample	Weighted Z
5	0.106 (3.33)	0.105 (3.28)	0.359 (10.73)	0.281 (7.41)	NA (NA)	0.07 (2.84)	0.068 (2.85)
10	0.11 (3.13)	0.105 (3.07)	0.084 (3.98)	0.105 (3.68)	0.196 (6.13)	0.061 (2.72)	0.077 (2.7)
20	0.111 (2.75)	0.107 (2.73)	0.08 (2.38)	0.092 (2.52)	0.081 (4.28)	0.046 (2.2)	0.082 (2.38)
30	0.112 (2.19)	0.109 (2.18)	0.092 (2.13)	0.096 (2.15)	0.069 (2.57)	0.035 (1.68)	0.079 (1.86)
40	0.116 (2.1)	0.11 (2.05)	0.1 (1.94)	0.102 (2.02)	0.074 (2.18)	0.028 (1.31)	0.082 (1.78)
50	0.115 (1.79)	0.11 (1.77)	0.101 (1.77)	0.099 (1.78)	0.068 (1.78)	0.024 (1.08)	0.073 (1.46)
60	0.122 (1.51)	0.119 (1.48)	0.108 (1.55)	0.105 (1.59)	0.067 (1.52)	0.023 (0.88)	0.065 (1.28)
70	0.127 (1.38)	0.126 (1.37)	0.115 (1.45)	0.112 (1.45)	0.064 (1.4)	0.023 (0.74)	0.052 (1.09)
FNR
n1	Modified t	Corrected Z	MLEE	MLELS	Paired only	Two-sample	Weighted Z
5	0.322 (0.95)	0.322 (0.95)	0.369 (0.43)	0.354 (0.85)	0.376 (0)	0.338 (0.77)	0.337 (0.81)
10	0.307 (1.02)	0.306 (1.01)	0.348 (1.01)	0.331 (1.2)	0.373 (0.31)	0.334 (0.78)	0.319 (0.94)
20	0.276 (1.11)	0.276 (1.1)	0.282 (1.53)	0.274 (1.54)	0.348 (1.07)	0.329 (0.84)	0.28 (1.22)
30	0.242 (1.18)	0.241 (1.15)	0.228 (1.52)	0.224 (1.47)	0.303 (1.57)	0.324 (0.83)	0.238 (1.36)
40	0.199 (1.08)	0.198 (1.07)	0.175 (1.25)	0.174 (1.26)	0.235 (1.64)	0.313 (0.82)	0.188 (1.27)
50	0.16 (0.96)	0.161 (0.94)	0.138 (0.96)	0.139 (0.94)	0.181 (1.43)	0.301 (0.8)	0.152 (1.06)
60	0.12 (0.81)	0.12 (0.79)	0.106 (0.8)	0.108 (0.82)	0.126 (1.15)	0.287 (0.73)	0.112 (0.89)
70	0.086 (0.71)	0.085 (0.74)	0.078 (0.73)	0.08 (0.74)	0.078 (0.84)	0.269 (0.59)	0.077 (0.7)

5. Discussion

This paper presents a simple yet robust method for partially matched samples based on p-values pooling, a popular approach in meta-analysis for combining results from multiple studies. Both the simulation results and the case study show that the p-values pooling based on the weighted Z-test achieves better operating characteristics including higher concordance relative to the oracle test, valid FDR control, smaller FNR (i.e., higher power) and higher area under ROC than existing methods across various distributions (Gaussian and non-Gaussian), correlations and degrees of missing matched samples. In addition, simulation results suggest that weighting by the square root of sample size under the heteroscedascticity assumption is robust and performs well in various scenarios.

One motivation of the proposed weighted Z-test for p-values pooling in partially matched samples is the flexibility of allowing users to choose their preferred statistical tests for analyzing the n₁ paired samples, and (n₂, n₃) unpaired samples. This enables users to utilize the vast statistical and computational tools that have been developed for analyzing the paired or independent two-sample data generated from the microarray or high throughput sequencing platforms separately. An alternative approach is to modify the existing algorithms to handle partially matched samples directly, however this is usually non-trivial and requires considerable effort.

The weighted Z transformation for p-values pooling assumes that the p-values are uniformly distributed. However, the p-values obtained from the non-parametric tests (Wilcoxon signed-rank or Mann-Whitney tests) or discrete distribution do not follow the uniform distribution. In such cases, this may reduce the power of the weighted Z-test (Lancaster [16], Trehub and Heilizer [17], Edgington and Haller [18]). Several extensions have been proposed to deal with discrete p-values (Lancaster [16], Kincaid [19], Mielke and Berry [20]). These methods can be adapted for partially matched samples scenarios for discrete p-values computed from count data such as RNA-Seq from the next generation sequencing instruments.

One limitation of the p-values pooling approach is in confidence interval estimation. Unlike the modified test statistics approaches which can be readily extended to obtain confidence intervals, such analog is not available for the p-values pooling approach. However, in large scale genomics study where hundreds or thousands of genes/biomarkers are being profiled, in many cases, the main interest is in estimating the p-values and FDRs of each gene/biomarker, followed by thresholding at a nominal FDR level and declaring a list of significant genes/biomarkers. In scenarios where the estimation of univariate mean difference and its corresponding confidence interval is the primary objective, we recommend the use of modified test statistics approaches reviewed in this paper.

Our motivating example comes from one of the many facets of cancer research in identifying biomarkers which are differentially expressed between tumor and matching normals. Another area of research which is closely related to the notion of partially matched samples is in the case-control genome-wide association studies (GWAS) that includes multiple control groups (Cessie et al. [21]), including (i) matching controls such as the family control to adjust for confounding genetic factors and (ii) unmatched population based controls. However, unlike the setup of this paper, where the unmatched samples constitute an independent dataset, in GWAS with multiple control groups, the same cases are used in comparison with the different control groups. In such cases, the p-values pooling approach needs to be adjusted to account for the correlation between the two individual p-values. We refer the readers to the work of Zaykin and Kozbur [22] which addresses the pooling of correlated p-values in GWAS, as well as a recent publication by Samawi and Vogel [23] for partially correlated samples in categorical data represented by contingency tables.

Appendix A

The two-sided p-values pooling using a weighted Z-test is based on the observation that the Z-test is symmetric. Here, we provide a justification on this with an example under the Normal distribution:

Let x₁, …, x_n ~ N(μ, σ²) and y₁, …, y_n ~ N(μ, σ²) be the independent and identically distributed observations from Study 1 and Study 2, respectively. For simplicity, we assume equal weighting and σ² = 1 is known.

To test H₀ : μ = 0 vs H₁ : μ ≠ 0, under the scenario of complete data, i.e., by combining Study 1 and Study 2, the two-sided p-value is $p=2\times [1-\mathrm{\Phi }(|{\sum }_{i=1}^n(x_i+y_i)/\sqrt{2n}|)]$ from the Z-test. Now, we will show how pooling individual one-sided p-values from Study 1 and Study 2 will yield the two-sided p-value.

Let $p_1^g$ and $p_2^g$ be the one-sided p-values for testing H₀ : μ = 0 vs H₁ : μ > 0. Then $p_1^g=1-\mathrm{\Phi }({\sum }_{i=1}^n{x}_i/\sqrt{n})$ and $p_2^g=1-\mathrm{\Phi }({\sum }_{i=1}^n{y}_i/\sqrt{n})$. By the proposed weighted p-value pooling approach, $Z_1={\mathrm{\Phi }}^{-1}(1-p_1^g)={\sum }_{i=1}^n{x}_i/\sqrt{n}$and $Z_2={\mathrm{\Phi }}^{-1}(1-p_2^g)={\sum }_{i=1}^n{y}_i/\sqrt{n}$. Thus the one-sided pooled p-value is $p_c^g=1-\mathrm{\Phi }[(Z_1+Z_2)/\sqrt{2}]=1-\mathrm{\Phi }({\sum }_{i=1}^n(x_i+y_i)/\sqrt{2n})$. Similarly, for testing H₀ : μ = 0 vs H₁ : μ < 0, the one-sided pooled p-value is $p_c^l=1-\mathrm{\Phi }(-{\sum }_{i=1}^n(x_i+y_i)/\sqrt{2n})=1-p_c^g$. Thus, the two-tailed pooled p-value $p_c^{\ast }$ is given by $\min (2\times [1-\mathrm{\Phi }(-{\sum }_{i=1}^n(x_i+y_i)/\sqrt{2n})],2\times [1-\mathrm{\Phi }({\sum }_{i=1}^n(x_i+y_i)/\sqrt{2n}])$, which is equal to p above. Equivalently,

$$p_c^{\ast }=\{\begin{array}{ll}2p_c^g,& \mathrm{if}{p}_c^g<1/2\\ 2(1-p_c^g),& \mathrm{otherwise}.\end{array}$$