Skip to main content
PMC home page
Annals of Botany logoLink to Annals of Botany
. 2013 May 30;112(3):515–526. doi: 10.1093/aob/mct119

Species coherence in the face of karyotype diversification in holocentric organisms: the case of a cytogenetically variable sedge (Carex scoparia, Cyperaceae)

Marcial Escudero 1,2, Jaime A Weber 1, Andrew L Hipp 1,3,*
PMCID: PMC3718211  PMID: 23723260

Abstract

Background and Aims

The sedge genus Carex, the most diversified angiosperm genus of the northern temperate zone, is renowned for its holocentric chromosomes and karyotype variability. The genus exhibits high variation in chromosome numbers both among and within species. Despite the possibility that this chromosome evolution may play a role in the high species diversity of Carex, population-level patterns of molecular and cytogenetic differentiation in the genus have not been extensively studied.

Methods

Microsatellite variation (11 loci, 461 individuals) and chromosomal diversity (82 individuals) were investigated in 22 Midwestern populations of the North American sedge Carex scoparia and two Northeastern populations.

Key Results

Among Midwestern populations, geographic distance is the most important predictor of genetic differentiation. Within populations, inbreeding is high and chromosome variation explains a significant component of genetic differentiation. Infrequent dispersal among populations separated by >100 km explains an important component of molecular genetic and cytogenetic diversity within populations. However, karyotype variation and correlation between genetic and chromosomal variation persist within populations even when putative migrants based on genetic data are excluded.

Conclusions

These findings demonstrate dispersal and genetic connectivity among widespread populations that differ in chromosome numbers, explaining the phenomenon of genetic coherence in this karyotypically diverse sedge species. More generally, the study suggests that traditional sedge taxonomic boundaries demarcate good species even when those species encompass a high range of chromosomal diversity. This finding is important evidence as we work to document the limits and drivers of biodiversity in one of the world's largest angiosperm genera.

Keywords: Carex scoparia, Cyperaceae, gene flow, holocentric chromosomes, karyotype evolution, microsatellites, sedge, simple sequence repeats, species coherence

INTRODUCTION

The sedge genus Carex (Cyperaceae), with >2000 species (Reznicek, 1990), is one of the four largest angiosperm genera worldwide (Judd et al., 2007). It has a centre of diversification in the cold and temperate areas of the northern hemisphere, where it is the most diversified angiosperm genus (Escudero et al., 2012a). Several recent studies have illuminated important mechanisms that shape Carex population genetic structure: isolation-by-distance (Escudero et al., 2010b; Gehrke and Linder, 2011; Jiménez-Mejías et al., 2011); long-distance dispersal or vicariance (Schönswetter et al., 2008; Escudero et al., 2009, 2010b, c; Gehrke and Linder, 2011; Jiménez-Mejías et al., 2011, 2012); self-compatibility and high selfing (Whitkus, 1988a; Friedman and Barrett, 2009; Escudero et al., 2010b; Arens et al., 2005); and chromosome differentiation (Whitkus, 1988a; Hipp et al., 2010; Escudero et al., 2010a; Jiménez-Mejías et al., 2011). Chromosome evolution has received particular attention (Hipp et al., 2009a) and has long been suggested to be an important driver of lineage diversification in Carex (Heilborn, 1924; Hipp, 2007; Escudero et al., 2010a, 2012a, b; Chung et al., 2012). Despite this fact, we have little understanding of whether or not population genetic patterns arise as a function of chromosome diversification in the genus. Previous studies on reproductive isolation between Carex species indicate that chromosomal differences do not play a deterministic role, but, instead, genetically determined pre- or post-mating barriers may be the norm (Whitkus, 1988a, b, 1991, 1992). More recent studies suggest that chromosome rearrangements in sedges have a cumulative effect on intraspecific gene flow and a potential role in speciation (Escudero et al., 2010a; Hipp et al., 2010). Understanding how these components of genetic differentiation correlate and/or interact is key to understanding the biodiversity of temperate zone's largest angiosperm genera.

Holocentric chromosomes – chromosomes with diffuse rather than solitary, localized centromeres – have been reported from sedges and rushes (Cyperaceae and Juncaceae, which together form a clade) and five other angiosperm clades, as well as scattered clades in the algae, bryophytes, Rhizaria, nematodes, velvet worms and arthropods (Mola and Papeschi, 2006; Hipp et al., 2013). Diffuse centromeres allow rapid evolution of chromosome rearrangements via fission (agmatoploidy), fusion (simploidy) and translocations (reviewed in Hipp et al., 2009a). Consequently, Carex exhibits a nearly continuous range of chromosome numbers (2n = 12–124; Roalson, 2008; Hipp et al., 2009a; Rotreklová et al., 2011) and substantial chromosome variation within many species (Ohkawa et al., 2000; Roalson, 2008; Escudero et al., 2010a). In monocentric chromosomes, chromosome fragments without centromeres are unable to segregate normally, which will result in a loss of genetic material and probably inviable gametes. In holocentric chromosomes, diffuse centromeres allow that all fragments segregate normally during meiosis, and eventually changes in chromosome number may become stabilized through backcrossing or selfing, or even crossing among individuals that have undergone convergent rearrangements (Luceño, 1994). Moreover, non-bivalent associations of holocentric chromosomes often segregate normally during meiosis, reducing the selective pressure against fissions and fusions of chromosomes (Faulkner, 1972; Luceño, 1993). A diffuse centromere thus has the potential to reduce or eliminate the underdominance of chromosome rearrangements, allowing them to become fixed at a higher rate than in organisms with monocentric chromosomes.

Chromosome rearrangements in monocentric chromosomes have been shown to limit gene flow (Rieseberg et al., 1995, 1999; Noor et al., 2001a, b, 2007; Machado et al., 2002, 2007a, b; Navarro and Barton, 2003a, b; Ayala and Coluzzi, 2005; Basset et al., 2008; Lowry and Willis, 2010), but it is not well known how rearrangements in holocentric chromosomes affect gene flow patterns. In at least two Carex species, deep genetic breaks are absent within the species despite the fact that interpopulational estimates of cytogenetic difference and molecular genetic distance for those same species are positively correlated (Hipp et al., 2010). Similarly, cytogenetic study of a cytogenetically diverse butterfly species suggests that chromosome diversity has arisen within the species from 8500 to 31 000 years ago (Lukhtanov et al., 2011). These findings suggest that chromosome rearrangements may not be sufficient for speciation in holocentric organisms, but they may nonetheless contribute to genetic differentiation between populations. It is not known, however, whether cytogenetic diversification affects population genetic structure within holocentric organisms. It is also not known whether cytogenetic diversity arises frequently within populations and then goes to fixation, or is shared among populations due to migration. Stated another way: are chromosomally variable sedges cohesive species in which genes can migrate relatively freely among populations, or collections of populations that are all differentiated and more or less reproductively isolated from one another?

In this study, we present population-level sampling of molecular genetic markers [simple sequence repeats (SSRs) or microsatellites] and chromosome counts in Carex scoparia Schkuhr ex Willdenow to investigate the patterns of genetic structure among and within populations. We quantify patterns of cytogenetic and molecular genetic variation at regional (within the greater Chicago region, <350 km maximum pairwise distance) and local scales (within populations), to investigate patterns of genetic connectivity among populations, and evaluate the relative effects of geographic distance and cytogenetic differentiation on gene flow. Our findings demonstrate that in spite of cytogenetic differentiation among and within populations, there is both isolation-by-distance and migration among populations separated by >100 km, and genetic admixture within individuals, suggesting a history of gene flow between populations. Our demonstration of genetic connectivity between karyotypically divergent populations in the species is a finding of theoretical and practical significance in the evolution of biodiversity in one of the world's largest and most ecologically widespread angiosperm genera.

MATERIALS AND METHODS

Study species

Carex scoparia (Carex sect. Ovales, Cyperaceae) grows in wet to occasionally dry, open habitats, often in sandy and/or acidic soils. The species is distributed across much of the northern half of North America at low elevations (0–2000 m), predominantly in eastern North America, and ranges in chromosome number from 2n = 56 to 2n = 70 (Mastrogiuseppe et al., 2002). A previous study (Hipp et al., 2010) based on chromosome counts and amplified fragment length polymorphism (AFLP) genotypes of exemplars from each of 35 populations across a large portion of the species' distribution demonstrated that there are no strong molecular genetic disjunctures within C. scoparia sensu stricto (s.s.), though there is strong separation between C. scoparia and C. waponahkikensis M.Lovit & A.Haines (Lovit and Haines, 2012), previously known as C. scoparia var. tessellata Fernald & Wiegand. It also demonstrated that chromosome rearrangements (conservatively estimated as differences in chromosome number) explain 5·3 % of the population genetic variance in the species, approximately equal to the proportion of genetic variance explained by geographic distance. A recent study of chromosome number and genome size in the species based on the Midwestern populations we are using in the present study demonstrated that chromosome number variation in C. scoparia evolves via fission, fusion and possibly by translocations, rather than by duplication and deletion of chromosomes (Chung et al., 2011).

Sampling

Samples for this study come from 461 individuals representing 22 populations of the greater Chicago region in the Midwestern USA (Fig. 1A), and two additional populations from upstate New York (Table 1). The Chicago region sample includes 5–28 (mostly 15–24) individuals per each of 22 populations in south-eastern Wisconsin, north-eastern Illinois and north-western Indiana. Samples were collected from the widest spatial range practical at each site visited. For the cytogenetic study, we sampled 3–6 individuals from each of the Chicago and Northeast populations, 82 individuals in total (Table 1). Forty-one new chromosome counts are presented in this study and 41 counts were previously published (Chung et al., 2011). All counts were performed following the technique of Cooperrider and Morrison (1967), as described by Rothrock and Reznicek (1996), Hipp et al. (2010) and Chung et al. (2011).

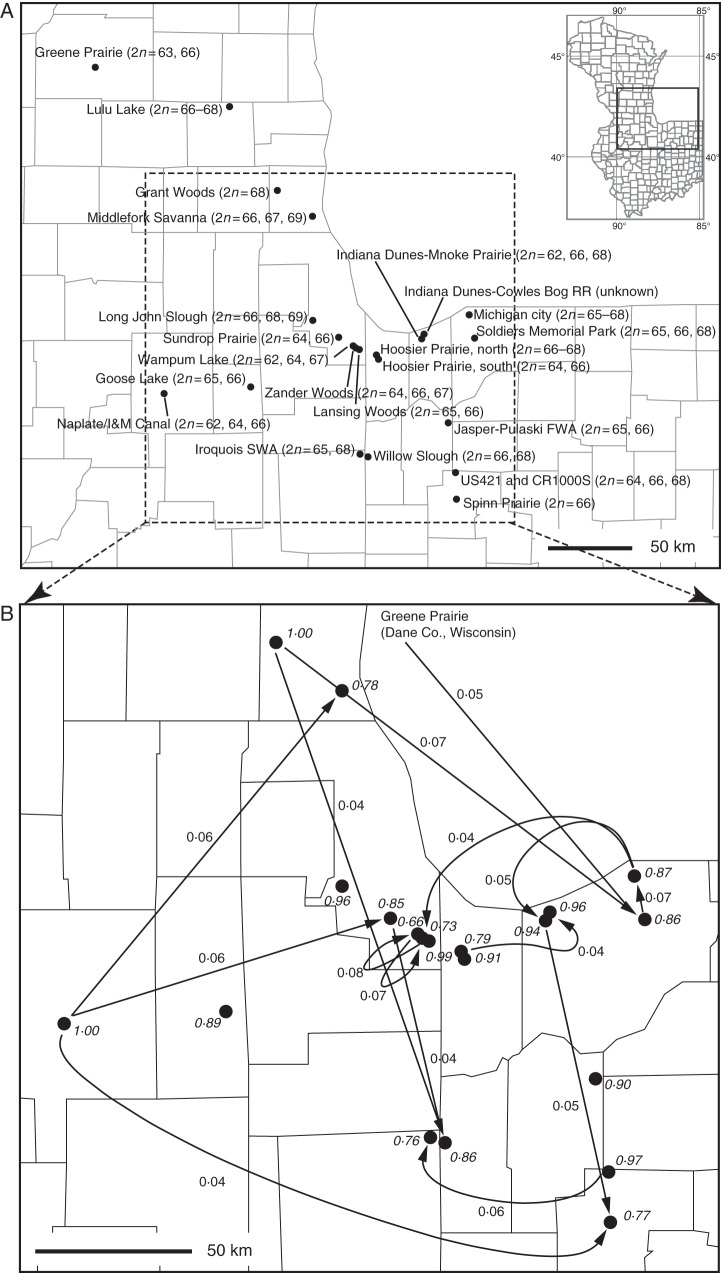
Fig. 1.

Fig. 1.

Open in a new tab

(A) Map of sampled Midwestern populations. Diploid (2n) chromosome counts from each population are shown (see Table 1). (B) Chicago region detail. Arrows and rates in bold indicate all inferred gene flow events >4 % between Midwest populations (inferred from admixture BAPS analysis based on 24 geographical population partition); italics and non-bold indicate the proportion of endogenous genetic variation inferred for each population. Lines on the map delimit counties.

Table 1.

Sample size (NSSR), gene diversity (HS), observed heterozygosity (HO) and inbreeding (FIS) from the SSR study; sample size (NCYT), diploid chromosome numbers (2n) and meiotic configuration for samples with irregularities, mean chromosome number (2nPOP) and variance (σ2) from the cytogenetic study.

Population NSSR HS (s.e.) HO (s.e.) FIS (s.e.) 2n (Voucher) NCYT 2nPOP σ2all individuals σ2excluding migrants
Goose Lake (IL, 41.359583/–88.315900) 28 0·480 (0·093) 0·188 (0·037) 0·533 (0·068) 65 (2n = 31II = 1III, 2830N), 66 (2830D, J, W) 4 65·75 0·25 0·25
Grant Woods (IL, 42·387900/–88·128067) 5 0·000 (0·000) 0·000 (0·000) NA 68 (2879A) 1 68 NA NA
Hoosier Prairie, North (IN, 41·526361/–87·442680) 24 0·517 (0·057) 0·102 (0·025) 0·798 (0·045) 66 (2863B, H, Q), 67 (2n = 32II + 1III, 2863M), 68 (2863A) 5 66·6 0·8 0·8
Hoosier Prairie, South (IN, 41·504783/–87·437267) 15 0·447 (0·065) 0·006 (0·006) 0·989 (0·010) 64 (2864M), 66 (2864A, F) 3 65·33 1·33 2
Indiana Dunes–Cowles Bog RR (IN, 41·636817/–87·100533) 12 0·241 (0·066) 0·061 (0·016) 0·579 (0·122) – 0 NA NA NA
Indiana Dunes–Mnoke Prairie (IN, 41·617983/–87·108550) 24 0·370 (0·069) 0·049 (0·011) 0·752 (0·091) 62 (2865W), 66 (2865S), 68 (2865F, H, O) 5 66·8 3·2 3·2
Iroquois SWA (IL, 41·008500, –87·548525) 20 0·593 (0·052) 0·241 (0·031) 0·539 (0·073) 65 (2n = 31II + 1III, 2894K), 68 (2894H) 2 66·5 4·5 4·5
Jasper-Pulaski FWA (IN, 41·172383/–86·930767) 21 0·461 (0·072) 0·074 (0·021) 0·802 (0·043) 62 (2893O), 64 (2893A, C, G) 4 63·5 1 1
Lansing Woods (IL, 41·555500/–87·554217) 21 0·254 (0·078) 0·078 (0·035) 0·764 (0·073) 65 (2n = 31II + 1III, 2880N), 66 (2880A, N, R) 3 65·83 0·08 0·08
Long John Slough (IL, 41·708633, –87·879417) 21 0·456 (0·046) 0·117 (0·016) 0·732 (0·028) 66 (2878I), 68 (2878A, C), 69 (2n = 33II + 1III, 2878F) 4 67·75 1·58 1·58
Lulu Lake (WI, 42·826867/–88·462550) 15 0·256 (0·072) 0·018 (0·009) 0·930 (0·029) 68 (2800), 67 (2n = 32II + 1III, 2807), 66 (2816, 2818) 4 66·75 0·92 0·92
Michigan City/IN CR 900N (IN, 41·737383/–86·784900) 23 0·292 (0·076) 0·043 (0·026) 0·888 (0·048) 65 (2n = 31II + III, 2890J, 2703), 66 (2890D), 67 (2n = 30II + 1III + 1IV, 2890A), 68 (2709, 2890I) 6 66·5 1·9 1·7
Middlefork Savanna (IL, 42·253200, –87·882633) 12 0·541 (0·076) 0·318 (0·045) 0·349 (0·074) 66 (2895A, C; 2n = 31II + 1IV, 2895K), 67 (2n = 32II + 1III, 2895H), 69 (2n = 32II + 2I + 1III, 2895I) 5 66·8 1·7 1·7
Naplate/IandM Canal (IL, 41·329700/–88·914233) 18 0·178 (0·074) 0·000 (0·000) 1·000 (0·000) 62 (2839B, I, O), 64 (2n = 30II + 1I + 1III/29II + 2III, 2839F), 66 (2839K) 5 63·2 3·2 3·2
Soldiers Memorial Park (IN, 41·615900/–86·747283) 22 0·344 (0·075) 0·127 (0·030) 0·580 (0·090) 65 (2n = 31II + 1III, 2889R), 66 (2889L*; 31II + 1III + 1I, 2889D), 68 (2889A) 4 66·25 1·58 0·33
Spinn Prairie (IN, 40·772083, –86·873900) 20 0·519 (0·077) 0·186 (0·028) 0·565 (0·068) 66 (2884B, F) 2 66 0 NA
Sundrop Prairie (IL, 41·619467/–87·698633) 20 0·348 (0·058) 0·055 (0·016) 0·837 (0·043) 64 (2891O), 66 (2891D, G, L) 4 65·5 1 0
US421 and CR1000S (IN, 40·911967/–86·880083) 20 0·361 (0·076) 0·082 (0·024) 0·659 (0·097) 64 (2882D), 66 (2882A), 68 (2882K) 3 66 4 4
Wampum Lake (IL, 41·576083/–87·589733) 20 0·526 (0·077) 0·045 (0·014) 0·922 (0·022) 62 (2875K; 2n = 28II + 2III, 2875G), 64 (2875A), 67 (2n = 32II + 2III, 2875R) 4 63·75 5·58 6·33
Willow Slough (IN, 40·993500, –87·494100) 25 0·568 (0·052) 0·058 (0·012) 0·877 (0·039) 66 (2690), 68 (2892C, 2n = 32II + 1IV, 2892I) 3 67·33 1·33 NA
Zander Woods (IL, 41·569700, –87·585967) 21 0·492 (0·065) 0·091 (0·022) 0·844 (0·032) 64 (2881O), 66 (2881H, L), 67 (2n = 33II + 1I, 2881D) 4 65·75 1·58 NA
Greene Prairie, Madison (WI, 43·026404/–89·437106) 17 0·529 (0·045) 0·314 (0·037) 0·315 (0·099) 63 (2652B†), 66 (2663, 2658-1, 2658-3‡) 4 65·25 2·25 3
Bishop Ville (NY; 42·34923/–77·75423) 20 0·248 (0·064) 0·023 (0·012) 0·937 (0·028) 64 (2718C), 66 (2718I) 2 65 2 2
Keaney Swamp (NY; 42·42712 / –77·90698) 17 0·472 (0·054) 0·091 (0·017) 0·744 (0·084) 64 (2731M) 1 64 NA NA
– 19·210 (0·996) 0·396 (0·016) 0·099 (0·007) 0·736 (0·017) – 3·4 65·8 1·9 2·03
Open in a new tab

Herbarium vouchers are archived at MOR. For the meiotic configurations the number (n) of bivalents, monovalents, trivalents and tetravalents during meiotic divisions are indicated by nII, nI, nIII and nIV, respectively.

* Missing SSR loci.

† Cytogenetic irregularities in meiosis I.

‡ Lacking SSR data.

DNA extraction and SSR protocols

Eleven SSR primer pairs (Hipp et al., 2009b) were used for the present study. For two of the loci (S177 and S102), the forward primer had an M13 tail attached to the 5' end to allow for labelling with 6-FAM fluorescent-labelled M13 primers (Schuelke, 2000). All other primer pairs had the forward primer directly labelled using 6-FAM. PCRs (21 µL) consisted of approx. 1–10 ng of genomic DNA, 1× MgCl2-free PCR buffer, 2·5 mm MgCl2, 0·2 mm each dNTP, 0·4 µg μL−1 bovine serum albumin (BSA), 0·16 µm labelled M13 primer, 0·16 µm reverse primer, 0·04 µm forward primer (with an M13 tail) and 0·65 U of Taq DNA polymerase (GoTAQ, Promega, Madison, WI, USA). Thermal cycling regimens for M13-labelled primer pairs were as follows: 94 °C for 4 min; 35 cycles of 94 °C for 30 s, Ta °C for 30 s (see Ta for each primer in Hipp et al., 2009b), 72 °C for 45 s; followed by eight cycles of 94 °C for 30 s, 53 °C for 30 s, 72 °C for 45 s; and a final extension at 72 °C for 10 min. Multiplex PCR was used for the remaining nine primer pairs, with the following PCR modifications: the forward primer for each locus was separately labelled, all primers were diluted to 0·01 µm (0·02 µm for S047), MgCl2 was diluted to 2·0 mm, BSA was not used, and the final round of eight PCR cycles at Ta = 53 °C was not used. PCR products and ROX-labelled GeneFlo 625 (CHIMERx, Milwaukee, WI, USA) size standard were suspended in formamide before running on an ABI3730 DNA Analyzer. Fragment analysis was conducted using GeneMapper version 4.0 (Applied Biosystems, Carlsbad, CA, USA).

Analyses I: genetic structure

Allele frequency and diversity were analysed using Genalex v.6 (Peakall and Smouse, 2006). For the entire data set at the population level as well as for a sub-set of individuals with known chromosome number (individual level), we calculated Da genetic distances (Nei's chord distance; Nei et al., 1983) from allele frequencies and used the resulting distance matrix to create Neighbor–Joining (NJ) trees. We assessed the reliability of the tree using 1000 non-parametric bootstrap replicates. Analyses were performed using MSA v. 4.05 (Dieringer and Schlötterer, 2003) and the NEIGHBOR and CONSENSE packages of Phylip v.3.7 (Felsenstein, 2007). A single-level analysis of molecular variance (AMOVA) for the Chicago region sample was performed in Genalex v.6, with individuals nested within populations (Peakall and Smouse, 2006). For each population in the Chicago region sample, we estimated molecular genetic diversity across loci using average observed heterozygosity (HO), gene diversity (HS) and inbreeding coefficient (FIS) (Genalex v.6, Peakall and Smouse, 2006). Mean chromosome number and chromosome variance in each population were also calculated, once including and once excluding migrants inferred using BAPS analyses, as described below.

Two model-based clustering approaches were used to identify population genetic structure within our data set: BAPS version 5.3 (Corander et al., 2006, 2008), which uses stochastic optimization in a Bayesian approach to find optimal population partitions under the assumption of random mating within populations; and STRUCTURE v2.3.2.1 (Pritchard et al., 2000), which uses Markov chain Monte Carlo (MCMC) to recover a posterior probability distribution of population partitions and population genetic parameters, assuming Hardy–Weinberg equilibrium and random mating within populations. In STRUCTURE analyses, we utilized the admixture, correlated allele frequencies model, using sampling locality as a population clustering prior (‘LOCPRIOR’ model; Hubisz et al., 2009). The local prior model is recommended for low genetic sampling within individuals or limited genetic structure. It provides an estimate of the importance of locality or other clustering prior to the clusters recovered in the posterior distribution and is robust to violations of the local prior. At the same time, the method is more sensitive to population structure when population structure in the data is not strong (Hubisz et al., 2009), making it well suited to data sets such as ours (11 SSR loci in this study). The allele frequencies parameter (λ) was estimated in an initial set of three independent runs, assuming K = 1 population, then set at the converged-upon value for all subsequent analyses per software recommendations. STRUCTURE simulations were run from K = 20 to 30 populations, with three replicates per run. We also ran analyses with the same parameters but no local prior for comparison and to evaluate whether our estimate of K (population number) is influenced by use of the local prior model, which it should not be (Hubisz et al., 2009). We studied the pattern of gene flow between our 24 geographic populations by running a BAPS admixture clustering analysis based on pre-defined population partitions, the 24 geographic populations. Minimum allowable population size was set at five individuals (the minimum population sampling in our data set), the number of iterations that were used to estimate the admixture coefficients for the individuals was 100 (as recommended in the manual), the number of reference individuals from each population was three and the number of iterations used to estimate admixture coefficients for the reference individuals was 20 (as recommended in the manual). We used Plot Gene Flow (Tang et al., 2009) to visualize gene flow events between populations. BAPS calculates simulation-based P-values for admixture coefficients under the null hypothesis of no admixed ancestry (Corander and Marttinnen, 2006). In this study, we apply a significance threshold of P < 0·01.

Analysis II: estimating population divergence times

To estimate divergence time between the Midwest (424 individuals) and Northeast (37 individuals) populations, we chose a random sub-set of 84 individuals from the Midwest sample, representing all populations. The size of the random sub-set was chosen to obtain a similar population sample size in the Chicago region and Northeast. We analysed only the five loci for which we could assume a stepwise mutation model (S181, S87, S180, S145 and S175), as these five microsatellite loci display a size pattern variation proportional to the motif size (Ohta and Kimura, 1973). We used the isolation-with-migration (IM) model implemented in the program IMa (Hey and Nielsen, 2004, 2007). The two-population IM model estimates gene flow and divergence times between two populations that are assumed to be descended from a common ancestor and exchanging genes only between themselves. In our previous work (Hipp et al., 2010), the Northeast and Midwest populations come out as independent groups (with the exception of population 3466), and in our current study the upstate New York populations separate distinctly from the populations of the Chicago region (bootstrap support = 96 %; Fig. 2). Moreover, both the Midwest and Northeast populations are on sites that were under ice <20 000 years ago during the last glacial maximum (LGM) (Dyke et al., 2002) and were probably colonized from a common pool of relictual and ancestral southern populations. However, the assumption that these populations are exchanging genes only with each other is presumably violated in our study: gene flow between the Northeast and Midwest populations is almost certainly occurring via intermediate populations. We expect that intermediate populations are more recently diverged from both the Northeast and Midwest populations, and that as a consequence, dating of divergence between the Northeast and Midwest populations may be biased downward (toward a more recent divergence estimate). Ongoing gene flow with an unsampled third species, ancestral to the two focal species, was found to have a relatively minor effect on IMa analyses of population divergence time in a simulation study (Strasburg and Rieseberg, 2010). Nonetheless, divergence time estimates presented in this study should be interpreted cautiously.

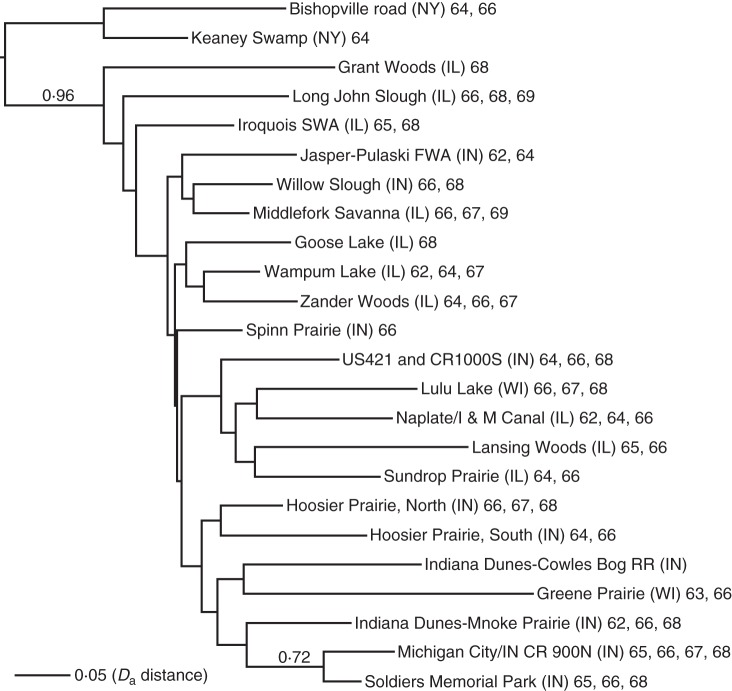
Fig. 2.

Fig. 2.

Open in a new tab

Neighbor–joining (NJ) tree from the Da distance matrix of 24 populations from the Chicago and Northeastern regions sample (461 individuals in total). Bootstrap values are shown above branches that have support >0·5. Each tip is labelled with the population name and chromosome numbers. This tree has been rooted using the populations from Northeastern region.

We used IMa to estimate (1) the marginal posterior probability densities of the population parameters of divergence time, t, where t = Tμ, with T being the time in years, and μ the mutation rate (mutation locus−1 year−1, assuming a 1 year generation time); (2) population differentiation indices of the ancestral population (θA) and the two extant lineages (θ1 and θ2), where θ = 4Neμ for diploid autosomal loci and Ne is the effective population size; and (3) the migration rate for each population, m1 and m2, where m is the migration rate per mutation rate (m = m/μ), and m1 = m1/μ and m2 = m2/μ. Priors used in 30 alternative IMa analyses conducted with one chain and for 2·5 million steps after a burn-in period of 0·1 million steps were as follows: θ1 = 100, θ2 = 100, θA = 100, m1 = 100, m2 = 100, t = 100, θ1 = 10, θ2 = 10, θA = 10, m1 = 10, m2 = 10, t = 10 for ten runs, and θ1 = 5, θ2 = 5, θA = 5, m1 = 5, m2 = 5, t = 5 for ten runs each. Final runs were conducted with estimated maximum value of parameters, 4–50 chains, 15 million steps and a previous burn-in period of 5 million steps, saving a total of 10 000 genealogies. We ran our analyses increasing the number of chains (4, 8, 15, 30 and 50) until Markov chains reached stationarity. At this point, the chains are presumed to sample from the true parameter posterior distribution. We used a geometric mode for selecting heating levels in Markov chains as recommended for >30 chains. We ran the 50 chain analysis three times to ensure convergence of parameter estimates across runs. We used a mutation rate range of 3 × 10−5 locus−1 year−1 to 6 × 10−4 locus−1 year−1, with a mean of 2 × 10−4 locus−1 year−1. This range was chosen based on microsatellite mutation rates in two cereal crops, durum wheat and maize (Thuillet et al., 2002; Vigouroux et al., 2002). These mutation rates were estimated using mutation accumulation experiments and have been used in previous IMa analysis with Carex species (King and Roalson, 2009).

Analysis III: correlations among chromosome divergence, genetic divergence and geographic distances

Correlation between genetic distances and cytogenetic and geographic distances was tested at population and individual levels. For analyses at the population level, we estimated pairwise genetic distances following Nei et al. (1983), great circle geographic distances using the Haversine formula (Sinnott, 1984), and cytogenetic differences as the pairwise absolute difference between mean chromosome number for each population. We assessed the relative contribution of geographic distance and cytogenetic differences to the variance in genetic distance using partial Mantel tests (Mantel, 1967; Smouse et al., 1986; Hipp et al., 2010). This approach estimates the partial effect of each predictor Xi on a response Y, holding all other Xi constant, and as such is analogous to multiple or partial regression. The significance of the partial coefficients of determination was estimated using 1000 Mantel permutations for each analysis.

At the individual level within populations, we calculated the Pearson product moment (Pearson's r) between pairwise genetic distances and pairwise cytogenetic differences for each population, and used the average r as our test statistic. The Type-I error probability was estimated by permuting individuals within populations 10 000 times, calculating the null distribution of r as the mean r over populations, and comparing observed mean r with the null distribution to obtain a two-tailed P-value. Individual-level analyses were conducted on data including all sets of individuals (‘full’ data set) and excluding individuals estimated to have <100 % of their genome originating within the population (‘no migrants’ data set). Analyses were conducted within R 2.13.0 using the multiple Mantel test implementation in the morton project (http://r-forge.r-project.org/projects/morton).

RESULTS

Genetic structure

Allele frequency and diversity statistics are summarized in Supplementary Data Table S1. The population-level NJ tree exhibits strong support for separation of the 22 Midwestern populations from the two New York populations (96 % bootstrap support; Fig. 2) and clustering of two Indiana populations (Michigan City/IN CR 900N and Soldiers Memorial Park, 72 % bootstrap; Fig. 2). No other groupings are strongly supported. The individual-level NJ tree similarly shows support only for separation of the New York populations from the Midwest populations and for a few within-population groupings of individuals (Supplementary Data Fig. S1). Gene flow analysis from BAPS admixture analysis based on the pre-defined partition of 24 geographic populations suggests that 66–100 % of genetic variance within each population is due to intrapopulation gene flow. Almost all interpopulation gene flow vectors >4 % (4–8 %) connect populations separated by >50 km (Fig. 1B). Whether this result reflects actual rates of gene flow or noise in the data bears additional study with more markers. Following BAPS documentation, in order to make this kind of admixture analysis reasonable, pre-defined clusters should be genetically distinct. However, our pre-defined clustering is based on geographic rather than genetic criteria. Nevertheless, when we cluster populations (not individuals) using BAPS mixture analysis (from K = 2 to K = 30), the optimal number of clusters is 23, and each cluster contains one geographic site, with the exception of Michigan City/IN CR 900N and Soldiers Memorial Park, which also clustered together in the NJ tree.

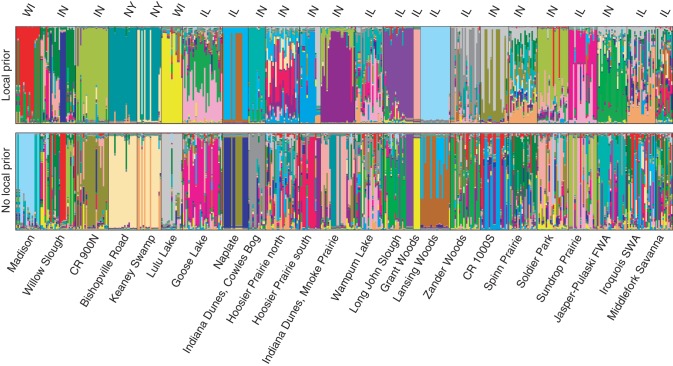
STRUCTURE (MCMC) analyses estimate the number of populations at K = 28 under the local prior model and K = 30 populations under the non-local prior model (posterior probability >0·999 for both models). As the number of sampling populations was 24, analyses were not conducted for values of K >30, and the optimal estimate of K may be >30. However, addition of populations above K = 24 does not appear to aid in interpreting population structure or sub-structure, but only increases within-individual molecular genetic diversity. For ease of interpretation, and because none of our conclusions or interpretations depends on precisely estimating K, we present only the K = 24 analysis results under the local prior and non-local prior models (Fig. 3). The estimate of the sampling informativeness parameter (r = 3·750 ± 0·222 in our study, whereas r ≤ 1 would suggest that locality is a good predictor of genetic grouping), congruence between the local prior and no local prior models, and visual inspection of the population genetic structure suggests that there is considerable migration among sampling sites. For four populations sampled (Long John Slough, Lansing Woods, Indiana Dunes–Mnoke Prairie and Soldier Park), the local prior model suggests less population admixture based on visual inspection (Fig. 3). All other populations show qualitatively similar patterns of sub-structure and admixture under both analysis models (Fig. 3A vs. 3B).

Fig. 3.

Fig. 3.

Open in a new tab

Admixture analysis from STRUCTURE analysis of 461 individuals from 24 populations (using correlated allele frequencies model). Results from both analyses, with and without sampling locality as a population clustering prior, are shown. Colours indicate different clusters (K = 24). Population names and US states are indicated.

The AMOVA for the Chicago region sample with two hierarchical levels apportions 32 % of the total genetic variance to among-site variation and 68 % to variation within populations. Gene diversity ranges from 0·000 to 0·593 (0·395 ± 0·016, mean ± s.e.) and observed heterozygosity ranges from 0·000 to 0·318 (0·099 ± 0·007). Inbreeding estimated as FIS is high, ranging from 0·315 to 1·000, with a mean value of 0·724 ± 0·017 (Table 1). Diploid chromosome number ranges from 2n = 60 to 2n = 69 in our data set. Mean population diploid chromosome number ranges from 63·2 to 68 (mean = 65·8) and population variance in 2n ranges from 0·00 to 5·58 (mean = 1·90) with migrants included, and from 0·00 to 6·33 (mean = 2·03) with migrants excluded.

Divergence time between populations

The IMa analysis was run until effective sample sizes were between 50 and 100 and the visual inspection of maximum likelihood graphs suggested adequate convergence and mixing of the Markov chains (50 chains). The best estimate of divergence time was t = 0·2356 (Table 2), which, based on t = Tμ, corresponds to a divergence time of 1178 years [95 % confidence interval (CI) 714–3850 years; hereafter in this paragraph, ranges in parentheses are 95 % CIs)]. While our 1 year generation time may be an underestimate, as it is based on observations in the greenhouse and in garden settings (pers. obs.), even assuming a 2 or 3 year generation keeps the upper bound on our divergence time CI under 12 000 years. Differentiation rates were estimated as θNortheast = 0·0248, θMidwest = 5·4782 and θAncestral = 14·8263, which, based on θ = 4Neμ, imply effective population sizes of NeNortheast = 31 (16–153) individuals, NeMidwest = 6848 (5718–137 308) individuals and NeAncestral = 18 533 (9329–209 335) individuals (Table 2). Finally, migration rate per mutation rate estimates are mMidwest to Northeast = 25·34 and m Northeast to Midwest = 11·61, which implies migration rates (m = m/μ) of mMidwest to Northeast = 5·07 (1·96–17·53) individuals per year and mNortheast to Midwest = 2·32 (1·27–5·48) individuals per year (Table 2).

Table 2.

Isolation–migration analyses

Estimate θEast (Ne) θMidwest (Ne) θAncestral (Ne) mEast (MEast) mMidwest (MMidwest) t (T, years)
Highest point 0·0248 (31) 5·48 (6848) 14·8 (18 533) 25·3 (5) 11·6 (2) 0·2356 (1178)
Mean 0·0433 (54) 52·0 (65 042) 44·1 (55 092) 44·8 (9) 14·4 (3) 0·3929 (1965)
95Low 0·0125 (16) 4·57 (5718) 7·46 (9329) 9·81 (2) 6·35 (1) 0·1428 (714)
95High 0·1227 (153) 109·8 (137 308) 167·5 (209 335) 87·7 (18) 27·4 (5) 0·7700 (3850)
Open in a new tab

Parameters of population differentiation (θEast, θMidwest and θAncestral), migration (mEast and mMidwest) and relative time since divergence (t) are shown. Absolute time estimations (T, years), effective population size (Ne) and population migration rate (MEast and MMidwest) are given in parentheses.

Correlations among chromosome divergence, genetic divergence and geographic distances

Chromosome number difference and geographic distance jointly explain 11·4 % (multiple R2) of the total variance in molecular genetic variance among the 22 Midwest populations. Almost all of this variance is explained by geographic distance (partial r = 0·334, two-tailed P = 0·024 based on 1000 Mantel permutations). Among populations, there is essentially no correlation between chromosome number difference and genetic differentiation (partial r = 0·041, two-tailed P = 0·373 based on 1000 Mantel permutations). This same result is supported by simple Mantel tests at the population level, suggesting that the result is not due to spatial autocorrelation in chromosome numbers (cf. Fig. 1A). At the individual level, only considering pairwise distances within populations, there is significant average correlation between genetic and chromosome distance when we consider populations with at least five individuals sampled for both chromosome counts and genotype (mean population r = 0·375 ± 0·141, two-tailed P = 0·028; n = 5 populations), while if we consider all populations with at least four individuals sampled for both chromosome counts and genotype (mean population r = 0·165 ± 0·119, two-tailed P = 0·167; n = 12 populations) or at least three individuals (mean population r = 0·100 ± 0·126, two-tailed P = 0·433; n = 18 populations) the average correlation is not significant. Excluding migrants from populations increases this correlation (for populations with at least four individuals, r = 0·275 ± 0·143, two-tailed P = 0·047, n = 9 populations; for populations with at least five individuals, r = 0·477 ± 0·143, two-tailed P = 0·015, n = 4 populations).

DISCUSSION

Population genetic structure

Populations from the Midwest exhibit detectable population genetic structure (Fig. 3), though the estimate of the sampling informativeness parameter (r = 3·750 ± 0·222 in our study, whereas r ≤ 1 would suggest that locality is a good predictor of genetic grouping) and visual inspection of the population genetic structure suggest considerable mixing among populations. The AMOVA results, according to which 32 % of molecular variance is apportioned among populations, support this finding. Patterns of gene flow based on admixture BAPS analysis similarly demonstrate that the majority of gene flow is from each population to itself (mean value 89 %, 66–100 %; Fig. 1B). Nevertheless, many population pairs exhibit significant rates of gene flow (P ≤ 0·01), such that 4–8 % of the total molecular variation within several populations is due to migration from populations 50–100 km distant (Fig. 1B). Geographic proximity plays a significant role in rates of gene flow within the region (among-population partial r = 0·334 with chromosome number as a covariate; two-tailed P = 0·024 based on 1000 Mantel permutations), while the BAPS analysis suggests that long-distance dispersal is not uncommon in the species. It is very difficult to know whether individuals with the same number of motif repeats actually share that number by descent. The presence of the same apparent allele in populations separated by >100 km could indicate long-distance gene flow or it could indicate independent mutations. Nevertheless, most of our inferred gene flow events involve more than one of our 11 microsatellites markers, reducing the possibility that what we are observing is homoplasy rather than gene flow. In fact, C. scoparia have small, lightweight, winged propagules (perigynia), which have a high potential for dispersal and colonization. This potential for occasional long-distance dispersal may help explain the previous report that, at broad geographic scales, the effect of chromosome differences on genetic differentiation does not attenuate with increasing geographic distance in either C. scoparia or the western North American C. pachystachya (Hipp et al., 2010). While we do not know what the long-term effect of these migrations is, our findings suggest that interpopulation migration at regional scales has the potential to play an important role in species cohesion despite high chromosome variation.

Carex scoparia exhibits a genetic signature of high inbreeding (FIS = 0·315–1·000; Table 1). These results are congruent with previous estimates of high selfing rates in Carex from studies based on hand pollinations and isozyme work (Whitkus, 1988a; Ohkawa et al., 2000; Friedman and Barrett, 2009) and microsatellite data (Escudero et al., 2010b; Arens et al., 2005). It is also in line with published summary data on population genetic parameters of plants based on microsatellite data (Nybom, 2004). For perennial plants, the mean observed heterozygosity value (HO = 0·53–0·63; Nybom, 2004) is generally higher than we find in C. scoparia (HO = 0·099 ± 0·007; current study, Table 1), while the expected heterozygosity (HS = 0·55–0·68; Nybom, 2004) is similar to our findings (HS = 0·396 ± 0·016; Table 1). For selfing plants, observed and expected heterozygosity (HO = 0·05 and HE = 0·41; Nybom 2004) are very close to our estimates for C. scoparia (HO = 0·099 ± 0·007 and HE = 0·396 ± 0·016; Table 1). Chromosome mutations have a higher probability of becoming fixed in selfing populations (Ohkawa et al., 2000; Arens et al., 2005; Friedman and Barrett, 2009; Escudero et al., 2010b), which can overcome the effects of selection in removing underdominant mutations from the population (Coyne and Orr, 2004; Gavrilets, 2004). The high chromosome variation we observe in Carex may thus be a consequence of those mutations being close to neutral mutations, as chromosome fission and fusion do not result in changes of genome size (Haldane, 1932; Chung et al., 2011, 2012); and/or relatively high fixation rates in inbreeding populations. Our observations of high chromosome number variation in combination with significant population structure, inbreeding and at least occasional long-distance dispersal support the role of inbreeding as an explanation for fixation of chromosomal variants in sedges by drift, without providing evidence for or against the role of selection.

Cytogenetic variation and gene flow patterns within populations

In this study, we estimate the age of the divergence between Northeastern and Midwestern populations at 1178 years ago (95 % posterior distribution 714–3850; Table 2), post-dating the LGM by at least 10 000 years (Dyke et al., 2002; Saeki et al., 2011). This period is significantly shorter than our previous estimate of a maximal average waiting time between chromosome rearrangements of 52 095 years (95 % CI = 20 223–103 065 years; Hipp et al., 2010), and it raises the question of how rapidly chromosome evolution proceeds in the species. The AFLP tree of individuals presented previously (Hipp et al., 2010) makes it impossible to rule out multiple origins of the Midwest populations sampled in this study. Similarly, in the current study, we cannot distinguish positively between two alternative (though not mutually exclusive) explanations for chromosomal diversity: (1) chromosome evolution within populations on very short time scales on one hand; and (2) ancestral chromosomal polymorphism and ongoing interpopulation migration on the other. Our finding of a positive correlation between molecular genetic distances and chromosome number differences within populations, while weak, is intriguing. This result might come about by one of at least two processes. First, it may be that cytogenetic diversity arises within populations and leads to molecular genetic diversification. Thus, we may be looking at the origins of population sub-division. To test this hypothesis, we would need to demonstrate molecular genetic differentiation between cytogenetically differentiated sub-populations, while also demonstrating that those sub-populations are together differentiated from other nearby populations in the area. On the other hand, populations that have higher rates of gene flow with other populations may simply exhibit both higher molecular genetic diversity and higher cytogenetic diversity, which would presumably also lead to a positive correlation between cytogenetic and molecular genetic diversity within populations. In our study, we find a higher correlation between cytogenetic differences and molecular genetic distances when we exclude migrants from analysis, which is evidence against this second hypothesis. However, our sample sizes for this test are quite small. Distinguishing between these alternative explanations for the relationship between cytogenetic and molecular genetic diversity will require more chromosomal data within populations.

Our study does provide preliminary evidence for rapid chromosome evolution as suggested by (1) chromosome differences among individuals with identical genotypes and (2) different chromosome numbers within one individual in this study (Table 1). This agrees with previous findings of different cytotypes among pollen mother cells of single anthers (Schmid, 1982; Luceño, 1992) and the previous report that cytogenetic mutations in Carex are much faster than ITS (internal transcribed spacer) mutations (Escudero et al., 2008). In combination with our result of a correlation between cytogenetic and molecular genetic divergence both within (current study) and among (Hipp et al., 2010) C. scoparia populations, this highlights the potential for chromosome diversification to drive molecular genetic diversification in sedges.

Conclusions

Our study demonstrates (1) the presence of chromosomal diversity within and among populations and (2) interpopulation gene flow between populations as a function of distance rather than of chromosome number differences. These findings complement our previous demonstration that chromosome rearrangements do not cause deep genetic breaks within the species (Hipp et al., 2010) to provide important evidence that this karyotypically diverse sedge species is genetically cohesive. The study also provides what we believe to be the first evidence that holocentric chromosome divergence influences population genetic structure at fine scales, suggesting that chromosome rearrangements may influence genetic structure within populations without driving strong genetic divergence between local populations. The role of chromosome evolution in speciation in this diverse genus remains a potent question.

From an applied standpoint, our study implies that we have good reason to be confident in estimates of species numbers in Carex that are based largely on ecological, biogeographic and morphological observations, the data of traditional taxonomy. Understanding the structure of biodiversity from the perspective of the clade or the community demands a valid estimate of species richness.

SUPPLEMENTARY DATA

Supplementary data are available online at ww.aob.oxfordjournals.org and consist of the following. Table S1: summary of allele frequency and diversity statistics. Figure S1: Neighbor–Joining tree from the Da distance matrix of 80 individuals from the Chicago region sample for which chromosome numbers were counted.

Supplementary Data
supp_112_3_515__index.html (1.1KB, html)

ACKNOWLEDGEMENTS

We thank two anonymous reviewers and the editor J. S. Heslop-Harrison for comments on the manuscript; land managers and ecologists too numerous to mention individually throughout the Chicago Region for help with permitting, population location and sampling; P. Rothrock and A. Reznicek for ongoing support of cytogenetic research into C. scoparia and for laying the groundwork for this study; and K. Feldheim and the staff of the Pritzker Laboratory for lab support. This research was funded by grants to A.H. from the National Fish and Wildlife Foundation (Midewin Tallgrass Prairie Restoration Fund Award #11439), US Fish and Wildlife Service and Illinois Conservation Foundation (Chicago Wilderness Award #FWS0603), and US National Science Foundation (NSF-DEB Award #0743157); and an MEC-Fulbright fellowship (FU2009-0946) to M.E.

LITERATURE CITED

  1. Arens P, Bijlsma R, Van't Westende W, Van Os B, Smulders MJM, Vosman B. Genetic structure in populations of an ancient woodland sedge, Carex sylvatica Hudson, at a regional and local scale. Plant Biology. 2005;7:387–396. doi: 10.1055/s-2005-865644. [DOI] [PubMed] [Google Scholar]
  2. Ayala FJ, Coluzzi M. Chromosome speciation: humans, Drosophila, and mosquitoes. Proceedings of the National Acadey of Sciences, USA. 2005;102:6535–6542. doi: 10.1073/pnas.0501847102. [DOI] [PMC free article] [PubMed] [Google Scholar]
  3. Basset P, Yannic G, Hausser J. Chromosomal rearrangements and genetic structure at different evolutionary levels of the Sorex araneus group. Journal of Evolutionary Biology. 2008;21:842–852. doi: 10.1111/j.1420-9101.2008.01506.x. [DOI] [PubMed] [Google Scholar]
  4. Chung K-S, Weber JA, Hipp AL. Dynamics of chromosome number and genome size variation in a cytogenetically variable sedge (Carex scoparia var. scoparia, Cyperaceae) American Journal of Botany. 2011;98:122–129. doi: 10.3732/ajb.1000046. [DOI] [PubMed] [Google Scholar]
  5. Chung K-S, Hipp AL, Roalson EH. Chromosome number evolves independently of genome size in a clade with non-localized centromeres (Carex: Cyperaceae) Evolution. 2012;66:2708–2722. doi: 10.1111/j.1558-5646.2012.01624.x. [DOI] [PubMed] [Google Scholar]
  6. Cooperrider TS, Morrison JH. Lactic–acetic–orcein as chromosome stain. Michigan Botanist. 1967;6:176–178. [Google Scholar]
  7. Coyne JA, Orr HA. Speciation. Sunderland, MA: Sinauer Associates; 2004. [Google Scholar]
  8. Corander J, Marttinen P. Bayesian identification of admixture events using multilocus molecular markers. Molecular Ecology. 2006;15:2833–2843. doi: 10.1111/j.1365-294X.2006.02994.x. [DOI] [PubMed] [Google Scholar]
  9. Corander J, Marttinen P, Mäntyniemi S. A Bayesian method for identification of stock mixtures from molecular marker data. Fisheries Bulletin. 2006;104:550–558. [Google Scholar]
  10. Corander J, Marttinen P, Sirén J, Tang J. Enhanced Bayesian modeling in BAPS software for learning genetic structures of populations. BMC Bioinformatics. 2008;9:539. doi: 10.1186/1471-2105-9-539. [DOI] [PMC free article] [PubMed] [Google Scholar]
  11. Dieringer D, Schlötterer C. MICROSATELLITE ANALYSER (MSA): a platform independent analysis tool for large microsatellite data sets. Molecular Ecology Notes. 2003;3:167–169. [Google Scholar]
  12. Dyke AS, Andrews JT, Clark PU, et al. The Laurentide and Innuitian ice sheets during the Last Glacial Maximum. Quaternary Science Reviews. 2002;21:9–31. [Google Scholar]
  13. Escudero M, Valcárcel V, Vargas P, Luceño M. Evolution in Carex L. sect. Spirostachyae (Cyperaceae): a molecular and cytogenetic approach. Organisms Diversity and Evolution. 2008;7:271–291. [Google Scholar]
  14. Escudero M, Valcárcel V, Vargas P, Luceño M. Significance of ecological vicariance and long-distance dispersal in the diversification of Carex sect. Spirostachyae (Cyperaceae) American Journal of Botany. 2009;96:2100–2114. doi: 10.3732/ajb.0900134. [DOI] [PubMed] [Google Scholar]
  15. Escudero M, Hipp AL, Luceño M. Karyotype stability and predictors of chromosome number variation in sedges: a study in Carex section Spirostachyae (Cyperaceae) Molecular Phylogenetics and Evolution. 2010a;57:353–363. doi: 10.1016/j.ympev.2010.07.009. [DOI] [PubMed] [Google Scholar]
  16. Escudero M, Vargas P, Arens P, Ouborg NJ, Luceño M. The east–west–north colonization history of the Mediterranean and Europe by the coastal plant Carex extensa (Cyperaceae) Molecular Ecology. 2010b;19:352–370. doi: 10.1111/j.1365-294X.2009.04449.x. [DOI] [PubMed] [Google Scholar]
  17. Escudero M, Valcárcel V, Vargas P, Luceño M. Bipolar disjunctions in Carex: long-distance dispersal, vicariance, or parallel evolution? Flora: Morphology, Distribution, Functional Ecology of Plants. 2010c;205:118–127. [Google Scholar]
  18. Escudero M, Hipp AL, Waterway MJ, Valente LM. Diversification rates and chromosome evolution in the most diverse angiosperm genus of the temperate zone (Carex, Cyperaceae) Molecular Phylogenetics and Evolution. 2012a;63:650–655. doi: 10.1016/j.ympev.2012.02.005. [DOI] [PubMed] [Google Scholar]
  19. Escudero M, Hipp AL, Hansen TF, Voje KL, Luceño M. Selection and inertia in the evolution of holocentric chromosomes in sedges (Carex, Cyperaceae) New Phytologist. 2012b;195:237–247. doi: 10.1111/j.1469-8137.2012.04137.x. [DOI] [PubMed] [Google Scholar]
  20. Faulkner JS. Chromosome studies on Carex section Acutae in northwest Europe. Botanical Journal of the Linnean Society. 1972;65:271–301. [Google Scholar]
  21. Felsenstein J. PHYLIP: Phylogenetic Inference Package, Version 3.67. Seattle: Department of Genome Sciences and Department of Biology, University of Washington; 2007. Available from the author. [Google Scholar]
  22. Friedman J, Barrett SCH. The consequences of monoecy and protogyny for mating in wind-pollinated Carex. New Phytolologist. 2009;181:489–497. doi: 10.1111/j.1469-8137.2008.02664.x. [DOI] [PubMed] [Google Scholar]
  23. Gavrilets S. Fitness landscapes and the origin of species. Princeton, NJ: Princeton University Press; 2004. [Google Scholar]
  24. Gehrke B, Linder HP. Time, space and ecology: why some clades have more species than others. Journal of Biogeography. 2011;38:1948–1962. [Google Scholar]
  25. Haldane JBS. The causes of evolution. Princeton, NJ: Princeton University Press; 1932. [Google Scholar]
  26. Heilborn O. Chromosome numbers and dimensions, species-formation and phylogeny in the genus Carex. Hereditas. 1924;5:129–216. [Google Scholar]
  27. Hey J, Nielsen R. Multilocus methods for estimating population sizes, migration rates and divergence time, with applications to the divergence of Drosophila pseudoobscura and D. persimilis. Genetics. 2004;167:747–760. doi: 10.1534/genetics.103.024182. [DOI] [PMC free article] [PubMed] [Google Scholar]
  28. Hey J, Nielsen R. Integration within the Felsenstein equation for improved Markov chain Monte Carlo methods in population genetics. Proceedings of the National Academy of Sciences, USA. 2007;104:2785–2790. doi: 10.1073/pnas.0611164104. [DOI] [PMC free article] [PubMed] [Google Scholar]
  29. Hipp AL. Nonuniform processes of chromosome evolution in sedges (Carex: Cyperaceae) Evolution. 2007;61:2175–2194. doi: 10.1111/j.1558-5646.2007.00183.x. [DOI] [PubMed] [Google Scholar]
  30. Hipp AL, Rothrock PE, Roalson EH. The evolution of chromosome arrangements in Carex (Cyperaceae) Botanical Review. 2009a;75:96–109. [Google Scholar]
  31. Hipp AL, Kettenring KM, Feldheim KA, Weber JA. Isolation of 11 polymorphic tri- and tetranucleotide microsatellite loci in a North American sedge (Carex scoparia: Cyperaceae) and cross-species amplification in three additional Carex species. Molecular Ecology Resources. 2009b;9:625–627. doi: 10.1111/j.1755-0998.2008.02480.x. [DOI] [PubMed] [Google Scholar]
  32. Hipp AL, Rothrock PE, Whitkus R, Weber JA. Chromosomes tell half of the story: The correlation between karyotype rearrangements and genetic diversity in sedges, a group with holocentric chromosomes. Molecular Ecology. 2010;19:3124–3138. doi: 10.1111/j.1365-294X.2010.04741.x. [DOI] [PubMed] [Google Scholar]
  33. Hipp AL, Chung K-S, Escudero M. Holocentric chromosomes. In: Maloy S, Hughes K, editors. Brenner's Encyclopedia of genetics. 2nd edn. New York: Academic Press; 2013. [Google Scholar]
  34. Hubisz MJ, Falush D, Stephens M, Pritchard JK. Inferring weak population structure with the assistance of sample group information. Molecular Ecology Resources. 2009;9:1322–1332. doi: 10.1111/j.1755-0998.2009.02591.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
  35. Jiménez-Mejías P, Escudero M, Guerra-Cárdenas S, Lye KA, Luceño M. Taxonomic delimitation and drivers of speciation in the Ibero-North African Carex sect. Phacocystis river-shore group (Cyperaceae) American Journal of Botany. 2011;98:1855–1867. doi: 10.3732/ajb.1100120. [DOI] [PubMed] [Google Scholar]
  36. Jiménez-Mejías P, Luceño M, Lye KA, Brochmann C, Gussarova G. Genetically diverse but with surprisingly little geographic structure: the complex history of the widespread herb Carex nigra (Cyperaceae) Journal of Biogeography. 2012;39:2279–2291. [Google Scholar]
  37. Judd WS, Campbell CS, Kellogg EA, Stevens PF, Donoghue MJ. Plant systematics: a phylogenetic approach. 3rd edn. Sunderland, MA: Sinauer Associates, Inc; 2007. [Google Scholar]
  38. King MG, Roalson EH. Discordance between phylogenetics and coalescent-based divergence modelling: exploring phylogeographic patterns of speciation in the Carex macrocephala species complex. Molecular Ecology. 2009;18:468–482. doi: 10.1111/j.1365-294X.2008.04033.x. [DOI] [PubMed] [Google Scholar]
  39. Lovit M, Haines A. A new name and status for Carex scoparia var. tessellata (Cyperaceae) Botanical Notes. 2012;14:1–5. [Google Scholar]
  40. Lowry DB, Willis JH. A widespread chromosomal inversion polymorphism contributes to a major life-history transition, local adaptation, and reproductive isolation. PLoS Biology. 2010;8:e1000500. doi: 10.1371/journal.pbio.1000500. [DOI] [PMC free article] [PubMed] [Google Scholar]
  41. Luceño M. Cytotaxonomic studies in Iberian and Macaronesian species of Carex (Cyperaceae) Willdenowia. 1992;22:149–165. [Google Scholar]
  42. Luceño M. Chromosome studies on Carex (L.) section Mitratae Kükenth. (Cyperaceae) in the Iberian Peninsula. Cytologia. 1993;58:321–330. [Google Scholar]
  43. Luceño M. Cytotaxonomic studies in Iberian, Balearic, North African, and Macaronesian species of Carex (Cyperaceae). II. Canadian Journal of Botany. 1994;72:587–596. [Google Scholar]
  44. Lukhtanov V, Dinca V, Talavera G, Vila R. Unprecedented within-species chromosome number cline in the Wood White butterfly Leptidea sinapis and its significance for karyotype evolution and speciation. BMC Evolutionary Biology. 2011;11:109. doi: 10.1186/1471-2148-11-109. [DOI] [PMC free article] [PubMed] [Google Scholar]
  45. Machado CA, Kliman RM, Markert JA, Hey J. Inferring the history of speciation from multilocus DNA sequence data: the case of Drosophila pseudoobscura and close relatives. Molecular Biology and Evolution. 2002;19:472–488. doi: 10.1093/oxfordjournals.molbev.a004103. [DOI] [PubMed] [Google Scholar]
  46. Machado CA, Haselkorn TS, Noor MAF. Evaluation of the genomic extent of effects of fixed inversion differences on intraspecific variation and interspecific gene flow in Drosophila pseudoobscura and D. persimilis. Genetics. 2007a;175:1289–1306. doi: 10.1534/genetics.106.064758. [DOI] [PMC free article] [PubMed] [Google Scholar]
  47. Machado CA, Matzkin LM, Reed LK, Markow TA. Multilocus nuclear sequences reveal intra- and interspecific relationships among chromosomally polymorphic species of cactophilic Drosophila. Molecular Ecology. 2007b;16:3009–3024. doi: 10.1111/j.1365-294X.2007.03325.x. [DOI] [PubMed] [Google Scholar]
  48. Mantel N. The detection of disease clustering and a generalized regression approach. Cancer Research. 1967;27:209–220. [PubMed] [Google Scholar]
  49. Mastrogiuseppe J, Rothrock PE, Dibble AC, Reznicek AA. Flora of North America North of Mexico. Vol. 23. New York: Oxford University Press; 2002. Carex L. sect. Ovales Kunth; pp. 332–378. Flora of North Americaial Committee. [Google Scholar]
  50. Mola LM, Papeschi AG. Holokinetic chromosomes at a glance. Journal of Basic and Applied Genetics. 2006;17:17–33. [Google Scholar]
  51. Navarro A, Barton NH. Accumulating postzygotic isolation genes in parapatry: a new twist on chromosomal speciation. Evolution. 2003a;57:447–459. doi: 10.1111/j.0014-3820.2003.tb01537.x. [DOI] [PubMed] [Google Scholar]
  52. Navarro A, Barton NH. Chromosomal speciation and molecular divergence – accelerated evolution in rearranged chromosomes. Science. 2003b;300:321–324. doi: 10.1126/science.1080600. [DOI] [PubMed] [Google Scholar]
  53. Nei M, Tajima F, Tateno Y. Accuracy of estimated phylogenetic trees from molecular data. II. Gene frequency data. Journal of Molecular Evolution. 1983;19:153–170. doi: 10.1007/BF02300753. [DOI] [PubMed] [Google Scholar]
  54. Noor MAF, Gratos KL, Bertucci LA, Reiland J. Chromosomal inversions and the reproductive isolation of species. Proceedings of the National Academy of Sciences, USA. 2001a;98:12084–12088. doi: 10.1073/pnas.221274498. [DOI] [PMC free article] [PubMed] [Google Scholar]
  55. Noor MAF, Grams KL, Bertucci LA, Almendarez Y, Reiland J, Smith KR. The genetics of reproductive isolation and the potential for gene exchange between Drosophila pseudoobscura and D. persimilis via backcross hybrid males. Evolution. 2001b;55:512–521. doi: 10.1554/0014-3820(2001)055[0512:tgoria]2.0.co;2. [DOI] [PubMed] [Google Scholar]
  56. Noor MAF, Garfield DA, Schaeffer SW, Machado CA. Divergence between the Drosophila pseudoobscura and D. persimilis genome sequences in relation to chromosomal inversions. Genetics. 2007;177:1417–1428. doi: 10.1534/genetics.107.070672. [DOI] [PMC free article] [PubMed] [Google Scholar]
  57. Nybom H. Comparison of different nuclear DNA markers for estimating intraspecific genetic diversity in plants. Molecular Ecology. 2004;13:1143–1155. doi: 10.1111/j.1365-294X.2004.02141.x. [DOI] [PubMed] [Google Scholar]
  58. Ohkawa T, Yokota M, Hoshino T. Aneuploidal population differentiation in Carex sociutu Boott (Cyperaceae) of the Ryukyu Islands, Japan. Botanical Journal of the Linnean Society. 2000;132:337–358. [Google Scholar]
  59. Ohta T, Kimura M. A model of mutation appropriate to estimate the number of electrophoretically detectable alleles in a finite population. Genetic Research. 1973;22:201–204. doi: 10.1017/s0016672300012994. [DOI] [PubMed] [Google Scholar]
  60. Peakall R, Smouse PE. GENALEX 6: genetic analysis in Excel. Population genetic software for teaching and research. Molecular Ecology Notes. 2006;6:288–295. doi: 10.1093/bioinformatics/bts460. [DOI] [PMC free article] [PubMed] [Google Scholar]
  61. Pritchard JK, Stephens M, Donnelly P. Inference of population structure using multilocus genotype data. Genetics. 2000;155:945–959. doi: 10.1093/genetics/155.2.945. [DOI] [PMC free article] [PubMed] [Google Scholar]
  62. Reznicek AA. Evolution in sedges (Carex, Cyperaceae) Canadian Journal of Botany. 1990;68:1409–1432. [Google Scholar]
  63. Rieseberg LH, Linder CR, Seiler GJ. Chromosomal and genic barriers to introgression in Helianthus. Genetics. 1995;141:1163–1171. doi: 10.1093/genetics/141.3.1163. [DOI] [PMC free article] [PubMed] [Google Scholar]
  64. Rieseberg LH, Whitton J, Gardner K. Hybrid zones and the genetic architecture of a barrier to gene flow between two sunflower species. Genetics. 1999;152:713–727. doi: 10.1093/genetics/152.2.713. [DOI] [PMC free article] [PubMed] [Google Scholar]
  65. Roalson EH. A synopsis of chromosome number variation in the Cyperaceae. Botanical Review. 2008;74:209–393. [Google Scholar]
  66. Rothrock PE, Reznicek AA. Documented chromosome numbers 1996: 1. Chromosome numbers in Carex section Ovales (Cyperaceae) from eastern North America. SIDA, Contributions to Botany. 1996;17:251–258. [Google Scholar]
  67. Rotreklová O, Bureš P, Repka R, et al. Chromosome numbers of Carex. Preslia. 2011;83:25–58. [Google Scholar]
  68. Saeki I, Dick CW, Barnes BV, Murakami N. Comparative phylogeography of red maple (Acer rubrum L.) and silver maple (Acer saccharinum L.): impacts of habitat specialization, hybridization and glacial history. Journal of Biogeography. 2011;38:992–1005. [Google Scholar]
  69. Schmid B. Karyology and hybridization in the Carex flava complex in Switzerland. Feddes Repertorium. 1982;93:23–59. [Google Scholar]
  70. Schönswetter P, Elven R, Brochmann C. Trans-Atlantic dispersal and large-scale lack of genetic structure in the circumpolar, arctic–alpine sedge Carex bigelowii s.l. (Cyperaceae) American Journal of Botany. 2008;95:1006–1014. doi: 10.3732/ajb.2007196. [DOI] [PubMed] [Google Scholar]
  71. Schuelke M. An economic method for the fluorescent labeling of PCR fragments. Nature Biotechnology. 2000;18:233–234. doi: 10.1038/72708. [DOI] [PubMed] [Google Scholar]
  72. Sinnott RW. Virtues of the Haversine. Sky Telescope. 1984;68:159. [Google Scholar]
  73. Smouse PE, Long JC, Sokal RR. Multiple regression and correlation extensions of the Mantel test of matrix correspondence. Systematic Zoology. 1986;35:627–632. [Google Scholar]
  74. Strasburg JL, Rieseberg LH. How robust are ‘isolation with migration’ analyses to violations of the IM model? A simulation study. Molecular Biology and Evolution. 2010;27:297–310. doi: 10.1093/molbev/msp233. [DOI] [PMC free article] [PubMed] [Google Scholar]
  75. Tang J, Hanage WP, Fraser C, Corander J. Identifying currents in the gene pool for bacterial populations using an integrative approach. PLoS Computational Biology. 2009;5:e1000455. doi: 10.1371/journal.pcbi.1000455. [DOI] [PMC free article] [PubMed] [Google Scholar]
  76. Thuillet A-C, Bru D, David J, et al. Direct estimation of mutation rate for 10 microsatellite loci in durum wheat, Triticum turgidum (L.) Thell. ssp. durum Desf. Molecular Biology and Evolution. 2002;19:122–125. doi: 10.1093/oxfordjournals.molbev.a003977. [DOI] [PubMed] [Google Scholar]
  77. Vigouroux Y, Jaqueth JS, Matsuoka Y, et al. Rate and pattern of mutation at microsatellite loci in maize. Molecular Biology and Evolution. 2002;19:1251–1260. doi: 10.1093/oxfordjournals.molbev.a004186. [DOI] [PubMed] [Google Scholar]
  78. Whitkus R. Experimental hybridization among chromosome races of Carex pachystachya and the related species Carex macloviana and Carex preslii (Cyperaceae) Systematic Botany. 1988a;13:146–153. [Google Scholar]
  79. Whitkus R. Systematics and evolution of the Carex pachystachya complex (Cyperaceae) PhD thesis, Ohio State University: USA; 1988b. [Google Scholar]
  80. Whitkus R. Chromosome counts of Carex section Ovales. Botanical Gazette. 1991;152:224–230. [Google Scholar]
  81. Whitkus R. Allozyme variation within the Carex pachystachya complex (Cyperaceae) Systematic Botany. 1992;17:16–24. [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

Supplementary Data
supp_112_3_515__index.html (1.1KB, html)
supp_mct119_mct119supp_fig1.pdf (446.7KB, pdf)
supp_mct119_mct119supp_table1.xlsx (2.3MB, xlsx)

Articles from Annals of Botany are provided here courtesy of Oxford University Press

RESOURCES