Thermostabilization of the β₁-adrenergic receptor Correlates with Increased Entropy of the Inactive State

Abstract

The dynamic nature of GPCRs is a major hurdle in their purification and crystallization, but thermostabilization can facilitate structure determination, as has been shown by the structure of the thermostabilized β₁-adrenergic receptor (β₁AR) mutant, m23-β₁AR, which has been thermostabilized in the inactive state. However, it is unclear from the structure how the six thermostabilizing mutations in m23-β₁AR affect receptor dynamics. We have used molecular dynamics simulations in explicit solvent to compare the conformational ensembles for both wild type β₁AR (wt-β₁AR) and m23-β₁AR. Thermostabilization results in an increase in the number of accessible microscopic conformational states within the inactive state ensemble, effectively increasing the side chain entropy of the inactive state at room temperature, while suppressing large-scale main chain conformational changes that lead to activation. We identified several diverse mechanisms of thermostabilization upon mutation. These include, decrease of long range correlated movement between residues in the G-protein coupling site to the extracellular region (Y227A^5.58, F338M^7.48), formation of new hydrogen bonds (R68S), and reduction of local stress (Y227^5.58, F327^7.37 and F338^7.48). This study provides insights into microscopic mechanisms underlying thermostability that leads to an understanding of the effect of these mutations on the structure of the receptor.

INTRODUCTION

G-protein-coupled receptors (GPCRs) are seven helical transmembrane (TM) proteins that activate G-proteins upon binding agonists, such as hormones or neurotransmitters. Their key role in signal transduction makes them useful targets for therapeutic treatment. Newly developed strategies for determining the structures of GPCRs ^1–3 will have a dramatic impact on the development of new drugs with enhanced specificity and better efficacy ⁴. However, determination of GPCR structures is still challenging due to their conformational flexibility, which plays an essential role in the activation of GPCRs. This conformational flexibility contributes significantly to the instability of GPCRs in detergents, hence decreasing the probability of obtaining well-ordered crystals ⁵. One strategy for improving the likelihood of obtaining crystals using lipidic cubic phase technology has been to engineer GPCR chimeras with T4 lysozyme inserted into intracellular loop 3 (ICL3) or by co-crystallization with antibody fragments ^6–7. The other strategy is to conformationally thermostabilize GPCRs so that the receptors are preferentially in a single conformational state and, in addition, tolerant of short chain detergents ideal for crystallography ⁸. Thermostabilized GPCRs are readily purified and ideal for biophysical studies such as analyses using surface plasmon resonance or for crystallization ^2,9–10. The structures of thermostable mutants of three class A GPCRs, the adenosine A_2A receptor and the avian β₁-adrenergic receptor (β₁AR), and the rat neurotensin receptor have been determined bound to either antagonists, agonists or biased agonists ¹¹. However, the structural basis for the difference in stability of the mutant GPCRs compared to the wild type is not clear. β₁AR, was stabilized by the inclusion of six thermostabilizing mutations ¹². The thermostabilization procedure was based on Ala/Leu scanning mutagenesis where every residue was mutated to Ala (except for Ala residues that were mutated to Leu), each mutant was expressed and its thermostability was determined relative to the wild type receptor. Once thermostabilizing mutations were identified, they were mutated to other amino acid residues to see if further improvements in thermostability were obtained. The best thermostabilizing mutations were then combined to give the optimally stable mutant m23-β₁AR. This is a time-consuming process, so if we understand the structural and kinetic basis for why the mutations were thermostablizing, then it might be possible to predict which residues in a model of a GPCR structure are thermostabilizing, thus facilitating an accelerated route to thermostabilization and structure determination.

The structural basis of thermostability of soluble proteins has been studied extensively from the perspectives of structure, biophysics and thermodynamics ¹³. In contrast, studies on membrane protein stability are less common, which is probably because they are far less tractable experimentally ^14–15. The physicochemical properties of membrane proteins dictate that detergents are essential for their solubilization from membranes and for their subsequent purification. The environment of the detergent micelle is not a perfect mimetic of a membrane, which often results in decreased stability of membrane proteins after purification ⁵. In addition, the ideal scenario for a thermodynamic analysis of protein stability would be to have a reversible folding-unfolding equilibrium, but this has been achieved for only a handful of membrane proteins ¹⁶. For example, a number of studies have been performed on the kinetics of unfolding and folding of bacteriorhodopsin ¹⁷, light harvesting complex ¹⁸, and bacterial porins ¹⁹, but it has not yet been possible to do this on GPCRs. Thus, to study the role of the thermostabilizing mutations in GPCRs, the only viable option currently available is to use computational approaches.

Molecular dynamics (MD) simulations of GPCRs have been used extensively to understand conformational changes and to provide insights into the mechanism of activation in GPCRs ^20–24. MD simulations have been used in conjunction with NMR data to explore the mechanism of activation of rhodopsin ²⁵ and they have also been used to sample the ensemble of conformations in a given potential energy minimum for GPCRs ^26–27. The role of thermostable mutations has been attributed to formation or breaking of inter-residue contacts at the site of mutation that stabilizes one selective receptor conformation over the others ⁸. However not all mutations that lead to thermostability conform to this concept. In this paper we aim to analyze the effect of mutations on the global scale by calculating the differences in the ensemble of conformations sampled by the wild type and the m23-β₁AR. We have used in total 2.10 μs all-atom MD simulations combined for both wild type β₁AR (wt-β₁AR) and the thermostable mutant m23-β₁AR, in explicit lipid and water to provide a rationale for how the mutations lead to thermostabilization of m23-β₁AR compared to wt-β₁AR.

METHODS

Preparation of Protein Structure for Simulations

The starting conformation of avian m23-β₁AR for the MD simulations was obtained from the protein databank (PDB ID: 2Y04). Initial conformations for the wild type structure simulations were obtained by mutating the residues in the crystal structure of the mutant back to the wild type using Maestro9.2 [Schrodinger Inc]. Residues within 5Å of the sites of mutation were minimized using MacroModel [Schrodinger Inc.] with position restraints on all backbone atoms and all residues further than 5Å from the site of mutation.

Details of the Molecular Dynamics Simulations

The receptor structures were solvated in explicit palmitoyl oleoyl phosphatidyl choline (POPC) lipid and water. The lipid was packed around the protein using inflategro package in GROMACS ²⁸. SPC water molecules ²⁹ were added on both sides of the lipid bilayer, and 11 chloride ions were added for both m23-β₁AR and wt-β₁AR. Ten simulations with different starting velocities on wt-β1AR and m23-β1AR in a POPC lipid bilayer were performed using GROMACS 4.0.7 ²⁸ and the GROMOS96 53a6 force field ³⁰. After the systems were equilibrated at the correct temperature and pressure, MD simulations of 110 ns were performed for each of the 10 unique initial conformations, using a NVT ensemble with a NoséHoover thermostat ^31–32. A total of 1.05μs of simulation was performed for each wt-β₁AR and m23-β₁AR. This is sufficient since our goal is to analyze the conformational ensembles sampled near the inactive state of the respective receptors. More details of the simulation conditions and a discussion on the convergence of individual MD trajectories is given in the supporting text S1.

Conformational Entropy and Mutual Information calculations

The use of internal coordinates for conformational entropy calculations has previously been shown to be a more successful strategy than using Cartesian coordinates ³³. We have neglected the contributions from bond and angle degrees of freedom since they tend to be relatively small. First order conformational entropy was calculated using the Gibbs Entropy ³³ for each torsion angle. We used 35 bins in the torsion angle distribution, that choice was based on convergence of the calculated entropy values. A correction for under sampling was applied as has been done previously ^34–35. For the equations used please refer to the supporting text S1.

Force Distribution Analysis

Forces on each residue were calculated using both the bonded and non-bonded components of the GROMOS96 53a6 force field. The force on each residue was calculated by averaging the force exerted by all the other residues within 3Å and omitting the residues that are directly bonded to the residue. The averaging was done for all the snapshots from the MD simulations. The forces were calculated between each atom pair following the procedure described by Stacklies et al. ³⁶. The residue wise forces were then binned and the population density at each bin was calculated.

Principal Component Analysis

The most dominant motions sampled during MD simulations can be described using only a few principal modes ³⁷. We used the Principal Component Analysis (PCA) to understand the complex multidimensional dynamics in reduced space. PCA analysis was performed using GROMACS, on the consolidated 1μs trajectory obtained by merging the ten different simulations for each wild type and mutant. Only Cα atoms in TM1 to TM7 (Table S1) were included in the PCA to reduce noise by the highly flexible loops and the N terminal end of TM1. Eigenvalues and eigenvectors were calculated from the covariance matrix, using the g_covar command in GROMACS. We performed PCA on the MD trajectories of wt-β₁AR and m23-β₁AR receptors separately.

RESULTS

Conformational ensembles of wt-β₁AR and m23-β₁AR in the inactive state

Class A GPCRs have seven helical transmembrane (TM) regions connected by extracellular loops (ECLs) and intracellular loops (ICLs) and they usually contain a short amphipathic helix called helix 8 (H8) parallel to the membrane surface after TM7. The m23-β₁AR is a thermostable mutant (thermostable by ~20° C compared to the wt-β₁AR) with six point mutations at the positions: R68S^1.59, M90V^2.53, Y227A^5.58, A282L^ICL3, F327A^7.37 and F338M^7.48. The superscripts refer to the Ballesteros-Weinstein number of the residues ³⁸, with the ICL3 superscript referring to residues in intracellular loop 3.. To compare the ensemble of conformations sampled during the 1.05μs each of dynamics for wt-β₁AR and m23-β₁AR, we performed Principal Component Analysis (PCA) on the Cα atoms of the TM domain (TM domains for β₁AR are defined in Table S1). We have used PCA to identify the dominant collective motions of the TM domain in both mutant and wild type receptors. The dominant motions in both receptors are a global pulsating motion involving the extracellular region of the TM domains, particularly TM5 and TM6 (referred to as PC1) and, fluctuations near the extracellular interface of TM2 and TM3 (referred to as PC2) (Fig. S1A). The distance between the intracellular regions of TM3 and TM6 in both m23-β₁AR and wt-β₁AR was determined to identify any movement related to receptor activation ^39–40, but it was found to be consistently close to the inactive state of the receptor (Fig. S1). This is in contrast to previous multiscale dynamics study on ligand free wild type β₂AR, where both inactive state and an active-like state were observed ²⁰. The dominant motion sampled during MD simulations can be described using the first few principal modes as shown by the fraction of variance captured by each of the PCs shown in Figure S3.

The microscopic sub-states sampled within the inactive state conformation for wt-β₁AR and m23-β₁AR were projected on to PC1 and PC2 (Fig. 1). One broad and densely populated conformational cluster was observed during the MD simulation of m23-β₁AR that showed an RMSD of ~1.5Å from the crystal structure ⁴¹. Within this broad cluster there are three sub-clusters or microscopic sub-states (Fig. S2). In comparison, wt-β₁AR has one densely populated conformational cluster and another relatively sparsely populated conformational cluster that shows partial disorder in TM1 and TM7 (Fig. S2). The RMSD of all the conformational clusters from the crystal structure (pdb: 2Y04), their calculated population, and their potential energies are shown in Fig. S2. However an increase in the number of clusters (clustered by PC) does not necessarily mean higher entropy unless we take into account the size of these clusters and the conformational diversity within individual clusters. Therefore to make the conformational diversity uniform among clusters, we clustered the conformations by RMSD in coordinates.

Figure 1.

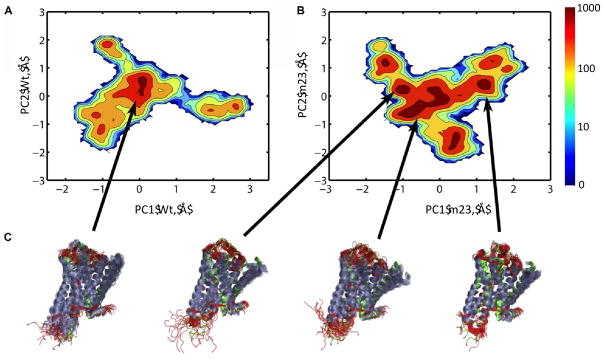
Comparison of the major motions observed in MD simulations of wt-β₁AR and thermostabilized m23-β₁AR. Conformational clusters, based on PC coordinates, were calculated from the MD simulations and are represented in 2-dimensions, projected on their respective principal components, PC1 and PC2: A. wt-β₁AR and B. the m23-β₁AR. Densely populated regions are colored in red, while sparsely populated regions are shown in deep blue. C. Representative ensemble of structures from each conformational cluster are depicted in cartoon representation (α-helices purple, non-helical regions red) aligned with the crystal structure of m23-β₁AR (green, pdb: 2Y04).

RMSD-based conformational clustering was performed to quantify the number of conformational clusters, the free energy difference between the conformational clusters and the number of transitions between these conformational clusters. We find that in the case of m23-β₁AR there are 5 conformational clusters of similar population (within 1.5kcal/mol) showing significant number of transitions to the inactive state cluster. The, wt-β₁AR on the other hand has only 3 similarly populated clusters with direct transition to the inactive cluster (Fig. S4). Furthermore, the average difference in free energy calculated from the population, between the inactive state cluster and the neighboring clusters that show transitions is 1.83 kcal/mol for m23-β₁AR, and 2.15 kcal/mol for wt-β₁AR (Fig S4). This is also reflected in an increased number of transitions from and to the inactive cluster in the mutant (7.1/100 snapshots) as compared to the wild type (5.8/100 snapshots). Based on these data we have generated a schematic representation of the difference in the free energy landscape for the inactive state (Fig. 2) and the inactive state-active state transition (Fig S5) for both wt-β₁AR and m23-β₁AR. The population of the inactive state cluster is higher in m23-β₁AR than in the wild type receptor. Thus, the dynamics of mutant m23-β₁AR shows higher population of the inactive state compared to the wild type, and does so by generating multiple microscopic sub-states (Fig. 2) within the inactive state. We speculate that these microscopic states would dissipate the extra thermal energy at high temperatures thus retaining the overall fold of the inactive state. In contrast, wt-β₁AR has lower population of the inactive state and fewer microscopic sub-states within the inactive state. The wild type receptor shows a population of other conformations well removed from the inactive state and are partially disordered and separated by large energy barriers. Therefore, at high temperatures wt-β₁AR could possibly increase the population of disordered states leading to protein aggregation, as observed by Serrano-Vega et al. ¹². The multiple sub-states in m23-β₁AR increases the localized entropy of the inactive state of the receptor, making the free energy of the inactive state more favorable. As shown in the section below, this increase in entropy comes from a reduction in correlated side chain movement between residues in EC region and the G-protein coupling region.

Figure 2.

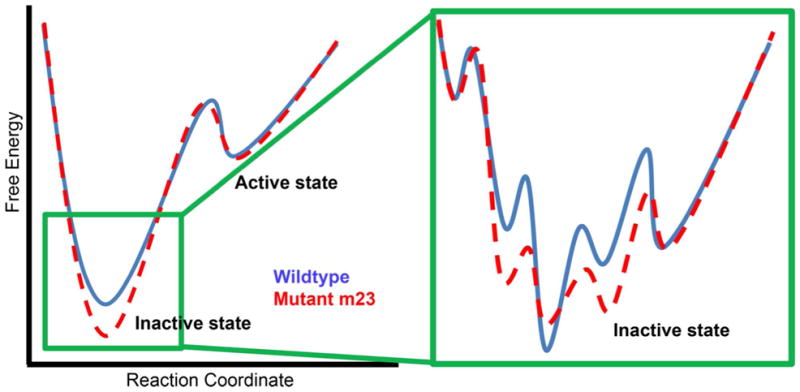
Schematic representation of the free energy landscape of the inactive state of β₁AR. The blue line represents the free energy profile for wt-β₁AR and the dashed red line is for the thermostable mutant m23-β₁AR. The schematic energy landscape is based on the data on the ensemble of conformations sampled in the MD simulations of these two receptors (Figure 1 and Figure S3).

Localized entropy differences between wt-β₁AR and m23-β₁AR stems from loss of correlated movement among residues in the mutant

To understand the basis for higher thermostability of the m23-β₁AR mutant compared to wt-β₁AR, we analyzed the enthalpic and entropic components of free energy of the ensemble of receptor conformations sampled in the MD simulations. There is no significant difference in the calculated average potential energy of the receptor when comparing the conformations sampled by wt-β₁AR (−2167±130 kcal/mol) compared to m23-β₁AR (−2140±126 kcal/mol). It should be noted that these potential energies were calculated in explicit lipid bilayer and water and not in detergents as done in experiments. The normalized potential energy distribution (Fig. S6A) shows a higher peak for the m23-β₁AR compared to the wt-β₁AR. This result, combined with the observation that the wt-β₁AR samples less number of microscopic sub-states (Fig. 1), suggests that increased entropic contribution could be a major reason of thermostabilization for the m23 mutant.

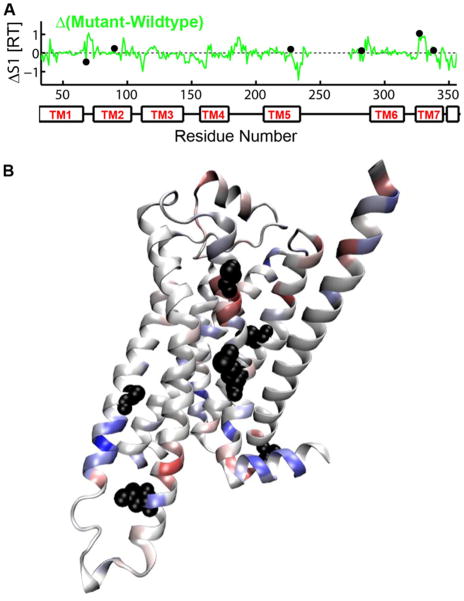
To investigate which thermostabilizing mutations contribute to the increased entropy of m23-β₁AR, we have calculated residue based torsional entropy as the sum of the entropy of the individual torsional degrees of freedom and the residue pairwise correlations that reduces the entropy ³³. Comparison of the residue entropy for wt-β₁AR and m23-β₁AR (Fig. 3) shows that the major differences in entropy is often found near the sites of mutation. To quantify this observation, we have reported the maximal change in entropy within 2 helical turns (±4 residues) of each thermostabilizing mutation (neighborhood entropy change). All of the mutations show neighborhood entropy changes in excess of 2.5σ (σ: standard deviation over all residues). The neighborhood entropy changes for individual mutations are 0.8 kcal/mol, z-score: 3.6 (R68S^1.59), 0.57 kcal/mol, z-score: 2.6 (M90V^2.53), 0.84 kcal/mol, z-score: 3.8 (Y227A^5.58), 0.57 kcal/mol, z-score: 2.6 (A282L^ICL3), 0.65 kcal/mol, z-score: 2.9 (F327A^7.37) and 0.59 kcal/mol, z-score: 2.7 (F338M^7.48). In addition, increased entropy in the mutant is observed in the extracellular half (0.95 kcal/mol more in the mutant) of the receptor (e.g. TM1, TM2 and TM7) while the entropy is reduced in the intracellular half of m23-β₁AR (1.92 kcal/mol more in the wildtype), definitions of EC and IC half are given in Table S2. The reduced torsional entropy in the intracellular region of the m23-β₁AR would be expected to lower the propensity for the mutant receptor to get activated. This was observed in the experiments of agonist induced activation and agonist binding affinity measurements by Serrano-Vega et al. ¹².

Figure 3.

The difference in the first order entropy (ΔS¹) for each amino acid in m23-β₁AR and wt-β₁AR. A. ΔS¹ plotted against the position in the amino acid sequence. Filled black circles show the location of the 6 thermostabilizing mutations in m23-β₁AR. B. The difference in first order entropy between wt-β₁AR and m23-β₁AR is depicted on a cartoon of the m23-β₁AR structure: regions in blue have lower entropy in m23-β₁AR compared to wt-β₁AR, while regions in red have higher entropy. The side chains of thermostabilizing residues are shown as black spheres.

Thermostable mutant m23-β₁AR loses correlated movement among residues involved in receptor activation

Certain residues in class A GPCRs have been shown to change their conformations upon activation and hence are proposed to act as ‘molecular switches’ ^{20,23–24,42–43}. To analyze if these residues are involved in activation leading to concerted motion between the ligand binding site and G-protein coupling site, we have analyzed the correlated movement of residue pairs during the dynamics of the wt-β₁AR and m23-β₁AR, using Mutual Information ^33–35. Correlation in movement between residues that are far removed in sequence leads to a reduction in entropy, because it reduces the number of unique conformational states sampled. Mutual Information has been used previously for the identification of allosteric communication pathways ^34,44 and the quantification of conformational entropy ³³.

Several of the mutation sites show differences in cross correlation with other residues in the receptor when compared between wt-β₁AR and m23-β₁AR (Fig. 4). We observe that the residue Y227^5.58 in wt-β₁AR shows many inter-residue correlations, the majority of which are lost upon mutation to alanine in m23-β₁AR (Fig. 4A). Y227^5.58 also undergoes conformational change upon activation in the wt-β₁AR and makes contact with Arg^3.50 on TM3 upon activation, and breaks the ionic lock between TM3 and TM6 (Fig. S7) ^39,45. Therefore mutation of this residue leads to preservation and stabilization of the ionic lock and hence the inactive state and a substantial increase in thermostability ²⁷. We observe a reduction in coupling (37% less than wild type) between the sites of the receptor correlated to Y227^5.58 and this contributes to the increased entropy in m23-β₁AR. Thus the increased entropy resulting from the loss of inter-residue correlation as well as the strengthening of the ionic lock in the inactive state could explain the pronounced effect of the Y227^5.58 A mutation on the stability of the inactive state. Likewise, the R68S mutation leads to a loss in correlation in m23-β₁AR (Fig 4B). We observed that the R68S mutation also leads to the formation of a hydrogen bond between TM1 and helix8 (H8) (Fig. S8). The mutated S68^1.59 forms a hydrogen bond with R355 on H8. Subsequent to our prediction, this hydrogen bond was also observed in a recent crystal structure ⁴⁶ (additional discussion in SI Text). F327A mutation (Fig. S9C) leads to an increase in inter-residue correlation between this residue and other residues in the receptor. In the wildtype receptor F327^7.37 is pointing into the lipid bilayer and, upon mutation to alanine, this interaction is lost and the residue becomes more correlated with the rest of the protein. As we show later in the paper, the net stress on F327^7.37 is high and hence the mutation F327A relieves this stress conferring thermostability.

Figure 4.

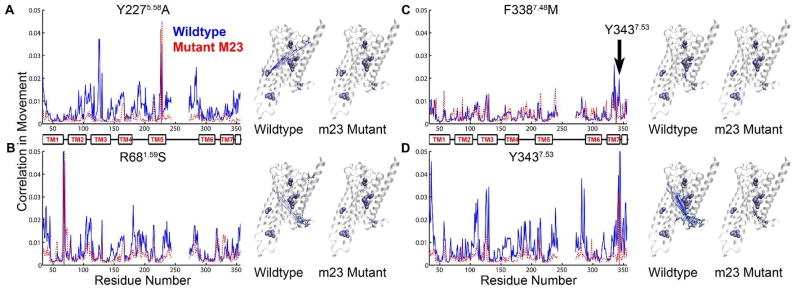
Calculated correlated movement of thermostabilizing residues with all the residues in the receptor. Each graph shows the calculated correlation in movement versus the amino acid number for both wt-β₁AR (solid blue line) and the thermostable mutant m23-β₁AR (dashed red line). Associated to the right of each graph are two cartoons of the β₁AR structure showing the side chains of thermostabilizing amino acid residues (space filling models, purple) and amino acid residues that show correlated movement (sticks; C, cyan; O, red; N, blue). In each figure, dashed lines link the Cα atom of the thermostabilizing mutation with the amino acid residue showing correlated movement: wt-β₁AR, blue; m23-β₁AR, red. Both A. the Y227A and B. R68S thermostabilizing mutations reduce correlated movement between the thermostabilizing residue and many residues throughout the receptor. C. The major effect of the F338M mutation is to cause a loss in correlated movement between the residue and Y343^7.53. D. The residue Y343^7.53, which is affected by the neighboring mutation F338M, shows reduced correlated movement to many residues in the receptor.

In the dynamics of the wt-β₁AR, we observed ²⁷ two possible microstates for F338^7.48 -one in which it shows π stack interaction with Y343^7.53 which in turn π stacks with F349^7.59; and the other in which there is no such π stacking with Y343^7.53. Y343^7.53 is part of the conserved NPxxY motif common to most class A GPCRs, and it is known to move upon activation in β₂AR ³⁹. However in the m23-β₁AR, the F338M mutation breaks its π stack interaction with Y343^7.53, resulting in strengthening of the π stacking between Y343^7.53 and F349^7.59 which is characteristic of the inactive receptor state ¹⁰. Here we also observe a loss of correlation of M338^7.48 with Y343^7.53 in m23-β₁AR (Fig. 4C) and this decouples M338^7.48 from the rest of the receptor (Fig. 4D), resulting in an increase in localized entropy and thereby stabilization. The other sites of mutation show less significant differences in mutual information (Fig. S9A–C). The stability of the two mutations M90V and A282L could not be explained by our studies. The mutation A282L is in the ICL3 which is truncated in the structure and hence shows large fluctuations.

Overall, the wt-β₁AR shows more inter-residue correlations (Fig. S9D), leading to a higher order network of correlated residues. We have calculated the reduction in entropy due to correlated motion shown in Table S3. As expected, the correlation between residues in the IC half or between IC and EC half (Table S2) is higher in the wt-β₁AR compared to m23-β₁AR (Fig. S9D)(Table S3). This may explain the reduced potential for the m23-β₁AR to attain an activate state conformation. m23-β₁AR also shows increased inter-residue correlations localized in the EC half of the receptor (Fig. S9D)(Table S3). Thus the communication between residue pairs in the intracellular half of the receptor is reduced as a result of the thermostabilizing mutations, and several residues that are known to play a role in receptor activation lose correlation, resulting in a more inactive like receptor (Fig. 4).

Dynamics of inter-residue contacts that are related to receptor activation suggest that m23 is less prone to get activated

We have measured the variation of several critical inter-residue distances over time from the MD simulations. Comparison of the distribution of these inter-residue contacts between wt-β₁AR and m23-β₁AR, shows that m23-β₁AR has a stronger preference for the inactive state. Most noticeably, the distance distribution of Y343^7.53 to F349^H8 has two peaks for the wt-β₁AR simulations, but only one peak corresponding to the inactive state in the m23-β₁AR simulations (Fig. 5A). The salt bridge known as the “ionic lock” between R139^3.50 of the conserved DRY motif on TM3, and E285^6.30 on TM6 is more frequently formed in the m23-β₁AR than in wt-β₁AR simulations, although this interaction is very dynamic in our simulations (Fig. 5B). Therefore we conclude that this ionic lock is not an essential feature of the inactive state either in the wild type or m23-β₁AR; in fact there is no ionic lock observed in the crystal structure of m23-β₁AR in complex with cyanopindolol ¹⁰. Fig. 5C shows the distance distribution between residues S212^5.43 to N310^6.55 that form a hydrogen bond in the agonist bound crystal structure of β₁AR (pdb ID: 2Y04), but not in the antagonist bound crystal structure (pdb ID: 2VT4). This suggests that the hydrogen bond may be important in agonist-induced activation of the receptor, which is corroborated by mutational analysis of Ser207^5.43 in β₂AR ⁴⁷. Simulations of wt-β₁AR showed more sustained hydrogen bond formation than in m23-β₁AR simulations (Fig. 5C), supporting the contention that m23-β₁AR is preferentially in an inactive state. We have also calculated the distance between the C_γ atoms F299^6.44 and P219^5.50 since this distance increased upon activation of β₂AR ³⁹. However, in both m23-β₁AR and wt-β₁AR simulations we find F299^6.44 exclusively in the inactive conformation. This is in agreement with MD simulations that were performed starting from the active state conformation of β₂AR where F282^6.44 returns to its inactive conformation quickly in the absence of G-protein ²³, indicating that F299^6.44 conformational change may occur late in the activation pathway.

Figure 5.

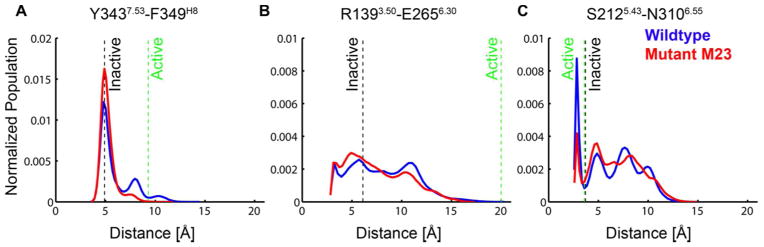
m23-β₁AR is more often in the inactive state as defined by distance distributions for inter-residue contacts related to receptor activation. The population of distances measured between specific atoms plotted; m23-β₁AR, red; wt-β₁AR, blue. Distances for the inactive state (black dashed line) were defined from the crystal structure of m23-β₁AR (PDB ID: 2Y04 and the active state distance was estimated as the corresponding distance in the β₂AR-Gs bound crystal (PDB ID: 3SN6 (green dashed line) A. Distance between C_γ atoms of Y343^7.53 -F349^H8; B. Minimum distance between R139^3.50 -E265^6.30 i.e. the ‘ionic lock’ at the intracellular end of TM3 and TM6. C. Oγ on S212^5.43 – Nδ on N310^6.55.

Stress Distribution in β₁AR correlates with the measured thermostability

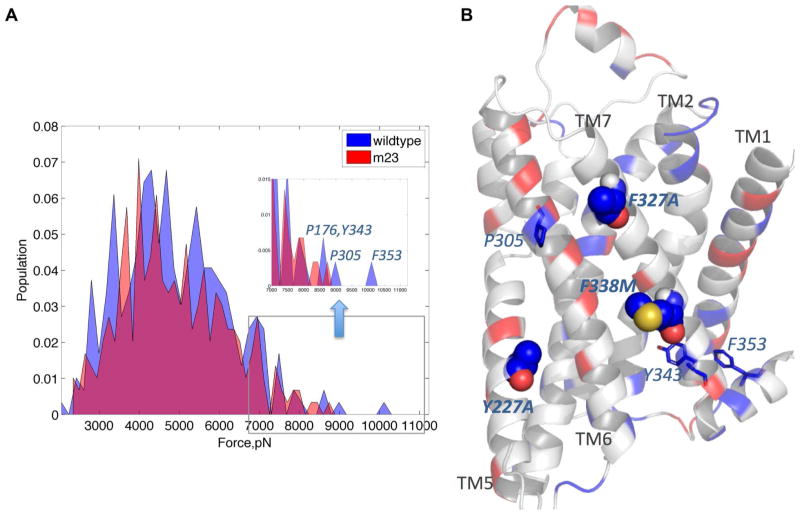
The distribution of the intramolecular repulsive and attractive forces within a protein structure governs how the protein reacts to thermal stress, since non-optimal distribution of internal stress can lead to structural destabilization at elevated temperatures ⁴⁸. Internal stress at certain regions/residues of the receptor is necessary for movement of those regions/residues during receptor activation ^36,49. Thus a balance of these internal forces is required to maintain receptor stability and activity. To understand the basis of thermostability, we have calculated the net force on each residue averaged over the snapshots of the MD simulations for both m23-β₁AR and wt-β₁AR. This average force is a measure of the intensity of localized stress in the structure. Fig. 6A compares the population distribution of stress at each residue within the wt-β₁AR and m23-β₁AR averaged over the trajectory of the MD simulations; positive and negative forces indicate repulsive and attractive forces, respectively. Although both wt-β₁AR and m23-β₁AR show a very similar force distribution, closer analysis shows that wt-β₁AR has an extended high stress or repulsive force region (in excess of 9000 pN; Fig. 6). The relative population of these high stress regions in wt-β₁AR is small and may not affect the folded structure at physiological temperature. However at high temperatures and in detergent, these high stress domains could form hot spots that lead to destabilization and possibly denaturation of the wild type receptor. The regions that show the highest stress in wt-β₁AR are P176^4.60, P305^6.50, Y343^7.53 and F353^H8 (Fig. 6B). Three of the strong thermostable mutations¹² show high stress in the wild type that gets relieved upon mutation: Y227A^5.58 on TM5 (thermostability index: 252), F327A^7.37 on TM7 (thermostability index: 180) and F338M^7.48 on TM7 (thermostability index: 191).

Figure 6.

A. Comparison of population density distribution of forces calculated on each residue. Forces are calculated by taking averages within 3 Å of each residue position, including both bonded and non-bonded force components; Populations (proportion of residues within each force range) are plotted with respect to the calculated force; wt-β₁AR, blue; m23-β₁AR, red; overlap, magenta. Regions of high stress in the wt-β₁AR are shown in the inset and the residues that contribute most to the peaks with high force values are shown. B. Differences in forces calculated between m23-β₁AR and wt-β₁AR are depicted on the structure of m23-β₁AR. Regions that show a change in force of more than 10 pN are highlighted. Regions of increased inter-residue forces in m23-β₁AR compared to wt-β₁AR, are shown in red and decreased stress are in blue. The thermostabilizing residues that show major stress reduction are shown as spheres and the other residues with significantly lower stress are shown as sticks.

Other regions that show significant stress in wt-β₁AR are P305^6.50 on TM6 and F353 on helix 8. P305^6.50 forms the hinge for the kink in TM6 and modulation of the proline kink could be crucial for the outward motion of TM6 leading to activation ^25,43. Thus reduced stress at P305^6.50 could lead to increased stability of the inactive state in m23-β₁AR. The residue F353^H8 forms π stacking interaction with Y343^7.53 and could be responsible for the stabilization of TM7 and helix 8 in the inactive state ²⁷. Comparison of the inactive and active state crystal structures of β₂AR (PDB: 2RH1 and 3SN6), shows that there is significant structural difference at the intracellular end of TM7 near the Y343^7.53 -F353^H8 interface (Fig. S8). Thus relaxation of stress near F353^H8 could stabilize the inactive conformation of TM7.

DISCUSSION

Conformational thermostabilization is a technique that results in conformational homogeneity in receptor mutants (8). This approach has now successfully been used for the structure determination of three GRPCs ^9–11,41,50. As the reasons for the increased stability of the receptor mutants were not obvious from the crystal structures, we have analyzed here the thermostabilized inactive-state m23-β₁AR. Using all-atom MD simulations, we have investigated the dynamics of wt-β₁AR and its thermostable mutant m23-β₁AR to understand the role of the mutations in conferring thermostability. The backbone flexibility of the thermostable mutant and the wild type receptor are similar. m23-β₁AR showed an increase in “localized flexibility” of the side chains within the inactive state (multiple microscopic states within the inactive state), effectively increasing the entropy of the inactive state. This aids in retention of the native functional state at higher temperatures by absorbing the extra thermal energy into localized fluctuations. Loss of correlated movement among residues could be a contributing factor behind the increase in the side chain movements.

In this study we present evidence that thermostabilization in β₁AR could be directly related to increased local entropy of the inactive state. Additionally, there are enthalpic contributions to stabilization by formation or breakage of localized residue networks through hydrogen bonds. Mutating residues that are points of high stress in the wild type receptor also leads to thermostabilization. The MD simulations in this study were done in explicit lipid bilayer and not in detergent solutions (as used in experiments), where there could be an enthalpic difference. Another point to be noted is that we have not examined the effect of the mutations on the enthalpy and entropy of the active state of the receptor, since there is no crystal structure of the active state of β₁AR. It is possible that these mutations have effects on active state conformations that are not investigated here. We have compared the enthalpic and entropic differences of only the inactive state of the wt-β₁AR and thermostable mutant m23-β₁AR.

Entropic stabilization of proteins has been found previously for thermophilic soluble proteins. Hydrogen/Deuterium exchange experiments on the hyperthermophilic rubredoxin ⁵¹, neutron scattering experiments on thermophilic and mesophilic dihydrofolate reductase ⁵² and α-amylase ⁵³, Fourier Transform-IR studies on thermophilic esterase ⁵⁴ and MD simulations on thermophilic homolog of subtilisin and esterases ^55–56 all have shown that the thermophilic proteins exhibit greater microscopic flexibility than their corresponding mesophilic homologs. These studies propose that thermostability comes from the entropic contributions that flatten the energy surface similar to the data (Figs. 1 and 2) presented in this work. Although there are folding and unfolding kinetic measurements for membrane proteins, there are no direct measurements of the relationship between thermal stability and internal equilibrium fluctuations in the conformational dynamics.

CONCLUSIONS

Our results provide valuable first insights into the one of the plausible mechanisms of thermostability in GPCRs. For instance, mutations that increase localized entropy while retaining the overall fold of the native state could have a higher propensity of being thermostable. Mutants that break networks of correlated residues that lead to activation have the potential to stabilize the inactive state of the receptor. Mutations that redistribute stress and/or form new favorable interaction networks can increase thermostability. Our study offers insight for four out of six mutations present in m23-β₁AR. However we could not explain the stability of A282L^ICL3 since this is present in the truncated sequence of ICL3. The other mutation that we could not understand is M90V^2.53. This residue is not involved in any inter-residue correlations in wt-β₁AR and is not in a region of high stress. However, we did observe some changes in the flexibility of residues surrounding M90V (Fig 3). Thus although we can offer insights into the themostabilization effected by the majority of thermostabilizing mutations in m23-β₁AR, there are clearly other factors that still need to be taken into account. For example, the role of the detergent micelle in stabilizing mutant receptors is unknown and this may lead to further insights into why some mutations that face the lipid bilayer are thermostabilizing. However, the results presented here provide a foundation for further studies on the stability of membrane proteins in a range of different environments.