Bards, Poets, and Cliques: Frequency-Dependent Selection and the Evolution of Language Genes

Abstract

The ability of humans to communicate via language is a complex, adapted phenotype, which undoubtedly has a recently evolved genetic component. However, the evolutionary dynamics of language-associated alleles are poorly understood. To improve our knowledge of such systems, a population-genetics model for language-associated genes is developed. (The model is general and applicable to social interactions other than communication.) When an allele arises that potentially improves the ability of individuals to communicate, it will experience positive frequency-dependent selection because its fitness will depend on how many other individuals communicate the same way. Consequently, new and rare alleles are selected against, posing a problem for the evolutionary origin of language. However, the model shows that if individuals form language-based cliques, then novel language-associated alleles can sweep through a population. Thus, the origin of language ability can be sufficiently explained by Darwinian processes operating on genetic diversity in a fi-nite population of human ancestors.

1 Introduction

Humans possess a unique and innate ability for complex communication called language, with several features of our anatomy appearing to have evolved for its use (Pinker and Jackendoff 2005; Nishimura et al. 2006; Corballis 2009). Given the large number of human features associated with language, it seems safe to assume that there are underlying genetic factors that have evolved at least in part for its production and use (Pinker and Bloom 1990). However, the literature concerning the evolutionary dynamics of such genes is surprisingly limited. Here I present a population-genetics model for the evolution of language-associated alleles and show how selection for improved communication can fix novel language-specific alleles. In contrast to previous predictions (Smith 2004; Smith and Kirby 2008), the model presented here finds that the obstacles posed by frequency-dependent selection can be overcome. I further argue that the interaction of selection with other evolutionary forces actually serves to increase the probability of fixation of language-specific genes. These results have broad implications for our understanding of the evolution of language ability, especially the demarcation problem: what aspects of language are specific to it and uniquely human (Hauser and Chomsky 2002; Pinker and Jackendoff 2005).

Complex language is a uniquely human ability. Although studies have found that certain species of animals possess the ability to learn rudimentary forms of language-like communication (Corballis 2009), their abilities are easily surpassed by very young children, who spontaneously acquire language through interacting with older humans (Darwin 1871; Hauser and Chomsky 2002; Pinker and Jackendoff 2005). Several parts of human anatomy appear to have evolved for the production and understanding of language. The most easily recognized are the face, mouth, and throat, which contain adaptations for the physical production of spoken language (Nishimura et al. 2006; Corballis 2009). Additionally, regions of the brain have been shown to be critical locations for cognition associated with language (Hagoort 2005; Corballis 2009). Given its complexity, there must be some genetic factors underlying language ability (Pinker and Bloom 1990), and these factors are likely to have evolved along the human lineage. FOXP2 is one such candidate because it is associated with deficits in language ability (Vargha-Khadem et al. 1995; Fisher et al. 1998; Lai et al. 2001; Fisher and Scharff 2009) and appears to have experienced adaptive selection in our lineage (Enard et al. 2002; Coop et al. 2008). Furthermore, several genes that are associated with auditory development and that show evidence of positive selection in the human lineage have been identified and are candidate genes for speech perception (Clark et al. 2003). Recently it was even proposed that specific ASPM and Microcephalin haplogroups were not only associated with tonal languages but actually biased populations to develop tonal languages (Dediu and Ladd 2007).

With little doubt, language—like all other complex adaptations—evolved gradually (Pinker and Bloom 1990; Pinker and Jackendoff 2005; Corballis 2009), and at various times during its evolutionary history, multiple language-ability phenotypes must have competed with one another in human populations. In these instances, some individuals communicated with an ancestral language ability and others with a derived language ability. Although each phenotype would acquire and use communication with different biases, communication between them would not necessarily be unintelligible.—Individuals with FOXP2-associated language disorders can still communicate with unaffected individuals (Vargha-Khadem et al. 1995).— During language acquisition, derived-phenotype individuals that are raised amongst ancestral-phenotype individuals would learn the existing ancestral language, but impose their own biases upon it, creating a distinctive idiolect. If there are other derived-phenotype individuals in the population, then their biases would be reinforced, and their idiolects could potentially merge into a new dialect.

Two well studied hypothesized transitions fall into this paradigm: gestures evolving into speech (Darwin 1871; Rizzolatti and Arbib 1998; Corballis 2009) and holistic communication into combinatorial language (Wray 1998; Nowak et al. 2000; Brighton 2002; Smith et al. 2003). In both instances, the ancestral form of communication was replaced by a derived—and fitter—form of communication.—Of course, “minor” transitions like improvements to the vocal tract or cognitive faculty would also fall into this paradigm.—Speech is more fit because it not only allows communication when individuals are not in direct sight of one another, but it also frees the hands for work (Corballis 2009). Likewise, combinatorial language (grammar, syntax, etc.) has been shown to offer at least two advantages over holistic language: it is cognitively more efficient when a wealth of ideas need to be communicated (von Humboldt 1836; Nowak and Krakauer 1999; Nowak et al. 2000) and produces more stable languages when children must acquire language from limited experience (poverty of input) (Brighton 2002; Smith et al. 2003). Unfortunately, this comes at a cost of increased risk for deception (Lachmann and Bergstrom 2004). Below I use a simple and intuitive population-genetics model to investigate the evolutionary dynamics of a novel language allele that produces a “fitter” language ability but arises in a population in which this fitness might not be able to be realized. While this model is described on the basis of language phenotypes, it can describe the evolutionary consequences of other types of social interaction.

2 Models and Analysis

Consider a population made up of “bards” and “poets,” where bards have the ancestral language-ability phenotype and poets have the derived phenotype. I do not propose that the phenotypic differences between bards and poets manifest in highly variable cultural aspects of language like verb-object versus object-verb orderings (Evans and Levinson 2009).—These have been shown to culturally evolve faster than biological adaptation can respond to (Christiansen and Chater 2008; Chater et al. 2009).—Rather they differ, perhaps slightly, in some fundamental cognitive or physical aspects of the language ability, e.g. in acquisition, production, or understanding of language.

Now consider that poets are able to communicate with one another more successfully than bards, such that a population of poets is likely to out compete a population of bards. In a mixed population, however, bards and poets interact with one another, and their successes also depend on how much their acquired languages overlap. In the most generous situation, poets that grow up amongst bards are able to completely learn the bardic language, while expanding upon it when communicating with other poets (complete overlap). Alternatively, the advantage of poets might come from thinking differently from bards, and although they might be able to learn the majority of the bardic language, their mastery of it could be limited, reducing the success of cross communication (partial overlap). If individuals' fitnesses are in part determined by their ability to communicate with other individuals, then bards and poets will experience positive frequency-dependent selection (Cavalli-Sforza and Feldman 1983).

While there is an enormous literature dealing with every variant of 2 × 2 interaction models in game theory and sociobiology, I will develop an explicitly genetic model in order to model directly the dynamics of language-associated alleles. I will assume that bards are homozygous for a recessive allele, BARD, and that poets have at least one copy of the correspondingly dominant allele, POET.—I also considered a model in which POET was recessive and a genic/haploid model that lacks dominance. They produce similar results, and I will note the differences where applicable.—The evolution of POET will be modeled via an extension of the dominant pairwise interaction model (Asmussen and Basnayake 1990; Asmussen et al. 2004). Pairwise interaction models derive an individual's fitness from its interactions with other individuals in the population. For each phenotype–phenotype interaction, there are partial-fitness coefficients for each of the actors. The total fitness of an individual is an average of their partial-fitness coefficients weighted by the frequency of their interaction with phenotypes in the population. The assumption of dominance in the model produces a two-phenotype system—ancestral and derived—that simplifies modeling. In the usage here, “phenotype” refers not to an individual's acquired language but rather the biases in its language ability. Poets are not born knowing a poetic language, but rather their biases result in them either acquiring it from other poets in the population or inventing it de novo, as described above. Additionally, I will not assume that poetic and bardic languages are mutually exclusive.

2.1 Complete Overlap Model

I will make the following assumptions: an infinitely large, unstructured population with random mating, no mutation, no migration, no genetic drift, and individuals interact randomly, such that the probability of each interaction type is proportional to phenotype frequencies. The impacts of violating the infinitely large and random mating assumptions will be discussed below. Let the partial fitness of two poets interacting be greater than two bards interacting, and let bards and poets receive equal fitnesses when interacting with one another—no phenotype can take advantage of the other phenotype. Let the partial fitness of poet–poet interactions be 1 + s, where s > 0 is the advantage that a poet receives from interacting with another poet. Sim-ilarly, let all other partial fitnesses be 1, i.e. complete overlap of language faculties. This produces the following partial-fitness matrix:

$$\begin{array}{ccc}& \text{Bard}& \text{Poet}\\ \text{Bard}& 1& 1\\ \text{Poet}& 1& 1+s\end{array}$$

Let p be the allele frequency of POET, and because it is dominant, poets occur with frequency p² + 2p(1 − p) and bards with frequency (1 − p)². The fitness of each phenotype is the average of its partial fitnesses weighted by its frequencies of interaction:

$$\begin{array}{c}{d}_{\text{poet}}(p)=(1+s)[p^2+2p(1-p)]+1{(1-p)}^2\\ d_{\text{bard}}(p)=1\end{array}$$

The marginal allele fitnesses are

$$\begin{array}{c}{w}_{\text{poet}}(p)=d_{\text{poet}}(p)\\ w_{\text{bard}}(p)=p{d}_{\text{poet}}(p)+(1-p)d_{\text{bard}}(p)\end{array}$$

The average fitness of the population is

$$\overline{w}(p)=[p^2+2p(1-p)]d_{\text{poet}}(p)+{(1-p)}^2{d}_{\text{bard}}(p)$$

and the allele frequency of the next generation is p′ = pw_poet(p)/w̄(p).

An equilibrium exists whenever p′ = p. Solving this equation finds two trivial equilibria at p = 0 and p = 1 that always exist. An equilibrium point is considered locally stable if populations with allele frequencies close to it move toward it and unstable if they move away. To determine stability it is trivial to demonstrate that p′ > p if p > 0. Therefore, p = 0 is unstable and p = 1 is stable. According to these dynamics, when p₀ > 0, POET will be driven to fixation. Thus complete overlap is always invadable by POET. However, since lim_{p→ 0} p′/p = 1, the spread of POET alleles is slow when they are rare, and thus fixation will be heavily influenced by stochastic fluctuations (cf. Cavalli-Sforza and Feldman 1983).

2.2 Partial Overlap Model

To study the dynamics of partial overlap, the previous model is modified to add a coefficient, c ∈ (0,1/s], which creates a fitness cost that occurs when bards and poets interact with one another. The partial-fitness matrix now becomes

$$\begin{array}{ccc}& \text{Bard}& \text{Poet}\\ \text{Bard}& 1& 1-\mathit{\text{cs}}\\ \text{Poet}& 1-\mathit{\text{cs}}& 1+s\end{array}$$

Consequently, the fitnesses of poets and bards become

$$\begin{array}{c}{d}_{\text{poet}}(p)=(1+s)[p^2+2p(1-p)]+(1-\mathit{\text{cs}}){(1-p)}^2\\ d_{\text{bard}}(p)=1{(1-p)}^2+(1-\mathit{\text{cs}})[p^2+2p(1-p)]\end{array}$$

These fitnesses produce an unstable polymorphic equilibrium at

$$\widehat{p}=1-\sqrt{\frac{1+c}{1+2c}}$$

and two stable trivial equilibria. According to these dynamics, when p₀ < p̂, POET will be driven to extinction, but when p₀ > p̂, it will be driven to fixation. Thus partial overlap is not invadable by POET, unless its frequency grows above a threshold via genetic drift or some other evolutionary means, echoing previous results (e.g. Smith 2004; Smith and Kirby 2008).

2.3 Cliquing Model

Under partial overlap of language faculties, POET is selected against when rare. However, in similar systems, assortative interactions have been found to encourage the spread of social traits (e.g. Hamilton 1975; Cavalli-Sforza and Feldman 1983; Wilson and Dugatkin 1997; Gardner and West 2010). In this system, assortative interactions manifest themselves in language cliques. Cliques are a reasonable addition because individuals are likely to prefer to interact with individuals with whom they can communicate successfully. This behavior can be active or passive, e.g. frequent interactions among kin, who are also likely to share the same language phenotype. If cliquing behavior is active, then language phenotypes are an example of a “greenbeard” (Gardner and West 2010).

The previous two models are essentially the results of Asmussen et al. (2004) restated for bards and poets. The dominant PIM model will now be extended to include a cliquing behavior governed by a parameter, f ∈ [0, 1]. Individuals are now assumed to interact randomly at a rate of 1 − f and within their clique with a rate of f (cf. Gardner and West 2010). Note that the previous two models become edge cases of this model. Under this cliquing model, the fitnesses of poets and bards are

$$\begin{array}{c}{d}_{\text{poet}}(p)=f(1+s)+(1-f)[p^2+2p(1-p)](1+s)+(1-f){(1-p)}^2(1-\mathit{\text{cs}})\\ =1+s-(1+c)s(1-f){(1-p)}^2\\ d_{\text{bard}}(p)=f+(1-f){(1-p)}^2+(1-f)[p^2+2p(1-p)](1-\mathit{\text{cs}})\\ =1-\mathit{\text{cs}}(1-f)[p^2+2p(1-p)]\end{array}$$

See Table 1.—Alternative formulations for recessive and haploid/genic POET models can be derived similarly.—From these fitnesses, a polymorphic equilibrium for bards and poets is found at a frequency of POET of

Table 1. Partial fitnesses and pairwise interaction rates with cliquing behavior.

Phenotype	Partial fitnesses		Interaction rates		Total fitnesses
	Bards	Poets	Bards	Poets
Bards	1	1 − cs	f + (1 − f)q2	(1 − f)(p2 + 2pq)	1 − cs(1 − f)(p2 + 2pq)
Poets	1 − cs	1 + s	(1− f)q2	f + (1 − f)(p + 2pq)	1 + s − (1 + c)s(1 − f)q2

Bards are recessive for ancestral allele BARD. Parameter s ≥ 0 is the selective advantage of two poets communicating with one another, and 0 ≤ c ≤ 1/s is the relative penalty of cross communication. The strength of cliquing behavior is represented by 0 ≤ f ≤ 1. The alleles POET and BARD have frequencies p and q = 1 − p in the population, respectively

$$\widehat{p}=1-\sqrt{\frac{1+(1-f)c}{(1-f)(1+2c)}}$$ (1)

which exists if f < c/(1 + c) and is always unstable. Instability is trivially proved by showing that p′ ≶ p if p ≶ p̂. By combining these results, the dynamics for two different initial conditions can be determined.

1. When c > 0 and 0 ≤ f < c/(1 + c), both p = 0 and p = 1 are stable, and p = p̂ is unstable. When p₀ < p̂, POET will be driven to extinction, and when p₀ > p̂, POET will be driven to fixation. Therefore, this situation is invadable by POET, only if its frequency is above the threshold of p̂.

2. When c ≥ 0 and c/(1 + c) ≤ f ≤ 1, p = 0 is unstable; p = 1 is stable; and the polymorphic equilibrium does not exist. When p₀ > 0, POET will be driven to fixation. This situation is always invadable by POET.

The behaviors of other formulations are identical except that $\widehat{p}=\sqrt{\frac{c(1-f)-f}{(1-f)(1+2c)}}$ if POET is recessive and $\widehat{p}=\frac{c(1-f)-f}{(1-f)(1+2c)}$ if POET is haploid/genic.

Poets will replace bards in the population, only if the frequency of POET is greater than p̂. At this point, selection for more fit communication will drive poets to fixation. Clearly, if c = 0, p̂ ≤ 0 and there is no threshold value of p for poets; as c increases the threshold also increases. More importantly, as f increases, the threshold value of p decreases, and when f ≥ c/(1 + c), the threshold disappears completely, and selection will drive poets to fixation even if they cannot communicate perfectly with bards, i.e. poets can invade a population of bards. For example, if c = 1/4 and f = 0, the threshold is about 9%; if f = 0.1, the threshold is about 5%; and if f = 0.2, it disappears.

Clearly, slight increases in cliquing behavior can have drastic effects on the location of p̂, and thus the evolvability of language abilities. These results indicate that the threshold resulting from incomplete communication between bards and poets can be reduced or eliminated by a preference that increases interactions among members of the same language phenotype. Additionally, lim_p→0 p′/p = 1 + fs (1 + c) − cs, indicating that the spread of rare POET alleles happens faster as f increases. Thus stronger cliquing behaviors decrease the influence of stochastic fluctuations in the population (cf. Cavalli-Sforza and Feldman 1983). The shape of Δp = p′ − p is actually concave with respect to f. At low values of p, stronger cliquing behaviors increase Δp, while at high values of p, the stronger cliquing behaviors decrease Δp. More specifically,

$$\frac{d\Delta p}{\mathit{\text{df}}}>0\text{if}p<1-\sqrt{\frac{c(1+s)}{1+c(2+s)}}$$

Note that p̂ is less than this threshold. Above this threshold, poets are common and bards are rare, and thus increasing cliquing behavior rewards bards more than poets.

2.4 Interaction with Genetic Drift

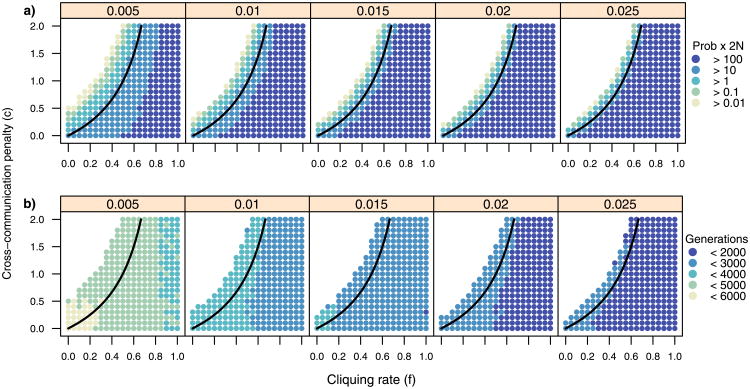
Selection is not the only evolutionary force, and another force like random genetic drift could raise POET above the threshold frequency, after which selection will drive poets to fixation and maintain them in the population. The interaction of the cliquing model with drift was explored using simulations. A Wright–Fisher simulation of this model was implemented, starting with 1 copy of POET in a population of 10000 diploids and running until fixation or elimination of POET. For each parameter set in Fig. 1, simulations were repeated until either 1000 successful sweeps of POET or until (sweeps + 1)/(trials + 1) < 0.01/2N. If 1000 sweeps occurred, their probability was estimated from the unbiased negative-binomial estimator. Additionally, the 5% quantile was estimated from the observed durations of the selective sweeps.

Fig. 1.

Selective sweeps of language-associated alleles occur for many different values of cliquing rates and interaction penalties. (a) Probability of occurrence of selective sweep. Each panel represents a different value for the selective coefficient (s) and contains 441 combinations of f and c. Points above the solid line are sets where p̂ > 0. For each set, the probability of a selective sweep occurring for POET in a population of size 10k was estimated in Simulation from the number of attempts it took to get 1000 selective sweeps. They are color-coded based on their ratio to the neutral expectation. Blank areas represent sets for which sweeps were too rare to study (2Nr < 0.01). (b) The 5% lower quantiles of the duration of selective sweeps for each set. Assuming the model is a reasonable description for the evolution of FOXP2 in humans, values below 4000 can be considered reasonable for its selective sweep

From the results (Fig. 1), I find that the probability of a selective sweep of POET occurring still depends on c, f, and s; however, selective sweeps occur regularly in some populations that have to surpass a threshold (above the solid line in Fig. 1a). The model presented here can also make predictions about the parameter values required to explain the selective sweep of FOXP2 in humans by using the duration of a sweep as a simple summary statistic. If we consider the result that the selective sweep of FOXP2 in humans began within the last 6000 generations (Enard et al. 2002) and assume that it finished before the out-of-Africa expansion of humans (roughly 2000 generations ago; Liu et al. 2006), then the duration of the sweep has an upper bound of 4000 generations. The majority of the points in Fig. 1b have lower 5% quantiles that are less than this bound and can be considered reasonable. It appears that s has to be at least 0.01, while b and f can vary as long as their relationship with drift allows for sweeps.

FOXP2 is just used an example of a language-associated gene that has undergone a selective sweep. The dynamics illustrated in this model could apply to any language-associated gene. For interpreting Fig. 1b, I have assumed that the modern allele is dominant over its ancestral state, but in reality, this is unknown in the case of FOXP2. We also do not know if the observed selective sweep was caused by the FOXP2 locus itself, or if there were interactions with genetic variation at other loci.

3 Discussion

I have developed a population-genetic model for the evolution of new language-associated alleles. In this model, “bards” have an ancestral language phenotype, and “poets” have a novel language phenotype that is potentially more fit. I find that if the poets' language abilities completely overlap bards', then selection will drive poets to fixation. However, partial overlap can select against poets when they are rare and can prevent them from invading the population. The ability of poets to spread can be greatly enhanced through assortative behaviors that create language-based cliques. Through simulations I explored the impact of genetic drift and estimated that the selective coefficient of FOXP2 would need to be at least 0.01 to explain a recent selective sweep.

In humans, genetic drift was probably more effective than predicted in the simulations since it only had to work in small tribes and not the entire population. After drift fixed POET in a few tribes, migration could spread the novel allele to other tribes (cf. Smith 2004). However, drift and migration alone are not sufficient to spread new language genes because migrants will be rare in a new tribe and selected against. Therefore, population-level events like rapid tribe growth and division, group migration, or war are needed for poets to efficiently spread outside their source tribes. Although this scenario is reminiscent of Wright's shifting-balance theory (Wright 1931) and suffers from the debate around it (Coyne et al. 1997; Whitlock and Phillips 2000), such events are common in human history, and their role in assisting language evolution cannot be entirely disregarded.

Although the cliquing model includes assortative interactions similar to assortative mating models, the results are simplified because mating still occurs randomly. Although it is not unreasonable to assume that there should be some level of assortative mating if there are cliques, the complexities of mate choice make it difficult to define what this level should be. For example, in a small tribe, language phenotypes will covary with relatedness, and inbreeding avoidance might prevent a language clique from becoming a mating clique. Assortative, within-clique mating should only reinforce the effects of language cliques.

Some researchers have argued that selection against language-specific alleles when they are rare indicates that language abilities are unlikely to evolve through selection for improved communication and that proposed language adaptations are thus neither specific to language nor adaptations for it (Smith 2004; Smith and Kirby 2008). They have further argued that language adaptations that do exist are likely to be cultural and not biological in origin. However, this hypothesis is called into question by the large number of universal anatomical features (physical and mental) of humans that are associated with language ability (Pinker and Bloom 1990; Vargha-Khadem et al. 1995; Fisher et al. 1998; Lai et al. 2001; Enard et al. 2002; Pinker and Jackendoff 2005; Nishimura et al. 2006; Coop et al. 2008; Corballis 2009). Not all of these can be explained by culture or as spandrels (Gould and Lewontin 1979). Because evolution is a process that results from many interacting forces, it would still be valid to call POET-like genes language-adapted even if drift or some other force had an important role in their evolutionary dynamics.

This model demonstrates that novel language alleles can be selected for even if they disrupt communication between ancestral and derived phenotypes. By forming cliques, the penalty of cross-communication is reduced or eliminated, making novel language alleles more likely to reach fixation. Furthermore, the interaction of selection with other evolutionary forces actually serves to increase the probability of fixation of language-specific alleles. However, this model is only the beginning, providing a framework for using classical population-genetic theory to study the evolution of the language ability and other social traits. Further research, utilizing more complex, frequency-dependent, population-genetic models and incorporating cultural transmission should allow for better understanding of the evolution of language and detection of language-associated genes.