Abstract
There is a substantial literature on the use of linkage disequilibrium (LD) to estimate effective population size using unlinked loci. The 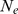 estimates are extremely sensitive to the sampling process, and there is currently no theory to cope with the possible biases. We derive formulae for the analysis of idealised populations mating at random with multi-allelic (microsatellite) loci. The ‘Burrows composite index’ is introduced in a novel way with a ‘composite haplotype table’. We show that in a sample of diploid size
estimates are extremely sensitive to the sampling process, and there is currently no theory to cope with the possible biases. We derive formulae for the analysis of idealised populations mating at random with multi-allelic (microsatellite) loci. The ‘Burrows composite index’ is introduced in a novel way with a ‘composite haplotype table’. We show that in a sample of diploid size 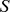 , the mean value of
, the mean value of 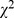 or
or 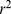 from the composite haplotype table is biased by a factor of
from the composite haplotype table is biased by a factor of 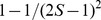 , rather than the usual factor
, rather than the usual factor 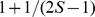 for a conventional haplotype table. But analysis of population data using these formulae leads to
for a conventional haplotype table. But analysis of population data using these formulae leads to 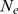 estimates that are unrealistically low. We provide theory and simulation to show that this bias towards low
estimates that are unrealistically low. We provide theory and simulation to show that this bias towards low 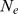 estimates is due to null alleles, and introduce a randomised permutation correction to compensate for the bias. We also consider the effect of introducing a within-locus disequilibrium factor to
estimates is due to null alleles, and introduce a randomised permutation correction to compensate for the bias. We also consider the effect of introducing a within-locus disequilibrium factor to 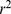 , and find that this factor leads to a bias in the
, and find that this factor leads to a bias in the 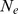 estimate. However this bias can be overcome using the same randomised permutation correction, to yield an altered
estimate. However this bias can be overcome using the same randomised permutation correction, to yield an altered 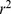 with lower variance than the original
with lower variance than the original 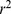 , and one that is also insensitive to null alleles. The resulting formulae are used to provide
, and one that is also insensitive to null alleles. The resulting formulae are used to provide 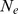 estimates on 40 samples of the Queensland fruit fly, Bactrocera tryoni, from populations with widely divergent
estimates on 40 samples of the Queensland fruit fly, Bactrocera tryoni, from populations with widely divergent 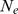 expectations. Linkage relationships are known for most of the microsatellite loci in this species. We find that there is little difference in the estimated
expectations. Linkage relationships are known for most of the microsatellite loci in this species. We find that there is little difference in the estimated 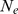 values from using known unlinked loci as compared to using all loci, which is important for conservation studies where linkage relationships are unknown.
values from using known unlinked loci as compared to using all loci, which is important for conservation studies where linkage relationships are unknown.
Introduction
The magnitude of linkage disequilibrium (LD) can be used to estimate effective population size [1]–[5]. In general, low populations sizes are expected to give rise to relatively high levels of LD, and similarly high population sizes to low LD levels. An important feature of this means of estimation is that measurement at a single point in time can provide information on effective size. Furthermore closely-linked loci give information on population sizes over historical periods of time, while loosely-linked loci estimate population sizes in the immediate past [3], [4].
Much recent attention has been paid to the use of unlinked loci for estimating population size, for which the term ‘Linkage Disequilibrium’ will inappropriately be used. There are three major advantages of studying unlinked loci. First, the majority of pairs of loci are unlinked. Secondly, these are the only locus pairs for which it is easy to estimate the recombination frequency, 50%. Finally, in the study of pest populations, and in the area of conservation, it is usually the most recent population sizes that are of interest, for which unlinked loci are the most relevant.
The principal problem in studying unlinked loci comes from the sample sizes needed to obtain accurate LD estimates. The expected disequilibrium is a function of 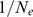 , where
, where 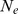 is the effective population size, assumed constant, and
is the effective population size, assumed constant, and 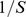 , where
, where 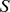 is the sample size [6]. Unless sample sizes are large, the latter can overwhelm the former.
is the sample size [6]. Unless sample sizes are large, the latter can overwhelm the former.
A second complication comes from the usual necessity to use diploid data. Most LD theory is based on haplotypes rather than diploid genotypes, which typically cannot be observed. Although the recognition of haplotypes may seem inappropriate for unlinked loci, the same distinction applies as for linked loci, because the information on population size comes from genes with the same parental origin rather than genes inherited from different parents. The passage from zygotic to to gametic parameters can be made using either the maximum likelihood estimator of Hill [7], or, as will be used here, the Burrows estimator as elaborated by Weir [8].
In preliminary investigations of the size of Queensland fruit fly populations, we found very low 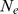 estimates for populations that are believed to be large. We traced this discrepancy to an excess of homozygous genotypes, believed to be due to the presence of null alleles at some of the microsatellite loci used in the study.
estimates for populations that are believed to be large. We traced this discrepancy to an excess of homozygous genotypes, believed to be due to the presence of null alleles at some of the microsatellite loci used in the study.
Because of these complications, the problem of finding an adequate estimator of 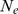 is fraught with potential biases. Waples and Do [9] have, however, shown that their LDNe program works well in estimating
is fraught with potential biases. Waples and Do [9] have, however, shown that their LDNe program works well in estimating 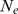 from simulated data. The program uses empirically derived correction factors rather than investigating the underlying reasons for the biases. The purpose of the present paper is to produce an analytical solution to account for the biases. We derive two sets of formulae that do this, depending on whether a ‘within-locus disequilibrium factor’ is used or not, and compare the application of these two sets to simulated and real data.
from simulated data. The program uses empirically derived correction factors rather than investigating the underlying reasons for the biases. The purpose of the present paper is to produce an analytical solution to account for the biases. We derive two sets of formulae that do this, depending on whether a ‘within-locus disequilibrium factor’ is used or not, and compare the application of these two sets to simulated and real data.
Materials and Methods
Queensland Fruit Fly Samples
Two data sets are analysed in the paper.
East coast Australian populations. The data are from 55 samples from towns in the state of NSW in the years 2002–2004 [10]. Some of these sample come from areas where the flies are endemic, and in other cases the outbreaks appear to be only temporary.
NorthWest. These flies were collected during the years 1999–2003 from Northern West Australia and the Northern Territory [11].
The data in the two cited papers have previously been summarised only in terms of single locus statistics. The present paper involves a two-locus analysis, which requires additional information from the original data sets. The original data sets are provided in Supporting Information, Data S1 and Data S2.
Computer Simulation
All simulations reported in the paper are forward Monte-Carlo simulations under the Wright-Fisher model. Parents were chosen randomly in each case, thereby allowing selfing and not assuming permanent mate bonding, an important aspect of population structure [6]. Most simulations involved a starting population with either 16 or 32 loci, each locus having the number of alleles chosen randomly between 2 and 8. Alleles were assigned randomly at different loci, assuming no systematic LD. Populations were simulated for 20 generations, followed by sampling without replacement of 32 individuals from the final population, and calculation of LD levels. Simulations were written in C, and are available on request.
Theory
Most of LD theory applies to gametes rather than genotypes. Fortunately a simple method, the ‘Burrows composite LD coefficient’, is available for handling genotypes. This coefficient has been defined by Cockerham and Weir [12] in terms of sums of genotype frequencies. It is convenient to introduce here a slightly different but simpler way of relating genotype frequencies to gamete frequencies. See Table 1 for a listing of symbols used.
Table 1. Symbols used in the text.
| Ne | Effective population size |
| S | Number of diploid individuals in a sample |
| n11 | Number of genotypes in a sample with aa at first locus and bb at second locus |
| n12 | Number of aa b– genotypes where – refers to non-b allele at the second locus |
| n21 | Number of a– bb genotypes |
| n22 | Number of a– b– genotypes |
| na, nb | Number of a and b alleles respectively |
| pa, pb | Allele frequencies in gametic and composite table, = na/2S and nb/2S |
| pab | Frequency of the ab haplotype |
| D | Gametic disequilibrium coefficient = pab – papb |
| r2 | Gametic correlation = D2/[pa(1– pa)pb(1– pb)] |
| M | Number of ab haplotypes in composite haplotype table = 4n11+2n12+2n21+ n22 |
| pab(comp) | Frequency of ab in composite haplotype table = M/4S |
| D(comp) | Disequilibrium coefficient from composite haplotype table = pab(comp) – papb |
| Δ | Burrows’ disequilibrium coefficient = 2D(comp) |
| r2(comp) | r2 value from composite haplotype table = D2(comp)/[pa(1– pa)pb(1– pb)] |
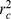
|
Composite r2 parameter = 4r2(comp) |
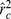
|
Estimate of 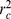 from sample from sample |
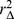
|
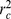 with single-locus disequilibrium = with single-locus disequilibrium = 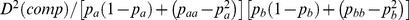
|
| ?2(comp) | ?2 calculated from composite haplotype table |
| pn | Frequency of null alleles at a locus |
| α | Half the difference between coupling and repulsion heterozygote frequencies |
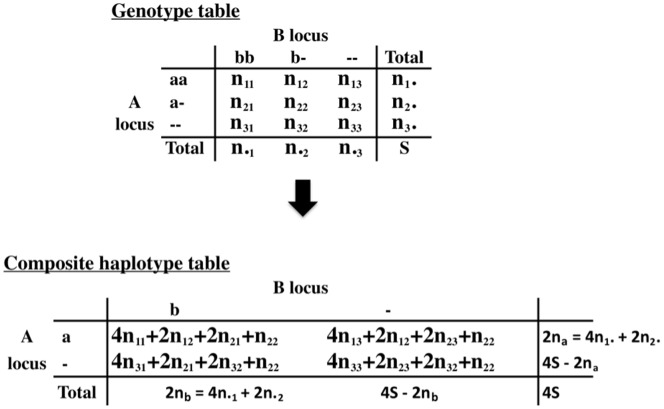
Figure 1 shows the principle for populating a ‘composite haplotype table’. Each genotype in Part (i) contributes the four possible gametes to the composite haplotype table in Part (ii). In the case of double heterozygotes, where the phase is usually unknown, each of the four possible haplotypes is represented. For all other genotypes the haplotypes are known, but each genotype nevertheless contributes four haplotypes. Note the use of  rather than
rather than  for the diploid sample total to emphasise the distinction between number in a population (
for the diploid sample total to emphasise the distinction between number in a population (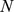 ) and number in a sample (
) and number in a sample (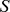 ). The normal haploid table cannot be written down from the genotypes in Figure 1, but the total would be
). The normal haploid table cannot be written down from the genotypes in Figure 1, but the total would be 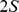 , and, for example, the number of
, and, for example, the number of  genes =
genes = 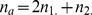 . The marginal totals in the composite table are double these.
. The marginal totals in the composite table are double these.
Figure 1. The composite haplotype table for a 2-allele observed sample.
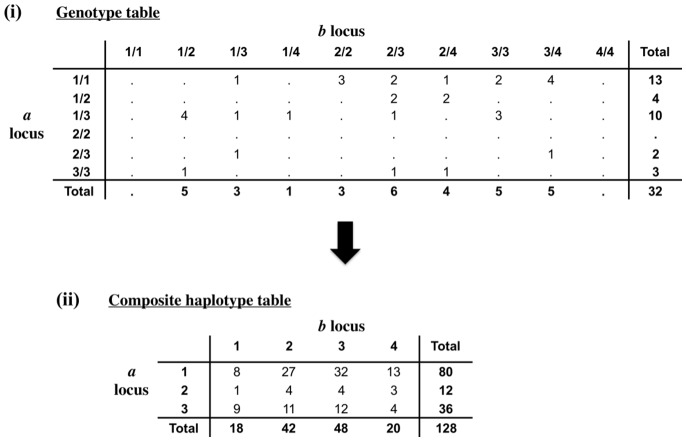
Figure 2 shows a numerical example of the composite haplotype table for one sample of size 32 from the Eastern Australia fruit fly data set, where one microsatellite,  , has 3 alleles and a second,
, has 3 alleles and a second, 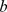 , has 4. Again the total in the haplotype table of Part (ii) of Figure 2 is 4x the total in the genotype table of Part (i), rather than 2x as would be found in a table where all haplotypes were known.
, has 4. Again the total in the haplotype table of Part (ii) of Figure 2 is 4x the total in the genotype table of Part (i), rather than 2x as would be found in a table where all haplotypes were known.
Figure 2. The composite haplotype table for an example of two microsatellites from the fruit y outbreak data set.
The usual LD coefficient can be calculated for the numbers in the composite haplotype table of Figure 1, and given the designation 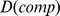 . It is:
. It is:
The LD coefficient of Cockerham and Weir [12], 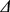 , is defined in terms of frequencies
, is defined in terms of frequencies 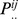 and
and 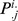 , and given as the sum of two coefficients,
, and given as the sum of two coefficients, 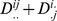 :
:
It can be seen from the definitions of 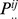 and
and 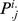 from [12], ignoring the sample-size correction N/(N−1), that this LD coefficient is double the value of
from [12], ignoring the sample-size correction N/(N−1), that this LD coefficient is double the value of 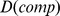 given above.
given above.
The intuitive justification for the composite haplotype table is most readily seen in the case of random mating (which is not assumed in the definition of 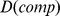 ). In a genotype such as
). In a genotype such as 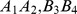 , the true haplotypes will be either
, the true haplotypes will be either 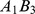 and
and 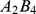 or alternatively
or alternatively 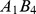 and
and 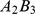 . Under random mating, whichever are the ‘false’ haplotypes are expected to occur at frequencies that are simply the products of the relevant gene frequencies. The frequencies contributed by the false haplotypes will dilute, but not bias, the haplotype frequencies. It is readily shown that this dilution will be simply a factor of 2. For example, following Figure 1, the frequency of the
. Under random mating, whichever are the ‘false’ haplotypes are expected to occur at frequencies that are simply the products of the relevant gene frequencies. The frequencies contributed by the false haplotypes will dilute, but not bias, the haplotype frequencies. It is readily shown that this dilution will be simply a factor of 2. For example, following Figure 1, the frequency of the 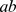 haplotype in the composite table,
haplotype in the composite table, 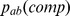 , is the true frequency of the
, is the true frequency of the 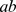 haplotype,
haplotype, 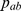 , except for the contribution from the double heterozygotes. The true contribution ought to be
, except for the contribution from the double heterozygotes. The true contribution ought to be 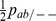 , whereas it is in fact
, whereas it is in fact 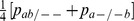 . Thus the difference between these two is the difference between
. Thus the difference between these two is the difference between 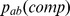 and
and 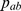 , giving.
, giving.
Under the assumption of random mating, it can be seen that.
where D is the usual LD parameter, equal to 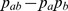 . Therefore
. Therefore
Subtracting 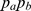 from each side,
from each side,
The LHS of this equation is, by definition, the disequilibrium coefficient from the composite table, 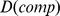 . So the equation is simply
. So the equation is simply
Since this is an expectation under the assumption of random mating, the equation can be written as:
| (1) |
where the expectation is taken over replicate populations of the same sample size.
The LD measure introduced by Hill and Robertson [13] is 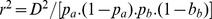 . An equivalent parameter can be calculated from the composite haplotype table. The marginal frequencies are the same as for the regular gamete table. So from (1) it follows that the expectation of
. An equivalent parameter can be calculated from the composite haplotype table. The marginal frequencies are the same as for the regular gamete table. So from (1) it follows that the expectation of 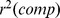 calculated from the composite table is
calculated from the composite table is
| (2) |
It is convenient to define a coefficient where, under random mating, the composite 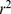 estimates the gametic
estimates the gametic 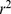 , rather than one-quarter of the latter. As pointed out above, the LD coefficient of Cockerham and Weir [12] does this. Therefore we define the statistic
, rather than one-quarter of the latter. As pointed out above, the LD coefficient of Cockerham and Weir [12] does this. Therefore we define the statistic 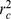 as
as
| (3) |
which from ( ), (
), ( ) and (
) and ( ) is calculated as
) is calculated as
| (4) |
The above definition of 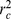 ignores an extra factor introduced by Weir [8]. This factor arises from the potential covariance of the two alleles at the
ignores an extra factor introduced by Weir [8]. This factor arises from the potential covariance of the two alleles at the  locus and similarly at the
locus and similarly at the 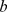 locus. These covariances are implemented through a ‘single-locus disequilibrium factor’,
locus. These covariances are implemented through a ‘single-locus disequilibrium factor’, 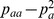 at the
at the  locus and
locus and 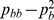 at the
at the 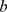 locus, which essentially measure deviations from expected homozygosity. The modified definition of
locus, which essentially measure deviations from expected homozygosity. The modified definition of 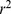 ,
, 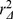 , is
, is
| (5) |
Because of difficulties in implementing this disequilibrium factor, its discussion is deferred to a later section under this label.
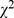 for the composite haplotype table
for the composite haplotype table
Owing to double-counting of genes, the composite gamete table has the property that all marginal totals are multiples of 2, while the overall total is a multiple of 4. Nevertheless a regular  can be calculated for such tables, and the resulting
can be calculated for such tables, and the resulting 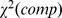 values for a
values for a  ×
× table has close to the expected distribution for
table has close to the expected distribution for 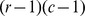 degrees of freedom (Appendix S1). It has the advantage of having more power than the
degrees of freedom (Appendix S1). It has the advantage of having more power than the 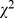 values calculated from the genotype table, owing to the large number of zero and unit values in the genotype table. Its use in independence tests may, however, be limited by its sensitivity to null alleles (see below).
values calculated from the genotype table, owing to the large number of zero and unit values in the genotype table. Its use in independence tests may, however, be limited by its sensitivity to null alleles (see below).
Weighting of 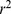 values
values
The calculation of LD for a microsatellite data set involves two levels of summation. There will usually be many loci, say 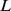 , and each of the
, and each of the 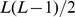 pairs yields a separate estimate of
pairs yields a separate estimate of 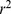 . However within each locus pair, say locus
. However within each locus pair, say locus 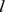 and locus
and locus  , there will be separate calculations for each pair of alleles. These two levels may be labelled as ‘between locus pairs’ and ‘within locus pairs’. Each needs to be separately treated in terms of weighting of the
, there will be separate calculations for each pair of alleles. These two levels may be labelled as ‘between locus pairs’ and ‘within locus pairs’. Each needs to be separately treated in terms of weighting of the 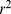 values.
values.
Between locus pairs
It is often the case that, through missing readings, different locus pairs will have reduced numbers of observations. The sample size for loci 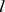 and
and  may be designated as
may be designated as 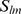 . Furthermore some loci will have large numbers of alleles and therefore provide more information than loci with small numbers of alleles. Waples and Do [9] have suggested the weighting
. Furthermore some loci will have large numbers of alleles and therefore provide more information than loci with small numbers of alleles. Waples and Do [9] have suggested the weighting 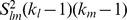 for the different
for the different 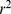 values, where
values, where 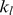 and
and 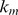 are the number of alleles at the
are the number of alleles at the 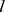 and
and  loci respectively. The overall estimate of
loci respectively. The overall estimate of 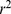 then becomes
then becomes
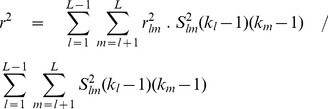 |
(6) |
A recent publication [14] suggests a slightly different weighting compared to that of Waples and Do [9], which would make a small difference to the overall 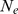 estimate.
estimate.
Within locus pairs
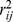 values for alleles
values for alleles  at locus
at locus 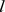 and
and 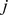 at locus
at locus  can be simply averaged to provide the
can be simply averaged to provide the 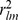 value. However this has the undesirable property that rare alleles exert a disproportionate influence on the overall
value. However this has the undesirable property that rare alleles exert a disproportionate influence on the overall 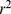 value. This effect that can be ameliorated by omitting low frequency alleles [9]. A more systematic way of avoiding this problem is to weight alleles according to their frequency. In the case where the frequencies of alleles
value. This effect that can be ameliorated by omitting low frequency alleles [9]. A more systematic way of avoiding this problem is to weight alleles according to their frequency. In the case where the frequencies of alleles 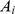 and
and 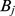 are respectively
are respectively 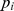 and
and 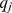 , a suitable weighting is
, a suitable weighting is 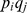 [15]. The overall
[15]. The overall 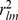 value then becomes
value then becomes
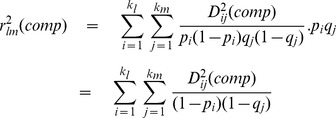 |
(7) |
Since 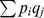 = 1, this value does not need to be normalised. And since the marginal frequencies are the same for the regular and composite tables, the same weighting applies to both.
= 1, this value does not need to be normalised. And since the marginal frequencies are the same for the regular and composite tables, the same weighting applies to both.
It is interesting to contrast this weighting proportional to gene frequencies to the normal 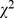 weighting of allele pairs for a
weighting of allele pairs for a  ×
× table. The
table. The 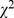 with
with 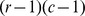 degrees of freedom can be expressed as the sum of
degrees of freedom can be expressed as the sum of  ×
× individual
individual 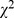 values each with 1 df, if the values are weighted by
values each with 1 df, if the values are weighted by 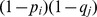 rather than
rather than 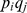 . Thus the
. Thus the 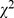 weighting gives rare alleles higher weight than common ones. Zhao et al [15] have compared these two measures, amongst others, for their use in QTL mapping, and recommend a standardised
weighting gives rare alleles higher weight than common ones. Zhao et al [15] have compared these two measures, amongst others, for their use in QTL mapping, and recommend a standardised 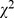 weighting for this case. However the higher weighting for rare alleles, as suggested from
weighting for this case. However the higher weighting for rare alleles, as suggested from 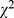 , performs poorly as just a simple measure of LD (Appendix S2).
, performs poorly as just a simple measure of LD (Appendix S2).
Because of the different weighting for 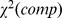 and
and 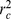 , there is no simple relationship between the two statistics. In general, however, significant values of
, there is no simple relationship between the two statistics. In general, however, significant values of 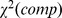 will lead to low estimates of
will lead to low estimates of 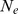 and non-significant values of
and non-significant values of 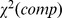 will be associated with high
will be associated with high 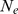 estimates. See [16] for a more detailed examination of the
estimates. See [16] for a more detailed examination of the 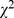 statistic.
statistic.
The estimation of 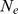
The theory for estimating 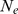 from unlinked loci has been developed by Weir [8], Weir and Hill [6] and Hill [3]. The effective size refers to a model Wright-Fisher population, and departures from this model, such as permanent pair bonding, make a difference of a factor of 2 in
from unlinked loci has been developed by Weir [8], Weir and Hill [6] and Hill [3]. The effective size refers to a model Wright-Fisher population, and departures from this model, such as permanent pair bonding, make a difference of a factor of 2 in 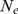 estimates [6]. Such pair bonding is, of course, unlikely in fruit fly populations. A model assuming discrete generations as considered here is, however, necessarily an approximation to real populations that are likely to have overlapping generations.
estimates [6]. Such pair bonding is, of course, unlikely in fruit fly populations. A model assuming discrete generations as considered here is, however, necessarily an approximation to real populations that are likely to have overlapping generations.
Taking no account, for the moment, of the effect of sample size, the key equation relating the expected LD level to 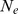 is
is
| (8) |
where  is the recombination frequency. This reduces to
is the recombination frequency. This reduces to
| (9) |
for unlinked loci, 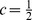 . The expectation for
. The expectation for 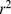 here assumes a balance between increase of
here assumes a balance between increase of 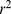 due to finite population size and loss due to recombination. All of the equations below assume this balance between drift and recombination. Equation (8) is derived using the ratio of expectations of
due to finite population size and loss due to recombination. All of the equations below assume this balance between drift and recombination. Equation (8) is derived using the ratio of expectations of 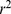 rather than the expectation of the ratio (see Hill [17]). However computer simulation shows that it works well for loosely linked or unlinked genes, those of interest in the present study. It is unbounded for low values of
rather than the expectation of the ratio (see Hill [17]). However computer simulation shows that it works well for loosely linked or unlinked genes, those of interest in the present study. It is unbounded for low values of 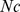 , when the expression given by Sved and Feldman [18]:
, when the expression given by Sved and Feldman [18]:
| (10) |
seems to work better. However for 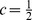 , the RHS of equation (10) reduces to
, the RHS of equation (10) reduces to 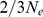 , which is double the value of equation (9) and clearly inaccurate at this end of the scale.
, which is double the value of equation (9) and clearly inaccurate at this end of the scale.
Equations (8)–(10) assume the measurement of haplotype or gamete frequencies. As previously indicated, diploid data may be taken into account using the composite LD measure. It follows from equations (1) and (4) that the expectation for this measure is identical to that of (8):
Sample size is a critical issue in determining LD levels [8], [6], [3]. This is especially the case for unlinked loci, where the levels of 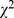 and
and 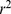 cannot be zero even if there is no association of loci in the population being sampled. The usual procedure in estimating true LD levels in the population is simply to subtract the level of
cannot be zero even if there is no association of loci in the population being sampled. The usual procedure in estimating true LD levels in the population is simply to subtract the level of 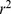 expected for zero LD with a particular sample size. As pointed out in [19], however, there is one circumstance where this procedure will not work. With complete LD in the population,
expected for zero LD with a particular sample size. As pointed out in [19], however, there is one circumstance where this procedure will not work. With complete LD in the population, 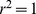 , as commonly found for the most tightly linked SNPs, the subtraction will falsely suggest
, as commonly found for the most tightly linked SNPs, the subtraction will falsely suggest 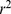 levels less than 1.
levels less than 1.
The effect on the equation for gametes (8) is to increase the expected value of 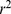 by a factor of
by a factor of 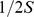 , where
, where 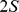 is the haploid sample size. The
is the haploid sample size. The 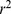 statistic in this case is shown as
statistic in this case is shown as 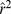 to indicate that it is an estimate that includes the effects of sampling
to indicate that it is an estimate that includes the effects of sampling
| (11) |
In fact the exact expectation for 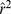 should include the term
should include the term 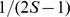 rather than
rather than 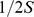 , equivalent to noting that the exact expectation of
, equivalent to noting that the exact expectation of 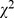 is
is 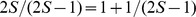 rather than 1 [20]. Weir [8] takes this factor into account in working with the ‘unbiased’ rather than ‘biased’ value of
rather than 1 [20]. Weir [8] takes this factor into account in working with the ‘unbiased’ rather than ‘biased’ value of 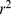 .
.
As shown in equations (1) and (3) of Appendix S1, the expectation for the composite 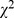 , or equivalently the composite LD coefficient
, or equivalently the composite LD coefficient 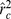 , involves the factor
, involves the factor 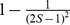 , rather than
, rather than 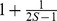 applicable to haploid data. This factor is very close to 1. Similarly the sampling correction factor for
applicable to haploid data. This factor is very close to 1. Similarly the sampling correction factor for 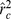 for a diploid sample of size
for a diploid sample of size 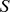 is close to
is close to  :
:
| (12) |
or for unlinked loci:
| (13) |
The estimate for 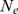 comes from inverting equation (13), where
comes from inverting equation (13), where 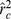 is calculated according to equation (6) and each
is calculated according to equation (6) and each 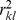 is calculated according to equation (7)
is calculated according to equation (7)
| (14) |
The effect of null alleles
Use of the composite disequilibrium index depends critically on the ability to distinguish heterozygous and homozygous genotypes. Unfortunately the presence of any null alleles makes this distinction difficult. Genotypes such as 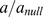 , will be incorrectly scored as
, will be incorrectly scored as 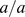 . Homozygous null genotypes are not easily detected, since it is difficult to distinguish between absence of a band and simple failure of the PCR reaction in the rare cases expected for homozygotes.
. Homozygous null genotypes are not easily detected, since it is difficult to distinguish between absence of a band and simple failure of the PCR reaction in the rare cases expected for homozygotes.
The expected effect of null alleles on the composite LD statistic can be quantified as in Appendix S3. This shows that a null allele at one of the two loci at a frequency 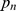 alters the expectation of equation (1) to:
alters the expectation of equation (1) to:
The statistic 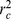 is increased by the factor
is increased by the factor 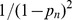 .
.
Although this effect may be small, it can readily be shown to overwhelm the calculations when the expected LD value is small due to high effective population size. In the case of an infinitely large population, the true value of 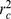 is expected to be just the sampling correction, which is approximately
is expected to be just the sampling correction, which is approximately  . A null allele at one of the two loci is expected to increase this value to
. A null allele at one of the two loci is expected to increase this value to 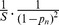 . Applying equation (13), the estimated value of
. Applying equation (13), the estimated value of 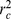 is then found by subtracting the usual
is then found by subtracting the usual  sampling contribution, giving
sampling contribution, giving
| (15) |
Applying numerical values to equation (15), for a sample size 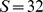 and null frequency
and null frequency 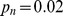 , the equation yields a value for
, the equation yields a value for 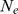 of 259. The actual population in this case should be infinitely large, so that a null allele frequency as low as 2% can have a strikingly large effect. A null allele at frequency 0.1, still difficult to detect, leads to a
of 259. The actual population in this case should be infinitely large, so that a null allele frequency as low as 2% can have a strikingly large effect. A null allele at frequency 0.1, still difficult to detect, leads to a 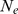 estimate of 45.
estimate of 45.
Simulations with null alleles
Simulations with null alleles have been carried out to test these expectations. These are 2-locus simulations with heterozygosities ranging from 50% to 87%. Under these conditions, equation (15) may slightly over-estimate the effect of null alleles. For example, in the above case with 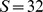 and
and 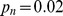 , simulation yields a value of
, simulation yields a value of 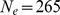 compared to expectation of 259, while
compared to expectation of 259, while 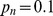 yields
yields 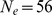 compared to 45.
compared to 45.
Simulation can also be used to check on more realistic cases where the value of 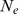 comes from multiple loci, rather than a two-locus simulation. These show that even low levels of null alleles at a single locus may have measurable effects. For example with 32 loci each with 5 alleles, the presence of just one locus amongst these having a null allele frequency of 10% can have a detectable effect, reducing the expected value of
comes from multiple loci, rather than a two-locus simulation. These show that even low levels of null alleles at a single locus may have measurable effects. For example with 32 loci each with 5 alleles, the presence of just one locus amongst these having a null allele frequency of 10% can have a detectable effect, reducing the expected value of 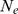 from infinitely large to less than 1,000. Much the same result is found for 5 loci each with a null frequency of 2%. Simulations also indicate that 8 out of 16 loci having null alleles at a particular frequency has much the same effect as one out of two loci in the simulations and calculations given above.
from infinitely large to less than 1,000. Much the same result is found for 5 loci each with a null frequency of 2%. Simulations also indicate that 8 out of 16 loci having null alleles at a particular frequency has much the same effect as one out of two loci in the simulations and calculations given above.
Correcting the effect of null alleles through permutation
A general formulation for the estimation of 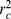 may be given as follows:
may be given as follows:
| (16) |
Here 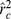 is the estimate derived from the data, and
is the estimate derived from the data, and 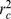 is the true measure of LD in the population, which is the quantity of interest in estimating
is the true measure of LD in the population, which is the quantity of interest in estimating 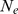 . The analysis above has shown that in the absence of null alleles, the correction factor is attributable purely to sampling, and is
. The analysis above has shown that in the absence of null alleles, the correction factor is attributable purely to sampling, and is 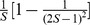 . The analysis on null alleles has shown that these will act as disturbing factors, whose effect can conveniently be subsumed into the correction factor in equation (16).
. The analysis on null alleles has shown that these will act as disturbing factors, whose effect can conveniently be subsumed into the correction factor in equation (16).
A randomising procedure can be suggested that will ameliorate the effect of null alleles. If the genotypes at each locus are independently randomly permuted amongst individuals, such as in the exact test of significance of LD, eg. [21], there can be no underlying LD. So the mean value of 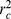 given by the average of many such randomly permuted samples is a direct estimate of the correction factor in (16) taking into account the actual genotype structure. If
given by the average of many such randomly permuted samples is a direct estimate of the correction factor in (16) taking into account the actual genotype structure. If 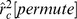 is the estimated value of
is the estimated value of 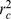 in such permuted samples, then equation (16) becomes
in such permuted samples, then equation (16) becomes
| (17) |
From equation (9), the estimate of 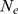 is then simply
is then simply
| (18) |
Both 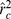 and
and 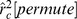 can be given with or without the sampling correction factor
can be given with or without the sampling correction factor 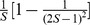 . In the data tables below, the factor has been subtracted from both in order to use equation (14) to estimate the value of
. In the data tables below, the factor has been subtracted from both in order to use equation (14) to estimate the value of 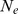 with no permutation. However for the value of
with no permutation. However for the value of 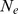 with
with 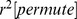 subtracted, the sampling factor cancels out and could have been omitted.
subtracted, the sampling factor cancels out and could have been omitted.
The permutation approach can be tested by simulation. This is shown in the first four lines of Table 2. All, except for the final two rows, involved 16 loci simulated for 20 generations, followed by sampling of 32 individuals. The first row shows the average 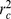 value for a range of population sizes from 32 to 1028. The second row shows the estimated
value for a range of population sizes from 32 to 1028. The second row shows the estimated 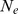 values using equation (14), with each of the
values using equation (14), with each of the 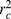 values calculated directly from the composite haplotype table according to equations (1) and (4). The
values calculated directly from the composite haplotype table according to equations (1) and (4). The 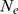 values are in good agreement with expectation.
values are in good agreement with expectation.
Table 2. Observed statistics from simulations with and without incorporating single-locus disequilibrium.
| Actual Ne | 32 | 64 | 128 | 256 | 512 | 1024 |
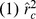
|
0.00993 | 0.00511 | 0.00255 | 0.00129 | 0.00065 | 0.00032 |
| (2) Ne (from equation 14) | 34 | 65 | 131 | 259 | 516 | 1036 |
| (3) Ne (null alleles) | 26 | 41 | 59 | 76 | 89 | 97 |
| (4) Ne (null alleles+permute) | 33 | 64 | 127 | 249 | 494 | 1025 |
(5) 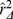 (diseq. included) (diseq. included) |
0.01067 | 0.00598 | 0.00352 | 0.00225 | 0.00163 | 0.00133 |
| (6) Ne (diseq. included) | 31 | 56 | 95 | 148 | 203 | 249 |
| (7) Ne (diseq. included+permute) | 35 | 68 | 134 | 265 | 523 | 1040 |
| (8) Ne (null alleles - diseq. included) | 31 | 56 | 96 | 147 | 206 | 248 |
| (9) Ne (nulls - diseq. corr.+permute) | 35 | 68 | 136 | 274 | 559 | 1127 |
(10) 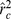 s.d. s.d. |
0.00655 | 0.00397 | 0.00285 | 0.00231 | 0.00205 | 0.00193 |
(11) 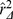 s.d. (diseq. included) s.d. (diseq. included) |
0.00468 | 0.00272 | 0.00186 | 0.00146 | 0.00126 | 0.00117 |
(12) 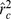 s.d. (32 loci) s.d. (32 loci) |
0.00454 | 0.00277 | 0.00195 | 0.00153 | 0.00134 | 0.00124 |
(13) 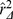 s.d. (diseq. included, 32 loci) s.d. (diseq. included, 32 loci) |
0.00299 | 0.00167 | 0.00108 | 0.00081 | 0.00067 | 0.00059 |
All used sample size S = 32.
The effect of introducing null alleles is shown in row (3). The simulations here involved choosing 8 of the 16 loci, and replacing 5% of alleles with null alleles in these. The 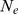 values calculated using equation (
values calculated using equation (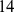 ) are drastically reduced, especially for the higher population sizes. However the permutation correction in row (4) essentially brings the estimated
) are drastically reduced, especially for the higher population sizes. However the permutation correction in row (4) essentially brings the estimated 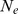 values back to their expected value.
values back to their expected value.
In the case of an infinitely large population, simulation is not necessary to justify the permutation approach for correcting for null alleles. The loci would be in linkage equilibrium in such a population, with a true value of 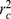 of zero. The only contributing factor to the observed value of
of zero. The only contributing factor to the observed value of 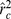 must be the correction factor, attributable to null alleles, plus the usual sampling factor of approximately
must be the correction factor, attributable to null alleles, plus the usual sampling factor of approximately 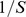 . Additional permutation of genotypes in a sample from a population with zero LD will not have any effect, so the
. Additional permutation of genotypes in a sample from a population with zero LD will not have any effect, so the 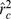 estimates with and without permutation will be identical and equal to
estimates with and without permutation will be identical and equal to 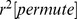 .
.
The case of an infinitely large population also serves to show that the permutation approach will NOT work in removing biases due to non-random mating. For example, a sample might consist of individuals from two independently randomly mating populations, where the substructure has not been recognised. Such a sample will give a reduced estimate of 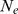 due to the induced LD [22] even though there may be no LD within each of the two contributing populations. However permuting the sample cannot resolve this issue. It can be seen that the value of
due to the induced LD [22] even though there may be no LD within each of the two contributing populations. However permuting the sample cannot resolve this issue. It can be seen that the value of 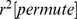 from the composite table will be zero, except for the normal sampling component of approximately
from the composite table will be zero, except for the normal sampling component of approximately 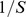 , assuming no null alleles. The application of equation (17) would then falsely indicate that the LD within populations was real and attributable to small population size. A valid correction could be produced if the sub-samples from the two populations could be independently permuted, which is possible in computer simulation but not with real data where the substructure is unknown.
, assuming no null alleles. The application of equation (17) would then falsely indicate that the LD within populations was real and attributable to small population size. A valid correction could be produced if the sub-samples from the two populations could be independently permuted, which is possible in computer simulation but not with real data where the substructure is unknown.
Taking account of all types of departure from random mating thus appears difficult. But Waples and England [23] have considered the case of migration into a random mating population, and shown that there is little effect on 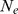 estimates in this case.
estimates in this case.
Including the single-locus disequilibrium factor
As mentioned above, a homozygosity correction term was suggested by Weir [8], as shown in equation (5). The effects of this term are shown in row (5) of Table 2, the 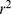 value, and row (6), the
value, and row (6), the 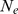 value. The latter shows a substantial bias in
value. The latter shows a substantial bias in 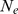 values, especially for the larger population sizes. The size of this discrepancy seems surprising, since, under random mating, the mean value of the homozygosity correction should be zero, and only a small correction should result. However there is a bias due to the fact that, in a finite-size sample, the expectation of
values, especially for the larger population sizes. The size of this discrepancy seems surprising, since, under random mating, the mean value of the homozygosity correction should be zero, and only a small correction should result. However there is a bias due to the fact that, in a finite-size sample, the expectation of 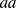 frequency is less than
frequency is less than 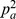 . This is most evident where there is a single
. This is most evident where there is a single  allele, giving
allele, giving 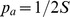 , but where the frequency of the
, but where the frequency of the 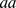 genotype must be zero.
genotype must be zero.
The obvious way of eliminating this bias would seem to be the use of 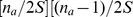 ] as the expected frequency of homozygotes. But simulation shows that this substantially over-corrects the bias. It is, however, possible, just as in the case of correcting the bias for null alleles, to use a permutation correction. This involves calculation of
] as the expected frequency of homozygotes. But simulation shows that this substantially over-corrects the bias. It is, however, possible, just as in the case of correcting the bias for null alleles, to use a permutation correction. This involves calculation of 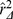 from equation (
from equation (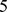 ), random permutation of genotypes in the sample, and calculation of
), random permutation of genotypes in the sample, and calculation of 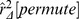 in permuted samples. The procedure may be summarised as:
in permuted samples. The procedure may be summarised as:
| (19) |
From equation (19), the estimate of 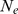 is
is
| (20) |
Simulation in row (7) of Table 2 shows that this correction works well for all 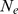 values.
values.
The homozygosity deviation factor, 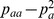 , was not specifically designed in [8] to take into account null alleles. It seems particularly vulnerable to their effect, since
, was not specifically designed in [8] to take into account null alleles. It seems particularly vulnerable to their effect, since 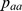 may be substantially over-estimated. However simulation shows that this factor dramatically improves rather than worsens the effect of null alleles. In contrast to the bias of the
may be substantially over-estimated. However simulation shows that this factor dramatically improves rather than worsens the effect of null alleles. In contrast to the bias of the 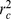 considered previously that lacks the disequilibrium correction, row (8), which introduces null alleles at the same frequency of 5% in half of the loci, gives almost the same
considered previously that lacks the disequilibrium correction, row (8), which introduces null alleles at the same frequency of 5% in half of the loci, gives almost the same 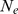 value as row (6) where there are no null alleles. As previously, the bias due to the factor can be eliminated by subtracting the permutation
value as row (6) where there are no null alleles. As previously, the bias due to the factor can be eliminated by subtracting the permutation 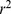 using equation (
using equation (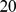 ), as shown in row (9).
), as shown in row (9).
A second advantage of the disequilibrium factor is that it reduces the variance of estimates. The 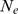 estimates given in Table 2 are based on large numbers of replicates. However the variability between individual simulation runs is high. Estimated standard deviations of
estimates given in Table 2 are based on large numbers of replicates. However the variability between individual simulation runs is high. Estimated standard deviations of 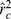 and
and 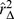 are given in rows (10) and (11). Both standard deviations are high in relation to the mean, but that associated with
are given in rows (10) and (11). Both standard deviations are high in relation to the mean, but that associated with 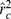 is especially so. Of course the magnitude of the standard deviations is heavily dependent on the choice of number of loci and heterozygosity levels. Doubling the number of loci from 16 to 32 substantially reduces standard deviations, row (12) and row (13), but the relativities between the two terms are maintained.
is especially so. Of course the magnitude of the standard deviations is heavily dependent on the choice of number of loci and heterozygosity levels. Doubling the number of loci from 16 to 32 substantially reduces standard deviations, row (12) and row (13), but the relativities between the two terms are maintained.
In summary of Table 2, only the original 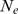 estimate from equation (14), where
estimate from equation (14), where 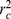 lacks the single-locus disequilibrium factor, gives unbiased
lacks the single-locus disequilibrium factor, gives unbiased 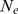 estimates. Nevertheless there is a strong reason for including the faxtor, provided that the bias in
estimates. Nevertheless there is a strong reason for including the faxtor, provided that the bias in 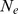 values is compensated, either by permutation as above, or by empirical correction as implemented in the computer program LDNe [9]. Weir’s insight in introducing this factor is vindicated by the increased accuracy of estimation and lowered sensitivity to null alleles.
values is compensated, either by permutation as above, or by empirical correction as implemented in the computer program LDNe [9]. Weir’s insight in introducing this factor is vindicated by the increased accuracy of estimation and lowered sensitivity to null alleles.
Results and Discussion
Results for the East coast populations are given in Table 3. Populations with low sample numbers, 15 or less, were omitted from the analysis, leaving 40 out of the original 52 samples. The table includes mostly samples from outbreak areas where the flies were not normally found, but also ten samples where the flies are endemic, including one from Queensland, the home range of the flies. The expectation is that these ten are samples from large populations.
Table 3. Summary of Ne estimated by various procedures for East coast outbreak populations of B.tryoni, with the most likely estimate shown by ⇓.
| S | No homozygote correction | Homozygote correction | Likelihood Significance | |||||
| Unlinked No permute Eqn. (14) | Unlinked permute Eqn. (18) | Unlinked permute Eqn. (20) ⇓ | All loci | |||||
| permute Eqn. (20) | LDNe | genotype | composite | |||||
| Albury03 | 27 | 60 | ∞ | ∞ | ∞ | ∞ | * | |
| Barooga03 | 33 | 40 | 30 | 40 | 20 | 20 | *** | |
| Condobolin02 | 42 | 40 | ∞ | ∞ | ∞ | ∞ | * | |
| Coota02 | 43 | 110 | ∞ | 450 | 340 | 510 | *** | |
| Corowa02 | 22 | 20 | 120 | 180 | 100 | ∞ | ||
| Cowra | 20 | 20 | 230 | 150 | 180 | ∞ | ||
| Deniliquin02 | 40 | 30 | 40 | 40 | 30 | ∞ | *** | *** |
| Deniliquin03 | 53 | 40 | 100 | 150 | 70 | 90 | * | *** |
| Deniliquin04 | 73 | 50 | 130 | 160 | 70 | 110 | * | *** |
| Dubbo02 | 26 | 30 | 180 | 130 | 160 | ∞ | ** | |
| Forbes02 | 34 | 40 | 250 | 180 | 170 | ∞ | ** | |
| Grenfell02 | 31 | 130 | ∞ | ∞ | ∞ | ∞ | *** | |
| Hay02 | 26 | 20 | 30 | 20 | 20 | 140 | *** | |
| Hay03 | 28 | 40 | 230 | 120 | 50 | 80 | * | *** |
| Henty02 | 20 | 20 | 120 | 60 | 50 | 190 | ** | |
| LakeCarg02 | 74 | 30 | 40 | 50 | 30 | 70 | ** | *** |
| Leeton03 | 82 | 70 | 110 | 160 | 70 | 80 | ** | *** |
| Narrandera04 | 25 | 30 | ∞ | 770 | 130 | 510 | * | |
| Parkes02 | 20 | 30 | 130 | 100 | 80 | 500 | ||
| Parkes03 | 41 | 30 | 140 | 140 | 190 | 310 | ** | |
| Temora02 | 20 | 20 | 120 | 160 | 150 | ∞ | ||
| TheRock02 | 20 | 30 | 410 | 170 | 100 | ∞ | ||
| Tumut | 20 | 20 | 670 | 470 | 270 | ∞ | * | |
| Wagga02 | 57 | 70 | 790 | ∞ | ∞ | ∞ | ||
| Wagga03 | 162 | 210 | 660 | 740 | 610 | 860 | ||
| Wahgunyah | 24 | 20 | 90 | 70 | 50 | ∞ | * | * |
| Wilcannia02 | 43 | 20 | 50 | 60 | 30 | 50 | *** | *** |
| Wodonga | 42 | 30 | 110 | 110 | 100 | 130 | *** | |
| WWyalong03 | 24 | 120 | ∞ | ∞ | 110 | ∞ | * | |
| Young02 | 49 | 110 | 170 | 380 | 400 | 440 | ** | *** |
| Coffs02¶ | 18 | 40 | 70 | 60 | 70 | ∞ | ||
| Foster02¶ | 34 | 40 | ∞ | ∞ | ∞ | ∞ | *** | *** |
| Grafton03¶ | 29 | 40 | 290 | 280 | 510 | ∞ | *** | |
| Maclean02¶ | 34 | 50 | 600 | 280 | 360 | ∞ | *** | |
| NSW03¶ | 42 | 90 | 380 | ∞ | ∞ | ∞ | ||
| QLD03¶ | 42 | 70 | 430 | 290 | 530 | ∞ | *** | |
| Sawtell02¶ | 34 | 120 | ∞ | ∞ | ∞ | ∞ | ||
| SWRocks02¶ | 33 | 40 | ∞ | ∞ | ∞ | ∞ | *** | |
| Syd03¶ | 42 | 130 | ∞ | ∞ | ∞ | 630 | * | |
| Taree03¶ | 30 | 40 | ∞ | ∞ | ∞ | ∞ | ||
Non-outbreak population.
Significant at 5% level.
Significant at 1% level.
Significant at 0.1% level.
The results are based on 29 microsatellites, a total of 29×28/2 = 406 locus pairs. Because of missing readings, not all pairs are present in all populations.
Amongst the 29 loci, 5 pairs are known to be closely linked, 51 pairs to be loosely linked, and 197 to be unlinked [24]. For the remaining 153 locus pairs, one or both chromosomes are unknown. Average values of 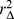 for the four classes are 0.0434, 0.0153, 0.0084 and 0.0096 respectively. As expected, average values are higher for the known linked loci.
for the four classes are 0.0434, 0.0153, 0.0084 and 0.0096 respectively. As expected, average values are higher for the known linked loci.
Values of 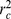 were calculated from the composite haplotype tables, and
were calculated from the composite haplotype tables, and 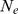 values (column 3) were then calculated from these values using equation (14). All populations, including the eight non-outbreak populations, show very low estimated population sizes. All are highly significantly different from infinite population size. The major conclusion from the above analysis, however, is that the existence of either null alleles or population sub-structure can cause cause
values (column 3) were then calculated from these values using equation (14). All populations, including the eight non-outbreak populations, show very low estimated population sizes. All are highly significantly different from infinite population size. The major conclusion from the above analysis, however, is that the existence of either null alleles or population sub-structure can cause cause 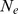 values to be substantially under-estimated.
values to be substantially under-estimated.
A direct test for null alleles is given in Table 4. The signal for null alleles is, eg. [25], excess of homozygotes over expectation. In a data set with multiple populations, a non-parametric test can be carried out based on number of populations where there is such an excess. Table 4 shows the results, revealing at least 10 out of 29 microsatelltes with significant excess of homozygotes, which, in the lack of systematic homozygote excess, can likely be attributed to null alleles rather than to population structure.
Table 4. Excess of homozygosity for different microsatellites.
| Rank | Microsatellite | Number of populations | |
| Homozygous excess | Out of | ||
| 1 | Bt2.9a | 36 | 39 |
| 2 | Bt6.1a | 33 | 36 |
| 3 | Bt15 | 36 | 40 |
| 4 | Bt4.1a | 36 | 40 |
| 5 | Bt1.7a | 35 | 40 |
| 6 | Bt2.6a | 33 | 40 |
| 7 | Bt2.6b | 31 | 38 |
| 8 | Bt3.2b | 30 | 37 |
| 9 | Bt1.6a | 31 | 39 |
| 10 | Bt32 | 30 | 39 |
| 11 | Bt10 | 30 | 40 |
| 12 | Bt7.9a | 29 | 39 |
| 13 | Bt6.12a | 27 | 40 |
| 14 | Bt5.10a | 27 | 40 |
| 15 | Bt8.5a | 26 | 40 |
| 16 | Bt11 | 25 | 40 |
| 17 | Bt7.2b | 23 | 39 |
| 18 | Bt1.1a | 20 | 40 |
| 19 | Bt9.1a | 20 | 40 |
| 20 | Bt14 | 18 | 40 |
| 21 | Bt8.6a | 18 | 40 |
| 22 | Bp78 | 18 | 40 |
| 23 | Bt17 | 17 | 40 |
| 24 | Bt4.3a | 16 | 40 |
| 25 | Bt4.6a | 15 | 38 |
| 26 | Bt6.8a | 15 | 40 |
| 27 | Bt8.12a | 15 | 40 |
| 28 | Bt6.10b | 14 | 40 |
| 29 | Bt5.8a | 9 | 38 |
Returning to Table 3, column 4 shows the values of 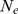 using
using  values corrected using equation (17). The correction factor in this case comes from 200,000 simulated populations for each outbreak sample. The
values corrected using equation (17). The correction factor in this case comes from 200,000 simulated populations for each outbreak sample. The 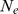 values clearly have a more realistic mixture of population sizes than the estimates based on the raw
values clearly have a more realistic mixture of population sizes than the estimates based on the raw 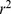 values. Positive values of greater than 1,000 are listed as infinite, as also are the
values. Positive values of greater than 1,000 are listed as infinite, as also are the 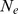 estimates associated with negative
estimates associated with negative 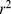 estimates. Lower values of
estimates. Lower values of 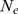 have been rounded to the nearest 10.
have been rounded to the nearest 10.
The disequilibrium factor is introduced in column 5. This column is marked as giving the most likely estimate of 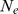 . As expected, all of the really small population size estimates come in the outbreak populations rather than in the endemic populations.
. As expected, all of the really small population size estimates come in the outbreak populations rather than in the endemic populations.
The 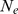 values in columns 3–5 are based on the unlinked locus pairs, including the 153 additional pairs likely to be loosely linked or unlinked. The values in column 6 are the equivalent corrected
values in columns 3–5 are based on the unlinked locus pairs, including the 153 additional pairs likely to be loosely linked or unlinked. The values in column 6 are the equivalent corrected 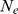 estimates based on all locus pairs. These can be directly compared to the values of
estimates based on all locus pairs. These can be directly compared to the values of 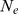 given by the LDNe program [9], also based on all locus pairs. There is good agreement for the smallest population sizes, although the LDNe program shows infinite sizes in a number of cases where the values of
given by the LDNe program [9], also based on all locus pairs. There is good agreement for the smallest population sizes, although the LDNe program shows infinite sizes in a number of cases where the values of 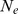 in column 5 are finite.
in column 5 are finite.
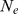 values in column 5, using unlinked loci, differ very little from values on column 6 using all loci. The expectation is that the use of linked loci will lead to under-estimation of
values in column 5, using unlinked loci, differ very little from values on column 6 using all loci. The expectation is that the use of linked loci will lead to under-estimation of 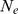 . Many, but not all, values in column 6 are slightly below those in column 5, but the differences are not large. This result seems fortuitous, given that linkage relationships are not as well established for many organisms, necessitating the use of all locus pairs.
. Many, but not all, values in column 6 are slightly below those in column 5, but the differences are not large. This result seems fortuitous, given that linkage relationships are not as well established for many organisms, necessitating the use of all locus pairs.
The final two columns of Table 3 show two different tests of significance, each based on the unlinked plus likely unlinked sub-sample of locus pairs. The first is the usual genotype likelihood test of LD [21], based on permutation of genotypes, with log likelihoods of the genotype tables summed over all relevant locus pairs. The second is a likelihood test based on permutation of genotypes, with likelihoods calculated on the composite haplotype tables. This test seems much more sensitive. Partly this is because, as indicated above and illustrated in Figure 2, the composite haplotype table is much denser than the genotype table, where all the zero and unit values do not contribute to the likelihood. However the second test is influenced by LD, but also by null alleles. The significant values are mostly associated with low population sizes, but there are exceptions to this in both directions. In general, the significance tests seem to be of limited value in judging whether population sizes are infinite or not.
The results from North-West samples [11] are given in Table 5. The results show a comparable proportion of high population numbers compared to the East coast populations of Table 3. Less has been known about these populations, but these results would suggest that, with the exception of the final two samples from Broome and Derby in West Australia, these are well-established outbreaks in most cases.
Table 5. Estimated Ne values for North-West population samples.
| S | No homozygote correction | Homozygote correction | Likelihood Significance | |||||
| Unlinked No permute Eqn. (14) | Unlinked permute Eqn. (18) | Unlinked permute Eqn. (20) ⇓ | All loci | |||||
| permute Eqn. (20) | LDNe | genotypea | composite | |||||
| K-Ke2002 | 22 | 30 | 160 | 270 | 90 | ∞ | *** | |
| K-Ke2003 | 39 | 20 | 60 | 90 | 100 | ∞ | *** | |
| K-Kl2000 | 77 | 70 | 240 | 290 | 160 | 190 | ||
| K-Kl2001 | 50 | 60 | 190 | 210 | 170 | ∞ | ||
| K-Kl2002 | 44 | 30 | 60 | 100 | 70 | 80 | ** | *** |
| K-Kl2003 | 50 | 50 | ∞ | ∞ | ∞ | ∞ | ** | |
| K-Km2002 | 27 | 20 | 420 | 280 | 90 | 50 | * | *** |
| N-DWN02 | 40 | 20 | 50 | 80 | 90 | 780 | ||
| N-DWN03 | 20 | 60 | ∞ | ∞ | ∞ | ∞ | *** | |
| N-DWN99 | 20 | ∞ | ∞ | ∞ | ∞ | ∞ | ||
| N-DWNBUSH02 | 30 | 40 | ∞ | ∞ | ∞ | ∞ | ||
| N-DWN-KTH03 | 19 | 60 | ∞ | ∞ | ∞ | ∞ | ||
| N-GOVE02 | 17 | ∞ | ∞ | ∞ | ∞ | ∞ | ||
| N-KAK02 | 40 | 40 | 80 | 120 | 120 | 440 | *** | |
| N-KTH03 | 20 | 30 | 100 | 230 | ∞ | ∞ | ||
| N-KTHGO02 | 28 | 80 | ∞ | 440 | 470 | ∞ | ** | |
| N-mDK02 | 27 | 40 | 300 | 180 | 270 | ∞ | ||
| N-mDKA02 | 20 | 80 | ∞ | ∞ | 150 | ∞ | ||
| N-mKKu03 | 36 | 30 | 100 | 120 | 80 | 200 | ** | |
| N-nDWN02 | 50 | 70 | 140 | 210 | 320 | ∞ | * | |
| N-nDWN03 | 20 | 90 | ∞ | ∞ | ∞ | 100 | *** | |
| N-nKTH03 | 20 | 30 | 170 | 270 | 420 | ∞ | ||
| Q-AT02 | 21 | 40 | ∞ | ∞ | ∞ | ∞ | ||
| Q-ATH99 | 21 | 110 | ∞ | ∞ | ∞ | 340 | ||
| Q-CT00 | 23 | 140 | ∞ | ∞ | ∞ | ∞ | * | |
| Q-CT99 | 17 | 50 | 90 | 280 | ∞ | ∞ | ||
| Q-LR00 | 24 | 80 | ∞ | ∞ | ∞ | 110 | ||
| Q-MB02 | 21 | 40 | ∞ | ∞ | ∞ | ∞ | ||
| Q-Qld00 | 94 | 110 | 260 | 260 | 390 | ∞ | *** | |
| Q-QLD01 | 55 | 70 | 280 | 280 | 630 | 300 | ||
| Q-QLD02 | 40 | 40 | 220 | 250 | 160 | ∞ | * | |
| Q-QLD03 | 42 | 40 | 250 | 110 | 140 | ∞ | ||
| W-Brm01 | 21 | 20 | 30 | 40 | 30 | 80 | ||
| W-Der01 | 17 | 10 | 10 | 10 | 10 | 10 | *** | ** |
Significant at 5% level.
Significant at 1% level.
Significant at 0.1% level.
Summary of the Findings
The Burrows composite index can be equivalently derived from a ‘composite haplotype table’ in which all genotypes sampled contribute four possible haplotypes.
Although the composite haplotype table has marginal totals that are even numbers due to double counting, a valid  ×
×
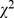 can be calculated for the table. The
can be calculated for the table. The 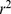 value calculated from this table,
value calculated from this table, 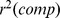 , needs to be multiplied by a factor of 4 to give
, needs to be multiplied by a factor of 4 to give 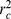 , a valid estimator of
, a valid estimator of 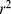 .
.
The expected 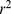 value calculated for the table is
value calculated for the table is 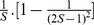 in the absence of LD. This contrasts with the sampling correction of
in the absence of LD. This contrasts with the sampling correction of 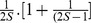 for
for 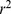 calculated when haplotypes can be recognised.
calculated when haplotypes can be recognised.
The overall calculation of 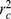 involves summation of values from different locus pairs. Within locus pairs, it involves summation of
involves summation of values from different locus pairs. Within locus pairs, it involves summation of 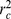 values for each pair of alleles. The weighting for the former is taken from [9], while a weighting proportional to gene frequencies is proposed for the latter.
values for each pair of alleles. The weighting for the former is taken from [9], while a weighting proportional to gene frequencies is proposed for the latter.
The results when this formula are applied to data from Queensland fruit fly give low 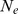 values in all samples, including ones from known large endemic populations. Null alleles are suggested as a cause for this discrepancy, and shown to be frequent in the data.
values in all samples, including ones from known large endemic populations. Null alleles are suggested as a cause for this discrepancy, and shown to be frequent in the data.
The effect of a null allele at frequency 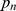 is shown to increase the composite
is shown to increase the composite 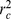 value by the fraction
value by the fraction 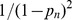 . Although this effect seems small, it will nevertheless overwhelm the calculations for large population sizes.
. Although this effect seems small, it will nevertheless overwhelm the calculations for large population sizes.
The 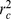 value can be corrected for null alleles using a comparison between the calculated
value can be corrected for null alleles using a comparison between the calculated 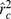 value and an equivalent
value and an equivalent 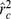 value calculated when genotypes in the sample are permuted at random. This correction is verified by simulation.
value calculated when genotypes in the sample are permuted at random. This correction is verified by simulation.
The single-locus disequilibrium factor suggested by Weir [8], equivalent to a homozygosity correction, is introduced into the calculation. This alters the value of 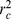 to
to 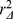 . Use of
. Use of 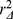 is shown to bias the
is shown to bias the 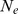 values due to the difficulty of calculating the single-locus disequilibrium factor using
values due to the difficulty of calculating the single-locus disequilibrium factor using 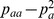 in a finite population.
in a finite population.
Simulation shows that this bias can be rectified using the same permutation approach as for null alleles.
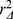 , and
, and 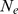 calculated from
calculated from 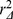 , have lower variances than
, have lower variances than 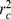 , and
, and 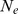 calculated from
calculated from 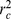 .
.
Simulation shows that the 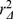 values are almost unaffected by null alleles, in sharp contrast to the
values are almost unaffected by null alleles, in sharp contrast to the 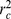 values.
values.
The estimates of 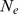 from both East coast and NorthWest populations are, as expected, mostly low for outbreak populations and high for endemic populations.
from both East coast and NorthWest populations are, as expected, mostly low for outbreak populations and high for endemic populations.
The calculations are based on loci known to be unlinked, but are not substantially changed when all locus pairs are considered. Linkage information is usually not available for non-laboratory organisms, and this result shows that lack of such information may not be critical in calculating 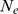 based on LD.
based on LD.
Although the LDNe program [9] is empirically based, it uses the single-locus disequilibrium factor, and appears to work well both with and without null alleles.
Supporting Information
The effect on the estimate of r2 from ?2 weighting compared to allele frequency weighting when introducing a single new mutant.
(TIF)
x 2 and r 2 for the composite haplotype table.
(PDF)
x 2 as a measure of LD for multiple alleles.
(PDF)
The effect of null alleles on r2.
(PDF)
Microsatellite data for East coast samples of Bactrocera tryioni (Queensland Fruit Fly).
(TXT)
Microsatellite data for NorthWest samples of Bactrocera tryioni (Queensland Fruit Fly).
(TXT)
Acknowledgments
Discussions with Ian Franklin, Bill Hill, Bill Sherwin and Robin Waples are gratefully acknowledged
Funding Statement
Funding from Australian Research Council Grant LP0219420. The funders had no role in study design, data collection and analysis, decision to publish, or preparation of the manuscript.
References
- 1. Sved JA (1971) Linkage disequilibrium and homozygosity of chromosome segments in finite popu-lations. Theor Popul Biol 2: 125–141. [DOI] [PubMed] [Google Scholar]
- 2. Sinnock P, Sing C (1972) Analysis of multilocus genetic systems in tecumseh, michigan. ii. consid-eration of the correlation between nonalleles in gametes. Amer J Hum Genet 24: 393–415. [PMC free article] [PubMed] [Google Scholar]
- 3. Hill WG (1981) Estimation of effective population size from data on linkage disequilibrium. Genet Res 38: 209–216. [Google Scholar]
- 4. Hayes B, Visscher P, McPartlan H, Goddard M (2003) Novel multilocus measure of linkage dise-quilibrium to estimate past effective population size. Genome Res 13: 635–643. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5. Waples RS (2006) A bias correction for estimates of effective population size based on linkage disequilibrium at unlinked gene loci. Conservation Genetics 7: 167–184. [Google Scholar]
- 6. Weir BS, Hill WG (1980) Effect of mating structure on variation in linkage disequilibrium. Genetics 95: 477–488. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7. Hill W (1974) Estimation of linkage disequilibrium in randomly mating populations. Heredity 33: 229–239. [DOI] [PubMed] [Google Scholar]
- 8. Weir BS (1979) Inferences about linkage disequilibrium. Biometrics 35: 235–254. [PubMed] [Google Scholar]
- 9. Waples R, Do C (2008) LDNe: A program for calculating effective population size from data on linkage disequilibrium. Molecular Ecology Notes 8: 753–756. [DOI] [PubMed] [Google Scholar]
- 10. Gilchrist AS, Meats AW (2010) The genetic structure of populations of an invading pest fruit y, bactrocera tryoni, at the species climatic range limit. Heredity (Edinb) 105: 165–72. [DOI] [PubMed] [Google Scholar]
- 11. Cameron EC, Sved JA, Gilchrist AS (2010) Pest fruit y (diptera: Tephritidae) in northwestern australia: one species or two? Bull Entomol Res 100: 197–206. [DOI] [PubMed] [Google Scholar]
- 12. Cockerham C, Weir B (1977) Digenic descent measures for finite populations. Genet Res 30: 121–147. [Google Scholar]
- 13. Hill WG, Robertson A (1968) Linkage disequilibrium in finite populations. Theor Appl Genet 38: 226–231. [DOI] [PubMed] [Google Scholar]
- 14. Peel D, Waples RS, Macbeth GM, Do C, Ovenden JR (2013) Accounting for missing data in theestimation of contemporary genetic effective population size (n(e) ). Mol Ecol Resour 13: 243–53. [DOI] [PubMed] [Google Scholar]
- 15. Zhao H, Nettleton D, Soller M, Dekkers JCM (2005) Evaluation of linkage disequilibrium measures between multi-allelic markers as predictors of linkage disequilibrium between markers and qtl. Genet Res 86: 77–87. [DOI] [PubMed] [Google Scholar]
- 16. Zaykin DV, Pudovkin A, Weir BS (2008) Correlation-based inference for linkage disequilibrium with multiple alleles. Genetics 180: 533–45. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17. Hill WG (1975) Linkage disequilibrium among multiple neutral alleles produced by mutation in finite population. Theor Popul Biol 8: 117–26. [DOI] [PubMed] [Google Scholar]
- 18. Sved JA, Feldman MW (1973) Correlation and probability methods for one and two loci. Theor Popul Biol 4: 129–132. [DOI] [PubMed] [Google Scholar]
- 19. Sved JA, McRae AF, Visscher PM (2008) Divergence between human populations estimated from linkage disequilibrium. Am J Hum Genet 83: 737–743. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20. Haldane J (1940) The mean and variance of chi-square, when used as a test of homogeneity, when expectations are small. Biometrika 31: 346–360. [Google Scholar]
- 21. Rousset F (2008) Genepop’007: a complete reimplementation of the genepop software for windows and linux. Mol Ecol Resources 8: 103–106. [DOI] [PubMed] [Google Scholar]
- 22. Nei M, Li WH (1973) Linkage disequilibrium in subdivided populations. Genetics 75: 213–9. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23. Waples RS, England PR (2011) Estimating contemporary effective population size on the basis of linkage disequilibrium in the face of migration. Genetics 189: 633–44. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24. Zhao JT, Frommer M, Sved JA, Gillies CB (2003) Genetic and molecular markers of the queensland fruit y, bactrocera tryoni. J Hered 94: 416–420. [DOI] [PubMed] [Google Scholar]
- 25. Chapuis MP, Estoup A (2007) Microsatellite null alleles and estimation of population differentia-tion. Mol Biol Evol 24: 621–31. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
The effect on the estimate of r2 from ?2 weighting compared to allele frequency weighting when introducing a single new mutant.
(TIF)
x 2 and r 2 for the composite haplotype table.
(PDF)
x 2 as a measure of LD for multiple alleles.
(PDF)
The effect of null alleles on r2.
(PDF)
Microsatellite data for East coast samples of Bactrocera tryioni (Queensland Fruit Fly).
(TXT)
Microsatellite data for NorthWest samples of Bactrocera tryioni (Queensland Fruit Fly).
(TXT)