Skip to main content
PMC home page
Scientific Reports logoLink to Scientific Reports
. 2013 Jul 24;3:2276. doi: 10.1038/srep02276

Perfect crystals grown from imperfect interfaces

Claudiu V Falub 1,7,8,a, Mojmír Meduňa 2,3,7, Daniel Chrastina 4, Fabio Isa 4, Anna Marzegalli 5, Thomas Kreiliger 1, Alfonso G Taboada 1, Giovanni Isella 4, Leo Miglio 5, Alex Dommann 6, Hans von Känel 1
PMCID: PMC3721082  PMID: 23880632

Abstract

The fabrication of advanced devices increasingly requires materials with different properties to be combined in the form of monolithic heterostructures. In practice this means growing epitaxial semiconductor layers on substrates often greatly differing in lattice parameters and thermal expansion coefficients. With increasing layer thickness the relaxation of misfit and thermal strains may cause dislocations, substrate bowing and even layer cracking. Minimizing these drawbacks is therefore essential for heterostructures based on thick layers to be of any use for device fabrication. Here we prove by scanning X-ray nanodiffraction that mismatched Ge crystals epitaxially grown on deeply patterned Si substrates evolve into perfect structures away from the heavily dislocated interface. We show that relaxing thermal and misfit strains result just in lattice bending and tiny crystal tilts. We may thus expect a new concept in which continuous layers are replaced by quasi-continuous crystal arrays to lead to dramatically improved physical properties.

Epitaxial heterostructures and nanostructures have become of immense interest in past decades because of their unique mechanical, electrical and optical properties. Traditionally, destructive techniques based on transmission electron microscopy (TEM) have been the methods of choice to analyse their crystal perfection, composition and strain1,2,3. With the advent of nanofocused X-ray beams4,5,6,7,8,9,10 and advanced X-ray diffraction (XRD) imaging techniques11,12,13,14,15,16 available at third-generation synchrotrons it has become possible to address individual crystals down to the nanoscale non-destructively. The role of strain induced by lattice misfit in determining the properties of epitaxial heterostructures and nanostructures can hardly be overemphasized. Its effects on the structural, optical and transport properties have been studied for decades17,18,19,20,21,22,23,24,25,26.

Here we show by scanning X-ray nanodiffraction how misfit and thermal strain of a highly mismatched layer-substrate system may evolve when the substrate is deeply patterned at a micron scale. We show that space-filling arrays of highly perfect single crystals can grow from heavily dislocated interfaces, provided that epitaxial growth conditions and substrate patterns are carefully matched as described in detail elsewhere27. As a prototypical case we take germanium epitaxially grown onto tall pillars a few microns in width, obtained by etching Si(001) substrates to much larger depths. For this system, the lattice mismatch between Si and Ge amounts to 4.2%28, while the difference of thermal expansion coefficients is 130% at 300 K29.

The Report is separated into three parts. First, we demonstrate how elastic relaxation of the thermal strain leads to diminishing lattice bending as the crystals gain in height. Second, we evaluate the net tilts of individual crystals emerging during the plastic relaxation of the misfit strain. Finally, by mapping the crystal quality on a nanometre scale, we provide evidence for perfect epitaxial single crystal growth from a heavily disordered interface.

We believe that the concept developed here may be the key to device applications heretofore simultaneously hampered by crystal defects, wafer bowing and layer cracks. Such applications may comprise X-ray detectors made from many tens of microns tall Ge crystals grown directly onto Si readout electronics; multiple-junction solar cells from III/V semiconductors stacked on a Ge bottom cell on top of a Si substrate; or power transistors, for example from cubic SiC grown on suitably patterned Si substrates.

Results

The Ge crystals forming the object of the present study were grown on deeply patterned Si(001) substrates under conditions favouring vertical over later growth (Methods, Supplementary Information S1). In the top view scanning electron microscopy (SEM) images of Fig. 1a, b and c, and the corresponding perspective views of Fig. 1d, e and f we show how such a Ge/Si heterostructure evolves with increasing deposition time. For low coverage (Fig. 1a and d) the separation of epitaxial Ge crystals is defined by the substrate geometry. The crystals then expand both laterally and vertically (Fig. 1b and e), but eventually lateral growth stops, leaving a quasi-continuous layer of Ge crystals separated by gaps which are just a few tens of nanometres wide (Fig. 1c and f; see also Supplementary Information S1).

Figure 1. Scanning X-ray nanodiffraction of arrays of epitaxial Ge crystals.

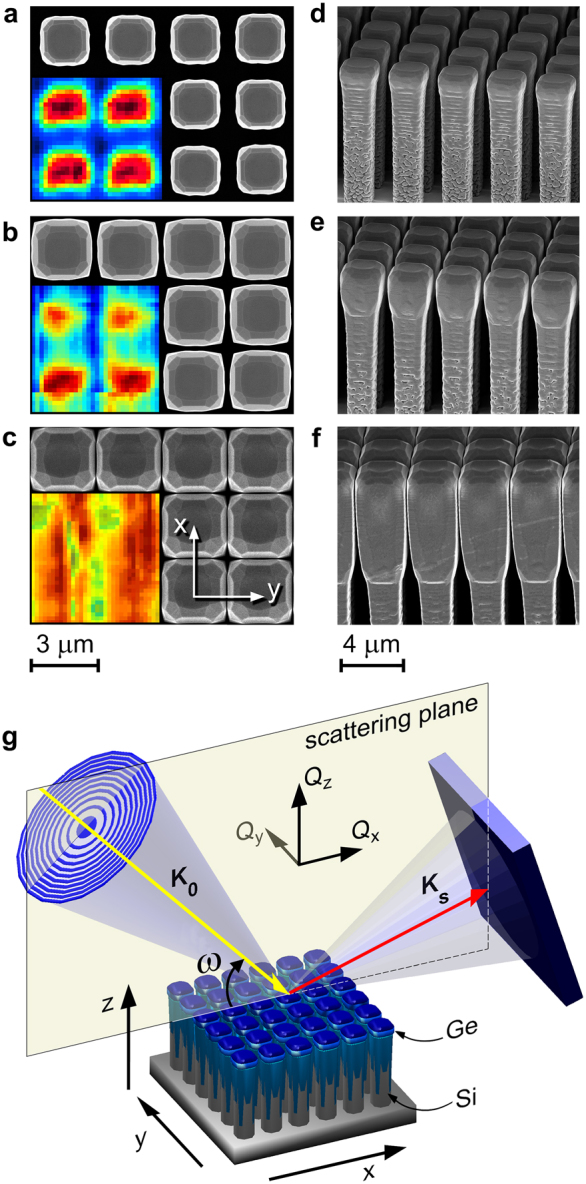
Figure 1

Open in a new tab

Top- and perspective-view SEM micrographs of 1.2 μm (a, d), 3.1 μm (b, e), and 7.3 μm (c, f) tall Ge crystals on patterned Si(001) wafer with 8-μm-tall and 2-μm-wide Si pillars, spaced by 1 μm. The insets in (a, b, c) show the total intensity for four crystals collected around the Ge(115) peak for all incidence angles. (g), Experimental setup at the ID01 beamline (ESRF). The primary beam (vector K0, incidence angle ω), focused down to ~ 300 × 500 nm by means of Fresnel zone plates, is moved across the Ge crystals array by a high-precision piezo-stage. The scattered beam (vector Ks) was collected by a 2D X-ray pixel detector.

We have previously studied such an array of closely spaced Ge crystals by laboratory high-resolution XRD measurements27. The information gained on strain and crystal quality was, however, obscured by averaging over thousands of crystals because of the large size of the X-ray beam, e.g. full-width-at-half-maximum (FWHM) ~ 1 mm (a brief summary can be found in Supplementary Information S2).

Here we shall discuss crystal quality and strain mapping at a microscopic scale as obtained by scanning X-ray nanodiffraction. A schematic of the scattering geometry is shown in Fig. 1g. The scattering plane with reciprocal space directions (Qx,Qz) is defined by the vectors K0 and Ks, forming the axes of the cones of incident and scattered X-ray beams, respectively. As a result of the beam focusing and the use of a two-dimensional (2D) detector, the scattered X-rays provide simultaneous information in all three directions Qx, Qy and Qz of reciprocal space (Supplementary Information S3-A). Individual Ge crystals were localized by recording the total intensity of an asymmetrical Ge(115) Bragg peak during sample translation in the (x,y) plane defined in Fig. 1g (Supplementary Information S3-B). The resulting intensity patterns are shown in the insets of Fig. 1a, b and c. They indicate that with increasing height, and therefore smaller gaps, the Ge crystals become more and more difficult to resolve.

Lattice bending close to the interface

Let us first focus on the elastic relaxation of the strain induced by the mismatch of thermal expansion parameters. As we shall see, it manifests itself most clearly for the thinnest sample with 1.2-μm-tall crystals of Fig. 1a and d. Figure 2a–d shows for such a sample the three-dimensional (3D) reciprocal space maps (RSMs) measured in the vicinity of the Si and Ge (115) reflections, projected onto the (Qx,Qy) plane parallel to the interface (see also Fig. 1g). For the Si(115) reflection, the peak positions are the same in all four panels. For the Ge(115) reflection on the other hand, the observed intensity maxima may be seen to correlate with the positions at which the X-ray beam hits the sample (see also Supplementary Movies 1 and 2). Indeed, the insets in the lower left corners, marking the beam positions, indicate one, two or four intensity maxima, when the beam is centred in the middle of a crystal (Fig. 2a), in the trench between two crystals (Fig. 2b and c) or at the trench crossing between four crystals (Fig. 2d), respectively. At first sight, it might appear reasonable to expect as many maxima as there are crystals simultaneously illuminated by the beam. In reality the situation must be more subtle, however, since equivalent Bragg planes on neighbouring crystals should give rise to a single peak if they were oriented exactly alike. To trace the origin of the multiple intensity maxima we recorded their shift in the reciprocal (Qx,Qy) plane while moving the beam along the real space y-axis in steps of 200 nm. This was repeated for various x-positions in steps of 400 nm. The data analysis revealed that the observed peak shift is due to concave bending of the Ge(001) lattice planes with a radius of curvature given by R = [(1/Qz)(dQξ/dξ )]−1, where ξ is any direction in the (x,y) plane (Supplementary Information S3-C). Averaged over four crystals R amounts to 770 ± 20 μm for the sample of Fig. 1a and d, corresponding to a tilt of the lattice planes towards the sidewalls of the crystals by ~ ± 0.1°. The lattice bending explains why more than one Ge crystal can contribute to an RSM. This is illustrated in Fig. 2e where close to a trench the (001) lattice planes of adjacent crystals can be seen to be tilted in opposite directions because of the bending. The same must be true of course for the {115} planes. For an X-ray beam incident close to such a trench the Bragg condition will be satisfied for two different values of the Qx component of the scattering vector, stemming from Bragg planes on both sides of the trench. A comparison with the lattice distortion calculated by 3D finite element method (FEM) reveals that the observed lattice bending can be explained by the elastic relaxation of the tensile strain developing in the Ge crystals during sample cooling after growth, because the thermal expansion coefficient of Ge exceeds that of the Si substrate (Supplementary Information S4). The FEM simulations were carried out for Ge crystals with a realistic morphology derived from SEM cross-sections. Figure 2e shows cross-sections through two neighbouring 1.2-μm-tall Ge crystals exhibiting the experimentally determined facet structure. The average bending of lattice planes derived from our X-ray analysis is indicated by the dashed curves. The curvature is exaggerated by a factor of 200 to render the bending clearly visible. The similarly exaggerated distortion of the (001) planes calculated by 3D FEM is shown in the same figure, along with the xz component of the rotation tensor in a colour code. The calculation reveals a gradual decrease of the bending towards the top of the Ge crystal, whereas the result of our X-ray analysis necessarily provides the bending averaged over the crystal as a whole.

Figure 2. Mapping lattice bending close to the interface.

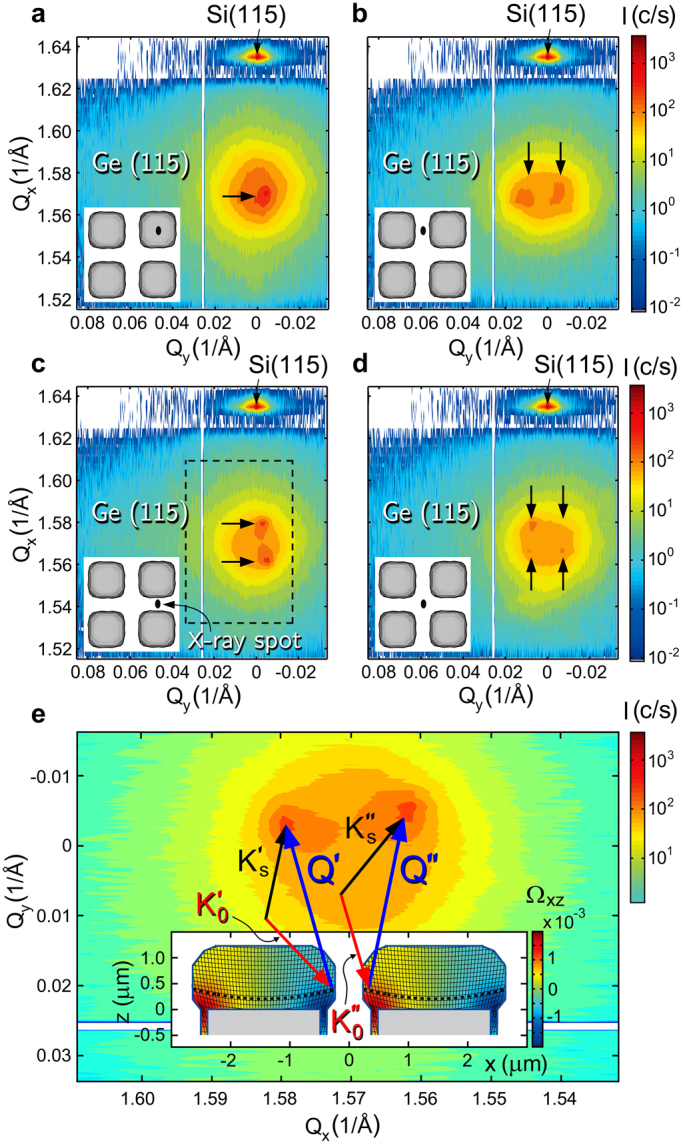
Figure 2

Open in a new tab

(a–d), Projections of the 3D RSM onto the (Qx,Qy) plane recorded at different (x,y) positions shown in the insets at the lower left. The arrows indicate the local maxima stemming from diffraction at lattice planes of adjacent crystals with opposite tilt. (e), Close-up view of the RSM projection area in (c) outlined by a dashed rectangle, rotated anticlockwise by 90°. The inset reveals how lattice bending of 1.2-μm-tall adjacent Ge crystals may give rise to multiple peaks in the RSM. Due to the tilted crystal planes in opposite directions at the trench between two adjacent crystals, the Bragg condition is fulfilled for two scattering vectors, Q′ and Q”. K0′ and K0” are the corresponding vectors of the incidence beam, whereas Ks′ and Ks” are the vectors of the exit beam. The lattice bending displayed by series of curved black lines was extracted from the rotation tensor obtained from FEM calculations. The colour maps represent cross-sections through the xz component of the 3D rotation tensor sliced through the middle of the Ge crystals (y = 0). The thick dashed black lines represent the experimental curvatures obtained from synchrotron nanodiffraction experiments. The position of the experimental curvature along the z-axis was chosen such that it matches the curvature calculated by FEM. The scale of the lattice bending was increased by a factor of 200 to make it better visible.

We have carried out similar analyses for the thicker samples of Fig. 1b–f (Supplementary Movies 3 and 4, Supplementary Information S4). For the 3.1-μm-tall crystals the lattice bending turns out to be much smaller. The measured radius of curvature amounts to R = (10 ± 8) mm. According to the FEM calculations, the lattice bending is now negligible near the crystal top. This explains the smaller observed lattice bending, since now the diffraction information stems from a much larger volume. Finally, for the 7.3-μm-tall crystals of Fig. 1c and f the average bending sampled by the X-rays becomes altogether negligible.

Random net tilts induced by misfit dislocations

After having discussed the elastic distortions of the crystal lattice as a mechanism to release thermal strain, we now come to the second topic of importance, namely the consequences of plastic strain release. Our analysis of RSMs such as those of Figs. 2a–d reveals that apart from the lattice bending there exists a net tilt of each crystal as a whole (Supplementary Information S5). In general, such tilts can be attributed to an imbalance of the number of misfit dislocations (MDs) with different Burgers vectors of mixed character at the interface30,31. For crystals of small height, such as those of Fig. 1a and d, it turns out, however, that the effect of lattice bending by far outweighs the effect of the net tilt (Supplementary Information S5-A). It is only for crystals several microns in height (Fig. 1c and f) that the net tilt clearly dominates. Unfortunately, for closely spaced crystals of this kind the inferior spatial resolution no longer allows their unambiguous localization by X-rays (see inset of Fig. 1c). We therefore had to find another way to accurately determine the net tilt. The key was to eliminate the majority of the Ge crystals from a space-filling array without disturbing the remaining crystals. We accomplished this by first etching the samples in H2O2. This caused the trenches to widen and material covering the sidewalls of Si pillars to be removed. In a subsequent step, we removed the Ge crystals from certain areas using micromanipulators, leaving but a few isolated ones for examination by scanning X-ray nanodiffraction (Supplementary Movie 5, Supplementary Information S1). Figure 3a shows an intensity map for the Ge(115) reflection, recorded while scanning the incident beam along the length of a selected crystal. Having thus determined where the beam hits the crystal, full 3D RSMs were acquired around the Ge(115) peak at chosen positions along the height of the crystal. Comparing the peak position in each one of these RSMs with the corresponding position of the Si(115) reflection, the net tilt of the Ge crystal could be accurately determined (Supplementary Information S5-B). We have carried out this procedure for three isolated Ge crystals. The directions, along with the magnitudes of their tilts, are shown in Fig. 3b and Table 1. Even though a statistically relevant number of Ge crystals could not be investigated, the results allow a comparison with results obtained by laboratory XRD. Now we have the final proof that the apparent mosaicity, leading to the observed peak broadening of ~ 0.1° along Qx27, is in fact caused by the random tilts of thousands of crystals sampled by the large X-ray beam.

Figure 3. Probing the random net tilts of Ge crystals.

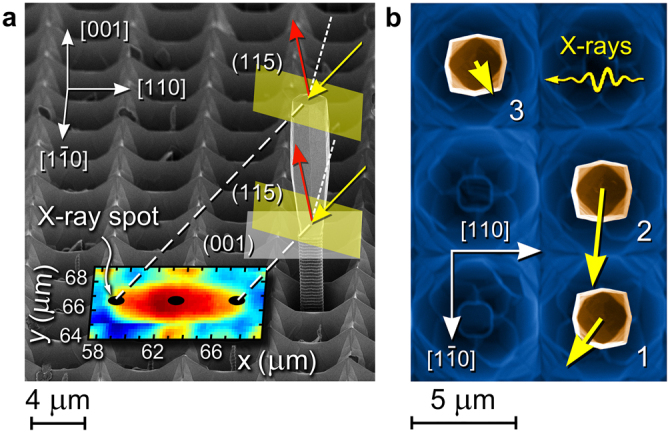
Figure 3

Open in a new tab

(a), Scattering geometry for the (115) Bragg reflection for an 8-μm-tall-Ge crystal on a patterned Si(001) wafer with 8-μm-tall and 2-μm-wide Si pillars, spaced by 4 μm. Neighbouring Ge crystals were removed. One (001) and two (115) planes are shown by transparent grey and green areas, respectively. The yellow arrows indicate the incident X-ray beams for two positions along the crystal height (bottom and top), and red arrows are the corresponding diffracted beams. The color map superimposed onto the perspective-view SEM micrograph represents the scattered intensity collected around the Ge(115) peak for an incidence angle of ω = 46.3° when the incident beam was moving along the length of the crystal. (b), Top-view SEM micrograph of three Ge crystals. The direction of incident X-rays is indicated (scattering geometry is similar to that shown in (a). The yellow thick arrows starting from the centre of each Ge crystal are the displacement vectors of the symmetry axes of the crystals from the [001] direction multiplied by 500 to enhance the visibility of local tilt.

Table 1. Net tilts of Ge crystals in Fig. 3b. χx and χy represent the tilts along the x- and y-direction, respectively.

Crystal χx (°) χy (°)
1 −0.023 ± 0.006 0.033 ± 0.005
2 −0.006 ± 0.001 0.068 ± 0.001
3 0.012 ± 0.001 0.023 ± 0.001
Open in a new tab

Perfect crystals emerging from imperfect interfaces

The ability to unambiguously address individual Ge crystals by scanning X-ray nanodiffraction provides us finally with the unique possibility to measure crystal quality at a nanometre scale. For this part of the study we chose Ge crystals with inclined top facets (Supplementary Information S1), since faceting has previously been shown to remove dislocations by deflecting them towards the sidewalls27,32,33,34. The full 3D RSM, along with its projections measured at the top of an 11-μm-tall, faceted Ge crystal is shown in Fig. 4. From this measurement we can appreciate the extraordinary quality of our epitaxial Ge crystals, despite their growth from a heavily dislocated interface. The apparent mosaicity, caused by individual crystal tilts, previously measured with laboratory sources, has vanished completely. As an example, we show cross-sections along Qx and Qz in Fig. 4. They exhibit similar widths both for the Ge(115) and Si(115) reflections, which, to our knowledge has never been seen before for a relaxed, highly mismatched heterostructure. The peak widths are in fact limited by the instrumental resolution (i.e. focusing by Fresnel Zone Plate induces a divergence of ~ 0.08° and angular size of the detector pixel ~ 0.003°) that is much broader than the Darwin width. Thus, for 11 keV X-ray photons the corresponding Darwin widths of diffraction curves for Si(115) and Ge(115) are 0.7” (ΔQz = 6 × 10−5Å−1) and 10” (ΔQx = 4 × 10−4 Å−1), respectively (Supplementary Information S6).

Figure 4. Three-dimensional X-ray nanodiffraction of a perfect epitaxial Ge crystal.

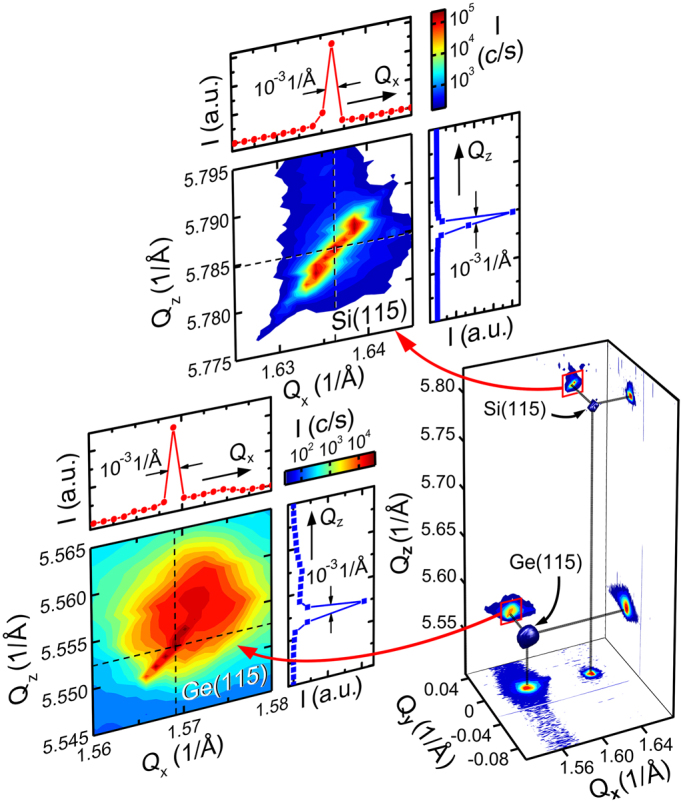
Figure 4

Open in a new tab

3D RSM around Si(115) and Ge (115) reciprocal lattice points and the corresponding projections onto the (Qx,Qz), (Qy,Qz) and (Qx,Qy) planes, recorded at the top of the 11-μm-tall Ge crystal of Fig. 3a. The Si and Ge peaks are plotted as iso-surfaces. The detailed region around the QxQz projection of Ge(115) reveals a very sharp peak, as sharp as the Si(115) peak, stemming from the defect-free epitaxial Ge crystal, superimposed onto a weaker, broader peak, corresponding to the defective, tensile-strained material in the trenches. The elongation of the sharp Si(115) and Ge(115) peaks is due to the divergence of the focused beam.

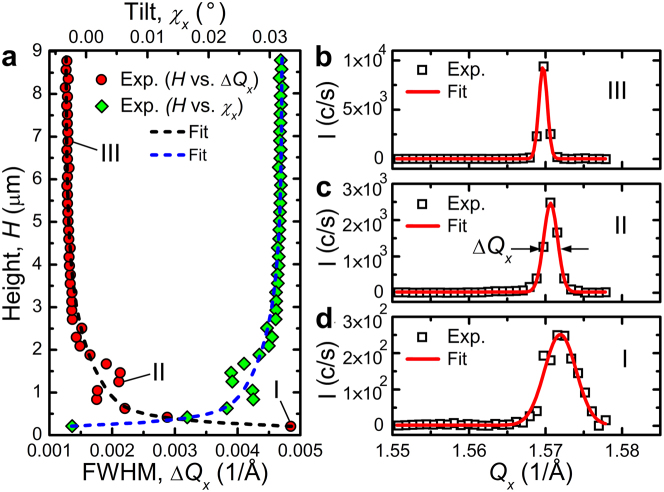
We have recorded the diffracted signal along the whole height of the 11-μm-tall Ge crystal in steps of ~ 200 nm from the interface to the top (see Supplementary Movies 6 and 7). The crystal was isolated by the etching and micro-manipulation procedure described above. Figure 5a shows the evolution of the peak FWHM, ΔQx, taken from the (Qx,Qy) cut (see also Fig. 4) through the RSMs measured as a function of crystal height. The dashed black curve indicates an asymptotic exponential decay of ΔQx from the interface towards the crystal top. It shows that at ~ 0.2 μm above the interface the peak width is ~ 0.0048 1/Å, and it drops by a factor of 1/e at a height of ~ 2.9 μm. The resolution-limited width is already reached at a height of ~ 4 μm. Three representative cross-sections, together with Gaussian fits from which the FWHMs were obtained, are shown in Fig. 5b–d. They were taken at the heights I, II and III indicated in Fig. 5a. The decrease of the peak width as we move away from the dislocated interface is a clear manifestation of decaying strain fields and of the escape of threading dislocations to the crystal sidewalls35. To the best of our knowledge this is the first demonstration of a perfect strain-free single crystal evolving from a heavily disordered interface. Interestingly, the peak positions measured at the three heights in Fig. 5a do not coincide. This is in perfect agreement with our analysis of crystal bending and tilt carried out above. Figure 5a shows in fact how the net tilt of a single crystal develops. At the interface it is practically negligible, but as soon as one moves away from the interface it increases quickly and tends to a value of ~ 0.032° in the dislocation-free region of the crystal.

Figure 5. Perfect single crystals emerging from imperfect interfaces.

Figure 5

Open in a new tab

(a), Full-width-at-half-maximum (FWHM) of the Ge(115) peak (ΔQx) and tilt (χx) along the Qx direction vs. crystal height. The experimental data are fitted with asymptotic exponential functions, 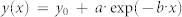Inline graphic, where a is positive and negative for y = ΔQx and y = χx, respectively (dashed black and blue lines). (b–d), Cross-sections through the Ge(115) peak along Qx at 3 different crystal heights (e.g. I, II and III) depicted in (a). The experimental data are fitted to single Gaussians.

Discussion

We have used an X-ray beam, focused to a spot a few hundred nanometres in size, to study strain and perfection of three-dimensional epitaxial Ge crystals on deeply-patterned Si substrates. We have shown that in the first few microns the crystal planes are bent as a result of elastic relaxation of the thermal strain which develops during cooling from the growth temperature. The strain caused by the large mismatch of the lattice parameters between Si and Ge is on the other hand released by dislocations at the Ge/Si interface, and these cause the crystals to become slightly tilted with respect to one another. Most importantly, after reaching sufficient height, the Ge crystals become indistinguishable from perfect, defect-free single crystals. In short, we have replaced defective continuous heterolayers by perfect crystals with individual tilts. We consider the example studied here as a model system for heterolayers from highly mismatched materials, unaffected by the usual problems of thermal cracks, wafer bowing and crystal defects. Moving from continuous to quasi-continuous heterolayers may therefore enable a wealth of applications, such as high-brightness light emitting diodes, power electronic devices, multiple-junction solar cells and radiation detectors, fabricated on large area silicon substrates, which heretofore have suffered from the shortcomings of the conventional approach.

Methods

Dense arrays of Ge crystals were grown by low-energy plasma-enhanced chemical vapour deposition (LEPECVD) onto micrometre-sized Si pillars micro-machined into Si(001) wafers by conventional photolithography and deep reactive ion etching (DRIE)27,36. Samples with isolated Ge crystals were fabricated by etching the dense arrays in 30 wt% H2O2 solution (90 seconds at 70°C) and by removing neighbouring crystals using micromanipulators inside a scanning electron microscope. Scanning X-ray nanodiffraction experiments were performed at the ID01 beamline of European Synchrotron Radiation Facility (ESRF) in Grenoble, using an X-ray beam (energy 11.07 keV) focused down to ~ 300 × 500 nm by means of Fresnel zone plates (FZP). For a certain reflection, e.g. symmetric (004) and asymmetric (115), and a fixed (x,y) position, the incidence angle of the X-ray beam was scanned while moving the beam across the sample. Since a two-dimensional pixel detector was used, three-dimensional reciprocal space maps could be constructed for each (x,y) position of the X-ray beam by rocking the incidence angle. For arrays of short Ge crystals lattice bending was determined by monitoring the position of the (115) diffraction peak along the Qy direction (i.e. perpendicular to the scattering plane) as a function of the y coordinate. Net tilts of tall isolated crystals were obtained by measuring the deviations of the peak position from their nominal value (i.e. 100% relaxed Ge with no tilt) in the (Qx,Qz) and (Qy,Qz) planes. FEM simulations were performed using the software COMSOL. The 3D models were constructed based on top-view and cross-section SEM images.

For further details, please see supplementary information (SI).

Author Contributions

C.V.F. and F.I. prepared the germanium crystal arrays with support from D.C. and G.I.; C.V.F., M.M., D.C., F.I. and T.K. designed and performed the synchrotron scanning X-ray nanodifraction experiments; M.M. performed the analysis of the synchrotron data with support from C.V.F.; C.V.F. performed the scanning electron microscopy and laboratory X-ray diffraction experiments, and analysed the data with support from H.v.K. and A.D.; T.K. and A.G.T. prepared the isolated Ge crystals with support from C.V.F.; A.M. and M.M. performed the FEM calculations with support from L.M.; C.V.F., M.M. and H.v.K. wrote the manuscript; C.V.F. prepared the manuscript figures with support from M.M. and H.v.K.; All authors reviewed the manuscript.

Supplementary Material

Supplementary Information

Supplementary information

srep02276-s1.pdf (2.8MB, pdf)
Supplementary Information

Supplementary movie 1

Download video file (4.8MB, mov)
Supplementary Information

Supplementary movie 2

Download video file (4.6MB, mov)
Supplementary Information

Supplementary movie 3

Download video file (4.5MB, mov)
Supplementary Information

Supplementary movie 4

Download video file (3.5MB, mov)
Supplementary Information

Supplementary movie 5

Download video file (4.2MB, mov)
Supplementary Information

Supplementary movie 6

Download video file (4.7MB, mov)
Supplementary Information

Supplementary movie 7

Download video file (4.1MB, mov)

Acknowledgments

Supported by the Swiss federal program funding Nano-Tera through project NEXRAY. One author wishes to acknowledge the projects INGO LA 10010 and Research4Industry (CZ.1.07/2.4.00/17.0006). We thank B. Batlogg for continuing support, the entire crew of the ID01 beamline at the European Synchrotron Radiation Facility (ESRF), Grenoble, in providing excellent user support for the scanning X-ray nanodiffraction experiments, Centre Suisse d'Electronique et Microtechnique (CSEM) for supplying the patterned Si substrates, A. Neels, T. Bandi for discussions about the laboratory high-resolution XRD experiments, D. Scopece for providing the code for building the 3D crystal structures used as input for the FEM simulations, O. Caha for helpful considerations about the diffraction theory, and the FIRST Center for Micro- and Nanoscience of ETH Zürich for making available its infrastructure. We are indebted to Pilegrowth Tech Srl for providing their technical expertise.

References

  1. Hytch M., Houdellier F., Hue F. & Snoeck E. Nanoscale holographic interferometry for strain measurements in electronic devices. Nature 453, 1086–1089 (2008). [DOI] [PubMed] [Google Scholar]
  2. Urban K. W. Studying atomic structures by aberration-corrected transmission electron microscopy. Science 321, 506–510 (2008) [DOI] [PubMed] [Google Scholar]
  3. Midgley P. A. & Dunin-Borkowski R. E. Electron tomography and holography in materials science. Nat. Mater. 8, 271–280 (2009). [DOI] [PubMed] [Google Scholar]
  4. Hanke M. et al. Scanning X-ray diffraction with 200 nm spatial resolution. Appl. Phys. Lett. 92, 193109 (2008). [Google Scholar]
  5. Mocuta C. et al. Beyond the ensemble average: X-ray microdiffraction analysis of single SiGe islands. Phys Rev B 77, 245425 (2008). [Google Scholar]
  6. Stangl J. et al. X-ray diffraction as a local probe tool. ChemPhysChem 10, 2923–2930 (2009). [DOI] [PubMed] [Google Scholar]
  7. Dubslaff M. et al. X-ray nanodiffraction at individual SiGe/Si(001) dot molecules and its numerical description based on kinematical scattering theory. Appl. Phys. Lett. 96, 133107 (2010). [Google Scholar]
  8. Hrauda N. et al. X-ray nanodiffraction on a single SiGe quantum dot inside a functioning field-effect transistor. Nano Lett. 11, 2875–2880 (2011). [DOI] [PMC free article] [PubMed] [Google Scholar]
  9. Segura-Ruiz J., Martinez-Criado G., Chu M. H., Geburt S. & Ronning C. Nano-X-ray absorption spectroscopy of single Co-implanted ZnO nanowires. Nano Lett. 11, 5322–5326 (2011). [DOI] [PubMed] [Google Scholar]
  10. Chrastina D. et al. Patterning-induced strain relief in single lithographic SiGe nanostructures studied by nanobeam X-ray diffraction. Nanotechnol. 23, 155702 (2012). [DOI] [PubMed] [Google Scholar]
  11. Pfeifer M. A., Williams G. J., Vartanyants I. A., Harder R. & Robinson I. K. Three-dimensional mapping of a deformation field inside a nanocrystal. Nature 442, 63–66 (2006). [DOI] [PubMed] [Google Scholar]
  12. Thibault P. et al. High-resolution scanning X-ray diffraction microscopy. Science 321, 379–382 (2008). [DOI] [PubMed] [Google Scholar]
  13. Robinson I. K. & Harder R. Coherent X-ray diffraction imaging of strain at the nanoscale. Nat. Mater. 8, 291–298 (2009). [DOI] [PubMed] [Google Scholar]
  14. Newton M. C., Leake S. J., Harder R. & Robinson I. K. Three-dimensional imaging of strain in a single ZnO nanorod. Nat. Mater. 9, 120–124 (2010). [DOI] [PubMed] [Google Scholar]
  15. Chamard V. et al. Three-dimensional X-ray Fourier transform holography: The Bragg case. Phys. Rev. Lett. 104, 165501 (2010). [DOI] [PubMed] [Google Scholar]
  16. Godard P. et al. Three-dimensional high-resolution quantitative microscopy of extended crystals. Nat. Commun. 2, 568 (2011). [DOI] [PubMed] [Google Scholar]
  17. Wei S.-H. & Zunger A. Optical properties of zinc-blende semiconductor alloys: Effects of epitaxial strain and atomic ordering. Phys. Rev. B 49, 14337–14351 (1994). [DOI] [PubMed] [Google Scholar]
  18. Fitzgerald E. A. et al. Influence of strain on semiconductor thin film epitaxy. J. Vac. Sci. Technol. A 15, 1048–1056 (1997). [Google Scholar]
  19. Dunstan D. J. Strain and strain relaxation in semiconductors. J. Mater. Sci Mater. Electron. 8, 337–375 (1997). [Google Scholar]
  20. Gil B. Stress effects on optical properties. Sem. Semimet. 57, 209–274 (1999). [Google Scholar]
  21. Ieong M., Doris B., Kedzierski J., Rim K. & Yang M. Silicon device scaling to the sub-10-nm regime. Science 306, 2057–2060 (2004). [DOI] [PubMed] [Google Scholar]
  22. Stangl J., Holý V. & Bauer G. Structural properties of self-organized semiconductor nanostructures. Rev. Mod. Phys. 76, 725–783 (2004). [Google Scholar]
  23. Roberts M. M. et al. Elastically relaxed free-standing strained-silicon nanomembranes. Nat. Mater. 5, 388–393 (2006). [DOI] [PubMed] [Google Scholar]
  24. Trotta R. Nanomembrane quantum-light-emitting diodes integrated onto piezoelectric actuators. Adv. Mater. 24, 2668–2672 (2012). [DOI] [PubMed] [Google Scholar]
  25. Minamisawa R. A. et al. Top-down fabricated silicon nanowires under tensile elastic strain up to 4.5%. Nat. Commun. 3, 1096 (2012). [DOI] [PubMed] [Google Scholar]
  26. Süess M. J. et al. Analysis of enhanced light emission from highly strained germanium microbridges. Nat. Photon. 7, 466–472 (2013). [Google Scholar]
  27. Falub C. V. et al. Scaling hetero-epitaxy from layers to three-dimensional crystals. Science 335, 1330–1334 (2012). [DOI] [PubMed] [Google Scholar]
  28. Mo Y.-W., Savage D. E., Swartzentruber B. S. & Lagally M. G. Kinetic Pathway in Stranski-Krastanov Growth of Ge on Si(001). Phys. Rev. Lett. 65, 1020–1023 (1990). [DOI] [PubMed] [Google Scholar]
  29. Slack G. A. & Bartram S. F. Thermal expansion of some diamondlike crystals. J. Appl. Phys. 46, 89–98 (1975). [Google Scholar]
  30. Dodson B. W. et al. Asymmetric Tilt Boundaries and Generalized Heteroepitaxy. Phys. Rev. Lett. 61, 2681–2684 (1988). [DOI] [PubMed] [Google Scholar]
  31. Young E. C. et al. Lattice tilt and misfit dislocations (1122) in semipolar GaN heteroepitaxy. Appl. Phys. Express 3, 011004 (2010). [Google Scholar]
  32. Park J.-S. et al. Defect reduction of selective Ge epitaxy in trenches on Si(001) substrates using aspect ratio trapping. Appl. Phys. Lett. 90, 052113 (2007). [Google Scholar]
  33. Bai J. et al. Study of the defect elimination mechanisms in aspect ratio trapping Ge growth. Appl. Phys. Lett. 90, 101902 (2007). [Google Scholar]
  34. Knoke I. Y., Meissner E., Friedrich J., Strunk H. P. & Müller G. Reduction of dislocation density in GaN during low-pressure solution growth. J. Cryst. Growth 310, 3351–3357 (2008). [Google Scholar]
  35. Marzegalli A. et al. Unexpected dominance of vertical dislocations in high-misfit Ge/Si(001) films and their elimination by deep substrate patterning. Adv. Mater., 10.1002/adma.201300550 (2013). [DOI] [PubMed] [Google Scholar]
  36. Rosenblad C. et al. Silicon epitaxy by low-energy plasma enhanced chemical vapor deposition. J. Vac. Sci. Technol. A 16, 2785–2790 (1998). [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

Supplementary Information

Supplementary information

srep02276-s1.pdf (2.8MB, pdf)
Supplementary Information

Supplementary movie 1

Download video file (4.8MB, mov)
Supplementary Information

Supplementary movie 2

Download video file (4.6MB, mov)
Supplementary Information

Supplementary movie 3

Download video file (4.5MB, mov)
Supplementary Information

Supplementary movie 4

Download video file (3.5MB, mov)
Supplementary Information

Supplementary movie 5

Download video file (4.2MB, mov)
Supplementary Information

Supplementary movie 6

Download video file (4.7MB, mov)
Supplementary Information

Supplementary movie 7

Download video file (4.1MB, mov)

Articles from Scientific Reports are provided here courtesy of Nature Publishing Group

RESOURCES