Experimental Observations of Dynamic Critical Phenomena in a Lipid Membrane

Abstract

Near a critical point, the time scale of thermally induced fluctuations diverges in a manner determined by the dynamic universality class. Experiments have verified predicted three-dimensional dynamic critical exponents in many systems, but similar experiments in two dimensions have been lacking for the case of conserved order parameter. Here we analyze the time-dependent correlation functions of a quasi-two-dimensional lipid bilayer in water to show that its critical dynamics agree with a recently predicted universality class. In particular, the effective dynamic exponent z_eff crosses over from ~2 to ~3 as the correlation length of fluctuations exceeds a hydrodynamic length set by the membrane and bulk viscosities.

Lipids self-assemble in water to form sheets that are two molecules thick, within which the lipids are free to diffuse. When composed of several lipid species, these two-dimensional (2D) liquid membranes can demix into coexisting liquid phases, termed L_o and L_d, over a range of temperatures and compositions, and can exhibit critical behavior [1-4]. Among 2D critical phenomena, composition fluctuations in membranes are rather unique in that their large sizes and long decay times are accessible to optical microscopy. For example, Fig. 1 and the Supplemental Material [5] show a vesicle (a spherical membrane shell) in which correlated regions reaching 10 μm persist for seconds [5]. Direct visualization of these equilibrium fluctuations has recently been used to show that static critical exponents for lipid membranes are consistent with the 2D Ising universality class [3,6]. Here we exploit the ability to visualize the dynamics of these fluctuations to examine for the first time the dynamic critical phenomena in this system. We find that although the statics are 2D phenomena, the critical dynamics are modified by hydrodynamic coupling to the surrounding three-dimensional (3D) fluid.

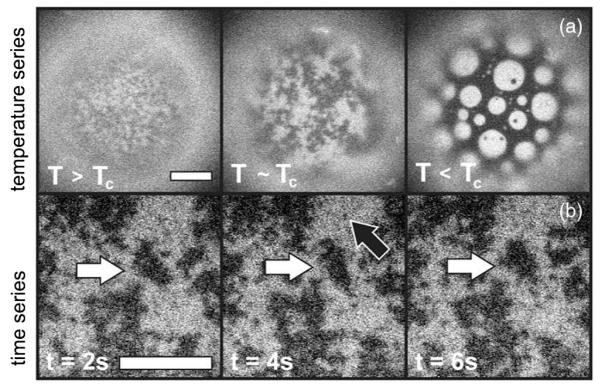
FIG. 1.

Fluorescence micrographs of vesicles of diameter 200 μm. (a) As temperature changes from T > T_c (T = 31.25 °C, T_c ≈ 30.9) to T ~ T_c (T = 31.0 °C), fluctuations in lipid composition grow. Below T_c, at T = 28 °C, domains appear. Scale bar = 10 μm. (b) A movie of composition fluctuations within a vesicle above T_c. Large fluctuations persist for seconds (white arrows), whereas small ones disappear by the next frame (black arrow). Scale bar = 20 μm.

Static critical exponents, which describe how observables such as correlation length vary as the critical point is approached, are identical for all systems in a given universality class, independent of their detailed microscopic physics [7,8]. For example, although membranes have a conserved order parameter and ferromagnets do not, membranes exhibit static exponents ν = 1.2 ± 0.2 and β = 0.124 ± 0.03, consistent with the expected 2D Ising values of ν = 1 and β = 1/8 [3]. Results in plasma membrane vesicles are also consistent with 2D Ising exponents ν = 1 and γ = 7/4 [6]. Systems that are in the same static universality class can fall into different dynamic universality subclasses determined by conservation laws constraining how fluctuations dissipate [9]. The critical exponent z for each dynamic subclass quantitatively describes the scaling of the dynamics. It relates how the correlation time τ_s diverges as temperature T approaches the critical temperature T_c, such that τ_s ∝ |(T − T_c)/T_c|−νz where ν is the static critical exponent. Experiments measure an effective exponent z_eff that approaches z as T → T_c and ξ → ∞. The dynamic subclasses relevant to 2D systems with conserved order parameter are notable equally for their wealth of theoretical predictions [9-11] and for the lack of experiments that systematically test those predictions.

Only a few previous measurements of dynamic critical exponents in 2D systems exist. Most experiments have been conducted on magnetic films. Using ferromagnetic films of ~ two monolayers, Dunlavy and Venus found νz = 2.09 ± 0.06, with ν = 1 [12]. Fewer experiments have been conducted on systems with conserved order parameter. Careful attempts to measure z were made in thin films of lutidine and water, but were unable to reach the 2D critical regime [13]. In plasma membrane vesicles from living rat basophil leukemia cells, fluctuation decay times were reported to be consistent with z ≈ 2 [6].

Here we obtain z_eff as T approaches T_c in a lipid membrane surrounded by water and compare to theory recently developed for an analogous system: a 2D critical binary fluid embedded in a noncritical bulk fluid [10,11].

This new theory incorporates three essential features of lipid bilayer dynamics: conserved order parameter, collective hydrodynamics, and hydrodynamic coupling between the bilayer and bulk [10,11]. Inclusion of only the first feature within an Ising model yields model B, in which composition fluctuations dissipate through the diffusion of microscopic constituents [9]. 2D model B predicts z = 4 – 2β = 3.75 [9], and numerical schemes give z = 3.80 and z = 3.95 [14,15]. Inclusion of the first two features, such that collective hydrodynamic motion replaces single particle diffusion as the dominant mechanism of order parameter relaxation, yields model H. 2D model H with coupling to only 2D momentum modes predicts z ≈ 2 [9]. The inclusion of all three features yields model HC, where HC denotes hydrodynamic coupling of the membrane to the bulk. This new version extends model H to account for the modes in both the 2D membrane and the 3D bulk fluid, with the result that z = 3 [10,11].

Intuition for the role of the coupling between the membrane and the bulk within model HC can be gleaned from an approximation for the 3D model H by Kawasaki [16]. The critical fluctuations are treated as spherical inclusions of diameter ξ that diffuse a distance ξ to equilibrate [9,16-18]. As such, the correlation time varies as τ ~ ξ²/D(ξ), where D(ξ) is the inclusion’s diffusion constant in a noncritical fluid. In three dimensions, D(r) ~ 1/r, where r is the inclusion’s radius. Using τ ∝ |(T − T_c)/T_c|^−νz ∝ ξ^z yields z ≈ 3. A more sophisticated theoretical treatment gives z = 3.065 [18]. Applying the same reasoning to 2D model H, in which the diffusion of inclusions has only a logarithmic dependence on r, yields z ≈ 2. Again, more sophisticated treatments produce similar values (see Ref. [5] for more detail). This argument can be extended to predict the value z should take in a 2D critical system embedded in a bulk fluid. Classic work by Saffman and Delbrück examined diffusion of an inclusion in a 2D liquid of viscosity η_2D immersed in a bulk fluid of 3D viscosity η3D, where hydrodynamic length L_h = η_2D/η3D is an important parameter [19,20]. When r ⪢ L_h, dissipation is primarily into the bulk and D(r) ∝ 1/r as in 3D model H. When r ⪡ L_h, dissipation is primarily into 2D hydrodynamic modes and D(r) ∝ ln(L_h/r), similar to 2D model H. Two groups have independently noted that when L_h is considered, z_eff for a 2D critical binary fluid embedded in bulk liquid crosses over from z_eff ≈ 2 when ξ ⪡ L_h to z_eff ≈ 3 when ξ ⪢ L_h [10,11].

The next four paragraphs demonstrate that the experimental results here are in excellent agreement with the recent predictions of model HC, namely that z_eff crosses over from ~2 to ~3 as T → T_c and ξ → ∞. Further experimental details follow the results.

A time series of the order parameter, $m(\overrightarrow{r},t)$, was extracted from videos of vesicles that were collected via fluorescence microscopy. For membranes, $m\left(\overrightarrow{r}\right)$ is the deviation from the average composition as reported by an image’s pixel gray scales. A time-correlation function $C(\overrightarrow{r},\tau )$, and its Fourier transform in space, the structure factor S(k, τ), were calculated for each wave number k.

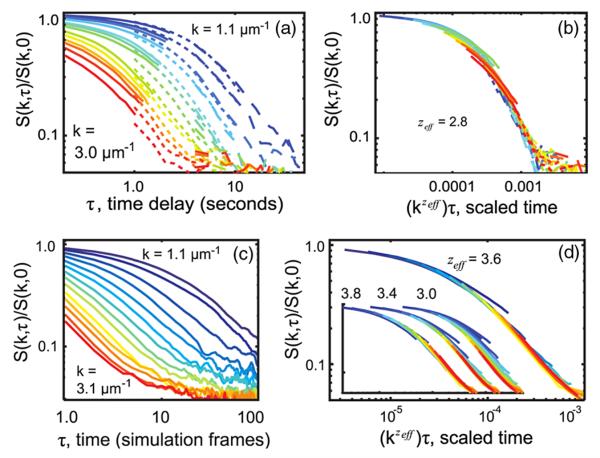
Curves of S(k, τ)/S(k, 0) vs k^z_effτ were plotted for a range of z_eff values. Figure 2(b) illustrates how the correct z_eff was identified: for a single value of z_eff, all experimentally measured curves at different k values [Fig. 2(a)] collapsed most fully onto a single curve, here at z_eff = 2.8 ± 0.2. Figure 3(a) shows z_eff values extracted in this manner from data over the entire measurable range of correlation lengths. In Fig. 3(a), z_eff rises from near 2 to near 3 as T → T_c, in accord with model HC [10,11].

FIG. 2.

(color online). (a) and (b) Rescaling experimental data closest to T_c by k^zτ collapses all curves to z_eff = 2.8, with consistent model HC. Normalized structure factors are shown for ξ = 13 ± 2.2 μm and three video rates: 10 frames per second (fps, solid lines), 2 fps (short dashed lines), and 0.5 fps (long dashed lines). Colors denote wave numbers k = 1.1 μm⁻¹ (top curve, blue) to 3.0 μm⁻¹ (bottom curve, red). (c) and (d) Simulations solely to verify technique. Structure factors of Kawasaki dynamics at T = T_c blurred in time to mimic experimental limitations collapse at z_eff = 3.6 ± 0.2, consistent with z = 3.75 for 2D model B. Colors range from k = 1.1 μm⁻¹ to 3.1 μm⁻¹. Insets show collapses used to determine bounds for z_eff and failure of collapse at z_eff = 3.

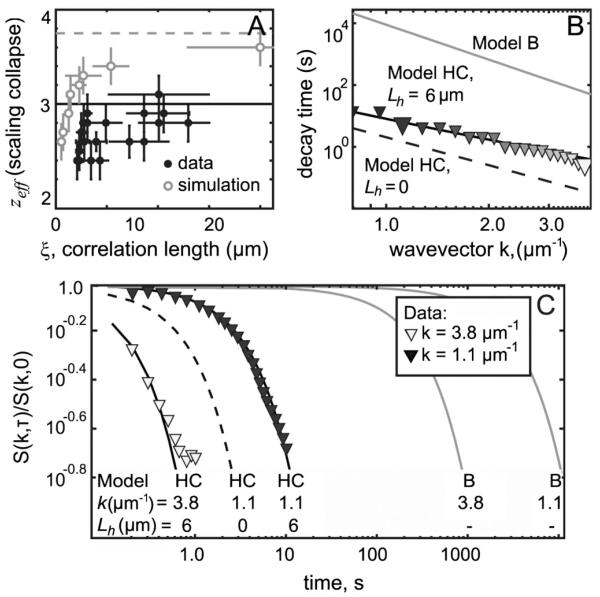
FIG. 3.

Data are in excellent agreement with model HC. (a) Filled symbols: dynamic exponent z_eff from scaling collapse of experimental data as in Figs. 2(a) and 2(b). Open symbols: model B simulation in which z_eff approaches 3.75. (b) Decay time, defined as when S(k, τ)/S(k, 0) = e⁻¹ Large symbols indicate wave numbers 1.1 and 3.3 μm⁻¹. (c) Normalized structure factors S(k, τ)/S(k, 0). In panels (b) and (c), experimental data denoted by symbols, 2D model B by gray lines, model HC (HC) with L_h = 6 μm by solid lines, and model HC with L_h = 0 by a dashed line.

Figures 2(c) and 2(d) validate this method by showing that standard simulations of model B Kawaski dynamics that are blurred to mimic experimental limitations and then analyzed in the same way as the experimental data give z = 3.6 ± 0.2 in agreement with the expected value of z = 3.75 (see Supplemental Material [5] for details). Simulations were run on a 400 × 400 biperiodic square lattice. The blur was achieved by averaging snapshots over 200 consecutive Monte Carlo sweeps, leaving a break of 800 sweeps without snapshots, and repeating the process, which reproduced the effects of a camera shutter opening for 100 ms of every 500 ms.

Excellent agreement between the predicted and measured structure factors provides even stronger evidence that model HC describes critical dynamics in membranes. Inaura and Fujitani give a prediction for the entire time-dependent structure factor S(k, τ) for model HC, taking as input η_2D, η_3D, and a mean-field approximation for the static structure factor, S(k, 0) [11]. The ratio S(k, τ)/S(k, 0) and its decay time will be compared between theory and experiment below. A feature of S(k, τ)/S(k, 0) is that it needs no correction due to the microscope’s point spread function. Ratios of S(k, τ)/S(k, 0) in the critical Ising model and in the mean-field approximation are similar, and do not depend strongly on the correlation length, as will be shown in a future manuscript.

The HC model with L_h = 6 μm fits the data over all experimentally accessible wave numbers. Figure 3(c) shows the ratio S(k, τ)/S(k, 0) at wave numbers 1.1 μm⁻¹ and 3.8 μm⁻¹. Figure 3(b) shows decay times, defined as when S(k, τ)/S(k, 0) = e⁻¹. All other models are excluded. Figure 3(a) rules out 2D model H because the measured z_eff rises close to 3, well above the predicted value of 2 for 2D model H. Figures 3(b) and 3(c) rule out 2D model B because the measured decay times are orders of magnitude shorter than the model predicts.

Developing model HC to completely describe membranes requires determining only membrane viscosity, η_2D, as an input since the viscosity of water, η_3D, is known. Figure 3(c) indicates that η_2D must be nonzero. In the small k limit, Inaura and Fujitani [11] predict a structure factor that depends only on η_3D. This parameter-free prediction, equivalent to taking η_2D = 0, underestimates time decays by a factor of 5–10 [dashed curve, Fig. 3(c)]. Setting the unknown, η_2D (or equivalently, L_h = η_2D/η_3D), as a single fit parameter within model HC over the entire measured range of k yields L_h = 6.0 ± 1.5 μm. This value is within the range found by tracking the diffusion of liquid domains across vesicle surfaces [21,22] and it is similar to values (2–4 μm) found by other methods, albeit for different lipid mixtures [23,24]. An essentially equivalent method of finding L_h is to calculate the model HC structure factor using the formalism of Hohenberg and Halperin [9], and to thereby extend model HC to incorporate Ising rather than mean-field statics. Within experimental uncertainty, this modest change has no effect (L_h = 5.5 ± 1.5 μm). This and other extensions of model HC, each leading to small corrections to the ratio S(k, τ)/S(k, 0), will appear in a future manuscript.

Using lipid bilayers to measure critical exponents introduces both complexities and advantages, which are outlined further in the Supplemental Material [5]. The first complexity is that the simplest bilayers that exhibit critical phenomena contain ternary lipid compositions. Strictly speaking, the ternary mixtures used here pass through isothermal critical mixing (plait) points rather than critical (col) points. A feature of 2D systems is that, unlike in 3D systems, no measurable change in critical exponents arises from the presence of a third component. Briefly, a small correction to scaling arises in systems that contain a third component at fixed composition rather than fixed chemical potential. Hence, T_c changes, and many effective critical exponents are renormalized by a factor of 1/(1 − α), as discovered by Widom [25] and generalized by Fisher [26]. For the 2D Ising case here, where α = 0, theory predicts only a logarithmic correction to singular behavior [25]. The second complexity is that when T is changed (as required in previous studies to find ν and β [3], but not required here), a bilayer with fixed composition does not necessarily follow a path with constant $\langle m\left(\overrightarrow{r}\right)\rangle$ [27]. However, since membrane phase diagrams are relatively symmetric over the range of temperatures probed, and since the measured values of ν and β were consistent with the 2D Ising model [3], deviations from a path of constant $\langle m\left(\overrightarrow{r}\right)\rangle$ are minor.

The first advantage of using lipid bilayers is that it avoids challenges of other systems. For example, lipid monolayers have confounding effects of dipole interactions, and the task of achieving simultaneous tunability and stability of surface pressure in a stationary monolayer is formidable. The second is that correlation lengths are large, partly because ξ₀ within the relation ξ = ξ₀|(T − T_c)/T_c|^−ν is on the order of the length of a lipid molecule rather than of an atom. Separately, there is an advantage in using 2D (or quasi-2D) experimental systems over 3D systems. The critical region is larger in 2D liquid-liquid critical systems than in analogous 3D ones, partially due to differences between critical exponents in 2D vs 3D Ising classes (ν = 1 and β = 1/8 in two dimensions vs ν ≈ 0.630 and β ≈ 0.325 in three dimensions [7]).

The methods used to produce the results in Fig. 3 follow. To optimize the movie quality, vesicles were spherical, free-floating, unilamellar, of radius >100 μm, and electroformed by the standard methods detailed in Ref. [3]. The vesicles were formed from mixtures along a line of plait points centered at 30% diphytanoylphosphatidylcholine (DiPhyPC, Avanti Polar Lipids, Alabaster, Alabama), 20% dipalmitoylphosphatidylcholine (DPPC), and 50% cholesterol (chol), with 0.5% fluorescent dye Texas red dipalmitoylphosphatidylethanolamine (TR-DPPE). Only vesicles near a plait point were analyzed, identified by micron-scale composition fluctuations visible over the largest observed range of temperatures (>1 °C) and by equal areas of coexisting liquid phases below T_c. Each vesicle analyzed fell on a slightly different plait point, so each had a slightly different T_c [28].

Images of membranes were captured via an epifluorescence microscope with a temperature-controlled stage and a mercury lamp source. Light exposure was minimized by employing a SmartShutter (Sutter Instrument, Novato, California) controlled through NIS-Elements (Nikon, Melville, New York), and by recording movies for at least two different frame rates at each temperature. Each frame was exposed 100–150 ms, with the shutter open 10 ms before and after exposures. The movies were collected from high to low temperature in steps of ~0.2 °C, equilibrated for at least two minutes. No consistent trend in intensity was observed throughout each movie, implying that the low light procedures used here eliminated significant photobleaching. To correct for lamp flickering, the mean brightness was subtracted from each frame. Spatial intensity gradients due to other vesicles outside the focal plane were removed by a long wavelength filter of 100 pixels.

The images were analyzed via custom matlab code (The Mathworks, Natick, Massachusetts). The vesicles were tracked and centered to remove drift (typically <25 μm/min). By eye, features exhibit no net translation, which implies no significant vesicle rolling. No difference in mean intensity or noise between pixels at edges vs centers of cropped images was observed, implying that the vesicles are so large that the membrane curvature over the images can be neglected [3]. Curvature corrections in smaller vesicles were minor [6].

The structure factor S(k, τ), the Fourier transform in space of the time-dependent correlation function, was found as previously described [3,29]. Briefly, a discrete transform was performed for each movie image, with a buffer of zero values to correct for image nonperiodicity. The transformed images were divided by the microscope’s finite point spread function to yield $m(\overrightarrow{k},t)$. The dynamic structure factor was generated at each τ by $S(\overrightarrow{k},\tau )=1∕2\langle m(\overrightarrow{k},t)\overline{m(\overrightarrow{k},t\pm \tau )}\rangle$, where $\overline{m(\overrightarrow{k},t)}$ is the complex conjugate of $m(\overrightarrow{k},t)$ [30]. $S(\overrightarrow{k},t)$ was then radially averaged to yield S(k, τ).

The structure factors were employed in two ways. First, the correlation lengths, ξ, were found by analyzing the structure factors at τ = 0. Specifically, a one-parameter fit for ξ was made until all data for k^(7/4)S(k) vs kξ collapsed onto the single curve for the exact numerical solution of the 2D Ising model [3,31]. Second, the effective dynamic scaling exponents, z_eff, were found by collapsing curves of S(k, τ) (see results above and the Supplemental Material [5] for details). Collapse works because, according to the dynamic scaling hypothesis, structure factors within the scaling regime can be written in the form, $S(k,\tau ,\xi )=k^{-2+\eta }\Omega ({\left(k\xi \right)}^{-1},k^z\tau )$, where Ω is a universal function (kξ)−1 and k^zτ [9]. Near T_c, where (kξ)−1 is near 0, the curves of S(k, τ)/S(k, 0) vs k^zτ collected over many wave numbers k should collapse via a one-parameter fit to produce the correct value of z. Here, Ω can also depend on kL_h, so that $S(k,\tau ,\xi )=k^{-2+\eta }\Omega ({\left(k\xi \right)}^{-1},k^z\tau ,k{L}_h)$. For the collapses in Figs. 2(a) and 2(b), z_eff refers to an effective z value that varies as ξ/L_h is changed. In Figs. 3(b) and 3(c), comparing the entire form of the structure factor to theoretical predictions directly verifies the value of z, as well as the dependence of the universal function on kL_h and k^zτ.

Conclusion

Directly imaging composition fluctuations enables measurement of effective dynamic critical exponents of a lipid membrane embedded in bulk water. The experimental structure factors are in excellent agreement with an emerging theoretical prediction in which 3D hydrodynamics affects critical slowing down in a 2D membrane. The theory invokes hydrodynamic coupling between the membrane and bulk fluid such that Ising degrees of freedom are coupled to momentum modes [10,11]. As predicted, a shift in z_eff from ~2 to ~3 as T → T_c and ξ → ∞ is observed.