Abstract
Critical events that occur rarely in biological processes are of great importance, but are challenging to study using Monte Carlo simulation. By introducing biases to reaction selection and reaction rates, weighted stochastic simulation algorithms based on importance sampling allow rare events to be sampled more effectively. However, existing methods do not address the important issue of barrier crossing, which often arises from multistable networks and systems with complex probability landscape. In addition, the proliferation of parameters and the associated computing cost pose significant problems. Here we introduce a general theoretical framework for obtaining optimized biases in sampling individual reactions for estimating probabilities of rare events. We further describe a practical algorithm called adaptively biased sequential importance sampling (ABSIS) method for efficient probability estimation. By adopting a look-ahead strategy and by enumerating short paths from the current state, we estimate the reaction-specific and state-specific forward and backward moving probabilities of the system, which are then used to bias reaction selections. The ABSIS algorithm can automatically detect barrier-crossing regions, and can adjust bias adaptively at different steps of the sampling process, with bias determined by the outcome of exhaustively generated short paths. In addition, there are only two bias parameters to be determined, regardless of the number of the reactions and the complexity of the network. We have applied the ABSIS method to four biochemical networks: the birth-death process, the reversible isomerization, the bistable Schlögl model, and the enzymatic futile cycle model. For comparison, we have also applied the finite buffer discrete chemical master equation (dCME) method recently developed to obtain exact numerical solutions of the underlying discrete chemical master equations of these problems. This allows us to assess sampling results objectively by comparing simulation results with true answers. Overall, ABSIS can accurately and efficiently estimate rare event probabilities for all examples, often with smaller variance than other importance sampling algorithms. The ABSIS method is general and can be applied to study rare events of other stochastic networks with complex probability landscape.
INTRODUCTION
Many critical events in biological processes occur rarely within the relevant physical time scale. Bacteriophage λ in E. coli1, 2, 3 can maintain a stable dormant lysogenic lifestyle when integrated into the E. coli genome, but can spontaneously transit to the lytic lifestyle of phage outburst2, 4, 5, 6, 7, 8 with a small probability (∼4 × 10−7 per cell cycle9). Crossing barrier in the free energy landscape in some slow-folding protein may be rare, but critical.10 In tumorigenesis, cells experiencing normal growth rarely transit spontaneously to uncontrolled tumor growth.11, 12 However, environmental changes, e.g., those resulting in the accumulation of DNA hypermethylation in promoter CpG islands,13, 14 can accelerate such transitions. Multi-stable cellular states of endogenous molecular-cellular networks and rare stochastic transitions between them may offer a general framework to study human diseases.15, 16 Accurate assessment of rare event probabilities is, therefore, important for understanding the machineries behind many critical biological processes.
It is challenging to study rare events from the viewpoint of mechanistic theory.17, 18 Here we study networks of biochemical reactions. In principle, the transition probability rates between two states can be calculated exactly, if the state space of biochemical reaction networks are completely accounted for, e.g., when the underlying discrete chemical master equation can be solved exactly.8, 19 However, when the state spaces and the transition matrices are too large to be efficiently computed, a widely used approach to study stochastic behavior of biochemical reactions is that of Monte Carlo sampling, first formulated as the stochastic simulation algorithm (SSA).21 However, the original SSA21 is ineffective for studying rare events, as most computing time is spent on following high-probability paths.22, 23
The techniques of importance sampling and reweighting can improve sampling efficiency significantly. They have been widely used in equilibrium sampling where the condition of detailed balance holds.24, 25 However, stochastic processes in reaction networks are generally not time reversible and the condition of detailed balance is not valid. Kuwahara and Mura developed the weighted SSA (wSSA) algorithm by applying the importance sampling technique to study stochastic reaction networks, in which each reaction rate is biased by a pre-determined constant, with the overall summation of reaction rates unchanged.22 As the probability for reaction selection can be biased such that rare events are sampled more frequently while the time scale of the underlying reactions is maintained, significantly improved sampling efficiency for rare events was reported.22, 23, 26 However, the choice of bias constants strongly affects the effectiveness of wSSA. When there are many reactions and the network is complex, the heuristic approach of determining bias constants by examining the reactions does not work.22 As there is no general guidance in how bias constants should be chosen, poor choices may lead to estimations that are less accurate than the original SSA.23
Daigle et al. developed the doubly-weighted SSA (dwSSA) algorithm, in which a multilevel cross-entropy (CE) method is used iteratively to provide estimates of bias constants.23 This is achieved by running long trial simulations until a fraction of the sampled trajectories reaches the target states.23 With this automated estimation, both reaction selection and the underlying time scale of reactions can be biased.23
A drawback of methods using constant biases such as wSSA and dwSSA is that the bias coefficients are global and state-independent, and are not influenced by the concentrations of molecules, which evolve with time. As the apparent rate of a reaction can vary dramatically depending on the copy number of molecules, the degree of bias for a reaction therefore needs to be adjusted according to the available copy numbers of reactants. With globally fixed bias constants, a network with reactions of a wide range of rates will have over- and under-biased reactions, depending on the states of the system. As a result, estimated properties of a network will have large variance, making these methods unsuitable for complex networks.27
Roh et al. developed a state-dependent biasing wSSA method (swSSA).27 By empirically classifying reactions into groups of favored, disfavored, and neutral reactions, biases in selection probability for reactions in the first two groups are calculated in a state-dependent fashion. The swSSA method can have better estimation accuracy and efficiency than the wSSA method,27 at the expense of about twice as many biasing parameters as that of the wSSA.27 Roh et al. further developed the state-dependent doubly weighted SSA method (sdwSSA), where reactions are further grouped into bins according to their selection probabilities, and are assigned different bias constants, which are automatically estimated using the cross-entropy method.26 However, the number of parameters to be estimated using sdwSSA is much larger than that of wSSA, dwSSA, and swSSA. For example, about 20 bias constants need to be estimated for a simple reversible isomerization system with only two reactions.26 Estimating a large number of bias constants needed for complex networks becomes difficult.
In this study, we describe an algorithm named adaptively biased sequential importance sampling (ABSIS) for efficient sampling of rare events. Based on the principle of sequential importance sampling, our approach adopts the look-ahead strategy, a technique well-established in polymer and protein studies,28, 29, 30, 31 to gather future information for design of bias parameters to enable effective barrier crossings.28, 29, 30, 31, 32, 33 By enumerating short paths from the current state, bias coefficients are generated based on analysis of these short paths. Unlike the dwSSA and sdwSSA methods, in which biases are fixed constants after parameter estimation, the biases in ABSIS for each reaction is dynamically determined based on exact calculation of the total probability of short κ-step forward- and backward-moving reaction paths, without the need of binning reaction rates. Reactions with higher probability of forward-moving are then encouraged, and reactions with higher probability of backward-moving are discouraged. Regardless of the number of reactions in the networks, we only need to assign two bias parameters for the whole network: the degree to encourage forward-moving reactions and the degree to discourage backward-moving reactions, which both can be estimated through an efficient parameter estimation algorithm.
We also take advantage of the recent development of a method that directly solves the discrete chemical master equation.8, 19 With a finite buffer, the rare event probability of a stochastic network of modest size can be computed exactly using this method, allowing us to have a gold standard to objectively assess the accuracy of estimated rare event probabilities through sampling. With errors computed based on exact numerical solutions, we show with four biological examples that the ABSIS method have improved or comparable accuracies compared to other methods (the dwSSA method, and the swSSA and sdwSSA methods when data available), at overall significantly reduced computational cost and much higher success rate.
This article is organized as follows: We briefly discuss the theoretical framework of reaction networks, the principle of sequential importance sampling, and details of the ABSIS method. We then apply our method to study four biological problems, namely, the birth-death process, the reversible isomerization model, the bistable Schlögl model, and the enzymatic futile cycle, and compare the accuracies of estimations and the success rates in generating reaction paths reaching the target states with the SSA and dwSSA methods. We conclude with remarks and discussions.
MODEL FRAMEWORK
Reaction networks
We assume a well-mixed biochemical system with constant volume and temperature. There are n different molecular species: . We use xi(t) to denote the copy number of molecular species Xi at time t. There are m possible different reactions in the system: . Each reaction Rk has an intrinsic reaction rate constant rk. The microstate of the system at time t is represented by a non-negative integer column vector: , where T denotes the transpose. An arbitrary reaction Rk (k = 1, 2, ⋯, m) with intrinsic rate rk takes the general form:
which brings the system from a microstate to . The difference between and is the stoichiometry vector of the reaction Rk: The stoichiometry matrix S for the reaction network is defined as: where each column represents a single reaction. The rate of reaction Rk that transforms microstate from to is determined by the intrinsic rate constant rk and the combination number of relevant reactants in the current microstate : assuming the convention .
State space and probability landscape
The state space S of a reaction network is defined as the set of all possible microstates that the system can visit from a given initial condition: . We denote the probability of each microstate at time t as , and the probability distribution at t over the whole state space as is also called the probability landscape of the network.8 It can be visualized as a time-evolving scalar surface over the state space, with the value at each state x taken to be . The volume integral under the surface at any arbitrary time t is always 1:
In general, there is no assumption of detailed balance. For a reaction network with arbitrary stoichiometries and a specific initial state , its probability landscape is governed by the discrete chemical master equation (dCME)
| (1) |
from which the time-evolving probability landscape and its steady state can be directly obtained.8, 19 Here A is the transition rate matrix .
Transition paths and transition probabilities
A transition path π(S, T) consists of a sequence of states: , starting from and ending at , along with a sequence of time points T = (t0, ⋅⋅⋅, tN) when each of these states are visited. Here N is the length of the transition path. When the beginning state and the ending state , as well as the sequence of states S and time points T are unambiguous from the context, we use π(0, N) to denote the transition path π(S, T) for convenience. This transition path is understood to move from state to state through a total of N steps following the specific sequence of states S and sequence of time points T. The sequence of time points can be alternatively specified by the corresponding sequence of time intervals: {τ0, τ1, ⋯, τN − 1} = {t1 − t0, t2 − t1, ⋯, tN − tN − 1}. In implementation, these time intervals are not predefined but are small random values generated by sampling Poisson processes, whose rates are governed by the underlying chemical reaction rates (see below). We assume that there is a unique reaction connecting each neighboring pair of microstates and along the reaction path. The probability p(π(S, T)) of a given transition path π(S, T) can be calculated as the product of the probability of the initial state , and the probabilities of all subsequent transitions between neighboring states ,
| (2) |
Assuming a Poisson process, the probability of each transition occurring during an infinitesimally small dτi − 1 after τi − 1 can be calculated as22, 34
| (3) |
where is the sum of rates of all reactions that could happen at the state , and is the probability that there is exactly one reaction occurring in next time interval τi − 1.35 The subscript k denotes the reaction Rk that connects state to state . The fraction is the probability that the kth reaction Rk occurs during τi − 1.22, 34 Taking together, the overall probability of the transition path π is
| (4) |
Macrostates and probability of rare transitions between macrostates
We define a macrostate B as a set of microstates: Here we are interested in biologically motivated macrostates. For example, in a bistable genetic switch system, most microstates belong to either the “on/off” or the “off/on” metastable states, each of which can be regarded as a macrostate. The probability of a macrostate B can be written as:
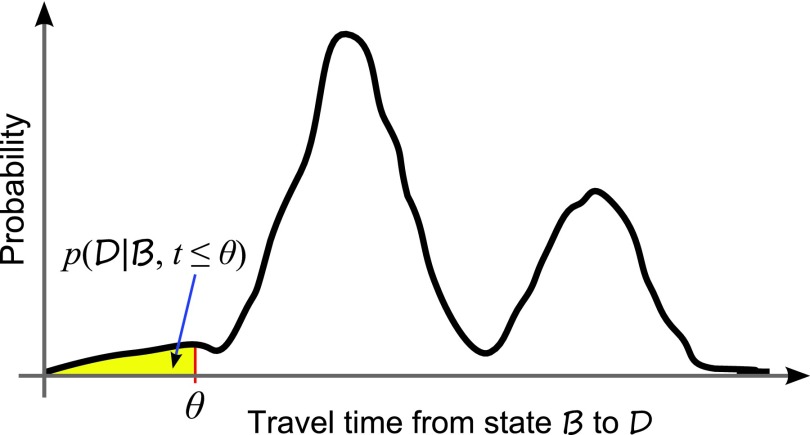
For a stochastic network, if a destination macrostate D can be reached from a beginning macrostate B, the probability of the system transiting from B to D is 1 if given infinite amount of time. However, we are interested in the probability of transition from B to D within a finite period of time θ. That is, we wish to estimate , which may be small (Fig. 1),
Figure 1.
Distribution of rare event transition paths. Rare event transition paths traveling from state B to D within time θ are of interest.
Calculating exact transition probability
The finite buffer dCME method can be used to enumerate the state space S of stochastic networks of modest size, and is optimal both in time complexity and in space requirement.8, 19 For these networks, we can directly solve the dCME. The transition probabilities of specific paths connecting two macroscopic states can therefore be calculated exactly. In this study, the probabilities of rare events in all examples are computed both by the finite buffer dCME method and by sampling methods. The results of the former are regarded as exact solutions, against which results from sampling methods are compared.
Weighted SSA and doubly-weighted SSA
There are potentially an enormous number of transition paths connecting two macrostates. In general, if enumeration is infeasible, exact calculation of the transition probabilities is not possible. One can estimate the probabilities through Monte Carlo sampling.
A number of sampling methods for rare events have been developed based on the principle of importance sampling. Kuwahara and Mura developed the wSSA algorithm,22 in which the rate of each reaction is biased by a pre-selected predilection constant αk, which will increase or decrease the rate of a specific reaction. This may affect the fraction of sampled paths reaching the target states. These paths are generated from the biased reaction rate . The biased probability of the reaction in the time step starting at state is calculated as
| (5) |
where reaction Rk leads to , and . A weight for correcting the bias is also kept for this reaction:
| (6) |
The true probability is then recovered as The biased probability p′(π(0, N)) for the full path is:
with the weight:
The true probability of the path is then: p(π(0, N)) = w(π(0, N)) · p′(π(0, N)).
In wSSA, bias is introduced through the second factor in Eq. 5, which represents the biased probability in selecting the next reaction in the wSSA scheme. The time scale of the Poisson process underlying the reaction, namely, the first factor in Eq. 5, remains unchanged.
In the doubly-weighted SSA method (dwSSA),23 both the selection probability and the Poisson time scale are biased, and the biased probability for each step in a dwSSA sampling path is:
| (7) |
where is the biased reaction rate. The weight for the kth reaction occurring at step i − 1 is obtained from dividing Eq. 3 by Eq. 7:
The biased probability for a full dwSSA path π(0, N) is:
and its weight is:
The true probability of the path p(π(0, N)) can be recovered as: p(π(0, N)) = w(π(0, N)) · p′(π(0, N)).
A key component of the dwSSA method is an automatic method to estimate the bias constant γk for each reaction Rk. A large number (typically 105) of full-length trial simulations are run, with some of them reaching the target macrostate. The number of each reaction that occurred in those simulations that reached the macrostate are counted and compared to the expected number of occurrence if one were to follow a Poisson process in the same given time under the same initial condition. Those reactions occur more frequently than expected are biased towards. Reactions that occur less frequently than expected are biased against. This procedure is repeated with the biases updated iteratively, until a predefined fraction (e.g., 2%) of full-length trial paths reaches the target macrostate. In the further developed swSSA and sdwSSA methods, the bias coefficient is not a constant, but depends on the copy numbers of molecules of the current state.26, 27 In order to assign more effective bias coefficients, a refined scheme of bias assignment is used in sdwSSA, in which each reaction is divided into multiple bins according to its probability to be chosen, with each bin assigned its own bias coefficient.26
There are a number of issues with these methods. First, estimation of the bias parameters relies on counting the number of occurrence of a reaction, which may not be possible or the estimate may not be reliable if reactions happens rarely. For example, gene binding and unbinding reactions in a toggle switch system bring the system from one metastable state to another. But this happens only once or twice during an extended time. It is challenging to sample these binding/unbinding reactions adequately using trial simulations, where limited runs are carried out. Second, as the estimated bias parameters are either constant or based on current state, no considerations for possible future barriers in the probability landscape is incorporated. This becomes problematic for complex systems, for example, those with multistabilities, where steep barriers need to be crossed. In these systems, the desirable bias may be quite different depending on the neighborhood where the system is currently located in the landscape. Third, there is a proliferation of adjustable bias parameters, for example, on the order of O(βm) for the sdwSSA method, with the number of bins β = 5–20 for each of the m reactions, making the assignment of bias coefficients a challenging task.26 As a result, often the overall amount of computation involved is substantial, the variance of samples generated is high, and the accuracy is still unsatisfactory.
Adaptively biased sequential importance sampling
Here we describe a new method called ABSIS for estimating rare transition probability between macrostates. Our approach is based on the look-ahead strategy and the principle of sequential importance sampling,31 which have found wide applications in studies of polymers and protein biophysics,29, 30 where challenging problems such as RNA loop entropy calculation, generation of protein folding transition state ensemble, and protein packing have been investigated.30, 33, 36 In ABSIS, bias for each reaction is calculated based on present and future information, and is adaptively adjusted automatically, resulting in more efficient sampling of rare events. It can be applied to stochastic networks with complex probability landscapes.
Perfect path sampling
Assume we wish to reach the macrostate D from the microstate . We can classify paths π(0, N) starting at and ending at into two sets and : those that reach the macrostate D before time θ form the set of paths , and those that do not form another set of paths .
Our goal is to assess the transition probability from the microstate to the macrostate D. It can be calculated as
where is an indicator function such that if , and 0 otherwise. Namely, it is 1 if a path π(0, N) starting from state reaches the macrostate D in time, and 0 otherwise. Perfect path samples for calculating then can be drawn as
In general, if our goal is to estimate certain property of the reaction paths, which is expressed as a scalar function of the microstate x, perfect sampling of the reaction paths for this estimation problem is then:
where , and forms the path π(0, N).
Optimal bias strategy and future-perfect adaptive weighting
Similarly, the probability that future paths after a reaction connecting the microstate to will reach the destination macrostate D in time is:
To estimate the transition probability , the next state can be sampled future-perfectly if we draw as
If our goal is to estimate the property f(·) of the reaction path that reaches the macrostate D, can be sampled optimally as
where .
κ-Step look-ahead bias strategy and adaptive weighting
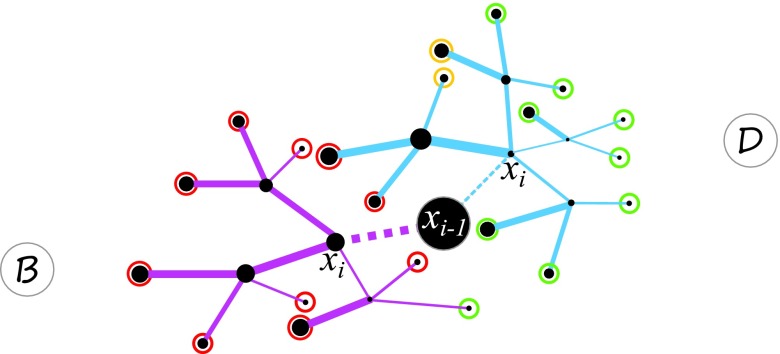
As it is usually impossible to enumerate and examine all paths up to time θ to calculate exactly, we approximate it by adopting a κ-step look-ahead strategy. Briefly, we analyze statistics of exhaustively generated short paths, and design biases based on estimations made on these short paths. We first classify κ-step paths π(i, i + κ), which all have the first step following a specific reaction connecting to , into three types: forward-moving paths , backward-moving paths , and non-moving paths (Fig. 2):
| (8) |
Here and are the distances between the states , and the target macrostate D, respectively. We define the distance For convenience, we use 1-norm distance. The forward-moving, backward-moving, and non-moving probabilities after κ-steps, given that the first reaction connects state and , can be calculated as
and
We can then have the approximations and which will be used to construct the bias functions for accelerating/decelerating the reaction rate and for selecting reaction. We can now have the approximation:
Figure 2.
Look-ahead strategy. Two reactions leading current state to next state are shown in dashed lines (blue and pink). All possible look-ahead paths of length κ = 2 for both reactions from two different next states are illustrated in solid blue and pink lines. State B is the initial state, and D is the target state. The thickness of lines indicates reaction rates. The color of circles at the end state of each path indicates moving forward (green, ), backward (red, ), and non-moving (yellow, ).
Bias function with κ-step look-ahead
Recall that the probability of a path p(π(i, N)) is computed as
To design bias functions that are fast to compute, we consider only the overall probability pr(π(i, N)) of reaction choices accumulated along the path, and ignore the rates of reactions for now:
We have
| (9) |
and
| (10) |
We can then design a bias function for selecting reaction k, and set as the biased reaction rate. The general biased probability for each step in the ABSIS sampling path is then:
| (11) |
Note that calculating the probability and is equivalent to follow a κ-step Markov process , where the probability transition matrix is:
in which A is the transition rate matrix of dCME in Eq. 1, , I is the identity matrix, and form the state space S for this κ-step Markov process starting from . The initial probability distribution for this Markov process is such that the probability for the current state is 1 and 0 for all other states.
Biasing strategy.
The bias in selecting reaction k that brings state to is based on the forward-moving and backward-moving probabilities. We first have
| (12) |
where , i′ is any reachable state from . Here λ1 ⩾ 0 and λ2 ⩾ 0 are the parameters for biasing towards forward-moving and against backward-moving reactions, respectively. Overall, there are only these two bias parameters, regardless which reaction k is considered. The surface maps of bias function with λ1 = λ2 = 0.5 for encouraging and discouraging reaction k at different values of , , and are shown in Figs. 3a, 3b.
Figure 3.
Surface map of bias function in Eq. 12 with λ1 = λ2 = 0.5. Bias strengths for encouraging reaction k at different values of forward-moving probability and are shown in (a). Bias strengths for discouraging reaction k at different values of backward-moving probability and are shown in (b).
The construction of is based on the following consideration. The rate ratio , which is the original probability of choosing the reaction k that reaches , is now modified by the forward probability at , obtained by looking κ-steps ahead. The term therefore represents the probability of selecting reaction k and moving forward. To encourage forward-moving reactions with lower reaction rates, we use the term instead. This is then further modified by so that reactions with higher forward-moving probability is favored proportionally (Fig. 3a). The bias coefficient λ1 is used to adjust the bias strength for forward-moving reactions. Larger λ1 gives stronger encouragement. As falls in the interval [0, +∞), we add the constant 1 so the function is now in the interval [1, +∞) when reaction k should be encouraged. Setting bias according to will increase the probability for a forward moving reaction to be selected. Overall, if a larger λ1 value is chosen, a slower reaction with higher probability of moving forward will be encouraged more (Fig. 3a).
Similarly, backward reactions are biased against, with stronger discouragement when using a larger λ2 value. The discouragement is also stronger for reactions with larger backward probability and larger rate ratio (Fig. 3b). To ensure fall within the interval (0, 1], a “min ” function is used here to add an upper bound for the bias. If neither advances nor backtracks the system, no bias is introduced.
Corrections of biases and biased reaction rates.
In principle, both reaction selection probability and the Poisson time scale can be biased. In this study, we focus on effects of directly biasing reaction selection probability alone. The effects of directly biasing specific reaction rates are the subject for future studies. Specifically, we now insist that the overall reaction rate of the system is unchanged, namely,
| (13) |
As and we use a normalizing constant α:
and the biased reaction rate is tentatively set to:
| (14) |
This ensures Eq. 13 holds.
As there are occasions where the bias changes direction after normalization, namely, from <1.0 to >1.0, or vice versa, we further insist that:
| (15) |
To satisfy this requirement, we partition all reactions into two disjoint sets based on whether their corresponding satisfy the above inequalities:
| (16) |
Inequalities in Eq. 15 are maintained by simply assigning no bias for all reactions in , and redistribute their surpluses and deficits evenly to all reactions in . As a result, the total reaction rate is unchanged. We have the final biased reaction rates:
| (17) |
where is given by Eq. 14. The final biased probability for each step in an ABSIS sampling path is then calculated as
| (18) |
Weights of ABSIS path
The weight for correcting the bias for taking the kth reaction at step i − 1 is obtained by dividing Eq. 3 by Eq. 18:
| (19) |
For the special case when the overall reaction rate is unchanged, namely, when , we have . The weight for a full ABSIS path is then:
| (20) |
The biased probability for a full ABSIS path π(0, N) is
The true probability of the path π(0, N) can be recovered as
The ABSIS algorithm
We summarize the ABSIS method in Algorithm 1.
In order to improve computing efficiency, we enumerate the κ-step look-ahead paths for each microstate when encountered. As implementation and data structure greatly affect computing speed, , , , , and are all calculated only once when the microstate is first visited, with their values stored in hash tables using the microstate as the key. All subsequent visits to the microstate need only to retrieve relevant values stored in the hash tables. This leads to dramatically improved time efficiency.
Determining look-ahead step κ and bias parameter λ1 and λ2
In ABSIS, we only have one look-ahead steps parameter κ, and two bias parameters λ1 and λ2 to be determined, regardless of the number of reactions and the overall network complexity.
The ABSIS
| // Input (X, R, , D, θ, κ, M, λ1, λ2) |
| Define network |
| Initialize hash table |
| j ← 0, total weight wM ← 0, weight square vM ← 0, |
| Number of successful paths Ns ← 0 |
| whilej < Mdo |
| Path length i ← 1 |
| Initialize path with the initial state |
| Time on current path t ← 0, weight of current path w ← 1 |
| whilet < θ and do |
| ifthen |
| Calculate reaction rates of state for all reactions |
| Enumerate all possible κ step paths π(i − 1, i + κ) starting from state using Algorithm of Ref 19. |
| Calculate and for each Rk using Eq. 9, 10 |
| Calculate bias strength for each Rk according to Eq. 12 |
| Calculate tentative reaction rate for all Rk according to Eq. 14 |
| Calculate final biased reaction rate for all Rk according to Eq. 17 |
| Calculate |
| end if |
| Retrieve , , , and from H using key |
| Generate two uniform random numbers and |
| t ← t + τi − 1, |
| i ← i + 1 |
| end while |
| ift < θ and thenwM ← wM + w, vM ← vM + w2, Ns ← Ns + 1 |
| end if |
| end while |
| return |
| return |
| return |
| return Success Rate: s = Ns/M |
Estimation of look-ahead steps κ and parameter search space l for ABSIS
| 1: // Input (X, R, , D, θ) |
| 2: Look-ahead step: κ ← 2 |
| 3: Maximum range of parameter search space for determining λ1 and λ2: l ← 1.0 |
| 4: Sample size: M ← 1000 |
| 5: Success rate: s ← 0 |
| 6: while 1 do ▷ Determine the optimal κ |
| 7: s ← s + success rate of ABSIS(X, R, , D, θ, κ, M, λ1 = 0.0, λ2 = 1.0) |
| 8: s ← s + success rate of ABSIS(X, R, , D, θ, κ, M, λ1 = 1.0, λ2 = 0.0) |
| 9: s ← s + success rate of ABSIS(X, R, , D, θ, κ, M, λ1 = 1.0, λ2 = 1.0) |
| 10: s ← s/3 |
| 11: ifs > 0.5 then |
| 12: break |
| 13: end if |
| 14: κ ← κ + 1 |
| 15: end while |
| 16: s ← success rate of ABSIS(X, R, , D, θ, κ, M, λ1 = 0.5, λ2 = 0.5) |
| 17: ifs > 0.8 then ▷ Determine the maximum range for parameter search: l |
| 18: l ← 0.5 |
| 19: end if |
| 20: return κ |
| 21: returnl |
To determine κ, we make the reasonable assumption that longer look-ahead paths lead to better bias parameters. Starting from κ = 2, we test different κ values with an increment of 1 using 103 ABSIS paths. We take the first value of κ that gives an average success rate s of >0.50 at three different parameters locations of (λ1, λ2) = (0.0, 1.0), (1.0, 0.0), and (1.0, 1.0). This is very efficient as it typically only takes 3 × 103 ABSIS paths to evaluate one κ. This is summarized in Algorithm 2.
To determine the optimal biasing parameters (λ1, λ2) ∈ [0.0, 1.0] × [0.0, 1.0], we use a grid search, where 103 paths are generated at each grid point. The sample variance, success rate, total path weight and total weight square are stored at each grid point. We assume that the success rate s of ABSIS increases monotonically with parameters λ1 and λ2, at the cost of reduced diversity among sampled paths. We first evaluate s at (λ1, λ2) = (0.5, 0.5) using 103 ABSIS paths. If s > 0.8, we focus on exploring more diverse paths and restrict our search space to (λ1, λ2) ∈ [0.0, 0.5] × [0.0, 0.5]. Otherwise, the search space remains as [0.0, 1.0] × [0.0, 1.0].
We start at (λ1, λ2) = (0.0, 0.0), and move first along the direction of λ2, and then continue at an increased λ1 value, all with an interval of Δ = 0.1. We stop our search along the λ2 direction if s > 0.8. If s at a specific point of (λ1, λ2) is 0.5 better than its visited neighbors in either the λ1 or the λ2 directions, we retrospectively increase the number of grid points in that direction with a finer interval of Δ′ = 0.02, and carry out searches on these grid points. After the search concludes, grid points with the smallest variance and s ∈ [0.1, 0.8] are taken as candidates.
We repeat this search process starting at (0.5, 0.5) again. The first candidate grid point that is again identified from a second independent search is taken as our final choice. When no candidate grid points are found in two independent searches, we repeat the overall search process, and update the stored sampling variances and success rates with results from new samples, until an optimal parameter pair is found. To further reduce computing costs, we skip grid points with previous s outside the range of [0.1, 0.8] when updating variance and success rates. The procedure for parameter estimation is summarized in Algorithm 3.
BIOLOGICAL EXAMPLES
Below we describe examples of applying ABSIS to four biochemical reaction networks. We show that ABSIS can provide accurate estimation of transition probabilities with efficient computation. Results are then compared with the true answer obtained from the finite buffer dCME method, and those obtained using other methods (the dwSSA,23 as well as the swSSA method27 and sdwSSA26 method when possible), with differences discussed.
Birth-death process
The birth-death process is a simple chemical reaction system that involves one molecular species and two reactions. Synthesis and degradation are the only reactions, and there is only one molecular species. The network and parameters are specified as follows:
| (21) |
We study the problem of estimating the rare event probability, p(x(t) = 80|x(0) = 40, t ⩽ θ), that the system transits from the initial state x(0) = 40 to the target state x(t) = 80 within the time threshold θ = 100. This same problem was studied in Daigle et al.23 and Roh et al.27
Estimation of Bias Parameters λ1, λ2 for ABSIS.
| 1: // Input (X, R, , D, θ, κ, l) |
| 2: Sample size: M ← 1000 |
| 3: Bias parameters: λ1 ← 0, λ2 ← 0 |
| 4: Grid size: Δ = 0.1 and refined grid size: Δ′ = 0.02 |
| 5: Initialize hash tables |
| 6: Initialize hash tables |
| 7: Total sample size for parameter estimation: Mtot ← 0 |
| 8: while 1 do |
| 9: while λ1 ⩽ ldo |
| 10: while λ2 ⩽ ldo |
| 11: fori = 1 → 2 do |
| 12: if (λ1, λ2) AND then |
| 13: λ2 ← λ2 + Δ |
| 14: i ← i + 1, and go to next iteration. |
| 15: end if |
| 16: [, ] = ABSIS(X, R, , D, θ, κ, M, λ1, λ2) |
| 17: Mtot ← Mtot + M |
| 18: ifthen |
| 19: |
| 20: else |
| 21: Update using samples |
| 22: end if |
| 23: ifthen |
| 24: Repeat line 16–22 for refined grids in [λ2 − Δ, λ2] with interval Δ′ |
| 25: end if |
| 26: ifthen |
| 27: Repeat line 16–22 for refined grids in [λ1 − Δ, λ1] with interval Δ′ |
| 28: end if |
| 29: end for |
| 30: λ2 ← λ2 + Δ |
| 31: end while |
| 32: λ1 ← λ1 + Δ |
| 33: end while |
| 34: ifthen Exit |
| 35: end if |
| 36: end while |
| 37: return λ1 and λ2 |
| 38: return total sample size: Mtot. |
Exact probability landscape and transition probability
We first enumerate the full state space S of the birth-death model of Eq. 21, starting from the initial state of x(0) = 40 using the finite state buffer dCME method with a buffer size of 200.8, 19 There are a total of 241 microstates. To calculate the exact rare event transition probability of p(80|40, t ⩽ θ), the 241 × 241 transition rate matrix A is modified by making the target states x = 80 as an absorbing state, following the approach of Ref. 20. The exact transition probability p(80|40, t ⩽ θ) can then be computed from the modified :
where the initial state probability landscape has and 0 for all other 240 states. p(80|40, t ⩽ θ) is obtained from . We use the matrix exponential software EXPOKIT37 to calculate p(80|40, t ⩽ θ) for θ = 100 numerically. The exact transition probability is found to be 2.986 × 10−7. This indicates that there would be only about 3 successful transition paths observed in 10 million sampled paths if the unmodified original SSA were used.
The calculated exact time-evolving probability landscape of the system is plotted in Fig. 4a. The blue and black curves show the landscapes at time t = 100 and at the steady state, respectively. There is one high probability region centered at x = 40 in both landscapes (green dots in Fig. 4a). The target state x = 80 (red dots in Fig. 4a) is located at a region with very low probability. Transitions from x = 40 to x = 80 is therefore of very low probability, as crossing a large barrier between these two states is necessary.
Figure 4.
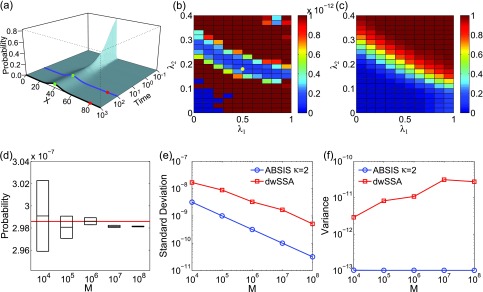
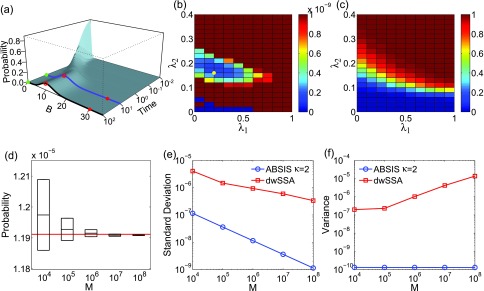
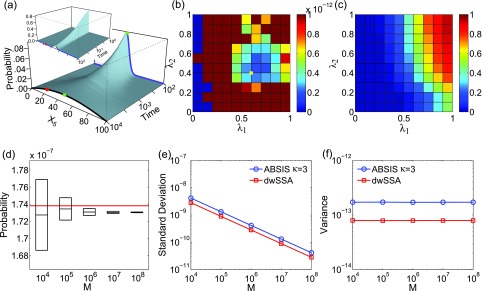
The birth-death model of Eq. 21. (a) Its time-evolving probability landscape. The blue and black curves highlight the landscape at t = 100 and at the steady state, respectively. There is one high probability region located at x = 40 in both landscapes (green dots), which is also the initial state. The target state (red dots) is outside the high probability region. (b) and (c) The variance (b) and success rate (c) of pilot ABSIS sampling during parameter search using a total sampling size of M = 9.2 × 104 and look-ahead path length of κ = 2. The yellow dot in (b) shows the location of the optimal parameters. (d) The estimated transition probability and sample convergence using ABSIS. The solid red line indicates the exact probability calculated from dCME. Black bars and heights of the box-plots are the mean and its standard deviations of estimated transition probability calculated from 4 independent ABSIS simulations, each for a different sample size of M = 104, 105, 106, 107, and 108, respectively. (e) Standard deviations of ABSIS (blue line) and dwSSA (red line) at different sample sizes. (f) Sample variances of the ABSIS (blue line) and the dwSSA (red line) method at different sample sizes.
Determination of look-ahead steps and bias parameters
The look-ahead steps for ABSIS is determined to be κ = 2, and the parameter search space is determined to be 0.5 by running Algorithm 2. The Algorithm 3 is then used to determine λ1 and λ2 from the search space [0, 0.5] × [0, 0.5]. The optimal parameters are determined to be λ1 = 0.50 and λ2 = 0.18, which have a success rate of 0.63. Figures 4b, 4c show the variances of sampling weights and success rates of reaching the target state at different values of λ1 and λ2. The optimal parameters λ1 = 0.50 and λ2 = 0.18 are located in the lowest variance region of the parameter space (yellow dot in Fig. 4b). The total sample size for parameter search is 9.5 × 104, which is much smaller than the reported sample size of 7 × 105 in dwSSA.23
Estimated transition probability
The estimated transition probability and variance from four independent simulations are plotted in Fig. 4d for sample size M of 104, 105, 106, 107, and 108 used for each simulation. The estimated rare transition probability with M = 107 is:
which is very close to the exact value of 2.986 × 10−7 (red line in Fig. 4d). In addition, ABSIS converge rapidly as the sample size increases.
We compare our results with those from the dwSSA method, which was implemented following Ref. 23. We use the exact bias constants of γ1 = 1.454 and γ2 = 0.686 as in Daigle et al.23 The probability estimated from dwSSA is 2.937 × 10−7 ± 0.017 × 10−7 using a sample size of M = 107, which is accurate but less so than that of ABSIS. Additionally, the ABSIS method has a higher success rate (0.63) than the dwSSA method (0.59). The comparisons of mean standard deviations between ABSIS and dwSSA calculated from four independent simulations using different sample size are plotted in Fig. 4e. ABSIS has a standard deviation about one order of magnitude smaller than dwSSA. In addition, ABSIS requires much less samples to achieve the same accuracy of dwSSA. For example, 104 samples of ABSIS has a smaller standard deviation than 106 samples of dwSSA. We also compare ABSIS estimation with the results from swSSA as reported in Roh et al.27 The estimation of 95% confidence interval from 105 samples of ABSIS is 2.986 × 10−7 ± 0.020 × 10−7, which is comparable to the estimation of swSSA 2.986 × 10−7 ± 0.019 × 10−7 using the same sample size.27
The sample variances of the ABSIS method when using different sample sizes are shown in Fig. 4f (blue line), along with variances using dwSSA sampling (red line, Fig. 4f). Overall, ABSIS gives consistently small variance. At M = 107, the variance (1.0 × 10−13) is two orders of magnitude smaller than the variance of 3.1 × 10−11 when using the dwSSA method. We further note that the variance of estimated transition probabilities using dwSSA seems to increase with the sample size.
Overall, our results show that the ABSIS method converges rapidly to the true transition probability when sample size is increased, whereas the dwSSA method converges less rapidly and has larger variance.
Bias mechanism of ABSIS
Examining the forward-moving probability (Figs. 5a, 5b, green lines) and the backward-moving probability (red lines) of both reactions R1 and R2 at different states helps to gain insight into how ABSIS works. The synthesis reaction R1 has a much higher forward-moving than backward-moving probability in majority of the states, and the degradation reaction R2 has a much higher backward-moving probability in majority of the states. These observations suggest that in most cases, one should bias to encourage reaction R1 and to discourage reaction R2.
Figure 5.
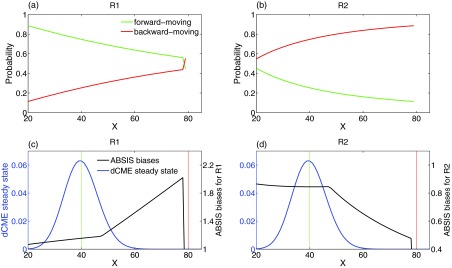
Forward and backward moving probabilities. (a) and (b) Probability of moving-forward and moving-backward for two reactions R1 and R2 in birth-death model. The x-axis is the system state, i.e., the copy number of molecular species X, and y-axis is the forward-moving (green lines) and backward-moving (red lines) probabilities of reaction R1 and R2 in each state. (c) and (d) The final ABSIS bias strengths for both reactions in birth-death model. Blue lines show the steady state probability landscape of birth-death model. The black lines in (c) and (d) show the curves of bias strengths for reactions R1 and R2, respectively. Green and red vertical lines indicate the start and end state.
As the system approaches the target state, the forward-moving probability of R1 (green line in Fig. 5a) decreases dramatically, while the backward-moving probability of R2 (red line in Fig. 5b) increases. This is due to the fact that the propensity for backward-moving becomes stronger as the rate of the degradation reaction R2 increases monotonically with the copy number of X, while the rate of the synthesis reaction R1 remains constant.
It is clear that constant biases will not work well for this problem, as the rare event transition requires overcoming the steep probability barrier between the two states of x = 40 and x = 80 (Fig. 5c, blue line). The optimal bias strengths will need to depend on the current propensity of forward moving, and should be adaptive.
For this problem, the ABSIS strategy of designing biases based on estimations from look-ahead paths works well. The bias strengths generated by the ABSIS algorithm for both reactions R1 and R2 are plotted in Figs. 5c, 5d (black lines), along with the steady state probability landscape (blue lines) as reference. In general, the biases for R1 are all favorable (Fig. 5c), and the biases for R2 are all unfavorable (Fig. 5d). However, the strength of the bias is adaptively adjusted following changes in the reaction propensity, as well as the need for overcoming the probability barriers. When approaching the target state, bias is set such that R1 is much more strongly encouraged to produce more X, whereas R2 is severely repressed to reduce the degradation of X.
Overall, by utilizing future information from κ = 2 look-ahead paths, ABSIS can identify automatically the reaction to encourage, as well as the reaction to discourage at any given state. The forward and backward-moving probabilities estimated from look-ahead paths can aid in crossing the probability barrier of rare event transitions. By adaptively changing biases according to changes in reaction propensity and future information about the probability barrier, the ABSIS method can provide estimates for the birth-death model with much smaller sampling variance compared to methods using constant biases such as the dwSSA method.23
Reversible isomerization
We also apply the ABSIS method to the reversible isomerization network taken from the Ref. 26, where the sdwSSA method was applied.26 The reversible isomerization network involves two molecular species and two reactions:
| (22) |
Our goal is to estimate the rare event probability that the system transitions from an initial state to any state with 30 copies of B within the time interval of t ⩽ 10.
Exact probability landscape and transition probability
We first enumerate the full state space S of the reversible isomerization model in Eq. 22, starting from the initial state using the dCME method. This reversible isomerization model is a closed system, therefore no buffer is needed. There are a total of 101 microstates in the state space S. The exact transition probability of the rare event is calculated by solving the matrix exponential problem using the EXPOKIT software,37 where is the modified transition rate matrix by making the target states absorbing states, following the approach of Ref. 20. The exact transition probability is found to be 1.1911 × 10−5.
The time-evolving probability landscape of the system is calculated, and its projection to B is plotted in Fig. 6a. The blue and black curves show the landscape at t = 10, and at the steady state, respectively. There is one high probability region centered at xB = 10 (red circles in Fig. 6a). The target state xB = 30 (red solid dots in Fig. 6a) is located in a region with very low probability. Transitions from xB = 0 (green dots in Fig. 6a) to xB = 30 therefore has very low probability, as a large barrier between these two states need to be crossed.
Figure 6.
Rare event estimation of the reversible isomerization network model. (a) Its time-evolving probability landscape projected to B. The blue and black curves show the landscape at t = 10, and at the steady state, respectively. There is only one high probability region in both landscapes, which is located at xB = 10 (red circles). The probability landscape at time t = 10 (blue curve) largely overlaps with that of the steady state (black curve). The initial state xB = 0 (green dots) is on the tail of the left-side of the probability peak, and the target state xB = 30 (red dots) is on the far right-side of the low probability region. (b) and (c) The variances (b) and success rates (c) of pilot ABSIS sampling during parameter search using a total sample size of M = 8.8 × 104 and look-ahead steps κ = 2. The yellow dot in (b) shows the location of the optimal parameters. (d) The estimated rare event probability and sampling convergence using ABSIS. The solid red line represents the exact probability calculated from directly solving dCME. The black bars and the box heights are the means and standard deviations calculated from 4 independent ABSIS simulations, for different sample sizes of M104, 105, 106, 107, and 108. (e) Standard deviations of ABSIS (blue line) and dwSSA (red line) at different sample sizes. (f) Sampling variances of ABSIS (blue line) and dwSSA (red line) for different sample sizes.
Determination of look-ahead steps and bias parameters
The look-ahead steps for ABSIS is determined to be κ = 2 and parameter search space to be l = 0.5 after running Algorithm 2. Algorithm 3 is used to determine λ1 and λ2 from the search space [0, 0.5] × [0, 0.5]. The optimal parameters are found to be λ1 = 0.20 and λ2 = 0.16, which have a success rate of 0.76. Figures 6b, 6c show the variances of sampling weights and success rates of reaching the target state at different values of λ1 and λ2. The optimal parameter pair λ1 = 0.20 and λ2 = 0.16 are located in the lowest variance region of the parameter space (yellow dot in Fig. 6b). The total sample size for parameter search is 9.1 × 104, which is much smaller than the reported 7 × 105 samples for parameter estimations for dwSSA and sdwSSA in Ref. 26.
Estimated transition probability
The estimated transition probability and standard deviation by averaging four independent simulations using different sample size of M = 104, 105, 106, 107, and 108 are plotted in Fig. 6d. ABSIS simulation provides accurate estimate of 1.1909 × 10−5 ± 0.0004 × 10−5 using the sample size of M = 107. In addition, ABSIS converges rapidly to the exact rare event probability computed from the dCME method (red line in Fig. 6d) as the sample size increases. When the same sample size M = 106 as that of Roh et al.26 is used, the ABSIS method gives the estimation of 1.192 × 10−5 ± 0.001 × 10−5, with its standard deviation about only one half of the estimation 1.193 × 10−5 ± 0.002 × 10−5 from the sdwSSA method.26 When using the same sample size M = 105 as in Roh et al.,27 the ABSIS method gives the 95% confidence interval estimation as 1.191 × 10−5 ± 0.007 × 10−5, which has a much smaller 95% confidence interval than the estimation of swSSA 1.190 × 10−5 ± 0.011 × 10−5 with the same sample size.27
We also compare our results with those from the dwSSA method. For dwSSA sampling, we use bias constants (γ1 = 1.301, γ2 = 0.719) for the two reactions in the network as reported in Roh et al.26 The rare event probability estimated from dwSSA using the sample size of M = 107 is 1.278 × 10−5 ± 0.060 × 10−5, and the success rate is only 0.07. The comparisons of mean standard deviations between ABSIS and dwSSA calculated from four independent simulations using different sample size are plotted in Fig. 6e. ABSIS results show 1–2 orders of magnitude smaller standard deviation (Fig. 6e) than dwSSA in estimating the rare event probability. In addition, ABSIS requires much less samples to achieve the same accuracy of dwSSA. In this example, 104 samples of ABSIS has a much smaller standard deviation than dwSSA with 108 samples.
The ABSIS method gives more accurate estimations than dwSSA (1.191 × 10−5 vs 1.278 × 10−5 at M = 107, 1.192 × 10−5 vs 1.201 × 10−5 at M = 106, and 1.191 × 10−5 vs 1.075 × 10−5 at M = 105 compared to the exact value of 1.191 × 10−5), and has higher success rate (0.76) compared to the dwSSA method (0.07). The ABSIS method also gives estimations with much smaller standard deviations than swSSA (at M = 105, where data are reported in Ref. 27) and sdwSSA (at M = 106, where data are reported in Ref. 26). In addition, it gives consistently smaller sample variances (1.3 × 10−10 at M = 107), which is four orders of magnitude smaller than the variance 4.2 × 10−6 obtained when using the dwSSA method. The sample variance of ABSIS using different sample size is shown in log-scale in Fig. 6f (blue line), along with variances using dwSSA sampling (red line, Fig. 6f).
Bistable Schlögl model
Schlögl model is a one-dimensional bistable system first proposed in Ref. 38, and extensively studied subsequently.39, 40, 41 It is an auto-catalytic network consisting of one molecular species (X) whose concentration can change through four reactions:38, 39
| (23) |
where A and B are species with constant concentrations (set to a = 1 and b = 2, respectively). Values of reaction rate constants k1, k2, k3, and k4 are taken from Vellela and Qian.39 The volume of the system is fixed as V = 25. Following Vellela and Qian,39 the reaction rates are calculated using formulas , , A3(x) = bk3V, and A4(x) = k4x, respectively. Our task is to estimate the probability p(92|0, t ⩽ θ) that the Schlögl system transitions from an initial state x = 0 to the target state x = 92 within a given time threshold of θ = 2.
Exact probability landscape and transition probability
We first enumerate the full state space S of the Schlögl model of Eq. 23, starting from the initial state of x = 0 using the dCME method with a buffer size of 1,000. There are 1,001 microstates in the state space S. The exact transition probability of the rare event p(92|0, t ⩽ 2) is calculated by solving the matrix exponential problem using the EXPOKIT software,37 where is the modified transition rate matrix by making the target states x = 92 an absorbing state, following the practice of Ref. 20. The calculated exact transition probability is 5.419 × 10−5. That is, if 105 paths are sampled using the original SSA method, there will only be about 5 successful transition paths.
The calculated exact time-evolving probability landscape of the system is plotted in Fig. 7a. The blue and black curves show the landscape at time t = 2 and at the steady state, respectively (Fig. 7a). There are two high probability regions centered at x = 4 (red circle on black curve) and x = 92 (red solid dot on black curve), respectively, on the steady state probability landscape (black curve). They are separated by a low probability barrier. The probability landscape at time t = 2 (blue curve) shows a much sharper peak centered at x = 3 (red circle on blue curve). It is clear that transition paths from x = 0 to x = 92 within t = 2 have a steep barrier to cross.
Figure 7.
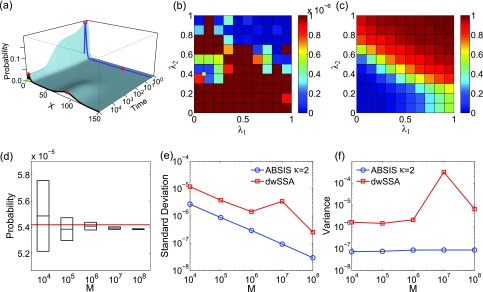
The Schlögl model. (a) Its time-evolving probability landscape. The blue and black curves show the landscape at t = 2 and at the steady state, respectively. There are two high probability regions at steady state (black curve) located at x = 4 (red circle on black curve) and x = 92 (red dot on black curve), respectively. The initial state x = 0 (green dot) is near the first peak, and the target state (red dot) is at the center of the second peak. (b) and (c) Variance and success rate of pilot ABSIS sampling during parameter search using a total sampling size of M = 3.28 × 105 and look-ahead steps κ = 2. The yellow dot in (b) shows the location of the optimal parameters. (d) The estimated transition probability and convergence behavior using ABSIS. The solid red line indicates the exact probability calculated from dCME. The black bars and the heights of boxes in the box-plots are the average means and standard deviations calculated from 4 independent ABSIS simulations, for a different sample size of M = 104, 105, 106, 107 and 108. (e) Standard deviations of ABSIS (blue line) and dwSSA (red line) at different sample sizes. (f) Sampling variances of ABSIS (blue line) and dwSSA (red line) for different sample sizes.
Determination of look-ahead steps and bias parameters
The look-ahead steps for ABSIS in Schlögl model is determined to be κ = 2, and the parameter search space is determined to be 0.5 after running Algorithm 2. Algorithm 3 is then used to determine λ1 and λ2 from the search space [0, 0.5] × [0, 0.5]. The optimal parameters are found to be λ1 = 0.10 and λ2 = 0.40, which have a success rate of 0.15. Figures 7b, 7c show the variances of sampling weights and success rates of reaching the target state at different values of λ1 and λ2. The optimal parameter pair λ1 = 0.10 and λ2 = 0.40 is located in the lowest variance region of the parameter space (yellow dot in Fig. 7b). The total sample size for parameter search is 3.28 × 105, which is much smaller than the typical sample size of 7 × 105 reported in dwSSA.23
Estimated transition probability
The estimated transition probability and variance by averaging four independent simulations using different sample size of M = 104, 105, 106, 107, and 108 are plotted in Fig. 7d. With the sample size M of 107, ABSIS simulation provides an accurate estimate of pABSIS(92|0, t ⩽ 2) = 5.394 × 10−5 ± 0.009 × 10−5, which is very close to the exact value of 5.419 × 10−5. In addition, ABSIS converges rapidly (Fig. 7e) as the sample size increases.
We also compare our results with those obtained using the dwSSA method. For dwSSA sampling, we followed the original authors' recommendation of choosing parameters such that the minimum fraction ρ of trajectories reaching the target states is 0.02.23 This gives the bias constants of γ1 = 1.115, γ2 = 0.967, γ3 = 1.171, and γ4 = 0.872 for reaction 1–4 in the network, respectively. The rare event probability estimated from dwSSA is 5.976 × 10−5 ± 0.342 × 10−5 using a sample size M = 107, which is less accurate than that of ABSIS (5.394 × 10−5 ± 0.009 × 10−5 vs. the exact value of 5.419 × 10−5). It also has a lower success rate of 0.02 compared to ABSIS (0.15). The comparisons of mean standard deviations between ABSIS and dwSSA calculated from four independent simulations using different sample sizes are plotted in Fig. 7e. ABSIS results show about one order of magnitude smaller standard deviation (Fig. 7e) than dwSSA. In terms of computing efficiency, ABSIS sampling is able to achieve better accuracy than dwSSA with 1/10 of samples.
The sample variance of ABSIS using different sample size is shown in Fig. 7f (blue line), along with variances using dwSSA sampling (red line). Overall, ABSIS sampling gives consistently small sample variances (8.712 × 10−8 at M = 107), which is roughly four orders of magnitude smaller than the variance 3.233 × 10−4 when using the dwSSA method.
Bias Mechanism of ABSIS
By examining the forward-moving probability (green lines in Figs. 8a, 8b, 8c, 8d) and the backward-moving probability (red lines) of all four reactions at different states, we found that the synthesis reactions R1 and R3 have much higher forward-moving than backward-moving probability in majority of the states, and the degradation reactions R2 and R4 have much higher backward-moving probability in majority of the states. These observations suggest that reactions R1 and R3 should be encouraged and reactions R2 and R4 should be discouraged.
Figure 8.
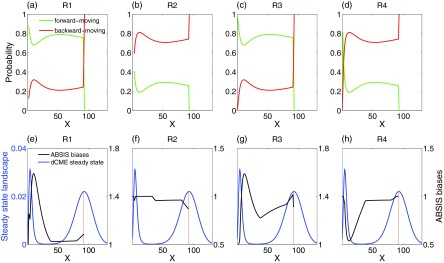
Forward and backward-moving probabilities and ABSIS biases for each reactions. (a)–(d) Probability of moving-forward and moving-backward for four reactions in Schlögl model. The x-axis is the system state, i.e., the copy number of molecular species X, and y-axis is the forward-moving (green lines) and backward-moving (red lines) probabilities of reaction R1–R4 in each state. (e)–(h) The final ABSIS bias strengths for reactions in Schlögl model. Blue lines show the steady state probability landscape of birth-death model. The black lines show the curves of bias strengths for four reactions, respectively.
Obviously, constant biases will not work well for this problem because of the steep barrier crossing region between the initial and the target state (blue curve in Fig. 8e). The optimal bias strengths should be adaptive and should be determined by the complex probability landscape of the system.
For the Schlögl model, the ABSIS strategy works well. The bias strengths calculated by the ABSIS algorithm for all four reactions are plotted in Figs. 8e, 8f, 8g, 8h (black curves), along with the steady state probability landscape as a reference (blue curves). The biases for R1 and R3 are all favorable (Figs. 8e, 8g), and the biases for R2 and R4 are all unfavorable (Figs. 5f, 5h). Interestingly, the strongest biased region of R1, R3, and R4 overlapped with the steepest barrier crossing region in the landscape (Figs. 8e, 8g, 8h), which shows that ABSIS can capture the urgent need for overcoming the probability barriers at the time. The insignificant bias of R2 is due to its smaller reaction rates, although it has a similar backward-moving probability as R4 (Fig. 8e).
Estimating rare event probability for Schlögl model is a difficult task for methods with constant biases, as reported in Ref. 34. However, by utilizing future information from 3-step look-ahead paths, ABSIS successfully estimated the probability of rare event transition in the bistable Schlögl model with accuracy and small sampling variance, and compares favorably to the constant biased dwSSA method.23
Enzymatic futile cycle
Enzymatic futile cycle is a ubiquitous network motif consisting of six different molecular species and six reactions. Samoilov et al. studied this network in detail.42 The molecular species, reactions, and corresponding reaction rate constants of the enzymatic futile cycle system are as follows:
| (24) |
Estimating rare event probability of the enzymatic futile cycle system has been the subject of recent studies using the wSSA method22 and the dwSSA method.23 Here the goal is to estimate the probability that the system starts from the initial state to any other states with exactly 25 copies of X5 within the time-threshold of θ = 100. The same task was also studied in Daigle et al. using dwSSA.23
Exact probability landscape and transition probability
We first enumerate the full state space S of the futile cycle model of Eq. 24, starting from the initial state using the dCME method. As the futile cycle model is a closed system, no buffer is needed for the dCME method. There are a total of 400 microstates in the state space S. The exact transition probability of the rare event p(x5 = 25|(1, 50, 0, 1, 50, 0), t < 100) is calculated by solving the matrix exponential problem using the EXPOKIT software,37 where is the modified transition rate matrix by making the target states absorbing states. The exact transition probability is calculated to be 1.738 × 10−7. That is, if we use the original SSA method, there will be only about 2 successful transition paths sampled in 10 million different sampled trajectories.
The time-evolving probability landscape of the system is calculated, and its projection to X5 is plotted in Fig. 9a. The inset figure in Fig. 9a shows the time-evolving landscape from time t = 1 to t = 100, and the main figure shows the time frame from t = 100 to t = 104. The blue and black curves show the landscape at t = 100, and at steady state, respectively. There is only one high probability region in the projected steady state probability landscape (black curve), which is centered at x5 = 50 (green dots). The probability landscape at time θ = 100 (blue curve) shows a much sharper peak centered at the same location x5 = 50. It is clear that transition paths from x5 = 50 to x5 = 25 within t ⩽ 100 have a steep barrier to cross, although there is no such barrier if sampling time is not restricted.
Figure 9.
The enzymatic futile cycle model. (a) Its time-evolving probability landscape projected to X5. The inset figure shows the time-evolving landscape from time t = 1 to t = 100, and the main figure shows the time frame from t = 100 to t = 104. The blue curves show the landscape at t = 100, and the black curve shows the landscape at steady state. There is only one high probability region, which is located at x5 = 50 (green dots). The probability landscape at time t = 100 (blue curve) shows a much sharper peak also centered at x5 = 50. The initial state with x5 = 50 (green dots) is at the height of the probability peak, and the target state at x5 = 25 (red dots) is in the low probability region to the left of the peak. (b) and (c) shows the variance (b) and success rate (c) of pilot ABSIS sampling during parameter search using a total sampling size of M = 2.11 × 105 and look-ahead steps of κ = 3. The yellow dot in (b) shows the location of the optimal parameters. (d) The estimated transition probability and convergence behavior using ABSIS. The solid red line represents the exact probability calculated from dCME. The black bars and the box-plots are the means and standard deviations calculated from 4 independent ABSIS simulations using a sample size of M of 104, 105, 106, 107, and 108. (e) Standard deviations of ABSIS (blue line) and dwSSA (red line) at different sample sizes. (f) Sample variances of ABSIS (blue line) and dwSSA (red line) at different sample sizes.
Determination of look-ahead steps and bias parameters
The look-ahead steps for ABSIS in the futile cycle model is determined to be κ = 3, and the parameter search space is determined to be l = 1.0 after running Algorithm 2. Algorithm 3 is then used to determine λ1 and λ2 from the search space [0, 1.0] × [0, 1.0]. The optimal parameters are determined to be λ1 = 0.60 and λ2 = 0.40, which have a success rate of 0.41. Figures 9b, 9c show the variances of sampling weights and success rates of reaching the target state at different values of λ1 and λ2. The optimal parameter pair λ1 = 0.60 and λ2 = 0.40 is located in the lowest variance region of the parameter space (yellow dot in Fig. 9b). The total sample size for parameter search is 2.11 × 105, which is much smaller than the reported sample size of 7 × 105 using dwSSA.23
Estimated transition probability
The estimated transition probability and standard deviation by averaging four independent simulations using different sample size of M = 104, 105, 106, 107, and 108 are plotted in Fig. 9d. ABSIS simulation provides an accurate estimate of 1.730 × 10−7 ± 0.001 × 10−7 with sample size M = 107, which is very close to the exact value of 1.738 × 10−7. The success rate is 0.41. In addition, ABSIS converges rapidly to the exact rare event probability (red line in Fig. 9d) as the sample size increases.
We also compared our results with those obtained using the dwSSA method. For dwSSA sampling, we use bias constants (γ1 = 1.000, γ2 = 1.003, γ3 = 0.320, γ4 = 1.003, γ5 = 0.993, and γ6 = 3.008) taken from Daigle et al.23 for the six reactions in the network. The rare event probability estimated from dwSSA is 1.741 × 10−7 ± 0.001 × 10−7 using a sample size M = 107, which is slightly better than the estimate from ABSIS, with a higher success rate of 0.67. The comparisons of mean standard deviations between ABSIS and dwSSA calculated from four independent simulations using different sample size are plotted in Fig. 9e. ABSIS results show about 1.5 times larger standard deviations (Fig. 9e) than dwSSA in estimating the rare event probability in futile cycle model. In terms of computing efficiency, ABSIS sampling needs about 1.5 times more samples to achieve the same accuracy as dwSSA with.
The sample variance of ABSIS using different sample size are shown in Fig. 9f (blue line), along with variances using dwSSA sampling (red line, Fig. 9f). ABSIS sampling gives consistently small sample variances (1.708 × 10−13 at M = 107), although it is about twice as large as the variance of 7.901 × 10−14 when using the dwSSA method. It has also a lower success rate of 0.41.
Bias mechanism of ABSIS
The enzymatic futile cycle network has different characteristics from the other networks studied here. This network includes two enzymes, and each has its active and inactive forms, which amount to a total of four enzyme molecular species, namely the first enzyme X1 and its inactive form X3, the second enzyme X4 and its inactive form X6. However, as each enzyme has only one copy in the system (X1 + X3 = 1, and X4 + X6 = 1), the occurrence of reactions is highly restricted by the availability of the enzymes. To study the biasing mechanism of the reactions, we project the forward-moving probability and the backward-moving probability of each reaction to the space of species X5 and fixed combinations of X1 and X4 (Figs. 10a, 10b, 10c, 10d, 10e, 10f for forward-moving probabilities and Figs. 10g, 10h, 10i, 10j, 10k, 10l for backward-moving probabilities). We found that the surfaces of forward and backward-moving probabilities are rather rugged. The forward and backward-moving probabilities for the same reaction can be very different for microstates with only one copy difference in X1 or X4. For example, the of R1 at X1 = 1, X4 = 0 (red histograms in Fig. 10a) is close to 1, but with only one copy difference in X4, the of R1 at X1 = 1, X4 = 1 is very close 0 (yellow histograms in Fig. 10a). This ruggedness is due to the fact that neighboring microstates have different available enzymes, therefore very different reactions occur according to Eq. 24. In fact, no microstates can have all six reactions occurring simultaneously. The ruggedness of the surfaces of forward and backward-moving probabilities requires biases with large fluctuations (as shown in Figs. 11c, 11f). Our bias scheme seems to offer no improvement for reducing sampling variance compared to dwSSA.
Figure 10.
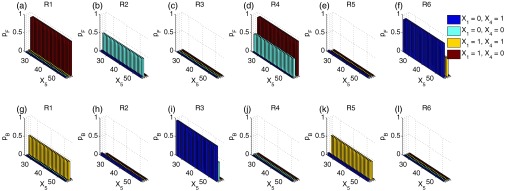
ABSIS forward and backward-moving probabilities for each reactions in the enzymatic futile cycle model. (a)–(f) Projected forward-moving probabilities of all six reactions on the space of X5 and four different combinations of X1 and X4 shown in different colors. (g)–(l) Projected backward-moving probabilities of all six reactions on the same space of X5 and four different combinations of X1 and X4.
Figure 11.

ABSIS biases for each reaction in futile cycle model. (a)–(f) The final ABSIS bias strengths for each reaction in enzymatic futile cycle model.
Although reactions R1, R2, R4, and R6 have overall larger forward-moving probabilities (Fig. 10) and should be encouraged, and reactions R3 and R5 have overall larger backward-moving probabilities and should be discouraged, the ABSIS biases for reactions R1, R2, R4, and R5 are all very close to 1, and only reactions R3 and R6 are significantly biased (Fig. 11), as they have the slowest rates among all six reactions and thus biased. Biases for R3 are clustered into two nearly flat biases with different mean 0.3364 and 0.4651, respectively (Fig. 11c). There are also two different nearly flat biases for R6 around the mean 2.6330 and 3.5129, respectively (Fig. 11f). In general, the current bias scheme used in ABSIS for the futile cycle network are not very different from the bias constants of dwSSA used in Daigle et al.23
Overall the ABSIS method is comparable to the dwSSA method for studying the futile cycle network. It can provide accurate estimates of the rare event probability. The sampling variance is constantly small at around 1.7 × 10−13, regardless of sample sizes. ABSIS also correctly identifies reactions that need to be encouraged and to be discouraged, although the sampling variance of ABSIS is about twice as large as that of dwSSA due to the ruggedness of the surfaces of forward and backward-moving probabilities.
DISCUSSIONS AND CONCLUSIONS
Sampling rare events is an important task for studying key events important for biological processes. In this work, we described a general theoretical framework for obtaining optimized bias in sampling individual reactions to estimate probabilities of rare events. We further developed a practical algorithm named ABSIS for efficient estimation of probabilities of rare events. By adopting a look-ahead strategy and by examining κ-step look-ahead paths following each reaction from the current microstate, we can estimate the reaction-specific and state-dependent forward-moving and backward-moving probabilities of the system. These probabilities are then used to adaptively adjust biases towards selecting each reaction. Overall, ABSIS is well suited for studying rare events in networks with complex probability landscape and steep probability barrier.
Our method addresses a major challenge in estimating rare event probability in biological networks, namely, the need to cross barriers on the probability landscape. As reactions in a network proceeds, the local neighborhood of the probability landscape changes, and different biases are often necessary for barrier-crossing. Unlike previous importance sampling methods such as sdwSSA26 and swSSA,27 in which biases are only based on reaction rates in the current state with no consideration of future information, the ABSIS method can detect barrier-crossing region in the probability landscape by incorporating future information. The bias introduced by the ABSIS method not only depends on the current state, but also depends on the need to cross the probability barrier, which is detected by the κ-step look-ahead strategy. The calculation of κ-step forward-moving and backward-moving probabilities is equivalent to solving a small local version of a chemical master equation of κ-steps.19
Our method also addresses the issue of proliferation of parameters and associated computational costs. Regardless of the number of reactions in the system and the complexity of the network, bias strengths for all reactions in ABSIS are adjusted using only two general parameters: λ1 for promoting forward-moving reactions, and λ2 for repressing backward-moving reactions. The biasing scheme is designed such that forward-moving reactions with lower reaction rates are encouraged, and backward-moving reactions with higher reaction rates are repressed. As κ is small, bias strengths can be determined without lengthy simulations.
We have applied the ABSIS method to four biological networks: the birth-death process, the reversible isomerization, the bistable Schlögl model, and the enzymatic futile cycle model. ABSIS can accurately and efficiently estimate rare event probabilities for all examples. For the birth-death process and Schlögl model, the rare event probabilities can be estimated by ABSIS with a variance of about 1/100 of that of the dwSSA method.23 For the reversible isomerization model, sampling variance of ABSIS is only about 1/10, 000 of that of the dwSSA. ABSIS also shows significant improvements in standard deviations in comparisons to dwSSA. For the reversible isomerization, ABSIS estimates the rare event probability with only about 1/100 standard deviation of that of dwSSA. For the birth-death model and bistable Schlögl model, the standard deviation of ABSIS sampling is less than 1/10 than that of dwSSA. In terms of computing efficiency, smaller standard deviation indicates ABSIS can achieve the same accuracy as dwSSA with only a small fraction of sample size that dwSSA needs.
Although ABSIS has no significant advantages over constant biasing methods such as dwSSA in studying the futile cycle model, as the current bias scheme in ABSIS gives nearly constant biases, the sampling variances of ABSIS are comparable to those of dwSSA. Future work includes designing more sophisticated bias functions that captures the ruggedness of the probability landscape, which may provide better solutions to problems such as the model of enzymatic futile cycle. In addition, replacing enumeration of κ-steps of the reactions with longer term look-ahead path sampling of comparable computational costs may help to explore potential for barrier-crossing at a longer time scale. Computational costs can be further reduced for larger networks if such long look-ahead sampling is strategically biased. It may also be possible to classify reaction networks based on their topology and rate constants and design different sub-schemes of bias.
ACKNOWLEDGMENTS
We thank Dr. Rong Chen and Dr. Ming Lin for thoughtful discussions and suggestions. This work was supported by National Science Foundation (NSF) Grant Nos. DBI 1062328 and DMS-0800257, and National Institutes of Health Grant Nos. GM079804 and GM086145.
References
- Kim K. Y. and Wang J., PLOS Comput. Biol. 3(3), e60 (2007). 10.1371/journal.pcbi.0030060 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ptashne M., A Genetic Switch: Phage Lambda Revisited, 3rd ed. (Cold Spring Harbor Laboratory Press, 2004). [Google Scholar]
- Tian T. and Burrage K., Proc. Natl. Acad. Sci. U.S.A. 103, 8372 (2006). 10.1073/pnas.0507818103 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Arkin A., Ross J., and McAdams H. H., Genetics 149(4), 1633 (1998). [DOI] [PMC free article] [PubMed] [Google Scholar]
- Aurell E., Brown S., Johanson J., and Sneppen K., Phys. Rev. E 65, 051914 (2002). 10.1103/PhysRevE.65.051914 [DOI] [PubMed] [Google Scholar]
- Aurell E. and Sneppen K., Phys. Rev. Lett. 88, 048101 (2002). 10.1103/PhysRevLett.88.048101 [DOI] [PubMed] [Google Scholar]
- Zhu X.-M., Yin L., Hood L., and Ao P., Funct. Integr. Genomics 4, 188 (2004). 10.1007/s10142-003-0095-5 [DOI] [PubMed] [Google Scholar]
- Cao Y., Lu H.-M., and Liang J., Proc. Natl. Acad. Sci. U.S.A. 107, 18445 (2010). 10.1073/pnas.1001455107 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Little J. W., Shepley D. P., and Wert D. W., EMBO J. 18, 4299 (1999). 10.1093/emboj/18.15.4299 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ghosh K., Ozkan S. B., and Dill K. A., J. Am. Chem. Soc. 129, 11920 (2007). 10.1021/ja066785b [DOI] [PubMed] [Google Scholar]
- Warren P. B., Phys. Rev. E 80, 030903 (2009). 10.1103/PhysRevE.80.030903 [DOI] [PubMed] [Google Scholar]
- Eftimie R., Dushoff J., Bridle B., Bramson J., and Earn D., Bull. Math. Biol. 73, 2932 (2011). 10.1007/s11538-011-9653-5 [DOI] [PubMed] [Google Scholar]
- Baylin S. and Herman J., Trends Genet. 16, 168 (2000). 10.1016/S0168-9525(99)01971-X [DOI] [PubMed] [Google Scholar]
- Jones P. and Baylin S., Nat. Rev. Genet. 3, 415 (2002). 10.1038/nrg816 [DOI] [PubMed] [Google Scholar]
- Ao P., Galas D., Hood L., and Zhu X., Med. Hypotheses 70, 678 (2008). 10.1016/j.mehy.2007.03.043 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Huang S., Ernberg I., and Kauffman S., Semin. Cell Dev. Biol. 20, 869 (2009). 10.1016/j.semcdb.2009.07.003 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Faradjian A. K. and Elber R., J. Chem. Phys. 120, 10880 (2004). 10.1063/1.1738640 [DOI] [PubMed] [Google Scholar]
- Allen R. J., Valeriani C., and ten Wolde P. R., J. Phys.: Condens. Matter 21, 463102 (2009). 10.1088/0953-8984/21/46/463102 [DOI] [PubMed] [Google Scholar]
- Cao Y. and Liang J., BMC Syst. Biol. 2, 30 (2008). 10.1186/1752-0509-2-30 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gross D. and Miller D., Oper. Res. 32, 343 (1984). 10.1287/opre.32.2.343 [DOI] [Google Scholar]
- Gillespie D. T., J. Phys. Chem. 81, 2340 (1977). 10.1021/j100540a008 [DOI] [Google Scholar]
- Kuwahara H. and Mura I., J. Chem. Phys. 129, 165101 (2008). 10.1063/1.2987701 [DOI] [PubMed] [Google Scholar]
- Daigle B., Roh M., Gillespie D., and Petzold L., J. Chem. Phys. 134, 044110 (2011). 10.1063/1.3522769 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Marshall A., in Symposium on Monte Carlo Methods, edited by Meyer M. (Wiley, 1956), pp. 123–140. [Google Scholar]
- Torrie G. and Valleau J., J. Comput. Phys. 23, 187 (1977). 10.1016/0021-9991(77)90121-8 [DOI] [Google Scholar]
- Roh M., Daigle B., Gillespie D., and Petzold L., J. Chem. Phys. 135, 234108 (2011). 10.1063/1.3668100 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Roh M. K., Gillespie D. T., and Petzold L. R., J. Chem. Phys. 133, 174106 (2010). 10.1063/1.3493460 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Meirovitch H., J. Phys. A: Mathematical and General 15, L735 (1982). 10.1088/0305-4470/15/12/014 [DOI] [Google Scholar]
- Meirovitch H., J. Chem. Phys. 89, 2514 (1988). 10.1063/1.455045 [DOI] [Google Scholar]
- Liang J., Zhang J., and Chen R., J. Chem. Phys. 117, 3511 (2002). 10.1063/1.1493772 [DOI] [Google Scholar]
- Lin M., Chen R., and Liu J., “Lookahead strategies for sequential Monte Carlo,” Technical Report (Rutgers University, Peking University and Harvard University, 2009).
- Liu J. S., Chen R., and Logvinenko T., Sequential Monte Carlo Methods in Practice, Statistics for Engineering and Information Science, edited by Doucet A., Freitas N., and Gordon N. (Springer, New York, 2001), pp. 225–246. [Google Scholar]
- Liang J., Zhang J., and Chen R., J. Chem. Phys. 117, 3511 (2002). 10.1063/1.1493772 [DOI] [Google Scholar]
- Gillespie D., Roh M., and Petzold L., J. Chem. Phys. 130, 174103 (2009). 10.1063/1.3116791 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gillespie D., J. Chem. Phys. 115, 1716 (2001). 10.1063/1.1378322 [DOI] [Google Scholar]
- Lin M., Zhang J., Lu H.-M., Chen R., and Liang J., J. Chem. Phys. 134, 075103 (2011). 10.1063/1.3519056 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sidje R. B., ACM Trans. Math. Softw. 24, 130 (1998). 10.1145/285861.285868 [DOI] [Google Scholar]
- Schlögl F., Z. Phy. 253, 147 (1972). 10.1007/BF01379769 [DOI] [Google Scholar]
- Vellela M. and Qian H., J. R. Soc., Interface 6, 925 (2009). 10.1098/rsif.2008.0476 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Vlad M. O. and Ross J., J. Chem. Phys. 100, 7268 (1994). 10.1063/1.466873 [DOI] [Google Scholar]
- Elderfield D. and Vvedensky D. D., J. Phys. A 18, 2591 (1985). 10.1088/0305-4470/18/13/034 [DOI] [Google Scholar]
- Samoilov M., Plyasunov S., and Arkin A., Proc. Natl. Acad. Sci. U.S.A. 102(7), 2310 (2005). 10.1073/pnas.0406841102 [DOI] [PMC free article] [PubMed] [Google Scholar]