Robust Analysis of High Throughput Screening (HTS) Assay Data

Abstract

Quantitative high throughput screening (qHTS) assays use cells or tissues to screen thousands of compounds in a short period of time. Data generated from qHTS assays are then evaluated using nonlinear regression models, such as the Hill model, and decisions regarding toxicity are made using the estimates of the parameters of the model. For any given compound, the variability in the observed response may either be constant across dose groups (homoscedasticity) or vary with dose (heteroscedasticity). Since thousands of compounds are simultaneously evaluated in a qHTS assay, it is not practically feasible for an investigator to perform residual analysis to determine the variance structure before performing statistical inferences on each compound. Since it is well-known that the variance structure plays an important role in the analysis of linear and nonlinear regression models it is therefore important to have practically useful and easy to interpret methodology which is robust to the variance structure. Furthermore, given the number of chemicals that are investigated in the qHTS assay, outliers and influential observations are not uncommon. In this article we describe preliminary test estimation (PTE) based methodology which is robust to the variance structure as well as any potential outliers and influential observations. Performance of the proposed methodology is evaluated in terms of false discovery rate (FDR) and power using a simulation study mimicking a real qHTS data. Of the two methods currently in use, our simulations studies suggest that one is extremely conservative with very small power in comparison to the proposed PTE based method whereas the other method is very liberal. In contrast, the proposed PTE based methodology achieves a better control of FDR while maintaining good power. The proposed methodology is illustrated using a data set obtained from the National Toxicology Program (NTP). Additional information, simulation results, data and computer code are available online as supplementary materials.

1 INTRODUCTION AND MOTIVATION

The classical rodent cancer bioassay used to detect toxicity or carcinogenicity of a chemical is often a slow and expensive process. For instance a typical carcinogenicity bioassay conducted by the National Toxicology Program (NTP) takes more than 2 years and costs several million dollars. It is widely acknowledged that humans are exposed to thousands of chemicals and yet less than 600 chemicals have been investigated by the NTP using the 2-year rodent bioassay. To speed up the process of screening chemicals, the NTP and other agencies as well as some chemical and pharmaceutical industries have begun conducting quantitative high throughput screening (qHTS) assays. Rather than using higher order animals such as rodents, qHTS assays typically treat cells or tissues to various doses of each chemical to determine toxicity of a chemical. Typically these assays are completed in a short period of time which results in substantial reduction of costs and time. Accordingly, in recent years, the design and analysis of qHTS data has been an active area of research (Zhang 2007; Michael et al. 2008; Qu 2010).

Typically, thousands of chemicals are processed at the same time in a qHTS assay and the resulting data are usually analyzed by fitting dose-response curves using the following function, known as the Hill function shown in Figure 1:

$$f(x,\mathit{\theta })={\theta }_0+{\theta }_1\frac{{\theta }_3^{{\theta }_2}}{x^{{\theta }_2}+{\theta }_3^{{\theta }_2}},$$ (1)

where x denotes the dose of a chemical, θ₀ is the lower asymptote, θ₁ is the diference between the mean response at baseline and the lower asymptote (also known as the efficacy of the chemical), θ₂ is the slope or shape parameter of the curve and θ₃ is the dose corresponding to 50% response to the maximum change from baseline (also known as ED₅₀). Throughout this paper x_min and x_max denote the smallest and the largest doses used in the study. In qHTS assays a possible response variable of interest is cell viability measured by intracellular adenosine triphosphate (ATP) levels (Xia et al. 2008). Often such responses are normalized relative to a positive control (−100%) and the vehicle control (0%) as follows:

$$y=\frac{y^0-N}{I-N}\times (-100)$$

where y is percent activity, y⁰ is raw data value, N is the median of the vehicle control, I is the median of a positive control (Inglese et al. 2006). Hence, the response is expressed as percentage and can be positive or negative.

Figure 1.

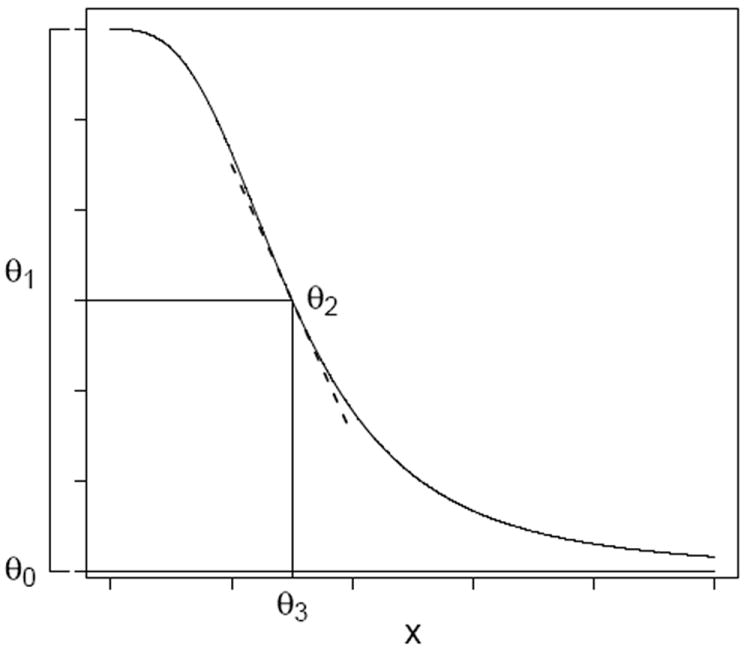
Hill function

Two common methods for analyzing qHTS data are the methods by Xia et al. (2008) and Parham et al. (2009). The former method, which will be referred to as the NCGC method, was developed by researchers at National Institute of Health Chemical Genomic Center (NCGC) and is widely used by researchers in the field. For each chemical, the NCGC methodology fits the Hill model using ordinary least squares and classifies the chemical into various curve classes on the basis of the ordinary least squares estimates (OLSE) θ̂ as follows:

• Class 1: If θ̂₁ > 30, θ̂₃ ∈ (x_min, x_max) and the curve does not have the lower asymptote.

• Class 2: If θ̂₁ > 30, θ̂₃ ∈ (x_min, x_max) and the curve has the lower asymptote.

• Class 3 (Inconclusive): If θ̂₁ > 30 and θ̂₃ ∉ (x_min, x_max).

• Class 4 (Inactive): If θ̂₁ < 30 then a chemical is classified as inactive.

Chemicals in Class 1 are declared to be active if the multiple correlation coefficient R² > 0.9. Chemicals in Class 2 are declared to be active if R² > 0.9 and θ̂₁ > 80. Chemicals that are neither classified to be active nor inactive are classified as inconclusive (Class 3). To define lower asymptote we quote Inglese et al. (2006) “To determine if the curve contained a lower bound asymptote, two points, representing the highest concentration tested and a half-log lower, were plotted according to the curve’s Hill parameters. If the slope of these points was > −10 and if the plotted concentrations were past the inflection, the curve was determined to contain a lower asymptote.”

A problem with the above strategy is that it ignores uncertainty associated with θ̂. To deal with some of these issues, Parham et al. (2009) first test H₀ : θ₁ = 0 against H_a : θ₁ ≠ 0 using a likelihood ratio test (LRT) (chi-squared with 3 degrees of freedom) at α = 0.05 with Bonferroni correction for multiple testing. They then classify compounds as follows:

• Active: If H₀ is rejected with θ̂₂ > 0, θ̂₃ < x_max and |y_xmax| > 10 where y_xmax is the response at x = x_max.

• Inactive: If either H₀ is not rejected or θ̂₂ < 0.

• Marginal: If a chemical is neither classified as active nor as inactive.

Throughout this paper we shall refer to the above methodology as “Parham methodology”. Although they use a formal procedure for testing θ₁, they too ignore uncertainty associated with the estimates of remaining parameters. Furthermore, they ignore the underlying variance structure by using OLSE even if the variances are heteroscedastic.

In practice, since qHTS assays consist of data on thousands of chemicals, it may not be realistic to assume that all data are homoscedastic. Williams et al. (2007) suggested the use of iterated weighted least squares (IWLS) methodology by modeling the variance as a function of dose. Although such a methodology is practical, it is well-known that when the error variance is nearly homoscedastic then IWLS may not perform well. To illustrate this point, we consider qHTS data on two chemicals from the NTP library of 1,408 chemicals (Tice et al. 2007). We label them as Chemical A and Chemical B. Since outliers are common in qHTS data, throughout this paper we use M-estimators (with Huber-score function) in place of least squares. Thus we use Ordinary M-estimator (OME) and Weighted M-estimator (WME), both of which will be defined precisely later in the paper. The following illustration would work equally well for OLSE and IWLSE.

Data for Chemical A, along with OME and WME fitted curves are presented in Figure 2(a). Similarly, plots for Chemical B are presented in Figure 2(b). The individual point estimates are summarized in Table 1. There are a total of 14 doses in the study which are 0.00059, 0.00294, 0.0147, 0.0328, 0.0734, 0.164, 0.367, 0.821, 1.835, 4.103, 9.175, 20.52, 45.87, and 91.74 with 3 replicates per dose. From Figure 2, it seems reasonable to assume that Chemical A data are possibly heteroscedastic as the variance seems to increase with dose, whereas Chemical B data are approximately homoscedastic. We performed a simple linear regression by regressing log of sample variance on the dose and found that the slope parameter for Chemical A is highly significant (p = 0.004) while the slope parameter for Chemical B is not (p = 0.33). The log linear model for the sample variance seems to be a simple parsimonious model to describe variance as a function of dose. Hence it is used throughout this paper.

Figure 2.

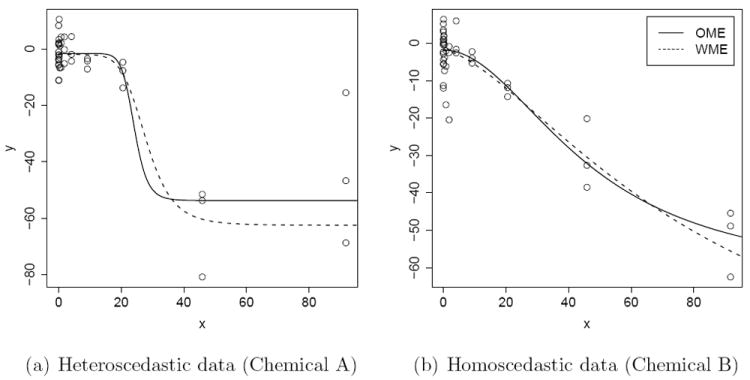
HepG2 cell triplicate data, potentially (a) heteroscedastic and (b) homoscedastic, from qHTS assays; the corresponding fitted curves using OME and WME methods.

Table 1.

Estimate and Standard Error for parameters of the models for HepG2 cell triplicate data using OME and WME methods.

PAR	Method	Chemical A (possibly heteroscedastic)			Chemical B (possibly homoscedastic)
		EST	SE	p-value	EST	SE	p-value
θ0	OME	-53.7	3.5	0.000	-63.7	15.7	0.000
	WME	-62.5	3.1	0.000	-103.1	74.8	0.088
θ1	OME	52.1	3.7	0.000	61.8	15.9	0.000
	WME	60.4	3.3	0.000	101.2	75.1	0.093
θ2	OME	11.6	201.3	0.477	2.0	0.7	0.004
	WME	6.6	2.6	0.008	1.5	0.6	0.009
θ3	OME	24.1	68.3	0.363	46.8	15.3	0.002
	WME	27.9	3.7	0.000	84.7	82.6	0.156

As seen from Figure 2, the fits based on OME and WME seem to be equally good. However, parameter estimates and their standard errors seem to differ substantially. Thus this example demonstrates that OME and WME (and their standard errors) can be drastically different from each other depending upon the underlying variance structure. In practice, one never knows a priori if the data are homoscedastic or heteroscedastic. Standard diagnostic tools are practically impossible to implement since thousands of models are to be fitted in an automated manner. Thus there is a need for a methodology which automatically chooses between OME and WME.

Recently, in Lim et al. (2012) we proposed the preliminary test estimation (PTE) procedure for possibly heteroscedastic nonlinear models. The basic idea is to select either OME or WME on the basis of a simple preliminary test for heteroscedasticity. Depending upon the outcome of the test, PTE uses either OME or WME. Motivated by the performance of PTE methodology in Section 2 we develop PTE based likelihood ratio type methodology to evaluate if a chemical is active or inactive. In addition to testing, we also propose PTE based confidence intervals for estimating various parameters of the Hill model. We derive suitable critical values for the PTE methodology. Extensive simulation studies are conducted in Section 3 to investigate the performance of the proposed methodology in terms of the false discovery rate (FDR), the power and coverage probabilities of confidence intervals.

It is important to note that unlike linear models, where statistical inference is based on exact distribution theory (under suitable model assumptions), in the case of nonlinear models one relies on the asymptotic theory. The asymptotic approximations are generally reasonable for moderately large tail probabilities. Unfortunately, however, the asymptotic approximations are not good for very small tail probabilities, which are of primary interest in multiple testing problems. This is particularly the case when the data are heteroscedastic. A possible alternative to asymptotic theory based methodology is to use a resampling based method such as bootstrap/permutation methodology. Unfortunately, in the case on nonlinear models, this is a computationally challenging process. Even in the absence of bootstrap, fitting nonlinear models requires a very large number of starting values to avoid convergence to local solutions. It is critical to get a solution as close to the optimum as possible – not only because one wants to estimate the model parameters as accurately as possible, but the uncertainty estimates depend upon the unknown parameters (unlike linear models). This has a downstream effect on statistical inference. Secondly, some of the model parameters can be very unstable/sensitive to the data (such as ED₅₀ and slope parameter). Estimates of these parameters are critical for toxicologists. Thus, even in the absence of bootstrap/permutation, the computation time to fit each model can be substantial. Since we are interested in far right tail probabilities (of the order 0.0001 or less), the number of bootstraps/permutations needed are of the order 100,000 or more to get an accurate estimate of small p-values. The current and future qHTS assays process 10,000 to 100,000 chemicals if not more. Thus the bootstrap/permutation based methods are practically infeasible for these assays. For this reason, it is more practical to use asymptotic theory based p-values although they are potentially inaccurate for small tail probabilities, especially when the data are heteroscedastic. As a consequence the FDR cannot be controlled by the Benjamini-Hochberg procedure (Benjamini and Hochberg 1995). Since p-values are inaccurate, we need to empirically determine which “black box” method could control FDR in this case. In this paper we concentrate on using a Bonferroni corrected threshold at level 0.05, which in our simulations below works quite well at assuring FDR control at the same level. The Bonferroni adjusted p-values obtained in this paper can be thought of as “scores” for each chemical, with small scores corresponding to a compound that is more likely to be active. Thus, although the methodology described here is inspired by large sample theory, the inability to obtain accurate p-values for small to moderate sample sizes renders this methodology to be a bit of a “black box”. We note that this problem is not unique to the qHTS context, but may arise in other settings where p-values are not exact but are based on asymptotic methods.

The proposed methodology is illustrated in Section 4 using an assay conducted on NTP’s library of 1,408 compounds. We conclude this paper in Section 5 by providing discussion and open problems. Notations and Proofs are provided in the Appendix. The regularity conditions and results of some additional simulation studies are provided in the online Supplementary Materials.

2 METHODOLOGY

The standard nonlinear regression model may be expressed as

$$y_{\mathit{ij}}=f(x_i,\mathit{\theta })+{\sigma }_i{\epsilon }_{\mathit{ij}},i=1,\dots ,k,j=1,\dots ,n_i$$ (2)

where y_ij is an observable response variable, x_i is a known constant, f(x_i, θ) and θ are defined in (1), σ_i is an error variance at x_i, and ε_ij is an unobservable random error assumed to be iid N(0, 1). The total sample size $n={\sum }_{i=1}^k{n}_i$.

Our experience with a sample of qHTS data suggests that σ_i depends upon x_i. To keep the variance model parsimonious, we use the log-linear model log σ_i = log σ(x_i, τ) = τ₀ + τ₁ x_i, where τ = (τ₀, τ₁)^t is a vector of variance parameters. However, the proposed methodology can be easily modified if a more complex model is justified.

An underlying assumption made by researchers in this field is that if a chemical is active then its mean response can be modeled by the Hill model. On the other hand, if the chemical is not active then it is assumed to have a constant mean response across dose groups. Therefore, one may formulate the statistical problem as a test of the following hypotheses:

$$H_0:E(y)=\beta (\mathrm{unknown})\mathrm{vs}.H_1:E(y)=f(x,\mathit{\theta }).$$ (3)

Assuming that the residuals are homoscedastic and normally distributed, the null distribution of the likelihood ratio test (LRT) for the above hypotheses can be approximated by central F-distribution (cf., Gallant 1987). More precisely, suppose θ̂ is the OLSE of θ under H₁ with ${\mathrm{SSE}}_1(\widehat{\mathit{\theta }})={\sum }_{i,j}{\{y_{\mathit{ij}}-f(x_i,\widehat{\mathit{\theta }})\}}^2$. Similarly, suppose β̂ is the sample mean under the null hypothesis and ${\mathrm{SSE}}_0(\widehat{\beta })={\sum }_{i,j}{(y_{\mathit{ij}}-\widehat{\beta })}^2$. Then the LRT L_OLSE = {(SSE₀(β̂)−SSE₁(θ̂))/3}/{SSE₁(θ̂)/(n−4)} is approximately central F distributed with (3, n − 4) degrees of freedom. The above test statistic can be approximated as L_OLSE = {η̂^t(Ĥ−H⁰)η̂/3}/{η̂^t(I_n − Ĥ)η̂/(n−4)}+o_P (1) = L^OLSE+o_P (1), where η̂ = Y − β̂1, Y = (y₁₁,…, y_k,nk)^t, β̂ = ȳ, 1 = (1,…, 1)^t, Ĥ = F̂(F̂^tF̂)⁻¹ F̂^t, F̂ = f_θ (θ̂) = {∂f (x_i, θ)/∂θ_j∣_θ=θ̂}, and H⁰ = 1(1^t1)⁻¹1^t. Since L^OLSE is not robust to outliers and influential observations, in this paper we make it robust by replacing OLSE by OME θ̃_n, in the above calculations, where OME is defined as (Lim et al. 2012): θ̃_n = Argmin {Σ_i,j h² (y_ij − f (x_i, θ)) : θ ∈ ℜ^p} where h is taken to be the Huber-score function. For a pre-specified positive constant k₀, $h\left(u\right)=u/\sqrt{2}$, if |u| < k₀, otherwise h(u) = {k₀(|u|−k₀/2)}^1/2. As commonly done, throughout this paper we take k₀ to be 1.5. We shall denote the resulting statistic by L^OME. Since OME and OLSE are asymptotically equivalent and OME is consistent and asymptotically normally distributed (Lim et al. 2012), the null distribution of L^OME can also be approximated by central F-distribution with (3, n − 4) degrees of freedom. Throughout this paper we shall refer to this modified LRT as the OME based methodology.

As often done, for heteroscedastic data we use the weighted version of L_OLSE by weighting the least squares with the estimated variances under the log-linear model as follows. First we estimate τ₀ and τ₁ in the log-linear model log σ_i = τ₀ + τ₁x_i by performing simple linear regression of log of residuals on dose using OLSE. Using these estimates we obtain WLSE of θ, denoted as θ̂ under H₁ and WLSE of β, denoted β̂ under H₀. Let L₀ = Σ_i,j (y_ij − β̂)²/exp(2τ̂₁x_i), L₁ = Σ_i,j (y_ij − f(x_i, θ̂))²/exp(2τ̂₁x_i) and β̂ = Σ_i,j y_ij exp(−2τ̂₁ x_i)/Σ_i n_iexp(−2τ̂₁x_i). Then the weighted version of L_OLSE is given by L^WLSE = {(L₀ − L₁)/3}/{L₁/(n−6)}. As done in the case of homoscedastic data, to robustify against outliers and influential observations, we replace the WLSE by WME in the above test statistic, where $\mathrm{WME}{({\widehat{\mathit{\theta }}}_n^t,{\widehat{\mathit{\tau }}}_n^t)}^t$, is defined as (Lim et al. 2012) ${({\widehat{\mathit{\theta }}}_n^t,{\widehat{\mathit{\tau }}}_n^t)}^t=\mathit{Argmin}\left[{\sum }_{i,j}\{h^2((y_{\mathit{ij}}-f(x_i,\mathit{\theta }))/\sigma ({\mathbf{z}}_i,\mathit{\tau }))+\log \sigma ({\mathbf{z}}_i,\mathit{\tau })\}:\mathit{\theta }\in {\Re }^p,\mathit{\tau }\in {\Re }^q\right]$. Under suitable regularity conditions, the asymptotic normality and consistency of WME is established in Lim et al. (2012). The WME version of L^WLSE is denoted as L^WME. Again due to asymptotic equivalence of WME and WLSE and the asymptotic equivalence of L^WLSE and L^WME, the null distribution of L^WME can be approximated by the approximate null distribution of L^WLSE (see Theorem 1).

As noted earlier, in practice one does not know if the data are homoscedastic or heteroscedastic. For this reason we now describe the PTE methodology.

As in Lim et al. (2012), we test for heteroscedasticity under the log-linear model log σ_i = τ₀ + τ₁x_i, by testing H₀ : τ₁ = 0 vs. H₁ : τ₁ ≠ 0 using $T_n={\widehat{\tau }}_{1n}/\sqrt{\mathrm{Var}\left({\widehat{\tau }}_{1n}\right)}$, which is approximately central t distributed with n − 2 degrees of freedom. Throughout this paper we perform this preliminary test at α = 0.5. Thus the PTE ${\widehat{\mathit{\theta }}}_n^{\mathrm{PT}}$ is defined as ${\widehat{\mathit{\theta }}}_n^{\mathrm{PT}}={\stackrel{\sim }{\mathit{\theta }}}_{n}I(|T_n|\le t_{\alpha /2,n-2})+{\widehat{\mathit{\theta }}}_{n}I(|T_n|>t_{\alpha /2,n-2})$, where I(·) is the usual indicator function. There is no special reason for choosing an α of 0.50. Our proposed methodology is flexible enough that one could use any level of significance in the pre-test. We use the pre-test as a model selection procedure and not a formal test. It mimics classical model selection procedures such as forward selection/stepwise regression etc. in the linear/logistic/Cox regression model literature. Most standard software packages (and applied researchers) typically set the default value to be larger than 0.05. For example, in its FORWARD selection method implemented in PROC REG, SAS sets it at 0.50 as the default value (http://support.sas.com/onlinedoc/913/docMainpage.jsp). Unlike in most instances, in the present context of pretesting for homoscedasticity vs. heteroscedasticity, the Type II error is more important than the Type I error. This is because, using a homoscedastic method for heteroscedastic data usually results in an inflated false positive rate. On the other hand, if we use a heteroscedastic method for homoscedastic data, then the damage done is potentially small because the estimate of the slope parameter of the log-linear variance model (corresponding to the dose) would be small enough that the dose may not contribute much to the variance. Thus the presumed heteroscedastic model would be “close to” homoscedastic case. Hence, we arbitrarily chose α to be 0.50.

The asymptotic covariance matrix of ${\widehat{\mathit{\theta }}}_n^{\mathrm{PT}}$, derived in Lim et al. (2012), is as follows:

$$\begin{array}{lll}\mathrm{Var}({\widehat{\mathit{\theta }}}_n^{\mathrm{PT}})& =& {\alpha }^{\ast }\mathrm{Var}({\stackrel{\sim }{\mathit{\theta }}}_n)+(1-{\alpha }^{\ast })\mathrm{Var}({\widehat{\mathit{\theta }}}_n)\\ & =& {\alpha }^{\ast }{\left(\frac{1}{n}{\mathbf{\Gamma }}_{4n}(\mathit{\theta })\right)}^{-1}\left(\frac{1}{n}{\mathbf{\Gamma }}_{33n}(\mathit{\theta })\right){\left(\frac{1}{n}{\mathbf{\Gamma }}_{4n}(\mathit{\theta })\right)}^{-1}+(1-{\alpha }^{\ast }){\left(\frac{1}{n}{\mathbf{\Gamma }}_{1n}(\mathit{\theta },\mathit{\tau })\right)}^{-1}\left(\frac{1}{n}{\mathbf{\Gamma }}_{31n}(\mathit{\theta },\mathit{\tau })\right){\left(\frac{1}{n}{\mathbf{\Gamma }}_{1n}(\mathit{\theta },\mathit{\tau })\right)}^{-1},\end{array}$$

where ${\alpha }^{\ast }=F_t\left(t_{\alpha /2,n-2}-{\tau }_1/\sqrt{\mathrm{Var}\left({\widehat{\tau }}_{1n}\right)}\right)-F_t\left(-t_{\alpha /2,n-2}-{\tau }_1/\sqrt{\mathrm{Var}\left({\widehat{\tau }}_{1n}\right)}\right)$, F_t is the cumulative distribution function of the t-distribution with n − 2 degrees of freedom, and Γ_1n (θ, τ), Γ_31n (θ, τ), Γ_33n (θ) and Γ_4n (θ) are defined in Appendix A.

The PTE based test statistic, which is robust to heteroscedasticity as well as outliers and influential observations, is given by L^PT = L^OME I(|T_n| ≤ t_α/2,n−2) + L^WME I(|T_n| > t_α/2,n−2). Using the fact that OME and WME are consistent and asymptotically normally distributed under the regularity conditions (Lim et al. 2012), we obtain approximate critical values for L^WME and L^PT in the following theorem.

Theorem 1

Suppose ε_ij ~ ^independent N (0, exp{2(τ₀ + τ₁x_i)}). Then,

1. Under the conditions [S1] – [S9] in the supplementary material, the distribution of L^WME under the null hypothesis H₀ can be approximated by the central F-distribution with (3, n − 6) degrees of freedom.

2. Under the conditions [S1] – [S11] in the supplementary material, lim sup_n→∞ P(L^PT > f_α1,3,n−6∣H₀) ≤ α₁ where f_α1,3,n−6 is the upper α₁ percentile of F-distribution with (3, n − 6) degrees of freedom and α₁ is the significance level.

The proof of the theorem is provided in Appendix B.

Our proposed methodology using OME, WME or PTE for screening chemicals in qHTS assays can be summarized as follows. For each chemical test (3) using L^T (i.e., L^OME, L^WME or L^PT) with Bonferroni correction for multiple testing. Chemicals that are significant based on this test are declared to be active while the remaining ones are declared to be inactive.

Once a chemical is declared to be active, researchers are interested in estimating individual parameters of the Hill model along with their confidence intervals. Standard errors and the critical values for the confidence intervals using OME and WME methodologies are available from Lim et al. (2012). However, Lim et al. (2012) did not derive the critical values for the confidence intervals centered at PTE, which are provided in the following theorem.

Theorem 2

For i = 1,…, 4 define $c_{{\alpha }_1}=t_{{\alpha }_1/2,n-6}\max \{\mathit{SE}({\stackrel{\sim }{\theta }}_i),\mathit{SE}({\widehat{\theta }}_i)\}/\mathit{SE}({\widehat{\theta }}_i^{\mathit{PT}})$. Then, under the conditions [S1] – [S11] in the supplementary material, $\lim {\inf }_{n\to \infty }P(|{\widehat{\theta }}_i^{\mathit{PT}}-{\theta }_i|/\mathit{SE}({\widehat{\theta }}_i^{\mathit{PT}})\le c_{{\alpha }_1})\ge 1-{\alpha }_1$.

The proof of the theorem is provided in Appendix B.

Note that we are constructing confidence intervals for parameters of those models that are selected by the above testing process. Consequently, one needs to be concerned about the overall coverage probability along the lines of Benjamini and Yekutieli (2005). Unfortunately, as noted earlier, the asymptotic p-values, especially those corresponding to far right tail of the distribution, are likely to be incorrect for small to moderate sample sizes. Thus, under the null hypothesis, the p-values are not necessarily uniformly distributed. As a consequence, procedures such as those of Benjamini and Yekutieli (2005) are not directly applicable. This presents an interesting problem for future research.

3 SIMULATION STUDIES

In this simulation study we compare the proposed PTE based methodology with the two existing methods, namely, NCGC and Parham methodologies as well as compare it with OME and WME based methodologies. Note that the WME and OME methods are similar to the PTE method. In contrast, NCGC and Parham are completely different methods. Our primary criteria of comparison are the estimated false discovery rate (FDR) and the power. As usual, for a given method, the estimated FDR is the proportion of true null hypotheses rejected among all rejected hypotheses and the estimated power is the proportion of cases in which the null hypothesis is correctly rejected among all cases where the null is false.

Since investigators are also interested in estimating parameters of the Hill model for chemicals that are considered to be active, in this paper we also compare the performance of the estimators, OME, WME and PTE in terms of coverage probability.

3.1 Study design

The design of our simulation study was modeled after a real qHTS data set obtained from the NTP. Thus our simulation experiment consisted of 14 doses (0.59 nM, 2.94 nM, 14.7 nM, 32.8 nM, 73.4 nM, 0.164 μM, 0.367 μM, 0.821 μM, 1.835 μM, 4.103 μM, 9.175 μM, 20.52 μM, 45.87 μM, and 91.74 μM) and 3 observations per dose. We generated 10,000 “chemicals” of which γ × 100% corresponded to “active” (i.e., none of the Hill parameters are zero) and the remaining (1 − γ) × 100% were true nulls which corresponded to no change in mean response across the dose groups. We now describe the selection of θ for the non-null data in our simulation study. To keep the parameters of our simulation study consistent with the NTP’s data on 1,408 chemicals, we first fitted a Hill model to each of these 1,408 compounds. From these we selected 100 patterns of curves that displayed various shapes of dose-response to get a reasonably broad selection of patterns. Since the observed responses of the NTP’s qHTS data were normalized using the positive control (set to be −100%) and the vehicle control (set to be 0%) obtained using dimethylsulfoxide (DMSO) (the solvent used for compound transfer) only, and since NCGC uses 30% as the minimum response to be active, θ₁ was chosen in the interval (32, 112). Motivated by Parham et al. (2009), θ₂ was chosen to range from 0.8 to 4.9 and θ₃ < x_max. Hence the 100 parameter sets so chosen include a wide range of patterns of shapes of Hill curves (see online supplementary materials for the values). The descriptive statistics of the parameters are presented in Table 2. We generated the null data by taking the mean response to be zero across all doses.

Table 2.

Summary statistics of 100 sets of parameters used in the simulation study.

Parameter	Range	Mean	Standard deviation
θ0	(−117, −31)	−74.420	26.377
θ1	(32, 112)	71.110	26.237
θ2	(0.8, 4.9)	2.467	1.060
θ3	(0.055, 83.49)	30.826	21.467

The patterns of variances considered in our simulation study were also deduced from the 1,408 chemicals data. For the selected 100 compounds, we tested for homoscedasticity and estimated the standard deviation for homoscedastic data sets. The range of the estimated standard deviation is between 2.9 and 48.6 and the median is 5.3. Thus, we considered five patterns of homoscedastic errors with standard deviation, σ = 4, 6, 8, 15 and 30, respectively.

To obtain patterns of variances to model heteroscedasticity, we fitted log-linear model for the variance (as described in the previous section) to the heteroscedastic data sets among the selected 100 compounds. The range of the estimated slope τ̂₁ of the log standard deviation is between −0.034 and 0.027 and the median is 0.007. Then, we arrived at four patterns of parameters, namely, (τ₀, τ₁) = (1.5, −0.015), (1, 0.01), (1, 0.02) and (3, 0.01). The ranges of σ_i with the choice of these parameters were (1.132, 4.482), (2.718, 6.803), (2.718, 17.027) and (20.086, 50.270), respectively.

In practice one generally does not know a priori what proportion of chemicals are heteroscedastic in a given qHTS assay. To keep our simulations realistic, we considered three patterns of proportion of heteroscedastic chemicals in a given run, namely, 10%, 25% or 50% heteroscedastic chemicals. The remaining are homoscedastic.

In summary we have 100 patterns of parameters with 9 patterns of variances for non-null data and 9 patterns of variances for null data. Thus we created a universe of 90,000 non-null data by generating 100 data sets for each of the 900 combinations of the patterns, and 9,000 null data by generating 1,000 data sets for each of the 9 patterns. From these 99,000 data sets, we obtained a random sample of 10,000 “chemicals” of which γ × 10, 000 were non-null and the remaining were null patterns. We repeated the simulation study 100 times and estimated the FDR and the power. We considered two different patterns of γ = 0.05 and 0.10 and three different patterns of the proportion of heteroscedastic data (as stated above).

For comparing OME, WME and PTE in terms of the coverage probability and the length of confidence interval, we used non-null data only. From 90,000 non-null data sets, we obtained a random sample of 10,000 non-null chemicals with three different patterns of proportions of heteroscedastic chemicals, which were 0.10, 0.25 or 0.50. Thus, either 10% or 25% or 50% of the non-null chemicals were heteroscedastic.

3.2 Results

The estimated FDR and power for the methods when γ = 0.10 are summarized in Figure 3. The results for the case of γ = 0.05 are provided in the supplementary material. The standard error of all FDR and power estimates provided in these figures was less than 0.005. In all the cases, the Parham method had a very high FDR compared to other methods. For example, when the proportion of non-null data is 0.10 and the proportion of heteroscedastic data is 0.50, the overall FDR of the Parham method is 0.421 and its FDR for heteroscedastic data is 0.475. On the other end of the spectrum, the NCGC method produced zero FDR in all cases. Accordingly it has a very low power. Additionally, we see from Table 3, both NCGC and Parham methods tend to declare a large proportion of chemicals to be inconclusive or marginal, thus requiring additional testing and resources to evaluate such chemicals.

Figure 3.

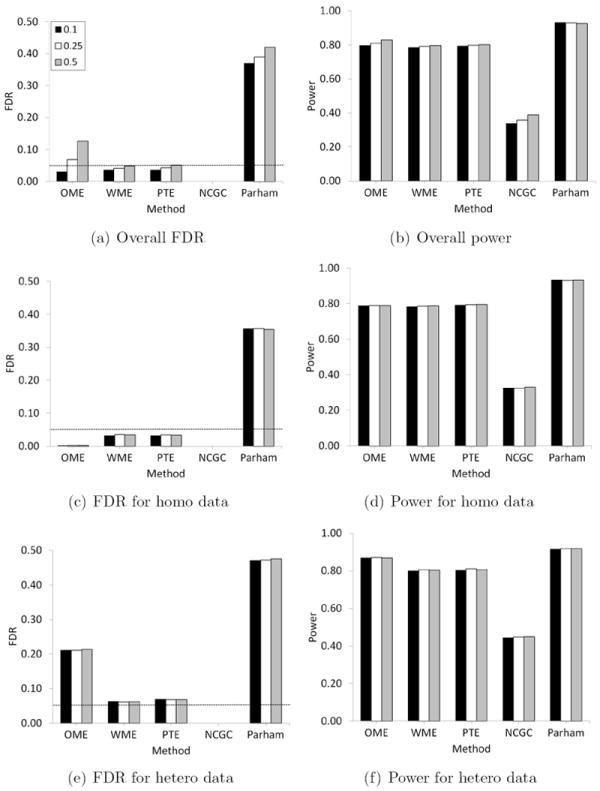
Estimated FDR and power for OME, WME, PTE, NCGC and Parham methods when the proportion of heteroscedastic data is 0.10, 0.25 and 0.50. Here γ = 0.10 and α = 0.05/10, 000.

Table 3.

Estimated proportion of inconclusive (marginal) data among non-null and null data based on NCGC and Parham methods with α = 0.05/10, 000.

γ	Hetero.	Method	Overall		Homoscedastic		Heteroscedastic
			Non-null	Null	Non-null	Null	Non-null	Null
0.10	0.10	NCGC	0.637	0.951	0.650	0.952	0.524	0.943
		Parham	0.069	0.285	0.068	0.295	0.077	0.198
	0.25	NCGC	0.616	0.950	0.647	0.952	0.521	0.943
		Parham	0.069	0.270	0.067	0.293	0.074	0.201
	0.50	NCGC	0.584	0.948	0.643	0.952	0.525	0.943
		Parham	0.072	0.246	0.066	0.294	0.077	0.199

The three alternative methods discussed in this paper, namely, OME, WME and PTE, had a better control of FDR in comparison to Parham method while maintaining reasonably good power in all the cases considered here. They were uniformly more powerful than NCGC method. The power of OME, WME and PTE based methods were almost same in every case but they differed in terms of FDR. As expected, the OME has the smallest FDR when the data are homoscedastic and generally has the largest FDR when the data are heteroscedastic. Overall, it has a larger FDR than WME and PTE based methods and hence we do not recommend its use for qHTS data. Interestingly, WME and PTE perform very similarly. This is largely due to the fact that for homoscedastic data the estimate of τ₁ used in the WME methodology is small enough for WME to perform similar to OME (and hence similar to PTE). However, when estimating confidence intervals for active chemicals, our simulation study reveals that PTE methodology outperforms WME (as well as OME) in terms of coverage probability (Figure 4). The coverage probabilities based on PTE are closer to the nominal level (0.95) than those based on OME and WME. One exception is the generally elevated θ₂ levels, in which PTE can be slightly higher and WME is close to nominal. The OME is subject to severe under-coverage especially for heteroscedastic data. For example, the lowest coverage probability based on OME for θ₀ is as low as 0.78 when 25% of the data are heteroscedastic. The WME is also subject to under-coverage in several cases, with the coverage probability as low as 0.90. On the other hand, the lowest coverage probability based on PTE is 0.93.

Figure 4.

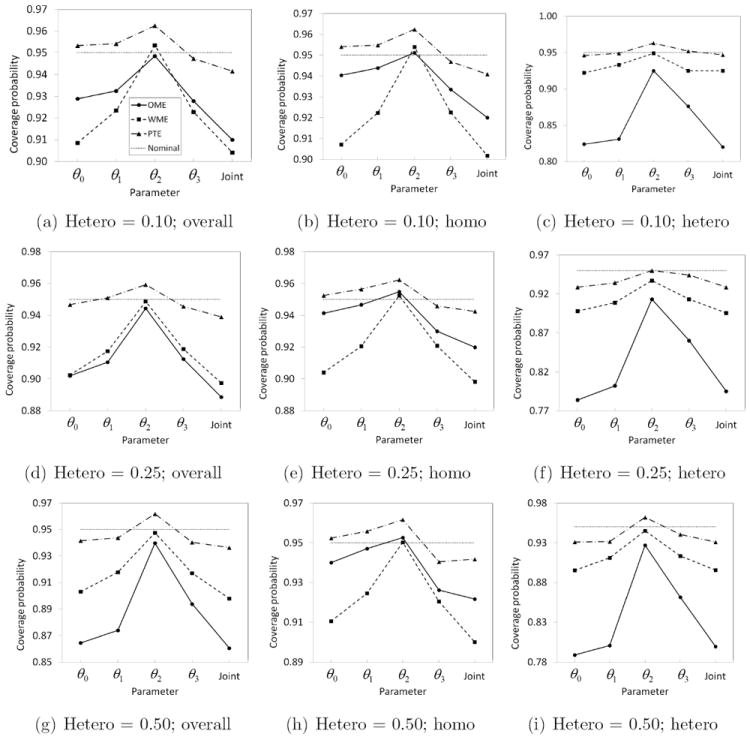
Estimated coverage probability based on OME, WME and PTE methods for non-null (overall, homoscedastic or heteroscedastic) data with 1 − α = 0.95 when the proportion of heteroscedastic data is 0.10, 0.25 or 0.50.

In summary, our simulation studies suggest that the proposed methodology based on PTE outperforms the existing methods of NCGC and Parham et al. (2009) by providing a better control of FDR while maintaining good power.

4 ANALYSIS OF HTS ASSAYS DATA

The NTP library of 1,408 compounds was established for evaluation in qHTS assays (Smith et al. 2007; Tice et al. 2007). These include solvents, preservatives, flavoring agents, therapeutic agents, inorganic and organic pollutants, pesticides, natural products, etc. Among 1,408 compounds, 1,353 are unique compounds and 55 are tested twice to evaluate the reproducibility of the assay. For details, we refer the reader to Xia et al. (2008).

We illustrate the proposed methodology using the HepG2 cell triplicate data obtained from the above experiment. For each compound, 14 different concentrations, listed previously in Section 3.1 and ranging from 0.00059 to 91.74 μM, were used. There were 3 replicates at each concentration thus resulting in a total sample size n = 42 observations.

The results of the analysis using all the methods discussed in this paper are summarized in Figure 5. According to our preliminary test 782 out of 1,408 compounds (56%) potentially have a heteroscedastic variance structure and the remaining 626 (44%) have a homoscedastic variance structure.

Figure 5.

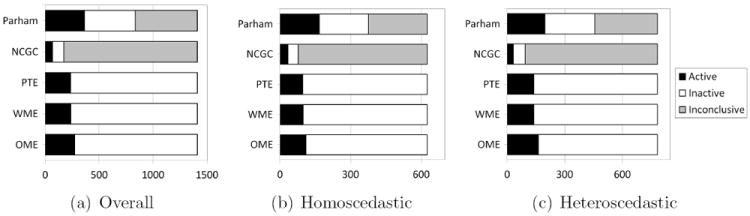
Screening results for 1,408 chemicals of HepG2 cell triplicate data using the NCGC, Parham, the proposed method based on OME, WME and PTE with α = 0.05/1408.

According to the NCGC method 5% of the 1,408 chemicals are active, while 26% are active according to the method of Parham et al. (2009). On the other hand, using the proposed OME, WME and PTE methodologies we discovered 19%, 17% and 17% of the 1,408 chemicals to be active, respectively. The NCGC method declared 88% chemicals as inconclusive while the Parham method declared 41% chemicals as marginal. For homoscedastic data, 5%, 27%, 18%, 16% and 15% of 626 chemicals are active while for heteroscedastic data, 4%, 25%, 21%, 18% and 18% of 782 chemicals are active according to the NCGC, Parham, OME, WME and PTE methods, respectively.

Venn diagrams of active chemicals declared by the various methods are provided in in Figure 6. From Figure 6(a), 205 chemicals were found to be active by OME, WME and PTE methods. Figure 6(b) shows that 66 chemicals were discovered by all three methods in the diagram.

Figure 6.

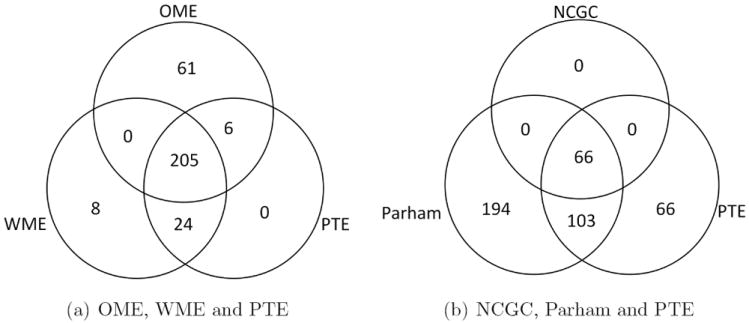
Venn diagrams of active chemicals using (a) OME, WME and PTE methods and (b) NCGC, Parham and PTE methods from qHTS assays.

5 DISCUSSION AND OPEN PROBELMS

With the advent of high throughput screening (HTS) assays and the need for fitting thousands of nonlinear regression models to classify chemicals into various toxicity categories, it is important that statistical methods are developed which are robust to various assumptions commonly made in classical regression analysis. This paper takes the first step in this direction. Based on the simulation studies and the example of real qHTS data (Section 4), it appears that the proposed methodology performs better than two currently available methods in terms of the false discovery rate and the power, which is desirable for the analysis of qHTS assays data. Although the PTE and WME performed equally well in terms of FDR and power, the PTE as an estimator outperforms both OME and WME in terms of the coverage probability of confidence intervals.

In the course of this investigation we identified several important research problems for future research. As noted in the introduction, the asymptotic p-values derived in the context of nonlinear models are not necessarily accurate for small to moderate sample sizes, especially those corresponding to small tail areas which are important for multiple testing problems. This problem is not unique to the present context, but may arise in other such multiple testing problems where asymptotic p-values are used. Unfortunately, resampling based procedures such as bootstrap/permutation methods are not practical in such situations for computational reasons.

A related problem is, for some data, especially the null data, the condition number of the information matrix can be extremely large. Note that, unlike linear models, in nonlinear models the information matrix is a function of the unknown parameters of the model. Toxicologists seem to recognize this issue and hence tend to discount/ignore data with either large slopes or large ED₅₀ values since they can’t trust those values (e.g., Parham et al. 2009). Analogous to SAM methodology for microarray data, in such cases we believe that the testing procedure can perhaps be modified by considering a shrinkage or a ridge type M-estimator in place of the regular M-estimator considered in this paper.

Although the theory of optimal designs is well developed in the case of linear and nonlinear models, it is has not been very well developed for high throughput screening assays with the exception of Qu (2010). Optimal designs developed in Qu (2010) are useful when the investigator is interested in making comparisons across chemicals. However, in the context described in this paper the problem of interest is not necessarily the comparison among thousands of chemicals but to screen chemicals that are potentially toxic. Hence the design issues discussed in Qu (2010) is not directly applicable here. Since the information matrix depends upon the unknown parameters of the model, the optimal design is not only a function of the dose but it is also a function of the unknown parameters of the model. The problem is exacerbated by the fact that the study involves not one nonlinear model but thousands of nonlinear models. Given that qHTS assays are being routinely conducted, it is important to derive suitable optimal designs. Since the condition number of the information matrix plays an important role, perhaps one may explore optimal designs by taking the objective function to be the expected value of the condition number of the information matrix. The expectation may be taken over a suitable prior distribution of θ, representing a wide range of chemicals.

APPENDIX A: NOTATIONS

In this appendix we define the notations used in the paper.

1. ${\mathbf{\Gamma }}_{1n}(\mathit{\theta },\mathit{\tau })={\gamma }_2{\sum }_{i=1}^n{k}^2({\mathbf{z}}_i,\mathit{\tau }){\mathbf{f}}_{\mathit{\theta }}(x_i,\mathit{\theta }){\mathbf{f}}_{\mathit{\theta }}^t(x_i,\mathit{\theta })$, where γ₂ = Eψ′ (ε)(≠ 0), k(z_i, τ) = 1/σ (z_i, τ), and f_θ (x, θ) = (∂/∂θ) f (x, θ).

2. ${\mathbf{\Gamma }}_{31n}(\mathit{\theta },\mathit{\tau })={\sigma }_{\psi 1}^2{\sum }_{i=1}^n{k}^2({\mathbf{z}}_i,\mathit{\tau }){\mathbf{f}}_{\mathit{\theta }}(x_i,\mathit{\theta }){\mathbf{f}}_{\mathit{\theta }}^t(x_i,\mathit{\theta })$, where ${\sigma }_{\psi 1}^2=E{\psi }^2(\epsilon )(<\infty )$.

3. ${\mathbf{\Gamma }}_{33n}(\mathit{\theta })={\sigma }_{\psi 3}^2{\sum }_{i=1}^k{n}_i{w}_1(x_i){\mathbf{f}}_{\mathit{\theta }}(x_i,\mathit{\theta }){\mathbf{f}}_{\mathit{\theta }}^t(x_i,\mathit{\theta })$, where ${\sigma }_{\psi 3}^2{w}_1(x)=E{\psi }^2(\sigma (\mathbf{z},\mathit{\tau })\epsilon )(<\infty )$.

4. ${\mathbf{\Gamma }}_{4n}(\mathit{\theta })={\gamma }_4{\sum }_{i=1}^k{n}_i{\mathbf{f}}_{\mathit{\theta }}(x_i,\mathit{\theta }){\mathbf{f}}_{\mathit{\theta }}^t(x_i,\mathit{\theta })$, where γ₄ = Eψ′ (σ (z, τ)ε)(≠ 0).

APPENDIX B: PROOFS OF THEOREMS

Proof of Theorem 1

(a) It is enough to show that the distribution of L^WLSE under H₀ is approximately central F-distribution with (3, n − 6) degrees of freedom. To begin with we assume τ₁(≠ 0) is known. Let $y_{\mathit{ij}}^{\ast }=y_{\mathit{ij}}/\exp ({\tau }_1{x}_i)$, g(x_i, θ) = f (x_i, θ)/exp(τ₁ x_i) and σ₀ = exp(τ₀). Then, the nonlinear regression model (2) can be expressed by $y_{\mathit{ij}}^{\ast }=g(x_i,\mathit{\theta })+{\sigma }_0{\epsilon }_{\mathit{ij}}$. Then, $L_1^{\ast }={\sum }_{i,j}{(y_{\mathit{ij}}^{\ast }-g(x_i,\widehat{\mathit{\theta }}))}^2={\mathit{\eta }}_1^t({\mathbf{I}}_n-{\mathbf{H}}^{\ast }){\mathit{\eta }}_1+o_P(1)$, where η₁ = Y* − g(θ), ${\mathbf{Y}}^{\ast }={(y_{11}^{\ast },\dots ,y_{k,n_k}^{\ast })}^t$, g(θ) = (g(x₁, θ), …, g(x_k, θ))^t (n × 1 vector), H* = G(G^tG)⁻¹G^t and G = g_θ(θ) = {∂g(x_i, θ)/∂θ_j}. Under H₀ in (3) the above regression model is replaced by $y_{\mathit{ij}}^{\ast }=\beta d_i+{\sigma }_0{\epsilon }_{\mathit{ij}}$, where d_i = 1/exp(τ₁ x_i). Then, $L_0^{\ast }={\sum }_{i,j}{(y_{\mathit{ij}}^{\ast }-\widehat{\beta }{d}_i)}^2={\mathit{\eta }}_0^t({\mathbf{I}}_n-{\mathbf{G}}^0){\mathit{\eta }}_0$, where $\widehat{\beta }={\sum }_{i,j}{d}_i{y}_{\mathit{ij}}^{\ast }/{\sum }_{i,j}{n}_i{d}_i^2$, η₀ = Y* − Dβ, D = (d₁, …, d_k)^t (n × 1 vector) and G⁰ = D(D^t D)⁻¹ D^t. If we apply the standard theory of the LRT in nonlinear regression models, under H₀ $L^{\ast }=\{(L_0^{\ast }-L_1^{\ast })/3\}/\{L_1^{\ast }/(n-6)\}$ is approximately following the central F-distribution with (3, n − 6) degrees of freedom.

Since τ₁ is unknown we replace it by its estimator τ̂_1n. Noting that τ̂_1n = τ₁ + o_P (1) and hence exp(τ̂_1n x_i) = exp(τ₁x_i) + o_P (1), we therefore have $L_1=L_1^{\ast }+o_P(1)$ and $L_0=L_0^{\ast }+o_P(1)$. Consequently, L^WLSE = L* + o_P (1). Therefore, under the null hypothesis H₀, L^WLSE is approximately distributed as central F-distribution with (3, n − 6) degrees of freedom.

(b) We show that the Type I error for the test statistic L^PT is bounded by α₁ in the following equation. Here the independence between T_n and (L^WME, L^OME) is needed, which can be deduced from the asymptotic joint normality of (θ̃, θ̂, τ̂_1n) (Theorem 2, Lim et al. 2012).

$$\begin{array}{l}P(L^{\mathrm{PT}}>f_{{\alpha }_1,3,n-6}\mid H_0)\\ =P(L^{\mathrm{WME}}>f_{{\alpha }_1,3,n-6},|T_n|>t_{\alpha /2,n-2}\mid H_0)+P(L^{\mathrm{OME}}>f_{{\alpha }_1,3,n-6},|T_n|\le t_{\alpha /2,n-2}\mid H_0)\\ =P(L^{\mathrm{WME}}>f_{{\alpha }_1,3,n-6}\mid H_0)P(|T_n|>t_{\alpha /2,n-2}\mid H_0)+P(L^{\mathrm{OME}}>f_{{\alpha }_1,3,n-6}\mid H_0)P(|T_n|\le t_{\alpha /2,n-2}\mid H_0)\\ \le P(L^{\mathrm{WME}}>f_{{\alpha }_1,3,n-6}\mid H_0)P(|T_n|>t_{\alpha /2,n-2}\mid H_0)+P(L^{\mathrm{OME}}>f_{{\alpha }_1,3,n-4}\mid H_0)P(|T_n|\le t_{\alpha /2,n-2}\mid H_0)\\ ={\alpha }_1.\end{array}$$

Proof of Theorem 2

For i = 1, …, 4, from the independence between T_n and (θ̃, θ̂) (Theorem 2, Lim et al. 2012),

$$\begin{array}{l}P\left(\frac{|{\widehat{\theta }}_i^{\mathit{PT}}-{\theta }_i|}{\mathit{SE}({\widehat{\theta }}_i^{\mathit{PT}})}\le c_{{\alpha }_1}\right)\\ =P(|{\widehat{\theta }}_i-{\theta }_i|\le c_{{\alpha }_1}\mathit{SE}({\widehat{\theta }}_i^{\mathit{PT}}),|T_n|>t_{\alpha /2,n-2})+P(|{\stackrel{\sim }{\theta }}_i-{\theta }_i|\le c_{{\alpha }_1}\mathit{SE}({\widehat{\theta }}_i^{\mathit{PT}}),|T_n|\le t_{\alpha /2,n-2})\\ =(1-{\alpha }^{\ast })P(|{\widehat{\theta }}_i-{\theta }_i|\le c_{{\alpha }_1}\mathit{SE}({\widehat{\theta }}_i^{\mathit{PT}}))+{\alpha }^{\ast }P(|{\stackrel{\sim }{\theta }}_i-{\theta }_i|\le c_{{\alpha }_1}\mathit{SE}({\widehat{\theta }}_i^{\mathit{PT}}))\\ =(1-{\alpha }^{\ast })P\left(|U|\le c_{{\alpha }_1}\frac{\mathit{SE}({\widehat{\theta }}_i^{\mathit{PT}})}{\mathit{SE}({\widehat{\theta }}_i)}\right)+{\alpha }^{\ast }P\left(|V|\le c_{{\alpha }_1}\frac{\mathit{SE}({\widehat{\theta }}_i^{\mathit{PT}})}{\mathit{SE}({\stackrel{\sim }{\theta }}_i)}\right)\\ \ge (1-{\alpha }^{\ast })P\left(|U|\le c_{{\alpha }_1}\frac{\mathit{SE}({\widehat{\theta }}_i^{\mathit{PT}})}{\max \{\mathit{SE}({\stackrel{\sim }{\theta }}_i),\mathit{SE}({\widehat{\theta }}_i)\}}\right)+{\alpha }^{\ast }P\left(|V|\le c_{{\alpha }_1}\frac{\mathit{SE}({\widehat{\theta }}_i^{\mathit{PT}})}{\max \{\mathit{SE}({\stackrel{\sim }{\theta }}_i),\mathit{SE}({\widehat{\theta }}_i)\}}\right)\\ =(1-{\alpha }^{\ast })P\left(|U|\le t_{{\alpha }_1/2,n-6}\right)+{\alpha }^{\ast }P(|V|\le t_{{\alpha }_1/2,n-6})\\ \ge (1-{\alpha }^{\ast })P(|U|\le t_{{\alpha }_1/2,n-6})+{\alpha }^{\ast }P(|V|\le t_{{\alpha }_1/2,n-4})=1-{\alpha }_1,\end{array}$$

where U and V are random variables following t-distributions with n − 6 degrees of freedom and n − 4 degrees of freedom, respectively.