Abstract
Objective
Local field potentials (LFPs) that carry information about the subject’s motor intention have the potential to serve as a complement or alternative to spike signals for brain-machine interfaces (BMIs). The goal of this study is to assess the utility of LFPs for BMIs by characterizing the largely unknown information coding properties of multichannel LFPs.
Approach
Two monkeys were implanted, each with a 16-channel electrode array, in the parietal reach region (PRR) where both LFPs and spikes are known to encode the subject’s intended reach target. We examined how multichannel LFPs recorded during a reach task jointly carry reach target information, and compared the LFP performance to simultaneously recorded multichannel spikes.
Main Results
LFPs yielded a higher number of channels that were informative about reach targets than spikes. Single channel LFPs provided more accurate target information than single channel spikes. However, LFPs showed significantly larger signal and noise correlations across channels than spikes. Reach target decoders performed worse when using multichannel LFPs than multichannel spikes. The underperformance of multichannel LFPs was mostly due to their larger noise correlation because noise de-correlated multichannel LFPs produced a decoding accuracy comparable to multichannel spikes. Despite the high noise correlation, decoders using LFPs in addition to spikes outperformed decoders using only spikes.
Significance
These results demonstrate that multichannel LFPs could effectively complement spikes for BMI applications by yielding more informative channels. The utility of multichannel LFPs may be further augmented if their high noise correlation can be taken into account by decoders.
Keywords: LFPs, BMIs, information redundancy, noise correlation
INTRODUCTION
An electrical signal sensed by a microelectrode inserted in the extracellular matrix of the cortex is typically decomposed into action potentials and local field potentials (LFPs). The action potential signal, often referred to as spikes, is generated by a few neurons near the tip of the electrode. The LFP is a low-pass filtered signal, cut off at 300 Hz or less, and largely reflects the sum of slow local synaptic currents in thousands of neurons surrounding the electrode tip (Mitzdorf, 1985; Poulet and Petersen, 2008). Both spikes and LFPs can carry important information about movements such as reach target location, hand kinematics, hand grasp type, reach onset time, and electromyograms (EMGs) of arm muscles (Mehring et al., 2003; Rickert et al., 2005; Scherberger et al., 2005; Heldman et al., 2006; Asher et al., 2007; Spinks et al., 2008; Hwang and Andersen, 2009; Bansal et al., 2011; Flint et al., 2012). Thus, both types of neural signals can potentially serve as command signals to control motor effectors (e.g., computer cursors, robot arms, paralyzed arms, etc.) in brain-machine interface (BMI) systems.
Most chronic BMIs implemented so far relied on spikes to decode the subject’s intended movements (Carmena et al., 2003; Musallam et al., 2004; Collinger et al., 2012; Ethier et al., 2012; Gilja et al., 2012; Hochberg et al., 2012). One serious challenge encountered by those chronic BMIs is that spike signals disappeared in many electrodes within a few months (Polikov et al., 2005; Simeral et al., 2011). Probable causes are neuro-degeneration following post-surgical glial scar formation near the electrodes, changes of the electrode location by uncontrolled physical perturbations including cardiac and respiratory pulsations, mechanical movement of the subject, and migration of neural tissue (Santhanam et al., 2007; Dickey et al., 2009; McConnell et al., 2009).
In this light, LFPs may be a reliable complement or alternative to spikes for chronic BMIs because compared to spikes, they are less likely affected by glial scarring or electrode location changes (Frien and Eckhorn, 2000; Leopold and Logothetis, 2003; O’Leary and Hatsopoulos, 2006; Stark and Abeles, 2007; Berens et al., 2008; Jia et al., 2011). The low electrode location sensitivity of LFPs, however, may pose a limitation on their utility for BMIs if multichannel LFPs recorded from different physical sites encode highly redundant information. The information redundancy in any neural population depends on the structure of noise and signal correlations between individual channels (Johnson, 1980; Zohary et al., 1994; Abbott and Dayan, 1999; Andersen et al., 2004; Averbeck et al., 2006; Quian Quiroga and Panzeri, 2009). Here, the noise correlation refers to the similarity between the trial-to-trial deviations from their respective average responses, whereas the signal correlation refers to the similarity in the mean responses across different stimuli or outputs. In general, information redundancy is larger when both signal and noise correlations are significant and in the same direction than when they are in the opposite directions or insignificant (Averbeck et al., 2006; Achtman et al., 2007; Quian Quiroga and Panzeri, 2009). For multichannel LFPs, only overall correlations (i.e., a combined measure of both signal and noise correlations) have been reported, and signal and noise correlations have not been examined separately (Destexhe et al., 1999; Mehring et al., 2003; Bansal et al., 2011; Eggermont et al., 2011).
Some studies directly assessed the utility of multichannel LFPs by decoding movement related parameters from multichannel LFPs and spikes and comparing the two decoding performances (Mehring et al., 2003; Bansal et al., 2011; Flint et al., 2012). The comparison results are inconsistent among studies, which is difficult to reconcile without knowing the underlying signal and noise correlations. Therefore, in this study, we measured signal and noise correlations across multichannel LFPs recorded in the macaque parietal reach region in which both LFPs and spikes were known to carry the subject’s intended reach target information (Snyder et al., 1997; Scherberger et al., 2005; Hwang et al., 2012). In addition, to assess the impact of these correlations on the utility of multichannel LFPs for BMIs, we examined the amount of reach target information that can be decoded from multichannel LFPs in comparison to spikes.
METHODS
Two male rhesus monkeys (Macaca Mulatta, Y and G) participated in this study. The California Institute of Technology Institutional Animal Care and Use Committee approved the animal procedures used in this study, which were performed in accordance with NIH guidelines.
Behavioral experiment setup
The monkeys sat in a primate chair and viewed visual stimuli presented on a vertical LCD monitor placed in the fronto-parallel plane, ~40 cm away from the eyes. Eye position was recorded with an infrared eye tracker (240 Hz; ISCAN, Burlington, MA) and hand position was recorded with a 19 inch translucent touch-sensitive screen (IntelliTouch; ELO Systems, Menlo Park, CA) placed in front of the LCD monitor. The visual stimulus presentation, online monitoring of eye and hand positions, and reward control were handled by a real-time LabView program running on a real-time operating system (National Instruments, LabView7.1 & LabView Real-Time).
Delayed reach task
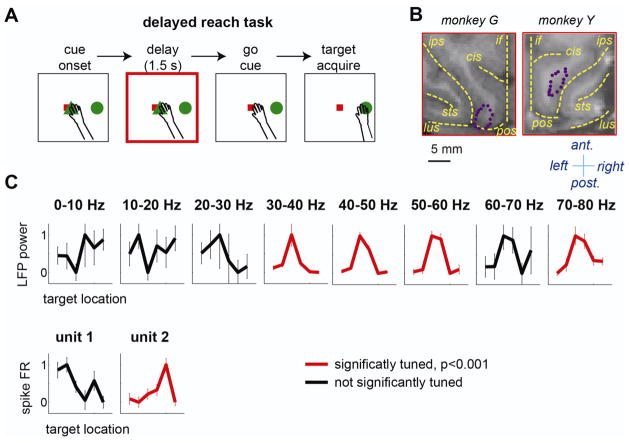
The monkeys began a trial by fixing their eyes on the eye-fixation target and touching the hand-fixation target in the screen center (Fig. 1A). After a 0.5 s fixation period, a green circle appeared in the periphery. After a delay period (1.5 ± 0.15 s), the hand-fixation target disappeared (go-cue), signaling the monkeys to reach to the green circle without moving their eyes. The monkeys were required to hold their hand within 3° from the green circle and their eyes on the fixation target for 0.3 s to receive a juice reward. Six target locations, evenly spaced around a virtual circle (10.3° eccentricity), were randomly interleaved. The monkeys made at least 11 successful trials per target location in each recording session, and completed 45 recording sessions (38 sessions by Y, 7 by G).
Figure 1.
A. Task sequence of the delayed reach task. The square and the triangle in the center represent the eye- and hand-fixation targets, respectively, and the circle in the periphery represents the reach target. B. The locations of 16 electrodes (purple dots) overlaid on the magnetic resonance image of each monkey’s brain. The yellow dashed lines indicate the intra-hemispheric fissure (if) and major sulci including the intra-parietal sulcus (ips), parieto-occipital sulcus (pos), lunate sulcus (lus), superior temporal sulcus (sts), and cingulate sulcus(cis). The anterior, posterior, left, and right directions are indicated. C. Tuning curves, the mean delay response for each of six target locations, of LFP and spike units recorded from the same electrode. The LFP power and spike firing rate (FR) in each tuning curve were normalized so that that the maximum is 1 and the minimum is 0. The error bars are the standard deviations.
Neural signal recording
The monkeys were implanted with a head holder and a recording chamber housing a 16-channel-movable-electrode array (Neuralynx, Bowsman, MT). We placed an array of 16 electrodes in PRR which covers the medial wall of the intraparietal sulcus (IPS) in monkey Y, and both the medial wall of IPS and the anterior wall of the parieto-occipital sulcus (POS) in monkey G (Fig. 1B). The electrode placement was guided by magnetic resonance images. The electrodes were spread over a 2×6.5 mm2 area of the dura for monkey Y and 3×5 mm2 for monkey G. Because each individual electrode was attached to its own dedicated screw-mechanism drive, the depth of each electrode was individually adjustable. To maximize the number of channels showing single unit activity, we moved the electrodes showing no discernible single units in the beginning of each session, up to 1 mm from the depth of the previous session or until clear single unit activity emerged, whichever occurred first. A commercial 16-channel neural signal recording system (Plexon MAP, Dallas, TX) was used to record and store neural signals. LFPs and spikes were separated by hardware bandpass filters in a preamplifier (LFP: 3.3–88 Hz and spike: 154 Hz – 8.8 kHz). To minimize potential contamination by the power line noise, LFP signals were filtered using a second-order notch filter with the center frequency at 60 Hz and the bandwidth of 0.6 Hz. In this study, each of the 16 channels corresponds to each of the 16 different electrodes. In some sessions, only 15 channels were functional because of faulty electrical connections.
Spike signal processing
For each channel, up to four spike units were isolated offline using a commercially available software package (Plexon Offline Sorter; T distributed expectation-maximization methods). The validity of the automatic isolation was checked by subsequent visual inspection. Each spike waveform was recorded as a 32-time-point vector (0.8 ms long). For each time point, we computed the mean and standard deviation of the amplitude. The signal-to-noise ratio (SNR) of a spike unit was defined as the ratio of the trough-to-peak amplitude of the mean waveform to twice the standard deviation averaged across the 32 points. Those with a SNR greater than 1.5 were included for analysis. By this criterion, both single unit (the spike signal of a single neuron) and multi-units (the compound spike signals of multiple indiscriminant neurons) were included. For each isolated spike unit, we counted its number of occurrences during the last 1 s of the delay period in each trial. These spike counts were used for all spike signal analyses in this study.
LFP processing
LFPs in PRR are known to carry reach target information via power modulation in various frequency bands(Scherberger et al., 2005). Thus, we transformed the time-domain LFP traces in the last 1 s delay period of each trial into frequency-domain power spectra using a multi-taper method (bandwidth = 5 Hz) (Pesaran et al., 2002). In this transformation, the single one second window was used for all frequencies. Since LFPs in different frequency bands often carry different information (Hwang and Andersen, 2011), each spectrum was converted to a 8×1 vector consisting of the average log-transformed powers in 8 frequency bands, 0–10 Hz, 10–20 Hz, …, 70–80 Hz. The 8 LFP powers were used for the main LFP signal analyses in this study.
Tuning analysis
Because the current study aimed to assess the extent to which LFP and spike signals in PRR are informative about the intended reach target, we examined the modulation of the neural signals as a function of the reach target, i.e., the reach target tuning (Fig. 1C). To determine the significance of the target tuning of a spike unit, we applied an ANOVA test on the spike count data, with the reach target as the single factor. If the significance level p<0.001 was satisfied, we rejected the null hypothesis that the mean spike counts were statistically equal across 6 targets. In other words, if the mean spike count for at least one target was significantly different from the others, the spike unit was considered to be significantly tuned to the reach target. Similarly, we applied the ANOVA test to the LFP power in each of the 8 frequency bands. If any frequency band met the signifance level p<0.001, the LFP channel was considered to be significantly tuned.
As noted above, the ANOVA test indicates whether or not the means of a neural signal differed for at least one target. To estimate how many reach targets each tuned LFP or spike unit could discriminate, we performed a 6-target decoding analysis described in the later section of the Methods. If a majority of the reach trials associated with a specific target was correctly decoded, we considered that the neural signal could discriminate that specific target. The number of targets that satisfied this condition was counted for each tuned neural signal as a measure to the number of targets that affected the neural signal.
Signal and noise correlations
For any two neural signals, the signal correlation was measured as the Pearson’s correlation coefficient between their tuning curves (Rickert et al., 2005). The tuning curve was a six-element vector with each element being the mean response for each of the six targets. To measure the noise correlation, we computed the response deviation of each trial from the mean response for the corresponding target. Then, we computed the Pearson’s correlation coefficient between the trial-by-trial deviations of the two signals (Zohary et al., 1994; Rickert et al., 2005).
All statistical test involving the correlation coefficients were applied to the z values after transforming the correlation coefficients through the Fisher transformation.
Offline reach target decoding algorithm
We used maximum likelihood decoders (Salinas and Abbott, 1994; Scherberger et al., 2005). The decoder input was a vector comprising the spike counts and/or the LFP powers. Thus, for N spike units and M LFP channels, the size of the input vector was N, 8 · M, or N + 8 · M depending on the input signal. The dimensionality of the input vector was reduced by selecting only those vector elements with significant reach target tuning based on the ANOVA test described earlier. If no element was significantly tuned, the element with the smallest p-value from the ANOVA test was selected. The decoder output was one of the six targets. In the maximum likelihood decoders, we used the following assumptions due to insufficient knowledge of the statistical properties of input vectors (Hwang and Andersen, 2012): 1) the prior probability across the six targets is uniform, 2) the conditional probability distribution of each input signal (i.e., spike count or LFP power) on any given target is normal, 3) the covariance of the normal distributions are the same across the six targets and only the means differ, and 4) the input signals are independent (i.e., the covariance matrix is diagonal). The last assumption was made because the sample size (the number of trials) in our study was too small in relation to the large dimensionality of the input signal to estimate a robust inverse of the covariance matrix although this assumption is invalid for multichannel LFPs as will be shown and described in the Results and Discussion. For the input signal of a given test trial, the log-likelihood that the signal was associated with each target was computed using the conditional probability function on each target that was estimated from the training data. Then the target associated with the maximum log-likelihood was selected as the decoder output. A decoder output was computed for every trial using all the other trials as training data. The decoding accuracy was computed as the proportion of the trials for which the decoder output was the actual reach target.
Neuron/LFP-channel dropping curves
In order to estimate how each additional signal source contributes to improving the reach target decoding accuracy, we computed neuron dropping curves and LFP-channel dropping curves (Wessberg et al., 2000). The neuron dropping curve represents the average six-target decoding accuracy as a function of the number of spike units or spike channels that were availble for decoding. Likewise, the LFP-channel dropping curve represents the average six-target decoding accuracy as a function of the number of LFP channels that were available for decoding. To estimate the average decoding performance for any number of channels N, the decoding accuracy was computed using 100 randomly selected combinations of N simultaneously recorded channels.
Trial shuffled multichannel LFPs
To examine the effect of noise correlations in LFPs on the decoding accuracy, we applied the same LFP-channel dropping curve analysis described above, using trial-shuffled signals in which LFPs from each channel were randomly shuffled among the same target trials.
Sequential multichannel LFPs
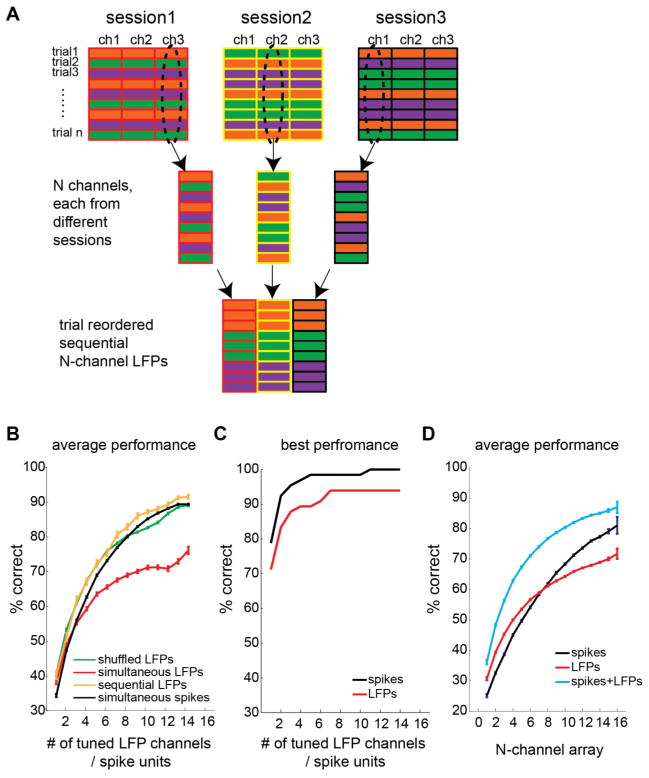
To compare the decoding accuracy between simultaneously recorded multichannel LFPs and sequentially recorded multichannel LFPs, we constructed sequential multichannel LFPs by combining LFP channels, each randomly selected from different recording sessions. To compute the decoding accuracy for sequential N-channel LFPs, we took the average decoding accuracy across 100 randomly selected combinations of N LFP channels, each from different recording sessions. Suppose we recorded 3 separate sessions, each with 3 LFP channels (Fig. 4A). An example of sequentially recorded 3-channel LFPs can be constructed using a combination of LFP channel 3 in session 1, channel 2 in session 2, and channel 1 in session 3. Then, trials in each selected LFP channel were reordered in such a way that the selected channels were combined with the same reach target sequence.
Figure 4.
A. The construction procedure for sequential multichannel LFPs. Each column represents a single channel. Each row represents a single trial. Different filling colors indicate different reach targets. A set of channels is selected from different sessions, and the trial sequences are reordered such that the selected channels have the same target sequence. B. The average decoding performance for each number of tuned LFP channels or tuned spike units, for the simultaneously recoded data, trial-shuffled data, and sequentially recorded data. C. The best decoding performance for each number of simultaneously tuned LFP channels or spike units. D. The average decoding performance for each number of simultaneously recorded electrodes, when using spike units, LFPs, and both signals. The error bars indicate the standard errors of means.
Data from the two monkeys are qualitatively similar, and thus we combined data from the two monkeys in the current paper unless specified otherwise.
RESULTS
Single channel LFPs provide more robust target information than single channel spikes
We first examined how LFPs and spikes encoded the reach target information at the single channel level. Figure 1C shows the tuning curves (i.e., the mean signal modulation as a function of the reach target) of a LFP and two spike signals recorded from the same electrode. The tuning curves of the LFP were computed separately for each of 8 frequency bands because different frequency bands could encode information in different ways (Rickert et al., 2005; Belitski et al., 2008; Hwang and Andersen, 2011; Hwang and Andersen, 2012). Consistent with our previous report (Hwang and Andersen, 2011), in the example channel, the delay period LFP in gamma bands (>40 Hz) was significantly tuned to the visible reach target (ANOVA, p<0.001). The delay period spike count of one spike unit was also significantly tuned to the reach target (ANOVA, p<0.001). Sixty-eight percent of all LFP channels recorded in this experiment showed significant target tuning in at least one frequency band. The most prevalently tuned frequency band was the 50–60 Hz band in which 57% of all channels showed significant target tuning. In contrast, only 34% of all recorded channels contained at least one spike unit with significant target tuning. More specifically, 58% of all recorded channels contained distinguishable single or multi spike units and among those channels, 58% contained at least one unit that was significantly tuned.
Next, to compare the quality of target tuning between single channel LFPs and single channel spikes, we performed reach target decoding analyses using each signal separately (Methods). When decoding six reach targets from any single channel LFP that was significantly tuned to the reach target, the mean decoding accuracy was 39±11.1%. The mean accuracy using any single significantly tuned spike unit was 34±10.4%. The difference was significant (Wilcoxon rank-sum test, p<0.001).
The two neural signals also differed in terms of the number of targets that they could discriminate (Methods). The single channel LFP shown in Figure 2A discriminated 4 targets. Notice the 4 bright diagonal elements, which indicates that a majority of the trials associated each of the 4 discriminable targets was decoded correctly. Of all tuned single channel LFPs, 43% could discriminate 4 or more targets, whereas only 20% of all tuned single spike units could discriminate 4 or more targets (Fig. 2B).
Figure 2.
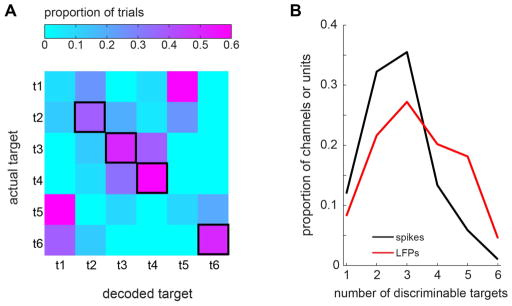
A. An example LFP channel which discriminated 4 reach targets. The matrix represents the 6-target decoding result from the example LFP channel. The color of each square represents the proportion of the trials for which the actual target corresponds to the row number and the decoded target corresponds to the column number. Each row is normalized such that the sum across the columns of each row is 1. The four squares with thick black borders indicate that a majority of trials in their corresponding row is decoded correctly, i.e., the actual target in each of those rows is discriminable. B. The distribution of the number of discriminable reach targets by single tuned LFPs or spike units.
Both signal and noise correlations are larger between LFP channels than between spike units
The single channel analysis results above appear to support the view that LFPs can serve as an alternative to spikes for BMI applications. However, to extract quality information for BMI control, it is necessary to pool signals from multiple channels (sites), and the amount of information in multichannel neural signals is not a simple sum of information carried by individual channels but depends on signal and noise correlations between channels (Johnson 1983; Zohary 1998; Bialek 2003). Thus, despite more target information at the single channel level, multichannel LFPs could be less efficient than multichannel spikes depending on their signal and noise correlations. We therefore characterized correlations between LFP channels in comparison to those between spike units.
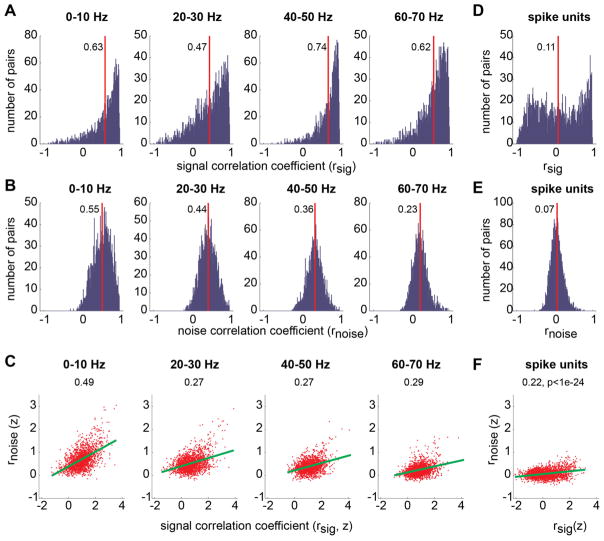
To systematically characterize correlations in multichannel LFPs, we computed their signal and noise correlations, separately as described in the Methods. The signal correlation coefficient measured the similarity between the tuning curves of two neural signals, whereas the noise correlation coefficient measured the similarity between the trial-to-trial deviations from their respective average responses. The correlation analysis was performed between all pairs of LFP channels that were simultaneously recorded and significantly tuned to the reach target (N=2025 pairs, 1539 for Y & 486 for G). We found that both the signal and noise correlation coefficients have significantly positive mean values in all frequency bands (t-test on Fisher’s z values, p<0.001; Fig. 3A–B). For instance, in the 40–50 Hz band, the mean signal and noise correlation coefficients between different LFP channels were 0.74 and 0.36, respectively. The mean noise correlation showed a small but significant decrease as the frequency increased (slope=−0.008, p<0.001). Furthermore, in all frequency bands, channel pairs with a strongly positive signal correlation coefficient tended to have a strongly positive noise correlation coefficient as well. The correlation coefficients between the noise and signal correlations range 0.29~0.49 and are significant (Spearman’s rank correlation, the significance levels were too small to measure; Fig. 4C), suggesting that multichannel LFPs in PRR carry the reach target information in a highly redundant manner (Averbeck et al., 2006; Achtman et al., 2007; Quian Quiroga and Panzeri, 2009).
Figure 3.
A. The histogram of signal correlations between all pairs of LFP channels (N=2025) were simultaneously recorded. LFP correlations were computed separately for each of the 8 frequency bands (only 4 bands are shown). The red line and the abutting number indicate the mean of the distribution. B. The histogram of LFP noise correlations. C. Signal correlation versus noise correlation. Each dot represents an individual LFP pair. The correlation coefficients are z-transformed. The green lines represent the linear regression. Spearman’s correlation between the two correlations is marked on the top of each plot. The significance level was virtually zero. D–F. The same as A–C but for all pairs of spike units (N=2243).
For comparison, we performed the same correlation analysis on all pairs of spike units that were simultaneously recorded and significantly tuned (N=2243 pairs, 2040 for Y & 203 for G). The mean signal and noise correlation coefficients between tuned spike units were 0.11 and 0.07, respectively, significantly smaller than those between tuned LFP pairs in all frequency bands (two-sample t-test, p<0.001; Fig. 2D–F). The higher signal and noise correlations between LFP channels than between spike units suggest that multichannel LFPs would encode target information in a more redundant manner than multichannel spikes.
Information gain by additional signal source is smaller for LFPs than spikes
Although we could decode the target information more accurately from single channel LFPs than single channel spike signals, the higher redundancy across multichannel LFPs than spike signals predicts that information gain by additional channels would be smaller for LFPs than spikes. To test this prediction, we decoded the reach target information from multichannel LFPs and multichannel spikes, and compared the decoding accuracy between the two types of neural signals. The LFP-channel and neuron dropping curves in Figure 4B represent the average target decoding accuracy as a function of the number of tuned LFP channels and tuned spike units, respectively. Because the purpose of the analysis was to compare information gain by additional signal sources that were informative on the reach target, we used only tuned neural signals in this analysis (see following sections for analysis regardless of tuning significance). Consistent with our prediction, the LFP-channel dropping curve fell below the neuron dropping curve for all numbers of channels/units greater than 3 although the LFP curve started off higher initially (Fig. 4B). In other words, the decoding accuracy from single LFP channels was higher than that from single spike units as described earlier, but decoding accuracy by incorporating additional channels increased more slowly for LFPs than spikes. For instance, the number of LFP channels required to achieve 70% accuracy was 9, whereas the number of spike units was 6. Therefore, the pool of LFPs is less efficient in providing the reach target information than the pool of spikes.
One may be interested in seeing the best possible, instead of the average, decoding performance. Figure 4B shows the best performance that can be achieved by each number of tuned neural signals. Multichannel spikes outperformed multichannel LFPs also in the best performance comparison. For spikes, the perfect decoding performance could be achieved using only 11 best units. For LFPs, the decoding performance reached 94% correct with 7 best channels.
The high noise correlation of multichannel LFPs contributes to information redundancy
In order to determine how much the noise correlation was responsible for the decreased efficiency of multichannel LFPs versus multichannel spike signals, we removed noise correlations in multichannel LFPs and computed an LFP-channel dropping curve. We constructed noise de-correlated multichannel LFPs by combining different LFP channels, each recorded in different sessions (Fig. 4A). These sequentially recorded multichannel LFPs produced decoding performance that was not significantly different from multiple spikes at any number of channels/units (Wilcoxon rank-sum test, p>0.1; Fig. 4B), suggesting that the high noise correlation between LFP channels rather than the high signal correlation is primarily responsible for the lower efficiency of multichannel LFPs compared to spikes. If indeed noise de-correlation effectively boosted decoding accuracy for the sequential LFPs, noise de-correlation of data within each session through a random shuffling among the same target trials would also result in a decoding accuracy boost. Consistent with this prediction, the trial-shuffled LFPs produced a decoding accuracy as good as the sequential LFPs (Fig. 4B).
Multichannel LFPs effectively complement spikes for reach target decoding
Although the simultaneous multichannel LFPs carried highly redundant information about the reach target, the target decoding accuracy monotonically increased with the number of tuned LFP channels, reaching up to approximately 75% for a six-target discrimination when using 14 tuned channels (Fig. 4B). The performance enhancement by adding each additional channel continued to be significant up to 6 channels (Wilcoxon rank-sum test on adjacent numbers of channels, p<0.001). After that, more than one additional channel was required to gain a significant improvement in the decoding accuracy. Thus, different LFP channels provide, though limited, non-redundant information regarding the intended reach target. Furthermore, multichannel LFPs are more efficient in the yield of tuned channels than spikes as shown earlier. Across all 45 recording sessions, the number of channels with tuned LFPs in each session was 10.8±3.23 (mean±s.d.) whereas the number of channels with tuned spike units was 5.3±2.07. These correspond to 69±21.5 and 34±13.6% of all channels. It was not necessary to record a tuned spike signal at the same electrode in order to record a tuned LFP. Nor was it necessary to record distinct action potentials. LFPs were tuned in 71% of the channels with untuned spike units, and in 47% of the channels without action potentials. These observations predict that multichannel LFPs, despite their high information redundancy, could play an effective complementary role to spikes for BMIs (Hwang and Andersen, 2010).
To test this prediction, we computed decoding performance from LFPs alone, spikes alone, and both LFPs and spikes. Unlike the LFP-channel and neuron dropping curves in the previous analysis, this analysis included all N channels, regardless of their significance of target tuning, in order to estimate the average decoding performance expected when N electrodes were implanted at random locations in PRR. Thus, this analysis took into account both the redundancy and the yield of tuned signals. The decoding accuracy using LFPs was better than or as good as the accuracy from spike signals up to 8 channels (Fig. 4D). Even after 8, the performance difference between the two signals was not as large as the previous analysis because the higher yield of tuned signals for LFPs compensates for the less efficient information decoding from multichannel LFPs than spikes. More importantly, decoding performance using both signals was higher than that using either signal alone. For instance, decoding accuracy using 8 channels was 77±0.2 (mean±s.e.m.), 62±0.3, and 61±0.2% respectively for both signals, spikes only, and LFPs only. All combinatorial comparisons showed significant differences (Wilcoxon rank-sum test, p<0.001). These results clearly demonstrate that multichannel LFPs can efficiently complement spikes when decoding the subject’s intended reach target.
Signal and noise correlations between LFP channels decrease with the physical distance
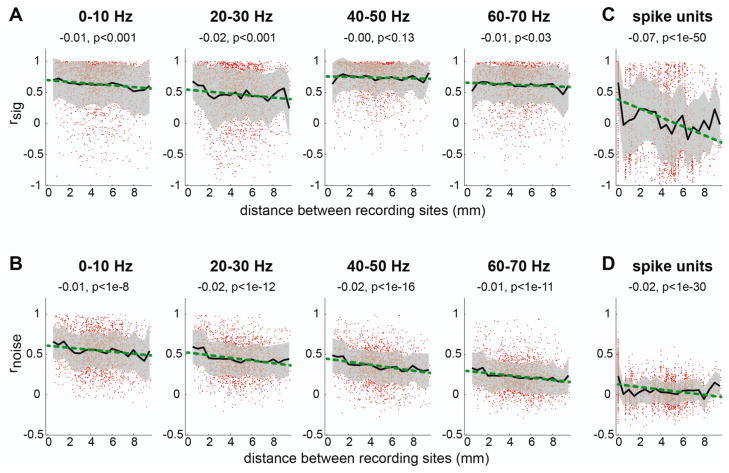
So far, we dealt with only the mean signal and noise correlations of LFPs and spike signals across all possible pairs. However, the physical distance between a pair was not constant and varied between 0.5 and 10 mm. Thus we examined the effect of distance on the correlations. Figure 5 shows the signal and noise correlation coefficients as a function of the distance between recording channels. For LFPs, we found that the slope of the linear regression was significantly negative for frequency bands below 40 Hz (p<0.001) but not in the more informative frequency bands (i.e., 40–60 Hz) (Fig. 5A). On the other hand, the noise correlation decreased with the distance between recording channels in all frequency bands (Fig. 5B).
Figure 5.
A. The signal correlation as a function of the distance between LFP channels. Each dot represents a single LFP site. The black line indicates the mean correlation coefficient for a given distance and the gray band indicates the standard deviation. The green line shows the linear regression on the distance and correlation coefficient. The slope of the linear regression and the significance level of the slope are indicated on the top of each plot. B. The same as A but for the noise correlation. C–D. The same as A–B but for spikes.
Compared to LFPs, the spike signal and noise correlations decreased at a much faster rate (Fig. 5C–D). The correlation coefficient for the distance of 0 was computed between pairs of spike units recorded at the same electrode. Notably, when the spike units recorded at the same electrode were excluded from the analysis, the mean signal and noise correlation coefficients were 0.03 and 0.03, respectively and neither was significantly different from 0 (t-test on Fisher’s z values; P>0.05; Fig. 5C). In addition, the regression slope became insignificant for both signal and noise correlations (p>0.05). Thus, pairs of spike units recorded from different sites in PRR are not significantly correlated, at least for the distance beyond the distance of 0.5 mm.
DISCUSSION
The current study, for the first time to our knowledge, measured noise and signal correlations between LFP channels. Both noise and signal correlations between LFP channels in PRR were significantly larger than those between spikes. To examine how these correlations impact their utility for BMI applications, decoding analyses were performed. We found that the target information decoded from multichannel signals was less accurate for LFPs than spikes. The underperformance of multichannel LFPs was mostly due to their larger noise correlation because noise de-correlated multichannel LFPs (sequentially recorded and shuffled LFPs) produced a decoding accuracy comparable to multichannel spikes. In other words, noise correlation between LFP channels significantly influences the amount of information that one can decode from multichannel LFPs. The result also confirms the previous warning that decoding performance estimated from sequentially recorded data should be used with caution (Quian Quiroga and Panzeri, 2009).
Correlations in LFPs in other areas of the brain
How can we generalize this finding from PRR to other brain areas? In the frontal eye field (FEF), trial-shuffled (i.e., noise de-correlated) versus original multichannel LFPs did not yield different accuracy when decoding eye movement targets (Markowitz et al., 2011). This suggests that the multichannel LFPs in FEF may not show significant noise correlations between channels. In M1, reach target decoding performance was similar between simultaneous and sequential multichannel LFPs (Mehring et al., 2003). This result also suggests that the noise correlation of LFPs in the frontal cortex may not be as significant as in PRR. By comparison, signal correlations across multichannel LFPs seem to be significant in M1 because the overall correlations across multichannel LFPs in M1 are as large as in PRR (Basal et al., 2011; Mehring et al., 2003).
Several studies in M1 also compared the decoding accuracy acquired from multichannel LFPs versus spikes. The results are mixed. Reach target was more accurately decoded from multichannel LFPs than spikes (Mehring et al., 2003). Decoding performance for the EMG patterns of arm muscles during reach and grasp was comparable between LFPs and spikes (Flint et al., 2012). When decoding hand kinematics during reach and grasp, multichannel spikes outperformed multichannel LFPs (Bansal et al., 2011). Such mixed results could occur if signal and noise correlations across multichannel neural signals differ depending on the parameter defined as the signal, which remains to be shown.
LFP noise correlations and frequency
We found that noise correlation between channels decreased with LFP frequency. In other words, for a given distance between two channels, LFP noise correlation is smaller for higher than lower frequency. This trend is similar to previous observations regarding the overall correlation between LFP channels in cat cerebral cortices (Destexhe et al., 1999; Eggermont et al., 2011). The smaller spatial extent of higher frequency LFPs are not attributable to biophysical filtering properties of the extracellular space because the electrical conductance of the extracellular space is relatively constant across frequencies (Logothetis et al., 2007). Instead the spatial extent might be determined by the size of the oscillation generators and the nature of neural events underlying them. For instance, Jia et al. (2011) found that the spatial extent can vary even for the same frequency LFPs depending on the task condition. Regardless of the exact mechanisms, the smaller noise correlation in higher frequency bands is suggestive of less redundancy in higher frequency LFPs, calling for future investigations of LFPs in even higher frequency than the frequency bands currently examined.
Noise correlation in spikes
The mean noise correlation between spike units in PRR was 0.07±0.165, and significantly different from 0. However, this significant correlation was mainly driven by the noise correlations between spike units recorded at the same electrode because the mean noise correlation became statistically insignificant after excluding pairs of units recorded from the same electrode. The mean noise correlation in PRR is substantially smaller than that reported for area MT, but comparable to those reported for the dorsal medial superior temporal area (MSTd) and primary visual cortex (V1) (Zohary et al., 1994; Ecker et al., 2010; Gu et al., 2011). The low noise correlation in PRR after factoring out the reach target-dependent signal correlation is consistent with the idea that the reach target is the major common variable that drives the activity of neurons in this region (Hwang et al., 2013).
Higher signal and noise correlations across LFPs than spikes
The finding that LFPs show higher signal correlation than spikes is consistent with the previous observation that LFPs show less sensitivity to changes in recording location than spikes in the same region (Frien and Eckhorn, 2000; Leopold and Logothetis, 2003; O’Leary and Hatsopoulos, 2006; Berens et al., 2008). The different sensitivity may be explained by their distinct signal origins. LFPs resemble sub-threshold membrane potentials of nearby neurons which are highly correlated with one another even if their spikes are not correlated (Penttonen et al., 1998; Lampl et al., 1999; Poulet and Petersen, 2008). The high correlation of the membrane potentials is likely due to shared synaptic inputs (Shadlen and Newsome, 1998), while the uncorrelated spikes may be explained by non-linear transformations (e.g., threshold and saturation) that are sensitive to small specific differences in the excitatory synaptic inputs between neurons (Poo and Isaacson, 2009; Yu et al., 2009; Renart et al., 2010). Moreover, summing the membrane potentials of thousands of neurons will further reduce the LFP sensitivity to recording locations (Mitzdorf, 1985; Poulet and Petersen, 2008).
Until the current study, noise correlations in LFPs have not been studied. The higher noise correlation in LFPs than spikes may reflect common synaptic inputs or global neuromodulatory signals to the region that are not specific to reach targets, such as arousal and motivation. The influence of such global signals would persist in the sum of local currents.
Decoders incorporating noise correlations
The decoding performance from multichannel LFPs in our study should not be viewed as the best possible performance that one can achieve. We used one of the most simplistic decoders, which was a maximum likelihood decoder based on a multivariate Gaussian model with multiple assumptions (e.g., noise independence between different channels, the same variance between conditional distributions on different targets, etc.; see Methods). Given that our independence assumption was inconsistent with the true statistical property of LFP data, the maximum likelihood decoder would not produce the best decoding performance. Therefore, it is possible that decoders taking advantage of noise correlations might improve the decoding accuracy for simultaneous multichannel data with significant noise correlations (Abbott and Dayan, 1999; Averbeck et al., 2006). For instance, it was previously shown that support vector machine (SVM) decoders which implicitly captured the characteristics of noise correlations among spike units in the primary visual cortex produced a decoding accuracy that was significantly enhanced in comparison to decoders with independent noise models (Graf et al., 2011). However, we cannot test SVM decoders on the data in the current study because of the small number of trials. An intriguing future research direction is to test the possibility that decoding algorithms incorporating the noise structure can improve decoding performance from multichannel LFPs with significant noise correlations.
Acknowledgments
This work was supported by NIH grant EY013337 and DARPA award N66001-10-C-2009. EJH was supported by NIH Career Development Award K99 NS062894. We thank Spencer Kellis, Arnulf Graf, Boris Revechkis, and Bardia Behabadi for scientific discussion, Tessa Yao for editorial assistance, Kelsie Pejsa for animal care, and Viktor Shcherbatyuk for technical assistance.
References
- Abbott LF, Dayan P. The effect of correlated variability on the accuracy of a population code. Neural Comput. 1999;11:91–101. doi: 10.1162/089976699300016827. [DOI] [PubMed] [Google Scholar]
- Achtman N, Afshar A, Santhanam G, Yu BM, Ryu SI, Shenoy KV. Free-paced high-performance brain-computer interfaces. J Neural Eng. 2007;4:336–347. doi: 10.1088/1741-2560/4/3/018. [DOI] [PubMed] [Google Scholar]
- Andersen RA, Musallam S, Pesaran B. Selecting the signals for a brain-machine interface. Curr Opin Neurobiol. 2004;14:720–726. doi: 10.1016/j.conb.2004.10.005. [DOI] [PubMed] [Google Scholar]
- Asher I, Stark E, Abeles M, Prut Y. Comparison of direction and object selectivity of local field potentials and single units in macaque posterior parietal cortex during prehension. J Neurophysiol. 2007;97:3684–3695. doi: 10.1152/jn.00886.2006. [DOI] [PubMed] [Google Scholar]
- Averbeck BB, Latham PE, Pouget A. Neural correlations, population coding and computation. Nat Rev Neurosci. 2006;7:358–366. doi: 10.1038/nrn1888. [DOI] [PubMed] [Google Scholar]
- Bansal AK, Vargas-Irwin CE, Truccolo W, Donoghue JP. Relationships among low-frequency local field potentials, spiking activity, and 3-D reach and grasp kinematics in primary motor and ventral premotor cortices. J Neurophysiol. 2011 doi: 10.1152/jn.00532.2010. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Belitski A, Gretton A, Magri C, Murayama Y, Montemurro MA, Logothetis NK, Panzeri S. Low-frequency local field potentials and spikes in primary visual cortex convey independent visual information. J Neurosci. 2008;28:5696–5709. doi: 10.1523/JNEUROSCI.0009-08.2008. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Berens P, Keliris GA, Ecker AS, Logothetis NK, Tolias AS. Comparing the feature selectivity of the gamma-band of the local field potential and the underlying spiking activity in primate visual cortex. Front Syst Neurosci. 2008;2:2. doi: 10.3389/neuro.06.002.2008. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Carmena JM, Lebedev MA, Crist RE, O’Doherty JE, Santucci DM, Dimitrov DF, Patil PG, Henriquez CS, Nicolelis MA. Learning to control a brain-machine interface for reaching and grasping by primates. PLoS Biol. 2003;1:E42. doi: 10.1371/journal.pbio.0000042. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Collinger JL, Wodlinger B, Downey JE, Wang W, Tyler-Kabara EC, Weber DJ, McMorland AJC, Velliste M, Boninger ML, Schwartz AB. High-performance neuroprosthetic control by an individual with tetraplegia. The Lancet. 2012 doi: 10.1016/S0140-6736(12)61816-9. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Destexhe A, Contreras D, Steriade M. Spatiotemporal analysis of local field potentials and unit discharges in cat cerebral cortex during natural wake and sleep states. J Neurosci. 1999;19:4595–4608. doi: 10.1523/JNEUROSCI.19-11-04595.1999. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Dickey AS, Suminski A, Amit Y, Hatsopoulos NG. Single-unit stability using chronically implanted multielectrode arrays. J Neurophysiol. 2009;102:1331–1339. doi: 10.1152/jn.90920.2008. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ecker AS, Berens P, Keliris GA, Bethge M, Logothetis NK, Tolias AS. Decorrelated neuronal firing in cortical microcircuits. Science. 2010;327:584–587. doi: 10.1126/science.1179867. [DOI] [PubMed] [Google Scholar]
- Eggermont JJ, Munguia R, Pienkowski M, Shaw G. Comparison of LFP-based and spike-based spectro-temporal receptive fields and cross-correlation in cat primary auditory cortex. PloS one. 2011;6:e20046. doi: 10.1371/journal.pone.0020046. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ethier C, Oby ER, Bauman MJ, Miller LE. Restoration of grasp following paralysis through brain-controlled stimulation of muscles. Nature. 2012;485:368–371. doi: 10.1038/nature10987. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Flint RD, Ethier C, Oby ER, Miller LE, Slutzky MW. Local field potentials allow accurate decoding of muscle activity. J Neurophysiol. 2012;108:18–24. doi: 10.1152/jn.00832.2011. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Frien A, Eckhorn R. Functional coupling shows stronger stimulus dependency for fast oscillations than for low-frequency components in striate cortex of awake monkey. European Journal of Neuroscience. 2000;12:1466–1478. doi: 10.1046/j.1460-9568.2000.00026.x. [DOI] [PubMed] [Google Scholar]
- Gilja V, Nuyujukian P, Chestek CA, Cunningham JP, Yu BM, Fan JM, Churchland MM, Kaufman MT, Kao JC, Ryu SI, Shenoy KV. A high-performance neural prosthesis enabled by control algorithm design. Nat Neurosci. 2012;15:1752–1757. doi: 10.1038/nn.3265. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Graf ABA, Kohn A, Jazayeri M, Movshon JA. Decoding the activity of neuronal populations in macaque primary visual cortex. Nat Neurosci. 2011;14:239–245. doi: 10.1038/nn.2733. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gu Y, Liu S, Fetsch Christopher R, Yang Y, Fok S, Sunkara A, DeAngelis Gregory C, Angelaki Dora E. Perceptual learning reduces interneuronal correlations in macaque visual cortex. Neuron. 2011;71:750–761. doi: 10.1016/j.neuron.2011.06.015. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Heldman DA, Wang W, Chan SS, Moran DW. Local field potential spectral tuning in motor cortex during reaching. IEEE Trans Neural Syst Rehabil Eng. 2006;14:180–183. doi: 10.1109/TNSRE.2006.875549. [DOI] [PubMed] [Google Scholar]
- Hochberg LR, Bacher D, Jarosiewicz B, Masse NY, Simeral JD, Vogel J, Haddadin S, Liu J, Cash SS, van der Smagt P, Donoghue JP. Reach and grasp by people with tetraplegia using a neurally controlled robotic arm. Nature. 2012;485:372–375. doi: 10.1038/nature11076. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hwang EJ, Andersen RA. Brain control of movement execution onset using local field potentials in posterior parietal cortex. J Neurosci. 2009;29:14363–14370. doi: 10.1523/JNEUROSCI.2081-09.2009. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hwang EJ, Andersen RA. Cognitively driven brain machine control using neural signals in the parietal reach region. Conf Proc IEEE Eng Med Biol Soc. 2010;1:3329–3332. doi: 10.1109/IEMBS.2010.5627277. [DOI] [PubMed] [Google Scholar]
- Hwang EJ, Andersen RA. Effects of visual stimulation on LFPs, spikes, and LFP-spike relations in PRR. J Neurophysiol. 2011;105:1850–1860. doi: 10.1152/jn.00802.2010. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hwang EJ, Andersen RA. Spiking and LFP activity in PRR during symbolically instructed reaches. J Neurophysiol. 2012;107:836–849. doi: 10.1152/jn.00063.2011. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hwang EJ, Bailey PM, Andersen RA. Volitional control of neural activity relies on the natural motor repertoire. Curr Biol. 2013;23 doi: 10.1016/j.cub.2013.01.027. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hwang EJ, Hauschild M, Wilke M, Andersen Richard A. Inactivation of the parietal reach region causes optic ataxia, impairing reaches but not saccades. Neuron. 2012;76:1021–1029. doi: 10.1016/j.neuron.2012.10.030. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Jia X, Smith MA, Kohn A. Stimulus selectivity and spatial coherence of gamma components of the local field potential. J Neurosci. 2011;31:9390–9403. doi: 10.1523/JNEUROSCI.0645-11.2011. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Johnson KO. Sensory discrimination: neural processes preceding discrimination decision. J Neurophysiol. 1980;43:1793–1815. doi: 10.1152/jn.1980.43.6.1793. [DOI] [PubMed] [Google Scholar]
- Lampl I, Reichova I, Ferster D. Synchronous membrane potential fluctuations in neurons of the cat visual cortex. Neuron. 1999;22:361–374. doi: 10.1016/s0896-6273(00)81096-x. [DOI] [PubMed] [Google Scholar]
- Leopold DA, Logothetis NK. Spatial patterns of spontaneous local field activity in the monkey visual cortex. Rev Neurosci. 2003;14:195–205. doi: 10.1515/revneuro.2003.14.1-2.195. [DOI] [PubMed] [Google Scholar]
- Logothetis NK, Kayser C, Oeltermann A. In vivo measurement of cortical impedance spectrum in monkeys: Implications for signal propagation. Neuron. 2007;55:809–823. doi: 10.1016/j.neuron.2007.07.027. [DOI] [PubMed] [Google Scholar]
- Markowitz DA, Wong YT, Gray CM, Pesaran B. Optimizing the decoding of movement goals from local field potentials in macaque cortex. J Neurosci. 2011;31:18412–18422. doi: 10.1523/JNEUROSCI.4165-11.2011. [DOI] [PMC free article] [PubMed] [Google Scholar]
- McConnell GC, Rees HD, Levey AI, Gutekunst C-A, Gross RE, Bellamkonda RV. Implanted neural electrodes cause chronic, local inflammation that is correlated with local neurodegeneration. Journal of Neural Engineering. 2009;6:056003. doi: 10.1088/1741-2560/6/5/056003. [DOI] [PubMed] [Google Scholar]
- Mehring C, Rickert J, Vaadia E, de Oliveira SC, Aertsen A, Rotter S. Inference of hand movements from local field potentials in monkey motor cortex. Nat Neurosci. 2003;6:1253–1254. doi: 10.1038/nn1158. [DOI] [PubMed] [Google Scholar]
- Mitzdorf U. Current source-density method and application in cat cerebral cortex: Investigation of evoked potentials and EEG phenomena. Physiol Rev. 1985;65:37–100. doi: 10.1152/physrev.1985.65.1.37. [DOI] [PubMed] [Google Scholar]
- Musallam S, Corneil BD, Greger B, Scherberger H, Andersen RA. Cognitive control signals for neural prosthetics. Science. 2004;305:258–262. doi: 10.1126/science.1097938. [DOI] [PubMed] [Google Scholar]
- O’Leary JG, Hatsopoulos NG. Early visuomotor representations revealed from evoked local field potentials in motor and premotor cortical areas. J Neurophysiol. 2006;96:1492–1506. doi: 10.1152/jn.00106.2006. [DOI] [PubMed] [Google Scholar]
- Penttonen M, Kamondi A, Acsady L, Buzsaki G. Gamma frequency oscillation in the hippocampus of the rat: Intracellular analysis in vivo. European Journal of Neuroscience. 1998;10:718–728. doi: 10.1046/j.1460-9568.1998.00096.x. [DOI] [PubMed] [Google Scholar]
- Pesaran B, Pezaris JS, Sahani M, Mitra PP, Andersen RA. Temporal structure in neuronal activity during working memory in macaque parietal cortex. Nat Neurosci. 2002;5:805–811. doi: 10.1038/nn890. [DOI] [PubMed] [Google Scholar]
- Polikov VS, Tresco PA, Reichert WM. Response of brain tissue to chronically implanted neural electrodes. J Neurosci Methods. 2005;148:1–18. doi: 10.1016/j.jneumeth.2005.08.015. [DOI] [PubMed] [Google Scholar]
- Poo C, Isaacson JS. Odor representations in olfactory cortex: “sparse” coding, global inhibition, and oscillations. Neuron. 2009;62:850–861. doi: 10.1016/j.neuron.2009.05.022. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Poulet JFA, Petersen CCH. Internal brain state regulates membrane potential synchrony in barrel cortex of behaving mice. Nature. 2008;454:881–885. doi: 10.1038/nature07150. [DOI] [PubMed] [Google Scholar]
- Quian Quiroga R, Panzeri S. Extracting information from neuronal populations: information theory and decoding approaches. Nat Rev Neurosci. 2009;10:173–185. doi: 10.1038/nrn2578. [DOI] [PubMed] [Google Scholar]
- Renart A, de la Rocha J, Bartho P, Hollender L, Parga N, Reyes A, Harris KD. The asynchronous state in cortical circuits. Science. 2010;327:587–590. doi: 10.1126/science.1179850. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rickert J, Oliveira SC, Vaadia E, Aertsen A, Rotter S, Mehring C. Encoding of movement direction in different frequency ranges of motor cortical local field potentials. J Neurosci. 2005;25:8815–8824. doi: 10.1523/JNEUROSCI.0816-05.2005. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Salinas E, Abbott LF. Vector reconstruction from firing rates. J Comp Neurol. 1994;1:89–107. doi: 10.1007/BF00962720. [DOI] [PubMed] [Google Scholar]
- Santhanam G, Linderman MD, Gilja V, Afshar A, Ryu SI, Meng TH, Shenoy KV. HermesB: a continuous neural recording system for freely behaving primates. IEEE Trans Biomed Eng. 2007;54:2037–2050. doi: 10.1109/TBME.2007.895753. [DOI] [PubMed] [Google Scholar]
- Scherberger H, Jarvis MR, Andersen RA. Cortical local field potential encodes movement intentions in the posterior parietal cortex. Neuron. 2005;46:347–354. doi: 10.1016/j.neuron.2005.03.004. [DOI] [PubMed] [Google Scholar]
- Shadlen MN, Newsome WT. The variable discharge of cortical neurons: implications for connectivity, computation, and information coding. J Neurosci. 1998;18:3870–3896. doi: 10.1523/JNEUROSCI.18-10-03870.1998. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Simeral JD, Kim S-P, Black MJ, Donoghue JP, Hochberg LR. Neural control of cursor trajectory and click by a human with tetraplegia 1000 days after implant of an intracortical microelectrode array. Journal of Neural Engineering. 2011;8:025027. doi: 10.1088/1741-2560/8/2/025027. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Snyder LH, Batista AP, Andersen RA. Coding of intention in the posterior parietal cortex. Nature. 1997;386:167–170. doi: 10.1038/386167a0. [DOI] [PubMed] [Google Scholar]
- Spinks RL, Kraskov A, Brochier T, Umilta MA, Lemon RN. Selectivity for grasp in local field potential and single neuron activity recorded simultaneously from M1 and F5 in the awake macaque monkey. J Neurosci. 2008;28:10961–10971. doi: 10.1523/JNEUROSCI.1956-08.2008. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Stark E, Abeles M. Predicting movement from multiunit activity. J Neurosci. 2007;27:8387–8394. doi: 10.1523/JNEUROSCI.1321-07.2007. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wessberg J, Stambaugh CR, Kralik JD, Beck PD, Laubach M, Chapin JK, Kim J, Biggs SJ, Srinivasan MA, Nicolelis MA. Real-time prediction of hand trajectory by ensembles of cortical neurons in primates. Nature. 2000;408:361–365. doi: 10.1038/35042582. [DOI] [PubMed] [Google Scholar]
- Yu Y-C, Bultje RS, Wang X, Shi S-H. Specific synapses develop preferentially among sister excitatory neurons in the neocortex. Nature. 2009;458:501–504. doi: 10.1038/nature07722. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zohary E, Shadlen MN, Newsome WT. Correlated neuronal discharge rate and its implications for psychophysical performance. Nature. 1994;370:140–143. doi: 10.1038/370140a0. [DOI] [PubMed] [Google Scholar]