Abstract
Objective
We aimed to improve the diagnostic accuracy of myocardial perfusion SPECT (MPS) by integrating clinical data and quantitative image features with machine learning (ML) algorithms.
Methods
1,181 rest 201Tl/stress 99mTc-sestamibi dual-isotope MPS studies [713 consecutive cases with correlating invasive coronary angiography (ICA) and suspected coronary artery disease (CAD) and 468 with low likelihood (LLk) of CAD <5%] were considered. Cases with stenosis <70% by ICA and LLk of CAD were considered normal. Total stress perfusion deficit (TPD) for supine/prone data, stress/rest perfusion change, and transient ischemic dilatation were derived by automated perfusion quantification software and were combined with age, sex, and post-electrocardiogram CAD probability by a boosted ensemble ML algorithm (Logit-Boost). The diagnostic accuracy of the model for prediction of obstructive CAD ≥70% was compared to standard prone/supine quantification and to visual analysis by two experienced readers utilizing all imaging, quantitative, and clinical data. Tenfold stratified cross-validation was performed.
Results
The diagnostic accuracy of ML (87.3% ± 2.1%) was similar to Expert 1 (86.0% ± 2.1%), but superior to combined supine/prone TPD (82.8% ± 2.2%) and Expert 2 (82.1% ± 2.2%) (P <.01). The receiver operator characteristic areas under curve for ML algorithm (0.94 ± 0.01) were higher than those for TPD and both visual readers (P <.001). The sensitivity of ML algorithm (78.9% ± 4.2%) was similar to TPD (75.6% ± 4.4%) and Expert 1 (76.3% ± 4.3%), but higher than that of Expert 2 (71.1% ± 4.6%), (P <.01). The specificity of ML algorithm (92.1% ± 2.2%) was similar to Expert 1 (91.4% ± 2.2%) and Expert 2 (88.3% ± 2.5%), but higher than TPD (86.8% ± 2.6%), (P <.01).
Conclusion
ML significantly improves diagnostic performance of MPS by computational integration of quantitative perfusion and clinical data to the level rivaling expert analysis.
Keywords: Myocardial perfusion imaging, SPECT automated quantification, coronary artery disease, total perfusion deficit, machine learning
INTRODUCTION
Myocardial perfusion SPECT (MPS) is the most commonly used noninvasive stress imaging modality for diagnosis of coronary artery disease (CAD).1 Prior studies have evaluated multiple MPS features, including semi-quantitative and quantitative perfusion and functional variables, for diagnosis of obstructive CAD.2–6 The American Society of Nuclear Cardiology (ASNC) recommends that the clinician should approach MPS interpretation in a systematic fashion, which should include review of raw and perfusion images, incorporation of quantitative and functional data, as well as consideration of clinical factors.7 However, manual combination of these data may lead to a significant inter-observer variability due to different levels of experience.8 Prior studies have demonstrated that quantitative analysis can be a useful supplement to the visual analysis;9 however, automated algorithms for combining and integrating perfusion, functional, and clinical variables have not been well developed.
Recent advances in machine learning (ML) research have resulted in algorithms that allow efficient combination of multiple input features in order to achieve optimal classification. In this study, we aimed to improve the diagnostic accuracy of MPS analysis by fully automated integration of several quantitative perfusion and clinical variables with an ensemble ML algorithm (LogitBoost). We demonstrate the improved diagnostic accuracy of this method over standard quantitative analysis, rivaling the accuracy of expert readers.
MATERIALS AND METHODS
Patient Population
The subjects who were referred to the Nuclear Medicine Department of Cedars-Sinai Medical Center, Los Angeles, California, from November 1, 2001, to June 30, 2005, for rest and stress electrocardiography (ECG) gating, for whom both supine and prone imaging 10 as well as informed consent were available, were consecutively selected. All patients with prior history of CAD or significant valve disease were excluded. Based on these selection criteria, 1,181 sequential studies were identified to form the study group. This population consisted of two subgroups of patients: 713 patients with correlative angiography and 468 patients with a low likelihood (LLk) of CAD. In the angiography group, MPS and coronary angiography had to be performed within 60 days without a significant intervening event. The majority of the patients in the angiography group underwent MPS prior to cardiac catheterization (96%). The LLk group consisted of patients who did not have correlating coronary angiography available, but had a low pretest likelihood of CAD (<5% for exercise MPS and <10% for adenosine stress MPS) by CADENZA (Advanced Heuristics, Inc, Bainbridge Island, Wash) analysis.11 The LLk patients were classified as normal for the purposes of this analysis. The clinical characteristics of the two groups are listed in Table 1. The data analyzed in this study were selected retrospectively from the existing database at Cedars-Sinai Medical Center. The retrospective use of clinical data in this study was approved by the Institutional Review Board and all patients provided written informed consent for the use of their clinical and imaging data for research purposes.
Table 1.
Baseline characteristics of the patients.
| Angiography Group | LLk Group | P - Value | |
|---|---|---|---|
| Number | 713 | 468 | N/A |
| Age (Years) | 64 ± 12 | 48 ± 11 | <.01 |
| Male % | 64 % | 41 % | <.01 |
| Female % | 36 % | 59 % | <.01 |
| Diabetes Mellitus % | 22 % | 10 % | <.01 |
| Hypertension % | 61 % | 36 % | <.01 |
| Hyperlipidemia % | 52 % | 38 % | <.01 |
| Smoking % | 6 % | 5 % | 0.46 |
| Exercise SPECT | 33 % | 56 % | <.01 |
| Adenosine SPECT | 67 % | 44 % | <.01 |
| Ejection Fraction (%) | 61.7 ± 13.2 | 65.7 ± 11.3 | 0.16 |
| Cath: 0-Vessel Disease | 291 (41%) | N/A | N/A |
| Cath: 1-Vessel Disease | 204 (29%) | N/A | N/A |
| Cath: 2-Vessel Disease | 149 (21%) | N/A | N/A |
| Cath: 3-Vessel Disease | 63 (9%) | N/A | N/A |
| Pre-Test Likelihood CAD | |||
| Low | 11% | 100 | <.01 |
| Intermediate | 80% | 0 | <.01 |
| High | 9% | 0 | <.01 |
Abbreviations: LLk- Low Likelihood, SPECT- Single Photon Emission Computed Tomography, N/A = Not applicable.
Rest MPS protocol
For rest imaging, weight- adjusted Tl-201(3.0–4.5 mCi) was injected intravenously and acquisition was performed 10 minutes after injection.
Exercise MPS protocol
Patients performed a symptom-limited exercise treadmill test with the standard Bruce protocol. At near-maximum exercise, 99mTc-sestamibi (25–40 mCi based on patient weight) was injected intravenously. Treadmill exercise was continued at maximum workload for 1 minute and at 1 stage lower for two additional minutes, when possible. 99mTc-sestamibi MPS acquisition was started 15–30 minutes after the radiopharmaceutical injection.
Adenosine MPS protocol
Adenosine MPS was performed as previously described.12 Adenosine was infused at 140 μg kg −1 minute−1 for 5 minutes. At the end of the second minute, 99mTc-sestamibi (25–40 mCi) was injected, and MPS acquisition was started approximately 60 minutes later. Whenever possible, during adenosine infusion, patients performed a low-level treadmill exercise, walking at 0% grade at 1–1.7 mph. With the latter protocol, imaging began 15–60 minutes after adenosine stress.
Image Acquisition and Reconstruction Protocols
The details of image acquisition and tomographic reconstruction have been previously described.14 All patients underwent separate acquisition rest 201Tl/stress 99mTc-sestamibi dual-isotope MPS as previously described.15 Stress scans were acquired with 64 projections at 25 seconds per projection for supine 99mTc acquisition, followed immediately by 15 seconds per projection for prone 99mTc acquisition. The rest 201Tl acquisition was performed with 64 projections (32 per each head) and 35 seconds per projection. Images were acquired on a dual-detector camera [Forte or Vertex (Philips Medical Systems, Andover, Massachusetts) or e.cam (Siemens Medical Systems, Malvern, Pennsylvania)]. High-resolution collimators were used. No attenuation or scatter correction was applied. Studies were reconstructed on the respective vendor platforms [Pegasys (Philips Medical Systems) or e.soft 2000 (Siemens Medical Systems)] by the commercial implementations of the iterative reconstruction. The reconstruction parameters were 12 iterations with Butterworth pre-filtering [cutoff, 0.66 cycles per pixel (pixel size = 6.9 mm) for supine 99mTc and 0.55 cycles per pixel for prone 99mTc; order, 5]. These parameters were optimized previously to provide optimal image quality for clinical scan reading.16
Short-axis images were automatically generated.17 In cases when the software failed to detect left ventricular contours as indicated by the quality control flag,18 manual contour correction was performed by an experienced technologist. In addition, if patient motion was noted during review of raw projections, motion correction (MoCo) software was applied.19 After reconstruction, the images were transferred for automated processing and quantification using Cedars-Sinai quantitative perfusion SPECT (QPS) software.20 No studies were removed from the consecutive series due to image quality issues.
Clinical Analysis
Pre-test probability of obstructive CAD was estimated using Diamond-Forrester criteria using age, sex, and symptoms.21 We also calculated the probability of obstructive CAD using ECG Diamond-Forrester criteria based on the degree of ST-depression on stress ECG.21 The post-ECG parameter as well as gender and age formed clinical input to the ML system.
Automated Analysis
Several quantitative parameters were obtained in a fully automated mode as described below. These parameters were used as an input into the ML algorithm.
Total perfusion deficit (TPD)
Supine and prone images were quantified separately using their respective supine and prone normal limits and a previously developed simplified approach.22 Briefly, an ellipsoidal model and contours derived by the quantitative gated SPECT (QGS) algorithm20 were used to extract polar map samples. An optimal normalization factor between the database cases and a test case was established by an iterative search and an abnormality threshold of 3.0 average (mean absolute) deviations was applied (approximately equivalent to 2.5 SD) to estimate the extent of hypoperfusion.22 This value is similar to the threshold used in other MPS quantification methods. The TPD measure was computed as the integral of polar map severities below the abnormality threshold, reflecting both extent and severity of the defect.
In addition to deriving separate TPD measures for supine and prone MPS, we computed the combined supine/prone TPD parameter, based on the findings of abnormality on both supine and prone images as previously described.14 Briefly, combined supine/prone TPD is calculated by limiting the TPD computation from the supine polar map to pixels, which have been quantified as abnormal on prone images. The same average deviation threshold (3.0) is used for supine and prone images (as in the analysis of separate images).14 Additionally, two exceptions for concomitant defect locations (anterior/apical supine defects and for inferior wall prone defects) have been built into the quantification process for males as previously established.14 The combined supine/prone parameter was expressed in the same units (percentage of the myocardium) as in the separate supine and prone TPD measures.
Stress/rest perfusion change
Stress-rest change was evaluated by the direct quantification of ischemia.3 The stress-rest count difference was assessed considering the voxels contained within only the stress contour volume since the rest scans were spatially aligned to stress scans. Following the spatial alignment and stress-rest image count normalization, we calculated stress/rest perfusion change based on the normal limits of changes as recently described.23
Transient ischemic dilation (TID)
Standard MPS processing was performed by the QPS/QGS software.20,24 The TID ratio was derived from stress/rest supine MPS as previously defined.25
Visual Analysis
Visual interpretation of MPS images was based on short-axis, horizontal, and vertical long-axis tomograms divided into 17-segments using QPS interactive 17-segment graph.20,26 MPS images were scored independently by two expert readers (Expert 1 with 30 years and Expert 2 with more than 10 years of clinical experience in nuclear cardiology as attending physicians) using a five-point scoring system (0, normal; 1, mildly decreased; 2, moderately decreased; 3, severely decreased; and 4, absence of segmental uptake). Visual reading was performed in two consecutive steps with the following information revealed to the expert readers at each step: Step 1: supine plus prone data, including stress and rest perfusion data, raw projection data, and gated functional data including gated images and stress plus rest ejection fraction (EF); and Step 2: all information provided in Step 1 as well as quantitative computer results and all clinical information including age, cardiac risk factors, type of stress, and clinical and ECG responses to stress. During the second step, readers could modify the stress and rest scores using the additional information that had been revealed to them. Subsequently, summed stress scores (SSS) and summed rest scores were calculated by summing the 17-segment stress and rest scores, respectively.
ML Algorithm
We have employed an ensemble-boosting ML algorithm, which is a meta-algorithm technique. A high performance of classification is obtained by the combination of weak learners (simple classification schemes), which produce a strong ensemble classification scheme by iteratively adjusting appropriate weights for each of the base-level classifiers. For the current analysis, we utilized a LogitBoost procedure27 with decision stumps as the base classifiers utilizing Waikato Environment for Knowledge Analysis (WEKA).28 This method has been shown to be superior to the originally proposed AdaBoost method29 and has been successfully applied to tumor classification with gene expression data.30 We utilized the following quantitative parameters—TID, combined supine/prone TPD, supine TPD, and optimized stress/rest change analysis as described previously.23 We also provided patient age, gender, and post-ECG probability of CAD computed as described in the previous section (seven features in total). Standard ten-fold stratified cross-validation was applied, and therefore no training data were used during testing of the model, but 10 different models were used to derive the final test results.31 No automated feature selection was performed and the same 7 features were used in the training and testing phase. Both LLk and angiography groups were included in the model to provide a balanced dataset for the ML with similar representation of normal and abnormal cases. The output in the form of continuous probability estimates was used to construct the receiver operator characteristic (ROC) curves. To assess the incremental diagnostic benefit of combining the clinical information and the quantitative features, the ML algorithm performance was compared to expert visual readings and to the combined supine/prone quantitative analysis. Furthermore, ML was used to combine only the 4 quantitative data features (without clinical features), which were compared to ML probability estimates combining all seven features to assess how clinical information influenced ML. In addition, we also combined quantitative perfusion with quantitative functional data including EF and segmental motion and thickening scores, as well as clinical data.
Conventional Coronary Angiography
Conventional invasive coronary angiography (ICA) was performed according to standard clinical protocols, within 60 days of the myocardial perfusion examination. All coronary angiograms were analyzed using quantitative coronary arteriography (QCA) by an experienced cardiologist. A stenosis of 50% or greater narrowing of luminal diameter of the left main or 70% or greater narrowing of the other coronary arteries by ICA was considered significant and was used as the gold standard for the detection of obstructive CAD.
Statistical Analysis
Continuous variables were expressed as the mean ± standard deviation, and categorical variables were expressed as percentages (%). The inter-observer agreement between visual and automated reads was assessed by kappa-test. Z-test for comparison of proportions was performed to compare the sensitivity, specificity, and accuracy. The normalcy was calculated based on the LLk population, and the normalcy rates were also compared using z-test. For all analyses, P values <.05 were considered statistically significant. ROC curves were analyzed to evaluate the ability of ML software vs visual scoring for forecasting obstructive CAD by QCA. The differences between the ROC areas under the curves (AUC) were compared using the Delong method.32
RESULTS
Contours were manually adjusted in 12% of the supine cases and 14% of the prone cases, with majority of these adjustments (9% for supine and 11% for prone) involving alteration of the mitral valve plane only.
Agreement Between Automated and Visual Analysis
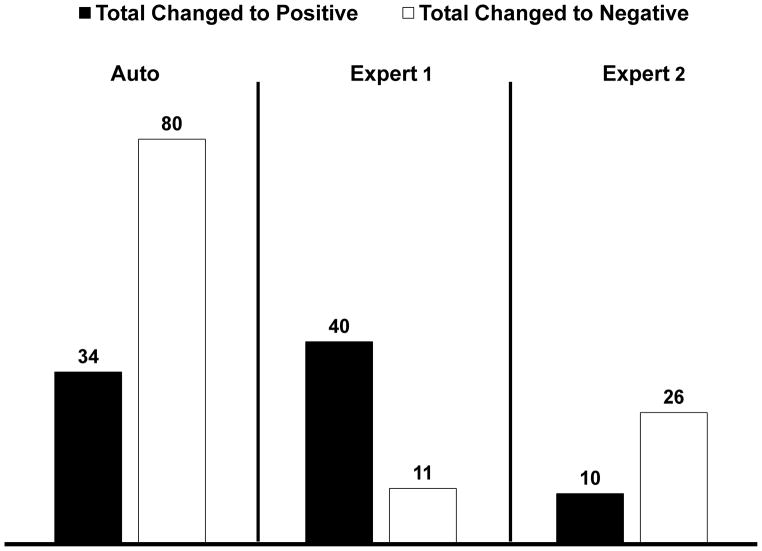
Figure 1 demonstrates the number of times the diagnosis was changed between the visual analysis without clinical and quantitative data (Step 1) and with all the data (Step 2) as well as between quantitative analysis and ML results. A supine/prone TPD value of ≥3%14 and SSS score of ≥4 were considered abnormal16,33 for the quantitative TPD and visual analysis. TPD threshold was not used by the ML method. The ML method combining quantitative and clinical data changed diagnosis in ~10% of cases as compared to combined supine/prone TPD parameter alone, while Expert 1 and Expert 2 changed the diagnosis in 4% and 3% of the cases between Step 1 and 2, respectively. The inter-observer agreement between the two expert readers, combined supine/prone, and ML is shown in Table 2. The overall inter-observer agreement between the two expert readers, quantitative, and ML was good (0.72–0.81).
Figure 1.
Comparison of the number of patients in whom the diagnosis was changed when all information including clinical variables was provided.
Table 2.
Agreements between the two expert readers, combined supine/prone TPD, and ML algorithm utilizing Kappa-test
| Kappa-Statistics | Total % Agreement | |
|---|---|---|
| Expert 1 vs. Expert 2 | 0.78 | 90% |
| Expert 1 vs. TPD | 0.80 | 91% |
| Expert 2 vs. TPD | 0.81 | 91% |
| Expert 1 vs. ML | 0.80 | 91% |
| Expert 2 vs. ML | 0.72 | 87% |
ML vs Quantitative Perfusion Analysis
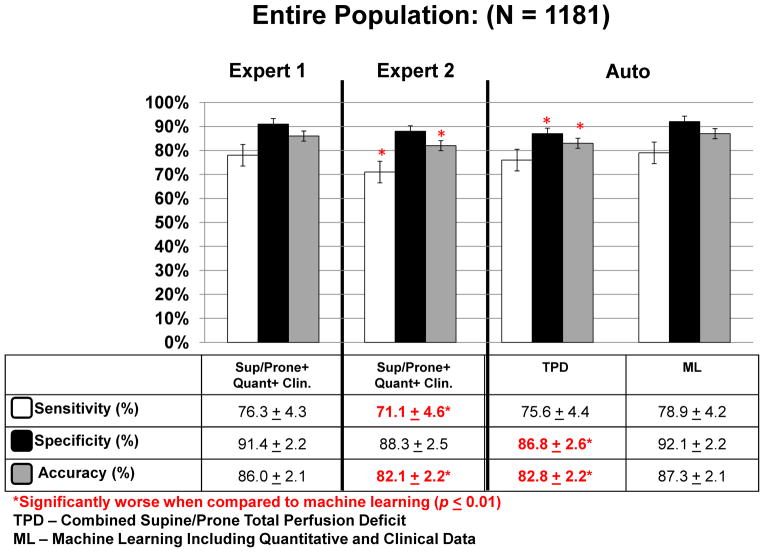
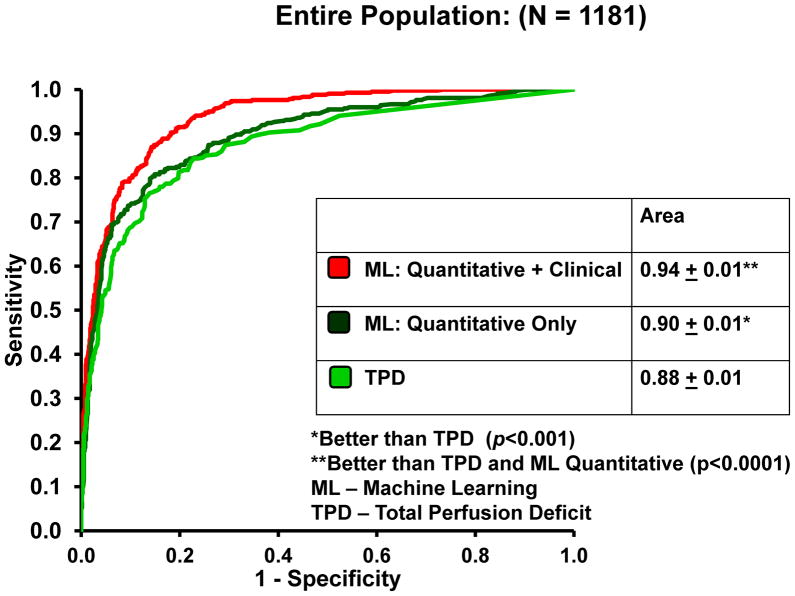
Figure 2 compares the sensitivity, specificity, and accuracy of the combined supine/prone TPD vs ML for the entire population cohort including angiography and LLK cases (N = 1,181). The specificity (92.1%) and accuracy (87.3%) of ML combining quantitative and clinical data was significantly higher than combined supine/prone TPD quantification (specificity: 86.8%, accuracy: 82.8%) (P<.01). The sensitivities of the two methods were similar. The ROC curves for TPD analysis (combined supine/prone), ML with quantitative features only, and ML combining quantitative and clinical data are shown in Figure 3A. The AUC for ML combining quantitative and clinical measurements (0.94 ± 0.01) was significantly better (P<.0001) than TPD (0.88 ± 0.01) and ML using quantitative data alone (0.90 ± 0.01). The ML using quantitative data alone was also significantly better than combined supine/prone TPD (P<.001). Furthermore, the AUC for ML combining quantitative perfusion and functional image features plus clinical information was 0.94 ± 0.01, which is similar to the result obtained without functional information; and also significantly better than TPD or ML using quantitative perfusion data only.
Figure 2.
Sensitivity, specificity, and accuracy of ML algorithm vs combined supine/prone TPD and visual expert analysis for detection of obstructive CAD for the entire cohort (N = 1,181).
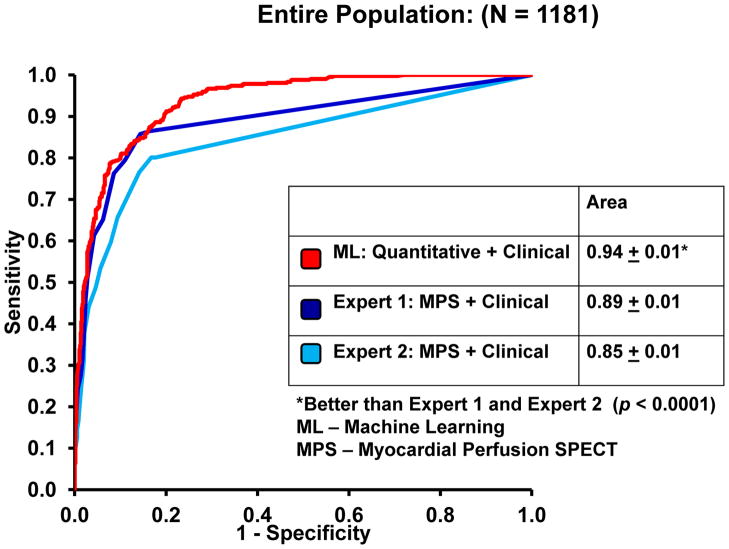
Figure 3.
The ROC curves comparing the ML algorithm vs combined supine/prone TPD (A) and expert visual analysis (B) for the detection of obstructive coronary artery disease.
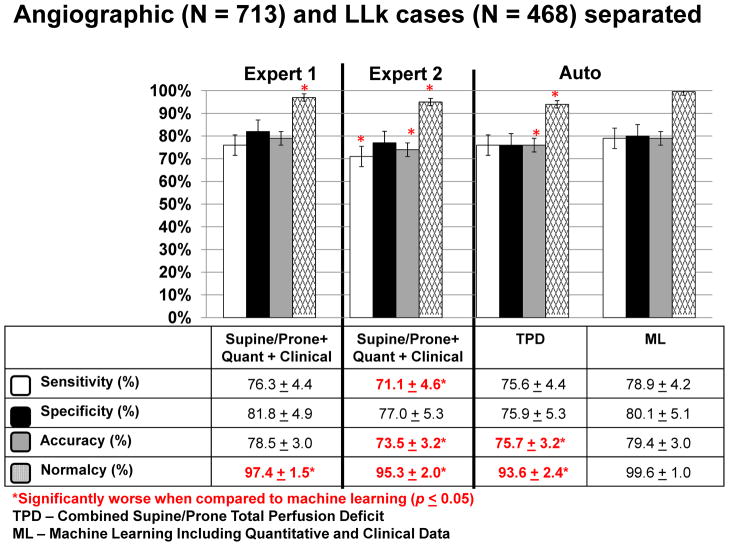
We also compared the diagnostic performance of the automated TPD analysis (combined supine/prone) vs quantitative/clinical ML analysis, separately in the angiographic population (N = 713) and LLK cases (N = 468) (Figure 4). The diagnostic accuracy of quantitative/clinical ML (79.4%) was significantly better than TPD (75.7%) (P<.05), while the specificities of the two methods were similar. The normalcy rate for the combined quantitative/clinical ML (99.6%) was significantly higher than combined supine/prone TPD (93.6%) (P<.01). In addition, the AUC for the quantitative/clinical ML (0.85 ± 0.01) was significantly better than combined supine/prone TPD (0.82 ± 0.01) (P<.001) in the separate angiographic population. Sensitivity comparisons were the same as in the overall population.
Figure 4.
Sensitivity, specificity, accuracy, and normalcy (based on LLk groups) of ML algorithms vs combined supine/prone TPD and visual analysis for obstructive CAD separately in the angiographic group (N = 713).
We compared the LogitBoost ML algorithm vs standard logistic regression using the same input variables and the same ten-fold stratified cross-validation process. The diagnostic performance of logistic regression resulted in sensitivity, specificity, and accuracy of 72.7%, 90.5%, and 84.2%, respectively. The sensitivity and accuracy of the logistic regression method was significantly lower than the LogitBoost method combining clinical and quantitative data (P<.05).
ML vs Visual Analysis
The sensitivity for visual read increased to 76.3% ± 4.5% vs 70.6% ± 4.5% in Step 2 vs Step 1, while specificity was unchanged (91.4% ± 2.2% vs 92.1% ± 2.2%) for Expert 1. Both sensitivity (71.1% ± 4.6% vs 73.7% ± 4.5%) and specificity (88.3% ± 2.5% vs 87.6% ± 2.6%) were unchanged for Expert 2 between Step 1 and Step 2. Figure 2 also compares the sensitivity, specificity, and accuracy of the quantitative/clinical ML algorithm vs the second reading step for each expert (with all clinical and quantitative information available) for the entire population cohort (N = 1,181). The diagnostic accuracy and sensitivity were comparable to Expert 1, but superior to Expert 2 (P<.01). The specificity of quantitative/clinical ML was similar in comparison to both experts. The ROC curves for detection of obstructive disease, comparing quantitative/clinical ML and visual reads for two experts, are shown in Figure 3B. The AUCs for ML were significantly better when compared to the visual analysis for both expert readers (P<.0001).
We also compared the diagnostic performance of the ML vs visual analysis (Step 2) separately in the angiographic population (N = 713) and LLK population for normalcy rate (Figure 4). The diagnostic accuracy of quantitative/clinical ML were similar to that of Expert 1 and superior to that of Expert 2 (P<.05) in the angiographic population. The normalcy rate (computed in the LLK population) for the ML (99.6%) was significantly higher than for both expert readers (P<.01). The AUC for ML (0.85 ± 0.01) was similar to the AUC for Expert 1 (0.84 ± 0.01) and was superior to the AUC for Expert 2 (0.79 ± 0.01) (P<.0001). Sensitivity comparisons were the same as in the overall population.
In order to verify the validity of the visual scoring threshold, we also assessed the diagnostic performance of ML vs visual analysis when SSS ≥3 was considered abnormal in the overall population.33 The sensitivity, specificity, and accuracy of the Step 2 score for the two experts were 79.4%, 89.1%, 85.6% and 76.5%, 85.9%, 82.6%, respectively. Analogous to the results obtained for the SSS ≥4 threshold, the sensitivity and accuracy of ML were superior when compared to Expert 2 (P<.01), but similar to Expert 1.
DISCUSSION
We were able to show significant improvements in the diagnostic accuracy for the detection of obstructive CAD utilizing ML algorithm, which combined multiple quantitative perfusion and clinical variables. The improvement of the overall diagnostic accuracy of MPS has a significant impact because it may allow better selection of interventions for the individuals who are at increased risk of events as well as avoiding unnecessary procedures.34 To our knowledge, this is the first large study to combine multiple clinical and quantitative features using ML algorithms. We were able to demonstrate that the diagnostic performance of ML algorithms combining clinical and perfusion data is significantly better than quantitative perfusion analysis alone. Furthermore, we compared the diagnostic accuracy of ML algorithm vs two experienced visual readers from high volume centers. In our study, the ML algorithms were at least as accurate or superior to the visual analysis (as compared to one expert). It has been demonstrated that the degree of variability in MPS interpretation is dependent on the reader’s experience.35,36 Therefore, it is feasible that these algorithms will also be superior when compared to less experienced readers. These algorithms can be easily incorporated with currently available standard nuclear cardiology software. In the future, this method could provide fundamental assistance in evaluation of MPS studies.
We note that the overall best visual accuracy obtained in this study was slightly lower (86%) than in the similar visual expert analysis recently reported by our group for the attenuation-corrected data (89%);37 however, in the current study, none of the data were removed due to poor image quality or motion artifacts. These studies were also performed in different populations, possibly reflecting differences in the referral patterns and different prevalence of the disease; therefore, further comparison of the supine-prone technique to attenuation-correction techniques is warranted.
Previous studies had examined the use of neural networks and rule-based analysis, older ML tools compared to the one used in this study, in the assessment of MPS.38–40 One study evaluated 135 patients who had undergone both 99mTc-sestamibi MPS and cardiac catheterization38 and showed an improvement in diagnostic performance by expert physicians when utilizing neural networks (decision support) in a small population. In another study, the diagnostic performance of a computer-assisted interpretation of MPS39 was compared to visual analysis in 655 patients undergoing MPS and coronary angiography where polar map characteristics were analyzed by a rule-based system. The diagnostic specificity of the automated system was noted to be higher than visual analysis (although only ~40%); however, the sensitivity of the visual analysis was higher. These methods focused on the interpretation of polar maps by automated rules or neural networks. In contrast, our approach was to integrate a small number of clinical and high-level quantitative parameters (which could be used for standalone diagnosis). One study40 reported the ability of a computer-based neural network to enhance the diagnostic accuracy of MPS in a small group of patients (N = 102) by combining interpretation of treadmill exercise tests and image analysis. Similar to our study, incorporation of clinical and exercise data significantly improved the predictive accuracy of the network compared to a network based on image data alone (P<.05). More recent ML algorithms have been applied in cardiovascular medicine to predict increased risk of decompensated heart failure41 and onset of atrial fibrillation.42 These techniques have also been used in gene mapping and cellular biology.43,44 However, they are not yet routinely used in cardiovascular imaging.
In our current study, we used boosting ML techniques. Boosting ML techniques combine multiple models, explicitly seeking models, which complement one another. Voting weighted by confidence is then used for classification to combine the output of multiple models. Boosting finds the models iteratively; it encourages new models to classify correctly the cases handled incorrectly by earlier models by assigning greater weights to these instances. In general, any type of ML could be used with boosting. The LogitBoost learning technique utilizes logistic regression as a base learner. Thus, a combination of different competing logistic regression models is used for the final prediction. We have demonstrated that such a technique is superior to the standard logistic regression approach.
We used a stratified ten-fold cross-validation for the evaluation of the ML algorithm which is a standard procedure in ML research. Cross-validation is often used to optimize the fitting process to create a stable model using a number of unknown parameters.31 In k-fold cross-validation (in this case ten-fold), the sample is divided into k-segments and k-1 segments are used as the training set and the remaining segment is used for validation.45 This process is repeated until all k-segments are tested. The average performance for the ten models is then reported, insuring that for a given model, no training data are used during the testing phase. The large amount of cases (1,181) and small amount of features (in this case 7) insure there is no over-fitting of the model. The split-sample technique would result in a smaller training and smaller evaluation set resulting in lower stability of the model and less certainty in the test results.46 Although the visual scoring threshold for disease detection was not trained on the current data, we have previously used established thresholds for abnormality. We also evaluated the alternative threshold for abnormality (SSS ≥3) for the visual experts, which did not change the results significantly. Furthermore, we reported the AUC comparisons, which are not dependent on the optimal threshold selection.
This study has several limitations. Coronary angiography was used as the gold standard for this study with its known limitations. In addition, patients with LLk of CAD were included in our analysis and were considered to have a normal angiogram. However, we also report the results for the angiography cases separately. Furthermore, we studied a population with suspected but not known CAD; however, the detection of CAD is typically useful only in this group. Attenuation correction was not used in this study; however, we used combined supine/prone analysis to guard against image artifacts. Additionally, the MPS protocol was dual-isotope imaging, which is limited by the difficulties in comparing rest and stress images due to differences in image resolution. Recently, this protocol has been employed less frequently due to the high amount radiation to the patient. Future studies using single-isotope protocols or low-dose MPS may be required to analyze the ML algorithms. The ML model was based on the presence of obstructive disease in any territory and did not distinguish per-vessel obstruction. In the future, we plan to apply these findings to individual coronary territories for assessment of localization of disease using ML. Furthermore, the clinical information provided to the physician did not result in as many changes in diagnosis as ML, possibly related to evaluation in a blinded fashion. Based on current recommendations and guidelines, the clinician was less likely to change the diagnosis drastically from definitely normal to definitely abnormal, while the ML did not operate with these constraints. Future studies are required to assess these differences further. Finally, although we had a large patient population, the results were obtained in only one center. Further multicenter evaluations will be required to confirm these results.
CONCLUSION
Computational integration of quantitative image measures and clinical data by ML improves diagnostic performance of automatic MPS analysis to the level rivaling expert analysis.
Acknowledgments
This research was supported in part by Grant R01HL089765 from the National Heart, Lung, and Blood Institute/National Institutes of Health (NHLBI/NIH) (PI: Piotr Slomka). Its contents are solely the responsibility of the authors and do not necessarily represent the official views of the NHLBI. Cedars-Sinai Medical Center receives royalties for the quantitative assessment of function, perfusion, and viability, a portion of which is distributed to some of the authors of this manuscript (DB, GG, PS). We would like to thank Dr Caroline Kilian and Arpine Oganyan for editing and proofreading the text.
References
- 1.Underwood SR, Anagnostopoulos C, Cerqueira M, Ell PJ, Flint EJ, Harbinson M, et al. Myocardial perfusion scintigraphy: The evidence. Eur J Nucl Med Mol Imaging. 2004;31:261–91. doi: 10.1007/s00259-003-1344-5. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Amanullah AM, Berman DS, Hachamovitch R, Kiat H, Kang X, Friedman JD. Identification of severe or extensive coronary artery disease in women by adenosine technetium-99m sestamibi SPECT. Am J Cardiol. 1997;80:132–7. doi: 10.1016/s0002-9149(97)00306-8. [DOI] [PubMed] [Google Scholar]
- 3.Slomka PJ, Nishina H, Berman DS, Kang X, Friedman JD, Hayes SW, et al. Automatic quantification of myocardial perfusion stress-rest change: A new measure of ischemia. J Nucl Med. 2004;45:183–91. [PubMed] [Google Scholar]
- 4.Slomka PJ, Nishina H, Berman DS, Akincioglu C, Abidov A, Friedman JD, et al. Automated quantification of myocardial perfusion SPECT using simplified normal limits. J Nucl Cardiol. 2005;12:66–77. doi: 10.1016/j.nuclcard.2004.10.006. [DOI] [PubMed] [Google Scholar]
- 5.Abidov A, Bax JJ, Hayes SW, Hachamovitch R, Cohen I, Gerlach J, et al. Transient ischemic dilation ratio of the left ventricle is a significant predictor of future cardiac events in patients with otherwise normal myocardial perfusion SPECT. J Am Coll Cardiol. 2003;42:1818–25. doi: 10.1016/j.jacc.2003.07.010. [DOI] [PubMed] [Google Scholar]
- 6.Johnson LL, Verdesca SA, Aude WY, Xavier RC, Nott LT, Campanella MW, et al. Postischemic stunning can affect left ventricular ejection fraction and regional wall motion on post-stress gated sestamibi tomograms. J Am Coll Cardiol. 1997;30:1641–8. doi: 10.1016/s0735-1097(97)00388-4. [DOI] [PubMed] [Google Scholar]
- 7.Holly TA, Abbott BG, Al-Mallah M, Calnon DA, Cohen MC, DiFilippo FP, et al. Single photon-emission computed tomography. J Nucl Cardiol. 2010;17:941–73. doi: 10.1007/s12350-010-9246-y. [DOI] [PubMed] [Google Scholar]
- 8.Danias PG, Ahlberg AW, Travin MI, Mahr NC, Abreu JE, Marini D, et al. Visual assessment of left ventricular perfusion and function with electrocardiography-gated SPECT has high intra-observer and interobserver reproducibility among experienced nuclear cardiologists and cardiology trainees. J Nucl Cardiol. 2002;9:263–70. doi: 10.1067/mnc.2002.121233. [DOI] [PubMed] [Google Scholar]
- 9.Berman DS, Kang X, Van Train KF, Lewin HC, Cohen I, Areeda J, et al. Comparative prognostic value of automatic quantitative analysis versus semiquantitative visual analysis of exercise myocardial perfusion single-photon emission computed tomography. J Am Coll Cardiol. 1998;32:1987–95. doi: 10.1016/s0735-1097(98)00501-4. [DOI] [PubMed] [Google Scholar]
- 10.Slomka PJ, Nishina H, Abidov A, Hayes SW, Friedman JD, Berman DS, et al. Combined quantitative supine-prone myocardial perfusion SPECT improves detection of coronary artery disease and normalcy rates in women. J Nucl Cardiol. 2007;14:44–52. doi: 10.1016/j.nuclcard.2006.10.021. [DOI] [PubMed] [Google Scholar]
- 11.Diamond GA, Staniloff HM, Forrester JS, Pollock BH, Swan HJ. Computer-assisted diagnosis in the noninvasive evaluation of patients with suspected coronary artery disease. J Am Coll Cardiol. 1983;1:444–55. doi: 10.1016/s0735-1097(83)80072-2. [DOI] [PubMed] [Google Scholar]
- 12.Amanullah AM, Kiat H, Friedman JD, Berman DS. Adenosine technetium-99m sestamibi myocardial perfusion SPECT in women: Diagnostic efficacy in detection of coronary artery disease. J Am Coll Cardiol. 1996;27:803–9. doi: 10.1016/0735-1097(95)00550-1. [DOI] [PubMed] [Google Scholar]
- 13.Berman DS, Kang X, Hayes SW, Friedman JD, Cohen I, Abidov A, et al. Adenosine myocardial perfusion single-photon emission computed tomography in women compared with men. Impact of diabetes mellitus on incremental prognostic value and effect on patient management. J Am Coll Cardiol. 2003;41:1125–33. doi: 10.1016/s0735-1097(03)00085-8. [DOI] [PubMed] [Google Scholar]
- 14.Nishina H, Slomka PJ, Abidov A, Yoda S, Akincioglu C, Kang X, et al. Combined supine and prone quantitative myocardial perfusion SPECT: Method development and clinical validation in patients with no known coronary artery disease. J Nucl Med. 2006;47:51–8. [PubMed] [Google Scholar]
- 15.Berman DS, Kiat H, Friedman JD, Wang FP, Van Train K, Matzer L, et al. Separate acquisition rest thallium-201/stress technetium- 99m sestamibi dual-isotope myocardial perfusion single-photon emission computed tomography: A clinical validation study. J Am Coll Cardiol. 1993;22:1455–64. doi: 10.1016/0735-1097(93)90557-h. [DOI] [PubMed] [Google Scholar]
- 16.Hayes SW, De Lorenzo A, Hachamovitch R, Dhar SC, Hsu P, Cohen I, et al. Prognostic implications of combined prone and supine acquisitions in patients with equivocal or abnormal supine myocardial perfusion SPECT. J Nucl Med. 2003;44:1633–40. [PubMed] [Google Scholar]
- 17.Germano G, Kavanagh PB, Su HT, Mazzanti M, Kiat H, Hachamovitch R, et al. Automatic reorientation of three-dimensional, transaxial myocardial perfusion SPECT images. J Nucl Med. 1995;36:1107–14. [PubMed] [Google Scholar]
- 18.Xu Y, Kavanagh P, Fish M, Gerlach J, Ramesh A, Lemley M, et al. Automated quality control for segmentation of myocardial perfusion SPECT. J Nucl Med. 2009;50:1418–26. doi: 10.2967/jnumed.108.061333. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Matsumoto N, Berman DS, Kavanagh PB, Gerlach J, Hayes SW, Lewin HC, et al. Quantitative assessment of motion artifacts and validation of a new motion-correction program for myocardial perfusion SPECT. J Nucl Med. 2001;42:687–94. [PubMed] [Google Scholar]
- 20.Germano G, Kavanagh PB, Slomka PJ, Van Kriekinge SD, Pollard G, Berman DS. Quantitation in gated perfusion SPECT imaging: The Cedars-Sinai approach. J Nucl Cardiol. 2007;14:433–54. doi: 10.1016/j.nuclcard.2007.06.008. [DOI] [PubMed] [Google Scholar]
- 21.Diamond GA, Forrester JS. Analysis of probability as an aid in the clinical diagnosis of coronary-artery disease. N Engl J Med. 1979;300:1350–8. doi: 10.1056/NEJM197906143002402. [DOI] [PubMed] [Google Scholar]
- 22.Slomka PJ, Fish MB, Lorenzo S, Nishina H, Gerlach J, Berman DS, et al. Simplified normal limits and automated quantitative assessment for attenuation-corrected myocardial perfusion SPECT. J Nucl Cardiol. 2006;13:642–51. doi: 10.1016/j.nuclcard.2006.06.131. [DOI] [PubMed] [Google Scholar]
- 23.Prasad M, Slomka PJ, Fish M, Kavanagh P, Gerlach J, Hayes S, et al. Improved quantification and normal limits for myocardial perfusion stress-rest change. J Nucl Med. 2010;51:204–9. doi: 10.2967/jnumed.109.067736. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Germano G, Kiat H, Kavanagh PB, Moriel M, Mazzanti M, Su HT, et al. Automatic quantification of ejection fraction from gated myocardial perfusion SPECT. J Nucl Med. 1995;36:2138–47. [PubMed] [Google Scholar]
- 25.Xu Y, Arsanjani R, Clond M, Hyun M, Lemley M, Jr, Fish M, et al. Transient ischemic dilation for coronary artery disease in quantitative analysis of same-day sestamibi myocardial perfusion SPECT. J Nucl Cardiol. 2012;19:465–73. doi: 10.1007/s12350-012-9527-8. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Cerqueira MD, Weissman NJ, Dilsizian V, Jacobs AK, Kaul S, Laskey WK, et al. Standardized myocardial segmentation and nomenclature for tomographic imaging of the heart: A statement for healthcare professionals from the Cardiac Imaging Committee of the Council on Clinical Cardiology of the American Heart Association. Circulation. 2002;105:539–42. doi: 10.1161/hc0402.102975. [DOI] [PubMed] [Google Scholar]
- 27.Friedman J, Hastie T, Tibshirani R. Additive logistic regression: A statistical view of boosting (With discussion and a rejoinder by the authors) Ann Stat. 2000;28:337–407. [Google Scholar]
- 28.Hall M, Frank E, Holmes G, Pfahringer B, Reutemann P, Witten IH. The WEKA data mining software: An update. SIGKDD Explor. 2009;11:10–8. [Google Scholar]
- 29.Freund Y, Schapire R. Experiments with a new boosting algorithm. Machine learning; Proceedings of the thirteenth international conference; Bari. 1996. pp. 148–56. [Google Scholar]
- 30.Dettling M, Bühlmann P. Boosting for tumor classification with gene expression data. Bioinformatics. 2003;19:1061–9. doi: 10.1093/bioinformatics/btf867. [DOI] [PubMed] [Google Scholar]
- 31.Geisser S. Predictive inference: An introduction. New York: Chapman & Hall; 1993. [Google Scholar]
- 32.DeLong ER, DeLong DM, Clarke-Pearson DL. Comparing the areas under two or more correlated receiver operating characteristic curves: A nonparametric approach. Biometrics. 1988;44:837–45. [PubMed] [Google Scholar]
- 33.Xu Y, Fish M, Gerlach J, Lemley M, Berman DS, Germano G, et al. Combined quantitative analysis of attenuation corrected and non-corrected myocardial perfusion SPECT: Method development and clinical validation. J Nucl Cardiol. 2010;17:591–9. doi: 10.1007/s12350-010-9220-8. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34.Klocke FJ, Baird MG, Lorell BH, Bateman TM, Messer JV, Berman DS, et al. ACC/AHA/ASNC guidelines for the clinical use of cardiac radionuclide imaging—executive summary: A report of the American College of Cardiology/American Heart Association Task Force on Practice Guidelines (ACC/AHA/ASNC Committee to Revise the 1995 Guidelines for the Clinical Use of Cardiac Radionuclide Imaging) Circulation. 2003;108:1404–18. doi: 10.1161/01.CIR.0000080946.42225.4D. [DOI] [PubMed] [Google Scholar]
- 35.Golub RJ, Ahlberg AW, McClellan JR, Herman SD, Travin MI, Mather JF, et al. Interpretive reproducibility of stress Tc-99m sestamibi tomographic myocardial perfusion imaging. J Nucl Cardiol. 1999;6:257–69. doi: 10.1016/s1071-3581(99)90037-5. [DOI] [PubMed] [Google Scholar]
- 36.Golub RJ, McClellan JR, Herman SD, Travin MI, Kline GM, Aitken PW, et al. Effectiveness of nuclear cardiology training guidelines: A comparison of trainees with experienced readers. J Nucl Cardiol. 1996;3:114–8. doi: 10.1016/s1071-3581(96)90003-3. [DOI] [PubMed] [Google Scholar]
- 37.Arsanjani R, Xu Y, Hayes SW, Fish M, Lemley M, Jr, Gerlach J, et al. Comparison of fully automated computer analysis and visual scoring for detection of coronary artery disease from myocardial perfusion SPECT in a large population. J Nucl Med. 2013;54:221–8. doi: 10.2967/jnumed.112.108969. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 38.Lindahl D, Lanke J, Lundin A, Palmer J, Edenbrandt L. Improved classifications of myocardial bull’s-eye scintigrams with computer-based decision support system. J Nucl Med. 1999;40:96–101. [PubMed] [Google Scholar]
- 39.Garcia EV, Cooke CD, Folks RD, Santana CA, Krawczynska EG, De Braal L, et al. Diagnostic performance of an expert system for the interpretation of myocardial perfusion SPECT studies. J Nucl Med. 2001;42:1185–91. [PubMed] [Google Scholar]
- 40.Scott JA, Aziz K, Yasuda T, Gewirtz H. Integration of clinical and imaging data to predict the presence of coronary artery disease with the use of neural networks. Coron Artery Dis. 2004;15:427–34. doi: 10.1097/00019501-200411000-00010. [DOI] [PubMed] [Google Scholar]
- 41.Candelieri A, Conforti D. A hyper-solution framework for SVM classification: Application for predicting destabilizations in chronic heart failure patients. Open Med Inform J. 2010;4:136–40. doi: 10.2174/1874431101004010136. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 42.Mohebbi M, Ghassemian H, Asl BM. Structures of the recurrence plot of heart rate variability signal as a tool for predicting the onset of paroxysmal atrial fibrillation. J Med Signals Sens. 2011;1:113–21. [PMC free article] [PubMed] [Google Scholar]
- 43.Stein DM, Hu PF, Chen HH, Yang S, Stansbury LG, Scalea TM. Computational gene mapping to analyze continuous automated physiologic monitoring data in neuro-trauma intensive care. J Trauma Acute Care Surg. 2012;73:419–4. doi: 10.1097/TA.0b013e31825ff59a. discussion 424–5. [DOI] [PubMed] [Google Scholar]
- 44.Lu Y, Wang X, Chen X, Zhao G. Computational methods for DNA-binding protein and binding residue prediction. Protein Peptide Lett. 2013;20:346–51. doi: 10.2174/0929866511320030013. [DOI] [PubMed] [Google Scholar]
- 45.Kohavi R. A study of cross-validation and bootstrap for accuracy estimation and model selection. Proceedings of the international joint conference on artificial intelligence; Montreal. 1995. pp. 1137–43. [Google Scholar]
- 46.Picaro R, Cook D. Cross-validation of regression models. J Am Stat Assoc. 1984;79:575–83. [Google Scholar]