Statistical resynchronization and Bayesian detection of periodically expressed genes

Abstract

We propose a periodic–normal mixture (PNM) model to fit transcription profiles of periodically expressed (PE) genes in cell cycle microarray experiments. The model leads to a principled statistical estimation procedure that produces more accurate estimates of the mean cell cycle length and the gene expression periodicity than existing heuristic approaches. A central component of the proposed procedure is the resynchronization of the observed transcription profile of each PE gene according to the PNM with estimated periodicity parameters. By using a two-component mixture-Beta model to approximate the PNM fitting residuals, we employ an empirical Bayes method to detect PE genes. We estimate that about one-third of the genes in the genome of Saccharomyces cerevisiae are likely to be transcribed periodically, and identify 822 genes whose posterior probabilities of being PE are greater than 0.95. Among these 822 genes, 540 are also in the list of 800 genes detected by Spellman. Gene ontology annotation analysis shows that many of the 822 genes were involved in important cell cycle-related processes, functions and components. When matching the 822 resynchronized expression profiles of three independent experiments, little phase shifts were observed, indicating that the three synchronization methods might have brought cells to the same phase at the time of release.

INTRODUCTION

The cell cycle program is encoded in the genomes of living organisms and is executed through the reciprocal interaction of gene expression and specific cellular processes. Saccharomyces cerevisiae (budding yeast) has been used as a major model organism to study which genes are expressed periodically during the cell cycle and how these genes in turn contribute to the cell cycle clock. Traditional experimental methods revealed over 100 genes that are cell cycle regulated in yeast (1). By taking advantage of recently developed microarray techniques, Cho et al. (2) conducted a genome-wide transcription analysis on synchronized yeast cells with a sequence of experiments covering about two mitotic cell cycles, from which they detected 421 periodic transcripts by visual inspection. Spellman et al. (1) applied additional synchronization techniques and identified 800 periodic transcripts by fitting to sinusoidal functions. Based on these time course microarray experiments, a number of strategies have been developed including clustering (3–6), the single-pulse model (7) and the partial least squares model (8). Despite these extensive efforts, there is still disagreement over whether these experiments are indeed informative on cell cycle-related genes (9) and, if so, which genes are periodically expressed in yeast cells. With the fast accumulation of functional genomics data, powerful statistical methods can help integrate information from various sources into a coherent picture of the molecular mechanisms underlying the cell cycle (10–13).

A significant hurdle in the identification of periodically expressed genes by microarray experiments arises from the substantial amount of noise in the observations. Although microarray technology can monitor transcription levels of thousands of genes simultaneously, only when the sampled cells are in good synchrony can time course readings reflect cell cycle course transcriptions. However, obtaining a pure synchronized population is non-trivial even for a single time point, and tight synchrony will decay gradually due to the diversity of individual cell growth rates. Consequently, expression profiles of periodically expressed genes observed from microarray experiments normally display a pattern that is relatively clear with a high and sharp peak within the first cell cycle, which becomes flatter or even undetectable in the ensuing cycles. With non-negligible synchrony decay, it is inappropriate to estimate the transcriptional periodicity directly from the microarray expression data without proper adjustment. In addition, efforts are also needed for handling the function fitting bias, the block/release effect and discrepancies between experiments. For example, the simple Fourier analysis may not fit a periodic profile that does not conform to a single sine wave. The same problem arises when applying the single-pulse model to periodic profiles with more than one peak. Even if the transcriptional periodicity could be accurately estimated within each data set, combining these poorly reproducible results can still be a challenging problem.

We propose a periodic–normal mixture (PNM) model, which is a linear combination of sinusoidal functions, to fit the transcription profile of every gene in cell cycle microarray experiments. Compared with the existing models such as simple sinusoid (1) or single-pulse (7), the PNM model is more flexible and provides a better fit to the data. For those periodically transcribed genes, the PNM model results in relatively small fitting errors (or residual), whereas, for non-periodically transcribed genes, the PNM residuals tend to be larger. We show that the sum of squares of the PNM residuals for a gene selected at random from the genome follows approximately a two-component mixture-Beta distribution: one component for those periodic transcripts and the other for non-periodic ones. We develop an empirical Bayes procedure based on this mixture-Beta distribution to determine genes that are periodically transcribed. Finally, we conduct phase matching of different experiments according to the resynchronized periodic transcripts.

We applied the PNM model to the budding yeast gene expression data sets, and obtained estimates of the cell cycle lengths and the rates of synchrony decay in five experiment series. Using an empirical Bayes procedure, we estimate that ∼32% of the 5510 tested genes may be periodically transcribed, among which 822 have a posterior probability of 0.95 or greater to be periodic. Among the 822 genes, 282 were absent from the list of 800 genes reported in Spellman et al. (1). Our gene ontology (GO) annotation analysis showed that many of these newly detected periodically transcribed genes are involved in important cell cycle-related processes, functions and components. Inter-experimental phase matching of these 822 adjusted profiles implies that the three synchronization methods might have brought cells to the same cell cycle phase at the time of release. The phase shift results were also used to infer the consensus transcription profiles of these periodically expressed genes.

MATERIALS AND METHODS

Data pre-processing

The data sets of five yeast cell cycle experiments, cdc28 (2), alpha, cdc15, elutriation (1) and fkh (10), were downloaded from the authors’ websites. For clarity, we name these data sets according to their synchronization methods. The first two time points of each data set were deleted in order to alleviate the block/release effect. The 90 and 100 min time points of the cdc28 data set were also deleted due to unsatisfactory hybridizations (4). The cdc28, alpha and cdc15 data sets were chosen for periodicity studies. From each of the three data sets, we discarded 1000 genes with least variation of expression level and also genes with 25% or more missing values (the model tends to over-fit with too much missing data). The remaining genes were centered and normalized with mean 0 and SD of 1. Out of a total of 6178 genes, 5510 passed the initial screening in at least two data sets, from which the periodically expressed genes were detected by fitting the PNM model and the two-component mixture-Beta model.

The PNM model

Let T be the length of the cell cycle period of a particular cell, and let ρ = 2π/T, which is called the cell cycle frequency or rate. We assume that the cell cycle rates of the yeast cell population follow a normal distribution, i.e. ρ ∼ N(µ,σ²). At time t, a cell reaches its cell cycle stage s = tρ. The transcription level V of a periodically expressed gene is described by a periodic function of stage (or time), i.e. V(s) = V(tρ) = V(tρ + 2nπ), which can be approximated by a linear combination of a few sinusoidal functions:

Because growth rates of cells within the population vary, the observed expression level of a gene at a certain time point is the summation of expression levels of that gene in cells residing in possibly different cell cycle stages, with the addition of an experimental noise ε. Thus, the observed expression level of a gene at time t, Y(t), can be modeled as:

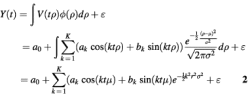
A particularly attractive aspect of assuming a normal distribution for the cell cycle rate is that the signal part of Y(t) can be represented as a linear combination of sinusoidal functions with exponential de-synchronization factors.

To compensate for the effect of synchrony decay, Spellman et al. (1) used 40 evenly spaced points around the estimated division time length to approximate the de-synchronization effect. Zhao et al. (7) assumed that the cell age (i.e. cell cycle time) follows a normal distribution with a standard deviation that grows exponentially along time. Here we argue that the main source of synchrony decay lies in the diversity of cell cycle frequency and, as shown by equation 2, that the synchrony of the cells decays exponentially in the square of time t (after the cells’ release) and the variance of the cell cycle rate σ².

Theoretically, the Fourier decomposition function 1 can approximate any continuous periodic function to infinite precision with an infinite number of sinusoids (K→∞). However, due to the limited number of measurement points, K must be limited to a small number to avoid over-fitting. We chose K = 3 here because the mean cell cycle length was estimated to be 60∼120 min in the three experiments considered in Spellman et al. (1), and there are only 9–12 measurement points in each cell cycle. When the cell cycle rate distribution (µ and σ) is known, the Fourier coefficients of each periodic transcript, a_k, b_k (k = 1, 2, 3), can be estimated from equation 2 using the least-square method.

Assessing the synchrony decay and the transcriptional periodicity

To estimate the synchrony decay, we started from a selected set of periodically expressed genes identified by traditional methods (1). The mean µ and SD σ of the cell cycle rate were inferred from the expression level of these genes by minimizing the total residual sum of squares (RSS):

where e_g² is the RSS for gene g, E denotes the selected set of periodically expressed genes, and t refers to the measurements in time. Different genes may have different transcription levels, V_g(tρ), but the cell cycle frequency distribution remains the same. Therefore, µ, σ, a_gk, and b_gk could be estimated iteratively by the following method. After computing µ and σ from the initial periodically expressed gene set, all genes in the data sets are fitted by the PNM model, and the top 100 genes with the smallest RSS are selected for another round of re-estimation of parameters µ and σ. The iterations are repeated until µ, σ and the top 100 genes become stable. The final µ and σ are then fixed in equation 2 to estimate the Fourier decomposition parameters a_gk, b_gk and the RSS e²_g for all pre-processed genes.

All of the five data sets were analyzed using the PNM model to estimate µ and σ. In the elutriation and fkh experiments, the data with regard to the second cell cycle are far from complete, and thus are not used to estimate the transcription periodicity. Only three data sets, namely cdc28, alpha and cdc15, were used in the following analyses.

Detecting periodically expressed genes

The periodic transcripts should have smaller RSS than the aperiodic transcripts. However, choosing a good threshold to separate the two groups of genes is non-trivial. Cho et al. (2) detected 421 periodic transcripts by visual inspection from one microarray experiment. Spellman et al. (1) combined three independent microarray experiments and significantly increased both the gene number and the reliability of the prediction. The ad hoc solution taken by Spellman et al. (1) is to sum up the periodicity measurements for each gene and design a cut-off value based on prior biological knowledge. Zhao et al. (7) chose a threshold for each experiment and overlapped the selected genes. His result contained three lists with increased reliability but a reduced number of genes. Due to the noisy nature of the experiments, we feel it necessary to develop a formal statistical procedure to combine different experiments and to identify periodically transcribed genes.

Note that the RSS of a periodic transcript g can be written as

Since Y(t) is normalized to have mean 0 and SD 1 before the model fitting step, the RSS is in fact equal to the ratio of two sums of squares:

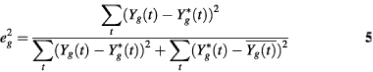
Hence, e_g² should follow a Beta distribution approximately. Similarly, for those aperiodic transcripts, when fitted by the PNM model, the RSS should also follow a Beta distribution but with different parameters. Therefore, the distribution of RSS in the whole data set could be approximated by a two-component mixture-Beta distribution. If we assume that the proportion of periodic transcripts is a fixed value across the three experiments, then the maximum likelihood estimates (MLEs) of the proportion of periodic genes, γ, and the parameters of the two Beta distributions, θ_ki, are the arguments that maximize the likelihood function

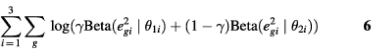
where e²_gi is the sum of squares of model fitting residuals of gene g in the i-th data set, and i = 1, 2, 3 corresponds to the three data sets: cdc28, alpha and cdc15, respectively. If γ is known, the posterior probability for gene g to be periodically expressed can be computed by the Bayes theorem:

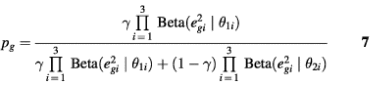
A gene with P_g ≥ 0.95 is declared as periodically transcribed.

Matching different experiments

We expect that expression profiles of most periodically expressed genes would be less varied under different synchronization techniques; otherwise, what can be found from the experiments would be no more than mere artifacts. Nevertheless, it is well known that different cell-arresting techniques may block cells at different checkpoints. The PNM resynchronized expression profiles enable us to compare the expression patterns shown in these different experiments, and to estimate the inter-experimental phase shifts by minimizing the matching errors.

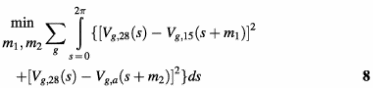
Here g refers to all the periodically expressed genes detected, s = tρ is the cell cycle stage, and V_g,28(s), V_g,15(s) and V_g,a(s) denote the transcription levels of the corresponding gene estimated from the three data sets. The cdc28 phase is used as a standard, since the data quality of cdc28 is relatively higher than that of the other two sets. The relative phase shifts of cdc15 and alpha (m₁ and m₂) can be estimated from equation 8. The transcription profile of a periodically expressed gene is estimated by the weighted average of the gene’s transcription patterns from the three data sets, with the phases adjusted:

Clustering of the periodic transcripts

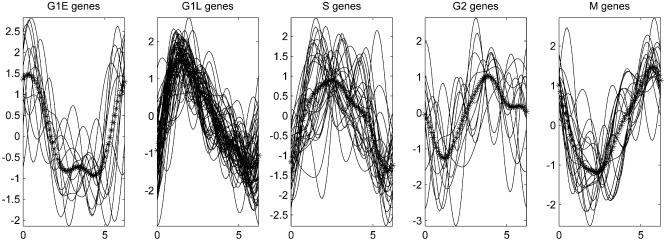
The periodically expressed genes detected by PNM can be assigned to five clusters based on their activation stages: M/G₁ (G₁ early), G₁/S (G₁ late), S, G₂ and M phases. We first selected five groups of well-studied genes with known activation stages. These genes and their active phases can be found in Table 1 of the Supplementary Material available at NAR Online. Five typical stage-specific transcription profiles were calculated by averaging the resynchronized transcription profiles of genes in each group. These five typical transcription profiles together with those of the genes that are used to derive them are plotted in Figure 1.

Table 1. The cell cycle period and synchrony decay in five microarray experiments.

	PNM	Spellman et al. (1)	Aach and Church (15)	Zhao et al. (7)
cdc28	83.2 ± 8.5	85		85
alpha	59.5 ± 5.2	66 ± 11	67.5 ± 6.5	58
cdc15	115.7 ± 11.1	110	119.0 ± 14.0	115
Elutriation	408.9 ± 52.3	390	422.5 ± 77.5
fkh	108.3 ± 18.7

The listed standard variations of T estimated by PNM are those at the end of the first cell cycle.

Figure 1.

Transcription profiles of five typical groups of stage-specific genes. Solid lines represent the transcription profiles of stage-specific genes. The line of asterisks represents the average transcription profile of the genes within each group.

The remaining periodically expressed genes are then assigned to the five groups by matching their profiles to the five typical stage-specific profiles according to the Pearson correlation coefficient. The clustering results can be found in Supplementary Table 1.

RESULTS AND DISCUSSION

The synchrony decay

Distributions of the cell cycle frequency in the five yeast cell cycle microarray experiments were estimated by the PNM model using equation 3, from which one can also derive the cell cycle period T and the rate of synchrony decay. The estimation results are listed in Table 1, together with some of the previous results. We see that PNM estimates of T are in close agreement with those reported previously. The synchrony decay at time t can be characterized by σt, where σ is the standard deviation of cell cycle frequency. For the data sets cdc28, alpha, cdc15 and elutriation, σ is estimated as ∼10% of µ, which means that by the time the cells complete their first cycle, the cell cycle stages of 95% of the cells in the population will span a range as wide as 40% of the whole cell cycle. This estimation is supported by the cytological observation that synchronized cdc28 yeast cells complete the first cell cycle in 70–110 min, a range of ∼48% of its cell cycle duration time (2). The large variation in cell cycle rate diversity results in such rapid synchrony decay that it is problematic to directly combine the information from the first cell cycle with that from the second one when measuring the periodicity of transcription profiles.

PNM resynchronization of genes

Although the Fourier transformation method adopted by Spellman et al. (1) and some other researchers (4,8,9,14) is powerful in periodicity analyses, it has been pointed out that cyclic patterns may not conform to a single sine wave (9). Similarly, the single-pulse model (7) is also too simplistic to capture the high-frequency information in periodic profiles.

The PNM model approximates periodic transcript expressions by Fourier decomposition, and describes the synchrony decay explicitly as an exponentially weighted mixture of periodic components (equations 1 and 2). It also facilitates a subsequent mixture-Beta method to reliably detect periodic transcripts. Furthermore, the PNM-based procedure estimates synchrony decay parameters by iteratively optimizing and selecting periodic transcript samples from the whole data set, which makes the result relatively independent of the genes chosen initially.

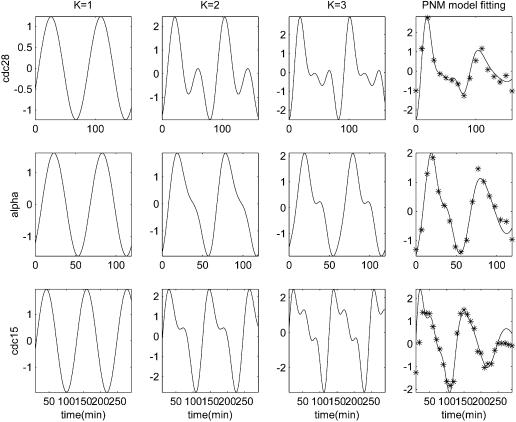
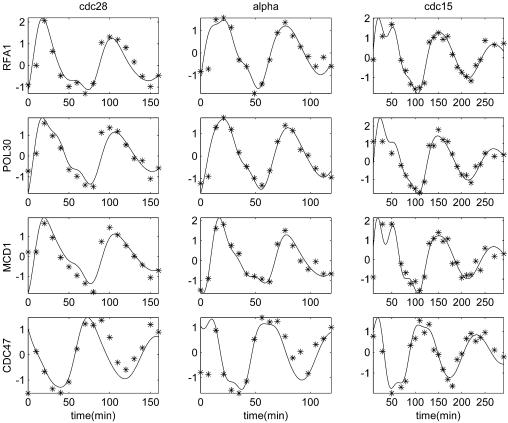
The PNM fittings of CLN2’s transcription profiles in the three data sets are shown in Figure 2. The PNM fittings of four other periodically expressed genes are plotted in Figure 3. The Fourier coefficients of all the periodically expressed genes detected by PNM can be found in Supplementary Table 1.

Figure 2.

The periodic–normal mixture model fitting of the CLN2 profiles in the three data sets: cdc28, cdc15 and alpha. Columns 1–3, transcription profile fitted with one, two and three sinusoids; column 4, the PNM fitting (K = 3 with normal mixture) to real observations. Solid curves are the PNM model and the asterisks are observations.

Figure 3.

The PNM model fittings of four periodically expressed genes in the three data sets: cdc28, cdc15 and alpha. Solid curves denote the PNM model and the asterisks denote observations.

Identification of the periodically expressed genes

The MLEs of the parameters in the mixture-Beta distribution for the RSS are listed in Supplementary Table 2. Both a numerical approximation method (Newton–Raphson) and the Metropolis–Hastings sampling approach were applied and they gave consistent results. Parameter γ is estimated as 32.3 ± 1.8%, implying that about one-third of the 5510 analyzed genes are periodically transcribed. Although this number is high, it is not too surprising that periodic transcripts make up about one-third of the whole yeast transcriptome given the importance of the cell cycle in the organization and replication of the cell. The posterior probability of every gene being periodically expressed was estimated by equation 7 with parameters fixed at their MLEs.

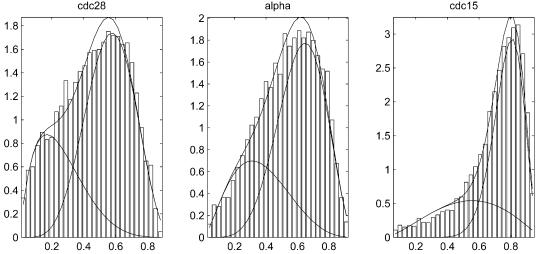
Figure 4 shows histograms of the RSS after fitting the PNM model to each gene in the three experiments. The approximations of these histograms by two-component mixture-Beta distributions are overlaid. It can be seen that in all three experiments, the two Beta distributions, corresponding to the periodic and aperiodic transcripts, overlap substantially due to the limited accuracy and stability of these experiments. Combining data from all the experiments improved the specificity of the prediction of periodic genes significantly. Using 0.95 as a cut-off, we obtained 822 genes whose posterior probabilities of being periodically transcribed, as computed using equation 7, are greater than or equal to the cut-off value. The list of 822 selected genes and their corresponding annotations can be found in Supplementary Table 1. Using a simulation method, we estimated that in the list of 822 genes we expect to see no more than eight false positives (details omitted).

Figure 4.

Histograms of model fitting residual sum of squares of the three data sets (cdc28, cdc15 and alpha) overlaid with the fitted mixture-Beta distributions.

Table 2 shows the comparison of our list of 822 cell cycle genes with the lists of such genes reported in some previous studies. Our list shares 540 genes with the list of 800 genes identified by Spellman et al. (1).

Table 2. PNM posterior probabilities of previously identified periodically expressed genes.

Method	No. of genes	PNM tested	Pmean	P > 0.95		Source
Traditional approach	104	102	0.865	78	76.5%	Spellman et al. (1)
Visual inspection	421	409	0.808	289	70.7%	Cho et al. (2)
Fourier transformation	800	788	0.822	540	68.5%	Spellman et al. (1)
SPM overlap-1	1106	1041	0.698	539	51.8%	Zhao et al. (7)
SPM overlap-2	260	257	0.963	229	89.1%	Zhao et al. (7)
SPM overlap-3	78	78	0.997	77	98.7%	Zhao et al. (7)

Pmean: mean posterior probability of each list. Pmean of PNM selected 822 genes is 0.992.

SPM overlap-1, 2, 3 are the lists of the genes which passed the SPM threshold one, two and three times in experiment cdc28, alpha and cdc15 according to the data from the authors’ website.

Overlaps of gene lists of traditional approach (T), Cho et al. (C), Spellman et al. (S) and Zhao et al. (Z) are: T–C 73, T–S 95, T–Z 88, C–S 304, C–Z 304 and S–Z 525.

As a control experiment, we performed two randomization tests to check the validity of the mixture-Beta model versus the single-Beta model. In the first test, we generated a set of RSS with the same size as the real data set by randomly sampling from a Beta distribution. In the other test, we permuted the time points of each gene to remove the time trend, fitted it by the PNM model, and calculated the model fitting RSS. These RSS are then fitted by the mixture-Beta distribution as done with the real data sets. In addition, these RSS were also fitted by a single-Beta distribution, and the differences between the log-likelihoods of the two models were calculated. Both tests were repeated 100 times, resulting in 200 log-likelihood differences. For comparison, the real data set was also fitted by a single-Beta distribution and the same log-likelihood difference was computed. We observed that the log-likelihood difference for the real data exceeded all of the 200 simulated ones, which strongly supports our use of the two-component mixture-Beta model.

The expression phases of the periodically expressed genes

According to previous studies, different synchronization techniques arrested yeast cells at different cell cycle phases: cdc28 at G₁/S, cdc15 at M phase and alpha at G₁ phase (1). However, this does not imply that the arrested cells will re-enter their cell cycle at the point where they were being blocked. We estimated the relative phase shifts m₁ (cdc15–cdc28) and m₂ (alpha–cdc28) by equation 8 and obtained m₁ = 2.1% and m₂ = 8.6% of one entire cell cycle. These results imply that in the three experiments, the yeast cells may have restarted their cell cycles from roughly the same phase. A possible explanation is that, although the former cell cycle program was blocked at different phase points, 120–210 min of arrest duration gave yeast cells enough time to overcome the blocking effect and hence the cells were fully prepared to enter the next cell cycle. Consequently, at the time of release, yeast cells can initiate the next cell cycle without finishing the former paused one. This prediction is supported by experimental evidence that in the cdc28 experiment, budding started at ∼30 min after release (0.36T, T = 83.2 min) (2), and in the cdc15 experiment, budding started within 50 min of release (before 0.43T, T = 115.7 min) (1). Although dumbbell-shaped cdc15 mutant cells appear to be arrested at late M phase without finishing the former division, at the end of arrest the undivided cells have already grown large enough to start the next division, and most of the G₁ functions have already been achieved. Therefore, after being released, the cells could get into S phase almost immediately. In fact, small buds appeared shortly after release in the cdc15 experiment as in the other two. The M phase-arrested appearance is simply a consequence of the physical separation of the nucleus and the cytoplasm that occurs due to the cell arrest techniques.

After estimating the relative phase shifts among the three experiments, we integrated the three transcription profiles and obtained the consensus transcription profile functions as weighted averages of the corresponding profiles from the three experiments using equation 9. These profile functions were used to estimate the expression phases of the genes which were assigned to five stage-specific profile classes (Fig. 5).

Figure 5.

Clustering of the 822 PNM-identified periodic transcripts into the five stage-specific groups.

Our phasing results match well with that of Spellman et al. (1) in most cases, with only ∼20% of the genes (110) assigned differently. Most of these 110 genes were assigned to the adjacent phases in Spellman et al. (1). For example, 32 of our M/G₁ genes were phased at G₂/M by Spellman et al. (1), but many of these genes, such as FAR1, CLN3 and pre-replication complex genes MCM2, MCM6, CDC54 and CDC47, are well known to be expressed at the stage immediately after exit, and peaked in early G₁. We assigned SWI4 to G₁/S instead of M/G₁, which agrees well with the observation that SWI4 was expressed in a positive feedback at START and peaked at G₁/S. More details can be found in Supplementary Table 1.

Annotation study of the periodically expressed genes

The biological roles of the 822 PNM detected periodically expressed genes as well as those detected by Spellman et al. (1) were analyzed using the Saccharomyces Genome Database (SGD) GO Term Finder (http://www.yeastgenome.org), and the P-value for each term was calculated. Table 3 lists the number and portion of genes annotated by GO as ‘cell cycle’ for both the PNM-identified and Spellman-identified genes. The GO terms that are significantly over-represented in the list of 822 PNM-identified cell cycle genes with P-values less than 10^–5 are listed in Supplementary Table 3. The results show that nearly all of the top significant terms are involved in the chromosome cycle, spindle cycle and bud cycle. On the other hand, far fewer periodically expressed genes are involved in the general transcription apparatus, protein synthesis, mitochondrion metabolism and other cytoplasmic processes. Only a small number of periodically expressed genes were involved in transportation, signaling or protein modification functions.

Table 3. Over-representation of the 822 periodically expressed genes in SGD Gene Ontology terms.

	No. of genes	Process knowna	Cell cycleb	Cell cycle/known (%)
Gene Ontologyc	5814	3999	496	12.4
PNM (P)d	822	524	146	27.9
Spellman et al. (S)e	800	529	141	26.7
S and Pf	540	353	121	34.3
P–Sg	282	171	25	14.6
S–Ph	260	168	17	10.1

^aThe number of genes with known process by Gene Ontology.

^bThe number of genes annotated as ‘cell cycle’ by Gene Ontology.

^cAll of the genes covered by Gene Ontology.

^dThe periodically expressed genes identified by the PNM model (P).

^eThe periodically expressed genes identified by Spellman et al. (S).

^fThe genes identified by both PNM and Spellman et al.

^gThe genes identified only by PNM but not by Spellman et al.

^hThe genes identified only by Spellman et al. but not by PNM.

Thirty-two additional GO terms were found in which all genes under these terms were in the list of 822 genes. Most of these GO terms are closely related to the cell cycle. They are absent from Supplementary Table 3 only because the total number of genes under these terms was too small. The terms with three or more genes are: pre-replication complex (eight genes), kinesin complex (six genes), DNA repair synthesis (four genes), DNA replication factor A complex (three genes), cation antiporter (three genes), septin checkpoint (three genes) and heteroduplex formation (three genes).

In addition to functional analyses of the entire set of genes identified by the PNM model, we also compared genes that were uniquely identified by Spellman et al. (1) with those uniquely identified by PNM analyses. After the elimination of unannotated open reading frames (ORFs) and those currently listed as dubious from both sets, analysis with GO Term Finder revealed that the PNM model uniquely identifies and significantly enriches for a number of additional ‘cell cycle’ genes (P = 2.1 × 10^–2, 25 genes), whereas Spellman et al.’s enrichment is less significant (P > 0.05, 17 genes). Although both approaches enrich for different sets of periodically expressed genes identifiably involved in the cell cycle that are listed under ‘growth and/or maintenance’ (PNM, P = 6.54 × 10^–10; Spellman, P = 3.00 × 10^–10), the PNM model uniquely identifies a number of functionally related groups of genes whose expression peaks during the cell cycle phase(s) in which such processes are known to occur. These include a number of genes found in categories such as the organization and biogenesis of the cell (P = 8.01 × 10^–7), cytoplasm (P = 1.89 × 10^–3), chromosome (P = 1.93 × 10^–3), nucleus (P = 2.97 × 10^–3), organelle (P = 2.93 × 10^–3) and mitochondrion (P = 5.79 × 10^–3), as well as those involved in mitochondrial genome maintenance (P = 1.43 × 10^–5), mitochondrial fission (P = 3.02 × 10^–3) and vacuole inheritance (P = 6.50 × 10^–3). Moreover, a substantive fraction of these genes has been shown to be essential for normal progression through the cell cycle.

In comparison, the approach of Spellman et al. uniquely identifies groups of periodically expressed genes involved in processes that are less identifiably cell cycle related, such as metabolism (organic acid, carboxylic acid and amino acid P = 9.63 × 10^–7) and, seemingly the meiosis-specific processes of, reproduction (P = 1.40 × 10^–6) and conjugation (P = 2.23 × 10^–6), which are probably responses to environmental stresses and external mating signals rather than to natural cell cycle needs. Although it is difficult to assess which approach may be better suited to identify cell cycle-specific genes, these analyses indicate that the PNM model uniquely enriches for functionally related genes that are readily identifiable as being involved in the cell cycle.

On the other hand, for many cell cycle-related GO terms (e.g. cell cycle and cell proliferation), only a small portion of genes (∼30%) belong to the list of 822 cell cycle genes. The remaining genes whose expression does not show significant cell cycle features may be weakly periodic genes, housekeeping genes, silent genes or genes that respond to signals other than cell cycle events. This implies that for many cell cycle events, only a small portion of the involved genes are transcriptionally regulated, leaving others to be regulated at post-transcriptional levels.

We found 166 adjacent pairs among the 822 periodically transcribed genes where the term ‘adjacent gene pair’ refers to a pair of genes on the same chromosome without any ‘chromosomal features’ between them (http://www.yeastgenome.org, SGD, April 19, 2003). ‘Chromosomal features’ include ORF, ARS, CEN, rRNA, tRNA, snRNA, snoRNA, RNA genes, LTRs and transposons. Fifty-four percent of the 48 co-upstream pairs and 52% of the 44 co-downstream pairs showed a similar expression pattern with a coefficient of correlation between the pair of genes greater than 0.5, e.g. the four pairs of histone genes. On the other hand, only 39% of the 74 serial pairs showed a similar expression pattern with a coefficient of correlation greater than 0.5. Furthermore, we found three pairs of genes that showed ‘inverse’ expression pattern with a coefficient of correlation lower than –0.5. These include CLB1–CLB6 and CLB2–CLB5, both of which are co-downstream, and IST2–RFC5, which are co-upstream. It may be interesting to investigate further how these adjacent gene pairs are co-regulated or reversely regulated by their shared upstream or even downstream regions.

SUPPLEMENTARY MATERIAL

Supplementary Material is available at NAR Online.