A biologist's view of the relevance of thermodynamics and physical chemistry to cryobiology

Abstract

Thermodynamics and physical chemistry have played powerful roles the past forty-five years in interpreting cryobiological problems and in predicting cryobiological outcomes. The author has been guided by a few core principles in using these concepts and tools and this paper discusses these core principles. They are (1) the importance of chemical potentials and of the difference between the chemical potentials of water and solutes inside the cell and outside in determining the direction and rate of fluxes of water and solutes. (2) The influence of the curvature of an ice crystal on its chemical potential and on the ability of ice to pass through pores in cell membranes, on the nucleation temperature of supercooled water, and on the recrystallization of ice. (3) The use of Le Chatalier's Principle in qualitatively predicting the direction of a reaction is response to variables like pressure. (4) The fact that the energy differences between State A and State B are independent of the path taken to go from A to B. (5) The importance of being aware of the assumptions underlying thermodynamic models of cryobiological events. And (6), the difficulties in obtaining experimental verification of thermodynamic and physical-chemical models.

“Mazur”, said a member of my Ph.D. thesis committee, “With your interest in cryobiology, you should consider taking a course in physical chemistry.” A “suggestion” by one's Ph.D. committee is not to be dismissed lightly. So early that summer I hied myself down to the University of Pennsylvania in Philadelphia to talk with the chemistry professor who was teaching it. (I was spending the summer on our family farm, about 40 miles away). He agreed to let me take his intensive 6-week course even though I lacked chemistry prerequisites. It turned out to be the wisest choice I had made career-wise, for it evolved into the single most valuable academic course from the view point of my subsequent devotion to cryobiology. It has been most valuable even though my knowledge of the field and the underlying analytical tools is primitive–freshman math, freshman physics, freshman chemistry. One advantage of this primitiveness is that it has forced me to identify and be guided by certain core concepts. I thought that perhaps a discussion of these core principles might prove useful to other cryobiologists, especially those who are biologists lacking intimate knowledge of physical chemistry and thermodynamics.

Chemical Potential

The first of these concepts is that of chemical potential. It is analogous to other forms of potential energy such as gravitational potential and electric potential. Potential energy has the capacity to do work; e.g., move a mass though a distance. Chemical potential (symbolized μ) has several important aspects. The first is that molecules move from a region where their chemical potential is high to a region where their chemical potential is low. Second, the rate at which they move is proportional to the magnitude of the difference in chemical potential, δμ. Third, when δμ = 0, that species of molecule is in equilibrium.

The term chemical potential and the symbol μ are shorthand for (Gibbs) free energy per mole; i.e, δμ = δF/mole [11, p. 208]. (Many writers use the symbol G in place of F). If δF is negative in going from state A to state B, that process or reaction will occur spontaneously. If δF is positive, the process will not occur spontaneously–rather the conversion of state B to A will be spontaneous. If δF = 0, states A and B are in equilibrium. A fundamental equation in thermodynamics is that the change in free energy in going from state A to B is equal to the amount of heat released or absorbed (enthalpy) minus the entropy (change in the degree of order). Formally,

$$\Delta \mathrm{F}=\Delta \mathrm{H}-\mathrm{T}\Delta \mathrm{S}$$ Eq. (1)

F and H have the units cal/mole or joules/mole; S has the units cal/mole-deg. Commonly, δF and δH have the same algebraic sign and are similar in value. But there are many exceptions, one of which is of direct cryobiological significance. Consider a mixture of ice and pure water at 0°C. There is no free energy change in going from ice to water at 0°C or the reverse; therefore δF = 0 and δμ = 0 and the system is defined as in equilibrium. Yet a large amount of heat (enthalpy) is released in going from water to ice (–1436 calories/mole) and an equally large amount is absorbed in going from ice to water. The only way the left and right sides of the equation can balance is for the entropy term (TδS) to be equal and of the same sign as the enthalpy. In other words, the conversion of water to ice is accompanied by a large release in heat (negative δH and a large decrease in entropy (negative δS) such that δF = 0. That makes intuitive sense since ice is more ordered than liquid water.

Alternative expressions for the chemical potential of water

Some of the equivalent expressions for chemical potential of water [11, 16] are

$${\mu }_{\mathrm{w}}-{{\mu }^{\mathrm{o}}}_{\mathrm{w}}=\mathrm{RT}\ln \mathrm{p}∕{\mathrm{p}}^{\mathrm{o}}=\mathrm{RT}\ln {\mathrm{a}}_{\mathrm{w}}=-\Pi {\mathrm{v}}_{\mathrm{w}}=\Delta {\mathrm{T}}_{\mathrm{f}}∕1.855=-{\text{RTv}}_{\mathrm{w}}\left[\Sigma \right]\phi \nu \mathrm{m}==-{\mathrm{v}}_{\mathrm{w}}\mathrm{RT}\mathit{M}.$$ Eq. (2)

In these equalities, superscript o refers to the pure solvent (here, water) and subscript w refers to water, p is the vapor pressure of water in the aqueous solution, a_w is the activity of water in the solution, R is the gas constant (1.987 calories/deg. mole= 0.0821 liter. atm/deg. mole), T is absolute temperature (K), v_w is the partial molar volume of water (0.018 liters/mole), Π is osmotic pressure, δT_f is the freezing point depression, 1.855 is the molal or osmolal freezing point depression for water, m is the molality, and M is the osmolality. The symbol ν is the number of species into which the solute dissociates (e.g., 1 for sucrose, 2 for NaCl, 3 for CaCl₂), and finally φ is the osmotic coefficient, values of which are tabulated for common solutes in sources like Robinson and Stokes [17, Appendices 8.3, 8.6, 8.10].

There are some subtlies in these equivalences. First, as written, the molality, m, has the units moles/liter of water. Its actual units are moles/kg. water, So for exactness, a density term has to be included. I omit it for simplicity and because the density of water is so close to 1 g/cm³. Second, the summation symbol in the fourth equivalence is (purposefully) ambiguous. In theory, the total osmolality of solutions that are more complex than binary is not equal to the summation of the osmolalities of its component binary solutions. This is because the solutes interact with each other and with water to affect the osmotic coefficient φ. However, in practice, Kleinhans and Mazur [10] have shown that for several ternary solutions (two solutes and water), the summation of the φνm's of the two underlying binaries yields osmolalities for the ternary that agree with experimental values to within ~5% at concentrations up to 30 to 50 wt %. My guess is that that will also apply to quartenary solutions. But surely, it will not be applicable to highly complex solutions such as those constituting cytoplasm, and will not be applicable to highly concentrated solutions.

There is a third subtlety. The first four equivalences (vapor pressure, activity, osmotic pressure, and freezing point depression) are all properties of the aqueous solution. Indeed they are so-called colligative properties (properties dependent on the numbers of molecules or ions and not their chemical nature). Each of these expressions involves certain simplifying assumptions [11, p.406][16]. But the fifth equivalence, –RTv_w[Σ] φνm), is different, for it is primarily expressed in terms of the mass concentration of solutes, the molality. The chief link between the two (properties and composition) is Raoult's Law, which for ideal solutions is p= p^o x₁, where x₁ is the mole fraction of water. The mole fraction of course can be converted to other measures of mass concentration such as molality and weight fraction. Raoult's law begins to yield increasingly inaccurate results as the solute concentration increases, and φ is an empirically determined factor to correct for that. As can be seen from this brief description of the equivalences, the osmolality is a hybrid quantitiy. In one sense, it is a property of the solution since its value can be derived from any one of several colligative properties. But in another sense, it is a measure of solute concentration since its value is closely related to the gravimetric concentration.

Another interesting equivalence is that p/p^o is numerically equal to the relative humidity. Although not of direct interest to cryobiology, it can be a matter of interest in freeze-drying and in drying from the liquid state. Note that at a relative humidity of 50% (a_w = 0.5), a solution will come to equilibrium when its water activity is reduced to half that of pure water. An a_w of 0.5 represents a very large driving force for water efflux, much larger than that occurring in osmosis in aqueous solutions. For example, a 1 molal solution of sucrose in water is 1.088 osmolal and the activity of its water (a_w) is 0.981.

Pictorial representations

I personally grasp phenomena better when I can visualize them than when they are just expressed mathematically. Consider some examples:

• ◦Osmotic changes in cell volumes in the presence of non-permeating solutes. Consider a re-sealed red cell ghost, the contents of which are 0.3 osmolal sucrose placed in a 1.3 osmolal solution of sucrose to which it is impermeable. (A ghost contains no macromolecular solids to complicate the issue). Since some of the solution is occupied by sucrose molecules, the number of water molecules per unit volume of solution will be higher inside the ghost than outside. The water molecules are in random motion. Since their initial concentration is higher inside the ghost than outside, more will move per unit time from inside-out than from outside-in, and the ghost will shrink. This will continue at a progressively lower rate until there is only an infinitesimal difference between the water concentrations inside and outside, at which point the chemical potentials of water inside and out will be the same, and equilibrium will have been achieved.
• ◦Osmotic changes in cell volumes in the presence of mixtures of permeating and non-permeating solutes. Fig. 1A depicts a cell, the cytoplasm of which is 0.3 osmolal impermeable salts immediately after being abruptly transferred from a solution of 0.3 osmolal PBS to a solution of 1.0 osmolal ethylene glycol (EG) in 0.15 osmolal PBS. The cell is assumed to be permeable to the EG but not to PBS salts. The chemical potential of the water in the cell (–RTM_T) exceeds that of water in the medium (−174.6 cal/osmole vs. −669.5 cal/osmole at room temperature). As a consequence, there is a driving force for water to leave the cell. On the other hand, the chemical potential of EG (~ = osmolal concentration) is higher outside the cell than inside the cell (where it is zero initially). This establishes a driving force for EG to enter the cell. The chemical potential of the PBS salts is higher inside the cell than outside, but they can not cross the plasma membrane in response because it is impermeable to them.

These initial conditions trigger the following responses, which we describe here as sequential steps even though they are in fact continuous:

• *The cell quickly loses sufficient water (and undergoes a concomitant reduction in volume) to make the total internal osmolality equal to the total external osmolality (1.15 Osm); i.e., the water volume is reduced to 26% of isotonic (Fig. 1B).

Fig. 1.

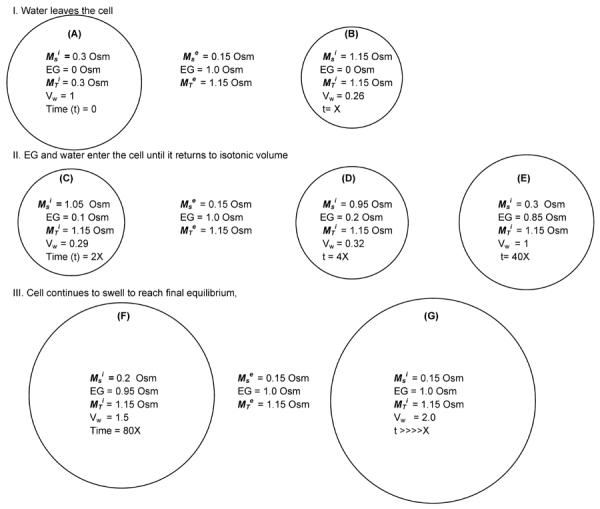
Schematic of changes in the osmolalities of water and solutes and in the volume of water in a cell abruptly transferred from isotonic (0.3 osmolal) PBS to a solution of 1 osmolal ethylene glycol (EG) in hypotonic salt (0.15 osmolal). The cell is assumed to be permeable to the former but impermeable to the later. The superscripts i and e refer to inside and outside the cell, M_s and M_T are the osmolalities of salt and the total osmolality (salt + EG). V_w is the volume of water in the cell relative to its volume in an isotonic cell. The time scale is arbitrary except to indicate that the swelling process in C–G is much slower than the shrinking process in A to B. The circles represent the variations in cell size but are not drawn quantitatively to scale.

An incremental number of moles of EG enter the cell (Fig. 1C). This transiently increases the total internal osmolality above that of the external and slightly decreases the chemical potential of the intracellular water; consequently, to reestablish equality of the chemical potentials of water, additional water has to move into the cell, which undergoes a further small increase in water volume; namely, to 28.6% of isotonic. However, the chemical potential of the external EG still exceeds that of the internal so more EG flows into the cell. Again, this slightly increases the total internal osmolality, and still more water has to move in to reestablish equality between the chemical potentials of external and internal water (Fig. 1D). The cell water volume is now 31.5% of isotonic. This cycle repeats. Fig. 1E is a snapshot of conditions when the cell water volume has returned to isotonic. However, the osmolality of the external EG (1.0 Osm) still exceeds that of the internal EG (0.85 osmolal) so EG along with water continue to move into the cell, albeit at a lower rate. Eventually, the cell attains equilibrium for all components (Fig. 1G). The chemical potentials of the salts and of EG are equal inside and out. And the cell water volume is twice the isotonic value because the osmolality of external salts is half of isotonic.

To obtain a quantitative picture of the kinetics of this process, one needs to apply a numerical solution to two coupled differential equations. This first describes the rate at which water leaves or enters the cell; namely,

$$\mathrm{dV}∕\mathrm{dt}={\mathrm{L}}_{\mathrm{p}}\mathrm{A}({{\mu }_{\mathrm{w}}}^{\mathrm{i}}-{{\mu }_{\mathrm{w}}}^{\mathrm{e}})∕{\mathrm{v}}_{\mathrm{w}}={\mathrm{L}}_{\mathrm{p}}\mathrm{A}({\Pi }^{\mathrm{e}}-{\Pi }^{\mathrm{i}})={\mathrm{L}}_{\mathrm{p}}\mathrm{A}\mathrm{RT}({\mathit{M}}^{\mathrm{e}}-{\mathit{M}}^i)$$ Eq.(3)

where L_P is the hydraulic conductivity for water (μm. min⁻¹. atm⁻¹), and superscripts e and i refer to external and internal, respectively. R is the gas constant in units of μm³.atm/deg.mole. (Again I have excluded the density term to convert mass to volume in the osmolality, and assume a value of 1)

The second equation describes the rate at which the CPA enters the cell; namely,

$${\mathrm{dn}}_{\mathrm{s}}∕\mathrm{dt}={\mathrm{P}}_{\mathrm{s}}\mathrm{A}({{\mathrm{m}}_{\mathrm{s}}}^{\mathrm{e}}-{{\mathrm{m}}_{\mathrm{s}}}^{\mathrm{i}})$$ Eq. (4)

where s refers to the CPA, n_s is moles of solute, P_s is the permeability coefficient of the solute (cm/min), and m is the molality of the solute. Kleinhans [9] has shown that equations 3 and 4 and simultateous solutions to them gives an accurate description of the kinetics of flow of solvent and solute in most cases. In other words, it is not necessary (and may be erroneous) to use the more complex equations of Kedem and Katchalsky's irreversible thermodynamics that require the introduction of a third parameter, the reflection coefficient, sigma.

An interesting and, at first thought, perplexing situation is that of a higher plant cell suspended in and equilibrated with water containing an extremely low concentration of solutes or none at all. The solute-dependent chemical potential of the external water (v_wRT[Σ]ϕνm) is higher than that of the intracellular water. Consequently, thermodynamically, water should move into the cell diluting the internal solution. However, to lower the solute concentration of the intracellular water to zero and thereby raise its chemical potential, μⁱ_w, to that of the outside water, the cell would have to swell to infinite volume. Since that is impossible, how is chemical potential equilibrium attainable? The answer is that the protoplast in the cell of a higher plant is enclosed within a rigid cellulosic wall. As the protoplast begins to expand in response to the osmotically driven water entry, the rigid wall begins to exert a hydrostatic pressure, and that pressure raises the chemical potential of the intracellular water to equal that of the external water. This means that Eq. (1) is incomplete in lacking a hydrostatic pressure term. The more complete expression is:

$${\mu }_{\mathrm{w}}={{\mu }^{\mathrm{o}}}_{\mathrm{w}}-{\mathbf{v}}_{\mathrm{w}}\mathbf{RT}\left[\Sigma \right]\varphi \nu m+{\mathbf{v}}_{\mathrm{w}}\mathbf{P}$$ Eq (5)

where P is the hydrostatic pressure. (Still fuller expressions for chemical potential can include terms for electric potential).

What is the melting point of ice?

“An absurd question” might be your instant reaction; “it is 0°C”. Well, yes and no. Yes, it is 0°C if no solutes are present, if the pressure is one atmosphere, and if the ice crystals are flat. However, it is below 0°C if solutes are present, if the pressure is greater than 1 atmosphere, or if the crystal is positively curved. The first is highly familiar and is a matter of major cryobiological significance. As indicated earlier, the melting point is lowered 1.86°C for each osmolal increase in solute concentration. The second is a small effect (1 atmosphere of excess pressure lowers the melting point 0.01°C) and is only rarely a matter of cryobiological significance. The third, curvature, is more subtle but is of major importance in cryobiology. The effect of radius of curvature of an ice crystal on its melting point in water is given by the Kelvin equation (also referred to the Gibbs-Thompson equation [Lord Kelvin's actual name was Thompson]; namely,

$$\Delta {\mathrm{T}}_{\mathrm{f}}=2\mathrm{v}{\sigma }_{\mathrm{SL}}{\mathrm{T}}_{\mathrm{f}}∕{\mathrm{rL}}_{\mathrm{f}}$$ Eq. (6)

where v is the molar volume of ice, T_f is the melting point of a planar crystal, σ_SL is the interfacial tension between liquid water and ice, r is the radius of the ice crystal, and L_f is the latent heat of fusion. Fletcher [3] has estimated the value of σ_SL to be about 20 ergs/cm². Consequently, if the curved crystal has a radius of 12 A°, its melting point will be about 10°C below that of a planar crystal. Details on the thermodynamic derivation of the equation are given by Mazur [13, pp 222–227]. Subsequently, Acker et al. [1] refined the equation by adding a term to handle the situation when the ice is in a solution.

Why should the melting point be suppressed by curvature? It is because the chemical potential or vapor pressure of the water molecules at the convex surface of a curved ice crystal exceeds that of water molecules at the surface of a flat ice crystal by an amount inversely proportional to the radius of curvature. The vapor pressure of ice falls faster with decreasing temperature than the vapor pressure of liquid. This is accounted for by another classical thermodynamic relationship, the Clausius-Clapyeron equation. It shows that dp/dT for ice depends on the latent heat of sublimation whereas that of water depends on the latent heat of vaporization, and the former exceeds the latter by the latent heat of fusion, L_f. For a planar ice crystal, the vapor pressures of ice and water become equal at 0°C, but for a 12 A° radius crystal, the two do not become equal until around −10°C. I visualize the situation as follows: A given water molecule on the surface of a planar ice crystal (infinite radius of curvature) can be pictured as being hydrogen bonded to an average of three neighboring water molecules, one on each side, and one below. But a given water molecule on the surface of a convex ice crystal has fewer neighboring water molecules. This means fewer intermolecular hydrogen bonds, and a higher “escaping tendency”, a term used synonymously with vapor pressure.

There are at least four areas where these curvature effects have important cryobiological ramifications. The first is the matter of ice propagating from the aqueous medium surrounding a cell into its interior through putative pores in the plasma membrane The second is the matter of ice propagating from one cell to another in multicellular assemblies through gap junctions between them. The third is in the matter of the temperature at which supercooled cellular water freezes and the fourth area deals with the conditions under which small internal ice crystals are converted into larger ones.

With respect to the first, and to some extent the third, we have shown [15] that mouse oocytes suspended in 1 to 1.5 M ethylene glycol or glycerol do not undergo IIF until the temperature has dropped close to −40°C. A temperature of −40°C is at or close to the temperature (T_h) of the homogeneous nucleation of a water drop with a volume equal to that in mouse oocytes. This is the temperature at which supercooled water nucleates spontaneously in the absence of nucleating agents. Why such a low temperature? One theory of the structure of liquid water is that periodically by chance small numbers of water molecules will transiently align themselves to form the tetrahedrally hydrogen-bonded structure that constitutes ice. A cluster of ice (often called an embryo) has a critical size. If it is smaller than that size, it will disappear; if it is larger than that size, it will grow. This is because two opposing forces are in play. The larger the volume or mass of the ice embryo, the larger its free energy; consequently, it is energetically favorable for it to shrink. However, the smaller the embryo, the greater becomes its surface free energy; consequently, it is energetically favorable for it to reduce its surface to volume ratio by growing. The critical size ice embryo is one where the two forces are equal and opposite. From a variant of the Kelvin equation (Eq. 6), one can show that the higher the temperature, the greater the radius of curvature has to be for an ice embryo to exist. But the larger the radius of curvature, the larger is the required size of the ice embryo, and the lower is the probability that it can form by random orientation. At T_h (~ −40°C), the critically sized ice embryo contains only a few water molecules; therefore, the probability of its forming spontaneously is very high (essentially 1).

But in mouse oocytes suspended in concentrations of EG or glycerol < 1 M and in many other cells, IIF occurs at temperatures well above T_h. In such cases, supercooled cell water is being nucleated heterogeneously; i.e., by a “foreign” agent. The general thought is that the surfaces of effective heterogenous nucleators contain chemical groups capable of hydrogen bonding with water molecules and spaced so as to coincide with the spacing of an ice lattice. We have argued that the most likely nucleator of intracellular water is external ice itself. The main differences between a heterogenous nucleator and a critical size embryo in homogeneous nucleation is that the heterogenous nucleator can be much larger than the critical size ice embryo, it doesn't have to form spontaneously, and it is stable at all temperatures below the melting point of the solutions. External ice crystals meet these requiremements as do the membrane fragments of the ice-nucleating bacterium, Pseudomonas syringii.

A second area where the reduced melting point of curved ice crystals plays a role is in the propagation of intracellular ice from one cell to an adjoining one in multicellular systems. Cells in these systems commonly form tightly apposed plasma membranes and usually these are penetrated by gap junctions which form a pore with a radius of some 7.5 to 9 A°. To penetrate such a pore, an ice crystal must assume a curvature of a comparable radius, and as Eq. 6 shows, such a crystal has its melting point suppressed by approximately 10°C. That means that if the temperature exceeds ~ −10°C, the ice crystal would melt in any attempt to grow through the pore. Acker et al [1] and Irimia and Karlsson [6] have examined the cell to cell propagation of ice in monolayers of tissue culture cells and in cell doublets and found that the temperatures at which these propagations occur are consistent with these predictions from the Kelvin equation. I say “consistent with” rather than “in agreement with” because one parameter that is not known is the contact angle that ice makes with the lining of the pore. That contact angle determines the relation between the radius of curvature of the ice and the radius of the pore.

The fourth area where the curvature of ice plays an important role is in determining the events that occur during the warming of vitrified cells or of cells in which very small ice crystals have formed during cooling. Small ice crystals have higher surface free energies than larger ones; consequently, in a mixture of crystal sizes, the larger crystals, over time, will tend to grow at the expense of smaller, or the smaller will fuse to produce a larger crystal. This process is referred to as recrystallization. The thermodynamic equations to describe the process have been derived by Kingery [8] and have a form similar to the Kelvin equation (Eq. 6). Kingery also measured the kinetics of the process in ice between −25°C and −2°C, and found it had a very high activation energy of 29 kcal/mole. Seki and Mazur [18] have found that partially dehydrated mouse oocytes do not undergo intracellular ice formation during cooling but turn black during warming, a process that definitely appears to be recrystallization. They too found the activation energy of the process to be very high; i.e., 27.5 kcal/mole.

Le Chatalier's Principle

In 1885, Le Chatalier developed the concept that “if a change occurs in a factor such as temperature or pressure, under which a system is in equilibrium, the system will tend to adjust itself so as to annul, as far as possible, the effect of that change.” Glasstone [5, p. 831] states that the principle is derived from the 2^nd law of thermodynamics and is applicable to all systems in equilibrium; e.g., solid-liquid, solid-solid as well as chemical reactions. For example, ice and liquid water are in equilibrium at 0°C at 1 atmosphere. Ice, however, has a 10% larger specific volume, so that the application of pressures > 1 atmosphere, suppresses the larger volume state (ice) and drives the equilibrium melting point to lower temperatures. Quantitatively, the effect is that each added atmosphere of pressure decreases the melting point by 0.01°C. Another example–The passage from initial state A to final state B usually involves moving through an intermediate activated state which has higher energy than either A or B. If this activated state has a larger volume than either states A or B, then by Le Chatalier's Principle the application of pressure will slow the reaction. If it has a smaller volume, pressure will accelerate the reaction [7, p. 26].

Energy Differences are Independent of the Path Taken

If we change a system from initial state A to final state B, the difference in energy between the two states in independent of the path taken to effect the change. Let me cite two examples, one rather self-evident; the other more subtle.

For the first example, consider a cell containing 0.3 osmolal salts (istotonic) and 1.0 osmolal EG and suspended in a solution of that same composition (State A). It is then transferred to a solution containing 0.3 osmolal salts and 0 EG. At equilibrium (State B), the cell will contain 0.3 osmolal salt and 0 EG. However, there are at least three paths that can be taken to arrive at State B. The first is that the cell can be abruptly transferred from solution A to solution B. The physical consequence is that the cell will undergo a large initial voume spike as water permeates followed by a slow decrease in volume as the EG diffuses out. The biological consequence of this path, however, may be that the cell can not withstand the volume spike. A second path is to dilute solution A in steps of specific volumes at specific intervals with 0.3 osmolal salt, and finally transfer them to Solution B. This path produces multiple volume spikes but they can be held to tolerable limits by the choice of the magnitude of the dilution steps and the intervals between them [4]. The third path is the so-called sucrose-dilution technique. With it, cells in solution A are transferred to a solution lacking EG but containing a non-permeating solute like sucrose, commonly at 0.5 M. The cells are held in this intermediate solution for a given time (commonly 5 or 10 minutes), and then transferred to solution B. The consequence of this path is that the cells undergo a small (and controllable) volume spike upon the initial dilution, progressive shrinkage with time as the EG flows out, and a rapid return to isotonic volume upon transfer to solution B if the holding time in sucrose has been sufficient for the outflow of nearly all the EG. Three different paths, but the same final equilibrium state. Note, however, although the three paths yield equivalent thermodynamic results, they may have very different biological consequences.

The second example is more subtle. Consider two samples at −22°C. One contains 1 g pure ice; the other contains 1 g ice mixed with sufficient NaCl so that when melted, the resulting solution is a eutectic solution (melting point −21.7°C). How much heat has to be absorbed by the two samples to warm them to 0°C and totally melt the ice? The answer for the first sample is simple. Since ice has a specific heat (c_p) of 0.5 cal/g/deg and a latent heat of fusion at 0°C of 79.7 cal/g, it will take 11 cal to warm the sample to 0°C and 79.7 calories to melt it at that temperature, for a total of 90.7 cal. In the case of the eutectic sample, it will melt totally at −21.7°C. The resulting water has twice the specific heat as ice, so it will take 22 cal to warm it to 0°C. The latent heat of fusion of ice at −21.7°C is reduced by the difference between the specific heats of ice and water times the number of degrees of warming[12, Eq. 27]. In other words, for the 1 g sample of ice in salt, L_{f @–21.7°C}) = L_f@0°C – ((1cal/deg– 0.5 cal/deg) ×22 deg) = 79.7 −11 cal = 68.7 calories. Thus it will take 68.7 + 22 or a total of 90.7 calories to melt the ice and warm the sample to 0°C –the same as in the case of pure ice where we first warm the sample to 0°C and then melt it. In other words, the energy differences are the identical regardless of the path.

The principle is the same for common cryobiological solutions containing intermediate concentrations of solutes, although the calculation is more complex owing to the fact that as warming continues above the eutectic point, the mass fraction of ice in the sample is progressively decreasing and the mass fraction of liquid water is progressively increasing. If desired, the actual masses of the two phases can be obtained from the phase diagram for the solution.

Assumptions in Physical-chemical and Thermodynamic Models

Physical-chemical models have been extremely powerful in analyzing and predicting cryobiologically relevant phenomena, but I think it correct to say that every one of them is based on underlying assumptions. Sometimes the assumptions are specifically stated; more often they are not. Sometimes the effects of varying the assumptions are evaluated; more often they are not. Sometimes, the effects of an invalid assumption are only minor; sometimes, however, they are crippling. In the preceding discussion of L_f vs. temperature, the assumption is that the specific heats of ice and water are independent of temperature. That is not the case, but the effect of incorporating the temperature dependence is small [12, Eq. 28], [2, p. 562], [5, p. 214] Many models involving osmotic responses and permeability require assumptions about the area of the cell surface (A). Some authors assume that A varies as V^2/3; others like me believe and provide supporting evidence that A is constant [14, pp. 83–85]. However, this choice of assumption has a relatively small effect on computed curves of cell volumes vs. time. Almost all investigators assume that the area of a cell calculated from measurements of its diameter is the true area. But in most cases it is not. The surface of most cells is covered with microvilli, folds, and pleats that make the true area as much as twice the geometric area calculated from measured diameters. The end result is that the Lp calculated from measurements of cell diameters is not a pure or true permeability coefficient but rather the product of A and that coefficient.

But some assumptions, especially those not recognized as such, can lead to totally invalid conclusions. For example, the assumption that osmotic relations and permeabilities are consequences only of passive flows can give highly erroneous results if some active process like cell volume regulation is involved. Similarly, the assumption that cells are permeable only to water and permeable solutes can lead to serious errors if that assumption breaks down. In general, pursuing the logic that if the cause is not A, it must be B is dangerous if it neglects the possibility of C or D.

Experimental Verification of Models

Physicists generally demand that to be accepted, a mathematical hypothesis must be experimentally verified. Witness, for example, the famous measurement of the bending of starlight passing near the sun that quantitatively confirmed some of Einstein's core equations on relativity. Another test of an hypothesis is that it have predictable consequences for future experiments. One difficulty with cryobiological models and hypotheses is that they often generate predictions that are not experimentally verifiable because of excess “noise” in the biological system. One good example of noise is the estimation of the volumes of cells subjected to osmotic changes both above and below 0°C. A list of possible sources of this noise would include errors in assuming that cells are spheres and remain so during swelling or shrinkage so that diameters can be translated into volumes, errors in the measurement of diameters, normal cell-to cell variation in the properties to be measured such as L_p or P_s, abnormal responses of some cells due to membrane damage. In the case of cells at subzero temperatures, there are added sources of noise such as partial obscuration of the image by external ice and shrinkage of cells in an anisotropic manner. The net result can well be that the prediction by a new model of some cryobiologically relevant property might differ from the prediction of that same property by an older model by say 25%, and yet not be distinguishable experimentally.

Conclusions

The intention of this article is to provide a bridge between a reader who may have little knowledge of thermodynamics and physical chemistry and authors who know the subjects in detail. There are certain core principles that should be kept in mind:

1. A central concept is that of chemical potential (μ). In suspensions or aggregates of cells in aqueous media, water molecules will move from regions where their chemical potential is high (e.g., a cell interior) to regions where it is low (e.g., a hyperosmotic surrounding medium). Equilibrium is attained where the μ_w of the two compartments is equal. A number of colligative properties are proxies for μ_w; namely, vapor pressure, osmolality, activity, and freezing point depression.

   Similarly, solutes will move from regions where the chemical potential of the solute is high to a compartment where its chemical potential is lower, provided that the solute can permeate the membrane demarking the two compartments. In the case of cells in solutions of permeating solutes, equilibrium requires that the chemical potentials of both water and solute become equal inside and outside the cell. The usual proxy for the chemical potential of a solute is its molality.

   If a series of experiments yield results that are not in accord with these rules, either a significant component of chemical potential has been neglected or a certain underlying assumption is invalid. As an example of the former, I cited the situation where higher plant cells apparently do not reach osmotic equilibrium when suspended in water. The anomaly is resolved by incorporating a hydrostatic pressure term to express the fact that a pressure is generated when the protoplast attempts to expand osmotically beyond the confines of the cell wall but can not do so because of the rigidity of the wall. An example of an assumption becoming invalid would be a case where a plasma membrane ceases to be semi-permeable.

2. Small ice crystals have small radii of curvature, and crystals with small radii have higher chemical potentials of their surface water than larger ones. This is relevant to cryobiology in two ways. One is that in order for an ice crystal to pass through a nanometer sized pore in a cell membrane, it must have a radius of curvature comparable to the radius of the pore. But because of their higher surface free energies, such crystals can exist only well below the normal freezing/melting point of the solution. The second is that the high surface free energies of small ice crystals is a major factor determining the very low temperature for the homogeneous nucleation of supercooled water, and is the major factor driving the recrystallization during warming of small internal ice crystals formed during cooling.

3. Visualizing a physical-chemical or thermodynamic process qualitatively can be an asset in understanding the process before deriving or analyzing the specific equations to describe it quantitatively. It is analogous to the value of algorithms in deriving formal computer code. There are several valuable tools and concepts to aid in the formulation of such thermodynamic algorithms. One is the concept of chemical potentials just discussed. A second is Le Chatalier's Principle. A third is the concept that the difference in energy in going from State A to State B is independent of the path taken.

4. Every physical-chemical or thermodynamic model contains assumptions. Sometimes they are specified and evaluated, but often they are not. The consequences of an assumption being invalid can vary from trivial to destructive. It is obviously impossible to list here the myriads of assumptions that are made. My personal policy is to treat assumptions like the reading of a page proof. You know text errors are there; the job of proofing is to find them.

5. As powerful and useful as physical-chemical and thermodynamic models have been to cryobiology, they present two dangers. The first is that experimental measurements of the characteristics of cells that models display are often too coarse or noisy to differentiate their fit to Model A vs. that to Model B. Historically, in astronomy, for example, it is only when the observations become sufficiently precise that one could conclude that Model A (e.g. Ptolomeic theory) is wrong and Model B (Copernican-Kepplerian) is correct. The second danger is that a model may be correct and still not describe experimental observations because some factor outside the confines of the model is affecting the results. One sort of factor could be the involvement of a biologically active process causing flows of solute and solvent against their chemical potential gradients. A specific example would be volume regulation, the process in which cells actively secrete or take up ions in response to osmotic challenges so as to restore their volumes to near isotonic.