Site-resolved stabilization of a DNA triple helix by magnesium ions

Abstract

Proton exchange and NMR spectroscopy have been used to define the effects of Mg²⁺ ions upon the stability of individual base pairs in the intramolecular parallel triple helix formed by the DNA oligonucleotide d(GAAGAGGTTTTTCCTCTTCTTTTTCTTCTCC). The rates of exchange of individual Watson–Crick and Hoogsteen imino protons in the DNA triple helix were measured in the absence and in the presence of Mg²⁺ ions. The results reveal that Mg²⁺ lowers the exchange rates of most imino protons in the structure by stabilizing the corresponding base pairs in their native closed conformation. Comparison of the DNA triple helix containing Na⁺ counterions to the same helix containing Mg²⁺ counterions shows that these stabilizing effects result, in large part, from Mg²⁺ ions closely associated with the DNA. Moreover, the effects are site-specific and depend on the number and location of protonated cytosines relative to the observed base. These findings provide new insights into the molecular roles of C⁺·GC triads in determining the stability of DNA triple-helical structures.

INTRODUCTION

Triple-helical structures offer a powerful approach for recognition of specific base sequences in DNA (1,2). These structures are formed by binding of an oligonucleotide strand into the major groove of a DNA duplex. Depending on the orientation of this third strand, two families of DNA triplexes can be distinguished (3). In the pyrimidine–purine–pyrimidine (Y·RY) family, the third strand is rich in thymines and protonated cytosines, and binds parallel to the purine-rich strand of the duplex. Due to the requirement for cytosine protonation, these structures are stable at acidic pH. In purine–purine–pyrimidine (R·RY) triple helices, the third strand is purine-rich and binds in the opposite orientation, anti-parallel to the purine strand of the duplex.

The formation and stability of DNA triple-helical structures are critically influenced by divalent cations, such as magnesium (4). Generally, the cations promote formation and increase stability of the triple-helical structure. For example, in the absence or at low concentrations of other cations, Mg²⁺ ions raise the melting temperature of Y·RY triplexes, and increase the equilibrium constant for the binding of the third strand to the duplex (5–10). The efficiency of Mg²⁺ ions in enhancing the stability of Y·RY triplexes is significantly greater than that of monovalent ions (8–10).

The effects of mono- and divalent cations on the stability of DNA triple helices have been explained by theoretical models derived from the counterion condensation theory or from solutions of the cylindrical Poisson–Boltzmann equation (8,11). In DNA triple-helical structures, the presence of the third strand creates a high linear charge density. Like in double helices, counterions accumulate in the vicinity of the DNA, or condense onto it, to neutralize and screen the phosphate charges. The resulting decrease in repulsive electrostatic free energy stabilizes the structure (12). Analysis of cation effects in Y·RY triple helices is complicated by the electrostatic potential created by the protonated cytosines in the third strand. Experimental evidence has demonstrated that the number of protonated cytosines and their location in the structure profoundly affect the stability of Y·RY triplexes and their dependence on cations (9,10,13–15). However, theoretical models have not yet been used to analyze cations effects in Y·RY triple helices containing protonated cytosines.

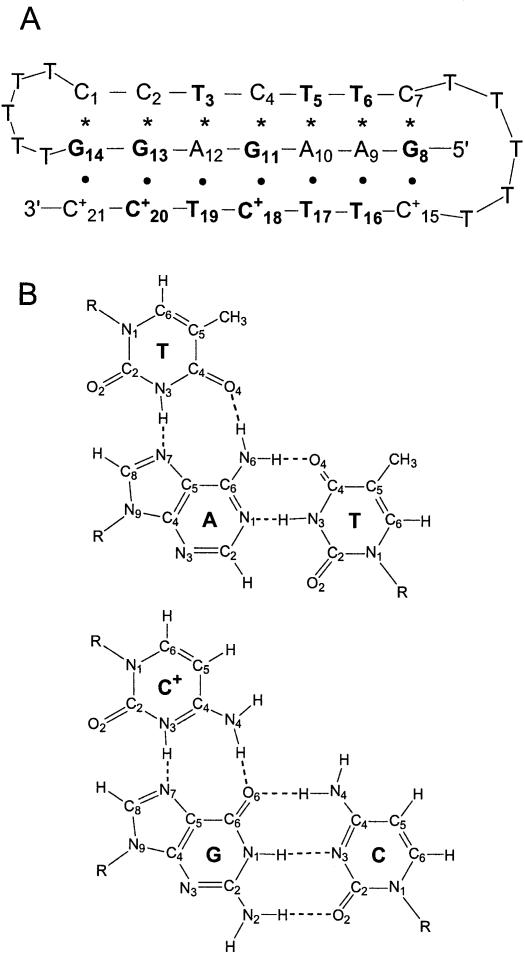
In the present work, we have addressed the question of the stabilization of DNA triple helices by Mg²⁺ ions using proton exchange and nuclear magnetic resonance (NMR) spectroscopy. The approach used allows characterization of Mg²⁺-induced effects on stability at the level of individual base pairs. The DNA oligonucleotide investigated is shown in Figure 1. Our previous structural studies have shown that this DNA assumes a single conformation in solution. The conformation is that of an intramolecular Y·RY triple helix in which the pyrimidine sequence C₁₅⁺ to C₂₁⁺ orients parallel to the purine ‘strand’ in the major groove of the duplex part of the structure (16).

Figure 1.

(A) Base sequence and folded conformation of the DNA triple helix investigated. Watson–Crick hydrogen bonds are indicated by asterisks, and Hoogsteen hydrogen bonds are indicated by dots. The imino proton resonances for the bases shown in bold are observable in the NMR spectra. The numbering of the bases is the same as that used in our previous characterization of this triple helix (16). (B) Structures of canonical T·AT and C⁺·GC triads (31).

MATERIALS AND METHODS

DNA samples

The DNA oligonucleotide was synthesized using phosphoramidite chemistry on an automated DNA synthesizer (Applied Biosystems model 381A). The DNA was purified by reverse-phase HPLC on a PRP-1 column (Hamilton) in 50 mM triethylammonium acetate buffer at pH 7 (with a gradient of 5–32% acetonitrile in 39 min). The counterions were replaced with Na⁺ or Mg²⁺ ions by repeated centrifugation (6–8 times) through Centricon YM-3 tubes (Amicon Inc.) using 0.5 M NaCl or 0.5 M MgCl₂ solutions. The DNA solution was desalted by repeated centrifugation (6–8 times) against water. The NMR samples contained DNA in water at a concentration of 1.6 mM [based on a calculated extinction coefficient of 261 O.D.₂₆₀/µmol (17)]. The pH of the sample (pH 4.6 ± 0.1) was measured at 5°C, before and after each NMR experiment.

NMR experiments

The NMR experiments were performed on a Varian INOVA 500 spectrometer operating at 11.75 T, at 5°C. This temperature is well below the range of temperatures in which melting of the triple helix occurs (namely, 35°C for the transition from triplex to hairpin duplex, and 48°C for the melting of the duplex, as measured by UV spectroscopy). One-dimensional (1D) NMR spectra were obtained using the Jump-and-Return pulse sequence (18). The imino proton exchange rates were measured by transfer of magnetization from water and in hydrogen/deuterium (H/D) exchange experiments.

In the experiments of transfer of magnetization from water, the exchange was initiated by inverting selectively the water proton resonance using a Gaussian 180° pulse (5.7–6.0 ms). A weak gradient (0.21 gauss/cm) was applied during the exchange delay following water inversion, in order to prevent the effects of radiation damping upon the recovery of water magnetization to equilibrium. At the end of the exchange delay, a second Gaussian pulse (1.7–1.8 ms) was applied to bring the water magnetization back to the oZ axis. The observation was with the Jump-and-Return pulse sequence. Twenty-two values of the exchange delay in the range from 2 to 600 ms were used in each experiment. The exchange rates were calculated from the dependence of the intensity of the proton resonance of interest on the exchange delay as we have previously described (19,20). The lowest exchange rate that can be measured reliably using this transfer of magnetization method is ∼0.3 s^–1 at 5°C (16).

In H/D exchange experiments, the DNA samples in water were dried down to 30–60 µl by flushing with argon, and the exchange was initiated by adding D₂O. The final volume fraction of D₂O was between 90 and 95%. In total, 96 transients were accumulated for each spectrum with a total acquisition time of 3.85 min per spectrum. The exchange rate was calculated from the dependence of the intensity of the corresponding resonance on the exchange delay (16). Due to the time elapsed between the initiation of the exchange and the first NMR spectrum (3–6 min), the fastest exchange rate that could be measured accurately in these experiments is 4 × 10^–3 s^–1.

Imino proton exchange in DNA

The exchange of DNA imino protons with solvent protons occurs via a structural opening reaction that brings the imino proton into an open state. In this state, the hydrogen bond holding the imino proton is broken such that the proton can be transferred to proton acceptors (21,22). The acceptors can be nitrogen atoms of other bases within the same DNA molecule or proton acceptors present in solution (e.g. OH^– and water) (22). The exchange rate observed experimentally depends upon the kinetic parameters of the opening reaction as (21):

k_ex = k_op × k_ex,open/(k_cl + k_ex,open)    1

where k_op and k_cl are the opening and the closing rate, respectively, and k_ex,open is the rate of exchange from the open state. Two kinetic regimes can be distinguished depending on how the rate of exchange from the open state compares with the rate of closing: (i) when k_ex,open << k_cl (EX2 regime), the observed rate of exchange is proportional to k_ex,open:

k_ex = K_op × k_ex,open    2

where K_op = k_op/k_cl is the equilibrium constant for the opening reaction of the base containing the imino proton. (ii) When k_ex,open >> k_cl (EX1 regime), the exchange occurs in each opening event and

k_ex = k_op    3

RESULTS

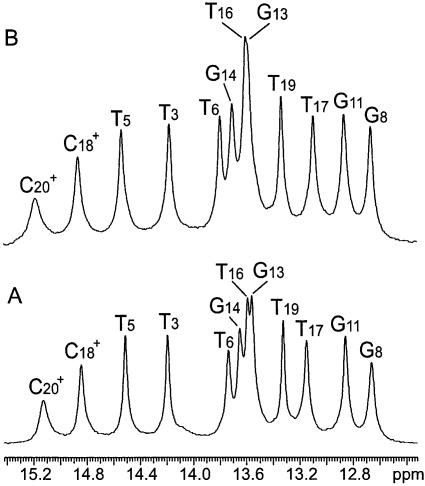
Figure 2 shows the NMR resonances of imino protons of the DNA triple helix investigated, in the absence and in the presence of 100 mM Mg²⁺. The resonances originate from imino protons involved in Watson–Crick hydrogen bonds (N₃H in thymines and N₁H in guanines) and in Hoogsteen hydrogen bonds (N₃H in thymines and protonated cytosines, Fig. 1). The resonances from the protonated cytosines in the first and in the last triad (i.e. C₂₁⁺ and C₁₅⁺) are not observed because they are broadened by fast exchange with solvent. Comparison of the two spectra in Figure 2, in the absence and in the presence of Mg²⁺, reveals only small differences in the chemical shifts of imino proton resonances. This indicates that Mg²⁺ ions do not change significantly the conformation of the triple helix.

Figure 2.

NMR resonances of imino protons in the DNA triple helix investigated in 90% H₂O/10% D₂O at pH 4.6 and at 5°C, in the absence of Mg²⁺ ions (A) and in the presence of 100 mM Mg²⁺ ions (B). The assignments of the resonances have been previously obtained by this laboratory (16).

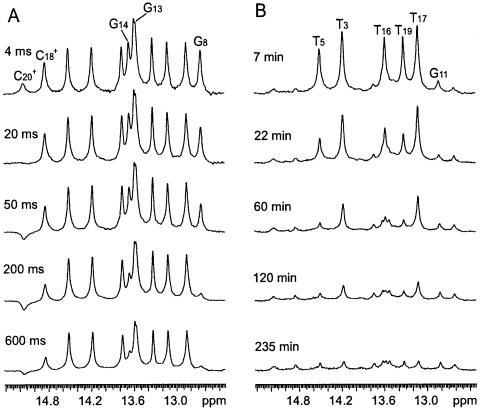
We have measured the rates of exchange of the imino protons in the DNA triple helix with solvent protons. The rates span five orders of magnitude, namely, from ∼5 × 10^–4 to ∼50 s^–1 at 5°C. The exchange of imino protons in the protonated cytosines C₁₈⁺ and C₂₀⁺, and in terminal guanines occurs on a time scale of seconds or faster. The exchange rates of these protons were measured in experiments of transfer of magnetization from water as illustrated in Figure 3A. In contrast, the exchange of imino protons in thymines and in the central guanine G₁₁ is much slower, and was measured in H/D exchange experiments (Fig. 3B).

Figure 3.

Selected imino proton spectra of the DNA triple helix in transfer of magnetization experiments (A) and in H/D exchange experiments (B). The exchange delay is given for each spectrum. The imino proton resonances that show changes in intensity in each experiment are indicated.

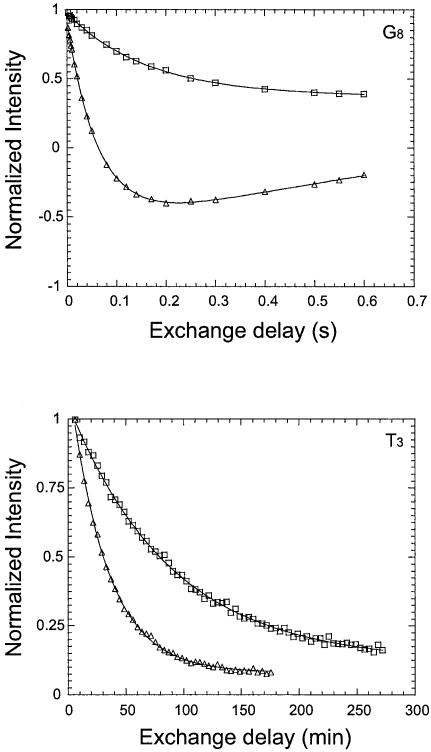
The effect of Mg²⁺ ions upon the exchange of imino protons was investigated using two samples of the DNA triple helix. In the first sample, the DNA contained Na⁺ as counterions [henceforth abbreviated DNA(Na⁺)]. The proton exchange rates for this sample were measured in the absence and in the presence of 100 mM Mg²⁺. The results are illustrated in Figure 4 with the exchange curves of imino protons in G₈ and T₃. Clearly, for both protons, the exchange in the presence of 100 mM Mg²⁺ is significantly slower than that in the absence of the ion (i.e. exchange rates 1.94 versus 13.0 s^–1 for G₈, and 2.1 × 10^–4 versus 5.2 × 10^–4 s^–1 for T₃). The exchange rates for all imino protons in this sample, in the absence and in the presence of 100 mM Mg²⁺ [k⁰_ex(Na⁺) and k^Mg_ex, respectively], are summarized in Table 1. Higher concentrations of Mg²⁺ did not induce further changes in the exchange rates. For the second DNA sample [henceforth abbreviated DNA(Mg²⁺)], the Na⁺ counterions were replaced with Mg²⁺. The exchange rates of imino protons were measured for a solution of this triple helix in water, and are given in the fourth column of Table 1 [k⁰_ex(Mg²⁺)]. For most imino protons, the exchange rates decrease in the presence of 100 mM Mg²⁺ ions, or when Na⁺ counterions are replaced with Mg²⁺. The exceptions to this trend are the imino protons in C⁺₂₀ and T₁₉. For C⁺₂₀, the exchange rate remains constant upon adding 100 mM Mg²⁺ to the DNA solution or upon replacing Na⁺ with Mg²⁺ counterions. For T₁₉, the exchange rate increases upon adding 100 mM Mg²⁺ ions. A larger increase in the exchange rate of this proton is observed upon replacing Na⁺ with Mg²⁺ counterions.

Figure 4.

Examples of the dependence of the intensity of imino proton resonances on the exchange delay. Upper panel: exchange of imino proton in G₈ measured in transfer of magnetization experiments. Lower panel: exchange of imino proton in T₃ measured in H/D exchange experiments. Triangles represent results for the DNA(Na⁺) sample in water, and squares represent results for the same sample in the presence of 100 mM Mg²⁺ ions.

Table 1. Effect of Mg²⁺ ions on the exchange rates of imino protons (s^–1) and the free energy changes in base-pair opening reactions (kcal/mol) in the DNA triple helix investigated at pH 4.6 and at 5°C.

Imino proton	k0ex(Na+)a	kMgexa	k0ex(Mg2+)a	δΔGMgope	δΔGop(Na+ → Mg2+)e
T3	(5.2 ± 0.3) × 10–4	(2.1 ± 0.3) × 10–4	(2.8 ± 0.2) × 10–4	0.50 ± 0.09	0.34 ± 0.05
T5	(1.68 ± 0.09) × 10–3	(6.0 ± 0.7) × 10–4	(7.0 ± 0.4) × 10–4	0.57 ± 0.07	0.48 ± 0.04
T6b	–	–	–	–	–
G14	4.3 ± 0.2	1.26 ± 0.04	2.21 ± 0.08	0.68 ± 0.03	0.37 ± 0.03
G13c	0.77 ± 0.01	<0.3	<0.3	>0.5	>0.5
G11d	>4 × 10–3	(1.4 ± 0.5) × 10–3	(2.2 ± 0.1) × 10–3	>0.6	>0.3
G8	13.0 ± 0.3	1.94 ± 0.08	3.1 ± 0.1	1.05 ± 0.03	0.79 ± 0.02
C20+	41 ± 1	37 ± 2	40 ± 1	0.06 ± 0.03	0.01 ± 0.02
T19	(9.9 ± 0.5) × 10–4	(1.38 ± 0.07) × 10–3	(1.7 ± 0.1) × 10–3	–0.18 ± 0.04	–0.30 ± 0.04
C18+	2.99 ± 0.09	1.73 ± 0.08	2.08 ± 0.08	0.30 ± 0.03f	0.20 ± 0.03f
T17	(3.6 ± 0.2) × 10–4	(2.1 ± 0.1) × 10–4	(2.4 ± 0.1) × 10–4	0.30 ± 0.04	0.22 ±0.04
T16	(1.5 ± 0.1) × 10–3	(4.9 ± 0.3) × 10–4	(6.5 ± 0.5) × 10–4	0.62 ± 0.05	0.46 ± 0.06

^ak⁰_ex(Na⁺) is the exchange rate for the DNA(Na⁺) sample in water; k^Mg_ex is the exchange rate for the same sample in the presence of 100 mM Mg²⁺; k⁰_ex(Mg²⁺) is the exchange rate for the DNA(Mg²⁺) sample in water.

^bThe exchange rate of imino proton in T₆ is too slow to be measured by transfer of magnetization (<0.3 s^–1) and too fast to be measured by H/D exchange (>4 × 10^–3 s^–1).

^cFor G₁₃, k^Mg_ex and k⁰_ex(Mg²⁺) decrease below 0.3 s^–1, and could not be measured in transfer of magnetization experiments.

^dFor G₁₁, k⁰_ex(Na⁺) is higher than 4 × 10^–3 s^–1, and could not be measured in H/D exchange experiments.

^eCalculated based on the assumption that Mg²⁺ ions do not affect the rates of exchange of imino protons from the open state of base pairs.

^fCalculated from the rate of opening.

DISCUSSION

Molecular origins of Mg²⁺ effects on imino proton exchange rates

The exchange of imino protons in DNA triple helices has been previously characterized by this and other laboratories (16,19,20,23). Under experimental conditions similar to those used in the present work, the exchange of most imino protons is in the EX2 regime (equation 2), where the observed exchange rate is proportional to the equilibrium constant for the opening reaction (K_op). In the open state of the base pair, the imino proton is transferred directly to water molecules or to nitrogen atoms in neighboring bases [for example, for Watson–Crick base pairs, imino protons in thymine and guanine are transferred to adenine N₁ and cytosine N₃, respectively (19)]. For protonated cytosines, the exchange is in EX1 regime (equation 3). This is because the imino proton is transferred, upon opening of the Hoogsteen C⁺·G base pair, to the N₇ atom of the guanine, and the rate of this transfer is very high. Thus, the observed exchange rate provides directly the rate of opening of the Hoogsteen C⁺·G base pair.

The changes in exchange rates observed in this work could originate from Mg²⁺-induced changes in the equilibrium constant of the opening reaction (K_op) and/or in the exchange rate from the open state (k_{ex, open}). Several observations suggest that the effects of Mg²⁺ ions upon exchange from the open state are small. In free deoxyribonucleotides, the exchange rates of imino protons are independent of Mg²⁺ concentration. For example, we have found that, under the experimental conditions used in this work (i.e. water at pH 4.6 and at 5°C), the exchange rates are 185 ± 6 s^–1 for the imino proton in guanosine 5′-monophosphate and 15.3 ± 0.1 s^–1 for the imino proton in thymidine 5′-monophosphate. These exchange rates are constant for Mg²⁺ concentrations up to 100 mM. In DNA structures, Mg²⁺ ions affect the local electrostatic potential at individual bases (24–26). However, these effects are not expected to influence the rate of exchange of imino protons from the open state because, as explained above, the acceptors involved in exchange (i.e. DNA bases and water) are uncharged. The absence of a significant effect of Mg²⁺ upon proton transfer rates in the open state is also suggested by the observation that the exchange rate of imino proton in C⁺₁₈ changes in the presence of Mg²⁺ (Table 1). The exchange of this proton is in EX1 regime (equation 3) and thus, is independent of the rate of exchange from the open state. Therefore, for this base, the effect of Mg²⁺ should result from an alteration of the rate of opening of the C⁺₁₈·G₁₁ base pair. These arguments suggest that Mg²⁺ does not influence significantly proton transfer reactions from the open state. Instead, it is more likely that Mg²⁺ ions change the imino proton exchange rates by affecting the equilibrium constant K_op and the energetics of the structural opening reactions for individual base pairs.

Effects of Mg²⁺ ions upon single-site energetics in the DNA triple helix

The effects of Mg²⁺ upon various sites in the DNA triple helix can be quantitatively compared by assuming that the changes in imino proton exchange rates result solely from changes in the equilibrium constant K_op. This constant is related to the free energy change in the opening reaction as (21):

ΔG_op = –RT ln K_op    4

Accordingly, when the exchange is in EX2 regime (equation 2), the changes in exchange rates can be recast as variations in the free energy changes ΔG_op at individual sites. For example, for the DNA(Na⁺) sample, when the change in exchange rate is induced by increasing the concentration of Mg²⁺ from 0 to 100 mM, the change in ΔG_op at any site is:

where the superscript ‘0’ refers to exchange and opening reactions in the absence of Mg²⁺ ions, and the superscript ‘Mg’ refers to the same reactions in the presence of 100 mM Mg²⁺. Similarly, when the change in exchange rate is induced by replacing Na⁺ counterions with Mg²⁺ counterions, the δΔG_op at any site is:

where the counterion closely associated with the DNA (Na⁺ or Mg²⁺) is indicated in parentheses. The calculated values of δΔG_op for each base in the DNA triple helix are shown in the last columns of Table 1. For most bases, the free energy change for opening increases in the presence of Mg²⁺. This suggests that Mg²⁺ stabilizes the DNA triple-helical structure by increasing the lifetime of most base pairs in their native, paired state.

An insight into the molecular origin of this Mg²⁺-induced stabilization of base pairs can be obtained by comparing the free energy variations observed upon replacing counterions, δΔG_op(Na⁺ → Mg²⁺), to the total free energy variations, δΔG^Mg_op, seen at 100 mM Mg²⁺. As shown in Figure 5, the δΔG_op(Na⁺ → Mg²⁺) values are linearly correlated to the δΔG^Mg_op values according to the following equation:

Figure 5.

Correlation between the changes in stabilization free energy observed upon replacing counterions, δΔG_op(Na⁺ → Mg²⁺), and the total δΔG^Mg_op changes observed at 100 mM Mg²⁺. The fitted line is: δΔG_op(Na⁺ → Mg²⁺) = (–0.06 ± 0.02) + (0.80 ± 0.02) δΔG^Mg_op

δΔG_op(Na⁺ → Mg²⁺) = (–0.06 ± 0.02) +     (0.80 ± 0.02) δΔG^Mg_op    7

This result suggests that the Mg²⁺ counterions closely associated with the DNA contribute approximately 80% to the total change in stabilization free energy induced by Mg²⁺ at each site. The remaining 20% of the effect results from bulk Mg²⁺ ions in solution.

The stabilizing effects of Mg²⁺ ions depend on the position of the base pair in the base sequence and in the structure. This observation is illustrated in Figure 6. A dominant factor in this dependence is the location of the base relative to the cytosines in the ‘third’ strand. Previous NMR investigations have shown that the pK values of third-strand cytosines in Y·RY triple helices are 5.5 or higher (15). Therefore, at the pH used in the present study (pH 4.6), the cytosines in the ‘third’ strand are mostly in the protonated state. The influence of these protonated cytosines is clearly evident for the other bases in the ‘third’ strand. When protonated cytosines are present on both sides of the base (like for T₁₉), the Mg²⁺-induced variations in ΔG_op are negative and the base pair is destabilized by Mg²⁺. When a thymine is placed next to a single protonated cytosine, the effect depends on its location. For example, the δΔG^Mg_op value for T₁₇ is half of that for T₁₆. This difference most likely reflects the effect of changing the position of the neighboring protonated cytosine from the 3′- to the 5′-side of the base. Protonated cytosines also influence the Mg²⁺-induced stabilization of the C⁺·G Hoogsteen base pairs themselves. For an isolated C⁺·G pair like C₁₈⁺·G₁₁, Mg²⁺ induces a total stabilization of 0.3 kcal/mol. In contrast, for the C₂₀⁺·G₁₃ pair whose neighbor is also charged, the change in stability is negligible (Table 1).

Figure 6.

Site-resolved energetic effects of Mg²⁺ ions upon the DNA triple helix investigated. Open columns represent δΔG^Mg_op values for Watson–Crick base pairs. Filled columns represent δΔG^Mg_op values for Hoogsteen base pairs. For G₁₁ and G₁₃, the lowest values of δΔG^Mg_op (Table 1) are shown.

Protonated cytosines have been previously shown to greatly affect the overall stability of Y·RY triple helices (9,13–15,27–30). Large numbers of protonated cytosines generally stabilize the structure. The highest stabilization is observed for triplexes in which C⁺·GC triads alternate with T·AT triads (10,28,30). The stabilization diminishes when cytosines are placed next to each other (9,13,15,29,30). The latter effect reflects the fact that the unfavorable electrostatic potential created by adjacent protonated cytosines overcomes the stabilizing electrostatic attraction between the protonated base and the negatively charged phosphodiester backbone. Recent results have demonstrated that the same unfavorable electrostatic potential, created by clustering protonated cytosines next to each other, also affects the Mg²⁺-induced increase in melting temperature. For example, Fox and co-workers (10) have compared the melting of several 15-triad intermolecular triple helices of different base sequences. The largest Mg²⁺-induced increase in melting temperature was observed for the triplex containing the C⁺TT repeat in the third strand (namely, 11.1°C upon addition of 50 mM MgCl₂). In contrast, for triplexes containing the C⁺C⁺T or C⁺TC⁺T repeats in the third strand, the corresponding increases in melting temperature were much smaller (i.e. 3.1 and 5.0°C, respectively). These findings are fully consistent with our conclusion that pairs of protonated cytosines, located either adjacent to each other or on both sides of the base, diminish or even eliminate the stabilization of base pairs by Mg²⁺ ions.

In summary, in the present work we have demonstrated that the exchange of imino protons is sensitive to the interactions of Mg²⁺ ions with DNA triple helices. Moreover, as we have shown, imino proton exchange can be used to probe the energetic effects of the ions at specific sites in DNA. The potential of this approach holds promise for future site-resolved investigations of interactions of metal ions with other nucleic acid systems.