Abstract
We present a new classification method for expression profiling data, called MIDClass (Microarray Interval Discriminant CLASSifier), based on association rules. It classifies expressions profiles exploiting the idea that the transcript expression intervals better discriminate subtypes in the same class. A wide experimental analysis shows the effectiveness of MIDClass compared to the most prominent classification approaches.
Introduction
Microarrays are a well established technology to analyze the expression of many genes in a single reaction whose applications range from cancer diagnosis to drug response. They are matrices, where known samples of DNA, cDNA, or oligonucleotides, called probes, combine with mRNA sequences. The expression level of genes is given by the amount of mRNA bounding to each entry. The aim is to find either sets of genes that characterize particular disease states or experimental condition or highly correlated genes that share common biological features. Microarray numerical data coming out from experiments are normalized and analysed [1]. Several algorithms and methods have been used for this analysis [2]. In particular statistical models should be suitable to correctly estimate the magnitude and the significance of differentially expressed genes [3]–[5]. Finally, specific supervised and unsupervised learning methods allow to investigate the predictive power of the candidate gene sets [6]–[8]. Several successful classification methods have been reported in the literature [9]–[13].
Support Vector Machines (SVM) [9] are powerful binary classification methods which take as input a training set of data, each belonging to one of two given classes. It finds support vectors for the classification by identifying a maximum separating hyperplane either when data are linearly separable or through kernel functions. SVMs can be successfully applied to multicategorial classification by using the “one-against-all” methodology [14].
Decision trees [10] are hierarchical models for supervised learning based on the idea that classification can be broken down into a set of progressive choices on the attributes. In a decision tree each internal node denotes a test on an attribute, each branch gives the outcome of the test and each leaf node stores the class label. Each path from the root to a leaf corresponds to a classification decision. When single tree classification shows low predicting power then decision forest classification can improve accuracy. Random Forests (RF) [13] build hundreds of trees. Each tree refers to a random variant of the same data. A single tree in the forest is built by using a bootstrap sample obtained from the training set.
The Nearest-Neighbor classifier [15] assigns to an unknown phenotype the label associated to the nearest sample tuple. The natural extension of the nearest-neighbor rule is the 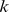 -Nearest-Neighbor classifier (k-NN). In this case, the new tuple label will be the most represented in the
-Nearest-Neighbor classifier (k-NN). In this case, the new tuple label will be the most represented in the 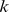 -nearest-neighbor tuples. The distance from the new tuple is used as a weight in the classification. This method tends to be slow for large training sets.
-nearest-neighbor tuples. The distance from the new tuple is used as a weight in the classification. This method tends to be slow for large training sets.
Diagonal Linear Discriminant Analysis [16] (DLDA) is a linear discriminant analysis method with future selection based on a diagonal covariance matrix which ignores potential correlation between different features.
Those classifiers make use of a so called black-box and rely on many genes to give good classification results. However, recently, Wang and Simom [17] explored the virtues of very simple single gene classification models for molecular classification of cancer. They first identify the genes with the most powerful univariate class discrimination ability and then construct simple classification rules for class prediction using those single genes. Their results show that in many cases the single gene classification yields more accurate classification results than classical approaches.
In this paper we present a new classification method, called MIDClass (Microarray Interval Discriminant CLASSifier) based on association rules. Association Rule Mining has been proven to be effective in many microarray applications[18]–[20]. In [18], authors extract significant relations among microarray genes annotated with metabolic pathways, transcriptional regulators and Gene Ontologies. In [19], McIntosh and Chawla employ quantitative association rules capable of dealing with numeric data representing cumulative effects of variables. In [20], Antonie and Bessonov classify using feature selection based on Support Vector Machines with recursive feature elimination in connection to association rules.
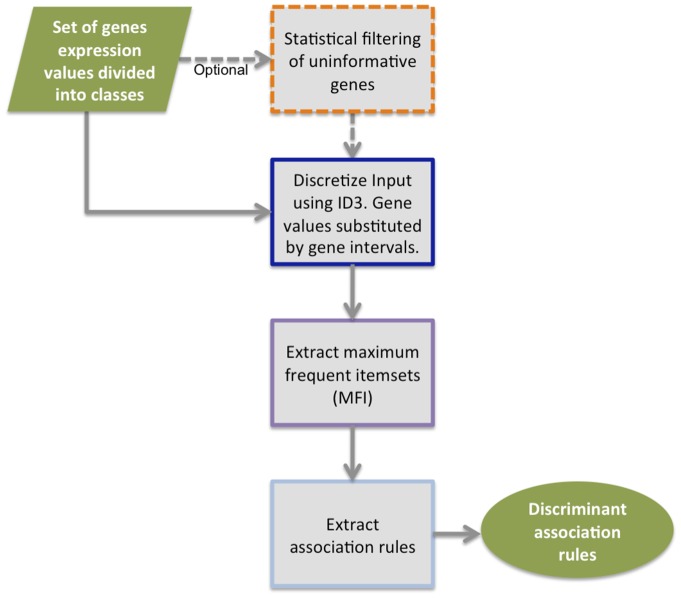
MIDClass is an association rule mining method [18], [19], [21] which classifies gene expression exploiting the idea that gene expression interval values could better discriminate subtypes in the same class. A flowchart of the proposed method is pictured in Figure 1. A wide experimental analysis shows the effectiveness of such a method compared to the above most prominent classification approaches. MIDClass is available at http://ferrolab.dmi.unict.it/midclass.html.
Figure 1. MIDClass flowchart.
Methods
Overview
Association rule mining finds sets of items (called frequent itemsets) whose occurrences exceed a predefined threshold in the dataset. Then it generates association rules from those itemsets with the constraints of minimal confidence. The market basket analysis [22] problem is an example of this kind of mining. Customers habits are classified by finding associations between the items placed in their shopping baskets.
In MIDClass items are gene expression intervals. Baskets are the phenotypes containing (i.e. described by) sets of gene expression intervals. The aim of MIDClass is to extract frequent maximal itemsets and then use them as rules whose antecedent is the conjunction of gene expression intervals and the consequence is the class-label.
Before mining, MIDClass preprocesses data. First, MIDClass applies the T-Test [23], [24] to filter those genes whose expression do not present any significant variability across the classes. Next, a discretization algorithm partitions the gene expression intervals into subintervals possessing strong discriminant power in each class. A flowchart of the proposed method on “Breast Cancer 2” Dataset is depicted in Figure 2.
Figure 2. Example of MIDClass flowchart on Breast Cancer 2 Dataset (data are partially shown).
Let 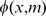 denote the expression value of sample
denote the expression value of sample  on the
on the  -th gene (an example of entry in M is shown as a black box). Samples are divided into classes corresponding to phenotypes disease. After discretization process, MIDClass constructs a matrix
-th gene (an example of entry in M is shown as a black box). Samples are divided into classes corresponding to phenotypes disease. After discretization process, MIDClass constructs a matrix 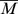 from
from 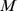 by replacing each
by replacing each 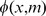 with the unique interval containing it.
with the unique interval containing it. 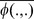 denotes an entry in
denotes an entry in 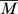 (an example of entry in
(an example of entry in 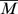 is shown as a black box). Then, MIDClass computes per class the possible sets of
is shown as a black box). Then, MIDClass computes per class the possible sets of 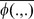 that are frequent and they have maximal size. MIDClass filters out gene expression intervals which size are below a given threshold. Since, association rules express interesting relationships between gene expressions and class labels, MIDClass uses them for classification. Therefore, MIDClass extracts a set of rules per class. Each rule has quantitative attributes on the antecedence part (i.e. discretized values) and one categorical attribute on the consequence side (i.e. the class
that are frequent and they have maximal size. MIDClass filters out gene expression intervals which size are below a given threshold. Since, association rules express interesting relationships between gene expressions and class labels, MIDClass uses them for classification. Therefore, MIDClass extracts a set of rules per class. Each rule has quantitative attributes on the antecedence part (i.e. discretized values) and one categorical attribute on the consequence side (i.e. the class 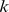 ). Finally, it returns only rules that have a maximal score. The score takes into account the number of items in each sample are contained in the rule together with the cardinality of the rule (the computation of the score is described in detailed in the Methods section).
). Finally, it returns only rules that have a maximal score. The score takes into account the number of items in each sample are contained in the rule together with the cardinality of the rule (the computation of the score is described in detailed in the Methods section).
Data format
MIDClass takes as input a matrix 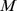 of
of  samples
samples 
 genes. Let
genes. Let 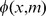 denote the expression value of sample
denote the expression value of sample  on the
on the  -th gene, with
-th gene, with 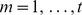 . Samples are divided into classes corresponding to phenotypes disease. Let
. Samples are divided into classes corresponding to phenotypes disease. Let 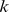 be a class label,
be a class label, 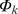 is the set of all values
is the set of all values 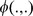 of genes associated to phenotypes of class
of genes associated to phenotypes of class 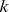 .
.
Statistical gene filtering
In order to select discriminant gene expression values MIDClass applies the T-Test [23], [24]. This step is critical for the reliability of the results, since the presence of not informative genes might negatively affect the classification and the computational performances. Notice that this step is done before running MIDClass . Other suitable statistical test can be applied. In particular, MIDClass uses the LIMMA package available in R through Bioconductor [25].
Discretization
For each gene  , MIDClass partitions its expression value
, MIDClass partitions its expression value 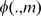 by a discretization algorithm. This produces a set of intervals and each expression value belongs to only one of them. Consequently, MIDClass constructs a matrix
by a discretization algorithm. This produces a set of intervals and each expression value belongs to only one of them. Consequently, MIDClass constructs a matrix 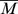 from
from 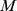 by replacing each
by replacing each 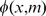 with the unique interval containing it.
with the unique interval containing it.
To perform such a discretization, since there is no best discretization method, MIDClass includes the following techniques [26]: ID3, EWIB, NONE. However, among the available discretization algorithms, in the tested datasets, ID3 showed to be one of the more robust. MIDClass uses ID3 as default discretization algorithm.
We denote by 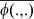 the entries in
the entries in 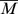 , with
, with 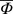 the set all possible
the set all possible 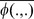 in
in 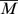 , and with
, and with 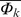 the set of intervals falling into the
the set of intervals falling into the 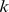 -th class. Note that, MIDClass classifies
-th class. Note that, MIDClass classifies 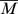 , i.e. it mines gene expression intervals rather than gene expression values.
, i.e. it mines gene expression intervals rather than gene expression values.
Extract maximal frequent itemsets
Let 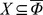 be an itemset (a set of pairs composed by gene and expression interval) and let
be an itemset (a set of pairs composed by gene and expression interval) and let 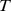 be a collection of itemsets (e.g. the set all possible itemsets). We denote by
be a collection of itemsets (e.g. the set all possible itemsets). We denote by 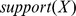 the percentage of itemsets
the percentage of itemsets 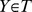 such that
such that 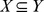 . The support measures how often
. The support measures how often 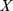 occurs in
occurs in 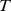 . Let
. Let 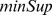 denote a threshold value given by the user whose experimentally default value is 0.4. If
denote a threshold value given by the user whose experimentally default value is 0.4. If 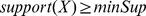 , then
, then 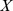 is claimed as a frequent itemset.
is claimed as a frequent itemset.
Let 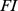 be the set of all frequent itemsets in
be the set of all frequent itemsets in 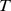 . If
. If 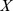 is frequent and there is no frequent superset of
is frequent and there is no frequent superset of 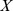 , then
, then 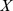 is a maximally frequent itemset. We denote by
is a maximally frequent itemset. We denote by 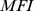 the set of all maximally frequent itemsets. MIDClass extracts only
the set of all maximally frequent itemsets. MIDClass extracts only 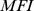 s by using the MAximal Frequent Itemset Algorithm (MAFIA) [27].
s by using the MAximal Frequent Itemset Algorithm (MAFIA) [27].
Since gene expression intervals may be too narrow and some time with a low significance, MIDClass allows users to tune the model by filtering out those that are below a certain threshold (Minimal Interval Size threshold – the default value is 0.05).
Extract association rules from maximal frequent itemsets
An association rule is an implication 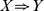 , where
, where 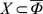 ,
, 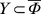 , and
, and 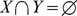 . Let
. Let  be the percentage of subsets in
be the percentage of subsets in 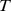 containing
containing 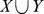 and let
and let  be the percentage of subsets of
be the percentage of subsets of 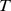 containing both
containing both 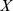 and
and 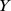 . Then,
. Then, 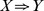 holds in the set
holds in the set 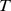 with support
with support  and it has confidence
and it has confidence  in
in 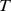 . The minimum confidence is a threshold value given as input by the user and whose default value is 0.05.
. The minimum confidence is a threshold value given as input by the user and whose default value is 0.05.
Association rules express interesting relationships between gene expressions and class labels. Therefore, MIDClass uses them for classification.
MIDClass identifies maximal frequent itemsets for each class 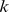 ,
, 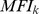 , by using
, by using 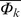 . Those itemsets generate the set of rules
. Those itemsets generate the set of rules 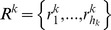 per class. The antecedence of each rule is the conjunction of the items (gene and expression interval) and the consequence is the membership of class
per class. The antecedence of each rule is the conjunction of the items (gene and expression interval) and the consequence is the membership of class 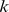 .
.
Extract discriminant association rules and classification
Let 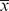 be an unknown discretized sample (i.e. genes expressions are represented by intervals), and let
be an unknown discretized sample (i.e. genes expressions are represented by intervals), and let 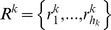 be the association rules for class
be the association rules for class 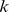 . For
. For 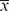 , MIDClass evaluates how many rules are satisfied, even partially, in each
, MIDClass evaluates how many rules are satisfied, even partially, in each 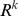 .
.
MIDClass assigns 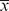 to that class
to that class 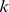 whose rules are maximally satisfied by the following scoring function.
whose rules are maximally satisfied by the following scoring function.
Given a class 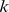 , MIDClass first evaluates
, MIDClass first evaluates 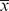 for each rule
for each rule 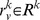 , by using the following function
, by using the following function 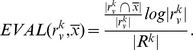 Notice that,
Notice that, 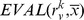 takes into account the number of items in the sample contained in the antecedent of the rule together with the cardinality of the rule
takes into account the number of items in the sample contained in the antecedent of the rule together with the cardinality of the rule 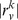 . The value is normalized by the number of rules,
. The value is normalized by the number of rules, 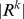 , in the class
, in the class 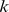 . Finally, the score assigned to the sample
. Finally, the score assigned to the sample 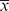 with respect to the class
with respect to the class 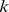 is set to be
is set to be 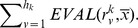
Results and Discussion
All tests have been run on a HP Pavilion with Intel Corei7, 8GB RAM and ubuntu 12.04.
Datasets and Preprocessing
We selected eleven gene expression datasets used in [17]. All datasets are publicly available and were downloaded from the BRB-Array Tools Data Archive for Human Cancer Gene Expression repository 2 (http://linus.nci.nih.gov/brb/DataArchive_New.html). In Table 1 we give the details of each dataset. In Table 2 we report the number of genes used by each classifier. Finally, in oder to compare MIDClass with the association rule mining based method reported in [20] we used the same Leukemia dataset [28]. Leukemia dataset contains the gene expression profile from the leukemia microarray study of Golub et al. [28]. It consists of 72 bone marrow tissues: 47 acute lymphoblastic leukemia (ALL) cases and 25 acute myeloid leukemia (AML) cases.
Table 1. Dataset description.
| Dataset | Description |
| Brain Cancer | 60 samples, 46 patients with classic and 14 patients with desmoplastic brain cancer |
| Breast Cancer 1 | 99 samples, patients that did (n = 45) and did not relapse (n = 54) |
| Breast Cancer 2 | 60 samples, disease-free (n = 32) or cancer recurred (n = 38) |
| Gastric Tumor | 132 samples, 103 tumor samples and 20 normal controls |
| Lymphoma | 58 samples. Patients that did (n = 32) and did not cured (n = 26) |
| Lung Cancer 1 | 41 samples, squamous cell lung carcinoma (21) or pulmonary carcinoid (20) |
| Lung Cancer 2 | 181 samples, 31 mesothelioma samples and 150 adenocarcinoma |
| Melanoma | 70 samples, 45 cases of malignant melanoma patients and 25 of non-malignant patients |
| Myeloma | 173 samples, 137 patients with bone lytic lesions,36 patients without |
| Pancreatic Cancer | 49 samples, 24 ductal carcinoma samples and 24 normal controls |
| Prostate | Cancer 102 samples, 50 non-tumor prostate and 52 prostate tumors |
Table 2. Number of genes used by classifiers in each tested dataset.
| Dataset | MIDClass | SGC-t | SGC-W | DLDA | k-NN | SVM | RF |
| Melanoma | 55 | 1 | 1 | 7200 | 7200 | 7200 | 7200 |
| Breast Cancer 1 | 8 | 1 | 1 | 17 | 17 | 17 | 15 |
| Brain Cancer | 239 | 1 | 1 | 14 | 14 | 14 | 14 |
| Breast Cancer 2 | 16 | 1 | 1 | 176 | 176 | 176 | 176 |
| Gastric Tumor | 23 | 1 | 1 | 848 | 848 | 848 | 848 |
| Lung Cancer 1 | 101 | 1 | 1 | 7472 | 7472 | 7472 | 7472 |
| Lung Cancer 2 | 55 | 1 | 1 | 3207 | 3207 | 3207 | 3207 |
| Lymphoma | 3 | 1 | 1 | 2 | 2 | 2 | 2 |
| Myeloma | 27 | 1 | 1 | 169 | 169 | 169 | 169 |
| Pancreatic Cancer | 22 | 1 | 1 | 56 | 56 | 56 | 44 |
| Prostate Cancer | 45 | 1 | 1 | 798 | 798 | 798 | 798 |
Performances
After MIDClass had generated the rules, we filter each rule by removing the genes intervals whose presence did not give any classification improvement. This step is implemented by applying a Leave-One-Out gene strategy [29].
To motivate the usage of gene intervals we run MIDClass on genes values discretized by using 1 for up regulated genes, −1 for donwregulated and 0 for normal expression values. We tested this model on the Breast Cancer 2 dataset obtaining very poor results (46% of accuracy).
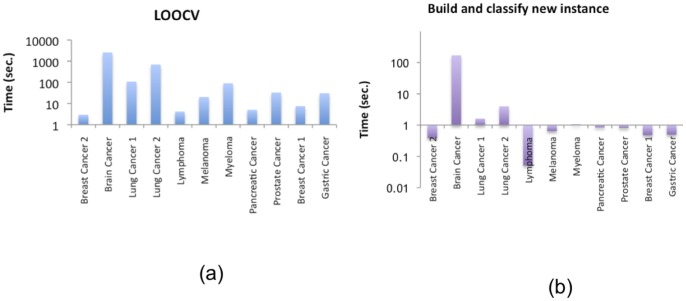
Concerning MIDClass running time, Figure 3 (a) reports the running time to build and establish the reliability of the model using the LOOCV on the tested dataset and Figure 3 (b) the time to execute MIDClass to create the model and classify a new instance.
Figure 3. Runninig time of MIDClass to (a) build and establish its reliability using the LOOCV and (b) to create the model and classify a new instance.
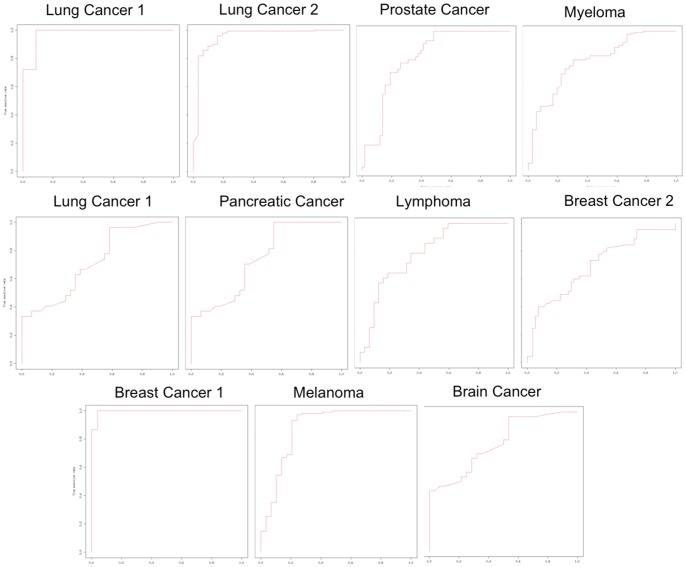
We compared our system against competitors using a Leave-One-Out-Cross-Validation (LOOCV). Using cross-validation one can better assess the performance of the classifier and predict how the classifier will generalize to a new independent data set. Table 3 reports the average accuracy obtained from LOOCV. Figure 4 reports the ROC curve of MIDClass on all the analyzed datasets.
Table 3. Comparisons of MIDClass , single gene classifiers and standard classifiers.
| Dataset | MIDClass | SGC-t | SGC-W | DLDA | k-NN | SVM | RF |
| Melanoma | 98.5 (ID3, 0.1, 2) | 97 | 96 | 97 | 97 | 97 | 97 |
| Breast Cancer 1 | 76 (ID3, 0.05, 1) | 63 | 69 | 61 | 53 | 52 | 43 |
| Brain Cancer | 83 (ID3, 0.01, 1) | 80 | 77 | 65 | 73 | 60 | 70 |
| Breast Cancer 2 | 90 (ID3, 0.05, 1) | 58 | 50 | 73 | 67 | 73 | 67 |
| Gastric Tumor | 94 (ID3, 0.05, 2) | 89 | 80 | 81 | 96 | 97 | 95 |
| Lung Cancer 1 | 98 (ID3, 0.05, 2) | 98 | 95 | 95 | 98 | 98 | 98 |
| Lung Cancer 2 | 99 (ID3, 0.01, 2) | 93 | 93 | 99 | 99 | 99 | 99 |
| Lymphoma | 69 (ID3, 0.1, 2) | 76 | 71 | 66 | 52 | 59 | 57 |
| Myeloma | 84 (ID3, 0.05, 2) | 68 | 67 | 75 | 78 | 74 | 79 |
| Pancreatic Cancer | 78 (ID3, 0.05, 1) | 69 | 90 | 63 | 61 | 65 | 55 |
| Prostate Cancer | 92 (EWIB, 0.01, 2) | 89 | 89 | 78 | 93 | 93 | 93 |
We report the average accuracy of all tested classifiers on the selected dataset obtained with standard LOOCV. The performances concerning the compared algorithms have been retrieved from [17]. Concerning MIDClass , in brackets we report the discretization algorithm, the MFI threshold and the 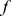 function (1:
function (1: 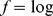 2:
2: 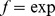 ).
).
Figure 4. MIDClass ROC curves.
Wang and Simon in [17] (here after Single Gene Classify) claim that in most of the cases a single gene is enough to obtain a better classification compared to the state of the art. However, we show that MIDClass outperforms the Single Gene Classify ( based on t-test (SGC-t) and based on WMW (SGC-W)) in almost all cases and in particular on those datasets in which it had poor performances (see Table 3). Table 3 shows also that MIDClass outperformed the standard methods (DLDA, k-NN, SVM and RF). The performances of compared systems have been obtained from [17]. Results in Table 3 also show that MIDClass in connection with ID3 in all datasets but one, Prostate Cancer, is more performant than EWIB. Finally, MIDClass in almost all cases outperformed all compared systems.
Comparing with the method in [20] in the Leukemia dataset, we observed that our rules have a high number of genes (an average of 10 genes compared to the 5 reported by the authors) and some genes were not present in our rules (such as RIN2,MNX1,LYN,GSTT2, GJA5,CD63 and CYFIP2). However, MIDClass yields a better classification performance ( MIDClass : 97.2% vs method in [20]: 95.52%).
Although MIDClass has been designed to afford two-class classification problems, we tested its performances in a multi-class classification problem. Following [14] we implemented the algorithm according to the One-Versus-All strategy. We performed a LOOCV on the SRBT dataset [30] obtaining 100% classification accuracy by using ID3, MFI threshold equals to 0.05 and Minimal Interval Size equals to 0.05. By comparing such results with the one yielded by ANMM4CBR [31] (around the 97%), MIDClass looks promising also for classifying multi-class instances.
Finally, in order to validate the use of gene intervals we conducted an experiment by substituting the intervals assigned to genes in the rules with their fold changes. We observed a strong degradation of the performances. Table 4 presents some of the MIDClass classification rules that have been used in the classification process of “Breast Cancer 2” dataset. For example, by substituting the intervals assigned to APS and IL17BR with their fold change we obtained a poorer classification performance equal to 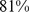 (originally it was
(originally it was 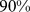 ).
).
Table 4. MIDClass classification rules in breast cancer 2 dataset.
| Rule | Genes | Class |
| Rule1 | IL17BR[0.79,0.98], DOK2[2.29,2.44], HOXB13[−0.68,−0.09], CHDH[1.58,1.89], | |
| SCYA4[7.64,8.13], GUCY2D[4.19,2.14E7], ABCC11[5.68,6.56], IL1R2[1.49,2.14E7], | ||
| APS[0.18,2.14E7] | NonRecurrence | |
| Rule2 | ABCC11[2.84,3.19], IL17BR[0.0,2.14E7], CHDH[0.94,1.2], GUCY2D[3.53,3.8], | |
| SCYA4[7.64,8.13], APS[0.18,2.14E7] | NonRecurrence | |
| Rule3 | DOK2[2.23,2.25], APS[−0.46,−0.38], IL1R2[1.09,1.38], IL17BR[0.0,−2.29], | |
| SCYA4[8.16,2.14E7], ABCC11 [5.68,6.56], HOXB13[1.1,2.14E7] | NonRecurrence | |
| Rule4 | IL17BR[−0.43,−0.34], CHDH [0.0,2.14E7], SCYA4[6.91,7.06], APS[−0.74,−0.64], | |
| GUCY2D[4.19,2.14E7], HOXB13[1.1,2.14E7] | NonRecurrence | |
| Rule5 | GUCY2D[0.56,0.7], APS[−1.34,−1.15], HOXB13[−2.2,−2.09], DOK2[2.0,2.11], | |
| ABCC11[4.96,5.25], SCYA4[6.91,7.06], CHDH[1.58,1.89] | NonRecurrence | |
| Rule6 | HOXB13 [−0.09,0.21], ABCC11 [3.61,3.97],APS [0.0,2.14E7],IL17BR [0.12,0.79] | Recurrence |
| Rule7 | GUCY2D [2.75,2.84],HOXB13 [0.56,0.85],ABCC11 [3.44,3.51], IL17BR [−1.03,−0.76], | |
| CHDH [1.2,1.35],APS [0.0,2.14E7],DOK2 [1.21,1.45] | Recurrence | |
| Rule8 | IL17BR [1.18,1.24],ABCC11 [0.0,2.14E7],APS [0.0,2.14E7], GUCY2D [3.07,3.25], | |
| DOK2 [0.0,1.2],CHDH [1.89,2.15],HOXB13 [−2.77,−2.58], IL1R2 [0.0,−0.37] | Recurrence | |
| Rule9 | GUCY2D [2.0,2.41], IL17BR [1.46,2.14E7],APS [−0.53, −0.46],CHDH [2.36,2.14E7], | |
| ABCC11 [0.57,2.84] | Recurrence | |
| Rule10 | SCYA4 [0.0,5.99], DOK2 [0.0,1.2],IL17BR [0.12,0.79] ,IL1R2 [0.0,−0.37], | |
| APS [−1.15,−0.74] | Recurrence |
Discussion of Biological Relevance
Table 4 presents some of the classification rules that have been used in the classification process of breast cancer 2 dataset. We assessed each gene in the rules in the breast cancer context by reviewing relevant literature and using IPA-Ingenuity Software (http://www.ingenuity.com/).
Most part of genes in Table 4 were related to breast cancer. For example, HOXB13, IL17BR and CHDH genes represented by Rule1 are correlated with ER status and all three genes exhibited an ER-dependent correlation pattern with HER2 status.
ER is a member of the nuclear hormone family of intra cellular receptors, it is a DNA-binding transcription factor which regulates gene expression. Binding of estrogen to ER stimulates proliferation of mammary cells, producing an increasing of cell division, DNA replication, and increases mutation rate. This causes disruption of the cell cycle, apoptosis and DNA repair processes eventually leading to tumor formation. The Human Epidermal growth factor Receptor 2 HER2/neu belongs to a family of four trans membrane receptor tyrosine kinases involved in signal transduction pathways that regulate cell growth and proliferation. Over-expression of this receptor in breast cancer is associated with increased disease recurrence and worse prognosis.
Previous studies shown that HOXB13 is negatively regulated by ER, likely through a different mechanism than gene activation[32]. On the contrary, IL17BR and CHDH are both positively correlated with ER expression, their extent of correlation is less than that for PR and pS2. Previously, the HOXB13:IL17BR index was found to be higher in HER2-positive tumors than that in HER2-negative tumors [33]. The relationship of these three E2-regulated genes to HER2 is notable because recent data from preclinical models indicate that crosstalk between the HER2 and ER signaling pathways directly contributes to the development of tamoxifen resistance [34], [35]. They are estrogen-regulated genes, and have a prognostic utility due to their complex regulation through both ER- and HER2-dependent pathways. These two pathways play a key role in breast cancer.
Another relevant gene reported by Rule10 is CCL4 (Gene Symbol SCYA4). It is a member of chemokines family and was present at high levels in breast cancer tissues compared to normal tissues [36]. This gene with CC chemokines CCL2 is also correlated to the grade of breast tumors [37]. High levels of CCL2 or CCL4 trigger macrophage, B and T lymphocytes recruitment to the tumor [36], [38], which is correlated with a poor prognosis [36]. A previous study also showed that CCL2 was correlated to lymph node status [38]. CCL2 -2518A/G promoter polymorphism has been shown to be correlated with staging and metastasis of breast cancer patients [39]. CCL4 displayed an expression inversely correlated to ER and to PR in breast cancer biopsies and is linked to HER2 status.
ABCC11 is associated with resistance to methotrexate and fluoropyrimidines, two classes of agents widely used for breast cancer treatments (see Rule10). Its transcripts were overexpressed in estrogen receptor-(ER-) positive breast cancers [39]. ABCC11-mediated transport of anticancer drugs, combined with its expression levels in a hormonally-regulated breast tissue, suggest that the pump expression may be regulated by xenobiotics. ABCC11 mRNA and protein levels were enhanced by DEX (dexamethasone) a potent anti-inflammatory factor widely used in cancer therapy, and by PROG (progesterone) in MCF7 (progesterone receptor-(PR-) positive) but not in MDA-MB-231 (PR-negative) breast cancer cells. This suggested a PR-signaling pathway involvement in ABCC11 regulation. Furthermore, ABCC11 levels were positively correlated with the PR status of postmenopausal patient breast tumors from two independent cohorts. Thus, in the subclass of breast tumors (Estrogen Receptor-(ER-) negative/PR-positive), the elevated expression level of ABCC11 may alter the sensitivity to ABCC11 anticancer substrates, especially under treatment combinations with DEX [40]–[42].
Interesting interaction between DOK2 and APS is represented by Rule10. These genes are not yet related to breast cancer although they are missexpressed in several breast cancer mRNA profiling. DOK2 is known as the substrate of chmeric p210bcr/abl oncoprotein characterizing chronic myelogenous leukemia with Philadelphia chromosome. Reduced DOK2 expression was recently reported in lung adenocarcinoma, suggesting that this protein acts as a tumor suppressor in solid tumors.
Finally, we mark that the use of gene intervals instead of gene fold changes not only improves the classification power of MIDClass as shown in Performances Section but reflect also the two operating modes of gene expression at the messenger level: baseline, and under-expression or over-expression. In addition, converting real gene expression data into a typically small number of finite values maintaining the variation of the original data, generates more intuitive rules that are able to catch possible individual variation.
Supporting Information
MIDClass user manual.
(PDF)
Acknowledgments
We would like to thank Professor Eiliv Lund, the main coordinator of the NOWAC study, for his helpful suggestions, and Dr. Stefano Forte for collaborating with us on the initial work of the project.
Funding Statement
This work has been partially founded by PO grant - FESR 2007-2013 Linea di intervento 4.1.1.2, CUP G23F11000840004. The funders had no role in study design, data collection and analysis, decision to publish, or preparation of the manuscript.
References
- 1. Onskog J, Freyhult E, Landfors M, Ryden P, Hvidsten T (2011) Classification of microarrays; synergistic effects between normalization, gene selection and machine learning. BMC Bioinformatics 12: 390. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2. Butte A (2002) The use and analysis of microarray data. Nature Reviews Drug Discovery 1: 951–60. [DOI] [PubMed] [Google Scholar]
- 3. Dudoit S, Yang Y, Callow M, Speed T (2002) Statistical methods for identifying differentially expressed genes in replicated cdna microarray experiments. Statistica Sinica 12: 111–140. [Google Scholar]
- 4. Cui X, Churchill G (2003) Statistical tests for differential expression in cdna microarray experiments. Genome Biology 4: 210. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5. Dudoit S, Shaffer J, Boldrick J (2003) Multiple hypothesis testing in microarray experiments. Statistical Science 18: 71–103. [Google Scholar]
- 6. Jiang D, Tang C, Zhang A (2004) Cluster analysis for gene expression data: A survey. IEEE Transactions on Knowledge and Data Engineering 16: 1370–1386. [Google Scholar]
- 7. Ben-Dor A, Bruhn L, Friedman N, Nachman I, Schummer M, et al. (2000) Tissue classification with gene expression profiles. Journal of Computational Biology 7: 559–583. [DOI] [PubMed] [Google Scholar]
- 8. Statnikov A, Aliferis C, Tsamardinos I, Hardin D, Levy S (2005) A comprehensive evaluation of multicategory classification methods for microarray gene expression cancer diagnosis. Bioinformatics 21: 631–643. [DOI] [PubMed] [Google Scholar]
- 9.Vapnik V (2000) The nature of statistical learning theory. Springer Verlag.
- 10.Han J, Kamber M (2006) Data mining: concepts and techniques. Morgan Kaufmann.
- 11. McCulloch W, Pitts W (1943) A logical calculus of the ideas immanent in nervous activity. Bulletin of Mathematical Biology 5: 115–133. [PubMed] [Google Scholar]
- 12.Duda R, Hart P, Stork D (1995) Pattern Classification and Scene Analysis 2nd ed. Wiley.
- 13. Breiman L (2001) Random forests. Machine Learning 45: 5–32. [Google Scholar]
- 14. Ramaswamy S, Tamayo P, Rifkin R, Mukherjee D, Yeang CH, et al. (2001) Multiclass cancer diagnosis using tumor gene expression signatures. Proceedings of the National Academy of Sciences 98: 15149–15154. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15. Fix E, Hodges J (1989) Discriminatory analysis. nonparametric discrimination: Consistency properties. International Statistical Review 57: 238–247. [Google Scholar]
- 16.Pique-Regi R, Ortega A, Asgharzadeh S (2005) Sequential diagonal linear discriminant analysis (seqdlda) for microarray classification and gene identification. In: Computational Structural Bioinformatics Workshop. 112–116.
- 17. Wang X, Simon R (2011) Microarray-based cancer prediction using single genes. BMC Bioinformatics 12: 1. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18. Becquet C, Blachon S, Jeudy B, Boulicaut J, Gandrillon O (2002) Strong-association-rule mining for large-scale gene-expression data analysis: a case study on human sage data. Genome Biology 3: research0067–research0067.16. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19. McIntosh T, Chawla S (2007) High confidence rule mining for microarray analysis. IEEE/ACM Transactions on Computational Biology and Bioinformatics 4: 611–623. [DOI] [PubMed] [Google Scholar]
- 20.Antonie L, Bessonov K (2011) Classifying microarray data with association rules. In: ACM Symposium on Applied Computing. 94–99.
- 21. Georgii E, Richter L, Rückert U, Kramer S (2005) Analyzing microarray data using quantitative association rules. Bioinformatics 21: ii123–ii129. [DOI] [PubMed] [Google Scholar]
- 22.Brin S, Motwani R, Ullman JD, Tsur S (1997) Dynamic itemset counting and implication rules for market basket data. In: ACM SIGMOD International Conference on Management of Data. 255–264.
- 23. Baldi P, Long A (2001) A bayesian framework for the analysis of microarray expression data: regularized t-test and statistical inferences of gene changes. Bioinformatics 17: 509. [DOI] [PubMed] [Google Scholar]
- 24. Tusher V, Tibshirani R, Chu G (2001) Significance analysis of microarrays applied to the ionizing radiation response. Proceedings of the National Academy of Sciences 98: 5116. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Smyth G (2005) Limma: linear models for microarray data. Bioinformatics and Computational Biology Solutions using R and Bioconductor. Springer, New York.
- 26. Garcia S, Luengo J, Sez J, Lpez V, Herrera F (2013) A survey of discretization techniques: Taxonomy and empirical analysis in supervised learning. IEEE Transactions on Knowledge and Data Engineering 25: 734–750. [Google Scholar]
- 27. Burdick D, Calimlim M, Flannick J, Gehrke J, Yiu T (2005) Mafia: A maximal frequent itemset algorithm. IEEE Transactions on Knowledge and Data Engineering 17: 1490–1504. [Google Scholar]
- 28. Golub TR, Slonim DK, Tamayo P, Huard C, Gaasenbeek M, et al. (1999) Molecular classification of cancer: class discovery and class prediction by gene expression monitoring. Science 286: 531–537. [DOI] [PubMed] [Google Scholar]
- 29.Kohavi R (1995) A study of cross-validation and bootstrap for accuracy estimation and model selection. In: International Joint Conference on Artificial Intelligence. volume 14, 1137–1145.
- 30. Khan J, Wei JS, Ringner M, Saal LH, Ladanyi M, et al. (2001) Classification and diagnostic prediction of cancers using gene expression profiling and artificial neural networks. Nature medicine 7: 673–679. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31. Yao B, Li S (2010) Anmm4cbr: a case-based reasoning method for gene expression data classification. Algorithms for Molecular Biology 5: 14. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.Wang Z, Dahiya S, Provencher H, Muir B, Carney E, et al.. (2007) The prognostic biomarkers hoxb13, il17br, and chdh are regulated by estrogen in breast cancer. Clinical Cancer Research 13. [DOI] [PubMed]
- 33.Ma X, Hilsenbeck S, Wang W, Ding L, Sgroi D, et al.. (2006) The hoxb13:il17br expression index is a prognostic factor in early-stage breast cancer. Journal of Clinical Oncology 24. [DOI] [PubMed]
- 34. Benz C, Scott G, Sarup J, Johnson R, Tripathy D, et al. (1992) Estrogen-dependent, tamoxifenresistant tumorigenic growth of mcf-7 cells transfected with her2/neu. Breast Cancer Research and Treatment 24: 85–95. [DOI] [PubMed] [Google Scholar]
- 35. Kurokawa H, Lenferink A, Simpson J, Pisacane P, Sliwkowski M, et al. (2000) Inhibition of her2/neu (erbb-2) and mitogen-activated protein kinases enhances tamoxifen action against her2-overexpressing, tamoxifen-resistant breast cancer cells. Cancer Research 60: 5887–94. [PubMed] [Google Scholar]
- 36. Chavey C, Bibeau F, Gourgou-Bourgade S, Burlinchon S, Boissiere F, et al. (2007) Estrogenreceptor negative breast cancers exhibit a high cytokine content. Breast Cancer Research 9: R15. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37. Qian BZ, Li J, Zhang H, Kitamura T, Zhang J, et al. (2011) CCL2 recruits inammatory monocytes to facilitate breast-tumour metastasis. Nature 475: 222–225. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 38. Lebrecht A, Grimm C, Lantzsch T, Ludwig E, Heer L, et al. (2004) Monocyte chemoattractant protein-1 serum levels in patients with breast cancer. Tumour Biology 25: 14–7. [DOI] [PubMed] [Google Scholar]
- 39. Ghilardi G, Biondi M, La Torre A, Battaglioli L, Scorza R (2005) Breast cancer progression and host polymorphisms in the chemokine system: role of the macrophage chemoattractant protein-1 (mcp-1)-2518 g allele. Clinical Chemistry 51: 452–5. [DOI] [PubMed] [Google Scholar]
- 40. Honorat M, Mesnier A, Vendrell J, Guitton J, Bieche I, et al. (2008) Abcc11 expression is regulated by estrogen in mcf7 cells, correlated with estrogen receptorexpression in postmenopausal breast tumors and overexpressed in tamoxifen-resistant breast cancer cells. Endocrine-Related Cancer 15: 125–138. [DOI] [PubMed] [Google Scholar]
- 41. Bortfeld M, Rius M, Knig J, Herold-Mende C, Nies A, et al. (2006) Human multidrug resistance protein 8 (mrp8/abcc11), an apical efflux pump for steroid sulfates, is an axonal protein of the cns and peripheral nervous system. Neuroscience 137: 1247–1257. [DOI] [PubMed] [Google Scholar]
- 42. McNamara S, Kilbride L (1999) Treating primary brain tumours with dexamethasone. Nursing times 95: 54–57. [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
MIDClass user manual.
(PDF)