Skip to main content
PMC home page
Molecular Systems Biology logoLink to Molecular Systems Biology
. 2011 Dec 20;7:561. doi: 10.1038/msb.2011.94

Queueing up for enzymatic processing: correlated signaling through coupled degradation

Natalie A Cookson 1,*, William H Mather 2,*, Tal Danino 2, Octavio Mondragón-Palomino 2, Ruth J Williams 3,4, Lev S Tsimring 4,†, Jeff Hasty 1,2,4,a,†
PMCID: PMC3737734  PMID: 22186735

Abstract

High-throughput technologies have led to the generation of complex wiring diagrams as a post-sequencing paradigm for depicting the interactions between vast and diverse cellular species. While these diagrams are useful for analyzing biological systems on a large scale, a detailed understanding of the molecular mechanisms that underlie the observed network connections is critical for the further development of systems and synthetic biology. Here, we use queueing theory to investigate how ‘waiting lines’ can lead to correlations between protein ‘customers’ that are coupled solely through a downstream set of enzymatic ‘servers’. Using the E. coli ClpXP degradation machine as a model processing system, we observe significant cross-talk between two networks that are indirectly coupled through a common set of processors. We further illustrate the implications of enzymatic queueing using a synthetic biology application, in which two independent synthetic networks demonstrate synchronized behavior when common ClpXP machinery is overburdened. Our results demonstrate that such post-translational processes can lead to dynamic connections in cellular networks and may provide a mechanistic understanding of existing but currently inexplicable links.

Keywords: ClpXP, protein degradation, queueing, synthetic biology

Introduction

Evolutionary pressure has driven organisms to develop into energy efficient machines, which conserve resources by minimizing biosynthetic costs and producing only the required amount of certain costly proteins (Warner et al, 2001; Vilaprinyo et al, 2010; Barton et al, 2010). An implication of maintaining only the minimal amount of critical machinery is the potential to overload important pathways during times of stress and to place unanticipated burden on important cellular workhorses. This can lead to the development of ‘waiting lines’ for biochemical processing which may cause apparent correlations between seemingly disconnected components that share the same processing pathways. In that sense, an analogy can be drawn to multiclass queueing theory (Kelly, 1979; Bramson, 1998; Williams, 1998; Bramson and Dai, 2001), which we employ here to provide a unifying model for describing how ‘waiting lines’ for processing by a common enzyme (the ‘servers’) can lead to correlations between two otherwise uncoupled proteins (the ‘customers’).

Generally, when strong correlated behavior is observed between two proteins in response to some perturbation, it is assumed that there is a direct coupling mechanism in place, such as correlated transcription. However, recent studies have revealed a lower degree of correlation between mRNA and protein levels than expected, indicating the need to search for other coupling mechanisms that may lead two protein species to follow similar trends in concentration (Gygi et al, 1999; Futcher et al, 1999; Greenbaum et al, 2003; Guo et al, 2008). Here, we use several experimental approaches along with a new application of queueing theory to reveal that a seemingly minor form of indirect coupling between cellular species can lead to surprisingly strong correlated behavior. As a model system, we use the native E. coli protease, ClpXP, as the ‘server’ and impose various static and dynamic conditions of underloading and overloading the cells with protein ‘customers’ targeted for destruction by this complex. We demonstrate that the transition from an underloaded to an overloaded regime can manifest itself in significant cross-talk between two independent networks, where the induction level of one protein substantially affects the mean and variability of the other protein. We also apply queueing theory to a native stress response system and demonstrate the use of this coupling property as a signaling mechanism to alert the cell to a dangerous environment.

The correlated behavior that arises from this type of indirect coupling can have many implications, both in the analysis of native cellular networks and in the design and construction of synthetic networks. For example, systems biology employs high-throughput technologies to reconstruct cellular networks and generate high level wiring diagrams (Alon et al, 1999; Golub et al, 1999; Ideker et al, 2001; Sauer, 2004; Li et al, 2004). While useful as tools for analyzing and understanding biological networks on a large scale, determining how these components are connected is the next critical step in understanding what the underlying interactions are and how they lead to the observed cellular behaviors. Similarly, the field of synthetic biology relies on a fundamental understanding of the relationship between cellular networks and the behaviors that emerge from their complex interactions (Elowitz and Leibler, 2000; Gardner et al, 2000; Hasty et al, 2002; You et al, 2004; Del Vecchio et al, 2008; Tabor et al, 2009; Tan et al, 2009; Danino et al, 2010; Kim and Sauro, 2010). As many of the emerging studies in synthetic biology aim to develop circuits that exhibit specific, dynamic behaviors, understanding and utilizing both direct and indirect coupling mechanisms will become essential to designing successful synthetic systems.

Results

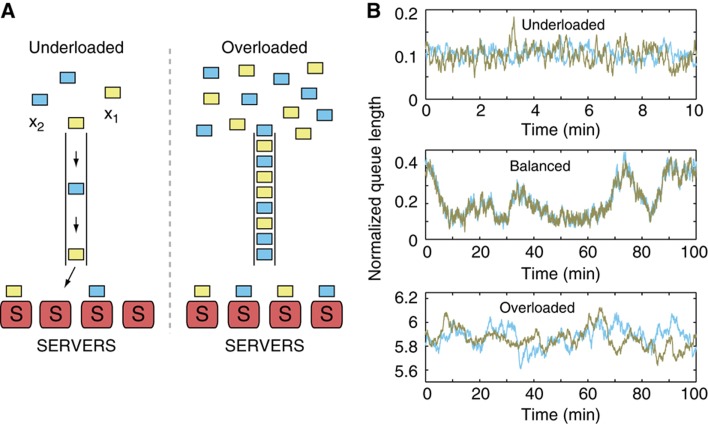
To illustrate how queueing theory can be used to analyze indirect coupling, suppose that two proteins X1 and X2 are involved in signaling pathways that do not directly interact, but they are processed downstream by the same enzyme. If the enzymatic ‘servers’ (S) are in abundance relative to the the number of target ‘customer’ molecules (x1 and x2), then there are no waiting lines and this corresponds to an underloaded system in queueing theory (Figure 1A, left). On the other hand, if the number of servers is small compared with the number of customers, then the system becomes overloaded as the customers must wait in line to be processed (Figure 1A, right). Such an overloaded system introduces coupling between the different types of customers. For example, consider an increase in the number of X1 molecules on the right side of Figure 1A. Conceptually, a rise in the number of X1 molecules will increase the mean waiting time for the processing of X2, leading to a decrease in the effective rate at which X2 leaves the system. In other words, for fixed arrival rate of X2, the mean number of X2 will increase as the number of X1 is increased, even though there is no direct coupling between the two protein species.

Figure 1.

Figure 1

Open in a new tab

Coupling via common enzymatic machinery: connection to queueing theory. (A) Rate-limited processing can couple the numbers of different job types in a queue. Different jobs (yellow and cyan squares) are forming a queue to be processed and removed from the queue by a fixed number of servers with finite processing capacity. If the arrival rate exceeds the maximum processing rate, the servers become overloaded, the queue lengthens dramatically, and the numbers of jobs competing for the attention of the servers become tightly correlated. (B) Individual stochastic trajectories for a queueing system in three different conditions demonstrate correlation resonance. We consider the system with L=100 servers, each with a processing rate of μ=10 min−1. Jobs renege, that is, abandon the system, at the first-order rate γ=ln2/20.0 min−1. Yellow corresponds to jobs of type 1 and count x1, while blue corresponds to jobs of type 2 and count x2. Trajectories are normalized by their arrival rates. (Top) Underloaded condition, with λ1=0.25 μL, the arrival rate of job 1, and λ2=0.5 μL, the arrival rate of job 2. The total rate of arrival Λ=0.75 μL is less than the total processing rate μL. (Middle) Balanced condition, with λ1=0.5 μL, λ2=0.5 μL, and Λ=μL. (Bottom) Overloaded condition, with λ1=0.75 μL, λ1=0.5 μL, and Λ=1.25 μL.

If the arrival of the two proteins X1 and X2 in Figure 1A is governed by Poissonian statistics, with production rates λ1 and λ2, respectively, the enzymatic system can be mapped to a queueing system where analytical formulae for the steady-state distributions can be derived (Mather et al, 2010; see Mather et al, 2011 for discussion of transients). While the resulting formulae are somewhat complex, they can be used to predict several generic properties that should arise in the context of coupled enzymatic processing. For example, for a fixed production rate λ2 of X2, the mean level of X2 increases as the production rate for X1 is increased. Initially, this increase is slow since the system is in the underloaded regime, but as waiting lines begin to lengthen, the system transitions to the overloaded regime and the mean of X2 rapidly rises as λ1 is increased. At the transition point between the underloaded and overloaded regimes (the ‘balance point’), the sum of λ1 and λ2 is equal to the processing capacity of the queueing network. Interestingly, queueing yields a fast, adaptive response for stress that is dynamic and noisy. Under certain conditions, fluctuations in X1 and X2 are highly coupled, with correlations peaking near the balance point (Figure 1B).

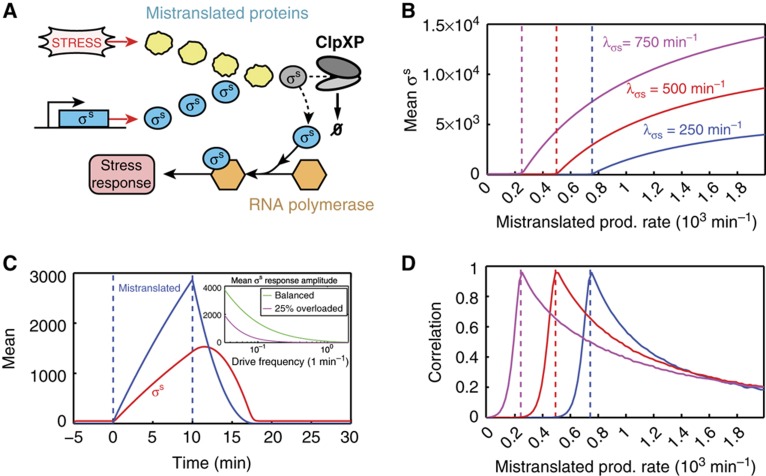
The stress response to nutrient starvation in E. coli has recently been shown to elicit a rapid and adaptive response through the saturation of downstream enzymatic machinery (Fredriksson et al, 2007); that is, in the context of queueing theory, the stressed system operates in the overloaded regime. This network relies on the functionality of the protease ClpXP, a well-studied example of shared enzymatic machinery that targets many types of proteins for degradation (Figure 2A; Levchenko et al, 2000; Sauer et al, 2004). In low stress conditions, the concentration of the master stress regulator, the sigma factor σs, is maintained at a low level through its rapid degradation via ClpXP. However, when the cell is subjected to nutrient starvation, an increased number of mistranslated proteins are targeted for degradation by ClpXP and they compete for a limited number of the proteases. This increases the half-life of σs, which builds up, signals starvation, and jump-starts the stress response. Queueing theory provides several insights into both the dynamic behavior of this response and the benefits that this type of indirect regulation can confer on a network. First, by looking at how the mean level of σs depends on the relative stress level (Figure 2B), we observe that queueing yields a very sensitive response that would normally be assumed to imply some type of strong cooperativity (i.e., a very high Hill coefficient). Second, looking at the temporal response of the σs level to a transient stress, it is clear that queueing confers a very fast and dynamic response. Importantly, the response is highly specific temporally, as σs only remains at a high level during the time that excess aberrant proteins are around (Figure 2C). Scanning the production rate of mistranslated proteins, positive correlations occur for a large range of parameters, peaking near the balance point (Figure 2D; Mather et al, 2010).

Figure 2.

Figure 2

Open in a new tab

The E. coli stress response network employs queueing as a signaling mechanism to ensure the most rapid response possible to adverse conditions. (A) Certain types of stress cause the accumulation of a large amount of aberrant proteins, which are targeted for rapid degradation and compete with the master stress regulator, σs, for a limited amount of ClpXP machinery. This leads to a decrease in the effective degradation rate of σs, allowing it to build up rapidly and initiate an immediate response. See the Supplementary Information for a precise definition of the model and for simulation details. (B) For a stochastic queueing model with 100 ClpXP molecules that each have processing rate μ=10 min−1, with cells dividing every 20 min, a scan of the mean steady-state level of σs with respect to the stress level (mistranslated protein production rate λm) demonstrates a very sensitive response of the system once the system has crossed the balance point (respectively colored dashed lines). Different σs basal production rates λσs are indicated in the figure. (C) The dynamic response of σs to a 10-min pulse of stress demonstrates that queueing provides for a very fast and dynamic response. Importantly, the response is highly specific temporally, as σs only remains at a high level during the time that excess aberrant proteins are around. We assume the basal rate λσs=500 min−1, while λm=1000 min−1 during the pulse of stress but λm=0 min−1 otherwise. (Inset) The mean response amplitude of σs to a periodic stress is strongest, especially at fast frequencies, when the system is on average near balance or slightly overloaded. The rate λm is taken to be a constant plus a sinusoid with amplitude 100 min−1 and given frequency. (D) The adaptive response leads to positive correlations between σs and mistranslated protein levels for a broad range of parameters, peaking near the balance point (respectively colored dashed lines). Parameters are the same as those used in (B).

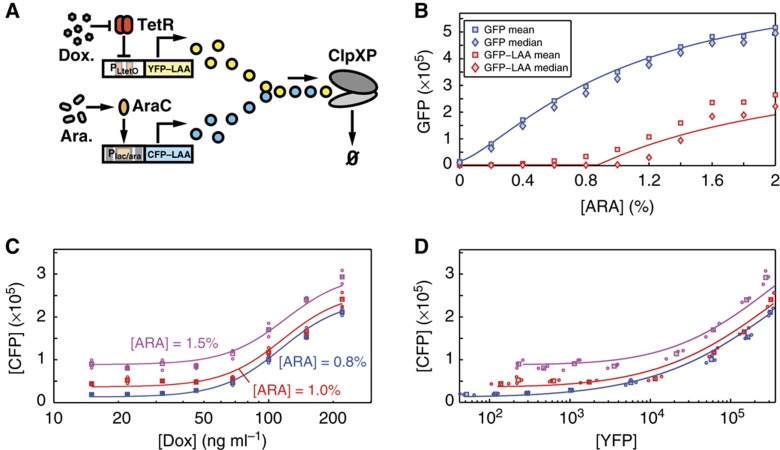
To systematically investigate the dynamic properties of a biological system in which queueing acts as a regulatory mechanism, we constructed a synthetic system to overexpress two different tagged proteins from separate and uncorrelated promoters (Figure 3A). The PLtetO−1 promoter, used to drive expression of YFP (yeast-enhanced yellow fluorescent protein, venus), is tightly repressible by the Tet repressor (TetR) and can be regulated over a range of up to 5000-fold by supplying doxycycline to the culture (Lutz and Bujard, 1997). The hybrid promoter, Plac/ara−1, used to drive expression of CFP (yeast-enhanced cerulean fluorescent protein), is tightly repressed by the Lac repressor (LacI) and activated by AraC. It can be regulated over a range of up to 1800-fold in the presence of IPTG and arabinose in the culture (Lutz and Bujard, 1997). For high expression from the Plac/ara−1 promoter, we used 1 mM of IPTG in all samples to fully relieve repression by LacI, and we used various levels of arabinose to tune the induction level of CFP. Both YFP and CFP were tagged on their C terminus with the well-characterized 11-residue ‘LAA’ tag (AANDENYALAA), marking them as targets for rapid degradation by ClpXP (Keiler et al, 1996). To ensure stable synthesis and maintenance of the regulatory proteins, the synthetic system was transformed into an E. coli DH5 α Z1 host that produces constitutive levels of TetR, LacI and AraC off of the chromosome (Lutz and Bujard, 1997), and controls were performed to ensure that there was no direct cross-talk between the two promoters (see Supplementary Figure S4).

Figure 3.

Coupled enzymatic degradation of yellow and cyan LAA-tagged fluorescent proteins by ClpXP machinery in E. coli. (A) Schematic network diagram of the synthetic circuit. YFP is produced by the PLtetO−1 promoter, which is repressed by TetR in the absence of doxycycline. CFP is produced by the Plac/ara−1 promoter, which is activated by AraC in the presence of arabinose. Both CFP and YFP molecules are tagged with identical LAA tags and are targeted for degradation by the ClpXP complexes. (B) Induction plots for a single fluorescent protein (GFP) produced by the Plac/ara−1 promoter. IPTG is held at 1 mM to fully relieve repression by lacI, and production is tuned by addition of arabinose. Blue and red symbols indicate untagged and LAA-tagged protein, respectively. Squares are mean protein counts, while diamonds are median protein counts. Solid lines are steady-state model fits to the data (including those in C and D). The red line stochastic queueing model prediction for enzymatic protein degradation compares favorably with the data. (C) Mean steady-state expression of CFP as a function of doxycycline concentration at three different levels of arabinose in triplicate flow cytometry measurements. Strong coupling is observed between CFP and YFP. Protein counts are reported using a combination of two-color flow cytometry and western blots. (D) The means of CFP and YFP increase simultaneously as the doxycycline concentration is increased. The color of the symbols corresponds to (C). In both (C) and (D), results for the stationary state of a fitted stochastic queueing model are included as solid lines. Supposing a doubling time τd≈30 min, we find an enzymatic degradation rate μ=7.6 × 103 min−1 for the model provides a good fit to the plotted results. Values for the production rates of YFP at given dox concentrations and for the production rates of CFP at given arabinose concentrations were determined from a best fit to the data. The qualitative result of this fit is that CFP only measurably increases when YFP becomes comparable in magnitude, consistent with a slightly overloaded queue. See Supplementary Information (Supplementary Figures S1, S5, and S6) for fitting details and parameters. Source data is available for this figure in the Supplementary Information.

Figure 3

Source Data for Figures 3c-d (23.5KB, xls)
Source Data for Figures 3b (30.5KB, xls)
Open in a new tab

Our queueing analysis of the enzymatic decay of highly expressed proteins predicts that at certain levels of expression, the mean level of one protein will be significantly coupled to the mean of the other. To test this hypothesis, we planned to hold production of one protein constant, while tuning the level of the other. As a first step, we acquired induction data for the Plac/ara−1 promoter driving GFP, to determine several arabinose levels to fix for the constant condition. Interestingly, we found a striking difference in the shapes of the induction curves for tagged and untagged variants of the fluorescent reporter (Figure 3B). While the untagged protein responded in the expected manner (Lutz and Bujard, 1997), the tagged protein data showed clear evidence of queuing as predicted by the theoretical model (Figure 2B), with a sharp bend in the curve indicating the balance point, where ClpXP transitions from the underburdened to overburdened state.

We then used two-color flow cytometry to generate induction curves for the two systems, fixing arabinose at three levels and tuning YFP production with doxycycline, and we were surprised by the extent to which the inducer for one species affected the other species. For example, as doxycycline was varied over a full induction range for YFP, we observed up to a 12-fold increase in the mean level of CFP (Figure 3C). Likewise, we observed unambiguously that the two proteins exhibited highly correlated behavior as we swept doxycycline and plotted the mean levels of CFP as a function of the mean levels of YFP (Figure 3D). This result highlights an important point in the general context of gene-regulatory and signaling networks; were this data collected in the absence of a mechanistic understanding, one would likely conclude that YFP is some form of inducer for CFP.

To place this queueing phenomenon in the context of native cellular behavior, it is important to develop a quantitative understanding of the system′s balance point and the processing capacity of ClpXP in healthy E. coli cells. To convert mean fluorescence data to a more informative protein count, we used a combination of flow cytometry and quantitative western blots (see Supplementary Figures S2 and S3) to calculate a scaling factor with which to directly compare YFP and CFP mean fluorescence levels as reported by the flow cytometer. We then employed western blots to determine a combined mean number of tagged YFP and CFP molecules per cell for various induction levels. The combination of these two approaches provides the numerical information necessary to translate the typical ‘arbitrary units’ to a number of proteins and yields a balance point value of 7.6 K tagged proteins produced (and degraded) per minute for this system. While healthy cells are believed to be in the underloaded regime (Moore and Sauer, 2005), in which they would not possess queues of excess tagged proteins, it is clear that certain stressful conditions, like carbon starvation, will push the degradation system far beyond the balance point (Neher et al, 2006; Ferenci, 2007; Fredriksson et al, 2007; Bougdour et al, 2008; Hengge, 2009). In fact, this appears to be a beneficial design feature of the E. coli stress response network, as the degradation delay allows the master regulator, σs, to build up rapidly for immediate response but to be removed and recycled quickly after the system is repaired.

The favorable comparison between model and experiment indicates that queueing theory provides a quantitative approach for describing coupled enzymatic processing (Figure 3B–D, solid lines). The model fits were derived through use of a fitting algorithm to determine model parameters μ, γ, K, a Hill function-based parameterization for λ1 (production rate of YFP for a given doxycycline), and the parameterization for λ2 (production rate of CFP for a given arabinose). Interestingly, although the model involves many parameters, the shape of the fitted curves depends only on a few parameters, particularly the enzymatic degradation rate μ (see Supplementary information). This indicates that the model describes the system well and that we are not overfitting the data.

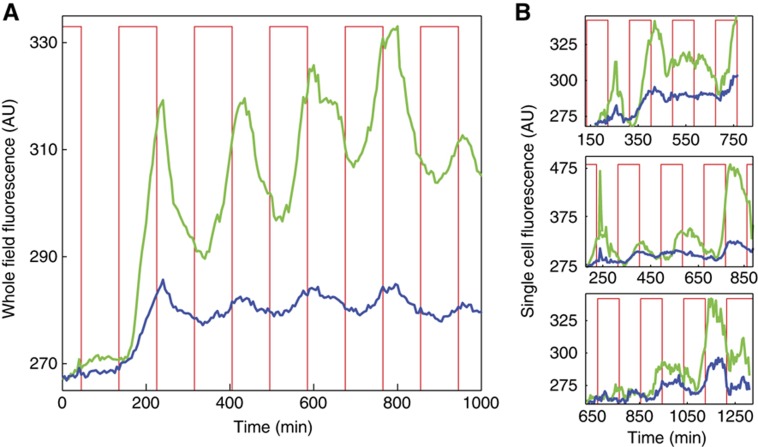
To further investigate the implications of enzymatic queueing, we designed a microfluidic platform based on previous designs (Bennett et al, 2008; Ferry et al, 2011) to drive and monitor the signaling responses of the two networks at the single-cell level. We drove production of YFP with a periodic square-wave signal of doxycycline (see Materials and methods summary) and used two-color microscopy to observe the response of both the YFP and CFP signals. Whole-field fluorescence of a population of E. coli cells demonstrates how the coupling of the two proteins through the shared degradation pathway serves to drive one system in response to the behavior of the other, as both the YFP (Figure 4A, green) and CFP (Figure 4A, blue) signals oscillate with the driving signal (Figure 4A, red). Similar trends can be observed in the fluorescence trajectories of individual cells (Figure 4B). Correlated behavior between the two reporters is observed in response to the driving signal as well as in long-term expression trends (Figure 5).

Figure 4.

Dynamic behavior of a synthetic signaling network. (A) Using a microfluidic platform capable of generating a time-dependent induction signal and multi-color single-cell fluorescence measurements, a large population of E. coli expressing the synthetic network were subject to a periodic series of doxycycline pulses (red), such that the system at zero doxycycline relaxed to a dim state, but the system at high doxycycline relaxed to a bright state. The total YFP and CFP fluorescence, integrated over the entire colony, demonstrates the direct response of the PLtetO−1 promoter, producing YFP (green) as TetR is periodically deactivated, as well as the indirect response of the CFP signal (blue) due to the time-dependent saturation of the ClpXP machinery. (B) Trajectories for several individual cells demonstrate the response at a single-cell level. Source data is available for this figure in the Supplementary Information.

Figure 4

Source Data for Figure 4 (38KB, xls)
Open in a new tab

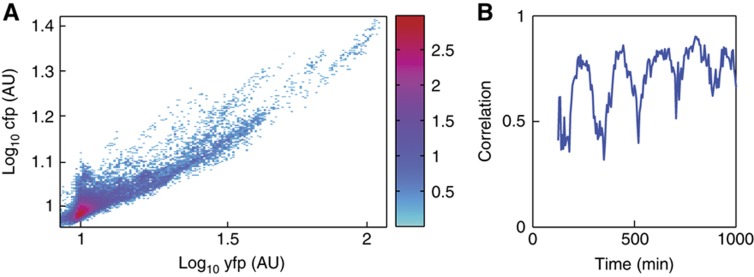
Figure 5.

Figure 5

Open in a new tab

Correlations between two independent reporter proteins. (A) A two-dimensional histogram depicts correlations between YFP and CFP levels in individual cells throughout the entire experiment duration from Figure 4. The value in each rectangular bin is log scaled (value of log10(1+n), with n the number of counts in a bin). (B) The Pearson's correlation coefficient between the two reporters as a function of time. Correlation is reported for the middle 80% of cells by CFP brightness (eliminating outliers that contribute bias to the correlation coefficient), and the estimated correlation coefficient for typical cells is observed to oscillate with the drive period.

Based on these results, we hypothesized that the effect of queueing through coupled enzymatic processing could have significant implications in the developing field of synthetic biology. As most synthetic biology approaches employ degradation tags to enforce the necessarily quick turnover of key network components, waiting times for processing by ClpXP (or similar machinery in other biological systems) may be exploited to generate synchronized behavior among seemingly independent circuits. To test this hypothesis, we constructed a synthetic two-color system involving two independently produced fluorescent proteins: one (GFP–LAA) produced periodically by a synthetic oscillator and the second (CFP–LAA) produced by a separately tunable promoter (Figure 6A). We built a new single-plasmid version of a previously reported synthetic oscillator (Stricker et al, 2008) with the activator (araC–LAA), repressor (LacI–LAA), and reporter (GFP–LAA) all on a p15A plasmid. For the second component, we placed the LuxI promoter driving CFP–LAA along with a constitutively produced LuxR on a high copy pUC19 vector, such that the expression of CFP is inducible by the addition of AHL to the medium.

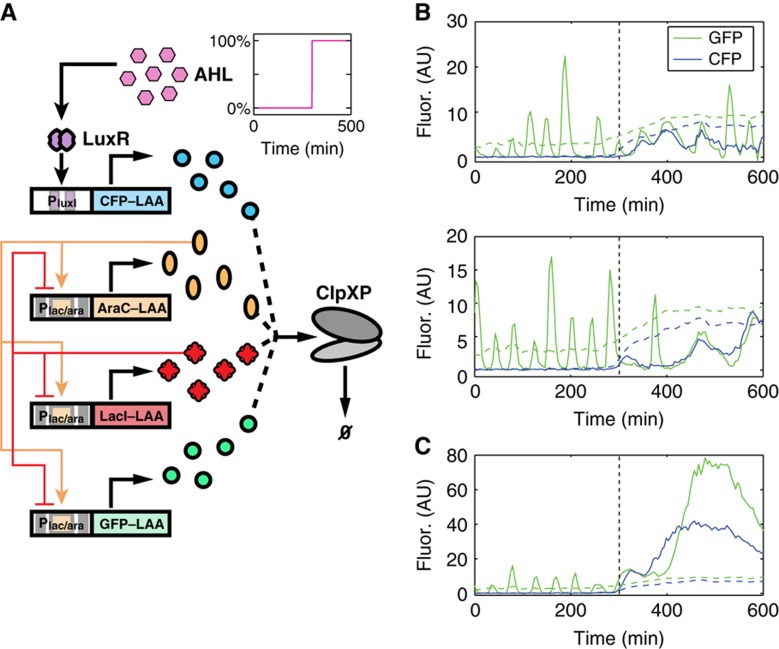
Figure 6.

Figure 6

Open in a new tab

Coupled degradation can serve to indirectly couple gene circuits. (A) Circuit diagram for a variant of a synthetic gene oscillator discussed previously (Stricker et al, 2008), expressed alongside an AHL-inducible, LAA-tagged CFP (see Supplementary Information for details). Competition for enzymatic degradation among LAA-tagged proteins allows CFP to interact with the oscillator by slowing the degradation of the oscillator components. Since fast enzymatic decay is thought to strongly influence the period and robustness of certain gene oscillators (Wong et al, 2007; Mather et al, 2009), the character of GFP oscillations should be closely tied to CFP expression. (B) Cells containing the circuit in (A) were grown in a microfluidic device to test the influence of CFP production on GFP oscillations (see Supplementary Information for details). Two single-cell trajectories for GFP and CFP fluorescence (solid lines) show regular oscillations in GFP fluorescence in the absence of external AHL, that is, at low CFP fluorescence. However, addition of 15 nm AHL (time of induction start is indicated by a vertical dotted line) introduces CFP into the system, causing the GFP oscillations to slow and the CFP signal to oscillate as a result of indirect coupling due to queueing. Coupling is also observed in the mean fluorescence across a region of cells (mean fluorescence as dashed lines), where increasing mean CFP fluorescence is associated with an increase in mean GFP fluorescence. (C) A representative trajectory where both CFP and GFP become and remain bright simultaneously. Positive coupling between trajectories is apparent.

We loaded this system into our microfluidic platform and imaged cells for several hours without AHL, and we found regular oscillations of GFP–LAA with an average period of 28 min, while CFP–LAA levels were negligible. However, following induction with 15 nM AHL, the mean levels of both CFP and GFP increased, and CFP trajectories rapidly became correlated with GFP trajectories. Some cells produced irregular oscillations of both colors with much longer periods, while others stopped oscillating altogether (Figure 6B and C). These results indicate that the additional production of tagged proteins by an independent circuit had a dramatic effect on the behavior of the synthetic oscillator, due to an increased burden on the degradation machinery.

Discussion

The steady-state induction characteristics and dynamic coupling observed in the two synthetic systems provide unambiguous evidence of how queueing for common enzymatic processing can induce coupling when there is a significant abundance of proteins relative to the number of functional enzymes. If such behavior was observed in a native or uncharacterized system, it would likely be assumed that these two proteins were coupled in a direct way, such as by coordinated gene expression or by a protein–protein interaction. As large-scale wiring diagrams have become a post-sequencing paradigm for depicting the interactions between vast and diverse cellular species, a major challenge is the deduction of the molecular interactions that underlie the observed correlations. Our results demonstrate that strong correlated behavior can be observed between two components that are only indirectly coupled via an overloaded enzymatic process and suggest that indirect coupling sources should be considered when evaluating native systems or designing and constructing functional synthetic networks.

By quantifying the number of tagged proteins observed in our experiments instead of using the typical ‘arbitrary units,’ we were able to generate a more precise numerical queueing model and to approximate the true ‘balance point’ in the natural system, above which the number of tagged proteins will likely lead to correlated behavior. While healthy cells are believed to be in the underloaded regime, in which they would not possess significant queues of excess tagged proteins, it is clear that stressful conditions can push the degradation system beyond the balance point, causing correlations between many proteins as a result. In fact, this may be a beneficial design feature of some stress response networks, where the degradation delay allows the required proteins to build up rapidly for immediate response but to be removed and recycled quickly after the system is repaired. There are likely many other examples of enzymes that exist in small numbers by design to confer specific behaviors to biological networks. For example, the yeast scaffold protein Ste5 is maintained in limited amounts to concentrate its targets near the common backbone (Chapman and Asthagiri, 2009).

Similarly, it may be beneficial to exploit these indirect links when designing new synthetic systems. As many of the interesting studies in synthetic biology focus on the creation of circuits that exhibit precise, dynamical behavior, targeted degradation of key network components has become an almost essential characteristic of synthetic systems. Since our study demonstrates how the use of degradation tags can lead to unexpected correlations, the results will have important implications on efforts to establish a ‘forward engineering’ methodology. That is, it may be both critical to consider coupled degradation in the modeling of genetic circuits and potentially interesting to intentionally incorporate waiting lines into the design criteria of novel synthetic systems to enhance the desired behavior.

Materials and methods

Strains and flow cytometry

The plasmids were constructed using the pZE24-mcs2a cloning plasmid, which has a kanamycin resistance marker and the hybrid Plac/ara−1 promoter upstream of a multiple cloning site (mcs) (Lutz and Bujard, 1997). For the dual-color plasmid, pNO-2cLAA, the sequence for CFP was tagged by PCR with a carboxy-terminal ssrA tag (AANDENYALAA) (Keiler et al, 1996) and inserted between the KpnI and HindIII sites of the mcs, creating pZE24-CFP–LAA. The YFP fragment was similarly tagged and inserted onto the pZS31-mcs2a cloning plasmid, which contains a chloramphenicol resistance marker and the PLtetO−1 promoter upstream of an mcs. The fragment of this plasmid containing the marker gene and PLtetO−1 driving YFP was copied by PCR and inserted into the SacI site of pZE24-CFP–LAA, creating the final plasmid pNO-2CLAA, containing the independently controlled fluorescent proteins. The plasmids for comparing the tagged and untagged GFP induction curves were constructed similarly on the same plasmid backbone.

For the synthetic oscillator coupled to a constitutive system, the medium copy oscillator (pTDCL8) was constructed by combining oscillator components from pJS167 and pJS169 (Stricker et al, 2008) onto a single p15A plasmid. The pJS167 module (from SacI up to AvrII) was copied by PCR with Kan resistance and flanking AvrII and NheI sites, and it was inserted via ligation at the AvrII site of the pZA14-LacI vector, maintaining uniqueness of the AvrII site and creating an undigestable AvrII-NheI hybrid site. The pLuxI-CFP plasmid (pZU25-CFP–LAA) was constructed by building pZE25-CFP–LAA and inserting the promoter+CFP module by PCR onto a pUC19 vector via flanking AvrII sites (U=pUC19, 5=luxIp promoter).

Flow cytometry data were taken with a Becton-Dickinson LSR II Cell Analyzer, fitted with 405 and 488 nm lasers. The cells were grown overnight in non-inducing medium: LB plus kanamycin for plasmid selection. The cells were passed in the morning into LB plus kanamycin plus various levels of inducer, doxycycline, arabinose/IPTG, or both. The cells were grown in a 37°C shaker at 300 r.p.m. After 3 h, the cells were harvested by centrifugation, resuspended in sterile PBS, and put on ice until they were ready to be sampled. Using the LSR II, 100 000 cells were assayed using MATLAB (The MathWorks, Inc.) and interfacing software. The SBML file of the model used is archived at BioModels (MODEL1111150000).

Microfluidics and microscopy

Image acquisition was performed on a Nikon Eclipse TI epifluorescent inverted microscope outfitted with fluorescence filter cubes optimized for YFP and CFP imaging and a phase-contrast-based autofocus algorithm. Images were acquired using a Photometrics CoolSNAP HQ2 cooled CCD camera, controlled by Nikon Elements software. For the signaling experiment, images were acquired every 1 min in phase contrast, to provide the optimal temporal coverage to suit the automated tracking program. Fluorescent images in the CFP and YFP channels were acquired every 5 min. The cells were imaged inside a microfluidic device with an upstream switch, with the ability to mix or switch between two different media sources. A custom application written in LabVIEW (National Instruments, Austin, Texas) controlled linear actuators, to which two reservoirs containing inducing and non-inducing medium were attached. Using this algorithm, a square wave of 3 h period was generated, subjecting the cells to alternating 90 min terms of 220 ng ml−1 and 0 ng ml−1 doxycycline. For the synthetic circuit experiment, CFP–LAA was induced with 15 nM AHL (N-3-Oxo-hexanoyl-homoserine lactone) from the LuxI promoter as described in the main text. Cells were imaged every 30 s in brightfield and every 4.5 min in both CFP and YFP channels. Controls were performed to ensure that IPTG and Dox did not affect the incorrect promoter and that lacI and tetR do not repress the incorrect promoter, as well as to ensure there was not significant overlap between the CFP and YFP channels, even when imaging CFP and GFP.

The microfluidic experiments were performed as previously described (Danino et al, 2010). Briefly, 50 μl of an overnight culture was diluted in 50 ml of LB (Difco)+antibiotics the day of the experiment. When cells reached an OD600 of 0.1, cells were spun down and resuspended in 5 ml of fresh media and loaded into the device. Image processing was performed using a custom application tied into the ImageJ image processing suite. Images were segmented by creating a binary mask to identify individual cells, and cells were tracked from frame to frame using a combination of quantitative characteristics. The output of this process is the single-cell trajectory information provided in the main text.

Supplementary Material

Supplementary Information

Supplementary figures S1-6

msb201194-s1.pdf (1.3MB, pdf)
SBML Model
msb201194-s2.xml (4.6KB, xml)
Review Process File
msb201194-s3.pdf (161KB, pdf)

Acknowledgments

This work was supported by the National Institutes of Health and General Medicine (R01GM079333), the San Diego Center for Systems Biology (P50GM085764), and the Department of Energy Computational Science Graduate Fellowship (DE-FG02-97ER25308) (NAC). Research of RJW was supported in part by NSF grants DMS-0825686 and DMS-0906535. LT was supported, in part, by ONR MURI grant N00014-07-0741. We would like to thank Colin Lam, Ivan Razinkov, and Arthur Prindle for assistance in plasmid construction and Jangir Selimkhanov for developing the cell tracking code.

Footnotes

The authors declare that they have no conflict of interest.

References

  1. Alon U, Barkai N, Notterman D, Gish K, Ybarra S, Mack D, Levine A (1999) Broad patterns of gene expression revealed by clustering analysis of tumor and normal colon tissues probed by oligonucleotide arrays. Proc Natl Acad Sci USA 96: 6745. [DOI] [PMC free article] [PubMed] [Google Scholar]
  2. Barton M, Delneri D, Oliver S, Rattray M, Bergman C, B ‘ahler J (2010) Evolutionary systems biology of amino acid biosynthetic cost in yeast. PloS One 5: e11935. [DOI] [PMC free article] [PubMed] [Google Scholar]
  3. Bennett MR, Pang WL, Ostroff NA, Baumgartner BL, Nayak S, Tsimring LS, Hasty J (2008) Metabolic gene regulation in a dynamically changing environment. Nature 454: 1119–1122 [DOI] [PMC free article] [PubMed] [Google Scholar]
  4. Bougdour A, Cunning C, Baptiste P, Elliott T, Gottesman S (2008) Multiple pathways for regulation of σS (RpoS) stability in Escherichia coli via the action of multiple anti-adaptors. Mol Microbiol 68: 298–313 [DOI] [PubMed] [Google Scholar]
  5. Bramson M (1998) State space collapse with application to heavy traffic limits for multiclass queueing networks. Queueing Syst 30: 89–148 [Google Scholar]
  6. Bramson M, Dai JG (2001) Heavy traffic limits for some queueing networks. Ann Appl Probab 11: 49–90 [Google Scholar]
  7. Chapman S, Asthagiri A (2009) Quantitative effect of scaffold abundance on signal propagation. Mol Syst Biol 5: 313. [DOI] [PMC free article] [PubMed] [Google Scholar]
  8. Danino D, Mondragón-Palomino O, Tsimring L, Hasty J (2010) A synchronized quorum of genetic clocks. Nature 463: 326–330 [DOI] [PMC free article] [PubMed] [Google Scholar]
  9. Del Vecchio D, Ninfa A, Sontag E (2008) Modular cell biology: retroactivity and insulation. Mol Syst Biol 4: 161. [DOI] [PMC free article] [PubMed] [Google Scholar]
  10. Elowitz MB, Leibler S (2000) A synthetic oscillatory network of transcriptional regulators. Nature 403: 335–338 [DOI] [PubMed] [Google Scholar]
  11. Ferenci T (2007) Sensing nutrient levels in bacteria. Nat Chem Biol 3: 607–608 [DOI] [PubMed] [Google Scholar]
  12. Ferry M, Razinkov I, Hasty J (2011) Microfluidics for synthetic biology from design to execution. Methods Enzymol 497: 295. [DOI] [PMC free article] [PubMed] [Google Scholar]
  13. Fredriksson A, Ballesteros M, Peterson C, Persson O, Silhavy T, Nystrom T (2007) Decline in ribosomal fidelity contributes to the accumulation and stabilization of the master stress response regulator σS upon carbon starvation. Genes Dev 21: 862. [DOI] [PMC free article] [PubMed] [Google Scholar]
  14. Futcher B, Latter G, Monardo P, McLaughlin C, Garrels J (1999) A sampling of the yeast proteome. Mol Cell Biol 19: 7357. [DOI] [PMC free article] [PubMed] [Google Scholar]
  15. Gardner TS, Cantor CR, Collins JJ (2000) Construction of a genetic toggle switch in Escherichia coli. Nature 403: 339–342 [DOI] [PubMed] [Google Scholar]
  16. Golub T, Slonim D, Tamayo P, Huard C, Gaasenbeek M, Mesirov J, Coller H, Loh M, Downing J, Caligiuri M, Bloomfield CD, Lander ES (1999) Molecular classification of cancer: class discovery and class prediction by gene expression monitoring. Science 286: 531. [DOI] [PubMed] [Google Scholar]
  17. Greenbaum D, Colangelo C, Williams K, Gerstein M (2003) Comparing protein abundance and mRNA expression levels on a genomic scale. Genome Biol 4: 117. [DOI] [PMC free article] [PubMed] [Google Scholar]
  18. Guo Y, Xiao P, Lei S, Deng F, Xiao G, Liu Y, Chen X, Li L, Wu S, Chen Y (2008) How is mRNA expression predictive for protein expression? A correlation study on human circulating monocytes. Acta Biochim Biophys Sin 40: 426–436 [DOI] [PubMed] [Google Scholar]
  19. Gygi S, Rochon Y, Franza B, Aebersold R (1999) Correlation between protein and mRNA abundance in yeast. Mol Cell Biol 19: 1720. [DOI] [PMC free article] [PubMed] [Google Scholar]
  20. Hasty J, McMillen D, Collins JJ (2002) Engineered gene circuits. Nature 420: 224–230 [DOI] [PubMed] [Google Scholar]
  21. Hengge R (2009) Proteolysis of σS (RpoS) and the general stress response in Escherichia coli. Res Microbiol 160: 667–676 [DOI] [PubMed] [Google Scholar]
  22. Ideker T, Thorsson V, Ranish J, Christmas R, Buhler J, Eng J, Bumgarner R, Goodlett D, Aebersold R, Hood L (2001) Integrated genomic and proteomic analyses of a systematically perturbed metabolic network. Science 292: 929. [DOI] [PubMed] [Google Scholar]
  23. Keiler K, Waller P, Sauer R (1996) Role of a peptide tagging system in degradation of proteins synthesized from damaged messenger RNA. Science 271: 990. [DOI] [PubMed] [Google Scholar]
  24. Kelly FP (1979) Reversibility and Stochastic Networks. John Wiley and Sons: Chichester [Google Scholar]
  25. Kim K, Sauro H (2010) Fan-out in gene regulatory networks. J Biol Eng 4: 1–14 [DOI] [PMC free article] [PubMed] [Google Scholar]
  26. Levchenko I, Seidel M, Sauer R, Baker T (2000) A specificity-enhancing factor for the ClpXP degradation machine. Science 289: 2354. [DOI] [PubMed] [Google Scholar]
  27. Li S, Armstrong C, Bertin N, Ge H, Milstein S, Boxem M, Vidalain P, Han J, Chesneau A, Hao T, Goldberg DS, Li N, Martinez M, Rual JF, Lamesch P, Xu L, Tewari M, Wong SL, Zhang LV, Berriz GF et al. (2004) A map of the interactome network of the metazoan C. elegans. Science 303: 540. [DOI] [PMC free article] [PubMed] [Google Scholar]
  28. Lutz R, Bujard H (1997) Independent and tight regulation of transcriptional units in Escherichia coli via the LacR/O, the TetR/O and AraC/I1-I2 regulatory elements. Nucleic Acids Res 25: 1203–1210 [DOI] [PMC free article] [PubMed] [Google Scholar]
  29. Mather W, Bennett M, Hasty J, Tsimring L (2009) Delay-induced degrade-and-fire oscillations in small genetic circuits. Phys Rev Lett 102: 068105. [DOI] [PMC free article] [PubMed] [Google Scholar]
  30. Mather W, Cookson N, Hasty J, Tsimring L, Williams R (2010) Correlation resonance generated by coupled enzymatic processing. Biophys J 99: 3172–3181 [DOI] [PMC free article] [PubMed] [Google Scholar]
  31. Mather W, Hasty J, Tsimring L, Williams R (2011) Factorized time-dependent distributions for certain multiclass queueing networks and an application to enzymatic processing networks. Queueing Syst 69: 313–328 [DOI] [PMC free article] [PubMed] [Google Scholar]
  32. Moore SD, Sauer RT (2005) Ribosome rescue: tmRNA tagging activity and capacity in Escherichia coli. Mol Microbiol 58: 456–466 [DOI] [PubMed] [Google Scholar]
  33. Neher S, Villén J, Oakes E, Bakalarski C, Sauer R, Gygi S, Baker T (2006) Proteomic profiling of ClpXP substrates after DNA damage reveals extensive instability within SOS regulon. Mol Cell 22: 193–204 [DOI] [PubMed] [Google Scholar]
  34. Sauer R, Bolon D, Burton B, Burton R, Flynn J, Grant R, Hersch G, Joshi S, Kenniston J, Levchenko I, Neher SB, Oakes ES, Siddiqui SM, Wah DA, Baker TA (2004) Sculpting the proteome with AAA+ proteases and disassembly machines. Cell 119: 9–18 [DOI] [PMC free article] [PubMed] [Google Scholar]
  35. Sauer U (2004) High-throughput phenomics: experimental methods for mapping fluxomes. Curr Opin Biotechnol 15: 58–63 [DOI] [PubMed] [Google Scholar]
  36. Stricker J, Cookson S, Bennett MR, Mather WH, Tsimring LS, Hasty J (2008) A fast, robust and tunable synthetic gene oscillator. Nature 456: 516–519 [DOI] [PMC free article] [PubMed] [Google Scholar]
  37. Tabor J, Salis H, Simpson Z, Chevalier A, Levskaya A, Marcotte E, Voigt C, Ellington A (2009) A synthetic genetic edge detection program. Cell 137: 1272–1281 [DOI] [PMC free article] [PubMed] [Google Scholar]
  38. Tan C, Marguet P, You L (2009) Emergent bistability by a growth-modulating positive feedback circuit. Nat Chem Biol 5: 842–848 [DOI] [PMC free article] [PubMed] [Google Scholar]
  39. Vilaprinyo E, Alves R, Sorribas A (2010) Minimization of biosynthetic costs in adaptive gene expression responses of yeast to environmental changes. PLoS Comput Biol 6: 184–1037 [DOI] [PMC free article] [PubMed] [Google Scholar]
  40. Warner JR, Vilardell J, Sohn JH (2001) Economics of ribosome biosynthesis. Cold Spring Har Symp Quant Bio 66: 567–574 [DOI] [PubMed] [Google Scholar]
  41. Williams RJ (1998) Diffusion approximations for open multiclass queueing networks: sufficient conditions involving state space collapse. Queueing Syst 30: 27–88 [Google Scholar]
  42. Wong W, Tsai T, Liao J (2007) Single-cell zeroth-order protein degradation enhances the robustness of synthetic oscillator. Mol Syst Biol 3: 130. [DOI] [PMC free article] [PubMed] [Google Scholar]
  43. You L, Cox RSI, Weiss R, Arnold FH (2004) Programmed population control by cell-cell communication and regulated killing. Nature 428: 868–871 [DOI] [PubMed] [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

Supplementary Information

Supplementary figures S1-6

msb201194-s1.pdf (1.3MB, pdf)
SBML Model
msb201194-s2.xml (4.6KB, xml)
Review Process File
msb201194-s3.pdf (161KB, pdf)

Articles from Molecular Systems Biology are provided here courtesy of Nature Publishing Group

RESOURCES