Molecular Origins of Cofilin-linked Changes in Actin Filament Mechanics

Abstract

The actin regulatory protein cofilin plays a central role in actin assembly dynamics by severing filaments and increasing the concentration of ends from which subunits add and dissociate. Cofilin binding modifies the average structure and mechanical properties of actin filaments, thereby promoting fragmentation of partially decorated filaments at boundaries of bare and cofilin-decorated segments. Despite extensive evidence for cofilin-dependent changes in filament structure and mechanics, it is unclear how the two processes are linked at the molecular level. Here, we use molecular dynamics simulations and coarse-grained analyses to evaluate the molecular origins of the changes in filament compliance due to cofilin binding. Filament subunits with bound cofilin are less flat and maintain a significantly more open nucleotide cleft than bare filament subunits. Decorated filament segments are less twisted, thinner (considering only actin), and less connected than their bare counterparts, which lowers the filament bending persistence length and torsional stiffness. Using coarse-graining as an analysis method reveals that cofilin binding increases the average distance between the adjacent long-axis filament subunit, thereby weakening their interaction. In contrast, a fraction of lateral filament subunit contacts are closer and presumably stronger with cofilin binding. A cofilactin interface contact identified by cryo-electron microscopy is unstable during simulations carried out at 310K, suggesting that this particular interaction may be short-lived at ambient temperatures. These results reveal the molecular origins of cofilin-dependent changes in actin filament mechanics that may promote filament severing.

Introduction

Actin filament assembly plays essential functional roles in cell motility, cell division, endocytosis and intracellular transport. Assembled filaments form networks that help determine the shape and mechanical integrity of cells. Numerous actin-binding proteins facilitate actin filament assembly, disassembly, and organization.^1–5 Among these proteins, cofilin plays a crucial role in actin (dis)assembly dynamics through severing filaments, which accelerates filament turnover by increasing the number of filament ends, where subunits both bind to and dissociate from filaments.

The mechanism by which cofilin severs actin filaments has been explored extensively using biochemical, structural, and computational approaches.^6–31 Changes in actin filament bending and twisting mechanics^16,24,27,28 appear to be related to filament severing by vertebrate cofilin.²⁸ Existing data favor a model in which stress accumulation promotes severing at regions with mechanical discontinuities, such as near boundaries between stiff, bare actin and compliant, cofilin-decorated segments.^26,28,30 This model explains why partially decorated filaments fragment more readily than bare filaments.^17,18,23

Cofilin alters the (average) structure of actin filaments.^{6,9,10,20,22,27,29,31} Reconstruction of negatively stained samples reveals that cofilin occupancy changes the average filament twist by ~5 degrees per subunit⁶ and may induce a (~12 degree) change in the average subunit tilt.⁹ As a result, longitudinal filament contacts are reorganized,^{10–12,21,24,25} which increases the fluctuation dynamics of the C-terminus and the DNase I binding-loop located within subdomain 2.^15,16 Longitudinal contacts between subdomains 3 and 4 of neighboring subunits along the long-pitch helix, however, are minimally affected.²⁹ Lateral filament contacts are also reorganized.^8,14 Electron microscopy image analysis of negatively stained samples¹² and time-resolved spectroscopic studies¹⁶ suggest that cofilin-dependent structural changes reflect redistribution of equilibrium conformers populated by bare actin, though evidence for novel conformations exists.¹⁶

Cofilin binding and subsequent conformational changes depend strongly on the chemical state of the actin-bound nucleotide and, therefore, cofilactin conformational changes are linked to occupancy of the high affinity nucleotide binding site.^10,20,22,29 Solution studies suggest the nucleotide clefts of cofilactin filament subunits adopt a more open conformation than those of bare actin filament subunits, resembling that of free actin monomers.^10,20 Three-dimensional reconstructions of filaments imaged by cryo-electron microscopy provide structural information that reveals that the cofilactin nucleotide cleft conformation is in a more open conformation than that of either G- or bare F-actin.²⁹

Computational studies have complemented actin and cofilactin experiments by providing quantitative connections between the properties, structure and interactions of actin filaments with atomistic detail.^27,31–35 Chu and Voth³² investigated how the persistence length of undecorated actin filaments varies with changes in D-loop conformation using molecular dynamics (MD) simulations. Pfaendtner et al.³³ refined this study using improved filament structures³⁶ and found that unfolding of the D-loop increased the persistence length regardless of the state of the bound nucleotide. A subsequent paper by Pfaendtner et al.²⁷, in which molecular dynamics simulations were performed starting from an early structure of cofilactin¹², showed that the persistence length of the cofilin-decorated filament is lower than that of the bare filament due to weakened longitudinal interactions. This study predicts that cofilin binding would cause the rearrangement of subdomain 2 of actin, resulting in weakened longitudinal interactions in the actin filament. This prediction was confirmed by the most recent high-resolution cofilactin filament structure where subdomain 2 rotates inward towards the other strand.²⁹ Wong and Sept deduced structural information about cofilin-decorated actin filaments using molecular docking and MD.³¹ More recently, the extensional and torsional stiffness of undecorated actin filaments have been evaluated using MD simulations.^34,35 These studies demonstrate how local conformational changes can propagate to affect macroscopic filament properties.

In this study, we extend the exploration of cofilin-induced changes in the persistence length of actin filaments begun by Pfaendtner et al.²⁷ using a more recently released cofilactin structure²⁹. We employ MD simulations and coarse-grained (CG) analysis to evaluate how cofilin-induced changes in actin structure affect both the bending and twisting dynamics of the filament and to identify the molecular determinants of this behavior and how these changes are modulated by cofilin binding. This work also advances previous investigations of actin filament mechanics and cofilin severing based on continuum mechanics interpretations.^24,28

Results and discussion

Cofilin binding opens the nucleotide-binding cleft of filament subunits by changing the dihedral angle twist

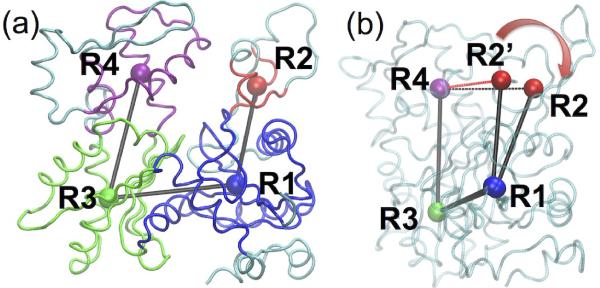
Cofilin binding alters the actin filament structure at both the subunit and filament level. When comparing the structures of subunits in the bare and cofilin-decorated filaments (hereafter called the cofilactin filament), we consider the local scale relatively rigid part of each actin subdomain:³⁷ residues 5–33, 80–147, 334–349 of SD1, residues 34–39, 52–59 of SD2, residues 148y1179, 273–333 of SD3, and residues 180–219, 252–262 of SD4. The centers of geometry (COGs) for these residues are labeled as R1, R2, R3, and R4 (shown in Figure 1(a)). Most of the equilibrated structural parameters of filament subunits (intersubunit bond distances, angle and dihedral; Table 1) do not deviate significantly from the crystal structures.^29,36 However, two differences emerge between the cofilactin and bare filament subunits. The equilibrated R2-R1-R3-R4 dihedral angles differ significantly (10.27±3.41° and 25.73±3.71° for bare actin and cofilactin, respectively. This dihedral angle R2-R1-R3-R4 is one measure of how widely the nucleotide binding cleft opens, as shown in Figure 1(b)). In the cryo-EM reconstruction²⁹ of cofilactin, subdomains 1 and 2 of the actin subunits rotate toward the adjacent strand to avoid steric clashes and the angle between vector R1-R2 and the twist axis of the filament differs by 16° between the two filaments as a consequence of this reorientation (Table 1).

Figure 1.

(a) Rigid portions of SD1, SD2, SD3 and SD4 of actin subunit are shown in blue, red, green and magenta, and the COG of each rigid groups is represented in a sphere of the same color, labeled as R1, R2, R3 and R4; (b) The dihedral angle R2-R1-R3-R4 opens from 10° (R2') to 25° after cofilin decoration, the distance of R2-R4 increases from 22.4 (R2') to 23.6 Å with cofilin binding.

Table 1.

Coarse-grained comparison of subunit geometries reveals two main differences between cofilactin and bare actin: the actin subunit dihedral angle and the orientation of the R1-R2 vector relative to the filament axis.

	Parameters	Actin Initial	Cofilactin Initial	Actin Equilibrated	Cofilactin Equilibrated
Bond (Å)	R1-R2*	22.82	23.03	22.99±0.39	23.36±0.45
	R1-R3	24.72	24.34	24.85±0.28	24.81±0.22
	R3-R4	24.99	24.73	24.97±0.28	24.89±0.27
Angle (°)	R1-R3-R4	74.22	71.55	74.42±1.96	73.21±1.34
	R2-R1-R3	103.09	100.61	102.06±2.06	97.82±3.12
Dihedral (°)	R2-R1-R3-R4	11.21	26.74	10.27±3.41	25.73±3.71
Angle (°)	R1-R2 vs. TA'	22.12	38.04	24.29±2.49	40.49±4.55
	R1-R3 vs. TA'	116.79	114.37	117.57±1.56	119.51±3.51
	R3-R4 vs. TA'	11.6	11.4	15.07±1.63	16.07±3.38

^*Residue sets

R1: 5–33, 80–147, 334–349; R2: 34–39, 52–59;

R3: 148–179, 273–333; R4: 180–219, 252–262.

TA': filament axis

Previous simulations33,37 demonstrate that bare actin filament subunits starting with a G-actin twist spontaneously flatten to a more F-actin-like conformation. With bound cofilin, however, the dihedral conformation of actin subunits remains stable during the simulation despite being in a G-actin-like orientation, suggesting that cofilin binding stabilizes this mode.

The filament subunit tilt angle, defined as the angle between the vector R3-R4 and the twist axis (see Methods), increases after ~100 ns of simulation from 11.6°^29,36 to 15.07°±1.63° for bare filaments and 11.4°^29,36 to 16.07°±3.38° for cofilactin filaments. The average bare and cofilactin subunit tilt angles differ only by 1°, but this angle fluctuates much more in cofilactin filament. The increased variability for cofilactin may be due to the larger rise per subunit in the cofilactin filament (see next section) that enables more rotational freedom for each subunit. In addition, the angle between the vector R1-R3 and twist axis of a cofilactin filament is 5° larger in the equilibrated state than in the initial state (see Table 1), and again exhibits more fluctuation than observed in the bare filament.

Cofilactin filaments are less twisted and thinner than the bare filaments

Structural differences at the filament level are assessed through the twist angle per subunit, crossover length of repeating unit, rise per subunit, and effective radius (Table 2). The equilibrated twist angle per subunit of bare filaments is larger than that of cofilactin filaments (165.84°±2.2° versus 163.7°±2.86°, respectively, comparable to the values of 166.1° and 162.1° seen in the filament reconstructions^6,29,36), indicating that cofilactin filaments are less twisted than bare filaments.^6,29,36 The reduced twist allows filaments to accommodate bound cofilin. Because of the reduced twist, each half-twist of the cofilactin filament contains fewer subunits than the corresponding bare actin filament, i.e., 11 vs. 13. The twist of the starting structure in the cofilactin simulation was 162.1°. However, if we enforce periodic boundaries for 11 subunits, this requires a twist of 163.6 to satisfy symmetry. Indeed, we observe, after simulation with periodic boundaries, that the average twist for 11 actin subunits increases to 163.7 ± 2.9. However, despite the 1.6° increase, the experimental value falls within one standard deviation of the observed simulation value. This finding is reasonable considering that the twist angles in the actin filament have been shown to adopt a broad distribution of values based on both experiments³⁸ and previous MD simulations.³⁹

Table 2.

Filament geometry and mechanical properties change significantly upon cofilin binding; MD simulations reproduce many differences previously observed experimentally.

	Persistence Length (μm)	Standard deviation of twist angle between subunit pairs (°)	Twist Angle per subunit (°)	Cross-over length (Å)	Rise per subunit (Å)	Filament Radius Rf (Å)	Dihedral Angle R2-R1-R3-R4 (°)*
Actin (MD)	9.9±2.1	4.24±0.9	165.84±2.0	358.24±0.52	27.57±0.25	16.33± 0.26	−10.27±3.41
Cofilactin (MD)	1.7±0.2	8.14±0.42	163.7±2.86	316.0±0.6	28.86±0.77	15.66±0.35	−25.73±3.71
Actin (Experiment)	9.8±0.14a	4.0b	166.1c	360c	27.5c	16.46c	−11.21c
Cofilactin (Experiment)	2.2±0.03a	16.8b	162.1d	303.6d	27.6d	16.04d	−26.74d

^*Residue sets: R1: 5–33, 80–147, 334–349; R2: 34–39, 52–59; R3: 148–179, 273–333; R4: 180–219, 252–262.

^aData from Ref. ²⁴.

^bData from Ref. ¹⁶.

^cData from Ref. ³⁶.

^dData from Ref. ²⁹.

Errors represent the standard deviations over all subunits and simulation time window.

The bare filament maintains its crossover length, while the cofilactin filament elongates during the simulation. The equilibrium crossover length of bare filaments is 358.24±0.52Å, and the rise per subunit is 27.55±0.6Å, in agreement with X-ray fiber diffraction analyses.³⁶ However, the cofilactin crossover length increases from 303.6Å to 316±0.6Å within first 20 ns of simulation (see Figure S1 in Supplemental Information, SI), i.e., the rise per subunit grows from 27.55±0.6Å^29,36 to 28.86±0.77Å. The rise per subunit of cofilactin is larger than that of bare filament, which may compromise longitudinal contacts between cofilactin subunits (quantified below in the last two Results sections). While this rise differs from the cryo-EM results, the difference is much smaller than the resolution of the cryoEM structure (9 Å). This difference may also arise due to a temperature effect; we found the rise per subunit from a shorter MD simulation at a lower temperature (123K) to be 27 Å, much closer to the rise observed in the cryo-EM structure.

In addition, after equilibration, the COGs of both filament subunits move closer to the twist axis (consistent with the filament elongation), and the actin component of the filaments become narrower with cofilin binding. Some of this change in the filament radius is observed in the starting structures (R_f =16.04 Å and 16.45 Å, data listed in Table 2; see Method Section for R_f); this difference is increased by the end of the simulation (R_f =15.66±0.35Å vs. 16.33±0.26Å). The final 0.7 Å difference in radius suggests a change in the lateral contacts of the filament.

Cofilin binding increases the bending and twisting dynamics of actin filaments

Analysis of the MD trajectory fluctuations using a correlation analysis indicates that cofilin binding makes actin filaments ~ 4-fold more compliant in bending and twisting. The filament orientation in the box did not change significantly during the simulation, remaining approximately aligned with the z-axis of the box. The bending persistence lengths of bare and cofilactin filaments determined by simulation, 9.9±2.1μm and 1.7±0.2μm, respectively, are in excellent agreement with experimental solution studies, 9.8±0.14μm and 2.2±0.03μm,²⁴ respectively (see Table 2).

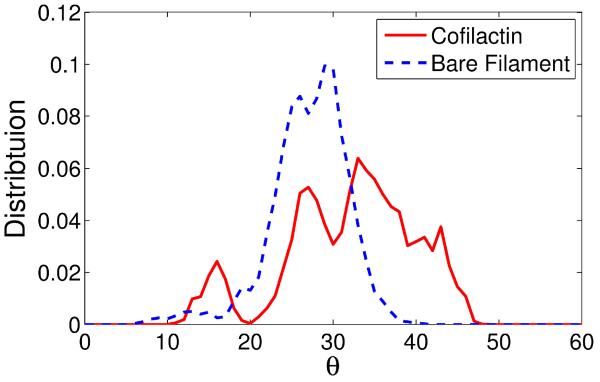
The probability distribution of twist angle between adjacent actin subunit pairs (Figure 2) yields the filament subunit torsional stiffness, which is inversely proportional to the square of the standard deviation (denoted std) of angles between nearest subunit pairs (see Methods section for a detailed description). While the distribution of the bare filament appears stable after a 50 ns of simulation (Figure S2(a)), the width of the distribution of the cofilactin filament stops expanding after 120 ns of simulation (Figures S2(b), S3(c)). The entire observed twist angle distribution of bare filaments is concentrated within the 20° to 35° range (Figure 2), while the range with bound cofilin is broadened, ranging between 10° to 50°. The std quantifies the width of the distribution: the std for bare filaments from our simulation is 4.24±0.9°, which is comparable to a 4° std for bare actin filaments obtained from solution studies¹⁶, image analysis⁴⁰, and single-molecule measurements;⁴¹ the std for cofilactin is 8.14±0.42° (Figure 2), which appears to be ~ 2-fold smaller than that obtained in solution experiments.¹⁶ However, as is explained in the Methods section, this std value may be underestimated due to either the choice of a Gaussian curve to fit the data or due to the limited sampling achievable during MD simulation. A simulation with a longer filament or over timescales an order of magnitude or more longer than those we performed may yield a better distribution; this is currently computationally infeasible.

Figure 2.

Comparison of twist angle distributions. The broader distribution of cofilactin subunits indicates that they are torsionally more compliant than bare filament subunits.

The distribution in Figure 2 displays multiple peaks for both filament types on the timescale of the MD simulation, reflecting coexistence of discrete local twist states,⁴² angular disorder, which has been observed by electron microscopy⁴⁰ and our previous MD study of the bare filament.³⁹

Cofilactin has a lower intersubunit contact density distributed across a smaller cross-sectional area than bare actin

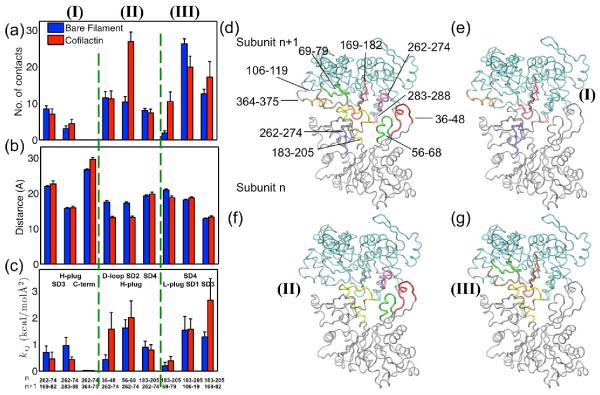
The actin filament bending and twisting mechanics are dictated by the strength, number, and area of longitudinal and lateral intersubunit contacts.^27,33,43,44 Therefore, the enhanced filament bending and twisting compliance observed with cofilin binding must be associated with reorganization and/or disruption of the filament intersubunit bonds. To quantitate and visualize these changes, we plot the distribution of contact densities at the cross-section with n, n+1, or n+2 (in the barbed to pointed end direction of filaments; Figure 3(f−i)), where a contact is defined to exist when a C-alpha atom is within 10 Å of an adjacent subunit's C-alpha atom.

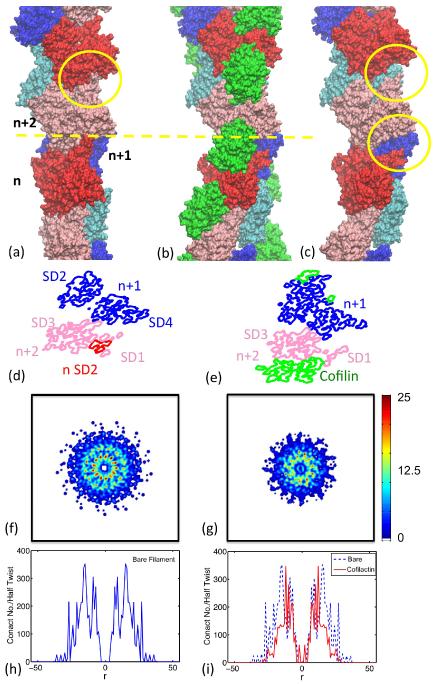
Figure 3.

There are fewer contacts in the cofilactin filament than in the bare actin filament and these occur within a smaller radius. Visualization of (a) bare, (b) cofilactin, and (c) cofilactin filaments, omitting the cofilin proteins, (d) a cross-section of the interface of bare filament, (e) a cross-section of the interface of a cofilactin filament. The actin subunits at the cross-section are labeled with n, n+1, or n+2, in the direction from the barbed to the pointed ends of the filament, and are plotted in red, blue and pink, respectively. Cofilin proteins are presented in green. Actin subdomain 2 is highlighted with a yellow circle for each subunit. Comparison of (d) and (e) shows that the binding of cofilin disrupts interactions between filament subunits, i.e. n-SD2 and n+2-SD1/SD3. The distribution of total number of contacts of a half twist of bare filament and cofilactin filament is projected onto the plane perpendicular to the filament long axis shown in panels (f) and (g). This distribution is further projected onto a single, radial dimension, which is plotted in panels (h) and (i) and which shows the total contact number as a function of the distance to the filament axis.

Cofilactin filaments (Figure 3(c)) have fewer longitudinal SD2(n)-SD1(n+2) and SD2(n)-SD3(n+2) contacts than bare filaments (Figure 3(a)) due to the rotation of subdomain 2 associated with cofilin binding. SD2 of the n^th subunit (red) in bare filaments (Figure 3(d)) is surrounded by SD1 and SD3 of n+2^th subunit (pink). SD2 is not observed in cofilactin (Figure 3(e)) because it is displaced by cofilin (green) and disordered.^10,11,25

A reduction in the net total intersubunit contact density with cofilin binding is readily visualized in the interface cross-section plots (Figures 3(f) and 3(g)). This reduction in total cofilactin intersubunit contacts explains how cofilin can make filaments more flexible and dynamic. However, cofilin could in principle make filaments more compliant by compromising both lateral and longitudinal interactions, or only one of the two (e.g. lateral or longitudinal), while stabilizing or not affecting the other. We therefore quantitate longitudinal and lateral contacts independently to distinguish contributions of lateral and longitudinal bonds to the filament stiffness.

Cofilactin filaments have fewer and weaker longitudinal subunit contacts than bare filaments

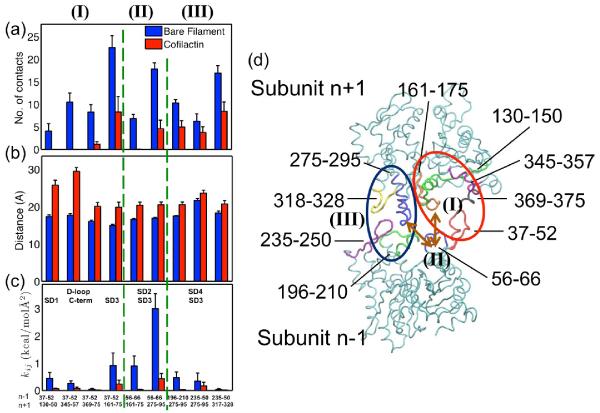
The distributions of intersubunit contacts (Figure 4) indicate two predominant longitudinal contact sites (plot in Figure 4(d)) in bare filaments. The first is between the D-loop (particularly residues 37–52) of the lower subunit and the hydrophobic groove (residues 130–150 and 340–375) of subunit n+2 between SD1 (including C-terminus) and SD3 (Set I in Figure 4). This contact can be divided into two distinct interfaces: one in which D-loop of the n^th subunit contacts SD1 of the (n+2)^th subunit, and the other where it contacts SD3 of the (n+2)^th subunit. The D-loop and major n+2 SD1 (i.e., residues 130–150) contact is present in bare filaments but not in cofilactin filaments (1^st pair of bars in Figure 4a), where only a few contacts remain between the D-loop and C-terminus (residues 345–357 and 369–375, 2^nd and 3^rd pair bars in Figure 4a). This reduction in contacts results from an ~8 Å greater distance separating the COG of residues bridging the D-loop and SD1 (Figure 4(b)). This result is consistent with the distance between residue 41 in the D-loop and residue 374 at the C-terminus increasing with cofilin binding^11,25,45 and a transient contact between residues 45 and 370 at physiological temperatures.²⁹

Figure 4.

Summary of actin subunit longitudinal contacts: (a) longitudinal contacts are significantly decreased in cofilactin; The bar provides the average of 11 or 13 pairs COG distance of the interacting groups of residues, and the error bar is the standard deviation of the mean; (b) Some local lateral contacts increase; (c) All distances between COG of interaction residues groups increase in cofilactin; (d) Schematic representation of residues contributed to longitudinal interactions between subunit n−1(bottom) and subunit n+1 (top). Residues 37–52, 56–66, 196–210, and 235–250 are highlighted in red, blue, green and magenta in subunit n−1; Residues 130–150, 161–175, 275–295, 318–328, 369–375 are highlighted in green, orange, blue, yellow, magenta and black in subunit n+1. Three groups of longitudinal interactions: (I) illustrates that residues in D-loop of subunit n−1 interact with residues in subunit n+1, highlighted in the red circle; (II) displays residues in SD2 of subunit n−1 interact with residues in SD3 of subunit n+1, highlighted by two brown arrows; (III) shows residues in SD4 of subunit n−1 interact with residues in SD3 of subunit n+1, highlighted in the black circle.

Cofilactin filaments also have 3-fold fewer number of contacts between the D-loop and SD3 (the 4^th pair of bars in Figure 4). The interacting groups in these regions (residues 37–52 and 161–175) move 3~4 Å apart with cofilin binding. Hence, the distance between 40(or 45) and 166–169 increases accordingly (Table 3), consistent with the broken contacts between 40 (or 45), and 166–169 observed in cryo-EM cofilactin.²⁹

Table 3.

Comparison of experiment and simulations for longitudinal and lateral filament contacts (errors represent standard deviations)

	Residue ID	Cryo-EM results (change in distance upon cofilin binding)	Equilibrium Distance (Å) Bare filament	Equilibrium Distance (Å) Cofilactin	Exp vs. MD
Longitudinal Contact
1. D-loop vs. C-term	41vs.374	Increase	13.09±1.5	22.02±4.22	Agree
	61 vs. 374	Increase	23.29±1.24	25.68±2.12	Agree
	45 vs. 370	Decrease	14.85±2.09	18.65±2.87	No
2. D-loopvs. SD1	45 vs. 169	Increase	9.74±1.74	13.93±4.24	Agree
	61 vs. 169	Increase	12.78±1.4	16.70±2.57	Agree
3. D-loop vs. SD3	62 vs. 288	Increase	7.52±1.13	13.38±2.37	Agree
4. SD4 vs. SD3	205 vs. 286	Unchanged	9.29±0.53	12.69±2.2	No
	241 vs. 322	Unchanged	11.03±1.76	12.73±1.93	Agree
Lateral Contact
1. H-plug vs. C-term	265 vs. 374	Increase	20.13±1.15	23.38±2.15	Agree

A second principal longitudinal contact area, between SD3 of subunit n+2 and SD2 and SD4 of the lower subunit n, weakens with cofilin binding (Sets II and III in Figure 4). This contact can also be subdivided into two parts: a) the contact between SD3 and SD2 (Set II in Figure 4), and b) the contact between SD3 and SD4 (Set III in Figure 4). The distance between SD3 (residues 161–175, and 275–295) and SD2 (residues 56–66) increases ~ 4 Å (Table 3), which lowers the average contact number in cofilactin 5-fold (the 5^th and 6^th pairs of bars in Figures 4(a) and 4(b)). The distance between SD3 (residues 275–295 and 317–328) and SD4 (residues 196–210 and 235–250) also increases by 2~3Å during the MD trajectory and the contact number decreases ~ 2 fold (the 5^th – 7^th pairs of bars in Figure 4(a) and 4(b)). This movement was not observed in the cryo-EM structure of cofilactin²⁹, which included similar contacts between SD4 and SD3 in bare and cofilactin filaments, suggesting this interaction is highly dynamic and characterized by a short kinetic lifetime at physiological temperature. The changes that we observe are less than the resolution of the cryo-EM image, suggesting that they are not wholly inconsistent with the structural results.

The heterogeneous elastic network model (HeteroENM, see Method section) method provides an alternative measure of the effective interaction strength between interacting pairs. The method coarse-grains interacting group residues (including bound ADP) into a series of CG sites connected with uniform harmonic springs and defines their interaction strength in terms of an effective spring constant (i.e. energy per area). The total number of longitudinal contacts decreases 3-fold from 103.5 pairs to 31.2 pairs with cofilin binding and the strength of these contacts decrease by as much as 20-fold (Figure 4(c)). This reduction originates from the greater separation distance between interacting pairs along with the increase in subunit rise, and the rotation of SD2, as described in the preceding text. Consequently the overall effective longitudinal interaction strength diminishes dramatically.

Cofilactin filaments have more and stronger lateral subunit contacts than bare filaments

The mechanism by which lateral (i.e. inter-strand, n to n+1 subunits) filament interactions respond to cofilin binding is somewhat controversial.^8,14,46 Some studies favor overall weakening of lateral interactions^8,14 while others suggest that they become stronger.⁴⁶ Our MD and CG analyses agree with aspects of both interpretations - some lateral interactions become weaker while others become stronger (Figure 5). There are three groups of lateral contacts (shown in Figure 5(d–g)). The first group (Figure 5e) consists of contacts between the H-plug (residues 262–274) of the n^th subunit and the n+1^th subunit unit (Set I in Figure 5a–c). In this group, the number of lateral contacts decreases in the cofilactin, and the distances between the COG of the H-plug and residues 169–182, and 364–375 slightly increase (Figure 5(b)), in accordance with the experimental observation that the distance between residues 265 (in the H-plug) and 374 (in the C-terminus) increases in cofilactin.¹⁴ The effective interaction strengths all decrease (Figure 5(c)), suggesting that the interaction between H-plug and C-terminus is weakened.

Figure 5.

Summary of actin subunit lateral contacts. (a) Partial lateral contacts increase; (b) Some lateral interacting groups become closer and (c) interact much more strongly in cofilactin. (d) Schematic representation of residues contributed to lateral interactions between subunit n in silver (bottom) and subunit n+1 in cyan (top). Residues 36–48, 56–68, 183–205, and 262–274 are highlighted in red, green, yellow and blue in subunit n; Residues 69–79, 106–119, 169–182, 262–274, 283–288, and 364–375 are highlighted in green, tan, red, magenta, pink, and orange in subunit n+1; (e)–(g) show the three groups (I–III) of interacting residues separately: (e) H-plug (blue) of subunit n interacts with SD3 (red and pink) and C-term (orange) of subunit n+1; (f) H-plug (magenta) of subunit n+1 interacts with D-loop (red), SD2 (green), and SD4 (yellow) of subunit n; (g) SD4 (yellow) of subunit n interacts with L-plug (green), SD1 (tan) and SD3 (red) of subunit n+1.

The second group (Figure 5f) includes contacts between H-plug of the n+1^th subunit and the nth subunit on the other strand, including the D-loop (especially residues 36–48), residues 56–68 of SD2, and residues 183–205 in SD4 of the n^th subunit (Set II in Figure 5a–c). In contrast to the findings for the first group, in the second group, the total contact numbers between these interactions increase (Figure 5(a)). In two of the three contact pairs, the interacting distances decrease (Figure 5(b)), and the effective interaction strengths increase (Figure 5(c)).

The third group of interactions (Figure 5g) is between SD4 of subunit n and the subunit n+1 (Set III in Figure 5a–c). SD4 interacts with the H-loop (residues 69–79), residues 106–119 of SD1, and residues 169–182 of SD3. The total contact number for these three groups increases (Figure 5(a)). The interacting distance decreases slightly in one contact pair (Figure 5(b)), and the effective interaction strengths increase for two of the pairs (Figure 5(c)). The increase of total contact density is consistent with the cryo-EM structure, which exhibits higher contact density in this region when cofilin and phalloidin are both present.⁴⁷ A later study²⁵ suggests phalloidin may not change the environment of H-plug, suggesting that cofilin alone is responsible for the increase in lateral contacts that are seen previously,⁴⁷ a conclusion that is supported by our results.

Overall, the total (average) number of lateral contacts increases from 82.3 in the bare filament to 104.7 in the cofilactin filament. Therefore, the greater flexibility of cofilactin filaments originates from a dramatic weakening or elimination of longitudinal subunit contacts. This is offset by a greater number and strengthening of lateral filament interactions.

Summary of total filament contacts

Two main differences account for the greater stiffness of bare actin filaments compared to cofilactin (Figure 3(f–i)). First is the presence of two high contact density rings in bare actin filaments (Figure 3(f); peaks in Figure 3(h), corresponding to contacts between SD4(n)-SD3(n+2), and SD2(n)-SD1/SD3(n+2), that reduce to a single narrow ring in cofilactin (Figure 3(g); peak in 3(i)). The missing outer ring in cofilactin corresponds to the disrupted SD2(n)-SD1/SD3(n+2) interactions, a consequence of the rotation of the SD2 domain. The second major difference originates from a reduction in the radial distribution of intersubunit contacts with cofilin binding (Figure 3). This geometric redistribution arises because cofilactin filaments are ~17% thinner than bare filaments – the effective radius of contacts (defined as

$$R_C=\int N\left(R\right)RdR∕\int N\left(R\right)dR$$

where N(R) is the number of contacts between R and R+dR comparing only the actin component of filaments) decreases from 15.26Å to 12.68Å with cofilin binding.

One of the four cofilin-actin interface contacts is transient at ambient temperatures

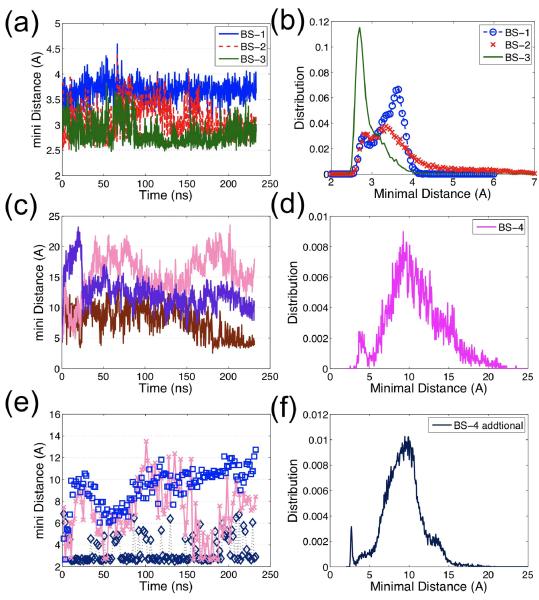
There is increasing evidence that actin filaments adopt multiple distinct and stable conformations.^16,39,48 Accordingly, bound cofilin is likely to adopt multiple binding modes, as inferred from spectroscopic lifetimes¹⁶ and cooperative binding kinetics.⁴⁹ We therefore carefully examined the stabilities of contacts between filament subunits and bound cofilin.

The highest resolution cofilactin structure to date²⁹ identifies four actin-cofilin contacts, two of which are termed G-actin binding sites (BS-1 and BS-2; see SI Table 2 for residues in each binding site, and Figure S4) and two termed F-actin binding sites (BS-3 and BS-4, plotted in Figure S5). The stability of each contact site is inferred from the minimal inter-residue atom (not including hydrogen) distances between the actin residues and the cofilin residues comprising each binding site (Figure 6). The distances in the two G-actin binding sites and in one of the F-actin binding site are very small (< 5 Å) and remain stable during ~ 200 ns of simulation (Figures 6(a–b)). However, the minimal inter-residue atom distance (not including hydrogen) of the F-actin binding site formed between actin residues 242–243 and cofilin residues 154–158 increases to >10 Å during the first 50 ns MD simulation (Figure 6(c–d)). We interpret this as an indication that this contact is weak and characterized by a short lifetime at ambient temperatures. Similar results have also been observed from another MD simulations started with a refined filament structure (see SI Structure refinement section for a detailed description of the refinement method^50,51 and the results). One alternative explanation of this behavior is that the low temperatures stabilize this contact.

Figure 6.

The minimal inter-residue distance (not including hydrogen) evolution and distribution for each binding site reflects the stability of binding sites: (a) The typical time evolution of the minimal inter-residue distance for G-actin binding sites, BS-1 (blue), BS-2 (red), and the stable F-actin binding site, BS-3 (green), demonstrates that each of these binding sites' distances is static, implying the binding site is stable; only one out of 11 curves is plotted for each binding site since all curves are very similar in terms of distance and stability. (b) The distance distributions of BS-1, BS-2, BS-3 for 11 pairs display small distance fluctuations (< 5 Å); (c) The evolution of three examples out of 11 distances for the unstable F-actin binding site, BS-4, shows that the distance of BS-4 is not as stable as that of BS-1 to BS-3; (d) The distance distribution of BS-4 (over all 11 pairs) has two peaks: one less than 5 Å (the initial configuration) and one larger than10Å. Figure 4(c) and (d) suggest that this binding site, BS-4, is unstable; (e) The time evolution of three examples of the distance between cofilin residues 151–158 and actin residues 50–65; (f) The distance distribution is similar to that of BS-4, indicating cofilin residues 151–158 may interact with other groups of actin residues, e.g. residues 55–57, 96–97, 206–208 and 214–216.

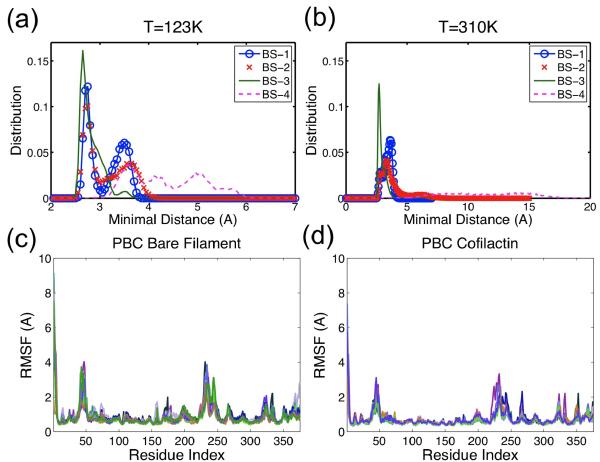
To investigate this possibility, MD simulations at temperatures slightly higher than those typically used for cryo-EM (123K) were performed. This system is equilibrated after about 20ns, based on the RMSD evolution (Figure S6). These simulations demonstrate that all four cofilactin binding site distances remain at < 6 Å after 40 ns of simulation (Figure 7(a)) (including the second F-actin site that dissociates during simulations carried out at ambient temperatures). Low temperatures thus appear to slow dissociation and stabilize the interactions, despite the fact that, overall, cofilin binding energetics display a weak temperature dependence.⁵² Actin residues 242–243 are located in a highly mobile coil region in both the bare⁵³ and cofilactin filaments (see Figures 7(c–d)); cofilin residues 154–158 lie in close proximity to other actin residues, including 55–57, 96–97, 206–208, 214–216 (Figure 6(e–f)), suggesting interactions at the second F-actin sites could be more transient and weak though still contribute to the filament binding affinity.⁵⁴

Figure 7.

Distance distribution of four cofilin-actin binding sites at (a) 123K and (b) 310K. Note the distance range ends at 7Å in (a) but at 20Å in (b). Peaks for BS-1 to BS-3 in (a) and (b) are similar, while for BS-4 are very different. These suggest that all four binding site are stable at low temperature, and BS-4 is not as stable as others at the physiological temperature. Residue RMSF distributions of (c) bare filament and (d) cofilactin filament exhibit a much higher RMSF in regions of N/C-terminus, D-loop, residues 230–250, and H-plug (residues 262–274). Each line represents RMSF data for one actin subunit.

Conclusions

This work focuses on analysis of the property-structure-interaction relationships deduced using all-atom MD simulations and CG analysis to identify the molecular origins of the cofilin-linked increase in bending and torsional flexibility of actin filaments. The mechanical properties calculated from all-atom MD simulations agree well with experimentally measured bending and torsional filament dynamics in actin and cofilactin filaments.^16,24 Opening of the nucleotide-binding cleft is one of the major structural differences between cofilactin and bare actin subunits; cofilactin re-opens from the flat/closed conformation observed in bare F-actin to the more open G-actin like conformation. Moreover, the tilt of each subunit in cofilactin fluctuates to a larger degree, probably due to increased rise per subunit and reduction in the number of longitudinal intersubunit contacts. The cofilactin filament becomes a narrower, more loosely twisted, and less inter-connected filament.

The MD simulations not only provide information about actin conformational changes induced by cofilin binding, but they also enable visualization and quantification of changes in the stability and connectivity of inter- and intra-strand contacts between actin subunits. Both the contacts between longitudinally adjacent subunits and those between laterally adjacent subunits are affected by cofilin binding. The number of longitudinal contacts decreases, and longitudinally adjacent subunits interact more weakly as previously reported in solution studies^{10–12,21,24,25} and in an earlier MD simulation study.²⁷ Some regions of laterally adjacent subunits separate when cofilin binds, and as a result the interaction between these subunits becomes weaker. Other subunit regions move closer together, and their interactions are strengthened. This is the first time that lateral interactions have been quantified computationally; previously only the longitudinal interactions between SD2 of subunit n and SD1 of subunit n+2 were quantified.²⁷ The net result of these changes in contacts is that the filament becomes easier to bend and twist. Reorganization of longitudinal contacts thus appears to be the dominant factor controlling filament flexibility.

The large-scale structural changes associated with cofilin binding include an increase in the subunit rise and an inward rotation of subdomain 2. Both these changes alter the contacts between actin subunits. As a result, the total radial interaction density distribution of cofilactin can be approximated as a much thinner elastic rod than bare actin. Continuum mechanics formalisms would therefore predict that cofilactin filaments would be easier to bend and twist than bare filaments.^16,24

The MD simulations provide information regarding the strength of cofilin-actin binding interactions that complements existing experimental data. We summarized the key parameters quantifying filament structures in Table 2 to show the difference between cryo-EM data (bottom row) and MD data (second row). Due to heterogeneity between subunits in an actin filament (further discussed in³⁹), the average value based on that of 11 actin subunits may not result in an accurate model for cofilactin, but for comparative purposes these averages are sufficient. We found the twist angle per subunit of cryo-EM data is within the range of uncertainty of the average value of simulation data; the cross-over length and the average rise per subunit based on simulation results are slightly larger than those of cryo-EM data; the average filament radius and dihedral angle R2-R1-R3-R4 from simulation are slightly smaller than those of cryo-EM data. In addition, one of the four actin-cofilin contact sites (lying between actin residues 242–243 and cofilin residues 154–158) is not stable during the simulation. Some contacts between SD3 and SD4 are also short-lived. Since the cooling rate of cryo-EM experiments is at about 10⁵–10⁶K/s, it takes about a millisecond to `freeze' the sample.⁵⁵ The changes that we observe in MD simulations occur in nanoseconds, suggesting that bound cofilin may re-equilibrate among its various binding modes during cooling.

Methods

Atomistic MD simulations of bare and cofilin-decorated actin filaments

Two actin filaments comprised of subunits with bound Mg²⁺-ADP were constructed: one bare and one with cofilin at a stoichiometric binding density of one cofilin per actin subunit. The bare filament, based on vertebrate (rabbit) skeletal muscle actin PDB entry 2ZWH³⁶ and containing 13-monomer subunits, was created as described previously.^39,56 The cofilactin filament containing 11 cofilin-bound actin subunits was created based on the 9-Å resolution three-dimensional reconstruction of cofilin-decorated actin (human non-muscle cofilin 2, bovine beta-actin) filaments, PDB entry 3J0S.²⁹ A high affinity Mg²⁺ cation was placed at the nucleotide-binding site, including the first solvation shell of explicit waters as detailed previously.⁵⁶ Each filament was solvated in explicit TIP3P water molecules,⁵⁷ with potassium and chloride ions included at a final concentration of 0.18 M using the solvate and autoionize tools in VMD.⁵⁸ The filament was aligned to periodically repeat along the z-direction, interacting with itself at the box edges. Hence, no water capping was present in the z-direction; however, a minimum layer of 8Å (because of the asymmetry of the filament, this equated to a distance of at least 40Å⁵⁶ between periodic images of the protein) and 15Å of solvent was positioned between the protein and the boundaries in the x and y directions of bare and cofilactin filaments respectively, to minimize self-interaction. The simulations consisted of ~ 473K and ~ 667K total atoms, respectively, including water solvent.

The MD simulations were performed using NAMD 2.9⁵⁹ and the CHARM 22/27 force field with CMAP correction.60 Electrostatic interactions were calculated using the particle mesh Ewald sum method⁶¹ with a cutoff of 12Å. An integration time step of 2fs was used while constraining all hydrogen-containing covalent bonds with the SHAKE⁶² algorithm. Each system was energy minimized, heated, and pre-equilibrated for 100ps in the canonical ensemble while harmonically restraining (with spring constant 1kcal/molŲ) the protein backbone, the nucleotide, the active site Mg²⁺, and water oxygen atoms. The NAMD barostat was then applied to maintain a pressure of 1 atm, and the system was simulated for an additional 200ps. Constraints were next released stepwise (with spring constant varying between 1kcal/molŲ to 0 in steps of 0.1 kcal/molŲ) over total 100ps before starting the production runs. The temperature was maintained throughout at 310K using a Langevin thermostat with 0.5ps⁻¹ damping coefficient. A total of 105 and 240ns of data were generated for the bare filament and cofilactin filament systems, respectively. From Figures S1, S2, and S3, all quantities, including RMSD, crossover length, and the standard deviation of angles between near subunit pairs, are seen to stabilize after ~ 50ns and ~ 120ns; only data after the system were equilibrated were taken for further analysis; most properties were obtained using the final 10ns of data, while the std for bare filament was obtained via the final 50ns data. All quantities presented in this manuscript are averaged value over all subunits and the simulation window.

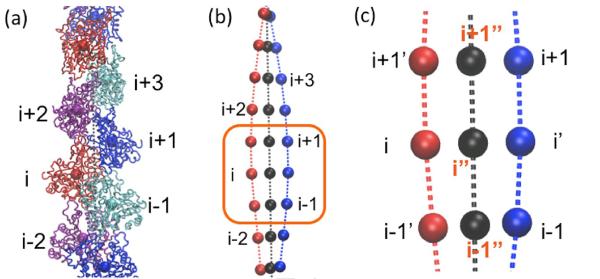
Calculating twist axis, twist angle per monomer, monomer rise, monomer tilt, persistence length, and torsional stiffness from MD simulations

To calculate experimentally measurable filament twisting properties from simulation trajectories, we linearize the actin filament as follows. Each subunit is CG onto a point at its COG. The COG of each strand is transformed to a smooth curve using a cubic spline. The projection of monomer i onto the other strand i' is defined by the point of the other strand with equal curvilinear distance to monomers i−1 and i+1. The twist axis curve connects the center point, denoted by i”, of i and i' (Figure 8). The twist angle of monomer i+1 referenced to monomer i is the projection of the angle between the vectors i−i” and (i+1)−(i+1)” onto the plane with norm directed along the vector i”−(i+1)”. The subunit rise is measured by the distance between points i” and (i+1)”. The subunit tilt is defined as the angle between the twist axis and the vector between the COGs of rigid segments of SD3 (residues 148–179 and 273–333) and rigid segments of SD4 (residues 180–219 and 252–262). The persistence length is then calculated from a cosine correlation analysis of filament tangent angles.⁴³ The distribution of angles between all nearest subunit pairs i−(i+1) and (i+2)−(i+3) is plotted to present the torsional flexibility (Figure 2). Note that the std of the distribution reported from experiments is the average value of data over all subunits of a much longer filament in a much longer time scale¹⁶ which is not accessible for MD simulations. However, we observe that, even though each angle is trapped at its local twist state (i.e., a local value of std strongly underestimates the torsional flexibility), the distribution over all subunits is broad and stops expanding (Figure S2(b)). We assume that each angle will go through all possible twist states given a sufficiently long simulation time, the best way to estimate std is to fit the distribution of all the angles using a Gaussian curve. However, this method of fitting the simulation data is expected to underestimate the actual standard deviation for two reasons. First, there are multiple distinct peaks present in the distribution, which means that fitting to a Gaussian curve undervalues the width of the distribution. Secondly, and more significantly, we can sample at most 11 unique configurations of the twist. Since subunits do not change their twist position during the timescale that we have simulated (see Figure S3(d)), it is entirely possible that there are additional stable configurations that we did not sample. Either of these changes would increase the calculated std.

Figure 8.

(a) Each actin subunit is coarse-grained into one bead (b) Each strand (one shown in red, the other in blue) is fitted to a curve using cubic spline; (c) the center of i−1 and i+1 on the blue curve, i' is the projection of the bead i of the red curve; the filament twist axis is defined by the black curve, which is connected by the center of each bead and its projection;

The effective filament radius was estimated by $R_f=\frac{1}{N_s}{\sum }_{i=1}^{N_s}{\left({r_x}^2\right(i)+{r_y}^2(i\left)\right)}^{1∕2}$, where N_s refers to the number of subunits in the filament (11 or 13) and r_x, r_y refer to the x and y coordinates of the COG of i^th actin subunit in the filament. This definition assumes that the filament is centered at the origin with the z direction aligned to the filament axis. It should be noted that here we only compare the radii of the actin component of the filaments--no cofilin was involved in the calculation.

CG interactions obtained using HeteroENM

The HeteroENM method⁶³ was used to extract interactions between each CG pair by modeling all interactions with harmonic springs whose stiffnesses are iteratively adjusted until the fluctuations of the CG model using normal mode analysis match the fluctuations observed during the all-atom MD simulation. The equilibrium distance of a spring equals the average distance between each CG pair ${\stackrel{‒}{x}}_{\mathit{ij}}=\overline{\mid x_i-x_j\mid }$, and the corresponding mean-square distancefluctuation is given by $\Delta x_{\mathit{ij}}^2=\overline{{(x_{\mathit{ij}}-{\stackrel{‒}{x}}_{\mathit{ij}})}^2}$, The spring constant k_ij is obtained by matching the mean-square distance fluctuation of CG sites, calculated from the normal-mode analysis $\left(\Delta x_{\mathit{ij},\mathit{NMA}}^2\right)$, with that from the MD simulations $\left(\Delta x_{\mathit{ij},\mathit{MD}}^2\right)$ through the following iterative algorithm

$$\frac{1}{k^{m+1}}=\frac{1}{k^m}-4\alpha (\Delta x_{\mathit{ij},\mathit{NMA}}^2-\Delta x_{\mathit{ij},\mathit{MD}}^2),$$ (2)

where m indicates the iteration. The normal mode analysis of the CG elastic network is performed with CHARMM version c32b2.⁶⁴ No distance cutoff is imposed to limit the interactions; thus HeteroENM would yield N_CG(N_CG−1)/2 spring constants for a system with N_CG sites. Initial values of the spring constants are set at k = 1 kcal/mol Ų before iterations of Eq. (2) which are continued until $\mid k_{\mathit{ij}}^{m+1}-k_{\mathit{ij}}^m\mid \le {10}^{-3}$.

Residues in each interacting groups (the complete list is provided in x-label of Figures 4(e) and 4(f) are coarse-grained into one CG site; residues between any two CG sites in the primary sequence are coarse-grained into another CG site. For instance, Figure 4(e) has x-labels 37–52, and 57–66, thus, residues 37–52 are coarse-grained into one CG site, residues 57–66 are coarse-grained into another CG site, residues between them, i.e., residues 53–56 are coarse-grained into one CG site. Notice Figures 4(e) and 4(f) have different x-labels, since the longitudinal and lateral interacting groups are different, bare and cofilactin subunits are coarse-grained into 22 CG sites to evaluate the longitudinal interactions using HeteroENM, and 17 CG sites for lateral interactions.

Highlights

• Cofilin binding increases actin filament flexibility.

• Cofilin binding opens the nucleotide-binding cleft of actin subunits.

• Cofilin weakens longitudinal subunit contacts and strengthens lateral contacts.

• Cofilactin intersubunit contacts have reduced density and cross-sectional area.

• Reorganization of longitudinal contacts appears to regulate filament flexibility.