Resilience of river flow regimes

Abstract

Landscape and climate alterations foreshadow global-scale shifts of river flow regimes. However, a theory that identifies the range of foreseen impacts on streamflows resulting from inhomogeneous forcings and sensitivity gradients across diverse regimes is lacking. Here, we derive a measurable index embedding climate and landscape attributes (the ratio of the mean interarrival of streamflow-producing rainfall events and the mean catchment response time) that discriminates erratic regimes with enhanced intraseasonal streamflow variability from persistent regimes endowed with regular flow patterns. Theoretical and empirical data show that erratic hydrological regimes typical of rivers with low mean discharges are resilient in that they hold a reduced sensitivity to climate fluctuations. The distinction between erratic and persistent regimes provides a robust framework for characterizing the hydrology of freshwater ecosystems and improving water management strategies in times of global change.

The river flow regime identifies the streamflow temporal variability at a station (1), which is the natural byproduct of the sequence of flow pulses conveyed to the stream network from the contributing catchment after rainfall. The flow regime is embodied by the probability distribution function (pdf) of daily flows (2–4), which provides information on the mean water availability, the extent of discharge fluctuations (5), and the frequency of high/low flows. Flow regimes not only constrain anthropogenic uses, such as energy production and irrigation, but shape form and functions of riverine ecosystems owing to the dynamic control of flow magnitude on stream habitats (1, 4, 6–8). In the past decades, natural and anthropogenic modifications of climate drivers (9), jointly with landscape changes, have led to increasingly nonstationary flow regimes (10–14). These ubiquitous and accelerating alterations of river flows challenge the sustainability of water uses (5, 15) and the ecosystem services provided by river biomes (6, 16, 17). However, streamflow alterations are not expected to be uniform (18, 19), owing to heterogeneous climate/landscape drifts and sensitivity gradients across diverse climate zones and regime types.

Here, the flow regimes of pristine rivers are analyzed using a mechanistic analytical model in which streamflow dynamics are driven by a catchment-scale soil–water balance forced by stochastic daily rainfall (2, 3). The analytical model indicates that the nature of flow regimes and their sensitivity to climate change can be discriminated based on the frequency of effective (i.e., flow-producing) rainfall events and the time scale of the hydrological response through which these rainfall inputs are propagated across catchments. This hypothesis is tested through extended climate and flow records taken from 44 US and Italian catchments belonging to the US Geological Survey/National Oceanic and Atmospheric Administration and the Regional Agency for Environmental Protection of the Veneto Region monitoring networks (Table S1). To comply with the basic assumptions of the mechanistic model (pertaining to the features of climate forcing and the dominant mechanisms of streamflow production), the choice of the catchments is restricted to unregulated, small/medium watersheds weakly influenced by snow dynamics (SI Materials and Methods). In this setting, flow-producing rainfall events result from the censoring operated by catchment soils on daily rainfall, and they are modeled as a spatially uniform marked Poisson process with mean depth α [L] and mean frequency 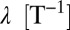. Although α quantifies the average daily intensity of rainfall events, λ is smaller than the underlying precipitation frequency because the soil–water deficit created by plant transpiration in the root zone may hinder the routing of some inputs to streams (Eq. S3). Therefore, λ crucially embeds rainfall attributes; soil/vegetation properties; and other climate variables, such as temperature, humidity, and wind speed.

The time scale of the hydrological response, defined as the mean water retention time in the upstream catchment, is operationally identified by the inverse of the flow decay rate 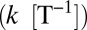observed during recessions, conveniently assumed to be exponential (2, 3, 20). The term k quantifies catchment-scale morphological and hydrological attributes [e.g., the mean length of hydrological pathways and upscaled soil conductivity (3)]. High k values imply low duration of the flow pulses released from the catchment after rainfall, typical of fast-responding catchments.

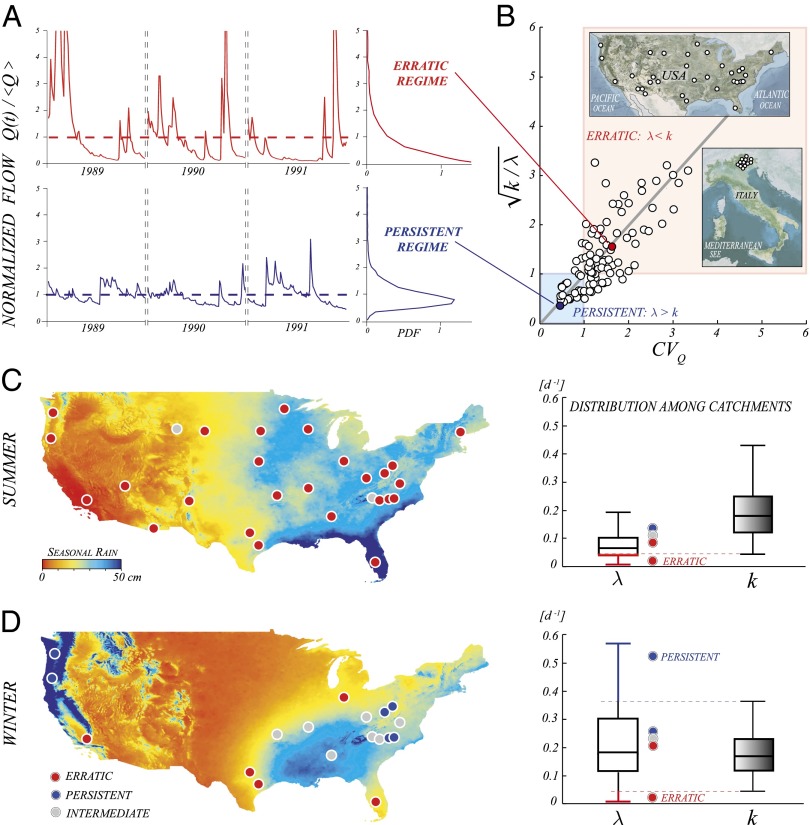
When flow-producing rainfall events are relatively frequent, such that their mean interarrival is smaller than the duration of the flow pulses delivered from the contributing catchment 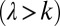, the range of streamflows observed at a station between two subsequent events is reduced, and a persistent supply is guaranteed to the stream from catchment soils. Therefore, river flows are weakly variable around the mean (Fig. 1A, Lower) and quite predictable. This type of regime (hereafter termed persistent) is typically expected during humid, cold seasons in slow-responding catchments (high λ, low k).

Fig. 1.

Analytical and empirical classification of river flow regimes as erratic or persistent. (A) Typical behavior of river flow dynamics in erratic and persistent regimes: Persistent regimes are characterized by enhanced frequencies of events that decrease the flow variability. (B) Ratio between the mean frequency of flow-producing rainfall events, λ, and the inverse of their mean response time, k, explains most of the observed intraseasonal flow variability 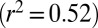, as documented by the scatterplot of the observed 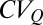vs. the corresponding estimate performed on the basis of the empirical values of 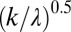, representing the theoretical prediction of the analytical model. Each circle identifies a given catchment during a season (spring, summer, fall, or winter). (Insets) Maps show the locations of the 44 study catchments. (C and D) Spatial distribution of the flow regimes among the US study catchments during summer (06/01–08/31) and winter (12/01–02/28), supported by the corresponding box plot of the frequency distribution of λ and k (outliers are not represented). In the two maps, based on the average value of 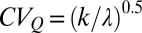, catchment regimes are classified as persistent 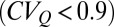, intermediate 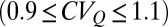, or erratic .

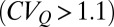When the mean interarrival between flow-producing rainfall events is larger than the typical duration of the resulting flow pulses 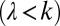, a wider range of streamflows is observed between events because the reach is allowed to dry significantly before the arrival of a new pulse. The temporal patterns of streamflows are thus more unpredictable (Fig. 1A, Upper), leading to erratic regimes with significant streamflow fluctuations. Under these circumstances, the preferential state of the system is typically lower than the mean. Erratic regimes are likely expected in fast-responding catchments during seasons with sporadic rainfall events (low λ, high k). However, this type of regime also can frequently be observed during hot, humid seasons (where relatively high rainfall rates are compensated by enhanced evapotranspiration).

The analytical mechanistic model on which the proposed classification of hydrological regimes is grounded allows the river flow pdf to be expressed as a gamma-distribution with shape parameter 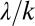and rate parameter 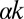(2, 3) (Materials and Methods). The parameters α, λ, and k (which we hereafter term hydroclimatic parameters) summarize the underlying morphological and hydroclimatic conditions, and can thus be evaluated based solely on rainfall, climate, and soil/vegetation information. However, to reduce the burden of the data requirement for their estimation, in this paper, λ, α, and k have been evaluated by combining rainfall and discharge data (Materials and Methods and Figs. S1 and S2). The reliability of the estimates of λ, α, and k has been checked a posteriori through comparison of the observed and theoretical distributions of daily flows (Figs. S3 and S4). The flow regime of the available combinations of catchments/seasons has then been classified as erratic or persistent depending on the long-term average of the ratio 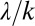. Due to the spatial and temporal heterogeneity of climate and landscape attributes, the estimated ratios 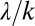span one order of magnitude. The majority of the cases analyzed (64 of 110 cases) are characterized by erratic regimes 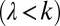. Remarkably, the estimated ratios 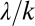explain most of the seasonal variability of daily flows observed in different catchments across regimes, quantified here through the coefficient of variation of daily flows (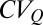). Fig. 1B shows that in the majority of the cases analyzed, the observed mean of the 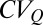(evaluated on a seasonal basis) matches the corresponding estimate of the mean of 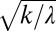, representing the theoretical prediction of the analytical model for the 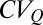. The limited number of observed data lying outside the screened area reveals that most cases classified as erratic (persistent) actually display, on average, a pronounced (reduced) flow variability. The reduced deviations from the theoretical prediction suggest the reliability of the proposed classification, which [although far from being perfect and applicable to all the settings (see below)] is able to frame the wide range of cases analyzed properly.

A strong seasonality of the flow regimes is observed owing to the underlying climatic controls, with regime shifts across seasons being the rule rather than the exception. Persistent regimes were found in most alpine catchments during the summer but were also detected in the United States, especially in the western and the northeastern United States, during the winter. Erratic regimes are widespread throughout the United States during the summer (Fig. 1C) and the fall, owing to larger rainfall interarrivals and to the enhanced transpiration rates. In some cases (especially winter and spring), the frequency of flow pulses was found to be close to the recession time constant, leading to 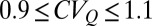. A significant number of these cases, classified as intermediate in Fig. 1 C and D, were found to be located in the southeastern United States. The 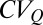(and thus the type of flow regime) is poorly correlated with the average seasonal rainfall but quite strongly anticorrelated 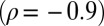with the mean specific discharge, 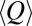, in agreement with the results of Destouni et al. (5). In particular, a large majority of the cases where 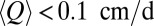were found to be erratic, thereby suggesting that a low 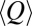may represent a sufficient but not necessary condition for the erraticity of the regime (Fig. S5). The smallest ratios 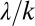(corresponding to extremely erratic regimes) were observed in the south/southwestern areas of the United States. Some of these cases (especially in the summer and the fall) are typically characterized by extremely low average discharges and were excluded from the analysis owing to the practical difficulties in estimating k from the few recessions available. Similarly, no catchments belonging to the mountainous northwestern area of the United States were included in the analysis, because their regime is typically affected by human regulation and/or snow dynamics (thereby violating the assumptions required by the analytical model).

To assess the regime sensitivity to interannual modifications of climate/landscape properties, we analyze how the flow regimes respond to long-term changes in the driving hydroclimatic parameters λ, α, and k. Interannual fluctuations of α quantify the interannual variability of the mean intensity of the events, whereas interannual modifications of λ describe the combined action of changes in precipitation (frequency and depths) and other climate variables affecting the soil–water balance (temperature, wind, humidity, and radiation). Dry and warm years, for instance, should likely result in drastically reduced frequencies of effective rainfall events. Similarly, the interannual variability of k quantifies interannual changes in soil responsiveness and the partitioning between fast/slow flows, jointly with possible changes in short-term rainfall dynamics. The interannual variability of λ and k may also mirror natural or human-triggered change in the landscape, such as shifts in soil cover and soil use. However, because the majority of the selected rivers belong to pristine areas that eschewed extensive anthropogenic interventions, the climate fluctuations in this study are most likely the primary driver of change.

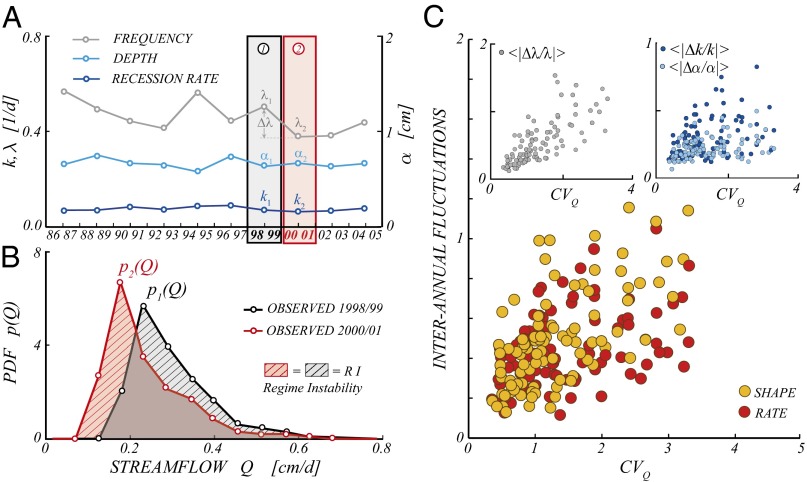
Climate time series typically feature complex, multiscaling behaviors (13, 21), which often make it difficult to separate natural fluctuations objectively from sustained trends. To circumvent this issue, we use the theory of superstatistics (22–24) and we assume that long-term climate/streamflow dynamics result from the juxtaposition of several stationary subperiods (each spanning a suitable number of years), within which the flow regimes are evaluated and classified based on the corresponding values of λ, k, and α. The combined effect of hierarchical fluctuations operating at different time scales is thus handled by assuming that the parameters defining the randomness of rainfall and transport processes during each subperiod (namely, 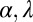, and k) may, in turn, vary across the different subperiods identified (Fig. 2A). Because the primary focus of this study is the regime responsiveness to hydroclimatic forcings (independent of their nature), the analyses have been carried out using two different aggregation time scales, namely, 2 y (representative of natural interannual fluctuations around stable states) and 8 y (representative of longer term fluctuations and sustained shifts). The corresponding variations of λ, α, and k between these periods will be referred to as hydroclimatic fluctuations, regardless of the underlying time scale. Fig. 2A shows the 2-y variability of λ, α, and k for a sample catchment considered in the study. Nonstationary features are particularly evident for the pulse frequency λ (which mainly mirrors interannual changes in rainfall and temperature; Fig. S2), a character shared by the majority of the catchments considered in this study. An example of the effects produced by hydroclimatic fluctuations on hydrological regimes is represented in Fig. 2B, where the observed shift in the streamflow distribution is primarily related to the observed decrease in the rainfall frequency. Quantitatively, the change produced by hydroclimatic fluctuations in the seasonal flow distributions (which we term flow regime instability) is evaluated here through the regime instability index (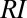), defined as the relative fraction of probability shifting from one flow range to another in response to hydroclimate fluctuations (cross-hatched areas in Fig. 2B). The 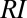is a synthetic measure of the fluctuations of the seasonal flow distribution (including mean, variance, and frequency of high/low flows) over different periods/years (Materials and Methods). Provided that both the ecological functions of riverine environments and the anthropogenic exploitability of running waters are strongly constrained by the entire distribution of observed flows (4, 15), the 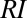is a meaningful measure of the potential impact of time-variant flow regimes on stream habitats and anthropogenic water uses.

Fig. 2.

Hydroclimatic fluctuations produce flow regime instability. (A) Hydroclimatic fluctuations in the Piave River at Cancia, Italy, during the summer, identified by the underlying fluctuations of λ, α, and k across consecutive, disjointed groups of 2 y (representing the variability of the number, magnitude, and response time of flow-producing rainfall events). (B) Experimental evidence of the effect of hydroclimatic fluctuations on the streamflow distribution: The frequency changes are particularly evident for the range of flows, 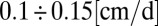, that had not been observed during 1998–1999 but became relatively frequent during 2000–2001. (C) Relative magnitude of the long-term variability of hydroclimatic parameters λ, α, and k (including the shape and rate parameters of the flow pdf: 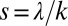and 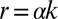) increases with the seasonal .

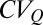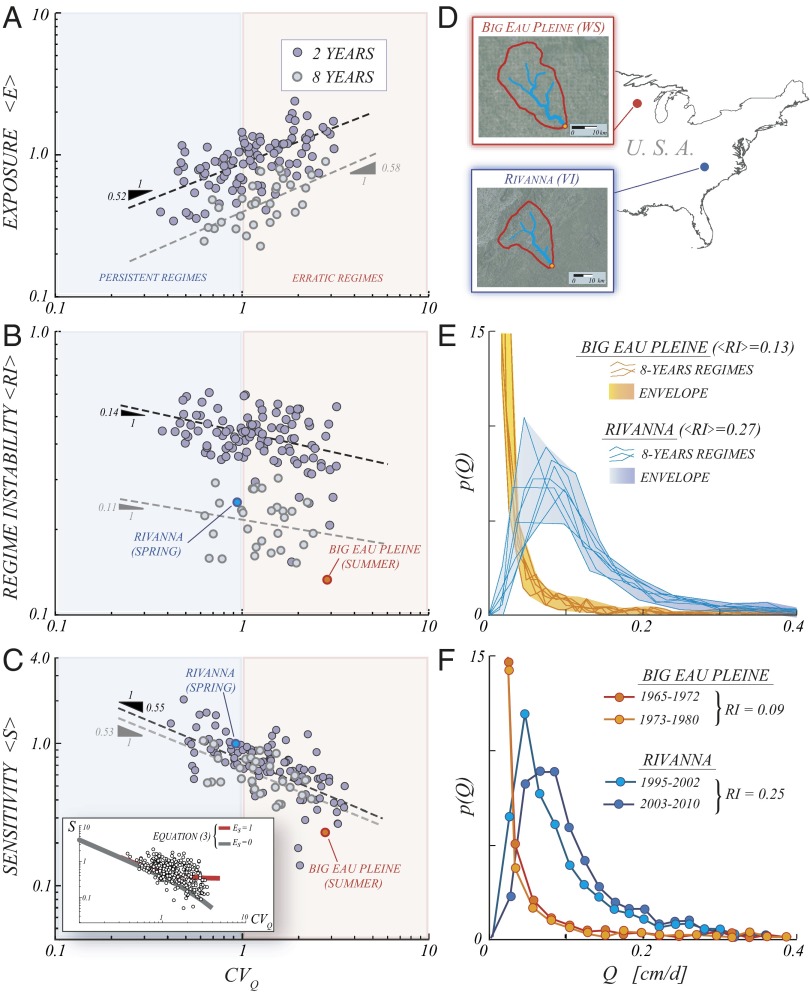
The magnitude of the hydroclimatic fluctuations driving regime instability can be quantified using different metrics. Here, we first analyze the relative interannual fluctuations of λ, α, and k to identify the interannual variability in the number, magnitude, and response time of flow-producing rainfall events. On this basis, the relative interannual fluctuations of the shape and rate parameters of the streamflow distribution (which are explicitly related to λ, α, and k through the analytical model) can be estimated. This allows evaluation of the actual extent of hydroclimatic fluctuations, properly discounting self-compensating external changes like the simultaneous increases of λ and k (i.e., more frequent but faster events) that maintain unaltered the flow variability. Finally, to summarize the overall exposure to climate change into a single indicator, we defined the exposure index (E) representing the sum of relative variations of the shape and rate parameters of the flow distribution (disregarding their sign). The E synthetically represents the extent of the observed hydroclimatic fluctuations (and thus the potential exposure to change), evaluated from the perspective of the analytical model for the flow distribution (Materials and Methods). Irrespective of the specific metric considered, owing to the enhanced nonlinearity of the relevant climatic/hydrological processes, the relative magnitude of hydroclimatic fluctuations sensibly increases with the flow variability, 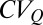(Figs. 2C and 3A). Erratic regimes are thus characterized by higher mean exposures than persistent regimes, with a significance of 0.05 (SI Materials and Methods).

Fig. 3.

Resilience of erratic flow regimes to climate change. Average exposure (A), regime instability (B), and sensitivity (C) for any available combination of catchments/seasons, plotted as a function of the seasonal 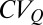. Dashed lines identify the least-squared regressions, whose slopes are indicated in the figure. The average 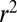values for E, 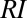, and S are 0.37, 0.1, and 0.41, respectively. Erratic flow regimes, notwithstanding their enhanced exposure to climate change, are characterized by lower sensitivity and lower regime instability. (C, Inset) Agreement between the observed sensitivities and the pattern predicted by the analytical model (SI Discussion). (D) Reduced sensitivity of erratic regimes identifies their ability to buffer climate change (hydrological resilience), as evidenced by the comparison of the streamflow pdfs observed in two streams with contrasting regimes: the Rivanna River (persistent) and the Big Eau Pleine River (erratic). (E) Comparison of the temporal evolution of the seasonal flow pdfs in these catchments during the past 50 y indicates that the flow pdfs observed in the Big Eau Pleine River during different periods are much more similar to one another with respect to the regime successions recorded in the Rivanna River. (F) Resilience of erratic flow regimes is also shown by the different responsiveness of the 8-y flow pdfs to a reference change 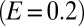of the underlying hydroclimatic parameters.

To assess the impact of hydroclimatic fluctuations on the hydrological cycle across different geographic regions and temporal scales, we have analyzed the seasonal flow regimes of the 44 test catchments during subsequent nonoverlapping periods of 2 and 8 y, and we have then computed the corresponding average regime instability indices, 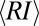(Materials and Methods). The plot of the average 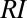vs. 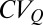shows that erratic regimes display a lower regime instability compared with persistent regimes, notwithstanding their larger exposure to climate change (Fig. 3B). Hence, erratic regimes bringing highly unpredictable discharges during each season may be more stable (and thus not equally unpredictable) across different years.

The ratio between regime instability and exposure provides a measure of the changes observed in the flow regime in response to a given (unit) perturbation of hydroclimatic parameters, and thus represents the regime sensitivity to climate change. High sensitivities imply that the underlying hydroclimatic fluctuations are amplified by flow regimes, with relevant modifications in the frequencies associated with discharges of any size. Reduced sensitivities, instead, indicate the ability of flow regimes to buffer changes in the external forcing, a feature that is referred to as hydrological resilience. The hydrological resilience of river regimes provides a robust basis for characterization of the expected response of riverine ecosystems to external disturbances (ecological resilience), and the related socioeconomic impact. Fig. 3C shows a clear pattern of sensitivity across regimes with the mean regime sensitivity of erratic regimes, 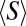, which is smaller than the mean sensitivity of persistent regimes (with a significance of 0.05). The structural resilience of erratic regimes identifies the reduced responsiveness of the whole streamflow pdf to interannual hydroclimatic fluctuations (Fig. 3 D–F), a feature that cannot be automatically transposed to other flow metrics (e.g., the mean flow). Interestingly, when the time scale used to analyze the regime instability increases (from 2 to 8 y), the average exposures and instabilities decrease consistently, although maintaining their characteristic dependence on the 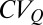. Remarkably, the sensitivity pattern does not appear to be altered (Fig. 3C), suggesting that the regime responsiveness to changes in the underlying climatic conditions depends only on the internal dynamics through which rainfall inputs are spatially and temporally integrated by watersheds. Because the regime sensitivity is strongly affected by the type of flow regime but is essentially independent of the time scale of the driving change, the observed sensitivity patterns should also apply to forthcoming climate shifts. The observed reduced sensitivity of the erratic flow regimes also complies with the reduced sensitivity of the corresponding analytical streamflow distributions to changes in the shape and rate parameters (Materials and Methods), as shown in Fig. 3C (Inset) (SI Discussion).

The analysis pinpoints that seasonality of flow regimes can be a critical issue for the description of river flow availability and the supply of water needs. Most catchments experience regime shifts across seasons, implying that the modes of water availability and the sensitivity to climate change may be radically different in diverse periods of the year. Even though the analytical approach underlying this study relies on significant simplifications, which pose concerns for applications to ephemeral streams or large basins and require a cautious approach to snow-dominated catchments, the proposed classification of flow regimes is deemed especially valuable. The diverse degree of flow variability of persistent and erratic flow regimes may have an impact on some key features of river ecosystems, particularly the temporal heterogeneity of habitat conditions and the river–floodplain connectivity, with significant implications for water quality and river food-web dynamics (25–31). The actual ability of stream biota to exploit riparian and riverbed resources may indeed be strongly influenced by the frequency and duration of low/high flows subsumed by the flow regime, notwithstanding the key role of geochemical, morphological, and biotic factors. In engineered rivers, the ability to characterize the underlying natural flow regimes can contribute to the assessment of the hydrological alteration produced by water infrastructures and the potential benefits of their decommissioning (32), thereby providing an objective support tool with which to embed environmental externalities in the definition of management strategies, services, prices, and incentives. The different sensitivity of erratic and persistent regimes may also bring important socioeconomic consequences, because the resilience of erratic regimes may contribute to buffer forthcoming changes of low flows in rivers with reduced water availability, thereby constraining the security of municipal, agricultural, and industrial water uses (5, 15). A proper classification of the flow regimes can also help to set targeted and flexible policy actions. For instance, minimum flow discharge prescriptions may not be suited to erratic regimes where, owing to the enhanced streamflow variability, any fixed minimum flow is typically disproportionate to the incoming flows during several weeks per season (being too small during high flows but too large under low-flow conditions). An objective characterization of flow regimes and their responsiveness to external forcing may thus offer important clues to the hydrology of freshwater ecosystems and the management of water resources.

Materials and Methods

Analytical Characterization of the Flow Regime.

Daily stream flow dynamics are assumed to result from the superposition of a sequence of flow pulses triggered by precipitation, suitably censored by (catchment-scale) soil moisture dynamics. In particular, the sequence of streamflow-producing rainfall events during a given season is approximated by a Poisson process similar to the overall rainfall (2), characterized by frequency λ and exponentially distributed depths (with mean α). The reduced frequency of effective rainfall events λ with respect to the precipitation frequency 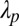(Eq. S3) expresses the ability of the soil to filter the rainfall forcing by exploiting some inputs to fill the soil–water deficit created by plant transpiration (thereby hindering the routing of these inputs). If subsurface environments are assumed to behave like a linear storage with rate constant k, each pulse determines a sudden increase of the stream flow followed by an exponential-like recession with rate k. Under these circumstances, the specific (per unit catchment area) discharge at time t, , is expressed by:

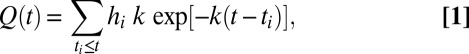where the couples 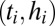identify the arrival time and the depth of the ith pulse, and define a 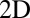Poisson process whose mean measure is 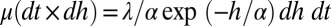. The steady-state pdf of Q can be derived through the Campbell theorem (33) as a Gamma-distribution with shape parameter 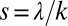and rate parameter 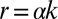(2, 3):

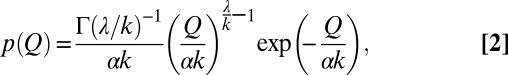where 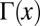is the complete Gamma-function of argument x. Because the exponent of the power-law term in Eq. 2 is positive only for 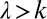, the shape of the river flow pdf is radically different in the two regimes (Fig. 1A): monotonic for erratic regimes 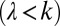and hump-shaped in the case of persistent regimes 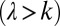. Eq. 2 is also able to explain the different degree of variability associated with erratic/persistent regimes. According to Eq. 2, the 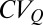can be analytically expressed as 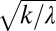(SI Materials and Methods), implying that persistent regimes are characterized by a 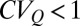, whereas erratic regimes are featured by a 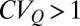. Significant assumptions are required to derive Eqs. 1 and 2, which express analytically the flow pdf in terms of three physically based measurable parameters embedding rainfall, soil, vegetation, and morphological attributes of the contributing catchment. Most of these assumptions, however, can be suitably relaxed, allowing power-law recessions (34), spatial/temporal variables k (3, 20), and heterogeneous rainfall/landscape attributes (3) to be tackled properly in the same framework. The above approach proved robust in predicting the observed streamflow pdfs in many temperate catchments under a variety of climate and morphological conditions (SI Materials and Methods). Model performances were satisfactory also in the catchments investigated in this study (Fig. S2).

Catchment Selection and Flow Regime Classification.

In this study, 44 medium/small catchments with synchronous discharge and rainfall records were selected throughout the United States and the Italian Alps (Fig. 1B and Table S1). In the selection, highly engineered rivers were excluded from the analysis as well as snow-impacted regimes typical of cool/mountain regions. For each available combination of catchments and seasons (identified on the basis of calendar dates as described in the legend for Fig. 1) the parameters λ, k, and α have been objectively evaluated from rainfall and discharge data: α is estimated as the mean observed rainfall depth, k is derived from observed recessions, and 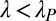is directly estimated from the mean discharge and the mean rainfall depth (Figs. S1 and S2 and SI Materials and Methods). The estimate has been repeated for the available nonoverlapping groups of 2 and 8 y contained in the datasets. The corresponding analytical streamflow pdfs (Eq. 2) and their moments were then computed and compared with the corresponding observed flow statistics. The scatterplot in Fig. 1B was built by comparing the observed and analytical 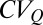values (long-term averages of 2-y periods) for each catchment and season. Based on the average value of 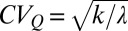, the catchment regimes of Fig. 1 C and D were classified as persistent 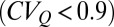, intermediate 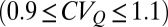, or erratic 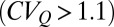. Provided that the estimate of k for extremely erratic regimes based on recessions may be biased owing to the limited number of events available within each season, we limited all the quantitative analyses shown in the paper to the range .

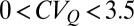Exposure to Climate Change and Regime Instability.

The analyses allowed an objective estimate of the observed interannual variability of λ, α, and k, and of the corresponding fluctuations of the shape and rate parameters that define the seasonal flow regime (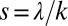 and 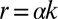). On this basis, we calculated the exposure to climate change through the exposure index E, defined as the sum of the modulus of the relative variations of r and s: 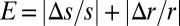(SI Materials and Methods). Note that according to the definition, the highest exposures are associated with the largest variations of the relevant hydroclimatic parameters, particularly the long-term changes of the ratio 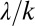(Fig. 2). Similarly, the interannual fluctuations of the river flow pdf were computed on the basis of the available discharge records through 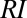the . The 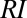defines the fraction of probability shifting from one flow range to another in response to climatic fluctuations. Specifically, the 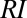between two subsequent periods (say, periods 1 and 2) characterized by the flow pdfs 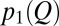and 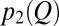is proportional to the area comprised between the two flow pdfs: 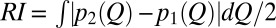(SI Materials and Methods and Fig. S3). The extreme cases 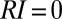and 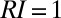, respectively, identify cases in which the flow regimes of the considered periods are perfectly overlapping and completely disjoint. The exposure and the regime instability were calculated for each combination of catchment/season (Fig. S6) at different time scales (namely, 2 and 8 y) and were then averaged to get the points shown in Fig. 3 A–C. Note that to reduce the scattering of the points, all the cases where 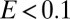( 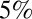of the cases analyzed) were excluded from the analysis (SI Materials and Methods).

Sensitivity.

The sensitivity of the flow regime to climate change is computed as the ratio between the regime instability and the exposure: 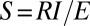. Reduced sensitivities identify the hydrological resilience of flow regimes. The sensitivity to climate change can be also characterized analytically through the stochastic analytical model embedded in Eq. 1, starting from the definition of regime instability and expressing the difference between the flow regimes in the two reference periods [ 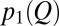and 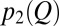] as a function of the underlying variations of λ, α, and k via a first-order Taylor expansion. If the observed changes of the shape and rate parameters of the flow pdfs ( 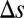and 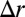) have the same sign, the sensitivity can be expressed as (SI Materials and Methods):

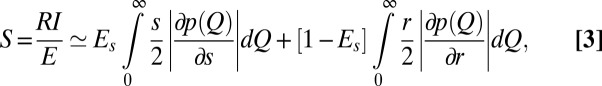where 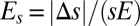represents the contribution provided by the variability of 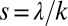to the overall E. The two integrals on the right-hand side can be calculated using Eq. 2, and both of them are found to be monotonic, increasing functions of 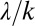the ratio (SI Materials and Methods). Eq. 3 shows that the regime sensitivity is controlled by the ratio 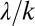and explains theoretically the observed reduced sensitivity of erratic flow regimes to climate change (SI Discussion). Fig. 3C (Inset) (SI Materials and Methods and SI Discussion) compares the theoretical dependence of S on the 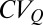given by Eq. 3 (where s is expressed as 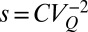) and the observed sensitivity pattern for the 2-y regimes (only changes of s and r with the same sign are considered, in agreement with the assumptions underlying Eq. 3).