DNA Hairpin Stabilization on a Hydrophobic Surface

Abstract

DNA hybridization in the vicinity of surfaces is a fundamental process for self-assembled nanoarrays, nanocrystal superlattices, and biosensors. It is widely recognized that solid surfaces alter molecular forces governing hybridization relative to bulk solution, and these effects can either favor or disfavor the hybridized state depending on the specific sequence and surface. Results presented here provide new insights into the dynamics of DNA hairpin-coil conformational transitions in the vicinity of hydrophilic oligo(ethylene glycol) (OEG) and hydrophobic trimethylsilane (TMS) surfaces. Single-molecule methods are used to observe the forward and reverse hybridization hairpin-coil transition of adsorbed species while simultaneously measuring molecular surface diffusion in order to gain insight into surface interactions with individual DNA bases. At least 35,000 individual molecular trajectories are observed on each type of surface. We find that unfolding slows and the folding rate increases on TMS relative to OEG despite stronger attractions between TMS and unpaired nucleobases. These rate differences lead to nearly complete hairpin formation on hydrophobic TMS and significant unfolding on hydrophilic OEG, resulting in the surprising conclusion that hydrophobic surface coatings are preferable for nanotechnology applications that rely on DNA hybridization near surfaces.

1. Introduction

DNA origami seeks to create nanometer-sized objects with complex geometries using Watson-Crick base pairing to guide self-assembly.^[1] The resulting structures can function as molecular ‘pegboards’ that template the spatial arrangement of multiple components to create novel experimental systems.^[2] Although origami has traditionally been self-assembled in solution, there is increasing interest in direct assembly on solid surfaces to avoid damaging the fragile nanostructures during transfer to surfaces for characterization or functional experiments.^[3] Furthermore, in order to preserve the perfection expected from solution-phase self-assembly, objects must remain stable and unaltered in the presence of distinctive and complex non-covalent surface interactions.

A related use of DNA-guided self-assembly is to template the formation of nanocrystal^[4–7] or carbon nanotube^[8] superlattices, where precise spatial arrangement of different components creates unique optical or electronic materials. In these systems, DNA must hybridize correctly in the vicinity of nanocrystal surfaces that, in addition to complex chemical surface properties, may exhibit high curvature or topographic features that can affect DNA hybridization.^[9] Indeed, the high error rate of self-assembly is a major challenge in this field^[10] and understanding the role of the surface in DNA hybridization can improve yields^[11] both by promoting the correct hybridized structure (potentially without multistep annealing procedures^[2]) and preventing surface-mediated unfolding of hybridized DNA. Additionally, many biosensors exploit DNA hybridization to detect analytes.^[12] While interfacial design has been explored in these systems from the perspective of preventing nonspecific adsorption^[13–14] or making ssDNA physically accessible to its complementary strand,^[15–16] the present work examines the direct influence of interfacial chemistry on DNA hybridization.

Although DNA hybridization has been extensively studied in solution, much less is known about interfacial hybridization.^[17] Recent efforts have addressed interfacial contributions such as electrostatics, conformational restriction due to confinement, and surface coverage.^[18–20] Relative to solution, surfaces were found to drive equilibrium either towards or away from the helical state depending on both the DNA sequence and surface properties, highlighting that surface effects represent combined contributions from many DNA-surface interactions.^[19–21] The present work uses single-molecule fluorescence tracking to observe both the conformational state and dynamic trajectory of a hairpin-forming DNA sequence on two different surface chemistries: a model hydrophobic surface (trimethylsilane, TMS) and hydrophilic oligo(ethylene glycol) (OEG). OEG monolayers are known to resist nonspecific DNA adsorption and to stabilize nanometer-sized particles while still allowing hybridization.^[22] In contrast, hydrophobic surfaces are expected to interact strongly with unpaired bases, resulting in a ‘base-down’ orientation that is often assumed to inhibit hybridization.^[23–24] This work makes direct measurements of the conformational states of individual DNA molecules that call the conventional wisdom into question with the finding that TMS favors the hairpin state more than OEG.

2. Results and Discussion

2.1. RET Tracking Identifies the Conformational State of DNA

DNA folding and unfolding transitions were studied using a hairpin-forming DNA sequence (h⁺DNA) labeled on the 5’ and 3’ ends with different fluorophores (Alexa488 and Alexa594) that comprised a resonance energy transfer (RET) pair with a Förster radius of ~5.4 nm in solution.^[25] We quantified the conformational state based on the relative end-to-end distance, d, which is proportional to the absolute end-to-end distance by a constant of order of the Förster radius as described in the Experimental Section. The 44-base sequence had a stem with 20 complementary base pairs, a 4-base turn/loop, and a calculated melting temperature of 55°C at a physiological salt concentration. In the random coil state, the 44-base sequence has an end-to-end distance that mostly exceeds the expected end-to-end distance for a well-folded hairpin, permitting us to distinguish between hairpin (folded) and coil (unfolded) states. Given that a double helix of B-DNA is 2.2–2.6 nm in diameter,^[26] one expects a fluorophore spacing of 3–4 nm for the hairpin state after accounting for short tethers used to attach the dyes. For a two-dimensional self-avoiding random walk with a characteristic monomer size of 0.59 nm,^[27] 71% of the coil configurations have an end-to-end distance larger than 4.0 nm.^[28–29] Therefore, the majority of short end-to-end distance configurations represent hairpins while nearly all configurations with large end-to-end distances represent coils.

Fluorescence microscopy was used to acquire sequential frames of DNA molecules at 25°C as they adsorbed to, diffused on, and desorbed from self-assembled monolayers of TMS or OEG. Our results represent data from 40,000 individual molecular trajectories on TMS and 35,000 trajectories on OEG. Images of the same surface region were acquired simultaneously in two wavelength channels that were sensitive to fluorescence emission from either Alexa488 or Alexa594 in order to determine RET efficiency and the relative end-to-end distance. Dynamic changes in RET efficiency, corresponding to conformational changes, were often observed during the surface residence of individual molecules.

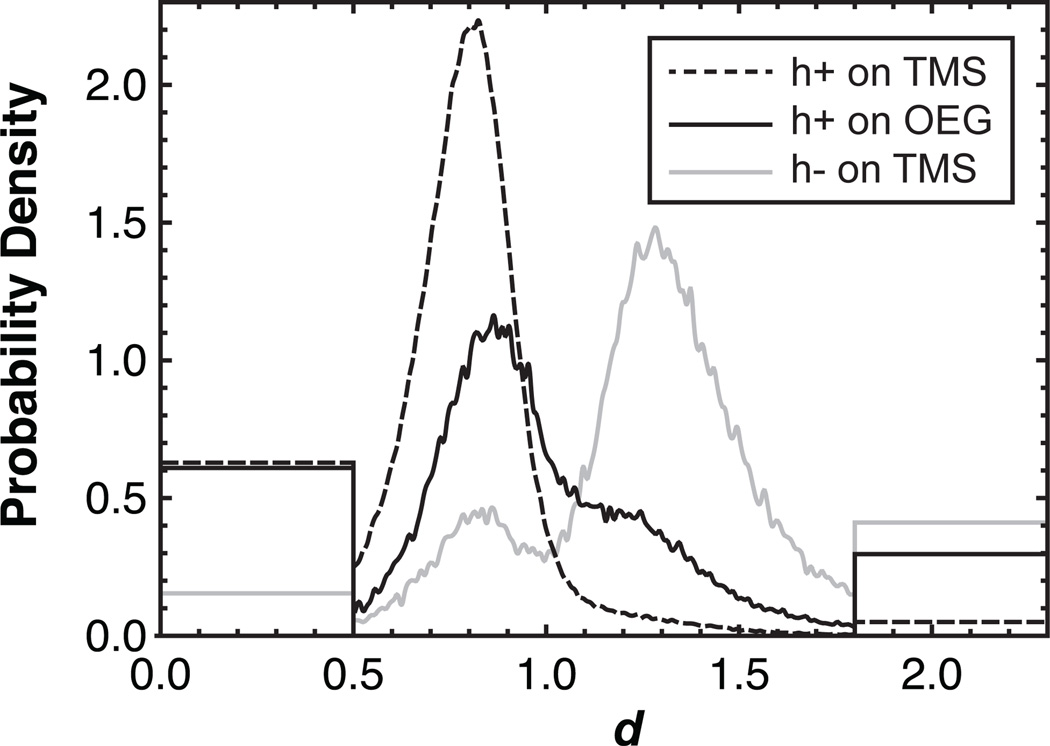
To observe surface effects on the hairpin-coil equilibrium, we compiled all the individual observations of the molecules’ relative end-to-end distances into a probability distribution of d-values in Figure 1. On TMS, this distribution strongly favored d<1 with a sharp peak at d=0.8 indicating that the h⁺DNA was nearly always in the hairpin configuration. Correspondence between conformational state and RET efficiency or d-value is conceptualized in Figure 2a. In contrast, OEG showed a significant shoulder at higher d, a region dominated by random coil conformations. This indicated that the hairpin was significantly less stable on the hydrophilic OEG surface.

Figure 1.

Surface influence on DNA hairpin formation. The probability density of observing a given relative end-to-end distance is shown for h⁺DNA on TMS and OEG as well as h⁻DNA on TMS. The ‘box-like’ ends of the distribution represent molecules that presented essentially zero intensity in one channel or the other, leading to apparent d-values of zero or infinity. This measurement artifact stems from difficulties quantifying low fluorescence intensity in either channel and to account for this we represent these molecules with step distributions at extreme d-values. The area under each ‘box’ is proportional to the number of molecules found in these extreme states and the cumulative area under the ‘boxy’ and ‘smooth’ parts of each distribution integrates to unity.

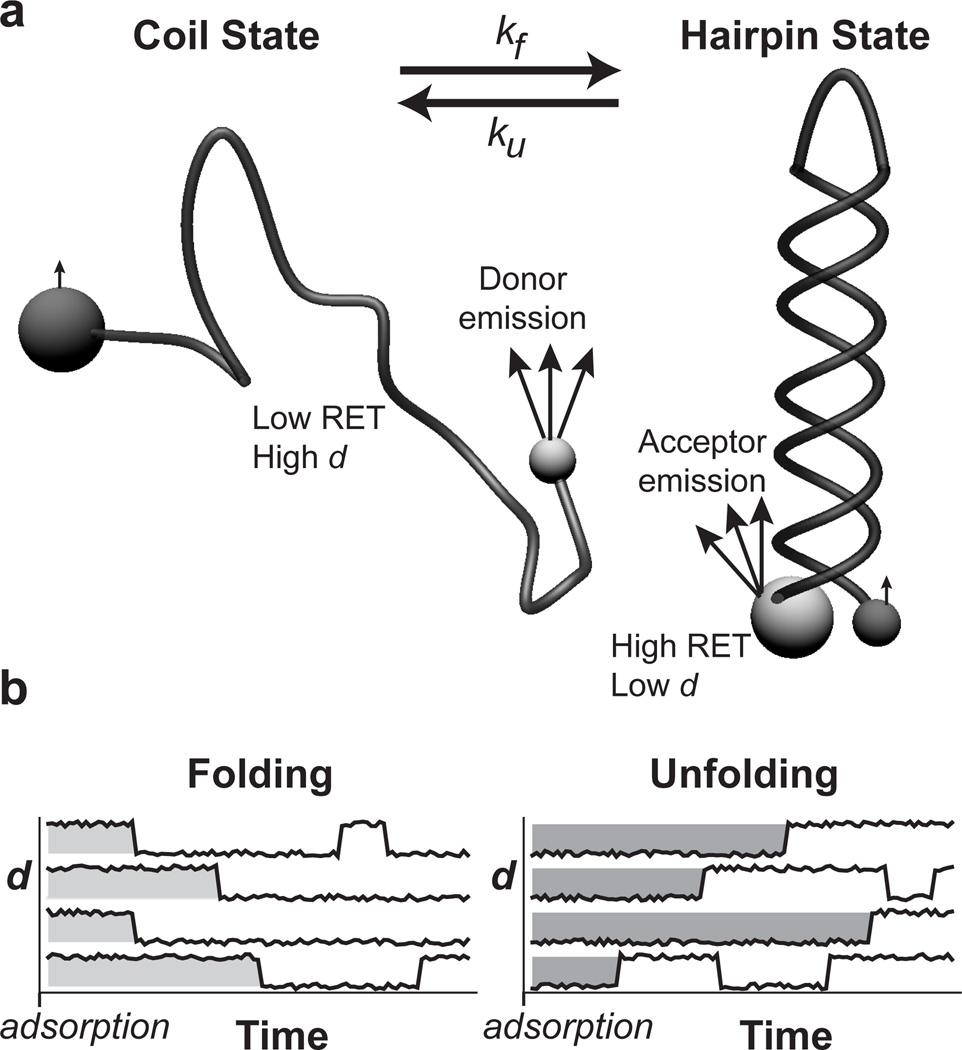
Figure 2.

RET identifies DNA conformation. (a) DNA is end-labeled with two different fluorophores such that RET can be used to distinguish between hairpin and coil states that may interconvert. Small spheres represent donor fluorophores while acceptors are shown as large spheres. Light grey indicates strong fluorophore emission while dark grey indicates weak emission. The hairpin state has a small end-to-end distance that yields high RET efficiency while the majority of coil conformations have large end-to-end distances and low RET efficiency. (b) The distribution of ‘initial-state residence times’ (see Figure 3) is extracted from trajectories of many individual molecules. Molecules are grouped by their initial state in the frame in which they first appear. The initial-state residence time for each molecule is then recorded as the time it takes to convert to the opposite conformational state from its initial state. Subsequent state changes are ignored for reasons described in the Experimental Section.

For comparison, a non-hairpin-forming control sequence (h⁻DNA) was observed on TMS to obtain the distribution of d-values expected for a random coil. Data acquired using the h⁻DNA sequence are useful controls because they are subject to possible artifacts from dye attachment as well as from data processing and analysis. Such artifacts are also possible in h⁺DNA, but comparison with h⁻DNA identifies which effects represent real differences in the behavior of the two sequences. This h⁻DNA control showed a dominant peak at d=1.3, indicating that higher d did in fact correspond to the coil state. The appearance of a small peak in the control near d=0.8 may represent a distinct conformational state with a short end-to-end distance, but may also result from our ability to better detect molecules appearing brightly in one channel or the other rather than dimly in both channels. This effect would anomalously lower the probability distribution near d=1.

Relative end-to-end distance is sufficient to compare the two conformational states in this work; we empirically find a d-range corresponding to the hairpin and coil states. However, it is helpful to consider absolute physical distances and how they relate to the measured d-values. In particular, if one naively uses the value of the Förster radius in solution (i.e. μ=5.4 nm), the hairpin peak at d=0.8 would correspond to a distance of 4.3 nm, slightly larger than the expected 3–4 nm as described above.

We adopted empirical quantitative criteria for assigning conformations to hairpin (d<0.9) and coil (d>1.1) states based on d-value, with the range 0.9≤d≤1.1 left as indeterminate. This allowed the equilibrium folded fraction (θ) to be calculated from the respective distributions, giving values of θ_TMS=0.94 and θ_OEG=0.64 for h⁺DNA on TMS and OEG, respectively. For comparison, θ₀=0.20 for h⁻DNA on TMS indicating that these criteria may erroneously identify up to 20% of random coil conformations as hairpins. Although the criteria for identifying conformational state are somewhat arbitrary, they provide a straightforward way to quantify the data in Figure 1 and the fractions given above vary by less than 0.02 for any symmetric interval about d=1 that is less than 0.3 d-units wide.

Figure 1 clearly indicates that adsorption to OEG significantly destabilizes the hairpin state while TMS maintains a much higher fraction of hairpin structure. These results are surprising if one adopts the conventional perspective of OEG as a hydrated uncharged ‘neutral’ surface, with some capacity for hydrogen bonding. This view would lead one to conclude that near-surface conformational restriction of the coil state would drive equilibrium towards the hairpin,^[20] not away from it as was observed here. Additionally, near-complete hybridization on TMS is also surprising, since one might imagine that hydrophobic base-surface interactions could stabilize the random coil state. Such a mechanism has been proposed for the catalytic role of hydrophobic interfaces in the unfolding of proteins.^[30] Our observations suggest that other factors, such as near-surface conformational restriction or the details of water structure, must influence the hairpin-coil equilibrium on TMS.

2.2. Kinetics of the Hairpin-Coil Transition

To determine if the hairpin was favored on TMS by a slower unfolding rate, faster folding rate, or both, we measured the kinetic rates of folding and unfolding. As described in the Experimental Section, trajectories were grouped according to their initial state and aligned at their adsorption times in order to measure the residence time in the initial state for each trajectory (see Figure 2b). That is, the time prior to unfolding was measured for molecules adsorbing as hairpins while the time prior to folding was measured for molecules initially appearing in the coil state. Observations of ‘initial-state residence times’ were used to construct probability distributions for unfolding and folding events as a function of time. The kinetic rates of folding and unfolding were subsequently extracted from these distributions.

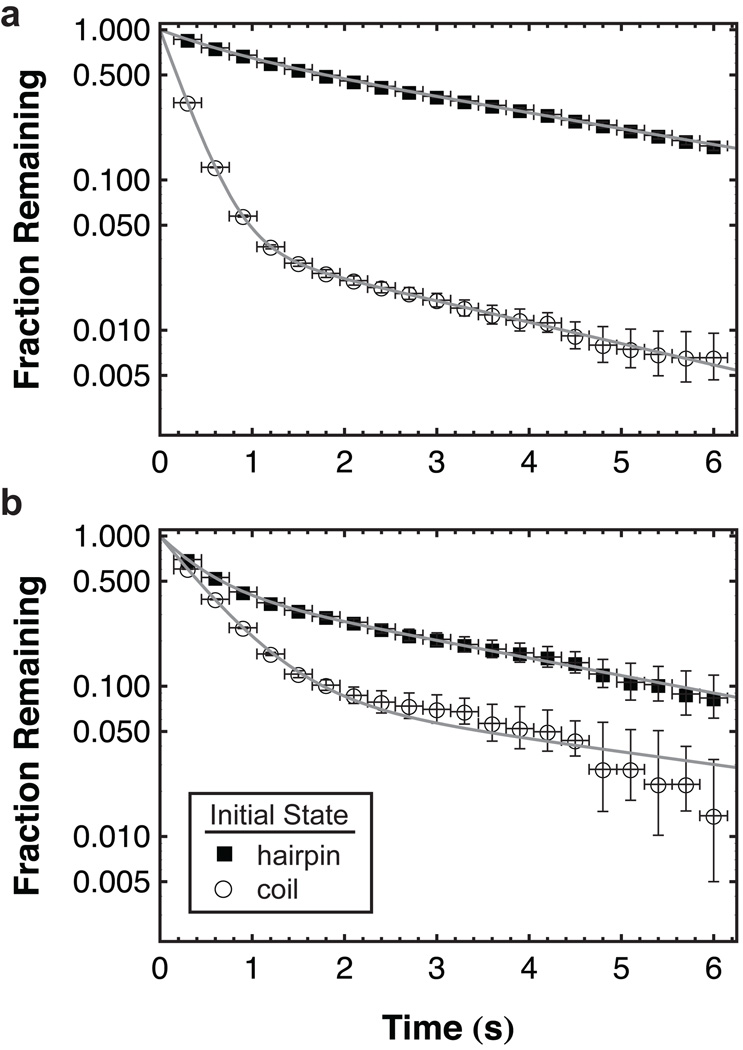
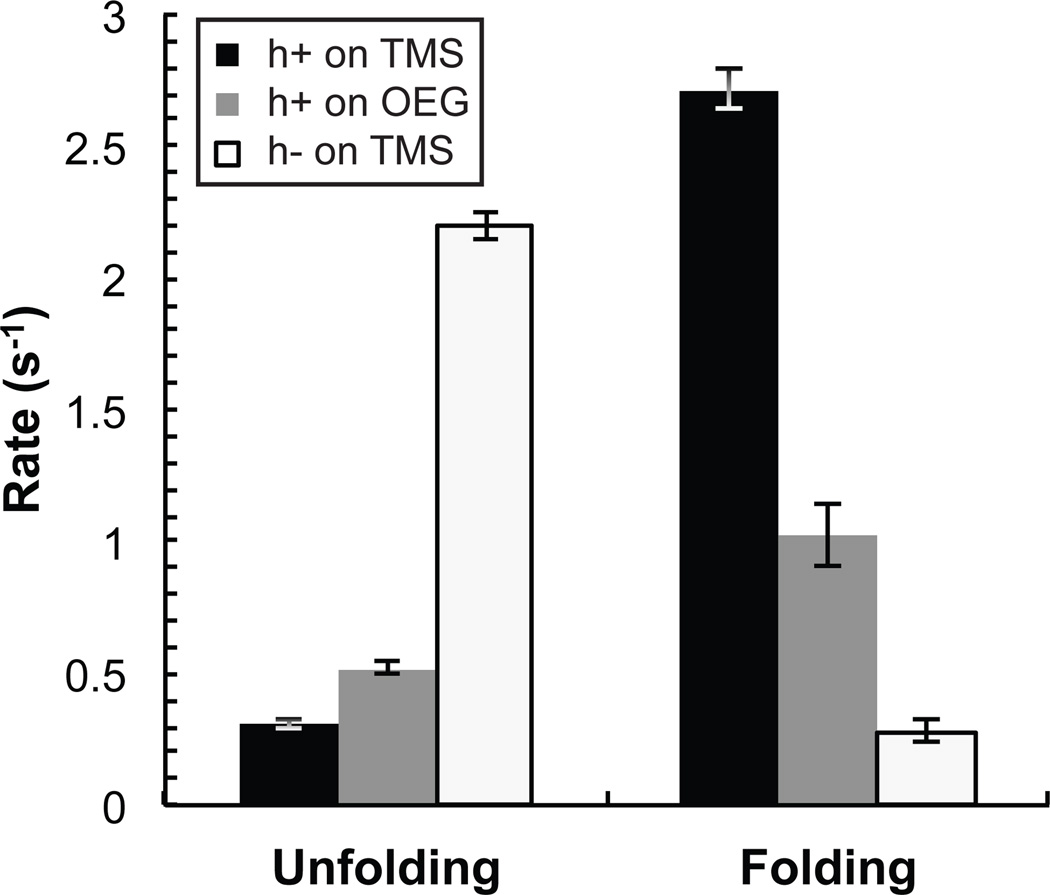
‘Initial-state residence time’ probability distributions are shown for TMS and OEG in Figure 3 in cumulative form, such that the value on the vertical axis corresponds to the fraction remaining in the initial state. Corresponding mean unfolding and folding rates (k_u and k_f, respectively) are displayed in Figure 4 where hairpins are shown to unfold approximately twice as fast while folding nearly three times slower on OEG relative to TMS. As expected for a non-complementary DNA sequence, the apparent unfolding rate for h⁻DNA was significantly faster while the apparent folding rate was significantly slower than the rates measured for h⁺DNA on either surface. This control indicates that although end-to-end distance fluctuations of a random coil may cause apparent folding and unfolding, this phenomenon cannot explain our measured rates for h⁺DNA.

Figure 3.

Kinetics of hairpin folding and unfolding. The integrated probability distribution of initial-state residence times is shown for molecules that are initially either hairpins or coils on (a) TMS and (b) OEG. From these distributions, the rate constants for folding and unfolding processes are extracted. Horizontal error bars represent uncertainty in assigning the initial-state change time due to finite time resolution. Vertical error bars are based on the number of observations that each data point represents (i.e. the number of initial-state residence times observed greater than a given time). From this number of observations, 68% confidence intervals were determined for a Poisson distribution in order to determine the percentage of error. Fits are shown for each dataset using equation 3 with N=2.

Figure 4.

Mean rate constants for folding and unfolding. The mean rate constants are shown for h⁺DNA on OEG and TMS and h⁻DNA on TMS. Error bars represent the standard deviation of the mean rate when calculated using several subsets of all trajectories.

On the semi-log scale in Figure 3, an exponential decay, indicating a single first-order process, would appear as a straight line. While only slight deviations from mono-exponential behavior were found for unfolding on both surfaces, multi-exponential decays were observed for folding. In the case of multiple competing folding pathways, variation in the mean could indicate either a change in the rates associated with each pathway or the fraction of molecules choosing one pathway over another. This distinction is important when trying to understand differences between analogous processes on different surfaces. An analysis of the multi-exponential folding decays found that both mechanisms were responsible for the near-tripling of the mean rate on TMS relative to OEG. A fast and a slow folding time scale was observed on each surface and the rate associated with the fast pathway on TMS (3.99±0.03 s⁻¹) was more than double that on OEG (1.89±0.05 s⁻¹). A similar trend was observed for the slower time scale: 0.33±0.01 s⁻¹ and 0.19±0.04 s⁻¹ on TMS and OEG, respectively. Additionally, unfolded coils chose the slow pathway more than twice as often on OEG (10±1%) relative to TMS (4.2±0.3%). Although further study is necessary to fully understand these observations, sensitivity to heterogeneous behavior gives this technique the ability to provide new insights into complex hairpin folding pathways.^[31–32]

Overall, the larger observed hairpin fraction on TMS is due to the fact that unfolding is twice as fast while folding slows nearly three-fold on OEG relative to TMS. From the balance between measured folding and unfolding rates, the steady-state folded fraction can be estimated from the calculation θ_ss=k_f /(k_f+k_u). The results give θ_ss,TMS=0.90±0.04 on TMS, θ_ss,OEG=0.66±0.08 on OEG, and θ_ss,o=0.14±0.02 for h⁻DNA on TMS, which are consistent with direct measurements of θ in the previous section.

Our measured folding and unfolding rates are slow relative to reported rates ranging from ~10⁻⁵ −10⁻² s.^[33–35] These measurements are typically made in solution using techniques sensitive to fast dynamics, such as fluorescence autocorrelation methods in which molecules diffuse through an observation volume within milliseconds; therefore sequences with fast conformational dynamics are deliberately chosen. However, evidence indicates that important DNA dynamics occur on much slower timescales.^[36–37] Additionally, surface effects may change the relevant timescales for DNA dynamics and there is currently no comprehensive theory to predict the strength of such effects. For example, a DNA hairpin with a 9 base pair stem gave dynamics of 10⁻² −10⁻¹ s when immobilized on a surface.^[38] In the present work, the observation of heterogeneous behavior in the same molecule at different times suggests that some timescales of DNA dynamics are readily captured with our time resolution, and this sensitivity to relatively slow dynamics is an important complement to fluorescence autocorrelation methods.

2.3. Mechanisms of Surface-Induced Conformational Change

The underlying mechanisms of surface-induced changes in DNA folding and unfolding kinetics may be complex. For any folding or unfolding transition, a surface may change the free energy of the initial state, final state, or a multitude of intermediate states through a combination of entropic and enthalpic contributions. While our current data cannot uniquely identify these effects, it is helpful to consider possible reasons for the observed differences in kinetic rates between TMS and OEG.

Minimally, hairpin unfolding requires hydrogen bond breakage and our data suggest that this process occurs more slowly on hydrophobic TMS. It has been shown that water near a hydrophobic surface is more susceptible to density fluctuations such that an adsorbing macromolecule can more easily ‘dry’ the space between it and the interface.^[39] With lower water density and a subsequent lowering of the dielectric constant,^[40] the dry region would strengthen electrostatic dipole-dipole interactions that underlie hydrogen bonding between complementary bases near TMS relative to OEG. A related explanation is that a dry interface between DNA and TMS may prevent water from accessing the hydrophobic core of the helix, making it more difficult for water molecules to stabilize the transition state associated with the breaking of base-base hydrogen bonds.^[41]

Regarding the folding transition from coil to hairpin, this process requires one or more correct base pairs to contact each other in conformations amenable to stable hydrogen bonds and nucleation of adjacent base-base pairing. A surface could inhibit this process through favorable base-surface interactions that compete with base-base pairing. However the observation of faster folding on hydrophobic TMS (where favorable hydrophobic base-surface interactions are expected) suggests that base-surface attraction is not the only relevant factor. For example, a surface could facilitate folding through previously studied excluded volume effects^[20] whereby the restriction of conformational freedom near a surface reduces the entropy of a random coil monomer thus raising the coil state free energy relative to that of the hairpin state.

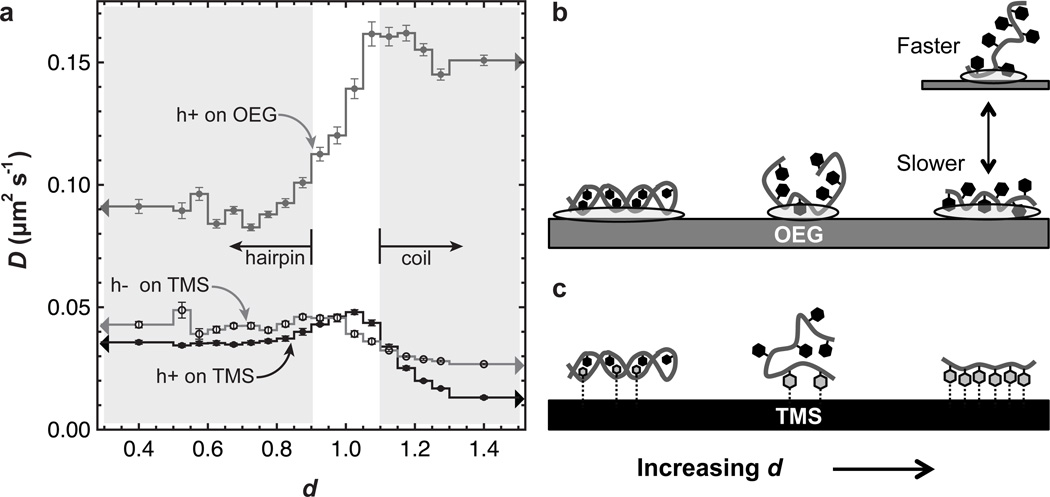
The use of mobile DNA has the advantage that mobility itself permits an independent assessment of DNA-surface interactions. In the crudest sense, low mobility represents stronger DNA-surface interactions; however, more information is available from detailed analyses of individual trajectories. To analyze mobility, the squared displacement of each trajectory step was sorted by the d-value exhibited during the displacement; these data were analyzed to extract the diffusion coefficient (D) as a function of d as shown in Figure 5a. In general, diffusion on OEG was significantly faster than on TMS, indicating that DNA interacts more strongly with TMS. The dependence of D on d provides additional detail. In particular, Figure 5a shows larger surface-specific differences in D for d-values corresponding to random coil states, where nucleobases are potentially more exposed to the surface, than for d-values corresponding to hairpins, where bases are somewhat hidden from the surrounding environment by the phosphate backbone. Thus, a reasonable conclusion is that differences between TMS and OEG stem from differences between the surface interactions with nucleobases, rather than the backbone. As discussed below, this conclusion is strengthened by the observation that while D was relatively invariant to the end-to-end distance (within the random coil regime) on OEG, D decreased significantly with increasing d on TMS.

Figure 5.

Effect of molecular extension on diffusion. (a) The diffusion coefficient for a given range of d is shown for the hairpin-forming sequence on TMS and OEG. The range at high d includes all d-values for d>1.3 while the range at low d includes all d-values for d<0.5. Error bars are discussed in the Experimental Section. Potential explanations for the trends in (a) are depicted in (b) and (c). (b) Ovals indicate areas of DNA-OEG interaction and these are larger for the hairpin, leading to slower diffusion. At short-to-intermediate end-to-end distance, coil DNA adopts a 3D ‘micellar’ structure with weaker OEG interactions and faster diffusion. Highly extended coils can lie flat on the surface (stronger surface interaction, slower diffusion) or extend into solution (weaker surface interaction, faster diffusion) and both are possible on OEG causing relatively fast average diffusion over the ensemble of extended conformations. (c) Dashed lines indicate hydrophobic interactions between the grey DNA bases and TMS. Some hydrophobic interactions are possible between the surface and the major and minor grooves of hairpin DNA. Like on OEG, self-avoiding character makes it difficult for coil DNA to lie flat while still having a short-to-intermediate end-to-end distance, causing relatively few contact points with the surface and faster diffusion. Many favorable hydrophobic base-TMS interactions cause highly extended coils to lie flat rather than extend into solution, leading to slow diffusion.

In the partial detachment paradigm of interfacial diffusion, an adsorbed molecule must detach (at least partially) in order to change its interfacial position; therefore slower diffusion is associated with stronger molecule-surface attraction.^[42–43] Recent simulations of a self-avoiding random walk predict that attraction between the surface and individual bases leads to an inverse relationship between end-to-end distance and diffusion coefficient.^[29] Physically, this occurs because base-surface attraction favors configurations that are more two-dimensional with more base-surface contact points over those that extend away from the interface (Figures 5b,c) and decrease mobility via partial detachment. Our data therefore indicate that base-surface attractions are stronger on TMS than OEG and the chain likely exhibits more two-dimensional character on TMS. Mobility decreases more dramatically with increasing d for h⁺DNA than for h⁻DNA. This trend is expected due to a greater fraction of the more hydrophobic adenine in h⁺DNA^[44] and further supports the idea that hydrophobic base-surface interactions govern diffusion on TMS. On OEG, the random coil may adopt ‘micelle-like’ conformations in which bases preferentially interact with each other rather than the OEG monolayer. Such conformations would be prone to weaker surface interactions and faster overall diffusion. These differences between surfaces are reminiscent of sequence-specific conformational differences observed by Akca et al. of single-stranded DNA on graphene in which poly-A and poly-C adopted micelle-like configurations while poly-T and poly-G extended in the interfacial plane.^[44]

Combined evidence from diffusion and folding/unfolding rates indicates that 2D conformational restriction induced by base-surface attraction increases the folding rate on TMS relative to OEG. A mechanistic explanation remains unclear but one possibility is that reducing the dimensionality of the random coil may pre-align individual bases, causing them to explore productive folding pathways more often. Regardless of the mechanism, this result suggests that individual base-surface attractions can surprisingly increase the folding rate rather than slow it.

3. Conclusions

In total, this work has demonstrated that OEG, often thought of as a neutral surface coating, destabilizes the DNA hairpin state whereas hydrophobic TMS promotes nearly complete folding. Thus, nanotechnology applications that depend on DNA-directed self-assembly in the near surface environment should benefit from a hydrophobic surface coating, such as TMS, while OEG, and possibly poly(ethylene glycol) by extension, should be avoided. Our single-molecule RET technique assessed the state of DNA both with a measurement of the equilibrium distribution of end-to-end distances and a kinetic analysis of the folding and unfolding rates. The kinetic rates, when extrapolated to steady-state, predicted hairpin fractions that agreed well with the fraction calculated from end-to-end distance distributions. Further kinetic analysis showed that TMS favors the hairpin state both by slowing DNA unfolding and speeding folding relative to OEG. Analysis of interfacial mobility also indicates a surprising positive correlation between stronger base-surface interactions on TMS and a faster rate of folding. This result implies that the role of the surface in DNA folding is more complicated than simply restricting conformations available to the random coil state and future studies of these properties as a function of temperature may help to clarify the underlying mechanisms for our observations.

4. Experimental Section

Solutions of end-labeled DNA

End-labeled DNA was purchased from Invitrogen and was purified by the company using HPLC to greater than 95%. The DNA hairpin sequence was 5'-(AATATTAT)₂AATA(C)₄TATT(ATAATATT)₂-3' and was labeled on the 5’ end with Alexa 488 and on the 3’ end with Alexa 594. The control DNA sequence was 5'-A(T)₂₀(C)₄(T)₂₀A-3' and was labeled in the same manner as the hairpin sequence. DNA (5 × 10⁻¹¹ M) was dissolved in phosphate buffered saline (Gibco, pH 7.4, calcium and magnesium free) in order to achieve surface densities low enough to observe individual molecules but high enough to provide many molecules for tracking in each frame.

Surface preparation and characterization

Fused silica (FS) wafers were washed with cationic detergent (Micro 90, International Product Corp.) and thoroughly rinsed with water purified to 18 MΩ-cm. Wafers were then immersed in warm piranha solution for 1 hour followed by UV-ozone treatment for 1 hour. For deposition of TMS monolayers, cleaned FS wafers were exposed to hexamethyldisilazane vapors for 24 hours at room temperature. To form OEG monolayers, cleaned FS wafers were exposed to the vapors of a solution of n-butylamine (5%), methoxy(triethyleneoxy)propyltrimethoxysilane (10%), and toluene (85%) for 48 hours at room temperature. Following deposition, wafers were rinsed with toluene, dried under nitrogen and used for experiments.

In order to characterize the surfaces, static contact angles of TMS- or OEG-functionalized FS were measured with a custom-built contact angle goniometer. A drop of deionized water (1 µL) was deposited on the surface and at least six drops on three independent samples were averaged for reported values here. After the piranha and UV-ozone treatment, clean FS had a contact angle of ~0°. The static contact angle of TMS-functionalized FS was 96 ± 4° while that of OEG-functionalized FS was 28 ± 2°. The value for TMS indicates a hydrophobic surface and is consistent with previously published values.^[43,45] The contact angle for OEG is 15–20% smaller than values found on monolayers of longer methoxy-terminated ethylene oxide chains,^[45–47] yet recent ellipsometric measurements of this monolayer indicate layer thickness near the contour length of OEG even at a contact angle as low as 18°.^[48]

Single-molecule total internal reflection fluorescence microscopy (TIRFM)

TIRFM measurements were performed using a custom-built prism-based illumination system, flow cell, Nikon TE-2000 microscope with 60× objective and 491 nm DPSS laser (Cobolt). The flow cell was maintained at 25.0 ± 0.1°C and flow was stopped after introduction of the DNA solution. Laser intensity was sufficiently high to resolve individual objects in either wavelength channel with a 0.3 s acquisition time. Dual-channel imaging was provided by an Optosplit II (Cairn Research) image splitter. In this device, a dichroic mirror (Chroma) with a nominal separation wavelength of 580 nm was used to separate fluorescence emission of donor and acceptor. Additional filters were then used to further select for fluorescence emission in each channel. The donor channel used a bandpass filter (Semrock FF01-529/28) centered at 529 nm with a 90% transmission width of 28 nm. The acceptor channel used a longpass filter (Semrock FF01-591/LP) with a 90% cut-on wavelength of 612 nm. After fluorescence emission was split and filtered, each channel was projected onto a separate region of an EMCCD camera (Photometrics) cooled to −70°C. Details regarding channel alignment and object identification and tracking are identical to those provided previously.^[29] For each DNA sequence and surface chemistry, multiple movies were acquired from at least three different preparations of the same surface chemistry.

Quantifying resonance energy transfer

Following our previous treatment of single-molecule RET data,^[29] the absolute end-to-end distance (r) can be calculated from the fluorescence intensity in each channel where $r=\mathrm{\mu }{\left(\frac{F_D}{F_A}\right)}^{1/6}$ and F_D and F_A are the intensities in the donor and acceptor channel, respectively. The constant, $\mathrm{\mu }=R_o{\left(\frac{F_A{|}_{r\to 0}}{F_D{|}_{r\to \infty }}\right)}^{1/6}$ depends on the Förster radius (R_o), and F_D and F_A measured at known separations. The expression adopts the simple form above when we use the acceptor intensity at zero separation and donor intensity in the absence of acceptor, but analogous expressions can be derived for other reference distances. While it is straightforward to measure donor intensity in the absence of acceptor, a second calibration intensity is difficult to measure due to the difficulty in fixing fluorophore separation with nanometer precision. Furthermore, a surface can potentially interact with the electronic structure of the dyes or can hinder rotation, changing R_o from its expected value. Due to these practical difficulties in determining μ, we chose to report our data using the relative end-to-end distance, $d=\frac{r}{\mathrm{\mu }}={\left(\frac{F_D}{F_A}\right)}^{1/6}$.

In our calculation of d, we neglected bleeding of the donor into the acceptor channel and direct excitation of the donor by the laser excitation source. This was motivated by the large spectral separation between donor and acceptor such that supplementation of acceptor signal by these anomalous processes was found to be relatively minor for the Alexa 488/594 RET pair.^[25] Our choice to neglect bleeding and direct excitation resulted in slightly elevated apparent values for F_A, thus lowering the apparent value of d. This error was greater for larger end-to-end distances, where the true value of F_A was expected to be small relative to the contribution from direct excitation while F_D was expected to be large (causing higher bleeding). The end result is that it became slightly more difficult to distinguish the random coil state from the hairpin state, but Figure 1 indicates that we were able to do so in spite of these errors.

Blinking and photobleaching

The photophysical phenomena of blinking and photobleaching must always be considered in fluorescence experiments involving single fluorophores. Photobleaching is the irreversible conversion of a fluorophore to a non-fluorescent state and limits the slowest observable dynamics by causing apparent desorption of a molecule. In other words, no timescale can be measured that exceeds the time constant for photobleaching. In this work, the slowest timescales for unfolding and folding processes (i.e. the reciprocal of k_f or k_u) were near 3 s. When we observed the residence time distribution of DNA on the surface (for more details on residence time distributions, see reference 42), distinct populations were observed with unique characteristic surface residence times. In each experiment, one population was observed with a characteristic residence time of 15 s or greater. While this characteristic residence time could result from either photobleaching or a unique DNA-surface interaction, this result meant that the characteristic time for photobleaching was at least 15 s, much longer than the folding or unfolding dynamics. Finally, previous work has examined photobleaching in fluorescein and rhodamine derivatives under imaging conditions similar to the current work.^[48] Photobleaching time constants were typically in the range of hundreds of seconds and the Alexa dyes used here are expected to be even more photostable. For both of these reasons, it is unlikely that photobleaching had any significant effect on our data.

With regards to blinking, our acquisition time of 0.3 s is roughly an order of magnitude greater than typical blinking timescales.^[49] Thus it is unlikely that blinking would cause a molecule to disappear and reappear due to fluctuations in its intensity. However, as blinking temporarily turns off one fluorophore or the other, it is possible to alter the measured d-value in a given frame. This phenomenon would tend to increase the apparent d-value because acceptor blinking will increase donor fluorescence (due to decreased RET) whereas donor blinking would cause a concomitant decrease in acceptor intensity. Consequently, blinking could occasionally cause a hairpin to appear to unfold, increasing the measured unfolding rate. However, our data clearly indicated that different sequences and different surfaces produced very different unfolding dynamics. In contrast, the factors typically affecting blinking (e.g. laser power and buffer solution) remained constant between experiments suggesting that any artifact introduced by blinking did not mask underlying differences in the behaviors of these systems.

Filtering of molecular trajectories

In order to track large numbers of individual molecules, we used automated object identification and tracking algorithms. It is therefore possible that anomalously high fluctuations in the image background were erroneously classified as fluorescent molecules in any one frame. However, it is unlikely that a noise fluctuation occurs in the same location in consecutive frames and extremely unlikely that the fluctuation persists through multiple frames. Thus, we ignored trajectories lasting less than 1.5 s (5 frames), essentially eliminating anomalous results due to noise while ensuring a large number of trajectories for good statistical significance. Ignoring short trajectories had the added benefit of eliminating a large fraction of molecules that had extremely weak interactions with the surface such that their behavior did not represent the interfacial phenomena that we sought to study.

Finally, for the purpose of assessing folding and unfolding kinetics, we eliminated all trajectories that did not exhibit a state change (using the d-criteria for hairpin and coil states listed previously) during their surface lifetime. This strategy inherently neglects objects that were mislabeled with only a donor or acceptor, thereby improving the quality of data. This filtering step was also important for accurate determination of kinetic rates as will become apparent below. Essentially if a conformational change was not observed during the molecule’s surface residence time, the ‘initial-state residence time’ could not be assigned with certainty. Including these trajectories would have caused the apparent folding and unfolding rates to be erroneously linked to the desorption rate. After all filtering steps were performed there were still over 40,000 trajectories on TMS and 35,000 on OEG for the hairpin sequence, while the hairpin control sequence on TMS retained over 11,000.

Constructing probability distributions of initial-state residence times

Kinetics were measured by first sorting trajectories by the initial conformation in their adsorbing frame, with hairpin and coil states identified by the d-value criteria above. Trajectories with initial indeterminate d-values were ignored. Although a large majority of molecules in solution should exist as hairpins rather than random coils, we believe that molecules that appeared as coils in the first frame could also have come from a population of hairpins that unfolded within a very short time (<<0.3 s) after adsorption. Trajectories were then aligned at their adsorption times and the residence time in the initial state was measured for each trajectory.

The number of frames for each trajectory to change conformational state was measured and initial-state residence times in units of frames were converted to units of time by the formula t_i=a(i−1) where i is the frame number in which the change was observed and a is the acquisition time of 0.3 s. The subtracting factor of 1 frame reflects the fact that a molecule likely changed state near the beginning of the frame in which it appeared to change, or even near the end of the previous frame. From this raw dataset of initial-state residence times, we constructed a probability distribution of initial-state residence times. Although this seems like a straightforward calculation, the ability of molecules to desorb from the surface creates an inherent bias in this probability distribution that must be accounted for. For example, all trajectories lasted for at least 1.5 s while longer trajectories were more rare. Because we only considered trajectories that exhibited a conformational change, it was inherently less likely to observe longer change times for which there were fewer trajectories that were long enough to observe that change time (t_i). Consequently we calculated the probability of a given change time, p(t_i), using equation 1:

$$p\left(t_i\right)=\frac{1}{\mathrm{\rho }}\frac{n\left(t_i\right)}{n(t_r>t_i)}$$ (1)

In equation 1, n(t_i) is the number of observations of a given change time, n(t_r > t_i) is the number of trajectories that exhibited a surface residence time (t_r) equal to or greater than the change time, and $\mathrm{\rho }=\sum _i\frac{n\left(t_i\right)}{n(t_r>t_i)}$ is a normalization factor that converts the relative probability into an absolute probability. Analysis of folding and unfolding kinetics is more straightforward when the raw probability distribution is converted to cumulative form.^[50] The cumulative distribution, f(t_j), can be constructed from the raw probability distribution as shown in equation 2:

$$f\left(t_j\right)=\sum _{t_i>t_j}p\left(t_i\right)$$ (2)

While hairpin folding and unfolding are expected to exhibit first-order kinetics, there may be N folding or unfolding pathways each with a unique characteristic time constant (τ). The cumulative probability distribution of initial-state residence times can be represented by equation 3 where x_k is the fraction of molecules that follow a pathway with time constant τ_k.

$$f\left(t\right)=\sum _{k=1}^N{x}_k{e}^{-t/{\tau }_k}$$ (3)

Equation 3 was fit to the experimental distribution (equation 2) in order to extract the fractions and time constants for each pathway. The mean time constant was taken as $\langle \tau \rangle =\sum _{k=1}^N{x}_k{\tau }_k$ and the reported mean folding and unfolding rates are the reciprocal of <τ>. Reported folding rates for each pathway are the reciprocal of τ_k. Errors were determined by repeating the analysis on subsets of the composite dataset to determine the standard deviation for each rate.

The above method for calculating the mean initial-state residence time is preferable to a direct calculation given by $\langle t\rangle =\sum _i{t}_{i}p\left(t_i\right)$. Due to finite time resolution of our experiment, we ignore very short initial-state residence times causing the direct calculation to overestimate the true mean residence time. Importantly, this effect is greater for systems with faster kinetics. In contrast, the use of equation 3 to model the residence time distribution makes a reasonable assumption regarding the number of short residence times that would have been observed with infinite time resolution and is therefore less prone to introducing artifacts in the data.

Our analysis of change times ignores second and subsequent conformational changes. This is done because the number of opportunities to observe a given change time (i.e. n(t_r > t_i) in equation 1) depends both on the length of each trajectory as well as the previous change times in that trajectory and accounting for these effects is much more complicated than our chosen strategy. In theory, conformational dynamics well after adsorption may exhibit different kinetics than those shortly after adsorption. However, good agreement between values of θ and θ_ss suggest that our choice to focus only on initial changes did not significantly affect our reported kinteic rates.

Analysis of diffusive motion

For every diffusive step in every trajectory, the displacement (R) measured between frames i-1 and i was associated with the d-value measured in frame i. Although using the d-value from frame i as opposed to i-1 might seem like an arbitrary choice, the former choice better represents the average conformation of the molecule while it was taking the observed diffusive step. Next, diffusive steps were binned by the d-values specified in the text and the mean-squared displacement (<R²>) was then calculated for each bin. The mean-squared displacement is proportional to the mean diffusion coefficient for a random walk such that D=<R²>/(4Δt) where Δt is the acquisition time of 0.3 s. The diffusion coefficient was corrected for static and dynamic localization errors that serve to elevate the apparent diffusion.^[51] Error for the diffusion coefficient was determined from the standard deviation when calculating <R²> from different subsets of each d-bin. This error estimate is preferred because random walk statistics dictates that the variance in the distribution of R² should equal <R²>, but this expected variation of R² is not an indicator of uncertainty in <R²>.