Abstract
Use of genetic methods to estimate effective population size (Ne) is rapidly increasing, but all approaches make simplifying assumptions unlikely to be met in real populations. In particular, all assume a single, unstructured population, and none has been evaluated for use with continuously distributed species. We simulated continuous populations with local mating structure, as envisioned by Wright's concept of neighborhood size (NS), and evaluated performance of a single-sample estimator based on linkage disequilibrium (LD), which provides an estimate of the effective number of parents that produced the sample (Nb). Results illustrate the interacting effects of two phenomena, drift and mixture, that contribute to LD. Samples from areas equal to or smaller than a breeding window produced estimates close to the NS. As the sampling window increased in size to encompass multiple genetic neighborhoods, mixture LD from a two-locus Wahlund effect overwhelmed the reduction in drift LD from incorporating offspring from more parents. As a consequence, 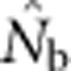 never approached the global Ne, even when the geographic scale of sampling was large. Results indicate that caution is needed in applying standard methods for estimating effective size to continuously distributed populations.
never approached the global Ne, even when the geographic scale of sampling was large. Results indicate that caution is needed in applying standard methods for estimating effective size to continuously distributed populations.
Keywords: genetic monitoring, inbreeding, isolation-by-distance, linkage disequilibrium, wahlund effect, wright's neighborhood
Introduction
The concept of effective population size (Ne) provides a way to quantify the evolutionary changes caused by random processes in finite populations (Charlesworth, 2009). Since its formal definition by Wright (1931) as the size of an ideal population that has played the same rate of genetic drift as an actual population of interest, Ne has a central role in studies of evolution and ecology. In addition to directly affecting the rates of loss of neutral genetic variability and frequency change of neutral alleles, Ne mediates the effectiveness of migration and selection, which are predictable in large populations but can be overwhelmed by drift in small ones.
The original concept of Ne envisaged a single population or a series of semi-discrete populations connected by limited migration. In many species, however, individuals are distributed more or less continuously across large landscapes, and matings occur more frequently among spatially proximal individuals. This type of demography produces a pattern of ‘isolation-by-distance' (IBD; Wright, 1943), in which genetic differentiation increases with distance, but there are no distinct breaks or discrete subunits within the global population. Species distributed in this fashion pose a particular challenge in applying the concept of effective population size. For example, recent research using the coalescent (for example, Barton and Wilson, 1995; Wilkins, 2004) has shown that evolutionary processes in continuously distributed populations exhibit both a short-term dynamic that is strongly dependent on the location of the samples and a long-term dynamic that is largely location independent. As a consequence, we expect at least two types of complications in estimating effective size in IBD systems: (1) estimators of short-term and long-term effective size might produce different results and (2) estimators of short-term (contemporary) effective size might be sensitive to the geographic scale of sampling.
For continuously distributed populations, Wright (1946) introduced the concept of a genetic ‘neighborhood' that describes the local area within which most matings occur. In a two-dimensional landscape, Wright's neighborhood size (NS) is
where D is density (number of individuals per unit area) and σ (mean squared distance along one axis between birthplaces of parents and their offspring) is a measure of dispersal (see Table 1 for notation and Appendix A for details). NS can be thought of as the number of reproducing individuals in a circle of radius 2σ. Assuming that dispersal is Gaussian, a circle of this size would include ∼87% of the potential parents of individuals at the center (Wright, 1946).
Table 1. Notation and terminology.
| Abbreviation | Description |
|---|---|
| BW | Breeding window—the square area, centered on the focal cell, within which mating occurs at random |
| Focal cell | The cell at the center of a breeding window where offspring are produced |
| b | Number of cells on one side of a breeding window; the total BW includes b2 cells |
| SW | Sampling window—the square area from which individuals are sampled |
| s | Number of cells on one side of a SW; the total SW includes s2 cells |
| Ne | Effective population size |
| Nb | Effective number of breeders responsible for the sample |
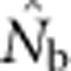 |
An estimate of Nb |
| NS | Wright's neighborhood size |
| σ2 | Mean squared axial parent–offspring distance; that is, the mean squared distance along one axis between birthplaces of parents and their offspring |
| D | Density—individuals per unit area. D was fixed at 1 in our model |
When matings occur preferentially within neighborhoods that are small relative to the global population distribution, genetic differentiation can build up across the landscape as a function of ‘isolation-by-distance' (Wright, 1943). Local genetic differences within continuously distributed populations can be substantial under some circumstances (Rohlf and Schnell, 1971), and this non-random mating affects rates of loss of diversity. Maruyama (1972) showed that, if σ2D>1, the global rate of loss of genetic variability is given approximately by 1/(2N), where N is the number of ideal individuals in the global system—that is, if dispersal is sufficiently high, the whole system loses genetic variability at the same rate as would a panmictic population of N ideal individuals. When dispersal rates are low enough that σ2D<1, however, the rate of loss of genetic variability is reduced to approximately σ2D/(2N). Thus, if breeding only occurs within small local neighborhoods, genetic variability in the global system is lost at a lower rate than would occur with a single panmictic population. This result is the continuous-distribution analogue of the familiar result for Wright's island model: population differentiation increases global diversity as subpopulations become fixed for different genetic variants.
Because Ne is difficult to measure directly in natural populations, a number of indirect genetic methods have been developed (Luikart et al., 2010; reviewed in Schwartz et al., 1998; Wang, 2005), and their use has surged in recent years with the increasing availability of large numbers of molecular markers (Palstra and Fraser, 2012). These methods can utilize information from a sample taken at one point in time (single-sample methods; for example, Tallmon et al., 2008; Waples and Do, 2008; Zhdanova and Pudovkin, 2008; Wang, 2009), or from allele frequency change between two or more samples (the temporal method; Nei and Tajima, 1981; Anderson, 2005). All these methods depend on simplifying assumptions, with one of the more important being that the focal population is randomly mating and closed to immigration. Although some estimators of contemporary Ne have been tested for robustness to violations of some underlying assumptions (Waples and Yokota, 2007; Waples and England, 2011), none has been tested for consequences of continuously distributed species with localized breeding. This lack of testing creates a serious data gap, given that spatial structure is known to affect other population genetic estimators such as those that attempt to define clusters of individuals (Novembre and Stephens, 2008; Frantz et al., 2009; Schwartz and McKelvey, 2009), detect bottlenecks (Leblois et al., 2006) or estimate demographic parameters (Leblois et al., 2004).
Here we consider how localized breeding within continuously distributed populations affects the most widely used single-sample estimator, which is based on LD (Hill, 1981). This analysis is timely, as use of single-sample estimators has increased exponentially in the last few years, whereas applications using the temporal method have remained flat (Palstra and Fraser, 2012). The LD method quantifies associations of alleles at different loci and assumes those associations are due to genetic drift caused by a finite number of parents. Results from applying the LD method are most easily interpreted in terms of the effective number of parents (EPs) that produced the sample (Nb; Waples, 2005). With random sampling from a single, unstructured population, 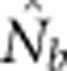 should be an unbiased estimate of Ne for the population as a whole. However, with localized sampling in a continuously distributed species, that will not generally be the case. We expect that as the geographic scale of sampling becomes large relative to the local breeding unit, two contrasting factors should affect genetic estimates based on LD. On one hand, a larger geographic sample should include progeny with more total parents, which should tend to increase
should be an unbiased estimate of Ne for the population as a whole. However, with localized sampling in a continuously distributed species, that will not generally be the case. We expect that as the geographic scale of sampling becomes large relative to the local breeding unit, two contrasting factors should affect genetic estimates based on LD. On one hand, a larger geographic sample should include progeny with more total parents, which should tend to increase 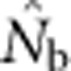 . On the other hand, if a sample includes progeny that result from local breeding within geographic areas separated by distances greater than typical parent–offspring dispersal, the amalgamation of genetically divergent individuals would create mixture LD (Nei and Li, 1973; Sinnock, 1975) that would tend to reduce
. On the other hand, if a sample includes progeny that result from local breeding within geographic areas separated by distances greater than typical parent–offspring dispersal, the amalgamation of genetically divergent individuals would create mixture LD (Nei and Li, 1973; Sinnock, 1975) that would tend to reduce 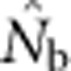 . It is not clear a priori whether one factor is generally more important or if their relative importance might vary with aspects of experimental design. To examine the consequences of using the LD method to estimate effective size in continuously distributed populations with local mating, we use simulated data to evaluate the following questions:
. It is not clear a priori whether one factor is generally more important or if their relative importance might vary with aspects of experimental design. To examine the consequences of using the LD method to estimate effective size in continuously distributed populations with local mating, we use simulated data to evaluate the following questions:
What are the relationships between
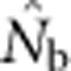 and the parameters NS and global Ne in a continuously distributed population?
and the parameters NS and global Ne in a continuously distributed population?How do these relationships vary as a function of the relative sizes of the genetic neighborhood and geographic sampling scales?
What errors of inference can result from a mismatch between the quantity one wants to estimate and the quantity that is actually estimated by
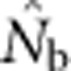 ?
?Can we identify indicators in the data to alert researchers to potential biases?
Materials and methods
Model description
We modified an individual-based model of a continuously distributed, constant-size population that has been used in other studies (Schwartz and McKelvey, 2009; Landguth et al., 2010) to comprise 90 000 diploid individuals distributed evenly (one per cell) across a 300 × 300 cell grid. This large grid allowed us to focus on local drift effects in small breeding neighborhoods within a 150 × 150 cell central area where edge effects were minimized. Diploid genotypes in the initial generation were assigned independently at each locus by randomly choosing among 99 equally likely alleles. This approach is equivalent to initialization with a K-allele model, with subsequent evolution occurring in absence of mutation. Choice of initial K=99 was arbitrary, but at the time of sampling yielded levels of per-locus allele richness and heterozygosities similar to those typically seen in microsatellite studies in natural populations (see Results; Tallmon et al., 2002; Schwartz et al., 2003; Purcell et al., 2006, 2009). Because the LD method uses information only on allelic state and not the evolutionary relationships among alleles, we did not try to mimic an explicit microsatellite mutation model. In addition, because we were primarily interested in evaluating bias rather than precision, we employed a high degree of replication of genetic drift by tracking 100 loci in each individual. Thus, the per-locus diversity reflects microsatellite variation, but our level of precision exceeds that of most studies in natural systems.
Parents were limited to a spatial area (which we call a breeding window (BW)) centered on a focal cell that represents the location of the offspring (Figure 1). We used four different square BWs with sides of b=3, 5, 7 and 9 cells. These BWs extend 1, 2, 3 and 4 cells ((b−1)/2 units) out in each direction from the focal cell, yielding BWs of BW=9, 25, 49 and 81 cells. Matings in each focal cell were simulated by randomly choosing one multilocus gamete with independent assortment from each of two individuals in the BW (selfing was not permitted) until a total of 101 offspring were produced. The window was then moved to an adjacent cell and the process was repeated for all 90 000 cells. Focal cells less than (b−1)/2 units from the edge of the matrix had fewer than b2 potential parents. In these cases, parents were drawn from the truncated neighborhood lying within the matrix. Individuals from these edge-affected focal cells were not directly used in any analysis, but they did contribute indirectly to breeding neighborhoods of more centrally located individuals. To reduce the consequences of edge effects, we collected data only from a centrally located 150 × 150 cell area that was at least 75 cells away from each edge. Cells directly influenced by edge effects occur only in the outer 1–4 rows depending on the BW size, and the total number of affected cells varied between 1% (BW9) and 5% (BW81) of the global population. Our boundaries are functionally equivalent to the reflecting boundary described by Leblois et al. (2006), who found that different boundary conditions had little influence on their results.
Figure 1.

Schematic depiction of a 3 × 3 SW (cross-hatched cells) nested within a 5 × 5 BW (shaded cells; any individual within two cells in any direction can be a parent of an offspring in a focal cell in the SW). Individuals from the outer ring of unshaded cells are within two cells of the sample window, and therefore all individuals within this 7 × 7 grid are potential parents of individuals in the sample. The numbers in each cell are the number of cells in the sample window to which a parent could potentially contribute offspring; these numbers thus reflect the relative probabilities of each cell being chosen as the parent of an individual in the sample.
When the breeding process was complete for all focal cells, all existing individuals were simultaneously replaced with one randomly selected offspring from the same cell, and the remaining 100 progeny individuals were set aside for sampling. Hence, population size was constant, breeding was simultaneous and generations were discrete. This process created a Wright–Fisher-like process within each BW and allowed for sample sizes that exceed the local effective size (as might occur for populations with Type III survival, or for which effective size is substantially less than census size).
We allowed the model to run for a 2000-generation burn-in period to establish quasi-stable genetic structure within the grid surface before sampling. We selected this burn-in period after evaluating the time necessary for spatial autocorrelation of genetic distance to stabilize (Appendix B). We considered the structure stable if spatial autocorrelation and Hedrick's (2005) standardized Fst (G′ST) did not change appreciably between sampled generations. At each time point and for each BW size, we calculated spatial autocorrelation of genetic distances among all individuals (a) in a centrally located 25 × 25 cell area across lag distances of 1–21 cells, using the program SPAGeDI Version 1.3 (Hardy and Vekemans, 2002). For all BWs, spatial autocorrelation established by no later than generation 50–100 and was relatively unchanged thereafter. We used 𝒢ℰ𝒩𝒪𝒟ℐ𝒱ℰ V.2.0b20 (Meirmans and Van Tienderen, 2004) to calculate G′ST among four, 10 × 10 cell sampling windows (SWs) located in the four corners of the 150 × 150 internal sampling grid. Change in G′ST values between sampled generations reached asymptotes in ∼40 generations in all BWs, but small increases in values through time were observed (Appendix B). We used a 2000-generation burn-in period that far exceeded the time needed for all spatial patterns to become fully evolved and stable.
We also used the spatial autocorrelation patterns to determine the array of SW sizes that would allow us to sample at scales below the spatial structure generated by the breeding neighborhood, at the scale of the neighborhood and across multiple neighborhoods. We chose square sample windows of size s2 where s=1, 3, 4, 5, 7, 8, 10, 22, 44 and 66 units, yielding sample windows of SW=1, 9, 16, 25, 49, 64, 100, 484, 1936 and 4356 cells, respectively. These windows yielded ratios of SW/BW ranging from 0.1 to 484.
In our model, the probability of being a parent of a new individual was uniform within the BW, which produces a rectangular distribution of parent–offspring distances constrained to be ⩽x (Appendix A). In contrast, most isolation-by-distance models allow for some chance of long-distance dispersal. To evaluate the consequences of this difference, for each BW, we sampled 1000 individuals at random from a central 200 × 200 cell area of the matrix after a burn-in period of 2000 generations. For each pair of individuals, we used the program SPAGeDi Version 1.3 (Hardy and Vekemans, 2002) to calculate both the Euclidean distance (x) and a measure of genetic differentiation (a) that is the individual analogue to the index FST/(1−FST) commonly used to characterize patterns of isolation-by-distance among samples (Rousset, 1997, 2000). We created bins of Euclidean distance values ranging from x=0–1, 1–2, … to x=49–50 (see Hardy and Vekemans (1999) for another example using this general binning approach). For each bin, we calculated mean x (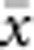 ) and mean a (
) and mean a (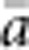 ) for all pairs of individuals separated by that binned Euclidean distance. Under the two-dimensional lattice model, theory predicts a linear relationship between a and ln(x), with slope equal to 1/(4πDσ2) (Rousset, 2000). We compared the empirical slope for
) for all pairs of individuals separated by that binned Euclidean distance. Under the two-dimensional lattice model, theory predicts a linear relationship between a and ln(x), with slope equal to 1/(4πDσ2) (Rousset, 2000). We compared the empirical slope for 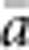 vs ln(
vs ln(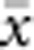 ) with the theoretical expectation. In calculating the empirical slopes, we excluded data for distances x⩽σ, as suggested by Rousset (2000).
) with the theoretical expectation. In calculating the empirical slopes, we excluded data for distances x⩽σ, as suggested by Rousset (2000).
After the 2000-generation burn-in, we collected samples for 100 consecutive generations. At each generation, we randomly sampled a total of 100 individuals from among the offspring that were set aside for sampling in each of the cells. When the sample window was one cell, all 100 individuals from that cell were used. When larger numbers of cells were sampled, individuals were apportioned randomly across the sample window. For each parameter set, we replicated the model runs 100 times and sampled at each of the 100 generations, producing 10 000 data points for each SW–BW combination. All model runs and 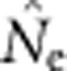 calculations were executed in parallel on the TerpCondor pool of the University of Maryland's distributed Lattice computing network (Bazinet et al., 2007).
calculations were executed in parallel on the TerpCondor pool of the University of Maryland's distributed Lattice computing network (Bazinet et al., 2007).
Estimation of effective size
We used the computer program L𝒟Nℰ (Waples and Do, 2008) to estimate effective size from LD, using the Burrows method (Weir, 1996) from a sample taken at a single point in time. Because our focus was on bias and the 100 loci provided more than ample precision, we included only alleles at a frequency >0.05. This cutoff value has been shown to produce little bias from rare alleles while maintaining moderate precision (Waples and Do, 2010). We took the harmonic mean effective size of all 10 000 estimates in each parameter set as a measure of central tendency of 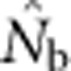 (see Discussion in Waples and Do (2010) regarding the appropriateness of using the harmonic mean in this context). We also calculated FIS for each sample as 1−Ho/He, where Ho is observed heterozygosity and He is expected heterozygosity.
(see Discussion in Waples and Do (2010) regarding the appropriateness of using the harmonic mean in this context). We also calculated FIS for each sample as 1−Ho/He, where Ho is observed heterozygosity and He is expected heterozygosity.
We compared 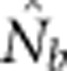 to theoretically expected values for local (NS) and global effective size, and to the total number of potential parents that contributed to a given sample (Table 2; Figure 2a). The number of potential parents is equal to the number of grid cells in a square with side dimension of s+(b−1). For example, for a 3 × 3 sample window (SW9) nested in a 5 × 5 BW (BW25), there are (3+4)2=49 potential parents (Figure 1). For the special case of SW1, all samples are taken from a single focal cell, and the number of potential parents is the BW size; these potential parents also represent ideal parents in that they all have an equal chance of producing any given offspring. In this situation, the realized variance in number of offspring produced per parent is binomial and, on average, effective size equals the number of potential parents. Because selfing was not allowed, in the scenarios with SW1, true Ne was BW+0.5+1/(2BW) (Balloux, 2004), leading to effective sizes of 9.6, 25.5, 49.5 and 81.5 for the four BWs (Table 2).
to theoretically expected values for local (NS) and global effective size, and to the total number of potential parents that contributed to a given sample (Table 2; Figure 2a). The number of potential parents is equal to the number of grid cells in a square with side dimension of s+(b−1). For example, for a 3 × 3 sample window (SW9) nested in a 5 × 5 BW (BW25), there are (3+4)2=49 potential parents (Figure 1). For the special case of SW1, all samples are taken from a single focal cell, and the number of potential parents is the BW size; these potential parents also represent ideal parents in that they all have an equal chance of producing any given offspring. In this situation, the realized variance in number of offspring produced per parent is binomial and, on average, effective size equals the number of potential parents. Because selfing was not allowed, in the scenarios with SW1, true Ne was BW+0.5+1/(2BW) (Balloux, 2004), leading to effective sizes of 9.6, 25.5, 49.5 and 81.5 for the four BWs (Table 2).
Table 2. Parent–offspring dispersal distance, neighborhood size (NS), effective population size, and effective number of breeders for each breeding window (BW) size.
Regression of
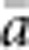 and ln( and ln(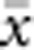 ) ) |
|||||||
|---|---|---|---|---|---|---|---|
| Expected |
Observed |
||||||
| BW | σ2 | NS | Ne | 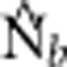 |
Slope | Slope | Intercept |
| 3 × 3 (BW9) | 0.67 | 8.4 | 9.6 | 9.7 | 0.119 | 0.100 | −0.043 |
| 5 × 5 (BW25) | 2.00 | 25.1 | 25.5 | 27.0 | 0.040 | 0.038 | −0.037 |
| 7 × 7 (BW49) | 4.00 | 50.3 | 49.5 | 49.6 | 0.020 | 0.019 | −0.025 |
| 9 × 9 (BW81) | 6.67 | 83.8 | 81.5 | 75.7 | 0.012 | 0.012 | −0.018 |
Notes: σ2 is the mean squared axial parent–offspring distance; Wright's NS=4πDσ2; Ne is the true effective size of the BW based on Balloux (2004) (Equation 10); and 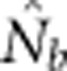 is the harmonic mean effective size estimated using LDNe.
is the harmonic mean effective size estimated using LDNe. 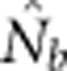 and Ne were calculated.
and Ne were calculated.
Expected and observed slopes of the regression of 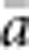 and ln(
and ln(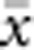 ) provides information on differences among individuals as a function of distance between our model and Wright's original concept of a genetic neighborhood.
) provides information on differences among individuals as a function of distance between our model and Wright's original concept of a genetic neighborhood.
Figure 2.
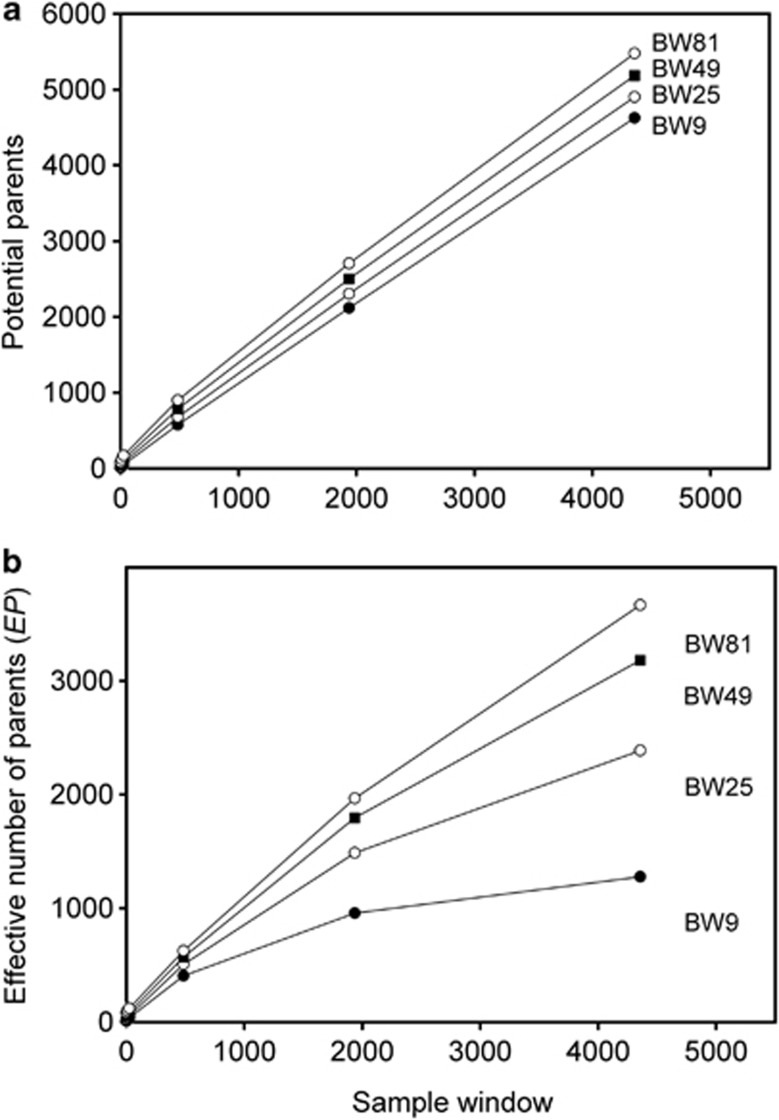
Number of potential parents as a function of the sizes of the sample window and BW. (a) Potential parent is an individual from any cell in generation t that can potentially contribute offspring to a sample taken in generation t+1 and is defined as (s+(b−1)2). (b) Number of effective parents as a function of the sizes of the sample window and BW. Effective parents accounts for the differential probability among potential parents of contributing to offspring in the next generation.
When SW>1, the probability of being a parent varied by location in the SW because potential parents for individuals in cells at the edge of the window can come from outside the sampling area itself, but those parents cannot contribute to all cells in the sample (Figure 1). We use a value, we call the effective number of parents (EP) to account for the effect of this unequal probability on 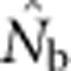 . We calculated EP for each BW–SW combination by randomly choosing a cell within the sample window, and then randomly choosing two parents for a new individual from within the BW centered on that focal cell. We repeated this process until we had a sample of 100 individuals; we then recorded the mean (
. We calculated EP for each BW–SW combination by randomly choosing a cell within the sample window, and then randomly choosing two parents for a new individual from within the BW centered on that focal cell. We repeated this process until we had a sample of 100 individuals; we then recorded the mean (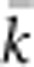 ) and variance (Vk) of the number of offspring (k) produced by each potential parent and used a standard formula for a monoecious population without selfing (Crow and Denniston, 1988)
) and variance (Vk) of the number of offspring (k) produced by each potential parent and used a standard formula for a monoecious population without selfing (Crow and Denniston, 1988)
 |
to calculate an inbreeding effective size for the parents that produced the sample (Figure 2b). These EP values were then compared with 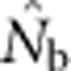 values from the samples generated from the model.
values from the samples generated from the model.
Results
The numbers of alleles per locus did not change appreciably over time through the 100-generation sampling period but did increase predictably with BW size (Table 3). At smaller BWs, numbers of alleles per locus in the final generation of our sampling runs (generation 2100) were consistent with levels found at microsatellite loci in many natural populations (Table 3). The slightly higher allele richness at larger window sizes than might be expected in natural populations would yield higher precision, but this was somewhat reduced by using a 0.05 frequency cutoff in LDNE estimates (described below). Observed heterozygosity ranged between 0.66 and 0.76 in the smallest BW size and between 0.93 and 0.96 for the largest BW size (Table 3). Mean FIS values from different model runs for BW9 ranged from −0.06 for SW1 to 0.22 for SW4356. FIS for BW81 ranged from −0.011 to 0.015 for the same SW sizes. The sample window at which mean FIS values became positive increased with increasing BW size from SW16 for BW9 to SW484 for BW81 (Table 3).
Table 3. Measures of genetic diversity as a function of the size of the breeding and sample windows.
|
Sample window |
||||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Breeding window (BW) | SW1 | SW9 | SW16 | SW25 | SW49 | SW64 | SW100 | SW484 | SW1936 | SW4356 |
| BW9 (Ho=0.720) | ||||||||||
| Alleles/locus | 5.08 | 6.86 | 7.50 | 8.04 | 9.02 | 9.47 | 10.31 | 14.65 | 21.65 | 28.13 |
| He | 0.674 | 0.674 | 0.729 | 0.743 | 0.766 | 0.777 | 0.791 | 0.849 | 0.900 | 0.926 |
| FIS | −0.064 | −0.011 | 0.012 | 0.030 | 0.059 | 0.071 | 0.090 | 0.152 | 0.198 | 0.221 |
| BW25 (Ho=0.872) | ||||||||||
| Alleles/locus | 12.16 | 14.07 | 14.76 | 15.39 | 16.56 | 17.09 | 18.09 | 22.97 | 29.75 | 35.37 |
| He | 0.850 | 0.859 | 0.863 | 0.867 | 0.874 | 0.878 | 0.884 | 0.909 | 0.931 | 0.944 |
| FIS | −0.025 | −0.015 | −0.011 | −0.006 | 0.003 | 0.007 | 0.015 | 0.041 | 0.064 | 0.076 |
| BW49 (Ho=0.925) | ||||||||||
| Alleles/locus | 20.99 | 22.55 | 23.12 | 23.72 | 24.82 | 25.36 | 26.38 | 31.35 | 37.67 | 42.44 |
| He | 0.911 | 0.914 | 0.915 | 0.917 | 0.920 | 0.922 | 0.925 | 0.937 | 0.949 | 0.956 |
| FIS | −0.015 | −0.012 | −0.010 | −0.009 | −0.005 | −0.003 | 0.000 | 0.013 | 0.025 | 0.033 |
| BW81 (Ho=0.948) | ||||||||||
| Alleles/locus | 29.44 | 30.58 | 31.03 | 31.50 | 32.39 | 32.84 | 33.72 | 38.19 | 43.67 | 47.54 |
| He | 0.938 | 0.939 | 0.940 | 0.940 | 0.942 | 0.943 | 0.944 | 0.951 | 0.958 | 0.963 |
| FIS | −0.011 | −0.010 | −0.009 | −0.008 | −0.007 | −0.006 | −0.004 | 0.003 | 0.011 | 0.016 |
Notes: Ho, mean observed heterozygosity; He, mean expected heterozygosity; and FIS, relative observed excess of homozygotes relative to Hardy–Weinberg proportions. Data are based on replicate samples of 100 individuals from each combination of breeding and SWs.
Model validation
Our model provided several opportunities for validation with theoretical predictions. We calculated the observed fraction of expected heterozygosity lost in the global population (90 000 individuals) after t=5000 generations and compared that with the fraction expected, based on the theoretical expectation that the fraction 1/(2Ne) of original heterozygosity is lost each generation. When the BW was 300 × 300, the entire population was panmictic and the fraction of heterozygosity lost was nearly identical to the theoretical expectation for a panmictic population of 90 000 (observed/expected loss=0.994). Maruyama (1972) predicted that the rate of loss of heterozygosity should essentially follow the panmictic expectation when σ2D>1 but should be reduced by the fraction σ2D when σ2D<1; our results were also in good agreement with this prediction. For BW81, σ2D>>1 (6.667; Table 2) and the rate of loss of heterozygosity was only slightly reduced relative to the panmictic expectation (observed/expected loss=0.941). For BW9 (σ2D=0.667; Table 2), Maruyama's theory predicts that the ratio of loss of heterozygosity should be reduced by one-third, and we found the observed rate to be 66% of that expected under panmixia.
Harmonic mean 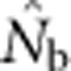 for SW1 samples for the four BW sizes agreed closely with theoretical expectations, as well as with the NSs associated with these four BWs (Table 2). Confidence intervals and root mean square error for
for SW1 samples for the four BW sizes agreed closely with theoretical expectations, as well as with the NSs associated with these four BWs (Table 2). Confidence intervals and root mean square error for 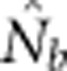 for individual replicates are shown in Appendix C.
for individual replicates are shown in Appendix C.
Also in accord with theory, the relationship between 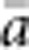 and ln(
and ln(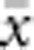 ) was almost perfectly linear (correlation >0.99) for all four BWs, and empirical slopes were close to the value of 1/(4πDσ2) expected for generalized dispersal models. The empirical slopes were within a few percent of the theoretical slope for BW25, 49 and 81, but for the smallest BW, the empirical slope was 16% lower than expected (Table 2). Thus, for the three larger BWs, the increase in genetic differentiation with distance was similar to expectations under Wright's neighborhood model, whereas for the smallest BW, genetic differentiation increased more slowly with distance than predicted. That is, although dispersal in our model was constrained to occur within the BW (Figure 1a), effects of parent–offspring dispersal in reducing genetic differentiation were equal to or slightly greater than under lattice models that allow long-range dispersal. Theory does not provide a general expectation for the intercept of the regression of a and ln(x). We found that the intercept decreased with the size of the BW (Table 2). In each case, the intercept was negative (range −0.018 to −0.043), which agrees with empirical data for the kangaroo rat (Dipodomys spectabilis; intercept=−0.162) analyzed by Rousset (2000).
) was almost perfectly linear (correlation >0.99) for all four BWs, and empirical slopes were close to the value of 1/(4πDσ2) expected for generalized dispersal models. The empirical slopes were within a few percent of the theoretical slope for BW25, 49 and 81, but for the smallest BW, the empirical slope was 16% lower than expected (Table 2). Thus, for the three larger BWs, the increase in genetic differentiation with distance was similar to expectations under Wright's neighborhood model, whereas for the smallest BW, genetic differentiation increased more slowly with distance than predicted. That is, although dispersal in our model was constrained to occur within the BW (Figure 1a), effects of parent–offspring dispersal in reducing genetic differentiation were equal to or slightly greater than under lattice models that allow long-range dispersal. Theory does not provide a general expectation for the intercept of the regression of a and ln(x). We found that the intercept decreased with the size of the BW (Table 2). In each case, the intercept was negative (range −0.018 to −0.043), which agrees with empirical data for the kangaroo rat (Dipodomys spectabilis; intercept=−0.162) analyzed by Rousset (2000).
Effects of sample and breeding window sizes
The number of potential parents increased nearly linearly as a function of the sample window size and was relatively insensitive to BW size (Figure 2a). However, not all potential parents have the same probability of producing an offspring. Accounting for these unequal contributions reduces the EP, and this reduction is most pronounced for smaller BW sizes (Figure 2b). For example, for BW9, increases in the sample window beyond 2000 cells produce only a small increase in EP. If no other factors were involved, the values of EP shown in Figure 2b would be the most reasonable a priori expectation for 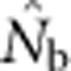 produced by a single-sample estimator.
produced by a single-sample estimator.
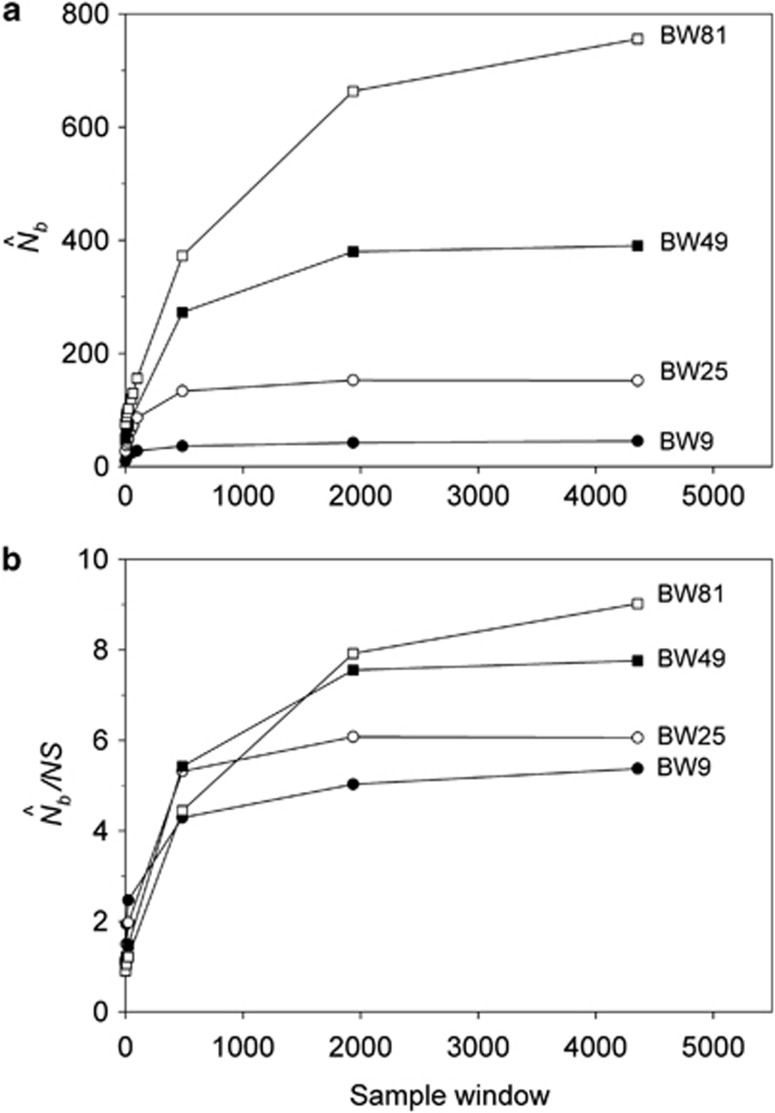
Analysis of our simulated data, however, showed that 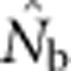 increased much more slowly with increases in the spatial scale of sampling than predicted based on EP (compare Figures 3a and 2b).
increased much more slowly with increases in the spatial scale of sampling than predicted based on EP (compare Figures 3a and 2b). 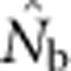 showed a pronounced asymptotic behavior, increasing with SW size until reaching a value characteristic of each BW size, after which increases in sample window size had relatively little effect. The most pronounced asymptote was seen in BW9 and occurred at
showed a pronounced asymptotic behavior, increasing with SW size until reaching a value characteristic of each BW size, after which increases in sample window size had relatively little effect. The most pronounced asymptote was seen in BW9 and occurred at 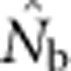 <50; for BW81, an asymptote is suggested but never quite reached even for the largest sample window. For each BW, the maximum
<50; for BW81, an asymptote is suggested but never quite reached even for the largest sample window. For each BW, the maximum 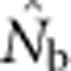 values were only ∼5–10 times larger than NS (Figure 3b), even though the sample windows considered were as much as 484 times as large as the BWs. For the largest SW BW81,
values were only ∼5–10 times larger than NS (Figure 3b), even though the sample windows considered were as much as 484 times as large as the BWs. For the largest SW BW81, 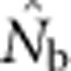 for was only 20.6% of the EP (756 vs 3667); for BW9,
for was only 20.6% of the EP (756 vs 3667); for BW9, 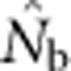 was only 3.5% of the EP (45 vs 1276) (Appendix C).
was only 3.5% of the EP (45 vs 1276) (Appendix C).
Figure 3.
(a) 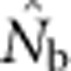 as a function of the size of the sampling and BWs.
as a function of the size of the sampling and BWs. 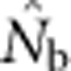 is the harmonic mean of estimates across 10 000 replicates of 100 generations of simulated data. Sample size was 100 individuals. Ninety-five percent confidence intervals for these estimates are provided in Appendix C. (b) As in a, but with the
is the harmonic mean of estimates across 10 000 replicates of 100 generations of simulated data. Sample size was 100 individuals. Ninety-five percent confidence intervals for these estimates are provided in Appendix C. (b) As in a, but with the 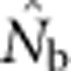 values standardized by Wright's NS for each BW (see Table 2).
values standardized by Wright's NS for each BW (see Table 2).
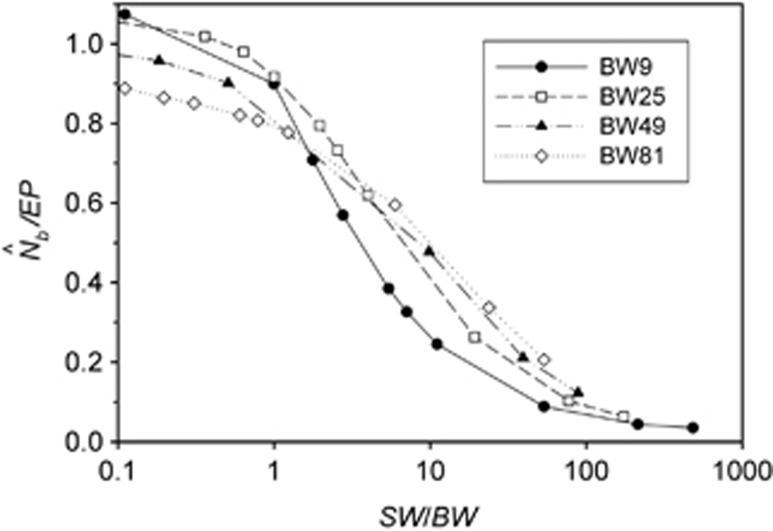
Two additional analyses help explain the discrepancy between 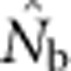 and EP. Plotting the ratio
and EP. Plotting the ratio 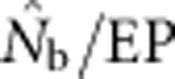 as a function of the ratio SW/BW yielded sigmoid curves with three distinct zones (Figure 4). For SW/BW⩽1,
as a function of the ratio SW/BW yielded sigmoid curves with three distinct zones (Figure 4). For SW/BW⩽1, 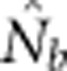 from the model was in close agreement with the EPs (
from the model was in close agreement with the EPs (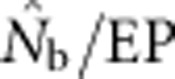 ∼1.0). As the sample window exceeded the size of the BW (1<SW/BW<10), the ratio
∼1.0). As the sample window exceeded the size of the BW (1<SW/BW<10), the ratio 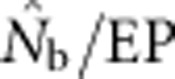 rapidly declined from near unity to 0.2–0.5. Finally, when the sample window was >10 times as large as the BW,
rapidly declined from near unity to 0.2–0.5. Finally, when the sample window was >10 times as large as the BW, 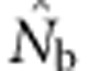 was a small fraction of the EPs, as noted above.
was a small fraction of the EPs, as noted above.
Figure 4.
The ratio of harmonic mean 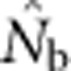 to the EP as a function of the ratio SW/BW.
to the EP as a function of the ratio SW/BW.
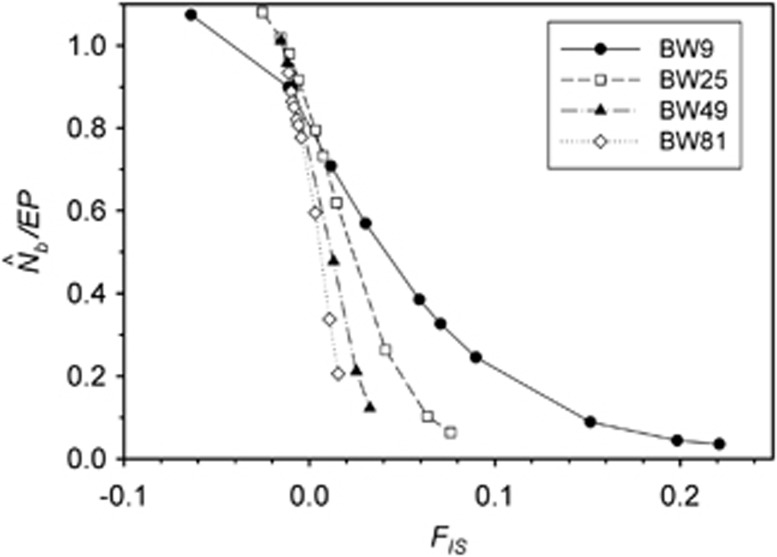
A plausible biological explanation for the results shown in Figure 4 is that the ratio 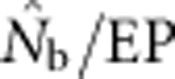 is very sensitive to the inbreeding coefficient for the sample (FIS; Table 2 and Figure 5). For FIS⩽0 (as expected for a randomly mating but finite population),
is very sensitive to the inbreeding coefficient for the sample (FIS; Table 2 and Figure 5). For FIS⩽0 (as expected for a randomly mating but finite population), 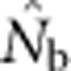 and EP were approximately equal. As FIS became positive (indicating heterozygote deficit),
and EP were approximately equal. As FIS became positive (indicating heterozygote deficit), 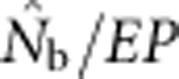 dropped sharply, particularly for larger BWs. For example, for BW=81, even a slightly positive FIS of 0.02 was associated with a substantial depression in estimated effective size (
dropped sharply, particularly for larger BWs. For example, for BW=81, even a slightly positive FIS of 0.02 was associated with a substantial depression in estimated effective size ( ⩽0.2; Figure 5). Thus, a deficiency of heterozygotes was associated with unusually small
⩽0.2; Figure 5). Thus, a deficiency of heterozygotes was associated with unusually small 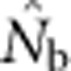 values relative to the number of parents contributing to a sample.
values relative to the number of parents contributing to a sample.
Figure 5.
The ratio 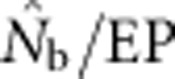 as a function of the inbreeding coefficient, FIS. For each BW size, the data points represent, from left to right, SW1 through SW4356.
as a function of the inbreeding coefficient, FIS. For each BW size, the data points represent, from left to right, SW1 through SW4356.
Discussion
Continuous distributions represent a major violation of a key assumption underlying most methods for estimating contemporary Ne—that samples have been taken from a single, unstructured population. Despite the fact that such distributions are common for natural populations of many widespread animal and plant species, the consequences for estimators designed for discrete populations have not been examined. This is a specific example of a more general problem with population genetics models and statistical tests that fail to account for spatial autocorrelation in allele frequencies (Meirmans, 2012). We have demonstrated that the relative geographic scales of sampling and local breeding in a continuously distributed population can dramatically affect estimates of effective size using the LD method, through interacting effects of genetic drift and population mixture on LD. If the samples are drawn from an area that is substantially larger than the area within which local, quasi-random mating occurs, effects of population mixture on 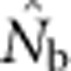 can far exceed effects of drift.
can far exceed effects of drift.
Two natural points of reference bracket the potential effective size estimates and place them in context: a local effective size related to Wright's NS and a global effective size related to the total number of individuals. We found that 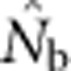 based on the LD method was close to Wright's NS when the SW was no larger than the area from which parents can be considered to be approximately randomly drawn (the BW). As the SW size increased relative to that of the BW, one might expect that the estimates of effective size would approach or reach the global effective size in proportion to the number of potential parents. This, however, was not the case:
based on the LD method was close to Wright's NS when the SW was no larger than the area from which parents can be considered to be approximately randomly drawn (the BW). As the SW size increased relative to that of the BW, one might expect that the estimates of effective size would approach or reach the global effective size in proportion to the number of potential parents. This, however, was not the case: 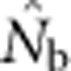 did not approach the number of potential parents. Alternatively, we could expect estimates to increase proportionally with the EPs (Figure 2b), given that the LD method primarily provides information about drift disequilibrium in the pool of parents responsible for the sample (Waples, 2005). We found, however, that
did not approach the number of potential parents. Alternatively, we could expect estimates to increase proportionally with the EPs (Figure 2b), given that the LD method primarily provides information about drift disequilibrium in the pool of parents responsible for the sample (Waples, 2005). We found, however, that 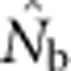 increased much more slowly than did even EP (compare Figures 3a and b with Figure 2b). When the sample window was × 10 as large as the BW,
increased much more slowly than did even EP (compare Figures 3a and b with Figure 2b). When the sample window was × 10 as large as the BW, 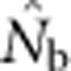 was only 20–50% of the EPs that produced the samples, and the discrepancy increased as SW size increased (Figure 4).
was only 20–50% of the EPs that produced the samples, and the discrepancy increased as SW size increased (Figure 4).
The primary factor that appears to be responsible for this deviation from expectation is a type of Wahlund effect that arises when genetically divergent individuals are included in a single sample. This effect is a general property of IBD models, but the effect will generally be small unless the size of the sample window exceeds the typical parent–offspring dispersal distance. At a single locus, this effect produces a deficiency of observed heterozygotes compared with Hardy–Weinberg expectations. When pairs of loci are considered, LD emerges due to mixture of offspring of genetically differentiated parents. The LD method assumes these disequilibria are due to genetic drift, and hence underestimates effective size.
The smallest SWs produced the opposite of the Wahlund effect—an excess of observed heterozygotes and slightly negative FIS values (Table 3 and Figure 5). When effective size is small, an excess of heterozygotes arises from random differences in allele frequency among parents of different sexes (Robertson, 1965); this phenomenon is the basis for the heterozygote-excess method for estimating effective size (Pudovkin et al., 1996). Balloux (2004) showed that an excess also arises from a lack of completely random mating in monoecious populations that lack selfing, as considered here. The slightly negative FIS values became positive as sample window size increased relative to BW size, indicating that the effect of a mixture of genetically divergent individuals more than offsets the heterozygote excess from a small number of local breeders.
Joint effects of drift and mixture on LD have been evaluated in discrete subpopulations connected by equilibrium, island-model migration (Waples and England, 2011). In that model, immigration produced two counteracting effects analogous to those considered here: it expanded the pool of parents and imported potentially divergent genotypes. Empirical results showed that 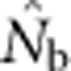 from the LD method was close to the local effective size unless migration rate (m) was >5–10%, at which point the estimate approached Ne for the metapopulation as a whole (Waples and England, 2011). The lack of an appreciable mixture LD effect presumably was due to basic properties of migration-drift equilibrium in the island model: if m is low, immigrants will be genetically divergent but rare, so they do not have a large overall impact; if m is high, immigrants will be genetically similar and thus produce little or no mixture LD.
from the LD method was close to the local effective size unless migration rate (m) was >5–10%, at which point the estimate approached Ne for the metapopulation as a whole (Waples and England, 2011). The lack of an appreciable mixture LD effect presumably was due to basic properties of migration-drift equilibrium in the island model: if m is low, immigrants will be genetically divergent but rare, so they do not have a large overall impact; if m is high, immigrants will be genetically similar and thus produce little or no mixture LD.
The isolation-by-distance model considered here differed in important ways from the island model considered by Waples and England (2011). In the latter study, all sampling was from one local subpopulation, and there is no way that equilibrium migration can import appreciable fractions of genetically divergent individuals. In the present study, in contrast, large SWs could include individuals produced by non-overlapping sets of parents, and the resulting mixture LD offset and eventually overwhelmed the reductions to drift LD from expanding the EPs. When Waples and England (2011) considered nonequilibrium, pulse migration at up to 10 times the equilibrium rate in their island model, they found that 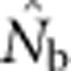 could be substantially depressed by mixture LD. This scenario somewhat mimics what happens as the sample window in our model expands beyond the BW size. In both cases, the sample includes genetically divergent individuals in proportions that greatly exceed what would occur locally under equilibrium conditions. We expect that a similar effect would be seen in the equilibrium island model if more than one subpopulation were included in a single sample.
could be substantially depressed by mixture LD. This scenario somewhat mimics what happens as the sample window in our model expands beyond the BW size. In both cases, the sample includes genetically divergent individuals in proportions that greatly exceed what would occur locally under equilibrium conditions. We expect that a similar effect would be seen in the equilibrium island model if more than one subpopulation were included in a single sample.
Other Neestimators
Two other single-sample estimators of contemporary Ne (the Approximate Bayesian Computation program ONeSAMP (Tallmon et al., 2008) and the sibship method of Wang (2009)) appear to have considerable potential but are too computationally demanding to easily evaluate in numerical studies like this one. Because the squared correlation of alleles at different loci (r2) is the most important genetic metric used by ONeSAMP (D Tallmon, personal communication), we expect that its performance under isolation-by-distance might be similar to that reported here. The sibship method should also be very sensitive to the size of the local BW, as a small NS should produce more full and half siblings than would occur in a large, randomly mating population. Results for the heterozygote-excess method are predictable; estimated effective size by that method is approximately −1/(2FIS) (Pudovkin et al., 1996; Balloux, 2004). Based on FIS values shown in Table 2, the estimates from this method would be close to the NS for the smallest SWs but would rapidly rise to undefined (infinite) values as the Wahlund effect erased the drift signal of heterozygote excess. We expect that estimates using the temporal method will also be sensitive to local breeding neighborhoods in continuously distributed species, but effects could be qualitatively different from those discussed here. This topic merits more detailed consideration in a separate study.
Applications
These results have direct relevance for anyone interested in using genetic methods to estimate effective size or study evolutionary processes in natural populations. The degree to which the potential biases resulting from a conflation of mixture and drift disequilibria represent a serious problem will depend on the study objectives, as well as on details of experimental design. In continuously distributed populations, using single-sample methods to derive an estimate of the global effective size is not likely to be feasible or appropriate unless the global population is panmictic or nearly so. If breeding is constrained to relatively small local areas (or, equivalently, if parent–offspring dispersal distance is small compared with the scale of the global population), then the LD method will underestimate global Ne regardless how much of the geographic range of the population is sampled. Even broad geographic sampling will produce an estimate that is some small but unknown multiple of the NS, and this can be a fraction of the total pool of parents that could have contributed to the sample (Figures 2a and 3). As discussed above, we expect that other single-sample estimators will produce qualitatively similar results.
Our results show that the LD method provides a good approximation of the NS as long as the scale of sampling is commensurate with the scale of local breeding. NS is a useful concept because it provides information about the geographic scale over which short-term evolutionary processes operate. A large number of empirical studies (Bradbury and Bentzen, 2007; Watts et al., 2007) have taken advantage of the increasing availability of numerous molecular markers to estimate NS and parent–offspring dispersal distance, using regression models (Rousset, 1997, 2000, 2008) that relate genetic divergence and geographic distance. Theoretical evaluations and modeling have demonstrated that this regression method is generally robust to assumptions about mutational processes and dispersal distributions, and empirical comparison of demographic and genetic estimates of σ2D for natural populations generally agree within a factor of two (Guillot et al., 2009). Recent development of maximum likelihood estimates based on the coalescent offer potential for even better estimates (Rousset and Leblois, 2012). On the other hand, Bradbury and Bentzen (2007) used simulations and meta-analysis of published empirical papers and found evidence for nonlinear patterns of isolation-by-distance in marine species at both very small and very large distances. Those authors suggested that these patterns might be common in species with limited dispersal but large geographic ranges.
Our results illustrate the importance of understanding the spatial structure of the target population to determine the optimal sampling strategy for the particular question of interest. Although researchers presumably match the geographic scale of sampling to the distribution of individuals in a population or species, they might have little idea about breeding structure or parent–offspring dispersal distances. Fortunately, it is possible to gain insights into the appropriate sampling scale using an iterative approach. We suggest that sampling initially occur based on multiple samples taken across a range of spatial scales to include individuals separated by a range of distances. These samples can first be used to test for positive spatial autocorrelation in allele frequencies, which can occur at fine spatial scales that can be missed if sampling is implemented only at large scales (Schwartz and McKelvey, 2009). Samples can be aggregated sequentially across different distance classes and used to estimate Nb and FIS. Examining the shape of the curve relating 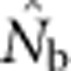 and sampling scale (as in Figure 3) can provide insight into the likely NS. The dramatic drop in
and sampling scale (as in Figure 3) can provide insight into the likely NS. The dramatic drop in 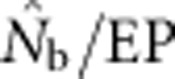 that occurs as FIS values become positive (Figure 5) indicates that the changing relationship between
that occurs as FIS values become positive (Figure 5) indicates that the changing relationship between 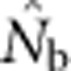 and FIS across spatial scales is a sensitive indicator of the scale at which a Wahlund effect and thus mixture disequilibrium occurs. It might also be useful to combine genetic sampling with non-genetic approaches such as global positioning system tracking of individuals to determine dispersal distances, home range sizes and other biological attributes of the sampled population.
and FIS across spatial scales is a sensitive indicator of the scale at which a Wahlund effect and thus mixture disequilibrium occurs. It might also be useful to combine genetic sampling with non-genetic approaches such as global positioning system tracking of individuals to determine dispersal distances, home range sizes and other biological attributes of the sampled population.
Our evaluations have focused on bias, because to date there have been no empirical evaluations of performance of any estimator of contemporary effective size when applied to species with continuous distributions. Precision also can be limiting for practical application; fortunately, considerable empirical information regarding precision of the LD method based on realistic samples of individuals, loci and alleles is available (England et al., 2010; Tallmon et al., 2010; Waples and Do, 2010; Antao et al., 2011; Waples and England, 2011). Results of these evaluations can be summarized as follows: (1) As is the case for all methods that estimate contemporary effective size, precision is inversely related to true Ne; (2) When Ne is small (<∼100), the drift signal is strong and precision can be high with amounts of data readily available from most field studies; (3) If Ne is large (>500–1000), precise estimates generally cannot be achieved without large sample sizes and large numbers of genetic markers; (4) The distributions of 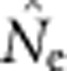 and
and 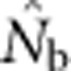 can be highly skewed toward large values, so the harmonic mean is the best measure of central tendency. Appendix C provides empirical confidence intervals for the simulated data shown in Figure 3 of this study.
can be highly skewed toward large values, so the harmonic mean is the best measure of central tendency. Appendix C provides empirical confidence intervals for the simulated data shown in Figure 3 of this study.
The results presented here should be broadly applicable to a wide range of patterns of individual isolation-by-distance in two dimensions. The lattice model with one individual per node is mathematically more tractable (Malécot, 1975; Rousset, 2000) and avoids the problem of clumped groups of offspring that grow larger over time that arise in other isolation-by-distance models (Felsenstein, 1975; Kawata, 1995). Although our implementation differs from that of Wright and others in not allowing for long-distance dispersal, the overall genetic differentiation patterns closely paralleled those found in other models (Table 2) and met theoretical expectations. Furthermore, Rousset (2000) has shown that the theoretical results for the lattice model were robust to highly leptokurtic dispersal distributions. Rousset (2000) cautioned that theoretical expectations might be less robust when individuals compared are separated by Euclidean distances much larger than σ, but we detected no change in the slope of the regression of 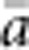 and ln(
and ln(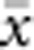 ) for
) for 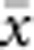 as large as 50 and σ=0.67–6.67.
as large as 50 and σ=0.67–6.67.
In summary, our results demonstrate that spatial variation in a continuous population can severely bias estimates of Ne generated with LD approaches, such that estimates are much closer to NSs than to global population sizes. If this same effect holds true with other approaches such as the temporal method, it might help explain why the literature is replete with estimates of tiny Ne/Nc ratios (for example, Hauser and Carvalho, 2008; Franckowiak et al., 2009; Nikolic et al., 2009; Palstra et al., 2009). Possible biological reasons for these discrepancies between estimated effective and census sizes include historic bottlenecks (Nikolic et al., 2009), fragmentation events, changing climate (Okello et al., 2008), fluctuating population size (Boessenkool et al., 2010), sweepstakes dispersal and recruitment (Hedgecock, 1994) and age structure (Palstra et al., 2009). However, because these anomalous results might also result from sampling issues, statistical artifacts or violations of assumptions, it is important to more fully explore these other potential factors. Thus, we advocate further performance testing of effective size estimators in continuously distributed populations and better understanding of the true structure of populations rather than assuming structure a priori.
Data Archiving
The data file containing all 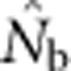 estimates and associated genetic diversity statistics is archived at the Dryad Repository (doi:10.5061/dryad.d9p7h). The model that generated the populations on which the
estimates and associated genetic diversity statistics is archived at the Dryad Repository (doi:10.5061/dryad.d9p7h). The model that generated the populations on which the 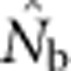 estimates are based is available upon request from K McKelvey (kmckelvey@fs.fed.us).
estimates are based is available upon request from K McKelvey (kmckelvey@fs.fed.us).
Acknowledgments
We thank the Genetic Monitoring Working Group for helpful discussions and feedback that greatly improved this work. This work was conducted as part of the Working Group on Genetic Monitoring: Development of Tools for Conservation and Management, jointly supported by the National Evolutionary Synthesis Center (NSF no. EF-0423641) and the National Center for Ecological Analysis and Synthesis, a Center funded by the US National Science Foundation (NSF no. DEB-0553768), the University of California, Santa Barbara, and the State of California. MWL is partially supported by the Maryland Agricultural Experiment Station.
Appendix A
Dispersal, breeding window size and neighborhood size
Wright's neighborhood size (NS) for a two-dimensional continuously distributed population is
NS=4πσ2D, where D is density (number of individuals per unit area) and σ2 is a measure of dispersal, reflecting the difference in location between birthplaces of parents and offspring. Specifically, σ2 is the variance of the signed parent–offspring distance along one axis (δ). In Wright's original neighborhood model, δ is normally distributed with a mean of 0 along both axes. Under those conditions, NS can be thought of as the number of reproducing individuals in a circle of radius 2σ, and a circle of this size would include about 87% of the parents of individuals at the center (Wright, 1946). The remaining ∼13% of parents therefore would have been responsible for relatively long-range dispersal of their offspring.
The model considered here has a number of similarities but also some differences compared with Wright's neighborhood model. Our model involves a regular lattice with exactly one individual per cell, so D=1 and that term drops out. In our model, the parents of an individual in a given focal cell are drawn with equal probability from any of the cells in the square breeding window (BW) with sides (b) of 3, 5, 7 and 9 cells, yielding BWs of BW=9, 25, 49 and 81. Parent–offspring dispersal, therefore, is not Gaussian in our model, but rather uniform within the range –n to +n. For example, for n=1, there are 3 × 3=9 potential parents in the square BW. Three of the potential parents have an X coordinate 1 cell to the left of the focal cell (δ=-1), three have an X coordinate the same as the focal cell (δ=0) and three have an X coordinate 1 U to the right of the focal cell (δ=+1). For BW9, therefore, 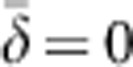 and σ2=0.667. In Wright's model, a neighborhood with the same density and same variance in dispersal would be of size NS=4π(0.667)=8.4, which is close to the nine ideal individuals in the comparable BW in our model. Table 2 shows that for each of the other BWs considered here, the NS having the same density and variance in dispersal is also quantitatively similar to the number of individuals in the BW.
and σ2=0.667. In Wright's model, a neighborhood with the same density and same variance in dispersal would be of size NS=4π(0.667)=8.4, which is close to the nine ideal individuals in the comparable BW in our model. Table 2 shows that for each of the other BWs considered here, the NS having the same density and variance in dispersal is also quantitatively similar to the number of individuals in the BW.
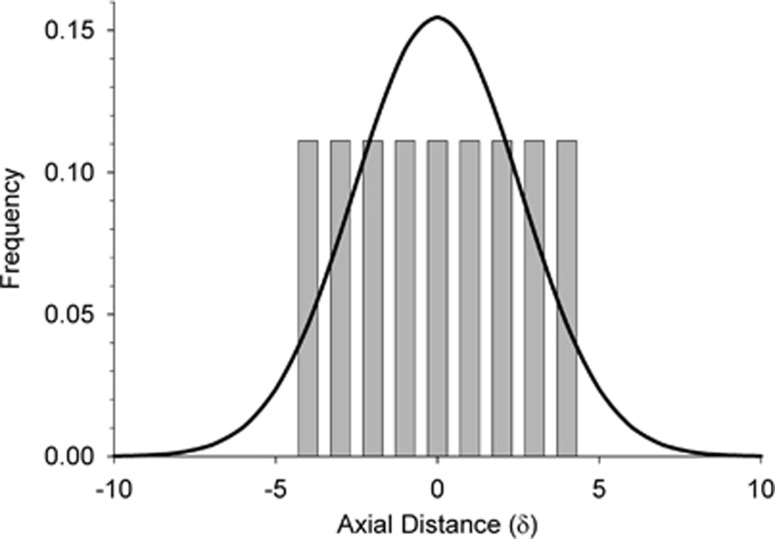
The major difference between the two models (distribution of parent–offspring dispersal distances) is illustrated in Figure A1, which compares patterns of dispersal for a 9 × 9 BW in our model with that expected under a neighborhood model with Gaussian dispersal. Both models have the same density and the same mean and variance in dispersal, but the neighborhood model has a higher fraction of long-distance dispersers, as well as a higher fraction that do not disperse at all.
Figure A1.
Distribution of axial dispersal distances (along the horizontal or vertical axis) for Wright's neighborhood model (curved line, assuming a normal distribution of dispersal) and our model (vertical bars) with BW81. In both models, the density of individuals (D)=1 and mean and variance of parent–offspring dispersal are 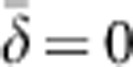 and σ2=0.667, respectively.
and σ2=0.667, respectively.
Appendix B
Development of spatial autocorrelation and local differentiation in the modeled landscape
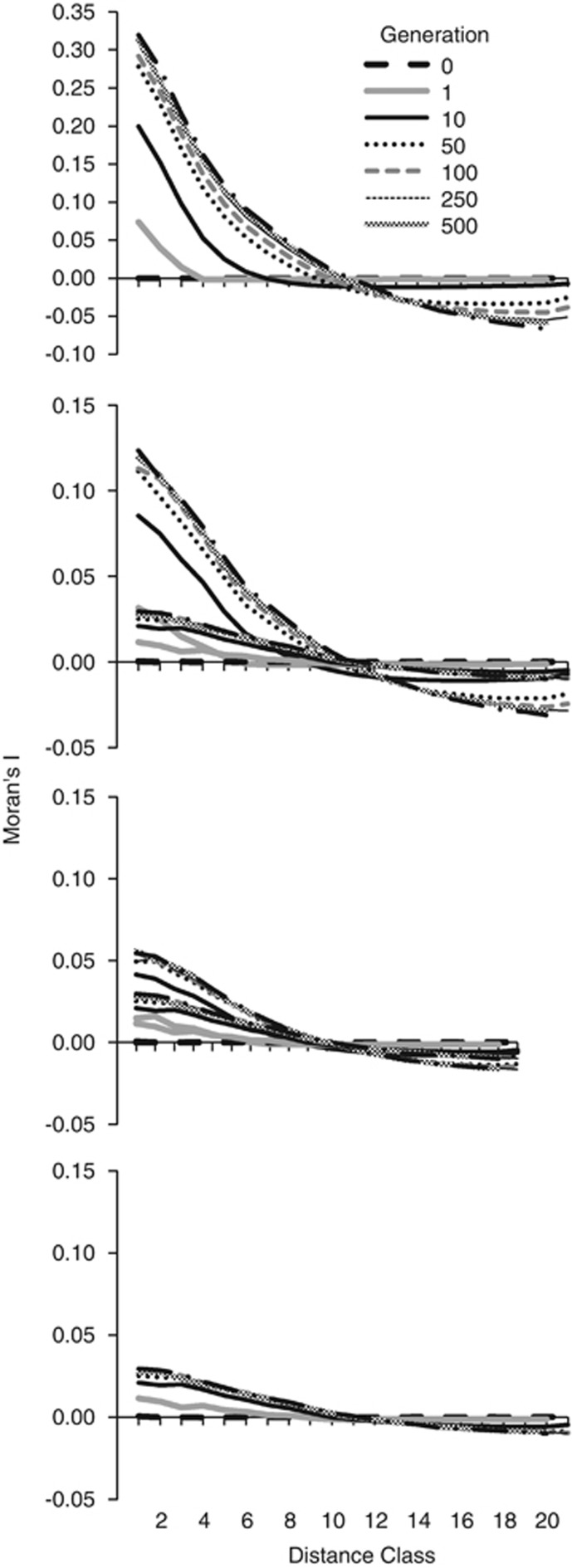
To determine the burn-in period, we quantified the number of generations necessary to establish genetic structure due to local mating within the continuous grid surface for the four breeding window (BW) sizes (BW9, BW25, BW49 and BW81). We used Moran's I to quantify spatial autocorrelation of genetic distance among all individuals in a centrally located 25 × 25 cell area across lag distances of 1–21 cells at generations 0, 1, 10, 50, 100, 250, 500 and 1000, using the computer program SPAGeDI (Hardy and Vekemans, 2002). We used the program 𝒢ℰ𝒩𝒪𝒟ℐ𝒱ℰ V.2.0b20 (Meirmans and Van Tienderen, 2004) to calculate Hedrick's standardized measure G′ST (Hedrick, 2005), GST and Hs among four 10 × 10 cell SWs that were located in four corners of the 150 × 150 internal sampling grid. We sampled 100 individuals from each ‘population' every 10 generations up to generation 200, and then every 100 generations up to generation 2000.
For all BWs, spatial autocorrelation was nonexistent at the start of the simulation but began establishing in 1 generation and was well established within 10 generations (Figure B1). The maximum magnitude of Moran's I was a function of the BW size, ranging from a maximum of 0.029 for BW81 to ∼0.32 for BW9. Between 50 and 100, generations were required to reach at least 90% of the maximum value of Moran's I for all BW sizes. The maximum lag distance at which Moran's I crossed 0 was ∼11. The number of generations required to reach this maximum decreased with increasing BW and within all BWs, and differences in the lag distance decreased with increasing generations. For BW9, the increases were minor after ∼100 generations; for BW25 and BW49, there was little change in the lag distance at which Moran's I crossed 0 after 50 generations; and for BW81, there was little change after 10 generations. Thus, the genetic structure as measured by autocorrelation was well established by generation 50–250 and then was relatively unchanged in subsequent generations in all BWs (Figure B1).
Figure B1.
Spatial autocorrelation of genetic distance (Moran's I) across selected gnerations between 0 and 1000 generations in four BW sizes. Note the y-axis scale difference between BW9 and the other BWs.
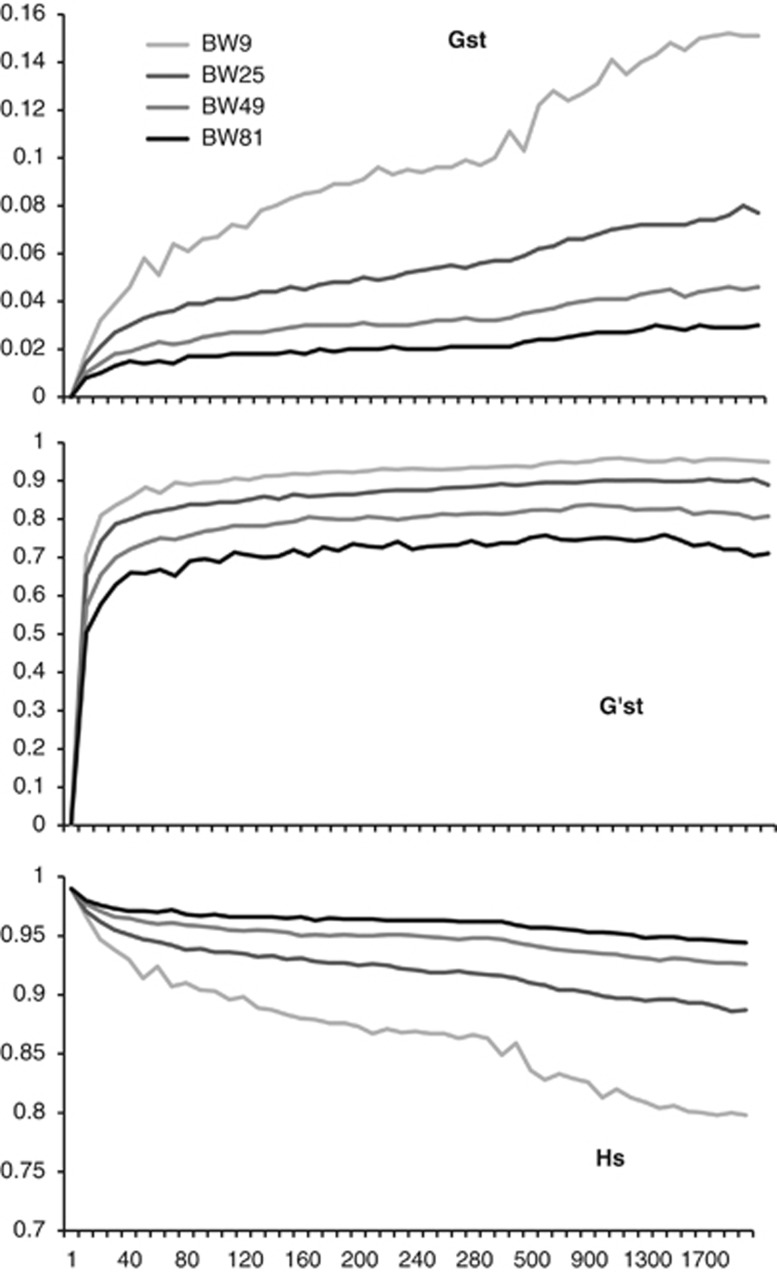
Values of GST and G′ST also indicated rapid development of population genetic structure in the grid surface, the magnitude of which was a function of BW size (Figure B2). GST continued to increase through time, and did so more rapidly than G′ST, especially for BW9. G′ST reached an asymptote by ∼30 generations. This differential increase was in large part due to continuing declines in HS that were strongest for BW9 (Figure B2). This relationship displays the expected interaction between HS and GST (MeirmgAans and Hedrick, 2011) that can confound interpretation of this statistic and illustrates how sampling from isolated locations within a continuous population yields gyetic structure indicative of isolation.
Figure B2.
GST, Hedrick's G′ST and HS for four 10 × 10 cell ‘populations' sampled from the continuous landscape as a function of BW size and number of generations in the modeled landscape.
Appendix C
Medians, 10th and 90th percentiles, and root mean squared error (RMSE) for estimates of number of effective breeders (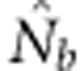 ) from 10 000 replicates of all breeding window (BW)–SW combinations. RMSE=sqrt[∑((1/(2
) from 10 000 replicates of all breeding window (BW)–SW combinations. RMSE=sqrt[∑((1/(2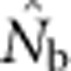 )−(1/(2NS))2] of the drift signal (1/(2
)−(1/(2NS))2] of the drift signal (1/(2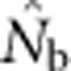 )). Bias of each estimate is assessed with respect to the true NS for each BW. See Wang (2009) for comparable data for another single-sample method.
)). Bias of each estimate is assessed with respect to the true NS for each BW. See Wang (2009) for comparable data for another single-sample method.
Table C1.
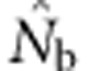 |
|||||||||
|---|---|---|---|---|---|---|---|---|---|
| SW | 2.5% | 10% | 50% | 90% | 97.5% | NS | 1/(2NS) | RMSE | |
| BW9 | 1 | 7.6 | 8.3 | 9.8 | 11.2 | 11.9 | 8.4 | 0.0595 | 0.00998 |
| 3 | 12.8 | 14.1 | 16.5 | 18.9 | 20.1 | 0.02899 | |||
| 4 | 14.7 | 16.1 | 18.8 | 21.6 | 23.1 | 0.03279 | |||
| 5 | 16.4 | 18.0 | 20.9 | 24.1 | 25.8 | 0.03548 | |||
| 7 | 19.6 | 21.2 | 24.2 | 27.5 | 29.3 | 0.03877 | |||
| 8 | 21.0 | 22.5 | 25.6 | 29.0 | 30.9 | 0.03988 | |||
| 10 | 23.1 | 24.7 | 27.9 | 31.4 | 33.4 | 0.04154 | |||
| 22 | 30.8 | 32.6 | 36.2 | 40.0 | 42.2 | 0.04566 | |||
| 44 | 36.5 | 38.5 | 42.4 | 46.5 | 48.9 | 0.04769 | |||
| 66 | 39.0 | 41.2 | 45.3 | 49.7 | 52.2 | 0.04845 | |||
| BW25 | 1 | 23.8 | 25.0 | 27.2 | 29.3 | 30.4 | 25.1 | 0.0199 | 0.00184 |
| 3 | 32 | 33.9 | 37.7 | 41.7 | 43.9 | 0.00669 | |||
| 4 | 36.4 | 38.8 | 43.4 | 48.1 | 50.8 | 0.00839 | |||
| 5 | 41.5 | 44.2 | 49.7 | 55.5 | 58.6 | 0.00985 | |||
| 7 | 54.1 | 57.6 | 65.0 | 72.9 | 77.3 | 0.01220 | |||
| 8 | 60.0 | 64.2 | 72.6 | 81.6 | 86.8 | 0.01301 | |||
| 10 | 71.7 | 76.8 | 86.8 | 97.8 | 103.7 | 0.01414 | |||
| 22 | 110.8 | 118.3 | 134.1 | 151.7 | 162.2 | 0.01618 | |||
| 44 | 126.8 | 135.3 | 153.1 | 173.2 | 185.5 | 0.01664 | |||
| 66 | 126.8 | 135.3 | 152.8 | 171.9 | 183.5 | 0.01663 | |||
| BW49 | 1 | 43.3 | 45.5 | 49.9 | 54.1 | 56.2 | 50.3 | 0.0099 | 0.00070 |
| 3 | 51.6 | 55.1 | 61.8 | 68.7 | 72.5 | 0.00193 | |||
| 4 | 56.1 | 60.0 | 67.9 | 76.2 | 81.1 | 0.00263 | |||
| 5 | 61.3 | 65.8 | 74.9 | 84.5 | 90.0 | 0.00328 | |||
| 7 | 74.9 | 81.0 | 93.3 | 106.6 | 114.0 | 0.00457 | |||
| 8 | 83.7 | 90.9 | 104.5 | 119.4 | 128.1 | 0.00514 | |||
| 10 | 103.7 | 112.5 | 130.0 | 149.6 | 161.3 | 0.00608 | |||
| 22 | 214.4 | 233.4 | 274.9 | 324.8 | 354.3 | 0.00811 | |||
| 44 | 296.2 | 323.8 | 382.4 | 455.9 | 500.5 | 0.00863 | |||
| 66 | 304.4 | 332.4 | 392.8 | 468.0 | 512.1 | 0.00866 | |||
| BW81 | 1 | 63.8 | 68.0 | 76.3 | 84.2 | 88.5 | 83.8 | 0.0060 | 0.00085 |
| 3 | 72.9 | 78.0 | 89.0 | 100.4 | 106.7 | 0.00064 | |||
| 4 | 77.1 | 83.4 | 95.7 | 109.0 | 116.6 | 0.00090 | |||
| 5 | 82.0 | 89.0 | 102.8 | 117.9 | 126.7 | 0.00120 | |||
| 7 | 94.0 | 102.7 | 120.1 | 139.8 | 151.3 | 0.00184 | |||
| 8 | 99.3 | 111.3 | 131.1 | 153.3 | 165.8 | 0.00217 | |||
| 10 | 120.2 | 132.5 | 157.7 | 185.5 | 202.4 | 0.00279 | |||
| 22 | 277.2 | 306.7 | 375.5 | 466.6 | 521.1 | 0.00463 | |||
| 44 | 463.2 | 526.2 | 673.6 | 880.5 | 1028.3 | 0.00521 | |||
| 66 | 521.7 | 591.6 | 761.9 | 1031.9 | 1243.3 | 0.00531 | |||
The authors declare no conflict of interest.
References
- Anderson EC. An efficient Monte Carlo method for estimating Ne from temporally spaced samples using a coalescent-based likelihood. Genetics. 2005;170:955–967. doi: 10.1534/genetics.104.038349. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Antao T, Perez-Figueroa A, Luikart G. Early detection of population declines: high power of genetic monitoring using effective population size estimators. Evol Appl. 2011;4:144–154. doi: 10.1111/j.1752-4571.2010.00150.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Balloux F. Heterozygote excess in small populations and the heterozygote-excess effective population size. Evolution. 2004;58:1891–1900. doi: 10.1111/j.0014-3820.2004.tb00477.x. [DOI] [PubMed] [Google Scholar]
- Barton NH, Wilson I. Genealogies and geography. Philos Trans R Soc Lond B Biol Sci. 1995;349:49–59. doi: 10.1098/rstb.1995.0090. [DOI] [PubMed] [Google Scholar]
- Bazinet AL, Myers DS, Fuetsch J, Cummings MP. Grid services base library: a high-level, procedural application program interface for writing Globus-based grid services. Future Gener Comp Syst. 2007;23:517–522. [Google Scholar]
- Boessenkool S, Star B, Seddon PJ, Waters JM. Temporal genetic samples indicate small effective population size of the endangered yellow-eyed penguin. Conserv Genet. 2010;11:539–546. [Google Scholar]
- Bradbury IR, Bentzen P. Non-linear genetic isolation by distance: implications for dispersal estimation in anadromous and marine fish populations. Mar Ecol Prog Ser. 2007;340:245–257. [Google Scholar]
- Charlesworth B. Effective population size and patterns of molecular evolution and variation. Nat Rev Genet. 2009;10:195–205. doi: 10.1038/nrg2526. [DOI] [PubMed] [Google Scholar]
- Crow JF, Denniston C. Inbreeding and variance effective population numbers. Evolution. 1988;42:482–495. doi: 10.1111/j.1558-5646.1988.tb04154.x. [DOI] [PubMed] [Google Scholar]
- England PR, Luikart G, Waples RS. Early detection of population fragmentation using linkage disequilibrium estimation of effective population size. Conserv Genet. 2010;11:2425–2430. [Google Scholar]
- Felsenstein J. Pain in the torus - some difficulties with models of isolation by distance. Am Nat. 1975;109:359–368. [Google Scholar]
- Franckowiak RP, Sloss BL, Bozek MA, Newman SP. Temporal effective size estimates of a managed walleye Sander vitreus population and implications for genetic-based management. J Fish Biol. 2009;74:1086–1103. doi: 10.1111/j.1095-8649.2008.02170.x. [DOI] [PubMed] [Google Scholar]
- Frantz AC, Cellina S, Krier A, Schley L, Burke T. Using spatial Bayesian methods to determine the genetic structure of a continuously distributed population: clusters or isolation by distance. J Appl Ecol. 2009;46:493–505. [Google Scholar]
- Guillot G, Leblois R, Coulon A, Frantz AC. Statistical methods in spatial genetics. Mol Ecol. 2009;18:4734–4756. doi: 10.1111/j.1365-294X.2009.04410.x. [DOI] [PubMed] [Google Scholar]
- Hardy OJ, Vekemans X. Isolation by distance in a continuous population: reconciliation between spatial autocorrelation analysis and population genetics models. Heredity. 1999;83:145–154. doi: 10.1046/j.1365-2540.1999.00558.x. [DOI] [PubMed] [Google Scholar]
- Hardy OJ, Vekemans X. SPAGeDi: a versatile computer program to analyse spatial genetic structure at the individual or population levels. Mol Ecol Notes. 2002;2:618–620. [Google Scholar]
- Hauser L, Carvalho GR. Paradigm shifts in marine fisheries genetics: ugly hypotheses slain by beautiful facts. Fish Fisheries. 2008;9:333–362. [Google Scholar]
- Hedgecock D.1994Does variance in reproductive success limit effective population size of marine organismsIn: Beaumont AR (ed).Genetics and Evolution of Aquatic Organisms Chapman and Hall: London; 122–135. [Google Scholar]
- Hedrick PW. A standardized genetic differentiation measure. Evolution. 2005;59:1633–1638. [PubMed] [Google Scholar]
- Hill WG. Estimation of effective population size from data on linked genes. Adv Appl Probability. 1981;13:4–4. [Google Scholar]
- Kawata M. Effective population size in a continuously distributed population. Evolution. 1995;49:1046–1054. doi: 10.1111/j.1558-5646.1995.tb04432.x. [DOI] [PubMed] [Google Scholar]
- Landguth EL, Cushman SA, Schwartz MK, McKelvey KS, Murphy M, Luikart G. Quantifying the lag time to detect barriers in landscape genetics. Mol Ecol. 2010;19:4179–4191. doi: 10.1111/j.1365-294X.2010.04808.x. [DOI] [PubMed] [Google Scholar]
- Leblois R, Estoup A, Streiff R. Genetics of recent habitat contraction and reduction in population size: does isolation by distance matter. Mol Ecol. 2006;15:3601–3615. doi: 10.1111/j.1365-294X.2006.03046.x. [DOI] [PubMed] [Google Scholar]
- Leblois R, Rousset F, Estoup A. Influence of spatial and temporal heterogeneities on the estimation of demographic parameters in a continuous population using individual microsatellite data. Genetics. 2004;166:1081–1092. doi: 10.1534/genetics.166.2.1081. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Luikart G, Ryman N, Tallmon DA, Schwartz MK, Allendorf FW. Estimation of census and effective population sizes: the increasing usefulness of DNA-based approaches. Conserv Genet. 2010;11:355–373. [Google Scholar]
- Malécot G. Heterozygosity and relationship in regularly subdivided populations. Theor Popul Biol. 1975;8:212–241. doi: 10.1016/0040-5809(75)90033-7. [DOI] [PubMed] [Google Scholar]
- Maruyama T. Rate of decrease of genetic variability in a 2-dimensional continuous population of finite size. Genetics. 1972;70:639–651. doi: 10.1093/genetics/70.4.639. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Meirmans PG, Hedrick PW. Assessing population structure: FST and related measures. Mol Ecol Resour. 2011;11:5–18. doi: 10.1111/j.1755-0998.2010.02927.x. [DOI] [PubMed] [Google Scholar]
- Meirmans PG, Van Tienderen PH. GENOTYPE and GENODIVE: two programs for the analysis of genetic diversity of asexual organisms. Mol Ecol Notes. 2004;4:792–794. [Google Scholar]
- Meirmans PG. The problem with isolation by distance. Mol Ecol. 2012;21:2839–2846. doi: 10.1111/j.1365-294X.2012.05578.x. [DOI] [PubMed] [Google Scholar]
- Nei M, Li WH. Linkage disequilibrium in subdivided populations. Genetics. 1973;75:213–219. doi: 10.1093/genetics/75.1.213. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Nei M, Tajima F. Genetic drift and estimation of effective population size. Genetics. 1981;98:625–640. doi: 10.1093/genetics/98.3.625. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Nikolic N, Butler JRA, Bagliniere JL, Laughton R, McMyn IAG, Chevalet C. An examination of genetic diversity and effective population size in Atlantic salmon populations. Genet Res. 2009;91:395–412. doi: 10.1017/S0016672309990346. [DOI] [PubMed] [Google Scholar]
- Novembre J, Stephens M. Interpreting principal component analyses of spatial population genetic variation. Nat Genet. 2008;40:646–649. doi: 10.1038/ng.139. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Okello JBA, Wittemyer G, Rasmussen HB, Arctander P, Nyakaana S, Douglas-Hamilton I, et al. Effective population size dynamics reveal impacts of historic climatic events and recent anthropogenic pressure in African elephants. Mol Ecol. 2008;17:3788–3799. doi: 10.1111/j.1365-294X.2008.03871.x. [DOI] [PubMed] [Google Scholar]
- Palstra FP, Fraser DJ. Effective/census population size ratio estimation: a compendium and appraisal. Ecol Evol. 2012;2:2357–2365. doi: 10.1002/ece3.329. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Palstra FP, O'Connell MF, Ruzzante DE. Age structure, changing demography and effective population size in Atlantic salmon (Salmo salar) Genetics. 2009;182:1233–1249. doi: 10.1534/genetics.109.101972. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Pudovkin AI, Zaykin DV, Hedgecock D. On the potential for estimating the effective number of breeders from heterozygote-excess in progeny. Genetics. 1996;144:383–387. doi: 10.1093/genetics/144.1.383. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Purcell JFH, Cowen RK, Hughes CR, Williams DA. Weak genetic structure indicates strong dispersal limits: a tale of two coral reef fish. Proc R Soc Lond B Biol Sci. 2006;273:1483–1490. doi: 10.1098/rspb.2006.3470. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Purcell JFH, Cowen RK, Hughes CR, Williams DA. Population structure in a common Caribbean coral-reef fish: implications for larval dispersal and early life-history traits. J Fish Biol. 2009;74:403–417. doi: 10.1111/j.1095-8649.2008.02078.x. [DOI] [PubMed] [Google Scholar]
- Robertson A. The interpretation of genotypic ratios in domestic animal populations. Anim Prod. 1965;7:319–324. [Google Scholar]
- Rohlf FJ, Schnell GD. An investigation of the isolation-by-distance model. Am Nat. 1971;105:295–324. [Google Scholar]
- Rousset F, Leblois R. Likelihood-based inferences under isolation by distance: two-dimensional habitats and confidence intervals. Mol Biol Evol. 2012;29:957–973. doi: 10.1093/molbev/msr262. [DOI] [PubMed] [Google Scholar]
- Rousset F. Genetic differentiation and estimation of gene flow from F-statistics under isolation by distance. Genetics. 1997;145:1219–1228. doi: 10.1093/genetics/145.4.1219. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rousset F. Genetic differentiation between individuals. J Evol Biol. 2000;13:58–62. [Google Scholar]
- Rousset F. GENEPOP'007: a complete re-implementation of the GENEPOP software for Windows and Linux. Mol Ecol Resour. 2008;8:103–106. doi: 10.1111/j.1471-8286.2007.01931.x. [DOI] [PubMed] [Google Scholar]
- Schwartz MK, McKelvey KS. Why sampling scheme matters: the effect of sampling scheme on landscape genetic results. Conserv Genet. 2009;10:441–452. [Google Scholar]
- Schwartz MK, Mills LS, Ortega Y, Ruggiero LF, Allendorf FW. Landscape location affects genetic variation of Canada lynx (Lynx canadensis) Mol Ecol. 2003;12:1807–1816. doi: 10.1046/j.1365-294x.2003.01878.x. [DOI] [PubMed] [Google Scholar]
- Schwartz MK, Tallmon DA, Luikart G. Review of DNA-based census and effective population size estimators. Anim Conserv. 1998;1:293–299. [Google Scholar]
- Sinnock P. Wahlund effect for the two-locus model. Am Nat. 1975;109:565–570. [Google Scholar]
- Tallmon DA, Draheim HM, Mills LS, Allendorf FW. Insights into recently fragmented vole populations from combined genetic and demographic data. Mol Ecol. 2002;11:699–709. doi: 10.1046/j.1365-294x.2002.01480.x. [DOI] [PubMed] [Google Scholar]
- Tallmon DA, Gregovich D, Waples RS, Baker CS, Jackson J, Taylor BL, et al. When are genetic methods useful for estimating contemporary abundance and detecting population trends. Mol Ecol Resour. 2010;10:684–692. doi: 10.1111/j.1755-0998.2010.02831.x. [DOI] [PubMed] [Google Scholar]
- Tallmon DA, Koyuk A, Luikart G, Beaumont MA. ONeSAMP: a program to estimate effective population size using approximate Bayesian computation. Mol Ecol Resour. 2008;8:299–301. doi: 10.1111/j.1471-8286.2007.01997.x. [DOI] [PubMed] [Google Scholar]
- Wang JL. Estimation of effective population sizes from data on genetic markers. Phil Trans R Soc. 2005;360:1395–1409. doi: 10.1098/rstb.2005.1682. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wang JL. A new method for estimating effective population sizes from a single sample of multilocus genotypes. Mol Ecol. 2009;18:2148–2164. doi: 10.1111/j.1365-294X.2009.04175.x. [DOI] [PubMed] [Google Scholar]
- Waples RS, Do C. LDNE: a program for estimating effective population size from data on linkage disequilibrium. Mol Ecol Resour. 2008;8:753–756. doi: 10.1111/j.1755-0998.2007.02061.x. [DOI] [PubMed] [Google Scholar]
- Waples RS, Do C. Linkage disequilibrium estimates of contemporary Ne using highly variable genetic markers: a largely untapped resource for applied conservation and evolution. Evol Appl. 2010;3:244–262. doi: 10.1111/j.1752-4571.2009.00104.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Waples RS, England PR. Estimating contemporary effective population size on the basis of linkage disequilibrium in the face of migration. Genetics. 2011;189:633–644. doi: 10.1534/genetics.111.132233. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Waples RS, Yokota M. Temporal estimates of effective population size in species with overlapping generations. Genetics. 2007;175:219–233. doi: 10.1534/genetics.106.065300. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Waples RS. Genetic estimates of contemporary effective population size: to what time periods do the estimates apply. Mol Ecol. 2005;14:3335–3352. doi: 10.1111/j.1365-294X.2005.02673.x. [DOI] [PubMed] [Google Scholar]
- Watts PC, Rousset F, Saccheri IJ, Leblois R, Kemp SJ, Thompson DJ. Compatible genetic and ecological estimates of dispersal rates in insect (Coenagrion mercuriale: Odonata: Zygoptera) populations: analysis of 'neighbourhood size' using a more precise estimator. Mol Ecol. 2007;16:737–751. doi: 10.1111/j.1365-294X.2006.03184.x. [DOI] [PubMed] [Google Scholar]
- Weir BS. Genetic Data Analysis II. Sinauer: Sunderland, Massachusetts, USA; 1996. [Google Scholar]
- Wilkins JF. A separation-of-timescales approach to the coalescent in a continuous population. Genetics. 2004;168:2227–2244. doi: 10.1534/genetics.103.022830. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wright S. Evolution in Mendelian populations. Genetics. 1931;16:97–159. doi: 10.1093/genetics/16.2.97. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wright S. Isolation by distance. Genetics. 1943;23:114–138. doi: 10.1093/genetics/28.2.114. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wright S. Isolation by distance under diverse systems of mating. Genetics. 1946;31:39–59. doi: 10.1093/genetics/31.1.39. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zhdanova OL, Pudovkin AL. The program NB_HETEXCESS to estimate small Nb from genotype frequencies in the progeny. J Hered. 2008;99:694–695. doi: 10.1093/jhered/esn061. [DOI] [PubMed] [Google Scholar]