Agent-based Bayesian approach to monitoring the progress of invasive species eradication programs

Abstract

Eradication of an invasive species can provide significant environmental, economic, and social benefits, but eradication programs often fail. Constant and careful monitoring improves the chance of success, but an invasion may seem to be in decline even when it is expanding in abundance or spatial extent. Determining whether an invasion is in decline is a challenging inference problem for two reasons. First, it is typically infeasible to regularly survey the entire infested region owing to high cost. Second, surveillance methods are imperfect and fail to detect some individuals. These two factors also make it difficult to determine why an eradication program is failing. Agent-based methods enable inferences to be made about the locations of undiscovered individuals over time to identify trends in invader abundance and spatial extent. We develop an agent-based Bayesian method and apply it to Australia’s largest eradication program: the campaign to eradicate the red imported fire ant (Solenopsis invicta) from Brisbane. The invasion was deemed to be almost eradicated in 2004 but our analyses indicate that its geographic range continued to expand despite a sharp decline in number of nests. We also show that eradication would probably have been achieved with a relatively small increase in the area searched and treated. Our results demonstrate the importance of inferring temporal and spatial trends in ongoing invasions. The method can handle incomplete observations and takes into account the effects of human intervention. It has the potential to transform eradication practices.

Invasive species can cause economic, social, and environmental losses (1), and eradication is therefore desirable. The duration of successful eradication programs varies depending on biological and management factors (2). If the invasion is detected early while it is confined to a small area, eradication can potentially be achieved almost immediately by treating the entire area. Black-striped mussels (Mytilopsis sallei) were eradicated soon after being discovered in a northern Australian marina by applying a highly toxic chemical to the entire marina (3). Such “brute-force” treatment methods may not be available when invasions have spread over a larger area owing to unacceptable impacts on nontarget species or human health or because of financial constraints. When large areas are potentially infested and surveillance is required to determine where to apply treatment, eradication can take many years. Some areas that might be infested are not regularly surveyed owing to the high cost of monitoring (observations are “incomplete”), and some individuals in surveyed locations are missed because surveillance methods are imperfect (4). These two factors create uncertainty about whether eradication efforts will succeed. An invasion may seem to be in decline but in fact be expanding in spatial extent and/or abundance, or declining more slowly than estimated, with a high risk of “escaping” to unmanaged areas. Invasions that expand in spatial extent or abundance over an extended period are not under control and may eventually become ineradicable without a change in management. Here, we focus on the problem of determining spatial and temporal trends in biological invasions with incomplete and imperfect observations obtained during an eradication program.

Three critical decisions arise during the course of eradication programs: whether to attempt eradication (5, 6), whether to declare eradication successfully completed (7–9), and whether to persist with the current eradication strategy. Decisions on whether to attempt eradication and when to declare success are made at the beginning and end of eradication programs and have received substantial attention in the invasion management literature. Much less attention has been given to the problem of determining whether to continue current eradication efforts given spatial and temporal trends in invader abundance (see refs. 2 and 10 for reviews of recent studies).

Many biological invasions occupy a large area at low density, with most individuals being in clusters that form as the result of local dispersal. Long-distance “jumps” by a small number of reproductive individuals create new clusters far from the founding cluster, and such jumps often are human-assisted (11). In such circumstances, there may be many unsurveyed sites that contain individuals despite the fact that surrounding areas have none, meaning that a large total area needs to be surveyed at high cost.

Hooten and Wikle (12) developed an invasion model motivated by a reaction–diffusion partial differential equation. Their main outputs are estimates of diffusion coefficients and parameters describing spatial variation in these coefficients. Although this model is certainly useful for modeling and simulation, the parameters estimated are abstract, and significant additional work is required to translate them into answers to such pressing questions as the number and location of undetected agents. A second problem is that the model does not take into account the effect of human intervention on the spread of the invasion. This is a major deficiency when an intensive eradication or management strategy is in place, because any effective strategy will affect the observed range and density of the invasion. Third, diffusion models implicitly consider the invasion to be composed of cumulative local movements and therefore do not allow for long-distance founding events. Such events can profoundly alter invasion dynamics and patterns of distribution (11, 13). The model of Schmidt et al. (14), codeveloped by one of the authors, most closely resembles the model we present here. In particular, it attempts to incorporate the effects of habitat suitability and human population density on the spread of the invasion and allows for long-distance founding events. However, the method still ignores the effect that the eradication effort has on the invasion. In addition, the inclusion of long-distance jumps results in a time complexity quadratic in the number of grid squares, greatly limiting the potential spatial resolution of the model. None of the existing methods has been used to determine whether an invasion subject to eradication efforts is in decline and, if not, the likely causes of failure.

The latter two methods are both intrinsically grid-based. In this paper, we present an entirely different approach that, unlike these earlier methods, is agent-based. Agent-based models explicitly incorporate autonomous agents and their actions and interactions to simulate systems or infer system-level parameters (15). Individual agents (in this case, nests) are explicitly considered in the model, including their exact position, times of founding and destruction, and phylogeny (tree of descent). The interactions between nests are restricted to founding events, making this a particularly simple agent-based model. The phylogeny of detected individuals is naturally considered only in terms of individual nests and could not be included in a grid-based model. Another advantage of an agent-based approach is that it allows maximum resolution on spatial and temporal scales, because there is no grid to limit resolution. The absence of a grid also facilitates efficiency without sacrificing generality. Although agent-based methods can be computationally expensive, if the interactions between agents are limited in number they require computational time linear in the number of agents. Grid-based methods that consider discrete spatial cells that might contain individuals, rather than considering individuals explicitly, require interactions to be limited in spatial extent, rather than in number, to achieve linear time complexity.

We apply the method to Australia’s largest eradication program, the campaign to eradicate the red imported fire ant (Solenopsis invicta) (RIFA) from Brisbane. The invasion was deemed to be almost eradicated in 2004 but subsequent discoveries of new infestations at ever-increasing distances from the invasion epicenter in the Port of Brisbane have called into question the feasibility of eradication. These new infestations also call into question whether the invasion was under control at any stage and, if not, whether corrective measures are available that can reverse the ongoing spread of the invasion. These are the questions we address here.

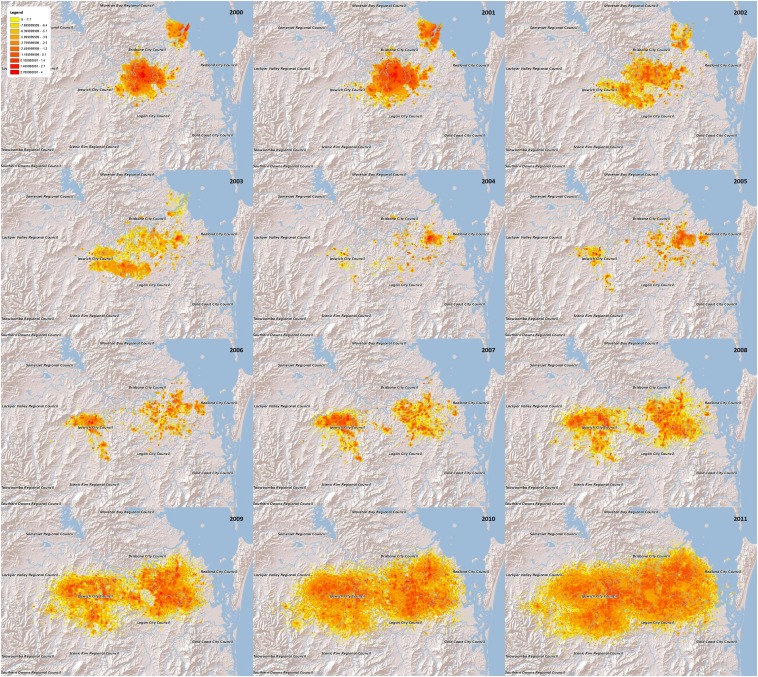
The fire ant eradication program in southeast Queensland is one of the larger eradication efforts to have been attempted in terms of its spatial extent and the amount of data collected, reflecting that over $250 million has been spent on the project to date. Fire ants are one of the world’s 100 worst invaders (16) and have the potential for extensive invasion worldwide (17). Our model was applied to a study region ∼190 km by 200 km (see Fig. 5) and data collected over 11 y (2001–2011). The data are in the form of point locations where detection of fire ant nests occurred and where surveillance activity took place by Biosecurity Queensland Control Centre (BQCC).

Fig. 5.

Heat maps for the posterior expected number of nests in grid cells 500 m by 500 m in December of each year 2000–2011. Brighter cells (yellows) have lower expected numbers of nests and darker cells (reds) have higher expected numbers. Color classes are on a logarithmic scale.

Results

Software implementing the method was validated using the method of Cook et al. (18), using 100 small to medium-sized simulated datasets, as discussed in Supporting Information (Fig. S1). We found no evidence of errors in the software. We also simulated a single large dataset, comparable in size to the real dataset analyzed below. Starting with a single nest in an urban area of Brisbane, we simulated unhindered expansion for 61 mo, with nests founded at an average rate of 0.25 per nest per month, and the distribution of founding distances shown in Fig. S2A. Relative establishment probabilities were set to 1.0, 0.9, 0.6, and 0.3 for the four habitat classes. We then simulated an eradication program lasting 95 mo, with a simple search and treatment strategy, similar to the strategy used by BQCC. The probability of passive detection in any given month was 0.02 for urban areas and 0.01 for rural areas. Whenever a passive detection occurred, a grid cell of side length 100 m containing the detected nest was searched, as were the eight grid cells forming a square around it. The 16 grid cells forming a larger square around those were treated. Where a grid cell was selected for both search and treatment, it was searched but not treated. Targeted search efficacy and treatment efficacy were both set to 0.8 (as suggested by BQCC). For each nest, an initial maturation period of 8 mo was imposed during which the nest cannot found other nests, and also a simultaneous initial period of 6 mo during which the nest cannot be detected by public or targeted search, although it can still be killed by treatment. These periods were based on expert opinion at BQCC supported by experimental studies (19) and were also assumed in our analysis of real data below.

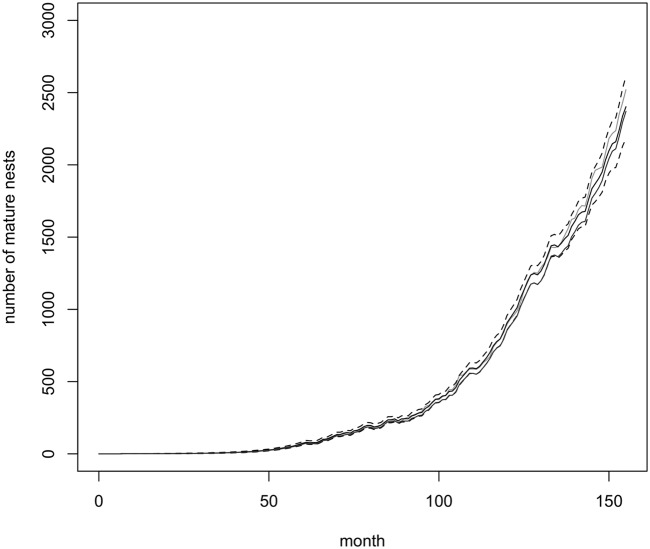
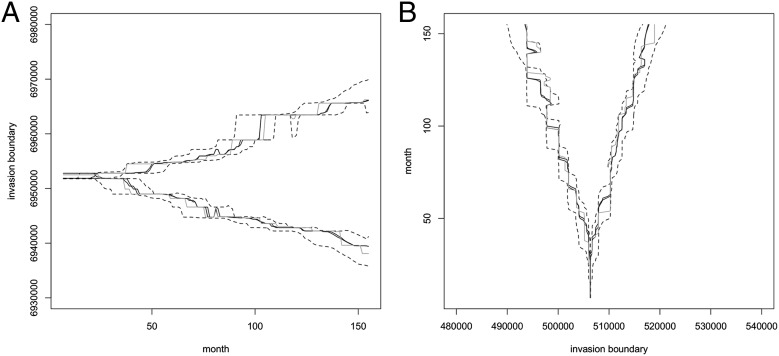
The method was then applied with additional constraints that search and treatment efficacies be greater than or equal to 0.8 (prior probabilities for these parameters were thus uniform between 0.8 and 1.0), and the reproductive rate was fixed at 0.25 founded nests per nest per month on average (the true value). Fig. 1 shows the actual trajectory of the simulated invasion in terms of number of mature nests and the inferred trajectory with 95% credible intervals. Also shown is the trajectory inferred without the additional constraints on search and treatment efficacies and reproductive rate. Similar results were obtained for immature nests (Fig. S2B). Fig. 2 shows the actual north, south, east, and west boundaries of the simulated invasion and the posterior median boundaries estimated with and without the additional constraints. Credible intervals for the inference with the additional constraints are also shown. Estimates of the establishment probabilities and passive detection probabilities are shown in Fig. S2 C and D, respectively.

Fig. 1.

The number of mature nests existing in each month of a simulated invasion consisting of 61 mo of unhindered expansion followed by 95 mo of a simple management strategy (light gray, highest solid line), the posterior median number of mature nests estimated using additional constraints that α₀ and α₁ are both greater than or equal to 0.8 and λ ≈ 0.25 (black, center solid line) with 95% credible intervals (black, dashed lines), and the posterior median number of mature nests estimated without the additional constraints (dark gray, lowest solid line).

Fig. 2.

(A) The northernmost and southernmost y coordinates of all mature nests in the simulated invasion, in each month (gray, solid lines), the posterior median northernmost and southernmost y coordinates of mature nests estimated using the additional constraints (black, solid lines) with 95% credible intervals (black, dashed lines), and the posterior median northernmost and southernmost y coordinates of mature nests estimated without the additional constraints (also black, solid lines). The trajectories inferred with and without the additional constraints are so similar that no attempt has been made to distinguish them. (B) The corresponding trajectories of the westernmost and easternmost x coordinates.

The method was then applied to the real data from the Brisbane fire ant eradication program, using prior information supplied by BQCC that the search and treatment efficacies were each greater than or equal to 0.8 and the reproductive rate was between two and four nests founded per nest per year. This prior information is essentially expert opinion, although influenced by experiments reported in the literature (19, 20). Separate inferences were performed with the reproductive rate set to 0.15, 0.2, 0.25, and 0.3 nests founded per nest per month, to test the sensitivity of the inference to this parameter.

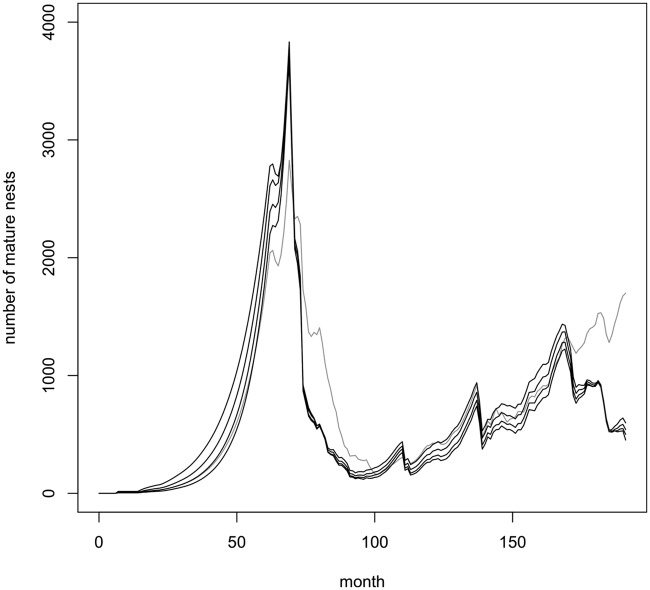
Fig. 3 shows the estimated invasion trajectory from January 1996 (month 0) to December 2011 (month 191) in terms of number of mature nests. The population declined sharply after the eradication program began in February 2000, and eradication was almost achieved by the end of 2003. However, the population recovered, reaching a second peak in the early months of 2010. Since then, the population again seems to be in decline. A similar pattern is observed for immature nests in Fig. S3C. Note that most of these trends are robust to variations in the prior information supplied, the important exception being the decline in numbers since 2010. This decline was observed for a range of values of the reproductive rate λ. However, in the absence of constraints on the search and treatment efficacies or reproductive rate, this decline was not observed, highlighting the need for sound prior information. Note also that at any specific time the number of immature nests is greater than the number of mature nests, indicating that most nests are killed by treatment before maturation. If the eradication program were to cease, these nests would reach maturity, and numerical expansion would dramatically accelerate. It is also clear that search and treatment should continue for at least 8 mo beyond apparent eradication of mature nests.

Fig. 3.

The posterior median number of mature nests existing in each month from January 1996 to December 2011, estimated using additional constraints that α₀ and α₁ are both greater than or equal to 0.8 and λ ≈ 0.15, 0.2, 0.25, and 0.3 (four black lines, top to bottom), and corresponding estimates without the additional constraints (gray line).

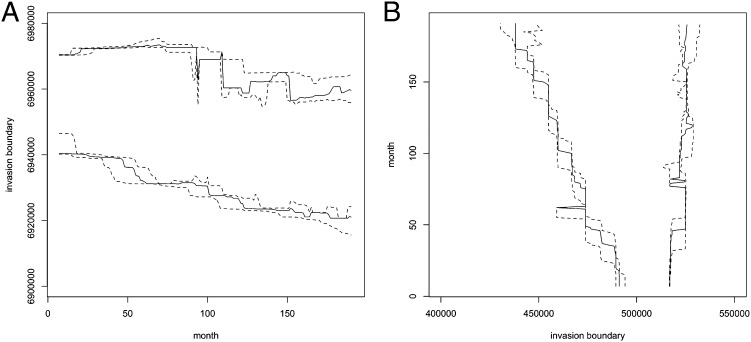
Equally important is the evolution of the spatial extent of the invasion. Fig. 4 shows trajectories of estimated posterior medians of the north, south, east, and west boundaries of mature nests. These estimates are almost unaffected by the inclusion of additional prior information. The boundaries of immature nests follow similar trajectories, 8 mo earlier (Fig. S3 A and B). Only the north boundary has been significantly pushed back, perhaps partly facilitated by the Brisbane River, which inhibits northward expansion. The east boundary has remained relatively static, again perhaps partly because the coastline bounds eastward expansion. However, the invasion front has advanced west and south in a steady, roughly linear manner, apparently unaffected by the sharp drop in nest numbers from 2001, or the recovery from 2004.

Fig. 4.

(A) The posterior median northernmost and southernmost y coordinates of all mature nests in each month from January 1996 to December 2011 estimated using additional constraints that α₀ and α₁ are both greater than or equal to 0.8 and λ ≈ 0.25 (solid lines) with 95% credible intervals (dashed lines). The trajectories inferred with other values of λ or without the additional constraints are so similar that they have not been plotted. (B) The corresponding trajectories of the westernmost and easternmost x coordinates.

Another way of visualizing the geographic expansion is via the annual sequence of heat maps shown in Fig. 5. Each map indicates the expected (i.e., posterior mean) number of mature RIFA nests in grid squares 500 m square. (Note that a grid is used here only for data presentation; it is not part of the model.) The darkest colors (reds) represent the highest expected numbers and the lightest colors (yellows) represent the lowest. Color bins are on a logarithmic scale, and the heat maps are overlaid on maps of the infested area. The maps indicate two distinct invasions in December 2000, with the smaller invasion near the mouth of the Brisbane River being virtually eradicated by 2004. The heat maps also illustrate that the decline and recovery of nest numbers affected the density, but not primarily the geographic range, of the invasion. However, interpreting these heat maps requires caution. Uncertainty about the location of nests increases in later years, because there are fewer data from later time points to inform the inference. Thus, the apparent rapid expansion in the later maps in part reflects increasing uncertainty rather than actual physical expansion. For this reason, the median boundary trajectories shown in Fig. 4 may be more useful than the heat maps for delineating the current extent of the invasion.

We also estimated the distribution of founding distances (Fig. S3D), the relative establishment probabilities (Fig. S3E), and the probabilities of detection by passive surveillance in urban and rural areas (Fig. S3F).

Our focus in this paper is on reconstructing the historical trajectory of an invasion to determine whether the current strategy is likely to succeed. However, we anticipate that the model will also be used to infer the likely locations of living nests, to inform eradication efforts. To assess the adequacy of the model for this purpose, we attempted to infer the number of nests and the location of the north, south, east, and west boundaries at the end of 2008, using only the data that were available at that time. Again, we used prior information that the search and treatment efficacies were greater than or equal to 0.8 and that the reproductive rate was 0.25 nests founded per nest per month (we did not investigate alternative values, because the analysis above convinced us that similar results would be obtained). The inferred numerical and geographic trajectories are shown in Fig. S4, with 95% credible intervals, and compared with the corresponding inferences using all data. It is clear that had this method been available in 2008 accurate and useful assessments of these quantities could have been made (although nest numbers would have been slightly overestimated). However, the 2008 heat map obtained using only the data available in 2008 differs substantially from that obtained using all of the data (Fig. S5). This reinforces the point that data from later time points reduce uncertainty about where nests were in 2008. In general, we recommend that heat maps are useful for identifying regions where nests are currently at high density, but not for delineating invasion boundaries.

The 2001–2008 dataset was also used to check two potential problems with the method. First, to investigate whether the sampler becomes trapped in a local mode, we ran it five times with different random starts. No evidence of an alternative mode was found, and results obtained were barely distinguishable. Second, we investigated the effect of raising the lower bound of the search and treatment efficacies to 0.85. Only small differences in the inferences were observed. Numerical and geographic trajectories for these tests are shown in Fig. S6.

Discussion

Our investigations with simulated data demonstrate the adequacy of the method for estimating the past trajectory and current extent of an invasion, in terms of numerical abundance and geographic range. A major finding of our analyses was that the estimated spatial extent of the invasion never declined. Fig. 4 suggests that if the strategies used thus far are not changed, the invasion will continue to expand, eventually becoming too large for affordable management. In fact, it may be that no strategy can stop the advance of the invasion front until eradication is almost achieved, which implies there is a limited time threshold beyond which eradication becomes infeasible. This is perhaps unsurprising, because the boundaries correspond to single nests, and unless these specific nests are killed, the boundary will not recede. Thus, even a highly effective management program faces an increasingly difficult task as time passes. A critical management decision that must be faced is whether to continue eradication efforts with improved strategies or to abandon the program and adopt more modest objectives. This depends heavily on the estimated increase in annual search and treatment area required to remove all individuals. A comparison of Fig. 5 with a map of the searched and treated areas in each year (Fig. S7) indicates that a relatively small area of additional surveillance and treatment was needed up until about 2005. The infested area has approximately doubled between 2004 and 2010, according to Fig. 4B.

The steady increase in the estimated area of required control efforts over time implies that a larger area needs to be searched or treated each year. This can be achieved by increasing program resources and/or by changing program methods, including the use of lower-cost methods that can be applied over larger areas. The eradication program is currently evaluating remote sensing as a new surveillance method, which has a much lower cost per hectare than currently used ground surveillance methods when applied over a large area. In addition to providing information required for determining how large an area to search, our methods can potentially be used to determine the effective placement of surveillance resources by identifying regions of high nest density and invasion boundaries. Periodically updating these estimates with information provided by remote sensing and passive surveillance and using the updated information to guide future surveillance will increase the effectiveness of management and may enable eradication.

Our model predicts a large number of immature nests, many of which will be too small to be visually detected. This highlights the importance of combining surveillance with treatment methods that do not rely on prior detection. Broadcast pesticide bait is taken by foraging ants back to their nests, and therefore this treatment method does not require prior visual detection of nests.

Two main forms of surveillance are applied to detect fire ants: passive surveillance by private citizens and active surveillance by trained personnel. Passive surveillance provides the first postborder line of defense against biological invasions and it is therefore critical to determine its effectiveness. The importance of passive surveillance is further emphasized by its large spatial coverage, which potentially allows for larger areas to be searched each year than do programs that rely solely on active surveillance. Previous studies have estimated the probability of detection with active surveillance using field experiments (20), but such experiments will typically not be available for estimating passive surveillance. No previous studies have estimated the probability of detection with passive citizen monitoring over large areas. This is a challenging inference problem, the main difficulty being the need to estimate the total number of nests in the region of interest. Our agent-based inference method is in principle well suited to addressing this problem and allowed us to make the first empirical estimates of passive surveillance detection probabilities.

Our study provides a rigorous, quantitative basis for determining whether eradication programs are on track and for diagnosing causes of eradication program failure. Our results demonstrate the importance of methods that consider the incompleteness and imperfection of observations for informing invasive species eradication and control programs.

Materials and Methods

The data collected during the Brisbane RIFA eradication program is exceptionally complete and detailed. For each nest i detected from 2001 to 2011, the precise map location (x_i, y_i), time of discovery t_i, and type of discovery d_i were recorded. The total number of nests detected was n = 7,068. Discovery times were encoded as integers in the range 61–191 representing months February 2001 to December 2011 and discovery types were encoded as 1 for targeted search and 0 for passive detection. Four maps were also available, precisely indicating (i) areas that were searched, (ii) areas that were treated, (iii) human land use types (urban and rural, divided into four subcategories), and (iv) habitat suitability for the ant (divided into four categories). The search and treatment maps were encoded as functions I₁(x, y, t) and I₂(x, y, t), taking the value 1 if position (x, y) was respectively searched or treated and 0 otherwise. The land-use and habitat maps were encoded as functions S(x, y) and H(x, y), each returning integer values in the range 1–4. Note that these latter two functions are in reality time-dependent, but here we assumed no change over time.

We constructed a detailed likelihood model in terms of the following unknown parameters: (i) the number U and locations (x_i, y_i) of all undetected nests alive at any time during 1996–2011 (note that the model includes an unhindered expansion phase 1996–2000); (ii) the mean number of nests founded per nest per month λ; (iii) the phylogeny of all nests, rooted in initial nests that existed at the beginning of 1996, and represented as a vector p_i identifying the parent nest for each nest i (p_i =-1 for initial nests); (iv) the time of founding f_i for each nest encoded as integers in the range 0–190 representing months from January 1996–November 2011 (f_i = −1 for initial nests); (v) the founding type J_i for each nest (undefined for initial nests and an integer in the range 1–4 for noninitial nests, representing four different scales of founding event); (vi) the proportion γ_j of founding events that are of founding type j; (vii) the distribution of founding distances in the x and y directions modeled as exponential distributions with parameters σ_Xj and σ_Yj, respectively, for each jump type j; (viii) treatment success rate α₀ and detection probabilities by targeted search α₁ and by passive search within each land use type (α₂–α₅ for land-use types 1–4); and (ix) nest establishment probabilities β₂–β₄ in each habitat suitability class 2–4, relative to the most suitable habitat, for which the relative establishment probability is defined as β₁ = 1.

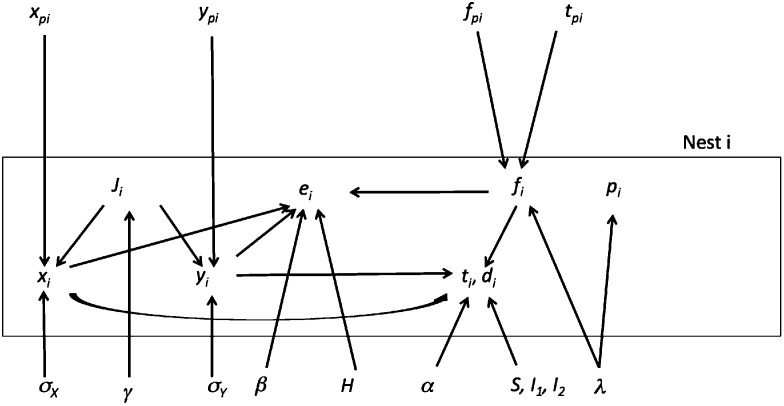
The conditional dependencies among the known and unknown parameters of a noninitial nest are shown in Fig. 6 and for an initial nest in Fig. S8. Parameters at the head of an arrow are conditionally dependent on parameters at the tail. A conditional distribution was defined for each arrow in these figures. Prior probabilities were defined for all unconditioned parameters (those with no incoming arrows). The mathematical forms of the prior and conditional distributions are provided in Supporting Information.

Fig. 6.

Model parameters associated with noninitial nests.

According to Bayes’ rule, the posterior distribution over the space of all unknowns is proportional to the product of the prior and conditional distributions just described. This posterior distribution was sampled using Markov chain Monte Carlo (MCMC). Each individual sample represents a complete and detailed reconstruction of the entire invasion history 1996–2011. We generated 10,000 such sampled histories. These can then be used to estimate posterior marginal distributions for quantities of interest.

The MCMC technique used was the generalized Gibbs sampler (21). This technique involves iteratively sampling conditional distributions over subsets of the target space. It is a broad generalization of the conventional Gibbs sampler: Whereas conventional Gibbs involves sampling from fixed coordinate subspaces, the generalization enables sampling from arbitrary subsets. In particular, it enables transdimensional sampling, that is, sampling from distributions for which the number of parameters is not known, as here. Most of the subsets selected for the sampler were one-dimensional, fixed-coordinate subspaces, resulting in conventional Gibbs parameter updates. Details of these are provided in Supporting Information. Here, we describe two updates that are not conventional Gibbs. The first is a subtree pruning and regrafting update, similar to updates used elsewhere in a phylogenetic context (22).

The sampler scans through a randomly ordered list of the nests, updating the parent nest for each nest i. Undetected nests (d_i = 2) that never founded a nest are not moved, but for all other nests, p_i is updated by detaching nest i with its descendents (pruning) and either selecting a new parent nest p (regrafting) or making the nest an initial nest. At the same time, the time of founding f_i and the type of founding J_i are also updated to values f and j, with all possibilities being considered except those that would violate natural constraints (for example, f must precede the month of founding for each descendant of nest i). An ordered list of the nests founded by p in month f is maintained, and nest i is added at a random position in this list. The conditional posterior probability that nest i is an initial nest is

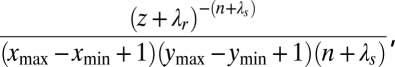where z is the total number of months after maturity summed over all nests excluding nest i, n is the total number of noninitial nests excluding nest i, x_min, x_max, y_min, and y_max are x and y bounds for initial nests, and λ_r and λ_s are, respectively, the rate and shape parameters for the prior distribution of λ. The conditional posterior distribution over the set of noninitial values (p, f, j) is proportional to

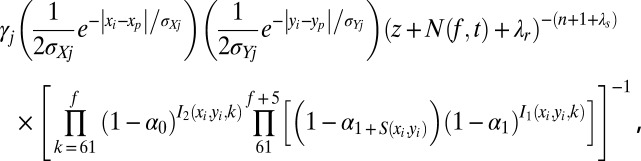where N(f, t) is the number of months during which nest i is mature. These expressions were obtained by conditioning the full posterior distribution over subsets consisting of allowed updates to (p, f, j).

The second update that does not fit within the conventional Gibbs framework involves adding or deleting undetected nests. It is similar to a Metropolis–Hastings move but differs in the systematic way that additions and deletions are considered and also includes a correction factor in the acceptance ratio determined by the generalized Gibbs methodology. The sampler scans through the list of nests, adding and deleting undetected child nests to each nest. It begins by considering deleting an undetected child of the first nest on the list. If there are no such undetected children, no change is made, and the deletion is considered to have failed. The sampler proceeds through the list of nests, deleting one undetected child per nest until a deletion fails, either because that nest had no undetected children or the proposed deletion was rejected. The sampler then attempts to add an undetected child and keeps adding undetected children to that same nest until an insertion fails, at which point it moves to the next nest on the list and begins deleting as before. This process is continued until the end of the list is reached.

Each time a deletion is attempted for nest i, the child k to be deleted is selected uniformly and randomly from the undetected children of that nest. If that child has children of its own, they become children of nest i. The sampler maintains an ordered list of children founded by each nest in each month; after a successful deletion, a random permutation of these lists is performed for the child lists of nest i in each month of the mature lifetime of the deleted nest. If nest i was killed by a treatment before the founding of one of these new children, the deletion automatically fails. Each time an insertion is attempted for nest i, the attempt fails immediately if i was not established or never reached maturity. Otherwise, a new nest is proposed for insertion at a random location in the ordered list of all nests and is given a founding month f selected randomly from the mature lifetime of nest i. The new founding type j is selected with probability γ_j, and the x and y coordinates are drawn from densities (1/2σ_Xj)exp(−|x − x_i|/ σ_Xj) and (1/2σ_Yj)exp(−|y − y_i|/σ_Yj), respectively. The nest is established with probability β_H(x,y) and if established the time of death t is determined by scanning through the months after f considering each treatment occurring at (x, y). Each treatment has probability α₀ of killing the nest, and if the proposed new nest survives all treatments then t = 9,999. Each child of nest i that was founded during the mature period of the proposed new nest then has probability 0.5 of becoming a child of the new nest. After a successful insertion, a random permutation of the lists of children founded in each month in the mature lifetime of the new nest is performed for both nest i and the newly inserted nest.

The probability of accepting a deletion is determined by the ratio

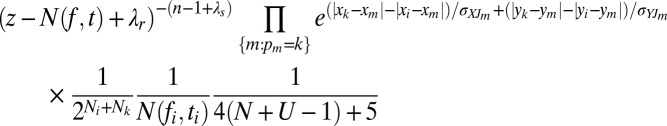to

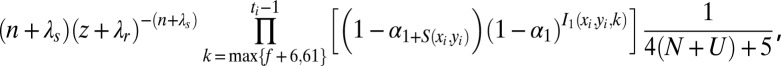where N_i and N_k are the number of nests founded by nests i and k, respectively, during the mature lifespan of nest k. If this ratio is greater than 1, the deletion is accepted, otherwise the deletion is accepted with probability equal to the ratio. For insertions, this ratio is inverted.