Lipid bilayer and cytoskeletal interactions in a red blood cell

Abstract

We study the biomechanical interactions between the lipid bilayer and the cytoskeleton in a red blood cell (RBC) by developing a general framework for mesoscopic simulations. We treated the lipid bilayer and the cytoskeleton as two distinct components and developed a unique whole-cell model of the RBC, using dissipative particle dynamics (DPD). The model is validated by comparing the predicted results with measurements from four different and independent experiments. First, we simulated the micropipette aspiration and quantified the cytoskeletal deformation. Second, we studied the membrane fluctuations of healthy RBCs and RBCs parasitized to different intraerythrocytic stages by the malaria-inducing parasite Plasmodium falciparum. Third, we subjected the RBC to shear flow and investigated the dependence of its tank-treading frequency on shear rate. Finally, we simulated the bilayer–cytoskeletal detachment in channel flow to quantify the strength of such interactions when the corresponding bonds break. Taken together, these experiments and corresponding systematic DPD simulations probe the governing constitutive response of the cytoskeleton, elastic stiffness, viscous friction, and strength of bilayer–cytoskeletal interactions as well as membrane viscosities. Hence, the DPD simulations and comparisons with available independent experiments serve as validation of the unique two-component model and lead to useful insights into the biomechanical interactions between the lipid bilayer and the cytoskeleton of the RBC. Furthermore, they provide a basis for further studies to probe cell mechanistic processes in health and disease in a manner that guides the design and interpretation of experiments and to develop simulations of phenomena that cannot be studied systematically by experiments alone.

The red blood cell (RBC) membrane consists of two components: a lipid bilayer and an attached 2D spectrin network that acts as the cytoskeleton. The resistance of the lipid bilayer to bending is controlled by the bending rigidity, 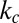, whereas the spectrin network’s resistance to shear strain is characterized by the in-plane shear modulus, 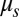. Under normal conditions, the cytoskeleton is tightly attached to the lipid bilayer from the cytoplasmic side. However, under certain pathological conditions, e.g., in sickle cell disease, the cytoskeleton may become dissociated from the lipid bilayer (1). Although the biomechanics of the two-component erythrocyte membrane have been studied extensively for decades (2), the mechanical properties of the interactions between the lipid bilayer and the cytoskeleton (such as elastic stiffness, viscous friction, and strength) via the pinning connections of transmembrane proteins are still largely unknown. This is at least in part ascribed to the fact that it is difficult to measure these interactions directly from experiments, because the length scale of these connections is too small compared with the characteristic length scale of the cell mechanical experiments.

The mechanical properties associated with the bilayer–cytoskeletal interactions strongly influence biorheology, erythrocyte function, and the onset and advancement of RBC diseases (3). For example, it has been hypothesized that the pathogenesis of hereditary spherocytosis is related to the weakened bilayer–cytoskeletal interaction strength, which leads to reduced spectrin density, and the loss of bilayer membrane resulting in reduced surface area (4). In addition, in sickle cell disease, the detachment of the RBC lipid bilayer from the spectrin network owing to hemoglobin polymerization also causes “budding off” of the bilayer, which in turn results in reduced cell deformability (1). Furthermore, when the RBCs pass through the interendothelial slits in the spleen, they undergo severe deformation. Here, the biophysical properties mediated by the bilayer–cytoskeletal interactions may play a significant role in the ensuing mechanical filtering process (5, 6).

Several computational approaches, including continuum formulations and particle-based numerical models, have been developed recently and applied to RBC simulations at different length scales; a review of these approaches can be found in ref. 7. These models may quantitatively mimic the mechanical properties of healthy and pathological RBCs under select experimental conditions and stress states. However, they do not lend themselves to detailed whole-cell investigations of a wide variety of biophysical problems involving the RBCs, such as the aforementioned issues of bilayer–cytoskeletal detachment or bilayer loss in hereditary spherocytosis due to defective protein attachments. In existing whole-cell models, the membrane is usually considered as a single-component shell with effective properties (8–10) that seek to estimate the combined effects of the lipid bilayer and the spectrin network. In situations where two-component molecular models have been invoked, the computational cost is prohibitively high, such that usually only a small portion of the cell membrane is modeled, a consequence of which is that the whole-cell response is not adequately and efficiently captured (11). Furthermore, such models are computationally too inefficient to be amenable to blood microrheology studies involving large numbers of RBCs in flow. For these reasons, there is a compelling need to develop a unique two-component, particle-based, whole-cell model to study the biophysics of RBCs arising from the interactions between the lipid bilayer and the spectrin cytoskeletal network. Such a model would provide a more reliable method and an overall modeling framework to extract mechanical properties of RBCs from a variety of independent experimental methods.

Currently there are no experimental techniques that directly measure the mechanical characteristics of the bilayer–cytoskeletal interactions. The specific characteristics of these interactions influence, in different ways, the mechanical property data inferred from several different experiments, such as micropipette aspiration and vesiculation (12, 13), membrane thermal fluctuations (14–16), tank-treading motion (17), and tethering of the lipid bilayer in channel flow (18). In the present study, we investigate the effects of the bilayer–cytoskeletal interactions in these experiments, using a unique two-component mesoscale RBC model implemented in dissipative particle dynamics (DPD).

Results and Discussion

We use the DPD formulation to develop the two-component model by extending the one-component RBC membrane model (19). This unique two-component model is capable of incorporating elastic and shear energy of the lipid bilayer and the cytoskeleton separately. In addition, we include both the normal and the tangential interactions between the lipid bilayer and the cytoskeleton as well as the membrane viscosities. This two-component mesoscale RBC model can also be implemented in conjunction with other methods such as the lattice Boltzmann method (20) and multiparticle collision dynamics (21). In this unique two-component RBC model, the membrane is modeled with two different components, i.e., the lipid bilayer and the cytoskeleton. Specifically, each component is composed of a 2D triangulated network with 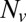vertices, where each vertex is represented by a DPD particle. In most simulations, we use 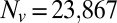so that each DPD particle on the triangulated network of the cytoskeleton represents a junctional complex in the RBC spectrin network (9). In contrast to the one-component DPD model, the lipid bilayer of the two-component model has no shear stiffness, but only bending stiffness and a very large local area stiffness. Similarly, the cytoskeleton has no bending stiffness, but possesses a large shear stiffness. Further details of the model are provided in Methods and in SI Text. Parameters are listed in Table S1.

We probe the bilayer–cytoskeletal interactions by applying the two-component DPD model to simulate four independent experiments on RBCs: (a) fluorescence-marked micropipette aspiration (12), (b) membrane fluctuations (14), (c) tank-treading motion in shear flow (17), and (d) bilayer–cytoskeletal detachment in channel flow (18). Because only one or two mechanical parameters in each simulation of these four experiments are relevant to the result, our approach provides a good protocol in investigating the effects of these parameters in isolation, in a systematic and controlled manner while, at the same time, validating the two-component model.

Fluorescence-Marked Micropipette Aspiration.

Using the two-component DPD model we are able to simulate, with the same set of input mechanical parameters, micropipette experiments that provide estimates of the area modulus (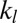 shown in SI Text) of the lipid bilayer (22) as well as the area and shear moduli ( 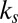and 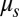shown in SI Text) of the cytoskeleton (12, 23). Such a simulation is not possible with the one-component model, in which the large local area modulus of the bilayer is absent. In micropipette aspiration, the local area modulus 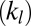of the lipid bilayer is measured as five orders higher (22) than the area or shear modulus ( 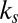or 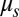) of the cytoskeleton (12, 23). To investigate the effect of slip between the lipid bilayer and the cytoskeleton on deformation, we perform detailed numerical simulations of the fluorescence-marked micropipette aspiration of RBCs (12). To our knowledge, this is a unique experiment in which the slip between the lipid layer and the cytoskeleton as well as the local area deformation of the cytoskeleton was quantitatively obtained. Details of the setup of the micropipette aspiration simulation can be found in SI Text.

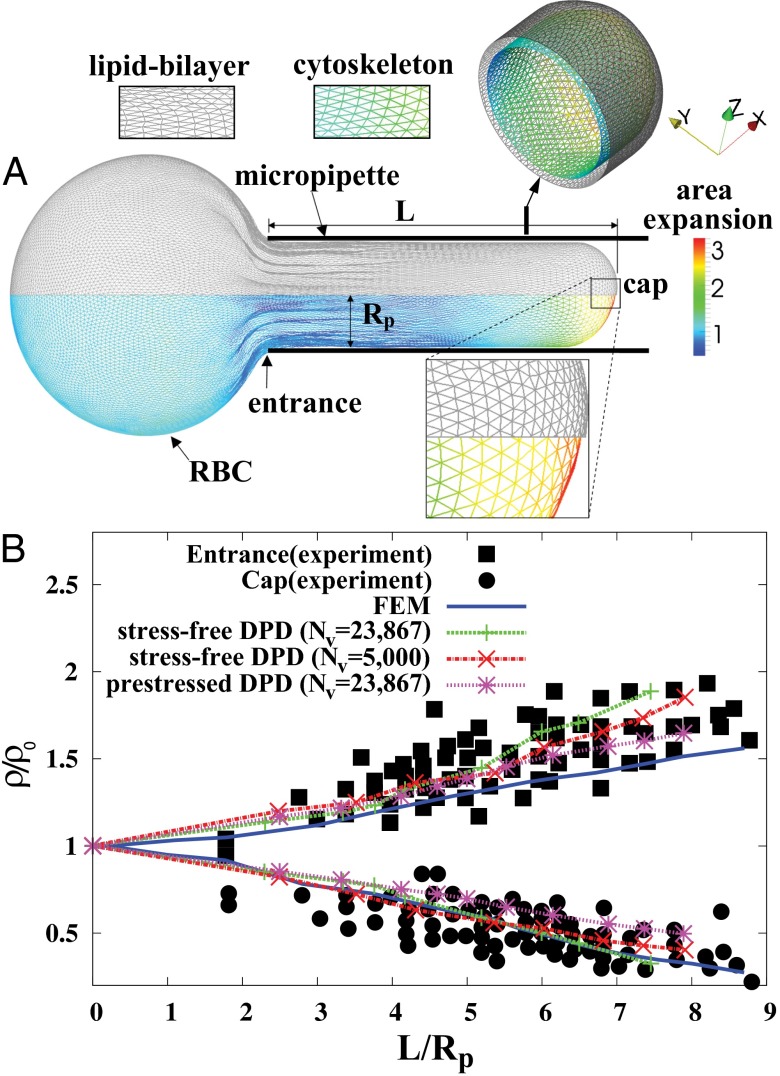
We use the two-component DPD model and compare the results with experimental data (12) and finite-element method (FEM) simulations (24) as shown in Fig. 1. We consider three cases in DPD simulations: N_v = 23,867 and N_v = 5,000 with a stress-free initial configuration and N_v = 23,867 with a prestressed initial configuration in which a negative isotropic stress 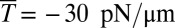is applied in the cytoskeleton. The cytoskeleton density is higher in the DPD simulations than in the FEM simulation with the same prestress 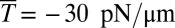in the cytoskeleton (24). The results of all three DPD simulation cases are in the range of experimental data, and the cytoskeleton deformation is smaller in the prestressed DPD case and the coarser DPD case with N_v = 5,000 as shown in Fig. 1B. The prestressed DPD case is closer to the FEM case in the entrance region, but the stress-free DPD case matches better with the FEM case in the cap region. The discrepancies may be due to the fact that the analysis of the deformation of individual spectrin molecules is performed in the DPD model with 23,867 DPD particles of the whole cell (25), whereas such details are absent in the FEM model. In addition to the cytoskeletal deformation, we are also able to quantify the maximum bilayer–cytoskeletal interaction force on one junctional complex (near the cap region) as 5.7 pN when 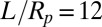. Such estimates of the interaction force between the lipid layer and the spectrin network provide valuable information about the vesiculation process in a micropipette (13). In vesiculation, detachment of the lipid bilayer from the cytoskeleton occurs due to the bilayer–cytoskeletal bond rupture during aspiration. In summary, the two-component model allows us to simulate accurately both micropipette aspiration experiments of measuring bilayer area modulus and cytoskeletal moduli with the same set of parameters, hence quantifying the cytoskeletal deformation and estimating the bilayer–cytoskeleton interaction force directly at the molecular level in the micropipette aspiration; this cannot be achieved using existing models.

Fig. 1.

Cytoskeletal area deformation during micropipette aspiration. (A) Simulated red blood cell in the micropipette. The gray triangular network is the lipid bilayer and the colored triangular network is the cytoskeleton. For clarity, only half of each triangular network is shown due to symmetry. The contour is the area deformation of the cytoskeleton. (B) Comparison of the two-component DPD model with the experiment (12) and the FEM model (24). The area expansion of the contour is defined as 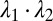, where 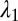and 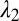are the principal stretches. 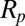is the pipette radius, ρ and ρ₀ are the current and initial protein densities in the cytoskeleton, L is the aspiration length under different pressures, and N_v is the number of DPD particles in each triangular network. Note that .

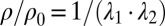Membrane Fluctuations.

Nanoscale fluctuations or “flickering” of RBCs have been studied theoretically and experimentally for decades (15, 26–30). Determining RBC membrane fluctuations provides a diagnostic capability to assess the health or pathological state of the whole RBC (14, 15). Membrane fluctuations experiments can probe the local mechanical properties of the lipid-bilayer membrane at different locations, such as central and rim regions, separately. This approach provides a noninvasive technique, in which the mechanical properties of the undeformed state are measured, whereas in micropipette aspiration the cell is subject to significant deformation.

The cell shape has a strong effect on the extent of thermal fluctuations (15), which, in turn, could be correlated with the healthy or pathological state of the cell. In addition, the interactions between the lipid bilayer and the cytoskeleton are usually simplified. For example, the cytoskeleton is often modeled as completely rigid (28), as a 3D network (31), or as a 2D Gaussian network (29). Friction and elastic interactions between the lipid bilayer and the cytoskeleton are usually ignored (30). Therefore, it is desirable to use whole-cell models to study thermal fluctuations with sufficient molecular details.

Recently, diffraction phase microscopy (DPM) has been used to map the instantaneous thickness of RBCs whereby nanometer levels of accuracy in the measurement of membrane fluctuations could be achieved at a temporal resolution of 1 ms (14, 15). In our previous work, the one-component DPD model was used to simulate healthy RBCs and RBCs parasitized to different intraerythrocytic asexual stages by the malaria-inducing parasite Plasmodium falciparum (32). Although the simulation results from the one-component model match well with the fluctuations of healthy cells at room and normal physiological temperatures, they underestimate thermal fluctuations of RBC membranes for healthy RBCs at febrile temperature and ring stage malaria-infected RBCs, unless the bending stiffness is artificially reduced significantly (32).

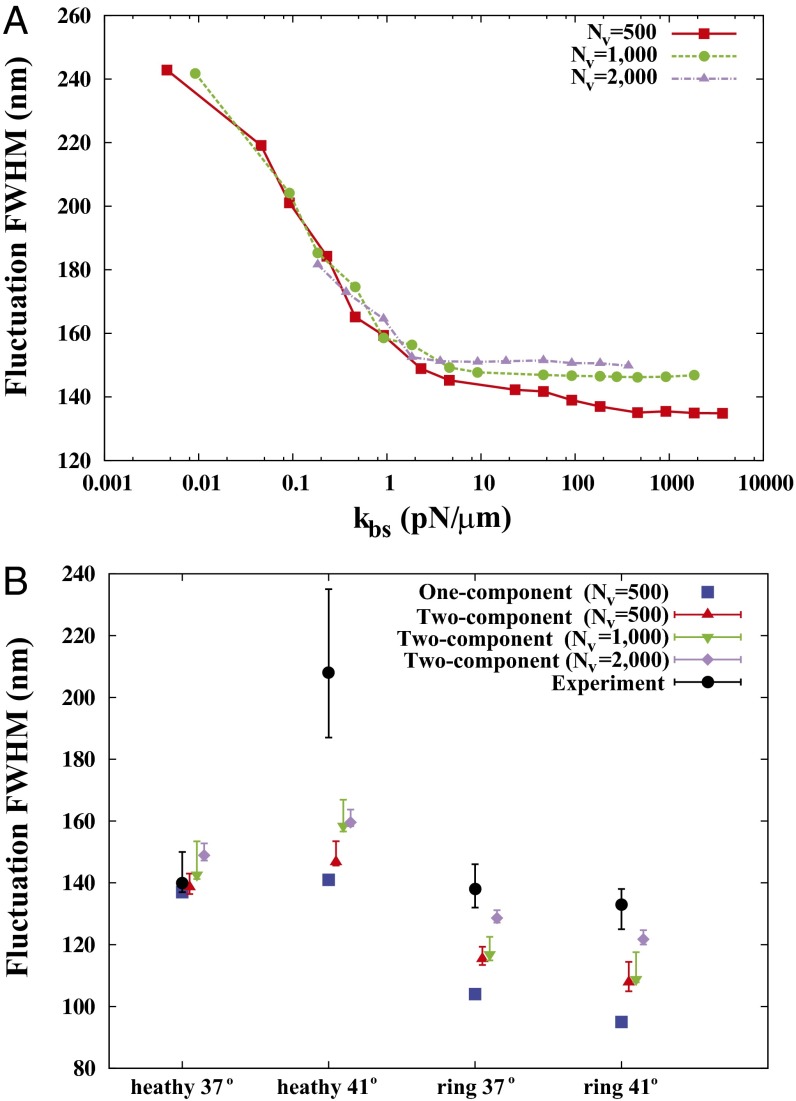
Fig. 2A shows the full width at half maximum (FWHM) (32) of membrane fluctuations for a healthy RBC at the normal physiological temperature (T ∼ 37 °C) for different values of the bilayer–cytoskeletal elastic interaction coefficient 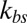and different levels of coarse graining with N_v = 500, 1,000 and 2,000, using the two-component model. The detailed simulation setup and coarse-graining procedure can be found in SI Text. We find that the amplitude of membrane fluctuations decreases with increased 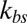(Fig. 2A) and approaches a constant limiting value after 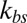reaches a critical value. This critical value of 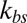is smaller for the model with N_v = 2,000, because the limiting lower-bound value of amplitude with large 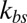is higher with N_v = 2,000 due to the finer resolution, so that it reaches this limiting value faster. It is also due to the fact that with the same value of 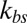, the effective elastic stiffness of a single junctional complex connection is larger with a higher resolution (SI Text). When 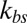is very large, there is a strong coupling between the bilayer and the cytoskeleton; i.e., they fluctuate as if they were one effective membrane, consistent with the analysis in ref. 33. If 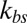is small, the bilayer–cytoskeletal coupling is weak. In the extreme case where 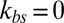, the amplitude of fluctuations is the same as that for a pure lipid bilayer. We also find that the FWHM value increases with finer DPD resolution but it is independent of the bilayer–cytoskeletal friction coefficient 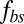, cytoskeleton viscosity 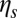, and bilayer viscosity 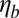, in agreement with existing theoretical models (34).

Fig. 2.

Membrane fluctuations. (A) Effect of the bilayer–cytoskeletal interaction stiffness 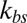on the full width at half maximum (FWHM) (32) of membrane fluctuations for the case of healthy RBCs at the physiological temperature (T ∼ 37 °C), using two-component models with N_v = 500, 1,000, 2,000. (B) Comparison of FWHM from simulations and experiments for different stages of malaria-infected RBCs at the physiological temperature (T ∼ 37 °C) and the febrile temperature (T ∼ 41 °C). The simulations are conducted using different two-component models with N_v = 500, 1,000, 2,000. The error bars of the simulations are obtained using different values of 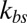(upper bound, k_bs = 4.6 pN/μm; midvalue, k_bs = 46 pN/μm; lower bound, k_bs = 460 pN/μm).

We compare our simulation results with experimental data and the one-component DPD model for healthy RBCs and RBCs parasitized to the ring stage (i.e., about 10–24 h following the invasion of the P. falciparum malaria parasite into the erythrocyte). These simulations for physiological (T ∼ 37 °C) and febrile (T ∼ 41 °C) temperatures are shown in Fig. 2B. The shear moduli of the RBC membrane for these different cases were measured experimentally in ref. 14, and they are shown in Table S2. The error bars of the simulations are obtained using different values of 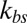(upper bound, k_bs = 4.6 pN/μm; midvalue, k_bs = 46 pN/μm; lower bound, k_bs = 460 pN/μm), as the FWHM value increases with decreased k_bs. Fig. 2B shows that the results of the two-component DPD model are more consistent with the experimental data, especially with more DPD particles and at a smaller value of 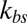. This result shows that the bilayer–cytoskeletal elastic interaction coefficient 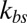indeed plays a key role in the thermal fluctuations experiments, and the discrepancy between the experimental data and the one-component RBC model can be significantly reduced by the two-component model.

Tank-Treading Motion of a RBC in Shear Flow.

Next we simulate the motion of a RBC in shear flow, known to exhibit complex dynamic behavior. This includes tank-treading (TT) motion, in which the RBC deforms to an ellipsoidal shape and the membrane circulates around while the inclination angle remains almost unchanged (35). An important characteristic of the TT dynamics of a RBC in shear flow is its frequency, i.e., the number of TT cycles per second. Although many experimental studies have been devoted to the measurement of TT frequency, considerable uncertainty exists with respect to the dependence of TT frequency (f) of RBCs on shear rate 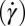. For example, Fischer et al. (35) and Tran-Son-Tay et al. (36) found that f increases linearly with 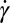. By contrast, Fischer (17) found that 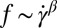with the scaling exponent β between 0.85 and 0.95. Another fundamental question is the importance of apparent slip between the lipid bilayer and the cytoskeleton during the TT motion of a healthy or diseased RBC, e.g., in hereditary spherocytosis where the transmembrane protein density may be significantly reduced (37). Here, we simulate the TT motion of a RBC in a shear flow to investigate the correct functional relationship between f and 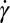and to quantify the effect of apparent slip by varying the bilayer–cytoskeletal friction. The detailed simulation setup and parameters can be found in SI Text.

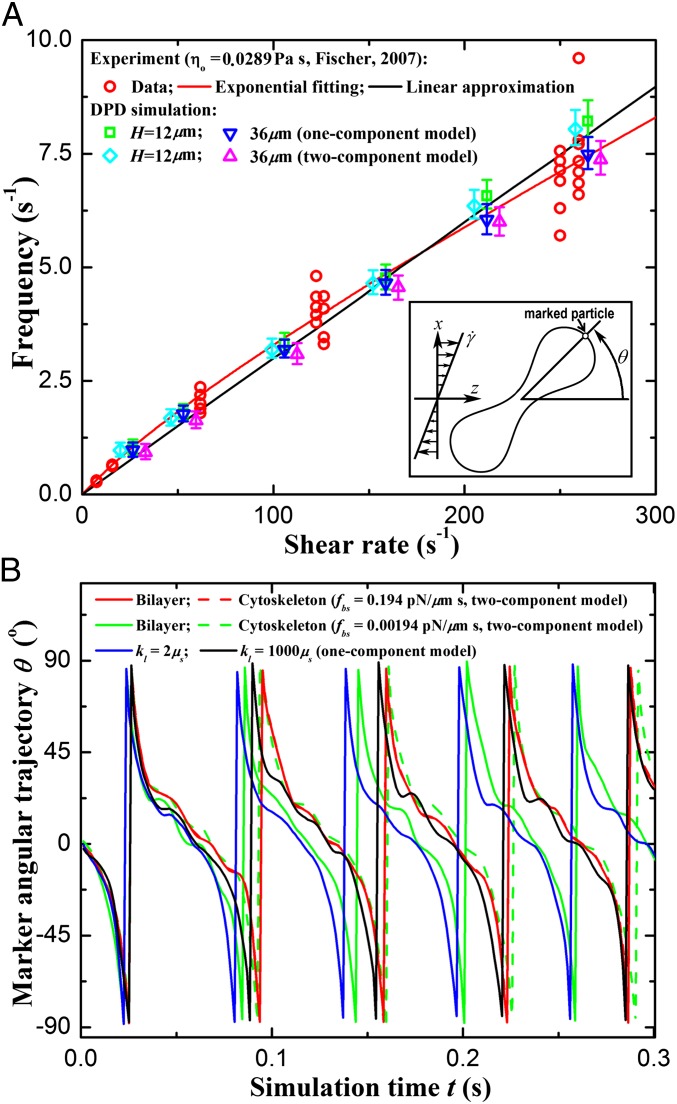
Fig. 3A shows that the TT frequency f increases linearly with 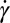for RBCs in a narrow gap flow with gap width H = 12 μm in both one-component and two-component RBC models but nonlinearly when we increase the gap width to H = 36 μm. These results are consistent with the experimental findings in refs. 35 and 36 for small gaps and with Fischer (17) in the experiment with a wide gap. Specifically, we observe a nonlinear dependence 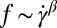with the exponent 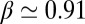in both RBC models. When the RBC rotates in shear flow, the velocity field of fluid flow around the RBC changes significantly (38). In a narrow channel, the strong confinement induces a flow parallel to the channel walls, resulting in enhanced local shear stress around the RBC. In a wide channel, the influence of solid walls on the local flow field around the RBC is very small or even negligible. Thus, there is a decrease in f compared with that for the RBC in a narrow channel. The functional relationship between f and 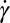is similar for both the one-component and the two-component models, although the values of f for the latter are somewhat lower.

Fig. 3.

Tank-treading motion of a RBC in shear flow. (A) TT frequency as a function of shear rate (the data of the two-component model are shifted horizontally for clarity; the error bars are obtained by increasing or decreasing membrane viscosities by 10% from their default values; 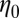is the suspending medium viscosity). Experimental data (red circles) from ref. 17 are shown. The TT frequency is investigated by tracking the marked particle in the RBC membrane. Inset shows the schematic diagram of the TT RBC in a shear flow. θ represents the angle between the position vector of the marked particle and flow direction. (B) Angular trajectory (θ) as a function of time. For the case with f_bs = 0.194 pN⋅μm⁻¹⋅s⁻¹, the bilayer and the cytoskeleton are represented by red solid and dashed lines, respectively. For the case with f_bs = 0.00194 pN⋅μm⁻¹⋅s⁻¹, they are represented by green solid and dashed lines, respectively. 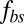denotes the friction coefficient of the bilayer–cytoskeletal interaction. The one-component model cases with local area modulus 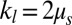and 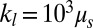are represented by blue and black solid lines, respectively, where 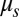is the shear modulus.

Next, we study the effect of the bilayer–cytoskeletal friction coefficient 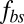as shown in Fig. 3B. To this end, we define the angular trajectory θ of a marked particle either on the lipid bilayer or on the cytoskeleton as an angle between the position vector of marked particles and the flow direction as shown in Fig. 3A, Inset. Fig. 3B shows θ as a function of time for different cases with the same initial position. We find that when using the value of f_bs = 0.194 pN⋅μm⁻¹⋅s⁻¹, which is derived on the basis of experimentally measured diffusivities of transmembrane proteins and the fluctuation dissipation theorem (39, 40), the two particles on the bilayer and the cytoskeleton move together. This is indicated by the overlapped red solid and dashed lines in Fig. 3B. Hence, there is no significant bilayer–cytoskeletal slip in this case. However, assuming a pathological RBC state where 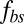is decreased by one or two orders of magnitude, an apparent bilayer–cytoskeletal slip occurs after a few TT cycles. Specifically, the TT frequency of the bilayer and the cytoskeleton with f_bs = 0.194 pN⋅μm⁻¹⋅s⁻¹ is greater than the frequency of the cytoskeleton but lower than the frequency of the lipid bilayer in the case with f_bs = 0.00194 pN⋅μm⁻¹⋅s⁻¹. For comparison, two cases of the one-component DPD model are also shown in Fig. 3B: one with the local area modulus k_l = 2μ_S and the other with k_l = 10³μ_S. We find that the frequency of the latter case is close to the case of the two-component model with f_bs = 0.194 pN⋅μm⁻¹⋅s⁻¹. This is because there is no bilayer–cytoskeletal slip with large 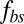and the local area deformation of the cytoskeleton is the same as that of the bilayer; hence we have local conservation of the surface area of the cytoskeleton in agreement with ref. 41. The frequency of the one-component model with area modulus 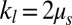is even greater than the frequency of the bilayer in the case of two-component model f_bs = 0.00194 pN⋅μm⁻¹⋅s⁻¹, because it is close to the case of the two-component model with f_bs = 0.0. In this case we do not have local conservation of the surface area of the cytoskeleton in contrast to ref. 41 but in agreement with ref. 42. Hence, our two-component model can be used to quantify the existence of slip and the cytoskeletal local surface area preservation depending on the RBC state, e.g., in health or in diseases with reduced transmembrane protein density (40). In summary, we resolved two-decades-old controversies on the dependence of TT frequency on shear rate and the role of bilayer–cytoskeletal slip, with the resolution of the latter achieved only by explicitly incorporating the bilayer–cytoskeletal friction in the two-component model.

Bilayer–Cytoskeletal Detachment in Channel Flow.

Another important and largely unresolved problem in RBC mechanics involves determining the forces needed to detach the lipid bilayer from the cytoskeleton (43). The prevalent description of this bilayer–cytoskeletal interaction strength is based on the definition of an adhesion energy 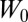(43, 44). Although this adhesion energy model matches well with experimental data, this description involving 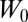does not provide mechanistic insights into the molecular origin of the bilayer–cytoskeletal interaction. The assumption in the adhesion energy model that the bilayer–cytoskeletal adhesion is a continuum property of the membrane is not rigorously true, because integral proteins are known to create discrete attachments of the spectrin network to the lipid bilayer. Therefore, we use our two-component model with N_v = 23,867 to predict the bilayer–cytoskeletal interaction force explicitly and directly at the molecular level when the bilayer–cytoskeletal bonds rupture occurs under a certain threshold value of shear stress (∼1.5 dyn/cm² or 0.15 pN/μm²) during the tethering process in channel flow (18). The detailed simulation setup can be found in SI Text.

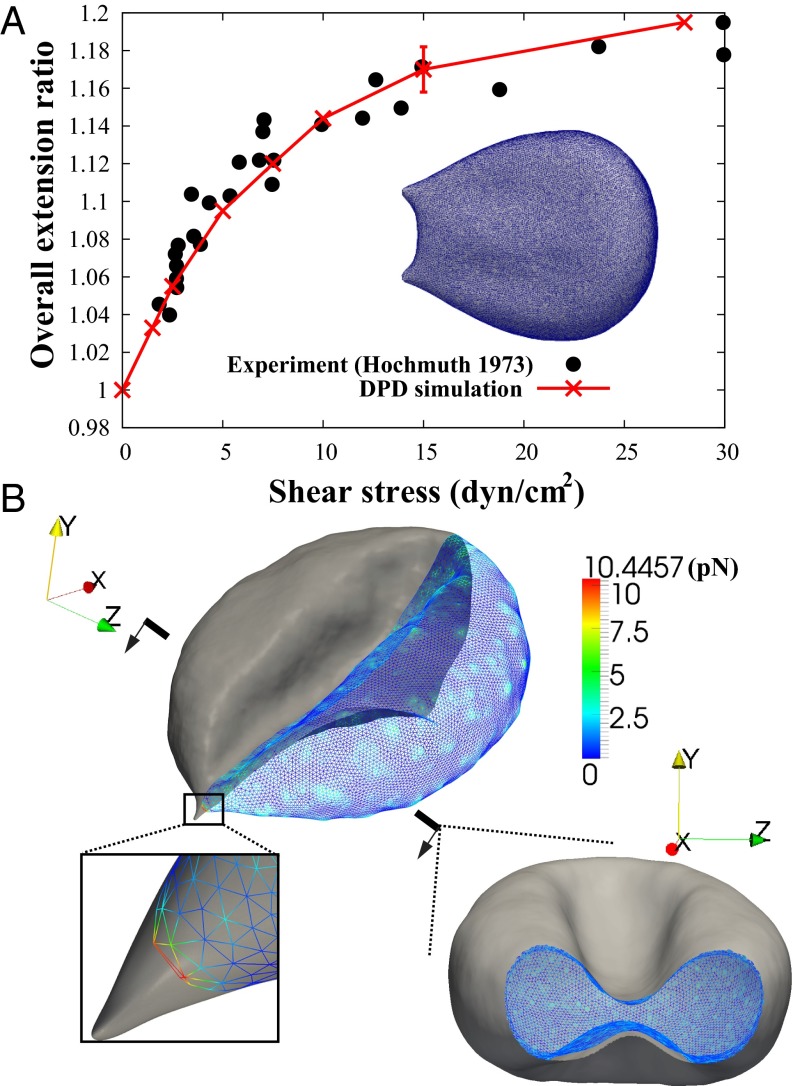
First, we model whole-cell stretching, with a line attachment between the cell and the substrate instead of a single-point attachment. The dependence predicted in the DPD simulation of the extension ratio of the RBC on the shear stress matches well with the experimental data shown in Fig. 4A. The extension ratio is defined as the ratio of maximum dimension between the current cell shape and the initial cell shape.

Fig. 4.

Bilayer–cytoskeletal detachment in channel flow. (A) Comparison of cell extension ratio between the DPD simulation and the experiment for the whole-cell stretching with a line attachment (18). The error bars are obtained by increasing or decreasing the default value of shear modulus 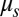by 10%. (B) Simulation of the bilayer–cytoskeletal detachment in channel flow. Inset shows the local view of the bilayer–cytoskeletal interaction near the attachment point. The bilayer is shown as a gray surface and the cytoskeleton is shown as a triangular network with the contour. The contour is the magnitude of the bilayer–cytoskeletal interaction force on a junctional complex. The unit of force is pico-Newtons (pN).

Next, we simulate the case with one attachment point. The bilayer–cytoskeletal interaction force applied on a single junctional complex in the case of critical shear stress (0.15 pN/μm²) is shown in Fig. 4B, and the bilayer–cytoskeletal interaction strength, i.e., the maximum force applied on a junctional complex, is estimated as σ_bs = 10.45 pN. Hwang and Waugh (43) reported that the bilayer–cytoskeletal adhesion energy 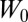is about 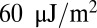. Following the scenario that during dissociation band 3 is separated from the bilayer, this adhesion energy is related to the energy to pull band 3 out. Taking into account the fact that band 3 is a chain that crosses the bilayer 14 times (45), the subsequent adhesion energy is the energy required to pull all these crossings sequentially out. Assuming that during the process the applied force decreases linearly from the critical contact force to zero as band 3 is completely taken out, the adhesion energy is given as 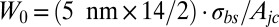, for a bilayer thickness of 5 nm, where 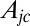is the area of a junctional complex. If the junctional complex is assumed to be circular with a diameter of 75 nm and area is A_jc = 0.004418 μm², then 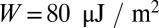, which is close to the value 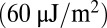obtained by Hwang and Waugh (43). In summary, these simulations lead to direct quantification of molecular-level mechanical forces involved in bilayer–cytoskeletal dissociation. Such quantitative assessment is essential for elucidating bilayer loss in RBC diseases such as hereditary spherocytosis (4) and sickle-cell anemia (1).

Conclusions.

In this work, we have presented a unique computational framework for simulating the interactions between the lipid bilayer and the cytoskeletal network of human RBCs. This mesoscale analysis, predicated on dissipative particle dynamics, is tested and validated through rigorous comparisons with experimental data from four different sets of independent experiments that probe different aspects of biophysical and rheological properties of RBCs. Furthermore, the present two-component model is compared with corresponding results obtained from prior one-component model predictions and with theoretical estimates, wherever appropriate. The capabilities and limitations of the two-component model are assessed.

By applying the two-component whole-cell model, we also reconciled and resolved several controversies and issues in RBC mechanics. First, we were able to realistically model the micropipette aspiration experiments of measuring both the area moduli of the cytoskeleton 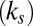and the lipid bilayer 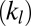, using the same set of input parameters, although these two area moduli differ by five orders of magnitude. Second, we found that the two-component model matches the thermal fluctuations experiments better than the one-component model due to the explicit incorporation of bilayer–cytoskeletal elastic interaction. Third, we found that the dependence of the tank-treading frequency on the shear rate follows a linear relationship for a narrow channel but a nonlinear one for a wide channel, hence reconciling a controversy in the literature (17). In addition, we demonstrated that the tank-treading motion is too fast for the bilayer–cytoskeletal slip to occur for healthy RBCs; however, we also showed that apparent bilayer–cytoskeletal slip occurs if the bilayer–cytoskeletal friction coefficient 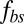is significantly reduced for certain diseases. Finally, we quantified the strength of the force per junctional complex by which the bilayer remains attached to the cytoskeleton at the molecular level during RBC tethering in the channel flow experiment.

Methods

In this unique two-component RBC model, the membrane is modeled by two different components, i.e., the lipid bilayer and the cytoskeleton. Specifically, each component is constructed by a 2D triangulated network with 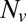vertices, where each vertex is represented by a DPD particle as shown in Fig. S1A. The potential of the RBC membrane including these two different components is written as

where 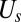is the spectrin’s potential energy from the cytoskeleton, 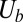is the bending energy from the lipid bilayer, 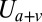corresponds to the area and volume conservation constraints from the lipid bilayer, and 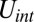is the potential energy of the interaction between the lipid bilayer and the cytoskeleton. The detailed expressions of 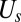, , 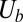and 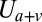can be found in SI Text.

The bilayer–cytoskeletal interaction potential 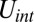can be expressed as a summation of harmonic potentials given by

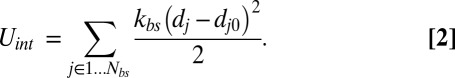Here 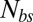is the number of bond connections between the bilayer and the cytoskeleton, i.e., the interactions between the transmembrane proteins (band 3 and glycophorin C) and spectrins; 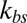denotes the spring constant of the bond; 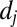is the distance between the vertex j of the cytoskeleton and the corresponding projection point 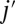on the lipid bilayer as shown in Fig. S1C; and 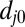is the initial distance between the vertex j and the point 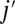. The vertex in the spectrin cytoskeletal network is projected onto the closest triangle face of the lipid bilayer, and the distance and relative velocity between the cytoskeleton vertex and its projection point on the lipid bilayer are obtained. The corresponding elastic force on the vertex j of the cytoskeleton is given as

where 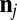is the normal direction of the lipid-bilayer surface at the projection point of vertex j.

The tangential friction force between the lipid bilayer and the cytoskeleton on the vertex j of the cytoskeleton is given as

where 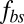is the tangential friction coefficient, and 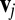is the relative velocity between the vertex j and the corresponding projection point 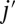on the lipid bilayer. Detailed descriptions of other aspects of the model, e.g., membrane viscosities, can be found in SI Text.