An integrated reweighting theory of perceptual learning

Abstract

Improvements in performance on visual tasks due to practice are often specific to a retinal position or stimulus feature. Many researchers suggest that specific perceptual learning alters selective retinotopic representations in early visual analysis. However, transfer is almost always practically advantageous, and it does occur. If perceptual learning alters location-specific representations, how does it transfer to new locations? An integrated reweighting theory explains transfer over retinal locations by incorporating higher level location-independent representations into a multilevel learning system. Location transfer is mediated through location-independent representations, whereas stimulus feature transfer is determined by stimulus similarity at both location-specific and location-independent levels. Transfer to new locations/positions differs fundamentally from transfer to new stimuli. After substantial initial training on an orientation discrimination task, switches to a new location or position are compared with switches to new orientations in the same position, or switches of both. Position switches led to the highest degree of transfer, whereas orientation switches led to the highest levels of specificity. A computational model of integrated reweighting is developed and tested that incorporates the details of the stimuli and the experiment. Transfer to an identical orientation task in a new position is mediated via more broadly tuned location-invariant representations, whereas changing orientation in the same position invokes interference or independent learning of the new orientations at both levels, reflecting stimulus dissimilarity. Consistent with single-cell recording studies, perceptual learning alters the weighting of both early and midlevel representations of the visual system.

Almost all perceptual tasks exhibit perceptual learning, improving people’s ability to detect, discriminate, or identify visual stimuli. These improvements due to practice are the basis of visual expertise. Practice improves the ability to perceive orientation, spatial frequency, patterns and texture, motion direction, and other stimulus features (1–4). Learned perceptual improvements generally show some specificity to the feature and to the retinal location of training. Specificity of trained improvements to retinal location and feature in behavioral studies of texture orientation (5, 6) or simple pattern orientation judgments (7, 8) inspired early researchers to posit that practice altered the responses of early visual representations (V1/V2) with small receptive fields, retinotopic structure, and relatively narrow orientation and spatial frequency tuning (6).

However, the generalization of learned perceptual skills over retinal locations is almost always practically advantageous, and is sometimes observed (9). Whether perceptual learning reflects changes in retinotopic representations in early visual cortical areas (6) or alternatively—as we have suggested elsewhere—is primarily accomplished through selective readout or reweighting of stable early representations (10–14), the theoretical challenge is not explaining specificity, but rather explaining how and under what circumstances learning transfers over locations.

An integrated reweighting theory (IRT) of perceptual learning and transfer, developed and tested here, is designed to account for learning at multiple locations (Fig. 1) and other related learning phenomena. The IRT proposes an architecture of perceptual learning in which higher level location-independent representations are trained at the same time as location-specific representations. Transfer to new retinal positions/locations is fundamentally different from transfer over stimulus features. Position transfer is mediated through reweighting of more broadly tuned location-independent representations, whereas transfer between different stimulus features reflects the similarity, conflict, or independence of the optimal weight structures in two tasks for both location-specific and location-independent representations. The perceptual learning mechanism is implemented as augmented Hebbian reweighting (13, 14) that dynamically optimizes connections between stable stimulus representations and a task decision. Reweighting operates on both levels of representations simultaneously. This is a computational model of perceptual learning that uses both multiple levels of representation and multiple locations to make predictions about location and feature transfer. The IRT predicts differential transfer to new features, locations, or both. Learned improvements in a task for the same feature transfer relatively well to a new location based on learned reweighting of the location-independent representations. Switches of feature in the same location show far less transfer as they require learning either new or conflicting weight structures for both location-independent and location-specific representations. Switches of both feature and location may show intermediate transfer if conflicting weight structures must be learned for the location-independent representations. Direct tests of the IRT predictions lead to our experiment. The computational IRT provides quantitative predictions for learning and transfer specialized for each experimental protocol. A computational model is necessary to generate predictions for learning and transfer that reflect the stimuli and judgment (15), the extent of initial training (16), and other aspects of each experimental protocol.

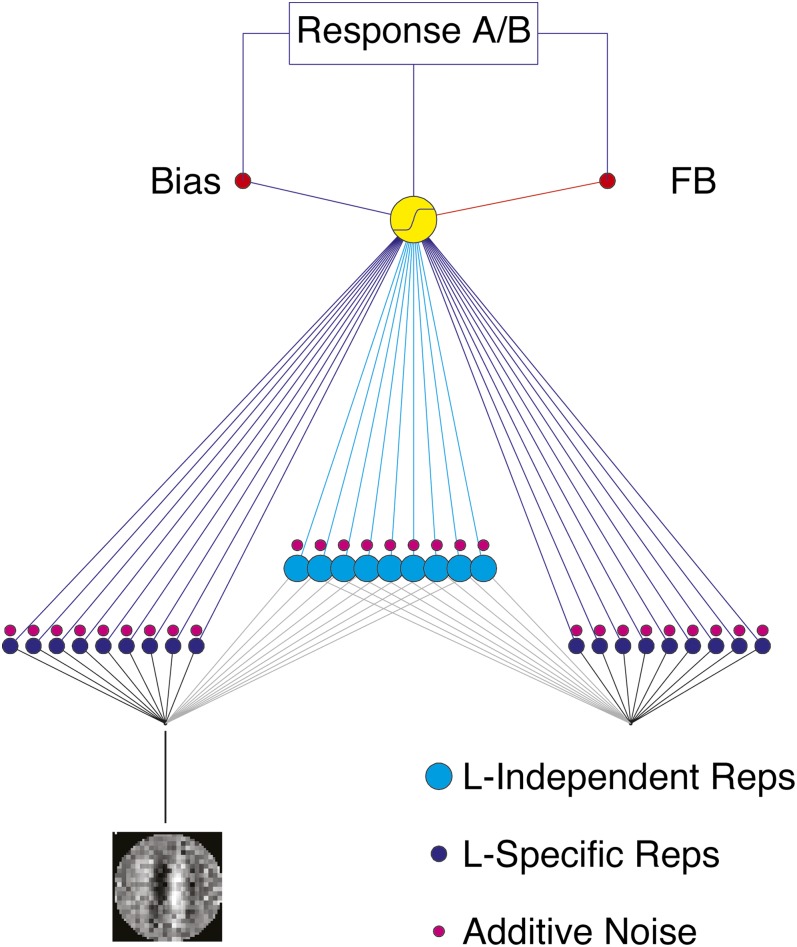
Fig. 1.

A schematic of the IRT includes location-independent representations (turquoise) and several location-specific representations (blue), each with internal additive noise (red). Learning reweights the connections from representation activations to a decision unit using Hebbian learning, with the benefit of bias control and feedback (SI Materials and Methods, Model Implementation of the Integrated Reweighting Theory). The location-independent weights to decision mediate location transfer, whereas the similarity of the optimized weight structure for different stimuli mediate feature/orientation transfer.

Previous behavioral studies of transfer after perceptual learning have generally changed either stimulus feature, such as orientation, or position at the task switch, but not both (5, 7, 8, 10, 11, 15, 17, 18). Schoups et al. (7) were the first to claim surprising specificity of learned peripheral orientation discrimination to positions separated by only a few degrees of visual angle. However, a review of all of the literature suggests a more nuanced picture. Many cases (8, 10, 11) exhibit only partial specificity—and so partial transfer—to visual field quadrant, or from preliminary foveal training to peripheral locations, with some residual specificity to each location (7), even when both orientations and locations are switched (5, 15). No prior study provides ideal experimental comparisons; still the literature overall is suggestive of greater specificity for orientation feature switches than for position switches. Two cases (7, 8) report higher specificity for an orientation switch; one hyperacuity bisection task showed the opposite but also involves a shift from fovea to periphery (17). Switched orientations at fovea led to full specificity (19), as did learned motion directions, despite a slightly speeded learning rate at transfer (20). The results are more complex if sequences of tasks are trained, often leading to transfer where none occurred before (11, 21, 22). The basis of these complex training effects is currently under investigation (Discussion).

A quantitative test of the IRT framework requires controlled comparisons to evaluate differential transfer. The current experiment compares the extent of transfer to switches of position (P) and switches of orientations (O), or both (OP), in strictly comparable experimental conditions. All transfer is not equal. As predicted by the IRT architecture, there is greater transfer of the same orientations to a new location than to new orientations within the same location. The computational IRT model of orientation judgment incorporating both location-specific and location-independent representations provides a close qualitative and quantitative account of the learning and transfer data.

Results

Observers judged small differences in the orientation of Gabor patches in periphery as clockwise or counterclockwise relative to an oblique reference angle (R° ± 5°) (see Fig. S1 for stimuli). Observers were assigned randomly to three groups. After eight blocks (two per session) of practice with one set of orientations and positions, observers were switched in one of three ways (P, O, or OP), and trained for another eight blocks. All together, each observer completed about 10,000 trials (Materials and Methods). High-precision orientation judgments, such as (R° ± 5°), yield partial specificity and partial transfer of learning when both reference angle and location are switched (15). This leaves room to see either more or less transfer and specificity for the other conditions. Throughout practice, discrimination was tested with and without external noise in the stimulus (“no noise” and “high noise”; Fig. 2), to assay learned stimulus enhancement and external noise exclusion, respectively (10, 11, 18, 19). Performance with and without external noise reveals different limiting factors in learning that can show distinct profiles of learning and transfer (18, 19, 23). Accounting simultaneously for both high and low noise within the context of the detailed training protocol of the experiment is a strong challenge for quantitative tests of the IRT model.

Fig. 2.

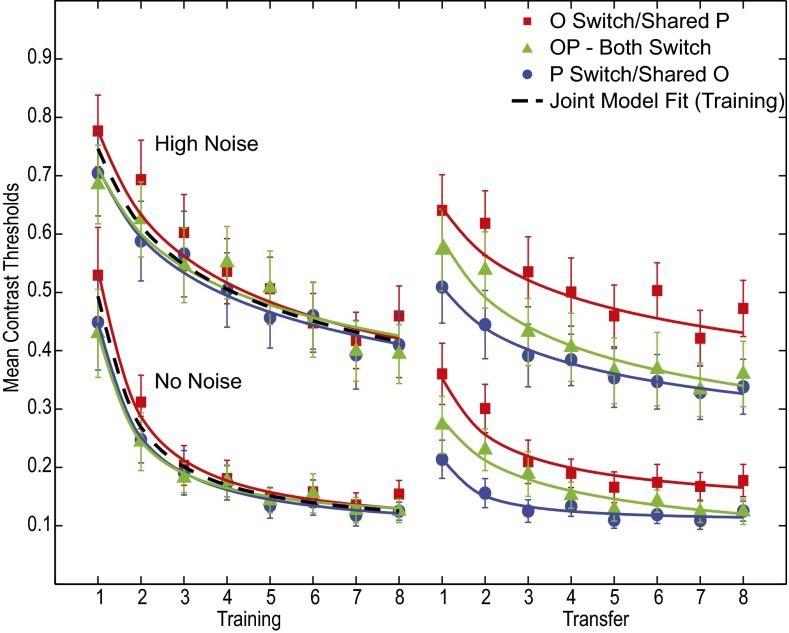
Contrast thresholds at 75% accuracy for the initial training phase (Left) and subsequent practice during the transfer phase (Right) after the task switch of the position (P), orientation (O), or both (OP), averaged over observers. Higher contrast threshold curves are for tests in high external noise, whereas lower contrast threshold curves are for tests without external noise. Error bars are estimated by Monte Carlo methods, and smooth curves represent best fitting power functions of practice.

Fig. 2 shows average contrast thresholds to achieve 75% correct as a function of practice for the initial training phase (Fig. 2, Left) and the postswitch transfer phase (Fig. 2, Right). The error bars were estimated from the data using Monte Carlo methods (n = 1,000). Power function improvements in contrast thresholds, fit by least-squares methods, are shown as smooth curves. Gabor patches are harder to see in the presence of visual noise and have higher threshold contrasts in both the initial training phase [(F(1, 64) = 149.24, P < 0.0001] and the postswitch transfer phase [F(1, 64) = 79.57, P < 0.0001]. (The IRT model fits low and high external noise conditions jointly with the same model parameters; see below.) Observers were randomly assigned to groups, so the initial performance of the groups should be statistically equivalent, and it is [F(2, 30) = 0.393, P > 0.6 in high noise and F(2, 30) = 0.454, P > 0.6 in no noise]. Initial training data in each noise condition and all groups were well fit by the same power function learning curves [F(6, 15) = 2.09, P = 0.12, F(6, 15) = 0.733, P = 0.63, in no noise and high noise, respectively].

Orientation discrimination contrast thresholds improved with practice in the initial training phase in both high external noise and no external noise tests (all P < 0.001, by t test). Performance also improved with practice in the transfer phase in both high noise (all P < 0.001) and no noise (P < 0.001, 0.003, and 0.05, respectively). If practice only changes the tuning of early visual representations, then stimuli should be represented with independent neural coding in all groups, and all conditions should show high, nearly maximal, levels of specificity. In contrast, in the IRT architecture, the three types of transfer will not in general be equivalent. Consistent with the IRT, the three transfer groups (O, P, and OP) differed in their transfer/specificity at the task switch. The same orientation stimuli switched to a new position (P, blue curves) led to the best performance at the switch point, showing considerable transfer or low specificity, consistent with transfer in the IRT through learned reweighting of location-independent representations that are still useful in the new location. Different orientation stimuli at the same position (O, red) led to the worst performance at the switch point, showing little transfer or high specificity, consistent with the need to learn either completely new or incompatible weights for the new orientations. The conditions differ at the first point after the task switch [t(30) = 2.04, P < 0.05 in high noise, and t(30) = 1.90, P = 0.07 in no noise], over the first two blocks of training after the switch for both high and low noise (P ∼ 0.013 and 0.09, respectively), and over all eight transfer blocks in high noise (P ∼ 0.01). The contrast thresholds for the position and orientation switch group (OP) were intermediate, and closely replicate the data of refs. 15, 16. This suggests that the learned weights for the location-independent representations are (slightly) incompatible and must be relearned, whereas reweighting of location-specific representations in the new location are independent of prior learning. Individual observer results were generally consistent with these patterns.

The practice effects on contrast thresholds were fit with power functions that estimate differential transfer; this quantitative analysis of the whole pattern of learning, detailed next, supports the conclusions above. Elaborated power functions, 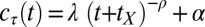, provide an excellent account of threshold improvement for aggregate data (15, 16, 19), where 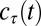is the contrast threshold at practice block t, 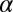is the asymptotic (minimum) threshold after extensive practice, 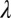is the initial incremental threshold above 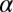, ρ is the learning rate, and transfer of prior experience is summarized by transfer factor 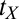, which is set to 0 for initial training (see ref. 15 for a description). The 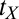s quantify transfer in blocks, ranging in this experiment between zero (no benefit of prior training or full specificity) and eight (full transfer or no specificity). The estimates of 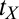at the task switch in high noise were 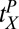= 6.04, 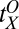= 0.59, and 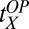= 2.47 (with 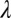= 0.56, 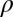= 0.45, 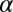= 0.20, r² = 0.865) and in low noise were 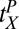= 2.63, 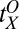= 0.37, and 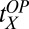= 1.09 (with 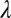= 0.38, 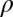= 1.06, 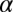= 0.08, r² = 0.945). The three groups share 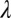, , 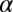and 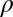, the initial performance, asymptotic level, and effective learning rates for each external noise level. Transfer is very high (transferring about six of eight blocks) for position switches (P), low (about one of eight blocks) for orientation switches (O), and intermediate (about 2.5 of 8 blocks) for changing both (OP) in high external noise, and about half these values in low noise trials. Correspondingly, performance level at the switch estimated from independent power functions were 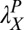= 0.30, 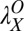= 0.48, and 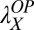= 0.36 in high noise (with baseline 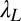= 0.55 in the initial learning phase, r² = 0.915) and were 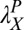= 0.12, 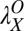= 0.27, and 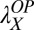= 0.18 in low noise (with baseline 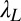= 0.38, r² = 0.959) (all Ps < 0.0001 by nested model tests). In sum, the power function analyses are consistent with the prior analyses and provide quantitative estimates of transfer.

Next, we develop a computational implementation of the IRT theory of perceptual learning and transfer. Our previous models of perceptual learning explain perceptual learning in a single location as incrementally optimized reweighting of outputs of early visual representations to influence a perceptual decision (10, 11, 24). The representations themselves often remain unchanged (6). A review of the literature in neurophysiology is broadly consistent with this idea (12), although modest representation retuning may also sometimes occur. A representation system (13, 14) operates on images of the experimental stimuli and computes activations of orientation and spatial-frequency tuned representation units. A decision unit integrates the weighted activation of these units and (nonlinearly) selects a behavioral response (i.e., “left” or “right” orientations). Connection weights are incrementally updated on each trial of a simulated version of the actual experiment through a Hebbian mechanism, augmented by feedback and bias correction. This augmented Hebbian reweighting model (AHRM) accounts for perceptual learning in alternating noise backgrounds (13), for the role of feedback (14, 25, 26) (see ref. 12 for a review), for the effects of external noise (11, 18), and for differential magnitudes of learning in high and low noise tests (11, 18). This original AHRM gives a powerful account of perceptual learning under varying training conditions for a single location. It provides no account for transfer of perceptual learning to new locations.

The IRT and architecture were developed to model learning and transfer across as well as within locations. This architecture has a broadly tuned location-independent representation as well as location-specific representations. The IRT simulation uses augmented Hebbian learning (13, 14) to simultaneously optimize the weights on location-independent representations and location-specific representations. The representation system for oriented pattern stimuli (such as the Gabors in the experiment) computes the normalized activation of noisy spatial frequency and orientation-sensitive units (see SI Materials and Methods, Model Implementation of the Integrated Reweighting Theory). Learning transfers to a new location or position when performance in a new location inherits useful location-independent weights; subsequent improvement occurs because the location-specific weights in the new location need to be learned. To summarize again, switching orientation in the same location requires retuning weights for the new orientations at both levels, and transfer (or interference) depends on the consistency, independence, or inconsistency of the optimal weight structures for the two sets of stimuli (14, 27). An IRT account of transfer of spatial, vernier, or bisection judgments (28, 29), or motion direction, would require alternative representation system modules suited to those tasks, but the architectural principle of the theory is general. Similarly, the details of the learning algorithm could be altered while retaining the general principles of the proposed architecture and theory.

The IRT simulation incorporates representation modules from the earlier single-location model (13). It takes an image and computes activations in different spatial-frequency and orientation tuned units that span the stimulus space via coarse sampling. Bandwidths are set from physiological estimates of early cortical areas, and we incorporate nonlinearities, internal noises, and selection of the spatial region of the oriented Gabor stimulus. The location-independent representations are noisier and more broadly tuned. The tradeoff for representing information from many locations is a reduction in the precision. Broader tuning is also motivated by the role of precision in the specificity of transfer to new locations, as well as by physiology (15). The weighted activations and input from a bias-control unit are passed through a nonlinear activation function to generate a binary response (i.e., left or right) on each trial. Weights from both the location-specific and location-independent units to the decision unit are updated after each trial. Feedback improves learning in low accuracy conditions, but is not necessary for learning if the internal response without it is often correct. The model and related equations are described in SI Materials and Methods.

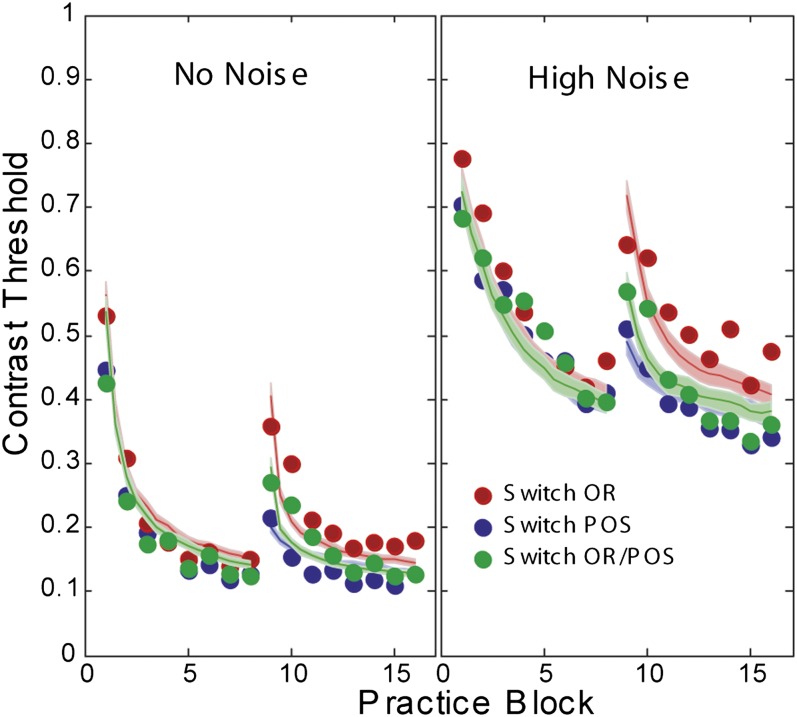
Examples of activation computed for the location-specific and the more broadly tuned location-invariant IRT representations are shown in Fig. S2. Best fitting simulated predictions of the IRT, shown in Fig. 3, provide a close account of the average human data (r² = 0.952), with model parameters listed in Table 1. The low noise (Fig. 3, Left) and high noise (Fig. 3, Right) test data are separated for clarity of the graph, but they are intermixed in both the experiment and the modeling. Many of the general representation parameters were set a priori; others such as the learning rate are used to fit the observed rate of perceptual learning. The IRT model correctly predicts the ordinal patterns of the different transfer conditions under essentially all tested parameter sets; the fine-tuning of parameters matched performance levels and learning rate more closely. Internal representation noise parameters differed very slightly between the three subject groups to account for sampling differences; all other parameters are constant. Simulated model runs use random trial histories and response choices from the specific experimental design; incorporating observer variability in parameters would broaden the confidence bands, but not alter the basic pattern of predictions.

Fig. 3.

Predictions of the best fitting IRT with the experimental data points. Model parameters of the best fitting model were estimated by grid search methods and are listed in Table 1.

Table 1.

Parameters of the best-fitting IRT model

Parameters	Parameter values
Parameters set a priori
Orientation spacing Δθ	15°
Spatial frequency spacing Δf	0.5 octave
Maximum activation level Amax	1
Weight bounds wmin wmax	±1
Location-specific initial weights scaling factor winit	0.127
Location-independent initial weights scaling factor winitI	0.254
Activation function gain γ	3.5
Location-specific orientation bandwidth	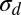30°
Location-independent orientation bandwidth	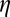48°
Location-specific frequency bandwidth hf	1 octave
Location-independent frequency bandwidth hfI	1.6 octave
Radial kernel width hr	2 dva
Parameters adjusted for the data
Normalization constant k	3e-6
Scaling factor a	0.167
Location-specific internal noise 1 σ1	2.5e-7
	3.5e-7
	2.5e-7
Location-specific internal noise 2, σ2	0.01
	0.02
	0.01
Location-independent internal noise 1 σI1	3.5e-6
Location-independent internal noise 2 σI2	0.15
Decision noise σd	0.01
Learning rate η	6e-4

 Location specific internal noises are for the three transfer conditions: P, O, and OP. dva, degrees of visual angle.

Perceptual learning pruned weights on irrelevant orientations and amplified weights for informative orientations of both location-specific and location-independent units—as seen in the initial weights, weights at the switch, and weights at the end of training on the new task (Fig. S3, SI Materials and Methods). Performance transfers over position via the learned location-independent weights, then all weights, including those for the new location-specific representations, are further optimized. For switches of orientation, both the location-specific and the location-independent weights are tuned for now irrelevant orientations, and both require learning of the new orientations, and unlearning of those previously learned weights that are inappropriate for the new orientations. If both dimensions are switched, then the location-specific weights are learned anew, whereas the location-independent weights must be retrained. This eliminates any conflict in learned weights between the training and the transfer tasks for the location-specific representations.

Discussion

Specificity to trained stimuli and locations is central in claims about neural mechanisms of perceptual learning. Specificity and transfer are also important in determining the value of perceptual learning for training of expertise and rehabilitation. Qualitative theories claiming that perceptual learning adapts or retunes neurons in early visual cortex imply widespread observations of specificity to position and stimulus features and equal and high specificity for all task switches involving distinct neural populations. A consideration of the literature led us instead to hypothesize that transfer to new locations was mediated by reweighting of information from location-independent representations, and to develop and test a new IRT and transfer architecture. We specified broader tuning and higher noise for the location-independent representation based on findings in the literature that the required precision of the transfer task is an important determinant of transfer over locations; high-precision tasks benefit less from transfer (5, 15).

The experiment directly compares switches of position only (P), orientation only (O), and both dimensions (OP) within the same task and training structure. Our findings of greater specificity for orientation changes than for position changes are generally in line with the prior literature (7, 8, 18) (but see ref .17), while controlling for extraneous factors in prior comparisons. The results are qualitatively and quantitatively consistent predictions of the IRT. No noise and high noise testing were intermixed in this study and therefore influence and reflect the same learned weight structures. High noise conditions naturally produced the larger magnitude of perceptual learning and differences in specificity observed under noisy test conditions, reflecting the impact of external noise on imperfectly tuned weight templates for the tasks. If trained separately (18, 23), noisy test environments limit the ability to find a stable optimized weight structure (10, 11). Transfer of stimuli or tasks within the same location are accounted for within the same IRT architecture. That consistency of weight structures determined stimulus/task transfer was an explicit prediction of the AHRM for perceptual learning in training locations, necessary to account for persistent switch costs in alternating noise conditions (13, 14) (see also refs. 12, 27). Parallel predictions would hold for tasks other than orientation judgments, such as spatial, vernier, pattern, motion, or texture judgments, although several of these require a different representation subsystem.

The computational implementation of the IRT architecture makes it possible to generate predictions for and understand apparently inconsistent results based on the exact details of the experimental paradigm. The exact extent of training and transfer can depend on the amount of training, the accuracy of performance during training, the availability of feedback, and the mixture and specific schedules of training different stimuli and tasks, For example, our results are potentially related to, but differ from those of ref. 21, which reports nearly full transfer of an orientation task to a new transfer location after “pretraining” that primes the second location, suggesting to those authors a role for intermediate-level coding in visual perceptual learning. The IRT architecture is extensible—it should make predictions about this and many other transfer phenomena, such as the “double training” method. Several such cases are being investigated in their own computational studies (30), where the IRT framework has accounted for several of the so-called double-training results as learned task-specific reweighting followed by up-regulation of location-independent weights through training with tasks requiring broad tuning. Details of the IRT implementation may need to evolve as this literature is expanded.

Neurophysiologists have also sought the neural signature of perceptual learning of orientation (31–35). Single-unit responses in early visual cortex before and after perceptual learning report largely identical location, size, and orientation selectivity between trained versus untrained regions of V1 and V2 (but see refs. 25, 36). Among these, a small change in slope in V1 neurons (34), not seen in other cases, is often cited as key evidence for changes in orientation tuning of neurons primarily responsive to the trained orientation. Any small alterations in early visual representations following extensive training do not account for the large behavioral changes (13). In contrast, alterations in tuning curves have been seen in V4 (35). Analogously, in a visual motion task, extensive training left sensory responses in MT largely unaffected, but altered those of lateral interparietal cortex (LIP) (37). Overall, the neurophysiology suggests that although small changes in very low-level representations may sometimes occur, they are insufficient in general to account for the substantial behavioral changes. Instead, changes or decision structures at a higher level of the visual hierarchy are suggested (12); or perceptual learning may alter feed forward connections and correlation structures, possibly before V1 (38). The neurophysiology has examined changes in cortical regions as the result of training for a single task in a single location, and has not widely studied transfer and subsequent retraining.

The IRT and architecture provide an explanatory structure for and good quantitative fit to differential transfer for location and stimulus features. Transfer to new locations uses location-independent representations as the scaffold. We speculate that these location-independent representations are consistent with “object” representations of anterior inferotemporal (IT) in the ventral visual pathway. Our 5°-eccentric test locations are (center to center) separated by about 7°. In comparison, receptive field sizes at similar eccentricities are estimated at less than 1° for V1, 1–2° for V2, and 3–4° for V4 (39), although some estimates are as high as 6° for V4, so position transfer in this experiment seems more consistent with properties of IT (40–42). This parallels conclusions that learning in the motion system localizes to LIP rather than middle temporal area (MT) (37). Visual psychophysics generates critical information about functional properties of perceptual learning and transfer that support conjectures about neural substrate that need to be tested and refined with physiological or brain imaging investigations.

The IRT framework does not aim to reconstruct detailed neural pathways of the visual system or the decision-making and action-selection circuits that collectively produce the behavior. It is inspired by computational models of V1, V4, and higher visual areas, whereas tuning properties of the representational units reflect tuning properties in these cortical regions (43, 44). Our design strategy is to simplify the model to essentials and test the ability to predict the patterns in data. Further model development might take several directions. Although some perceptual learning paradigms such as the current study did not require consideration of recurrent connections (38), recurrent connections from decision to sensory representation units may play a role in segmentation, attention, and conscious awareness (45, 46), and future studies may incorporate them to account for the properties of learning in other paradigms as another form of learning through reweighting. Applications of the IRT in different stimulus domains, such as motion direction discrimination or vernier, would require representation modules appropriate for those domains. Also, more complex experimental designs are likely to require attention gating of different inputs to the decision. Finally, the current IRT architecture approximated location-independent activation by submitting the stimulus directly to the location-independent units. The development of a full hierarchical stimulus analysis in which the location-independent units receive their input from location-dependent units would itself be a major research project. However, the current IRT architecture provides a strong computational framework that can make predictions about a wide range of transfer phenomena.

Conclusions

Dosher and Lu, and others (10–14, 24) suggested an alternative to altered early cortical representations in visual perceptual learning—the “reweighting hypothesis”—in which perceptual learning incrementally optimizes the connections between sensory representations and decision. Most quantitative models of perceptual learning are based on reweighting or some other form of selection from stable early representations (13, 14, 26, 29, 47–50). As learning continues, only the most relevant neural representations survive in decision. Even if early representations are slightly modified, reweighting will be necessary to optimize performance—indeed reweighting will be all of the more necessary if sensory representations are altered. The IRT models transfer through an expanded architecture incorporating both location-specific and location-independent representations for both original learning in a single retinal position and transfer to new positions and stimulus features. The architecture implies a special status for transfer over locations based on the location-independent representations of midlevel visual analysis, validated in the current experiment. It provides a theoretically motivated basis for considering the quantitative and qualitative properties of transfer in a wide variety of task combinations. The computational IRT model makes quantitative predictions for learning and transfer that are sensitive to the exact stimuli and the details of the training procedure, providing a framework for understanding new training paradigms. Application of the model to each new experimental condition will further test the range of phenomena explained by this perceptual learning system.

Materials and Methods

Observers discriminated the orientation (±5° clockwise or counterclockwise from –35° or +55°) or Gabor patches presented either with or without external noise either in the NW/SE or NE/SW corners (5.67° eccentric) on a computer screen. Contrast thresholds at 75% correct were measured using adaptive staircase methods. After training for four sessions (4,994 trials) on one task, they switched orientation, position, or both (O, P, or OP with 12, 11, and 10 observers) and trained for four sessions. Error feedback was provided. Details are in the SI Materials and Methods.

The IRT Matlab simulation takes grayscale images, computes activity in location-specific and location-independent representation units, generates a response, and then updates the weights. The simulated experiment exactly replayed the procedure in the human experiment. Representation parameters were set a priori for the location-specific representations (13, 14), at bandwidths of 30° for orientation and 1 octave in spatial frequency, spaced every 15° and every one-half octave, respectively. Bandwidths of location-independent representations, estimated from preliminary fits, were 1.6 times the location-specific values, and the activation function parameter 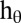was set to 3.5. Observed threshold learning curves were fit with a scaling factor (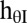), two parameters for internal additive noise (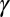) and for internal multiplicative noise (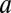), one each for location-specific, and one for location-independent representations, a decision noise (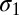), and a learning rate (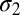). These parameters were adjusted to yield the best least-squares fit of the model to the average data (SI Materials and Methods). The predicted performance curves were based on 1,000 iterations of the model experiment.