Elucidating Solvent Contributions to Solution Reactions with Ab Initio QM/MM Methods

Abstract

Computer simulations of reaction processes in solution in general rely on the definition of a reaction coordinate and the determination of the thermodynamic changes of the system along the reaction coordinate. The reaction coordinate often constitutes of characteristic geometrical properties of the reactive solute species, while the contributions of solvent molecules are implicitly included in the thermodynamics of the solute degrees of freedoms. However, solvent dynamics can provide the driving force for the reaction process, and in such cases, explicit description of the solvent contribution in the free energy of the reaction process becomes necessary. We reported here a method that can be used to analyze the solvent contributions to the reaction activation free energies from the combined QM/MM minimum free-energy path simulations. The method was applied to the self-exchange S_N2 reaction of CH₃Cl + Cl^-, showing that the importance of solvent-solute interactions to the reaction process. The results were further discussed in the context of coupling between solvent and solute molecules in reaction processes.

Introduction

Solvent plays vital role in the chemical reaction process in solution. ^1-6 Unlike gas-phase reactions where the collisions between reacting species and subsequent energy transfer between a finite number of modes determine the kinetics and thermodynamics of the reaction process, solvent molecules are active partners of solution reactions. Even without the need for forming covalent interactions, solvent molecules can directly participate the reaction process by providing strong electrostatic and steric interactions with the solute molecule. Moreover, the dynamics of the solvent molecules provide a thermal bath for the reactions of the central solute molecules. In general, the effects of the solvent molecules on the reaction process can be categorized into equilibrium, or static, and non-equilibrium, or dynamic, contributions. The equilibrium effect can be measured as the difference between the free energy profile of the reaction processes in solution and in gas-phase which reflects a static thermodynamic effects of solvation, while the non-equilibrium or dynamic effect involves the short-time dynamic details of the solute and solvent motions, such as the re-crossing of the reaction barriers of the solute molecule modulated by the instantaneous motion of the solvent molecules. The latter is often summarized in the transmission coefficient in transition-state theory. Note that by this consideration the term “non-equilibrium” effect is different from what was defined in Ref (7).

Even though both the equilibrium and non-equilibrium effects of the solvent molecule contribute to the reaction rate, it is generally believed that for many reactions, especially those catalyzed in enzymes, the thermodynamic equilibrium effect dominates the reaction rates. ^7,8 The importance of the equilibrium contribution of solvent to the reaction process has been well illustrated by the electron transfer reaction described by Marcus theory. ^9-13 In this case, the sole reaction coordinate is the solvent interactions to the electron transfer center. Not only the reaction thermodynamics and rates can be quantitatively predicted by the equilibrium thermodynamics based on the solvent interactions, but also the important idea of re-organization energy was developed to capture the importance of the energetic contribution of the solvent to the reaction processes.

More complicated pictures about the solvent contributions have been explored by several research groups lately, ^2,4-6,14-21 in particular the dynamical effects of the solvent molecules, the quantum mechanical effects of the nucleic motions, and the possible coupling between solvent and solute dynamics. Warshel and his coworkers have discussed the contributions of general solvent, as well as enzyme environment as special solvent, to the reaction processes. ^2,20,22-24 After realizing the importance of the solvent molecules in the reaction processes, they constructed a 2-dimensional reaction surface in which a solute and a solvent reaction coordinate were used together to describe the reaction progress. ² The results provided a clear picture of the reaction process, which is especially useful in distinguishing possible coupling between solvent and solute during the reaction processes. A comprehensive discussion on their methods and research progress can be found in Ref. 25..

Despite the advances of the research in solution reactions, most simulations of reaction process still rely on a common approach which first defines a reaction coordinate of the solute geometry, such as selective sets of bond distances, bond angles and dihedral angles. The thermodynamics of the target system along the reaction process characterized by the variation of reaction coordinate were then determined by classical simulation approaches such as thermodynamic integration ²⁵ or umbrella sampling. ²⁶ The resulting free energy profile for the reaction process can lead to direct comparison to the experimental data, and the structural information of the solute molecule at different states, such as reactant state, transition state and product state, can be used to complement experimental studies. However, this approach lacks the details of solvent dynamics in different reaction states, in particular the answer to the important question regarding the role of possible coupling between solvent dynamics and solute dynamics in the reaction processes. ^23,27

Bearing in mind the importance of explicit description of solvent contributions in the reaction process, we developed an approach to quantify the solvent contribution to the reaction process. We defined an interaction term as characterization of solvent degree of freedom to the reaction process and determine a 2-D potential of mean force (PMF) surface from combined quantum mechanical/molecular mechanical minimum free-energy path (QM/MM-MFEP) simulation. ^28,29 The method was applied to a prototype S_N2 reaction of CH₃Cl + Cl^-. Our results showed, in a quantitative manner, the importance of the solvent degree of freedom in the reaction processes. The 2-D PMF provides a reference for determining the coupling between solute and solvent dynamics in general.

Theory

The progress of a chemical reaction process can often be characterized by the geometrical change of a selected group of atoms. Within the QM/MM context, it is convenient to describe the progress of the reaction system, e.g. reactant, product, and transition states, by the conformations of the QM subsystem. Therefore, following the previously developed QM/MM-MFEP method, ^28,29 we simplify the thermodynamics of the entire system by defining the PMF of a QM/MM system in terms of the QM conformation as

$$A({\mathbf{r}}_{QM})=\frac{1}{\beta }ln\left[\int exp(-\beta E({\mathbf{r}}_{QM},{\mathbf{r}}_{MM}))d{\mathbf{r}}_{MM}\right],$$ (1)

where E(r_QM, r_MM) is the total energy of the entire system expressed as a function of the coordinates of the QM and MM subsystems, r_QM and r_MM, respectively. The gradient of the PMF, i.e. the free energy gradient, is then

$$\frac{\partial A({\mathbf{r}}_{QM})}{\partial {\mathbf{r}}_{QM}}={\langle \frac{\partial E({\mathbf{r}}_{QM},{\mathbf{r}}_{MM})}{\partial {\mathbf{r}}_{QM}}\rangle }_{E,{\mathbf{r}}_{MM}},$$ (2)

which appears conveniently as the ensemble average of the gradient of the QM atoms, a term that can be obtained from MD simulations of the MM atoms. The notation 〈X〉_E,rMM indicates an average over the MM degrees of freedom in the ensemble generated from the energy function E(r_QM, r_MM):

$${\langle X\rangle }_{E,{\text{r}}_{MM}}=\frac{\int X({\mathbf{r}}_{MM})exp(-\beta E({\mathbf{r}}_{QM},{\mathbf{r}}_{MM}))d{\mathbf{r}}_{MM}}{\int exp(-\beta E({\mathbf{r}}_{QM},{\mathbf{r}}_{MM}))d{\mathbf{r}}_{MM}}.$$ (3)

Note that Eq. (2) is exact and is independent of the form of the energy function of the target QM/MM system. As will be discussed later, the use of QM/MM notation is not a restraint to the type of question the method can be applied to, i.e., it can be extended to systems beyond a QM/MM description. Eqs. (1) and (2) form the foundation for all methods that optimize the molecular conformation on a PMF surface, ^30-38 including the QM/MM-MFEP method. ^28,29 The main computational cost of the PMF comes from the statistical sampling of conformations of the MM subsystem required for the calculation of the QM PMF and its gradient. In our sequential sampling and optimization approach with the QM/MM-MFEP method, we reduced the amount of MM sampling while still retaining the accuracy of the results by first carrying out MM phase-space sampling and then optimizing the QM subsystem in the fixed-size ensemble of MM conformations. The resulting QM optimized structures are then used to obtain more accurate sampling of the MM subsystem. This process of sequential MM sampling and QM optimization is iterated until convergence. The use of a fixed-size, finite MM conformational ensemble enables the precise evaluation of the QM potential of mean force and its gradient within the ensemble, thus circumventing the challenges associated with statistical averaging and significantly speeding up the convergence of the optimization process. ^28,29 The resulted reaction path contains discrete, sequential conformational states of the reaction process. The conformational states can be projected to any defined reaction coordinate, yielding a 1-dimensional free energy profile.

Our interest here is to examine the contributions of the solvent molecules in addition to the conventional picture of using solute geometry as the descriptors. Ideally, if there is a solvent degree of freedom S, we would like to be able to carry out extended QM/MM-MFEP simulations with S also being included as one active degree of freedom in the PMF description, i.e., A(r_QM,S). Let us assume that S is a collective degree of freedom for MM solvent molecules. Technically, the PME description will place several conditions on the selection of this solvent degree of freedom. First, the choice of this solvent degree of freedom must be physically meaningful and reflects the correct physics. Second, to optimize the structure on the extended PMF surface, one needs to be able to compute the PMF gradient for S,

$$\frac{\partial A({\mathbf{r}}_{QM},\mathbf{S})}{\partial \mathbf{S}}={\langle \frac{\partial E({\mathbf{r}}_{QM},\mathbf{S},{\mathbf{r}}_{MM})}{\partial \mathbf{S}}\rangle }_{E,{\mathbf{r}}_{MM}},$$ (4)

The derivative in the bracket can be computed by

$$\frac{\partial E({\mathbf{r}}_{QM},\mathbf{S},{\mathbf{r}}_{MM})}{\partial \mathbf{S}}=\frac{\partial E({\mathbf{r}}_{QM},\mathbf{S},{\mathbf{r}}_{MM})}{\partial {\mathbf{r}}_{MM}}\frac{\partial {\mathbf{r}}_{MM}}{\partial \mathbf{S}},$$ (5)

When S is a linear function of r_MM, the above term can be easily computed during MD simulations of r_MM. When S is a nonlinear function of r_QM, however, calculation of the last term on the right hand side of Eq. 5 becomes troublesome.

Warshel has developed a solvent term to describe the solvent contribution to the reaction process. Even though the term is defined in a rather complicated fashion, ² it is in fact in equivalent to the electrostatic interaction energy difference between the two exchanging atoms. For the self-exchanging reaction of CH₃Cl + Cl^-, that is,

$$\mathbf{S}=\sum _{i\in MM}\left(\frac{q_i{Q}_A}{r_{iA}}-\frac{q_i{Q}_B}{r_{iB}}\right).$$ (6)

Here q_i is the charge of MM atom i, A and B denote the two chlorine atoms of the reaction system, and Q_A and Q_B are the charges of the two atoms, respectively. Assuming the charges are invariant to the external MM charges,

$$\begin{array}{c}\begin{array}{cc}& \frac{\partial \mathbf{S}}{\partial {\mathbf{r}}_i}=\frac{-q_i{Q}_A}{r_{iA}^2}\frac{\partial r_{iA}}{\partial {\mathbf{r}}_i}-\frac{-q_i{Q}_B}{r_{iB}^2}\frac{\partial r_{iB}}{\partial {\mathbf{r}}_i}\end{array}\\ \begin{array}{cc}\frac{\partial E({\mathbf{r}}_{QM},\mathbf{S},{\mathbf{r}}_{MM})}{\partial \mathbf{S}}& =\sum _{i\in MM}\frac{\partial E({\mathbf{r}}_{QM},\mathbf{S},{\mathbf{r}}_{MM})}{\partial {\mathbf{r}}_i}/\left[\frac{-q_i{Q}_A}{r_{iA}^2}\frac{\partial r_{iA}}{\partial {\mathbf{r}}_i}-\frac{-q_i{Q}_B}{r_{iB}^2}\frac{\partial r_{iB}}{\partial {\mathbf{r}}_i}\right]\end{array}\end{array},$$ (7)

In the present work, we will combine this solvent degree of freedom with the original solute QM degrees of freedom for the QM/MM-MFEP calculations. Nonetheless, note the use of point charges of the two chlorine atoms in the expression; this requires a classical description of the QM system, which can be easily done in the EVB model, but may not be generally available for other QM methods. In the QM/MM-MFEP methods, this is not a problem since the QM ESP charges are used in the approximate QM/MM energy functions. ^28,29,39-41

To minimize the reactant state on the combined surface of S and r_QM, one has to carry out constrained molecular dynamics simulations for given values of S and r_QM. The constraining force for r_QM is easy to compute, as shown previously. But the constraining force for S is not so easy to compute. Instead of direct simulations with extended solvent degree of freedom S, we note that the inclusion of S in the QM/MM-MFEP simulations in principle should not alter the position of stationary points on the reaction PMF surface, because the chemical degrees of freedom are still relevant to the progress of chemical reactions, unlike the case of electron transfer process. The projection of the positions of the minimum on the direction of r_QM should be the same no matter S is included in the active degrees of freedom of the PMF or not. Therefore, we took a posterior approach. That is, we first carry out MFEP simulations in which solute geometry was fixed at discrete values r_QM on the reaction path, i.e., different states. For each state, the value of S was computed and recorded during the MD simulations. After the simulation, the probability distribution of S, P(r_QM,S), at each state i was computed. The probability distribution can be properly normalized to generate a 2-D PMF value,

$$\begin{array}{c}A({\mathbf{r}}_{QM})=-\frac{1}{\beta }ln\left[\int P({\mathbf{r}}_{QM},\mathbf{S})d\mathbf{S}\right]\\ A({\mathbf{r}}_{QM},\mathbf{S})=-\frac{1}{\beta }lnP({\mathbf{r}}_{QM},\mathbf{S}),\end{array}$$ (8)

Simulation details

The system setup was identical to previous simulations. ²⁸ B3LYP/6-31+G* was employed as the QM method for the solute molecule. The reaction path from previous QM/MM-MFEP simulation was used as the initial conformations. For each conformation on the path, 180 ps MD simulation was performed. During the simulation, S, as defined in Eq. 6, was computed and recorded for each MD step. The QM charges were determined by fitting QM electrostatic potentials as described.³⁹

Results and Discussion

Fig. 1 depicted the evolution of the solvent contribution S, for the reactant, transition, and product states, respectively. It is evident that the magnitude of S is on the order of a few tens of kcal/mol, much larger than the free energetics of the reaction process. The fluctuation of S is on the order of 10 kcal/mole, comparable to the barrier height of the reaction process.

Figure 1.

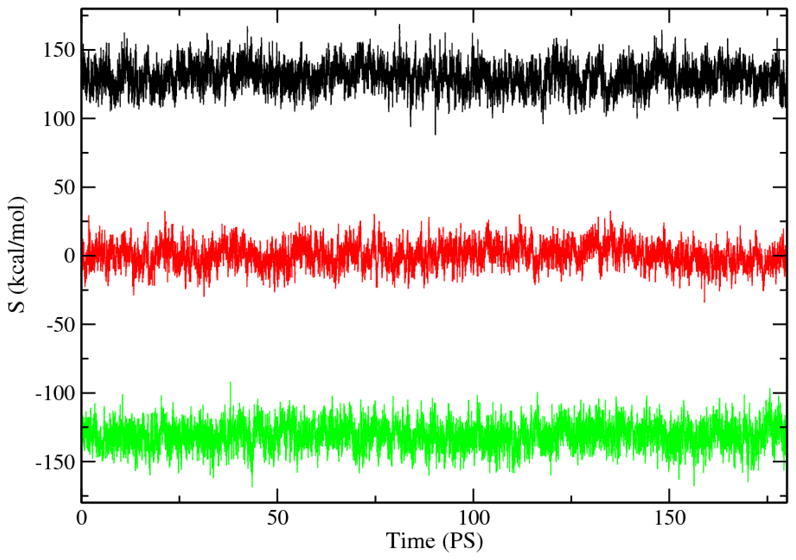
Evolution of S during the MD simulations of the reactant (black), transition (red), and product (green) states.

Fig. 2 depicted the 2-D PMF surface of the S_N2 reaction in solution. From the figure, it is obvious that the initial stages of the reaction proceed by the change of solute geometries. In the central region around transition state, both solute and solvent make very important contributions to the reaction process. This result is in agreement with previous simulations which noted that the variations of the charge of the two Cl atoms were small in the initial stage of the reaction process, thus the solvent interactions were constant and made minimal contribution to the reaction process. ² When the system is near the transition state, the charges change drastically and thus the solvent interactions play important energetic roles in this stage.

Figure 2.

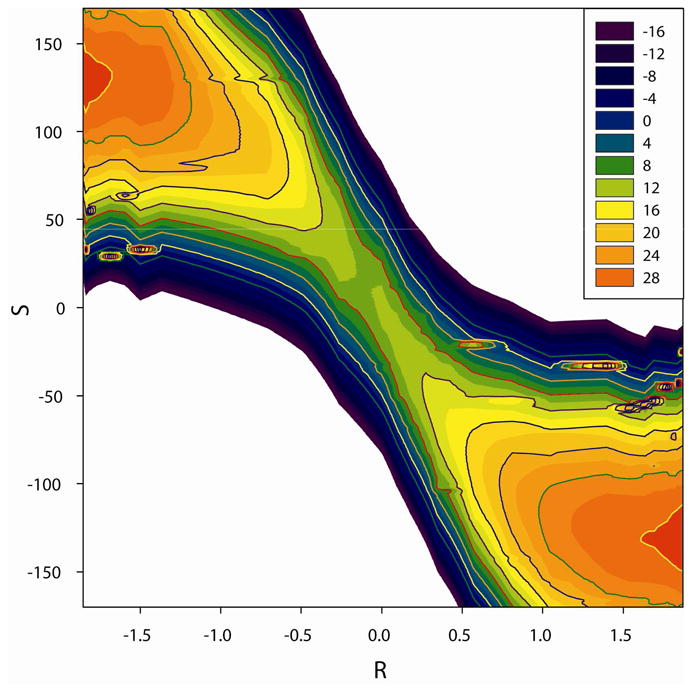
2-D potential of mean force surface for the S_N2 reaction in solution.

The 2-D PMF can be very useful in the future simulation study of solution and enzyme reactions. On one hand, the 2-D surface can allow further exploration of dynamic effects in the reaction process; as such, the non-equilibrium effect can be analyzed based on the detailed dynamics simulation on this surface. ⁴² On the other hand, this plot provides the most straightforward answer to the very challenging question in the current study of enzyme catalysis, that is, what is the role of conformational dynamics in the enzyme catalysis and can a specific motional mode couple with the catalytic process? In fact, a recent work started to attack this very important problem. ⁴³ Nonetheless, as noted in that work, this problem remains challenging to theoretical research because of several technical issues such as the convergence of the calculation and proper weighting of the conformational ensembles. Obviously, the method presented here offers one possible means for the further exploration of this subject.

If we treat the protein dynamics as the solvent degree of freedom in the current work, in our view, we can category three different scenarios for the possible coupling between enzyme conformational dynamics and enzyme catalysis (Fig 3).

Figure 3.

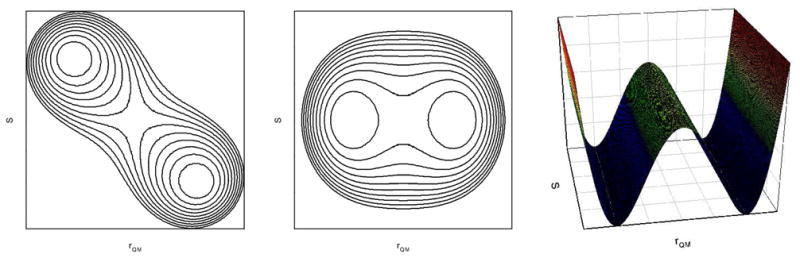
Three possible schemes for the coupling between solvent and solute degrees of freedom in the reaction processes. (a) direct coupling; (b) gated; and (c) completely independent.

The first scenario is a specific motional mode may couple with the catalysis, resulting a diagonal 2-D PMF plot for the geometrical degree of freedom of solute and the specific motional mode of proteins (Fig 3a). For some enzymes, or for some motional modes, the reaction may become “conformation gated” (Fig. 3b). That is, the catalysis only occurs when the protein conformations are within certain region of the phase space; outside this region, catalysis cannot occur. In contrast to this model, it is possible, at least in principle, that a reaction may proceed at any conformational state of the protein (Fig. 3c). The resulted 2-D plot contains two running low-free-energy channels along the solvent degree of freedom, one for the reactant state, and the other for the product state, respectively. For enzyme catalysis, the third scenario is very unlikely; otherwise, there is no meaning for the evolving of such complicated molecular machines.

As the direct coupling and gating mechanism are both possible for the enzyme catalysis, identifying the modes in the simulation of enzyme catalysis becomes crucial. As the direct simulations of conformational dynamics and catalysis are computationally very expensive, especially for the ab initio QM/MM methods, our approach provides an efficient way for addressing these issues. One may first carry out ordinary QM/MM-MFEP simulations to determine the reaction path and free energetics; afterwards, the trajectories obtained in the QM/MM-MFEP simulations can be used for the analysis of coupling scheme between any specific conformational motional mode and catalysis.

Our models (Fig. 3) provided the schematic pictures for different correlations between conformational dynamics and catalysis. As pointed out by Warshel, ^2,23 we also like to note that more complicated scenarios can be developed. As shown in Fig. 4, even though both cases can be regarded on some extent as coupled solvent and solute degrees of freedom for the reaction process, one can be regarded as solvent driven while the other can be regarded as solute driven. Therefore, extra care must be taken for the identification of the motional modes and analysis of the coupling.

Figure 4.

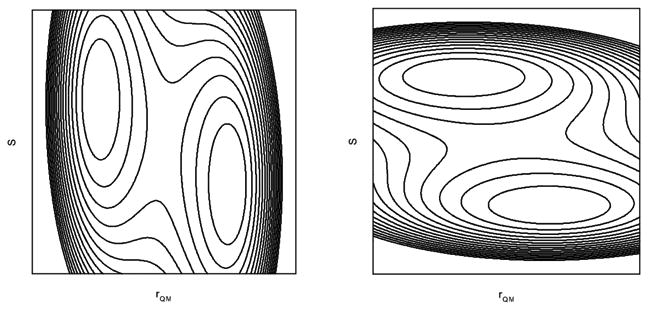
Different coupling schemes for solvent and solute degrees of freedom.

The focus of the current work is different from many previous researches. While many previous studies have demonstrated the complicated effects of the localized vibrations in the active site on the reaction rates, ^44-48 here we are more interested in the equilibrium or thermodynamic impact of large-scale motions on the reaction energetics. We believe that by properly choosing the active site, part or even most of the classical effects of active-site vibrations can be considered in the ordinary QM/MM simulations. However, because of the broad range of the timescales of the enzyme conformational motions, it is unlikely that large-scale, slow motions can directly couple to localized, fast vibrations in the active site. Therefore, the contributions of large-scale motions are most probably to be classical and might be explored by approaches described in the current and previous works.

The solvent coordinate used in the current work is an approximated energy term characterizing the electrostatic interactions of the solvent applied to the solutes. If one wants to explore the coupling between specific solvent coordinate, a more general and rigorous definition of solvent coordinate can be defined according the requirement discussed in (Eqs. (4) to (7). In the case of enzyme catalysis, it might be possible to use collective degree of freedom as the reaction coordinate, such as the distances and angles between different domains, or the shape and even radius of gyration of certain structural subsystems. ⁴³ This is also the conformational coordinate that can be designed to explore as in Fig. (3). It has been argued that the protein conformational motions are slaved by the solvent fluctuations; ⁴⁹ from this point of view, a general solvent coordinate might exist and remains to be defined.

Previous work has proposed plots similar to the coupling schemes discussed in the current work. ^50,51 From our understanding, there are some fundamental differences between the schemes discussed here and previously. ⁵⁰ The coupling schemes we discussed here are for the conformational dynamics in the catalytically-ready reactant and product states, while the conformational dynamics discussed in the previous work are in fact conformational transitions between discrete states along the whole reaction processes, starting from binding of the substrates to the formation of catalytically-active conformations Q_catalysis. In other words, we are more concerned with the role of conformational dynamics in an elementary reaction step while previous work more focused on the entire catalytic cycle. This difference might also indicate some current confusion on the definition of the coupling between conformational dynamics and catalysis.

Conclusion

We show here that posterior analysis of the results of QM/MM-MFEP simulation of solution reactions can be used to examine the important reactive degrees of freedom from solvent. Our method provides an efficient, quantitative and straightforward, though indirect, evidence for the challenging issue regarding coupling between protein dynamics and enzyme catalysis; it can play important roles in the future computer simulation of enzyme catalysis.