SweeD: Likelihood-Based Detection of Selective Sweeps in Thousands of Genomes

Abstract

The advent of modern DNA sequencing technology is the driving force in obtaining complete intra-specific genomes that can be used to detect loci that have been subject to positive selection in the recent past. Based on selective sweep theory, beneficial loci can be detected by examining the single nucleotide polymorphism patterns in intraspecific genome alignments. In the last decade, a plethora of algorithms for identifying selective sweeps have been developed. However, the majority of these algorithms have not been designed for analyzing whole-genome data. We present SweeD (Sweep Detector), an open-source tool for the rapid detection of selective sweeps in whole genomes. It analyzes site frequency spectra and represents a substantial extension of the widely used SweepFinder program. The sequential version of SweeD is up to 22 times faster than SweepFinder and, more importantly, is able to analyze thousands of sequences. We also provide a parallel implementation of SweeD for multi-core processors. Furthermore, we implemented a checkpointing mechanism that allows to deploy SweeD on cluster systems with queue execution time restrictions, as well as to resume long-running analyses after processor failures. In addition, the user can specify various demographic models via the command-line to calculate their theoretically expected site frequency spectra. Therefore, (in contrast to SweepFinder) the neutral site frequencies can optionally be directly calculated from a given demographic model. We show that an increase of sample size results in more precise detection of positive selection. Thus, the ability to analyze substantially larger sample sizes by using SweeD leads to more accurate sweep detection. We validate SweeD via simulations and by scanning the first chromosome from the 1000 human Genomes project for selective sweeps. We compare SweeD results with results from a linkage-disequilibrium-based approach and identify common outliers.

Introduction

The seminal paper by Maynard Smith and Haigh (1974) coined the term “selective sweep,” that is, the evolutionary process where a strongly beneficial mutation emerges and spreads in a population. As a consequence, the frequency of linked neutral or weakly selected variants will increase. The authors showed that, in sufficiently large populations, the hitchhiking effect drastically reduces genetic variation near the positively selected site, thereby inducing a so-called selective sweep. According to their deterministic model, diversity vanishes at the selected site immediately after the fixation of the beneficial allele. Additionally, the model makes the following predictions as the distance from the site of the beneficial allele increases: First, diversity accumulates, second, the distribution of the frequencies of segregating sites changes, and third, linkage disequilibrium (LD) patterns emerge around the target site of the beneficial mutation.

Neutral mutations are assumed to arise in a sufficiently large population at a rate of 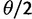, (, 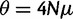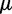being the mutation probability per site and per generation). According to the infinitely many sites model (Kimura 1969), they occur at previously monomorphic sites. Initially, they are present at each mutated site as single copy. The site frequency spectrum (SFS) of a population denotes the distribution of the expected number of polymorphic sites, 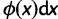, at which the derived allele has a frequency in 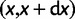, 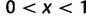. Kimura (1971) demonstrated that the SFS for the standard neutral model is given by 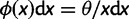. For the selective sweep model, Fay and Wu (2000) have shown that the frequency spectrum of neutral sites which are sufficiently close to the beneficial mutation shifts toward an excess of high- and low-frequency derived alleles in proportions 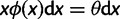and 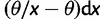, respectively. Although the aforementioned neutral and selective models assume a constant population size, analytical results for the SFS have also been obtained for scenarios in which the population is subject to deterministic size changes (e.g., Griffiths 2003). However, deriving an analytical approximation of the SFS when sites are subject to genetic hitchhiking (in populations with varying size over time) still remains a challenge.

Regarding analyses of DNA sequence data, the sample SFS (instead of the population SFS) is of interest. The sample SFS, 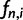, is the distribution of the expected number of sites at which there are i derived alleles, 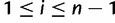, in a sample of n sequences. The relative frequencies are obtained from these absolute frequencies via division by the total number of segregating sites. If the derived allele can not be distinguished from the ancestral allele, the folded version of the SFS is used. 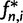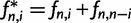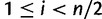The folded SFS, , is given by for and 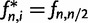for even n and 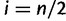. Kim and Stephan (2002) interpreted 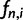as the probability of observing a single site where derived alleles are found in a sample of size n. The authors used the derivation of the SFS by Fay and Wu (2000) to develop the first composite likelihood ratio (CLR) test for detecting selective sweeps in typically small (up to a few hundred kilobases) genomic regions (henceforth called subgenomic regions). Nielsen et al. (2005) introduced two major modifications to the CLR method by Kim and Stephan (2002) for detecting selective sweeps in whole-genome data.

First, instead of using the model by Fay and Wu (2000) that relies on the population mutation parameter 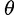, Nielsen et al. (2005) proposed a model that quantifies the frequency of an allele at a distance d from the beneficial mutation independently of 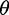by conditioning on the observation of a single nucleotide polymorphism (SNP). Second, instead of employing the theoretical result for the SFS (Kimura 1971) that assumes standard neutrality as also assumed by Kim and Stephan (2002), Nielsen et al. (2005) use the empirical SFS of the entire data set to obtain the neutral background. The first modification allows for applying the test to large-scale genome data, where 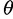can vary among regions. The second modification increases the robustness of the algorithm under demographic models (e.g., mild bottlenecks). It implicitly accounts for this by using the empirical SFS that is obtained from the entire genome. Nielsen et al. (2005) implemented their method in SweepFinder (http://people.binf.ku.dk/rasmus/webpage/sf.html, last accessed June 29, 2013). In the numerator of the CLR test, SweepFinder calculates the likelihood of a sweep at a certain position in the genome by optimizing 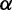. The denominator (the neutral model) is given by the product of the empirical SFS over all SNPs. As SNPs are assumed to be independent, the overall likelihood for the genetic hitchhiking model is calculated as the product over the per-SNP likelihood scores.

With next generation sequencing technologies, it has now become feasible to sequence whole genomes of thousands of individuals from a single species and to reliably detect the genomic locations of selective sweeps. Selective sweep prediction accuracy increases with the number of sequence samples. For instance, Jensen et al. (2007) showed that distinguishing selective sweeps from demographic events in samples of moderate size (50 samples) is easier than in smaller samples (12 samples). Nowadays, samples that comprise hundreds or even thousands (e.g., The 1000 Genomes Project Consortium 2012; http://www.1000genomes.org, last accessed June 29, 2013) of sequences are becoming available. Hence, selective sweep detection is expected to become more accurate. However, the increasing sample sizes and sequence lengths pose novel algorithmic, numerical, and computational challenges for selective sweep detection. Numerically stable implementations that can handle arithmetic over- and/or underflow are required. An efficient use of scarce computing and memory resources is also required. Furthermore, efficient parallel implementations are needed to analyze large data sets within reasonable times on state-of-the-art multi- and many-core processors.

At present, only a handful of tools that scale to thousands of whole-genome sequences is available. The implementation of the CLR test by Kim and Stephan (2002) can only be used for analyzing small subgenomic regions. Jensen et al. (2007) and Pavlidis et al. (2010) used the ω-statistic (Kim and Nielsen 2004), which relies on the LD signature of a selective sweep to detect positively selected sites. The respective implementations are also only able to handle subgenomic regions. SweepFinder (Nielsen et al. 2005) can analyze whole genomes efficiently, but only for up to a few hundred sequences. For larger sample sizes, execution times increase substantially. Moreover, SweepFinder can not analyze samples with more than 1,027 sequences because numerical problems associated to floating point underflow are not handled. Finally, SweepFinder only runs on a single core. To the best of our knowledge, the ω-statistic based OmegaPlus tool (Alachiotis et al. 2012) represents the sole publicly available high-performance implementation for detecting selective sweeps at this scale. OmegaPlus can efficiently analyze whole genomes from thousands of individuals by exploiting all available cores on a modern desktop or server. Even though both SweeD and OmegaPlus were designed to detect targets of recent positive selection, they are not equivalent, and OmegaPlus cannot substitute SweeD. First, in contrast to SweeD, OmegaPlus detects the LD signature of a selective sweep. Thus, OmegaPlus can be used only when haplotypes are known. In contrast, SweeD can analyze samples for which the allelic frequencies have been assessed. Thus, it can process unphased data sets or even pooled samples. Furthermore, Pavlidis et al. (2010) have shown that combining OmegaPlus with SweeD increases the power of selective sweep detection. Therefore, SweeD is expected to facilitate fast and accurate detection of recent positive selection.

New Approaches

In the following, we describe SweeD (Sweep Detector), our open-source tool for the SFS-based rapid detection of selective sweeps at the whole-genome scale. The SweeD code is based on SweepFinder (Nielsen et al. 2005) and incorporates the following new features and algorithmic techniques: Via respective program parameters the SFS can be calculated analytically for demographic models that comprise an arbitrary number of instantaneous population size changes and, optionally, also an exponential growth as the most recent event. Thereby, a neutral SFS can be obtained without the need to compute the empirical average SFS for the genome.

Moreover, SweeD can analyze thousands of genomes because we appropriately modified the numerical implementation. For a large number of genomes, the double precision floating-point range is frequently insufficient. This may lead to numerical over- or underflow. SweeD is able to analyze such large samples because it performs several calculations at the logarithmic scale.

The code can also parse several additional input file formats to read in simulated and real data sets. Regarding real data sets, it supports the FASTA and VCF formats. The VCF format is widely used in next generation sequencing projects, such as, for instance, the 1000 Genomes project (http://www.1000genomes.org). With respect to simulated data sets, SweeD supports ms (Hudson 2002) and MaCS (Chen et al. 2009) formats.

Furthermore, SweeD can exploit all available cores on a shared-memory multi-core processor to substantially expedite the analysis of huge data sets that comprise millions of SNPs and thousands of sequences.

Finally, SweeD offers a checkpointing capability that allows to resume an analysis from the point where it failed. Therefore, SweeD does not need to be re-run from scratch in such situations. This mechanism allows for saving CPU time and energy in the case of hardware failures or cluster queues with time limits.

Results and Discussion

In the following, we present a performance comparison between SweeD and SweepFinder, assess the efficiency of the parallel implementation, and provide a usage example.

Sequential Performance

For comparing the performance of SweeD versus SweepFinder, we generated simulated data sets with up to 1,000 sequences and 1,000,000 sites using msms (Ewing and Hermisson 2010). We slightly modified the source code of msms to obtain output files that can be parsed by SweepFinder (the modified version of msms is available at: http:/exelixis-lab.org/software.html, last accessed June 29, 2013). We generated data sets with and without selection. For neutral data sets, we used msms to perform simulations with a fixed number of SNPs (option -s). The recombination rate for the entire locus was set to a value of 5,000 and we assumed that there can be up to 5,000 recombination breakpoints (−r 5,000, 5,000). The number of recombination events is not critical for our study, because performance solely depends on the number of sequences and the number of SNPs. Therefore, we used small values for the recombination rate and the number of breakpoints to accelerate the simulations. Regarding simulations with selection, we used the same recombination rate as above and simulated a fixed number of SNPs (similar to the neutral simulations to obtain comparable results). The effective population size was set to N := 1,000,000. The location of the selected allele was placed into the middle of the simulated region (−Sp 0.5). The beneficial allele became fixed in the population at time 0.001 (in units of 4N generations) in the past. Selection intensity for homozygotes of type AA was 10,000, for heterozygotes (Aa) 5,000, and for the homozygotes of type aa 0. The command line parameters we used are provided in the supplementary material (supplementary section S1, Supplementary Material online). The programs were executed on an unloaded AMD Opteron 6174 processor with 12 cores running at 2.2 GHz under Ubuntu Linux.

As shown in table 1, SweeD outperforms SweepFinder on all data sets. The total execution times for both programs increase with the number of sequences and the number of SNPs. Run-times are dominated by two computationally expensive parts in both programs: 1) the pre-computation of a fixed number of likelihood values at given distances (in scaled units) around the position of the selective sweep, and 2) the computation of the CLR test at those positions as specified by the user via the -grid option. To precompute the likelihood values at certain distances around the position of the selective sweep, SweeD executes the arithmetic operations in a different order than SweepFinder. SweeD employs a lookup table to store these intermediate results such that they can be subsequently reused for the precomputation of the constant, fixed likelihood values. In contrast, SweepFinder recalculates these intermediate constant values on-the-fly. The performance benefit of using a lookup table can be observed when the number of sequences is increased, because the number of lookups (redundant recalculations in SweepFinder) is proportional to the number of sequences. For a small number of sequences, lookups, and recalculations need approximately the same time. As the number of sequences increases, the lookup-based approach outperforms the recalculation approach. SweeD and SweepFinder employ the same method to compute the CLR test at a specific position. However, we optimized the CLR computation in SweeD via low-level technical optimizations. Nonetheless, the computation of the CLR test as such is only marginally faster in SweeD.

Table 1.

Total Execution Times and Speedups for Simulated Data Sets with and without Selection.

Sequences	SNPs	SweepFinder		SweeD		Speedup
		Neutral	Selection	Neutral	Selection	Neutral	Selection
50	10,000	199.908	434.744	142.200	399.440	1.406	1.088
50	100,000	2,005.075	4,380.188	1,085.240	3,563.890	1.848	1.229
50	1,000,000	34,563.920	52,560.680	8,881.410	32,466.250	3.892	1.619
100	10,000	207.123	427.885	142.650	400.050	1.452	1.070
100	100,000	1,924.353	3,695.948	1,082.370	2,890.020	1.778	1.279
100	1,000,000	32,140.840	45,531.370	9,013.630	23,762.100	3.566	1.916
500	10,000	984.357	869.217	158.730	181.100	6.201	4.800
500	100,000	2,548.083	2,991.866	1,121.820	1,841.540	2.271	1.625
500	1,000,000	23,431.980	45,118.190	9,091.370	16,684.070	2.577	2.704
750	10,000	2,382.910	2,418.270	186.660	231.510	12.766	10.446
750	100,000	4,172.555	4,657.067	1,120.780	1,810.410	3.723	2.572
750	1,000,000	29,006.060	—*	9,181.570	20,601.350	3.159	—*
1,000	10,000	5,375.578	5,385.314	244.460	270.410	21.990	19.915
1,000	100,000	7,031.194	7,435.575	1,173.320	1,751.660	5.993	4.245
1,000	1,000,000	27,360.160	29,893.300	9,214.810	13,036.350	2.969	2.293

*SweepFinder terminated abruptly due to a failed assertion: “SweepFinder: SweepFinder.c:595: ln_likelihood: assertion P ≥ 0.0, P < 1.00000001 failed.”

Table 1 also shows that, for a small number of sequences, SweeD becomes faster than SweepFinder as the number of SNPs increases. This is because the order and the number of operations at each position, where the CLR is calculated, is different in SweeD (see section Arithmetic deviations from SweepFinder for more details). We obtained speedups between 1.07× and 3.90×. For larger numbers of sequences (1,000), the speedup of SweeD over SweepFinder drops from 22× (10,000 SNPs) to 2.9× (1,000,000 SNPs) with an increasing number of SNPs because a larger fraction of overall execution time is spent in CLR computations.

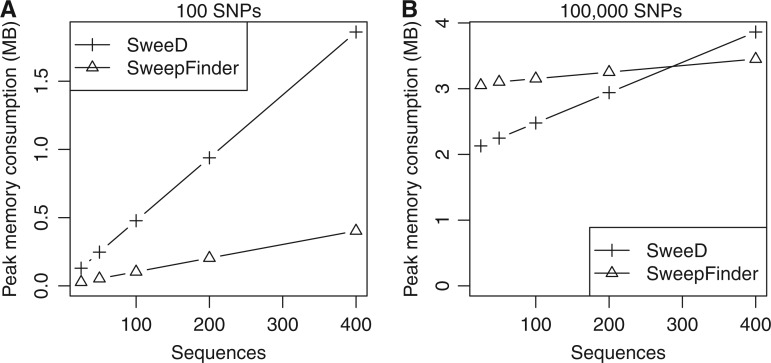
Due to the aforementioned lookup table, SweeD requires more memory than SweepFinder. Figure 1 shows the peak memory consumption for SweeD and SweepFinder as a function of the number of sequences for a data set of 100 SNPs (fig. 1A) and for a data set of 1,000,000 SNPs (fig. 1B). For these specific data sets and large sample sizes (400 sequences), SweeD consumes more memory (4.6 and 1.2 times, respectively) than SweepFinder. Nonetheless, the memory requirements only increase linearly with the number of sequences for both programs. Despite the larger memory footprint of SweeD, the additional memory for storing the lookup table is negligible with respect to the memory capacity of modern computers. For instance, the peak memory consumption for the data set of 1,000,000 SNPs and 400 sequences is less than 4 MB. Even for very large data sets, with 10,000 sequences, SweeD only requires approximately 24 MB. Thus, the analysis of very large population genetics data sets is feasible. SweeD uses the same suite of parsers as OmegaPlus for ms, MaCS, VCF, and FASTA files. As the parser suite is not yet fully optimized for memory efficiency, SweeD may exhibit temporary (during parsing and conversion into the internal SF data format) memory consumption peaks (depending on the input format), which exceed the amount of memory required for the actual computations. These temporary memory consumption peaks are not observed when data is in SF format.

Fig. 1.

Comparison of peak memory consumption between SweeD and SweepFinder. Simulated data sets of 100 SNPs (A) and 100,000 SNPs (B) and 25, 50, 100, 200, and 400 respective sequences were used for the measurements. Memory consumption was quantified with the massif tool of the valgrind software (Seward and Nethercote 2005). In most cases, SweeD consumes more memory than SweepFinder due to the lookup table implementation. However, memory consumption is in the order of MBs even for very large data sets.

Parallel Performance

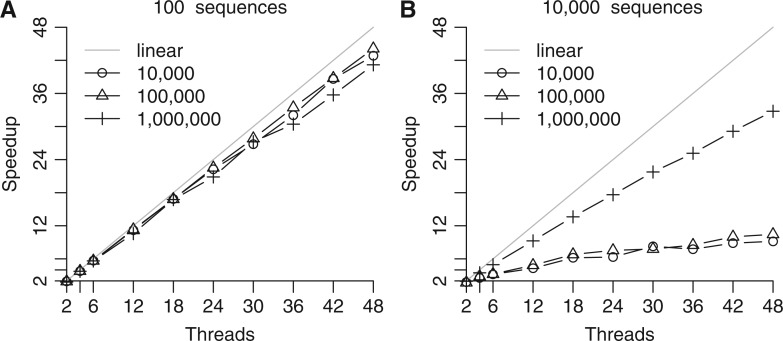
To assess the parallel efficiency of SweeD, we generated data sets with up to 10,000 sequences and 1,000,000 sites. Figure 2 shows the respective speedups for up to 48 cores/threads (4 AMD Opteron 6174 processors) on simulated data sets with 100 and 10,000 sequences, and 10,000, 100,000, and 1,000,000 SNPs, respectively. The execution times for the sequential analysis of the data set with 100 sequences are shown in table 1. The data sets with 10,000 sequences as well as 10,000, 100,000, and 1,000,000 SNPs required 8.5, 9, and 10.3 h, respectively.

Fig. 2.

Speedup measurements using up to 48 cores for the analysis of simulated data sets consisting of 100 (A) and 10,000 (B) sequences with 10,000, 100,000, and 1,000,000 SNPs, respectively.

As can be observed in figure 2A, the parallel implementation scales well with the number of cores, achieving speedups between 41× and 45× on 48 cores for the small sample of 100 sequences. In contrast, figure 2B shows speedups that only range between 7× and 32× for the large sample of 10,000 sequences on 48 cores. This is due to the small proportion of SNPs in the comparatively large number of sequences, which in turn leads to a significantly larger amount of time spent in the BFGS (Broyden–Fletcher–Goldfarb–Shanno; Fletcher 1987) algorithm that optimizes the neutral SFS. More specifically, the BFGS algorithm estimates the neutral SFS that maximizes the probability of the data set (i.e., the overall likelihood) given the input SFS and the data. This step is needed because the input data set may contain missing data, and thus the input SFS does not correspond exactly to the sample SFS. These likelihood computations have been parallelized. However, when the number of SNPs is small with respect to the number of sequences, substantially more iterations (and hence thread synchronization events) are required for the BFGS algorithm to converge. This step cannot be further parallelized because the iterative optimization procedure uses the likelihood values sequentially, that is, there exists a hard-to-resolve sequential dependency between iterations i and i + 1.

For example, when we analyze the data set with 10,000 sequences and 10,000 SNPs, the BFGS algorithm computes the likelihood of the input data set conditional on the SFS 4,477,114 times, whereas only 396 such likelihood calculations are required for the data set with 100 sequences and 10,000 SNPs.

The parallel efficiency of each iteration improves with an increasing number of SNPs because more computations are carried out per iteration/synchronization event. Therefore, for 10,000 SNPs and 10,000 sequences we observe the worst-case speedup of 7 due to an unfavorable combination of relatively few SNPs (low workload per iteration) and a large number of such parallel iterations (4,477,114). For the same sample size, but with 1,000,000 instead of 10,000 SNPs, the parallel efficiency improves and we obtain near-linear speedups (32×).

As a parallel implementation of SweepFinder is not available as a reference, we report on OmegaPlus performance as a rough reference. Compared with OmegaPlus, SweeD exhibits better parallel efficiency, as it scales well up to 48 cores in most cases. Parallel OmegaPlus only scales up to 12 cores (Alachiotis et al. 2012). Note however that, for a single core or a small number of cores (up to 12 in our tests), OmegaPlus outperforms SweeD due to algorithmic innovations and because it mostly relies on integer rather than on floating-point arithmetics.

Larger Samples Improve the Accuracy of Selective Sweep Detection

We examined the effect of sample size on the accuracy of sweep detection. For this purpose, we performed simulations for constant populations and populations with bottlenecks. We used msms (Ewing and Hermisson 2010) to simulate a single selective sweep in the middle of a 400-kb long genomic fragment. Selective sweep simulations were performed by conditioning on the trajectory of the beneficial mutation (option -pTrace). We did not use msms to generate the trajectory of the beneficial mutation because msms cannot guarantee the fixation of the beneficial allele when past population size changes have taken place. Furthermore, the most recent version of msms (v.3.2rc-b80) reported memory errors when reading in the trajectory of the beneficial mutation. Thus, we modified the source code of msms to use external trajectories of the beneficial allele, which were simulated with a modified version of the program mssel that was kindly provided by R. R. Hudson. The modified versions of both, mssel and msms are available at http://exelixis-lab.org/software.html (last accessed June 29, 2013).

To simulate the trajectory of the beneficial mutation we used uniformly distributed selection coefficients between the boundaries 0.001 and 0.005. The present-day population size is 1,000,000. Thus, α := 4Ns, where s is the selection coefficient and N the effective population size, ranges between 4,000 and 20,000, that is, strong selection. The beneficial mutation appears in the population at a uniformly distributed point in time between the present (time 0) and 150,000 generations in the past. The final frequency of a beneficial mutation exceeded 0.999. If the beneficial allele did not reach fixation, the simulation was rejected and a different uniformly distributed time point was chosen. Thus, the starting time points of the alleles that were not rejected may not be uniformly distributed.

For simulating selective sweeps in constant populations, we used the following parameter values: θ := 4Νμ = 4,000 (N is the effective population size, and μ the mutation rate for the whole fragment per individual and per generation) and ρ := 10,000. The beneficial allele is located at the middle of the simulated 400-kb fragment (i.e., at position 200,000). The command lines generating these data sets using msms are provided in the supplementary material (supplementary section S2, Supplementary Material online). Scripts that used to generate and analyze simulated data can be downloaded at http://exelixis-lab.org/software.html. Samples from populations with bottlenecks were also generated with msms. In the first scenario, the population size was decreased by a factor of 100 at time 0.0375 to attain its present-day level at time 0.03875 (time is measured in units of 4N generations and proceeds backwards; 0.0375 corresponds to 150,000 generations). We have simulated three additional bottlenecks to further generalize the results. The parameters of these bottleneck models (supplementary section S3 and fig. S1, Supplementary Material online) have been chosen to generate site frequency spectra that are characterized by 1) excess of low-frequency derived alleles, 2) excess of low- and high-frequency derived alleles, and 3) excess of intermediate- and high-frequency derived alleles.

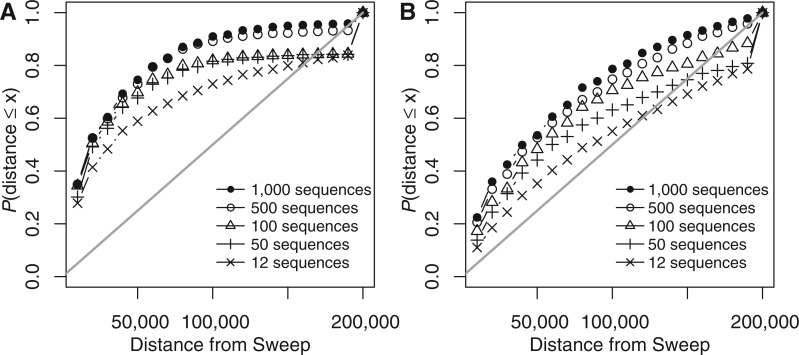
To estimate the accuracy of sweep detection as a function of increasing sample size n, we simulated 1,000 data sets for five sample sizes, n := 12, 50, 100, 500, and 1,000. For each simulated instance we used SweeD to infer the position where the likelihood ratio value is maximized. We then calculated the distance between the inferred and the true position (in the middle of the 400-kb fragment) of the selective sweep. Finally, we binned distances into bins with a size of 10 kb. Figure 3 shows the percentage of inferred selective sweeps at different distances from the true position for the first simulated bottleneck. Results for the three additional bottleneck models are shown in the supplementary material (supplementary fig. S2 in supplementary section S3, Supplementary Material online). As the simulated fragment length is 400 kb and the selective sweep position is located in the middle of the fragment, the maximum distance between the inferred and true position is 200 kb. As figure 3 and supplementary figure S3 (Supplementary Material online) show, greater sample size results in more accurate inferences of selective sweep positions, both, for constant populations and populations with bottlenecks.

Fig. 3.

Assessment of the accuracy of predicting the selective sweep position for various sample sizes. The x axis in both plots shows the distance d of the reported selective sweep position from the true selective sweep position. Distance is grouped in bins of size 10,000, i.e., d₁ = 10,000, d₂ = 20,000, … , d₂₀ = 200,000. For each bin i, the y axis shows the frequency of simulated data sets with a reported selective sweep position at a distance less than d_i. (A) Plot refers to a constant population model and (B) refers to a bottlenecked population model. Details regarding the simulation parameters are described in the main text. The straight line depicts the expected percentage of simulations at each bin, if the position of a reported selective sweep would be distributed uniformly along the simulated fragment of 400 kb. The figure shows that the accuracy of detecting selective sweeps increases with the sample size in both constant-size and bottlenecked populations. By comparing A with B, we see that the detection of a selective sweep is more accurate in constant-size than in bottlenecked populations.

Usage Example

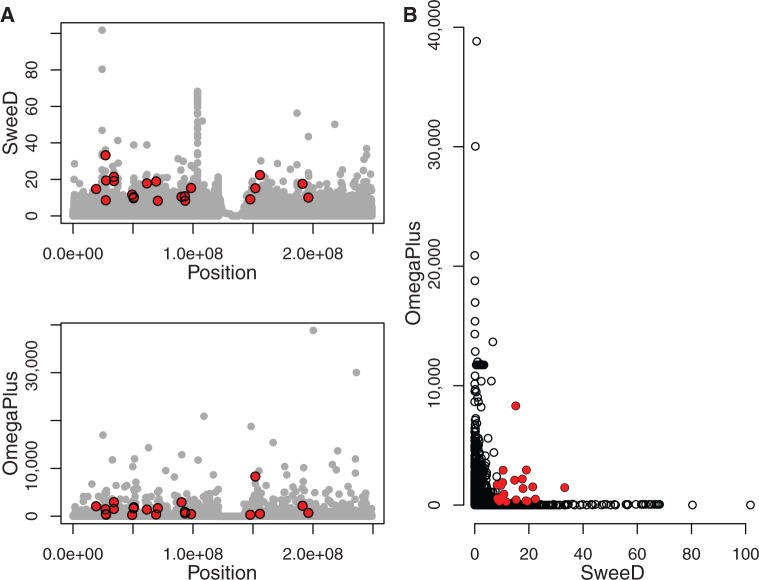
To demonstrate the capability of SweeD to handle real-world genomic data, we downloaded and analyzed the chromosome 1 data set from the 1000 Genome Project (http://ftp.1000genomes.ebi.ac.uk/vol1/ftp/phase1/analysis_results/integrated_call_sets/, last accessed June 29, 2013). This data set contains the genetic variation from 1,092 humans, that is, the sample size is 2,184. The size of the input file is 87 GB, and it comprises 2,896,960 SNPs. We carried out the analysis on an Intel Core i7-2600 processor with 4 cores (8 threads with hyperthreading) running at 3.4 GHz. We calculated the CLR test at 100,000 points (gridsize), and the SFS was obtained from the entire data set. The total execution time was 8 h and 15 min. In contrast to SweeD, SweepFinder fails to analyze this data set because of the large sample size (discussed in the section “Arithmetic deviations from SweepFinder”). We also analyzed this data set with OmegaPlus (command line flags: maxwin = 280,000, minwin = 1,000; see manual for further details on the OmegaPlus command line). OmegaPlus was faster than SweeD (total execution time: 2 h and 37 min). The OmegaPlus and SweeD results are illustrated in figure 4A. Figure 4B shows that for the entire human chromosome 1, the results of SweeD and OmegaPlus are only weakly correlated (Pearson correlation coefficient 0.0107, P value: 0.0007). Note that, this correlation is not visible in figure 4B because data points are too dense. Thus, there is no correlation between SweeD and OmegaPlus scores for the vast majority of positions on chromosome 1. Therefore, signals detected by SweeD substantially differ from those detected by OmegaPlus. Combining SFS-based (SweeD) with LD-based (OmegaPlus) tests increases the power of selective sweep detection (Pavlidis et al. 2010). This is because OmegaPlus and SweeD are complementary (despite the fact that they can be weakly correlated; see also Kim and Nielsen 2004, Pavlidis et. al. 2010), because they strive to detect different selective sweep signatures. We found outlier genomic regions at a significance threshold of 0.01 for both SweeD and OmegaPlus (shown in red in fig. 4). The genes in those genomic outlier regions are presented in supplementary table S1, Supplementary Material online (supplementary section S4, Supplementary Material online). Although combining SweeD with OmegaPlus is generally advantageous, there are cases where they should not be combined. For example, when samples are pooled, the usage of OmegaPlus is meaningless because the LD cannot be accurately computed. Also, when the sample size is small (e.g., less than 10 sequences), LD calculations may be noisy because the LD between several SNPs can be high by chance alone. In such cases, it is recommended to exclusively use a SFS-based program such as SweeD or SweepFinder.

Fig. 4.

Scan of the human chromosome 1 for selective sweeps. (A) The x axis denotes the position on chromosome 1, and the y axis shows the CLR evaluated by SweeD (upper panel) and the ω-statistic (bottom panel) evaluated by OmegaPlus. (B) The joint plot for SweeD and OmegaPlus. Red points denote outliers at a significance level of 1%. The genes located in the outlier regions are described in the supplementary material (supplementary table S1 in supplementary section S4, Supplementary Material online).

Usage of the Analytically Calculated SFS

SweeD can calculate the expected neutral SFS for the sample analytically, provided that we are confident about the demographic model of the population. This procedure can be computationally expensive on large sample sizes with respect to memory consumption and run times. However, it can be advantageous to use the analytically derived SFS instead of the average genome-wide SFS not only for small sample sizes. First, the empirical SFS might not represent the neutral demographic model accurately. This can happen when the length of the analyzed region (scaled in recombination units) is small. Second, using the empirical SFS may be problematic when multiple selective events have occurred in a genomic region. In this case, the empirical SFS is affected by both, demography and selection, whereas the null hypothesis interprets selection as neutrality and therefore becomes too conservative. In this case, it may be advantageous to initially infer the demographic scenario using another (predominantly neutral) part of the genome and based on this, estimate the neutral SFS for detecting selective sweeps. Third, there may be cases where selective sweep scans need to be repeated for individual genomic regions (e.g., autosomes) under the same demographic model. In such cases, the demographic model can be inferred from the whole set of autosomes. Thereafter, the neutral SFS can be estimated, and, finally, the regions can be scanned for selective sweeps using the same neutral SFS.

Alternatively, provided that we are confident about the demographic model, the neutral SFS can be calculated via simulations, for example, by using Hudson’s ms software. This approach has been used in Svetec et al. (2009) and Saminadin-Peter et al. (2012), where subgenomic regions where scanned for selective sweeps. Estimating the neutral SFS via simulations increases the workload and the time needed for the analysis. Initially, one needs to simulate neutral data with ms or msms to then calculate the average SFS from the simulated data. Moreover, the accuracy of the average SFS is low when a small number of simulated data sets is used. Thus, extensive simulations may be required to obtain an accurate estimate of the average SFS using this approach (fig. 5; supplementary fig. S3 in supplementary section S5, Supplementary Material online). Note that, figure 5 only shows the time needed for the simulations and not for the calculation of the average SFS from the simulated data. Thus, it represents a lower bound for the time required to obtain the average SFS via simulations. The demographic model represents a population bottleneck as described in the section “Larger samples improve the accuracy of selective sweep detection.” The population size was decreased by a factor of 100 at time 0.0375 to attain its present-day level at time 0.03875 (time is measured in units of 4N generations and proceeds backwards; 0.0375 corresponds to 150,000 generations). Command-lines that were used to calculate the SFS either by SweeD or by simulations are provided in supplementary section S6, Supplementary Material online.

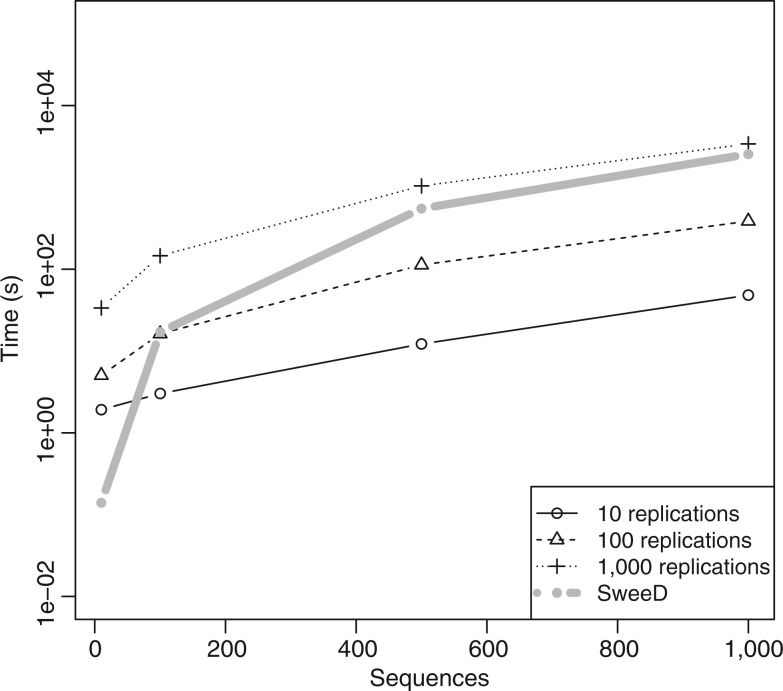
Fig. 5.

Comparison of the time (in seconds) required to estimate the average SFS by using either simulations or SweeD. The four thin black lines represent time needed by simulating a sample from a bottlenecked population 10 times (solid line), 100 times (dashed line), or 1,000 times (dotted line). Number of simulated replications affects the accuracy of estimation; more replications result in more accurate estimation (supplementary fig. S3 in supplementary section S5, Supplementary Material online). The thick gray line shows the time needed for SweeD (with the MPFR library) to estimate the average SFS of the same demographic scenario. The command line used for generating the simulated data sets is provided in the supplementary section S6, Supplementary Material online.

Detecting Selective Sweeps with Low-Coverage Sequencing Data

Modern, high-throughput sequencing technologies have revolutionized the field of population genomics. However, in many cases, the available sequence data from a single individual has low coverage. Thus, accurate genotyping and SNP calling becomes a challenging task. For example, the probability that only one of the two chromosomes of a diploid individual has been sampled is relatively high. The probability of wrong base-calls also increases. Downstream population genetics analyses are greatly affected by the quality of SNP data because summary statistics, such as the SFS, are affected by SNP- and genotype-calling. Therefore, we expect that selective sweep detection with SweeD will also be affected, and that the false positive as well as false negative rates will also increase. Several algorithms have been developed to improve the accuracy of genotype-calling for next generation sequencing data. The most sophisticated algorithms for reducing and quantifying the uncertainty associated with genotype-calling deploy probabilistic frameworks, which incorporate errors that may have been introduced in base calling, alignment, or assembly (Keightley and Halligan 2011; see Nielsen et al. 2011 for a recent review). SweeD does not use a probabilistic framework for calculating the SFS that takes into account uncertainty associated with low-coverage. A probabilistic framework might increase the accuracy of sweep detection at the cost of substantially higher execution times. We plan to assess the integration of a probabilistic framework similar to the one proposed by Keightley and Halligan (2011) in future releases of SweeD.

An alternative approach is to incorporate the effects of low-coverage sequencing into the calculation of the critical value of SweeD that corresponds to the 5% false positive rate. Typically, extensive simulations of neutral data follow a genome scan for selective sweeps to obtain the null distribution of SweeD scores. Simulations are usually performed using coalescent-based software such as Hudson’s ms (Hudson 2002) or msms (Ewing and Hermisson 2010). Modifying ms or msms to simulate low-coverage sequencing data could alleviate the effect of low-coverage on false positive and false negative rates. However, to the best of our knowledge, an implementation of a coalescent model that simulates low-coverage data is not available yet.

Conclusions and Future Work

SweeD is an improved, more stable, and scalable implementation of SweepFinder that allows for analyzing thousands of genomes. In contrast to SweepFinder, SweeD can also analytically calculate the SFS based on a user-specified demographic model. Furthermore, it can parse several common input file formats such as, ms, MaCS, FASTA, and VCF. In addition, SweeD leverages the computational power of multicore systems, shows good speedups, and thereby substantially decreases the time-to-solution. Finally, a checkpointing mechanism allows to resume analyses from where they were interrupted in the case of hardware failures or cluster queue time limitations, leading to time and energy savings.

Regarding future work, we plan to parallelize the calculations of the theoretical SFS and employ an out-of-core (external memory algorithm) approach to make these calculations feasible on off-the-shelf computers. Finally, we intend to evaluate the accuracy of scalable sweep-detection tools such as SweeD and OmegaPlus as a function of increasing sample size.

Materials and Methods

The SFS of Samples for Deterministically Varying Population Size

Analytical results for sample frequency spectra can either be directly derived via the coalescent or be obtained via binomial sampling from the population as derived within the diffusion framework. This is also the case for a neutral model of a population whose size varies over time. Here, 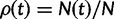denotes the ratio between the ancestral and the current population size at time t. Changes in population size can be included into the standard neutral model as the harmonic mean of the relative population sizes via time-rescaling 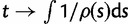in the respective coalescence probabilities or transition densities. Griffiths and Tavaré (1998) established the SFS within the coalescent framework, and Živković and Stephan (2011) found an equivalent solution based on diffusion theory (Evans et al. 2007) as

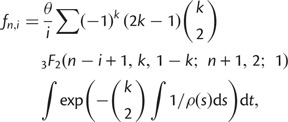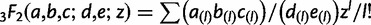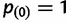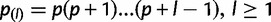where is a generalized hypergeometric function, in which and . For the standard neutral model, this equation reduces to 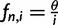. The relative site frequencies are obtained via division by the total number of segregating sites as 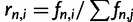. SweeD and SweepFinder use the relative site frequencies. The equations for the SFS can be applied to demographic models including various instantaneous size changes and multiple phases of exponential growth. They can also be used to calculate the composite likelihood of all considered sites of a data set based on a given demographic model in analogy to Kim and Stephan (2002).

Implementation

SweeD is implemented in C and has been developed and tested on Linux platforms. The parallel SweeD version uses Posix threads (PThreads). The checkpointing procedure relies on the DMTCP (distributed multithreaded checkpointing, Ansel et al. 2009) library.

Optional Computation of the SFS for a Given Demographic Model

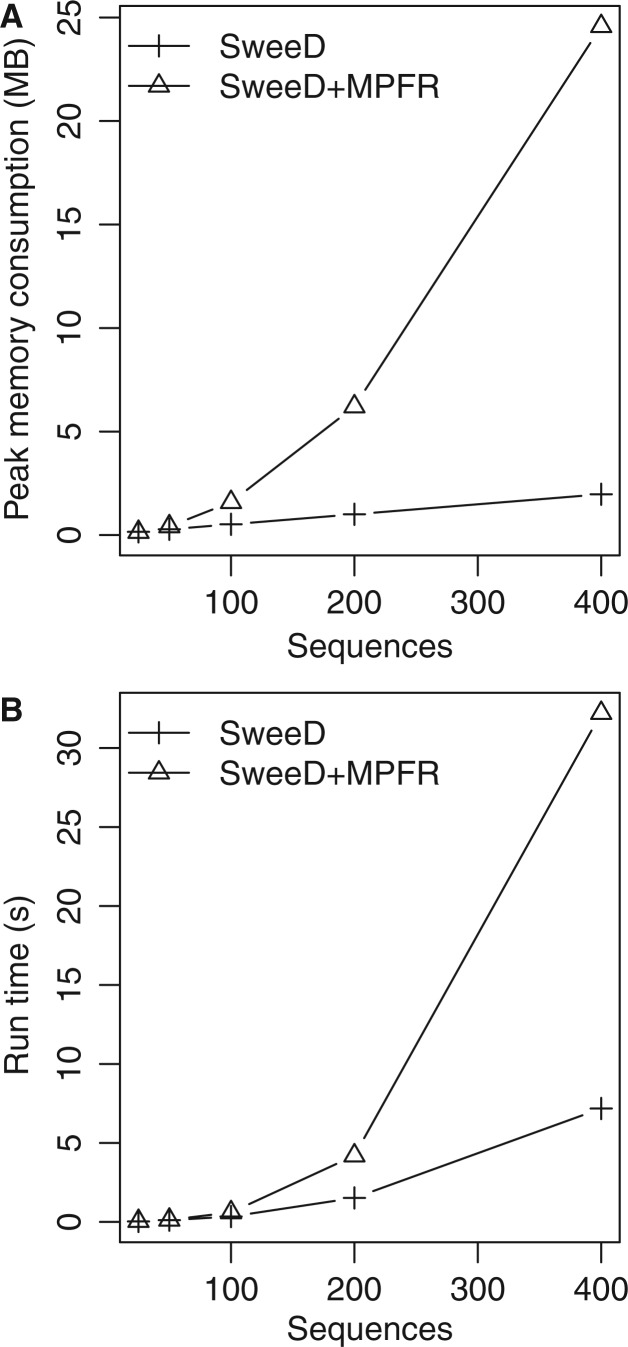
A new feature of SweeD that is not available in SweepFinder is the calculation of the theoretical sample SFS for a user-specified demographic model. The model can comprise an arbitrary number of instantaneous population size changes and, optionally, an exponential growth as the most recent event. For the calculation of the theoretical sample SFS, numerical issues can arise for samples exceeding 60 sequences. To solve recurrent issues with numerical precision that are related to the harmonic sum representation of the SFS, we used the MPFR (multiple-precision floating-point library with correct Rounding, Fousse et al. 2007) library. The MPFR library can be used to conduct arbitrary precision floating-point operations where required. Using arbitrary precision arithmetics, however, leads to increased run times and memory requirements for the analytical computation of the SFS compared with double precision floating point arithmetics. Although the run time differences are negligible for small sample sizes (up to approximately 50 sequences), computing times can increase substantially (up to 5 times in fig. 6B) with the number of sequences. We employed a lookup table to alleviate this performance issue by avoiding frequent recomputations of these values. This approach reduces run times by a factor that is approximately proportional to the number of sequences. However, the size of the lookup table also increases quadratically with the number of sequences and may induce excessive memory requirements (fig. 6A).

Fig. 6.

Comparison of memory consumption (A) and run-time (B) of SweeD (where the SFS is computed by the data itself) and SweeD using the MPFR library to calculate the analytical SFS. Simulated standard neutral data sets of 500 SNPs and 25, 50, 100, 200, and 400 sequences were used for the measurements. Memory consumption was quantified with the massif tool of the valgrind software (Seward and Nethercote 2005).

Parallelization

Multi-core systems can run several threads of execution in parallel which can decrease the run times of an application. However, substantial changes to the sequential code may be required to obtain an efficient parallel algorithm. Therefore, we focused on parallelizing the most compute-intensive parts of SweeD. As already described, SweeD computes the likelihood and optimizes the α parameter of the CLR test at several positions of the alignment. As the CLR calculations at different positions (CLR positions) are independent, they are equally distributed among the available cores. However, there is load imbalance among CLR computations because the inference of α parameters at CLR positions that are located close to a selected site requires a larger amount of arithmetic operations. When a CLR position is located near a positively selected site, the α parameter value that maximizes the likelihood of the sweep model is smaller (α is inversely proportional to the selection coefficient). However, the size of a genomic region that a selective sweep may affect is inversely proportional to α. Thus, more SNPs are required to compute α, when the α value decreases. Therefore, we distribute CLR positions in a cyclic way to cores to improve load balance. We plan to test whether more elaborate load balancing schemes, such as dynamic scheduling or guided scheduling can further improve parallel efficiency.

Arithmetic Deviations from SweepFinder

Since SweeD mainly represents a re-engineered version of SweepFinder, one would expect to obtain exactly the same output from both programs, when the same input data are analyzed. However, both SweeD and SweepFinder, heavily rely on floating-point arithmetics, which are not associative. In other words the following equality does not hold under floating-point arithmetics: A + (B + C) = (A + B) + C. Therefore, the order of floating point operations affects the final results. For each CLR position, both SweeD and SweepFinder compute the probability of each SNP (under the sweep and the neutral model) in a certain region around the CLR position. To calculate these probabilities, SweepFinder moves from left to right along the genome, whereas SweeD moves from the CLR position toward the boundaries of the region. Consequently, the order of operations is different. Therefore, slight numerical deviations between the respective results are to be expected.

There are two additional factors that contribute to the numeric differences between SweeD and SweepFinder. First, logarithmic operations are required in SweeD to ensure scalability for a large number (thousands) of sequences. To avoid arithmetic underflow as frequently observed in SweepFinder, several multiplications are implemented as sums of logarithms in SweeD. When the number of sequences is large, the operands in these multiplications approach the lower limit of the double-precision floating-point range, which can result in floating-point underflows. This is the main reason why SweepFinder cannot analyze data sets that comprise more than 1,027 sequences and exits with a failing assertion: “SweepFinder: SweepFinder.c:365: get_pstar: Assertion ‘sum <= 1.0 && sum > 0.0’ failed”.

Second, SweeD implements a linear instead of a cubic spline interpolation. Both SweepFinder and SweeD calculate the probability P(b) of observing a SNP with a frequency b at k fixed distances d (as scaled by α). For all other values of αd, P(b) is calculated by interpolating the probability values of the k fixed distances. SweepFinder uses k := 60 in conjunction with a cubic spline interpolation. We observed that the spline function calculates erroneous values for k := 60. By increasing the value of k, we found that, using a linear interpolation between distance points is sufficiently accurate to calculate P(b). Thus, we use k := 300 and a linear instead of a cubic spline interpolation in SweeD.

Checkpoint and Restart Capability

Because of the typical time limitations imposed by job submission queues on cluster systems, a checkpointing and restart capability represents an important feature of scientific codes. In typical cluster installations, job queues have 24 or 48 h time limits. A job submitted to a 24-h queue is killed immediately, if it takes longer, effectively wasting the energy spent during the past 24 h, since the user will have to resubmit the job to a queue with a higher time limit, say 48 h. However, if the application is checkpointed, the user can resume the job from the point, where its execution was interrupted to achieve time and energy savings.

SweeD uses the open-source checkpointing library DMTCP (Ansel et al. 2009) for this purpose. With the respective makefiles (with the file extension .CHECKPOINTS), users can compile the ‘checkpointable’ version of SweeD called SweeD-C. Note that the non-checkpointable version does not require the DMTCP library and is hence easier to compile and install. The checkpointable version takes one additional input parameter, the checkpointing interval, which defines how often checkpoints are created and stored during the execution of SweeD-C. To enable checkpointing, the dmtcp_coordinator process has to be started before executing SweeD-C. Subsequently, the program can be invoked as usual (with the additional parameter for the checkpointing interval). When an unexpected event such as a queue time-out or an electricity or processor failure interrupts the execution of the program, the user will be able to resume the execution by using the restart script provided with the DMTCP library.

Command Line Arguments and Output Files

SweeD is a command line tool and requires at least three parameters for a typical analysis: 1) a name for the run (-name), 2) the name of the input file (-input), and 3) the number of CLR positions (-grid).

In the following, we provide a few example command line invocations:

1. SweeD -name test -input file.sf -grid 10000

2. SweeD-P -name test -input file.sf -grid 10000 -threads 4

3. SweeD-C -name test -input file.sf -grid 10000 -checkpoint 1200

In the first example, SweeD is called with the minimum number of parameters to compute the CLR at 10,000 positions along the data set as provided in file.sf. In the second example, the parallel version of SweeD is called. Hence, we need an additional parameter to specify the number of cores/threads that shall be used. In the last example, we start the checkpointable version. This requires an additional parameter that specifies how frequently (in seconds) checkpoints should be stored. For more examples and a detailed description of all supported command line parameters please refer to the manual (http://exelixis-lab.org/software.html).

SweeD generates two output files: 1) an information file describing the data set (number of sequences, sites, etc.) and the analysis (e.g., execution time), and 2) a report file that contains the likelihood value and α-parameter for each CLR position. Finally, a warning file might be written, when ms or MaCS input file formats are used to report possible conflicting SNP positions, that is, SNPs that refer to the same alignment site.

Supplementary Material

Supplementary figures S1–S3, sections S1–S6, and table S1 are available at Molecular Biology and Evolution online (http://www.mbe.oxfordjournals.org/).