Assessing the Location of Surface Plasmons Over Nanotriangle and Nanohole Arrays of Different Size and Periodicity

Abstract

The increasing popularity of surface plasmon resonance (SPR) and surface enhanced Raman scattering (SERS) sensor design based on nanotriangle or nanohole arrays, and the possibility to manufacture substrates at the transition between these plasmonic substrates, makes them ideal candidates for the establishment of structure-property relationships. This work features near diffraction-limited Raman images and FDTD simulations of nanotriangle and nanohole arrays substrates, which clearly demonstrate that the localization of the hot spot on these SERS substrates is significantly influenced by the ratio of diameter/periodicity (D/P). The experimental and simulation data reveal that the hot spots are located around nanotriangles (D/P = 1), characteristic of localized SPR. Decreasing the D/P ratio to 0.75-0.7 led to the creation of nanohole arrays, which promoted the excitation of a propagating surface plasmon (SP) delocalized over the metal network. The optimal SERS intensity was consistently achieved at this transition from nanotriangles to nanoholes, for every periodicity (650 nm to 1.5 μm) and excitation wavelength (633 and 785 nm) investigated, despite the presence or absence of a plasmonic band near the laser excitation. Further decreasing the D/P ratio led to excitation of a localized SP located around the rim of nanohole arrays for D/P of 0.5-0.6, in agreement with previous reports. In addition, this manuscript provides the first evidence that the hot spots are positioned inside the hole for D/P of 0.4, with the center being the region of highest electric field and Raman intensity. The compelling experimental evidence and FDTD simulations offer an overall understanding of the plasmonic properties of nanohole arrays as SERS and SPR sensors, which is of significant value in advancing the diversity of applications from such surfaces.

Nanostructured surfaces have found use in various fields such as optics,¹ chemical and biological sensing,² photovoltaics,^3,4 and surface-enhanced spectroscopies⁵. The exquisite surface sensitivity of surface plasmons on nanostructured substrates is at the origin of optical phenomena, such as surface-enhanced Raman scattering (SERS). SERS is a versatile and highly sensitive analytical technique, which is capable of producing a vibrational fingerprint of the molecule under study.⁶ Significant literature supports the theory of Raman enhancement in SERS. A major contribution to the Raman enhancement can be attributed to the excitation of the localized surface plasmon resonance (LSPR) that occurs on nanostructured surfaces.⁷ As a result, an intense electromagnetic field is confined to specific regions on SERS substrates.^7,8 Molecules located within these regions of high electric field (so-called hot spots) contribute a major portion to the overall response of the substrate, without being the only contribution. The hot spots are significantly influenced by the size and shape of the nanostructured substrate and by geometrical parameters, such as the distance between nanoparticles (gap-effect).

Among the plethora of nanostructured surfaces that have been designed,⁹ nanotriangle,¹⁰ and nanohole arrays¹¹ exhibit good sensitivity to refractive index and so are suitable for SPR sensing. In addition, these nanostructures give large Raman enhancement factors necessary for SERS studies. Nanotriangle array-based sensors have been shown to be reliable and versatile substrates for LSPR sensing¹² and SERS¹⁰. In particular, nanohole arrays present a strongly enhanced light transmission at specific wavelengths that can be attributed to various plasmonic modes. As a result, an amplified electrical field is generated when an active plasmonic mode is excited, which can be of use in SERS and SPR experiments.¹³ Nanohole and nanotriangle arrays owe their interest to the availability of several fabrication methods capable of producing large areas of nearly defect-free substrates. The possibility of creating nanostructures ranging from nanotriangle to nanohole arrays by modified nanosphere lithography (NSL) has provided a tool to study the plasmonic properties at the transition between these nanostructures^14-16. While nanotriangles and nanohole arrays have been reported numerous times in the literature, no comparative studies have established their relative plasmonic properties.

Tuning the physical properties of nanostructured substrates, such as the diameter, height, thickness, and inter-particle spacing engineers the plasmon dispersion, which influences the excitation wavelength of the LSP, the sensitivity to refractive index, the SERS enhancement and SP mode (propagating or localized). For example, the modification of the size of Au nanoparticles on silicon substrate or of crescent-shape metallic nanoparticles resulted in the full control of tuning the SP excitation wavelength over a range from visible to infrared region.¹⁷ Furthermore, the plasmonic resonance of Ag nanocylinders was blueshifted by either increasing the height or reducing the diameter, which often results in the increase of optical absorption losses within the metal.¹⁸ Surface plasmon frequency can be engineered using double metallic configurations¹⁹ or metallo-dielectric configurations.²⁰ These examples demonstrated the strong influence of the substrate geometry on the LSP.

Substrates with surface features of a length scale longer than the dissipation length of the surface plasmon polariton exhibits properties characteristic of propagating surface plasmons. Some substrates, such as nanohole arrays, have features with length scales both in the nanoregime and the macro regime. Studying their plasmonic properties is thus of importance. The transition between localized and propagating SP modes was reported in nanovoid substrates supported on a metallic film by changing the normalized thickness of the voids.²¹ Nanovoids were prepared by NSL on a metallic film, leading to structures of relative similarity to nanotriangle and nanoholes. For example, structures with small normalized thickness resemble to nanotriangle arrays on a metallic film, while nanovoid substrates of large normalized thickness are similar to nanohole arrays. It was demonstrated that propagating SP modes were excited for small normalized thickness, which transition to localized SP mode located inside the voids for large normalized thickness. The excitation of localized and propagating SP modes was reported in nanotriangle and nanohole substrates based on sensitivity to refractive index and SPR spectra in the Kretschmann configuration.^14,22,23 However, nanotriangle and nanohole arrays are commonly excited by extinction or transmission spectroscopy for SPR and SERS experiments. It is thus important to establish the properties of these plasmonic substrates for fundamental knowledge and sensor design.

In addition to experimental properties, there is a strong interest in correlating the plasmonic properties to the predicted theoretical response. Recently, significant efforts have been undertaken to predict the localization of the regions with the strongest electromagnetic enhancement on the substrate, often referred to as “hot spots”. These hot spots are major contributors to the SPR and SERS response from molecular adsorbates. Thus, it is important to understand the structure-property relationship for different plasmonic substrates in order to better control the localization of molecular receptors on the surface of the substrate. Enhanced sensitivity may be accessible due to binding of the analyte at specific locations of a nanostructured substrate.²⁴ Numerical solutions have produced significant predictions for the localization of hot spots. For example, Schatz et al. performed DDA calculations on triangular dimers separated by a gap of 2 nm.²⁵ It was found that the hot spots were located at the tips of the triangles in nanotriangle substrates. In the case of triangle dimers, it was demonstrated that the maximum electric field enhancement occurs at the tip-to-tip region of the dimers. For nanohole arrays, simulations revealed that the hot spots were located around the rim of the nanohole.²⁶ Essentially, all simulations were performed on nanohole arrays, in which the diameter was nearly half the periodicity. No complete set of simulations has demonstrated the evolution of the hot spots localization in the transition from nanohole arrays.

Correlating simulations with experimental results provides compelling proof of the localization of the hot spots on nanostructures. Raman microscopy, although a very powerful analytical tool, has not been extensively exploited to image the localization of the regions of high Raman intensity on SERS substrates. These regions can be attributed to hot spots. Hot spots were first imaged by Qin et al. for barcodes of different spacing to understand the effect of plasmonic coupling on the SERS response.²⁷ The Raman images of film over etched nanospheres showed experimental evidence that the hot spots were indeed in regions where nanospheres were at closest proximity.²⁸ We have recently achieved correlated AFM and SERS images for nanotriangle and nanohole arrays,²⁹ which provided compelling evidence of the localization of hot spots on the SERS substrates. The Raman images map the regions of high plasmonic field and thus, can provide evidence of the plasmonic mode excited on substrates. In the work presented here, the measurement of SPR properties, SERS response, Raman images, correlated AFM and Raman images, and electric field distribution calculations obtained by finite-difference time-domain (FDTD) for nanotriangle and nanohole arrays of various periodicities provide a comprehensive overview of the plasmonic properties of these important substrates.

Experimental section

Fabrication of the Nanotriangle and Nanohole Arrays

Nanosphere lithography (NSL) is a simple method used to fabricate several different types of size-tunable nanoparticle arrays as it provides great control over the size, shape, and interparticle distance (gap). While some defects are present and depend on the deposition conditions,³⁰ crystalline regions composed of several domains with different orientation of the crystal lattice can create useful substrates of several mm² up to a cm². NSL has been utilized to fabricate nanotriangle arrays,³¹ and by adding a reactive ion etching step nanohole arrays can be created by reducing the size of the polymer nanospheres without altering the crystalline lattice of the NSL mask.^13,32,33 Thus, in this work, modified NSL was employed to investigate the surface plasmon properties^15,16 and SERS properties²⁹ of the transition from nanotriangle to nanohole arrays.

Glass microscope slides of 22 × 22 mm were first cleaned in a piranha solution (75% v/v H₂SO₄: 25% v/v H₂O₂) at 80°C for 90 minutes. After thoroughly rinsing with 18 M .cm water, they were sonicated in a 5:1:1 v/v solution of water/H₂O₂/NH₄OH for 60 minutes. The glass slides were once again thoroughly rinsed with 18 M .cm water and stored in water for extended periods of time, with replacement of the water every 48 hours. Nanosphere lithography (NSL) was employed to fabricate the nanohole arrays of various periodicity and diameter.^13,16 Using the clean glass slides as the substrate, NSL masks were prepared by drop coating of the nanospheres in solution. Considering the periodicity, a specific drop coating solution was prepared by mixing respectively water (18 M .cm MilliQ), ethanol (ACS grade) and a nanosphere stock solution (Thermo Scientific Particle technologies, 5000 series; 10% w/v) in different volume proportions (Table S3 in ESI). The drop size used in the drop coating process was also dependent on the periodicity. Finally, well-ordered regions were formed by drying the deposit at room temperature by covering the cover slip with the drop coating solution with a petri dish slightly raised by a pipette tip.

The size of the nanospheres was then tuned by etching the NSL masks with an oxygen plasma using a plasma cleaner (Harrick Plasma Cleaner PDC-32G) at high power (18 W) for 0 to 10 minutes for periodicities ranging from 650 to 1000 nm and for 0 to 18 minutes for 1500 nm nanospheres under a continuous oxygen flow of 15 mL/min. A 20-minute vacuum step prior to etching was necessary to remove air gases and to leave a low pressure of nearly pure oxygen.

Metallization of the substrate was achieved by depositing a 1 nm Cr adhesion layer followed by a 125 nm Au or Ag layer. Finally, removing the NSL mask by sonication in ethanol for a few seconds resulted in the nanostructured arrays. Four identical samples were prepared for each series for analytical purposes and the size (diameter and depth) of the nanoholes was estimated by atomic force microscopy (AFM) in contact mode and scanning electron microscopy (SEM).

Plasmonic Properties

The plasmonic properties were determined by reflectance measurements at normal incidence using a 6 around 1 reflectance probe. Illumination under halogen light source allowed the measurement of a reflectance spectrum ranging from 400 to 900 nm. For each sample, a spectrum was obtained by processing the reflectance data using a smooth Ag or Au film as the reference. Reflectance measurements were preferred due to the similarity of the Raman spectra measurements with an epi-microscope. Sensitivity was measured with sucrose solutions of different refractive indices, using transmission measurements with a custom-built flow cell and optical setup.

Raman Spectroscopy Measurements

Nanohole arrays were first immersed in an aqueous solution of 0.5 mM 4-nitrobenzene thiol (4-NBT) overnight. The 4-NBT was chosen as a control molecule because its Raman behaviour is well known. The samples were then rinsed with water followed by ethanol, dried under an Argon flux, and stored in the dark prior to their use. For each series (4 samples for each etch time), a Raman spectrum was measured with a Renishaw InVia Raman microscope using 633 and 785 nm excitation wavelengths. Spectra were acquired for 10 seconds at 1 % of the laser intensity, resulting in 0.57 mW for the 633 nm laser and 0.33 mW for the 785 nm laser. The laser power density was estimated at 0.84 MW/cm² for the 532 nm laser and at 0.34 MW/cm² for the 633 nm laser, with an illuminated area of approximately 0.068 μm² for the 532 nm laser and 0.097 μm² for the 633 nm laser. Four characteristic Raman peaks of 4-NBT (1082, 1112, 1350, and 1575 cm^-1) were used to investigate the intensity of the Raman response for each nanohole array sample. For comparison purposes, the Raman response was reported as a percentage compared to the nanotriangle response (where nanotriangle = 100%), prepared with the same NSL mask.

Near-Diffraction Limited Raman Microscopy Measurements

Raman analyses were carried out using WiTec alpha300 instrumentation, which facilitated the mapping of approximately 10 ×10 μm areas. The false colour Raman maps of intensity were obtained using a 532, 633 or 785 nm excitation laser. The approximate powers of the 532, 633 and 785 nm excitation lasers were 0.5 mW (1.2 % of total power), 0.3 mW (1.5 % of total power) and 1.2 mW (1.5 % of total power) respectively. The parameters were set as following: 0.005 s integration time, 100X objective (Olympus MPlan, NA = 0.9), which result in approximately 300 - 500 nm spatial resolution. The intensity of the v(C-C) stretch of 4-NBT at 1575 cm^-1 was mapped resulting in a false colour image of the Raman enhancement over the analysis area. Three maps were taken from three separate, identically prepared samples for each etch time and all maps from samples with the same etch time resembled one another to a high degree highlighting the reproducibility of the Raman response from the substrates.

Contact mode AFM analysis was performed on a NanoInk DPN5000 instrumentation. Images were obtained at 512 × 512 pixel resolution using a scan rate of 0.2. The scanned areas intentionally included crystallisation defects and/or scratches to act as a point of reference between the AFM and Raman images.

Finite Difference Time Domain (FDTD) Simulations

In the work described in this paper, Finite-Difference Time-Domain (FDTD) technique was employed for numerically calculating electromagnetic (EM) fields around nanotriangle and nanohole arrays in metallic thin films (Ag thin films) so as to study the effects of the diameters (D) and periodicities (P) of the nanohole arrays on the EM fields. We have previously employed FDTD for modeling EM fields around metallic nanostructures such as nanoparticles and nanopillar arrays.^14,17 While FDTD algorithms¹⁸ analyze structures by solving the differential form of coupled Maxwell’s equations, analyses described in these calculations incorporate the effects of dispersion relations, e.g. the effects of wavelength dependence of the dielectric constants of the metallic structures. Here, we employed an FDTD software called FullWAVE 6.0 by R-Soft to carry out the FDTD analysis for the nanohole arrays. This software enables FDTD analysis of the metallic media to include Debye or Lorentz models of dispersion relations of the dielectric constants of the metals.

In the FDTD simulations, we used an extended Debye dispersion model for determining the dielectric constants for silver.¹⁴ 3D FDTD solutions were obtained for electromagnetic fields around periodic hexagonal arrays of nanoholes (having different diameters and periodicities) in Ag films (50 nm thick Ag film, having a 5 nm thick Ti adhesion layer underneath the Ag film) deposited on a silica substrate. Electromagnetic fields (e.g. E and H fields in the x, y, and z directions) in the vicinity of the nanohole arrays were calculated assuming plane wave illumination being normally incident on the nanohole arrays, the wavelengths of the incident radiation being 532 and 633 nm. The magnitude of the incident electric fields was taken to be unity and the enhancement of electromagnetic fields, around the nanohole arrays, evaluated. The time steps employed in these simulations were selected to be small enough such that the Courant stability criterion¹⁸ was satisfied for the different grid sizes employed. For FDTD calculations involving the nanohole arrays, the grid sizes in x, y, and z directions (Δx, Δy, and Δz) were selected to be such that the value of the E field intensities around the nanohole arrays became independent of the grid sizes. In these simulations, the grid sizes in the x, y, and z directions were 5 nm, 5 nm, and 30 nm, respectively. The FDTD simulations were performed with the incident light being linearly polarized light along the x-axis of the figures (see bottom row of Figure 4). In our simulations, the diameters of the nanohole arrays in the Ag film were varied between 300 and 1500 nm (steps of 150 nm), while the periodicity of the nanohole arrays was 1500 nm.

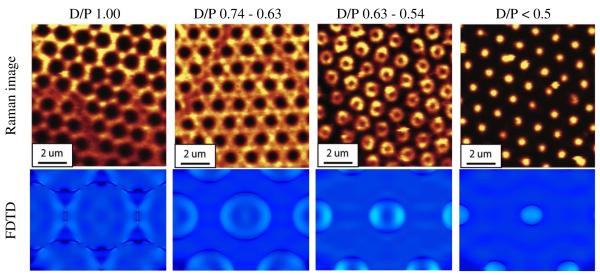
Figure 4.

(Top row) False color Raman microscopy images of a 10 × 10m region for nanohole arrays of decreasing D/P ratios from left to right respectively. (Bottom row) FDTD images of a 3 × 3m region for nanohole arrays corresponding to the same D/P regions as for the Raman images. For the Raman images and the FDTD simulations, the periodicity of the nanohole arrays is 1500 nm, illuminated with a 532 nm laser.

Results and discussion

General Properties of Nanohole Arrays

Nanohole arrays of different periodicities and diameters were fabricated by modified nanosphere lithography (NSL).^13,16,33 The initial size of the polystyrene spheres dictates the periodicity, while the duration of the etching process controls the diameter of the holes. A diameter/periodicity (D/P) ratio allows simple comparison of arrays of different periodicities. For example, a D/P of 1 corresponds to a nanotriangular structure, while a D/P of 0 is observed for a continuous film. It has been reported that the SERS, SPR, and LSPR results demonstrate that the transition from triangle to hole arrays occurs within a D/P ratio ranging from 0.75 to 0.60.²⁹ Therefore, a matrix of nanohole array samples was constructed with periodicities ranging from 650 to 1500 nm. Samples with D/P between 0.4 and 1.0 were investigated (Table 1). The investigation was limited to a lower boundary of D/P equal to 0.4 as the modified NSL method is incompatible with the fabrication of nanohole arrays of smaller D/P ratios. The transition region is of particular interest, as it exhibited an improved Raman response for nanohole arrays of 820 nm.²⁹ The physical aspect of the substrate changes significantly in this transition region. AFM images of samples with 1000 nm periodicity clearly demonstrated that samples with D/P ratio ranging from 0.74 to 0.77 consist of a network of nearly interconnected triangles, while a D/P with values around 0.60-0.63 exhibit a continuous network of holes (Figure 1). Therefore, these values of D/P will be used to define the upper and lower limit of the transition zone. To better understand the properties of plasmonic substrates in this transition region and to determine optimal SERS substrate among nanotriangle and nanohole arrays, a comprehensive characterization of nanohole arrays was undertaken.

Table 1.

Surface Plasmon Resonance Wavelength for Nanohole Arrays of Different Periodicities

650 nm		820 nm		1000 nm		1500 nm
D/P	λLSPR (nm)	D/P	λLSPR (nm)	D/P	λLSPR (nm)	D/P	λLSPR (nm)
1.00	OSRa	1.00	OSRa	1.00	OSRa	1.00	OSRa
0.72	513	0.77	OSRa	0.68	OSRa	0.71	OSRa
0.60	567	0.69	549, 700	0.61	OSRa	0.69	OSRa
0.46	510, 700	0.57	480, 668, 868	0.59	520	0.64	OSRa
0.45	542, 637	0.56	513, 895	0.53	520	0.64	OSRa
0.42	513, 747	0.52	507, 557, 640	0.50	498, 645, 740, 819	0.59	OSRa
		0.43	528, 670, 807, 842	0.46	498, 645, 740, 819	0.53	649

^aOSR: Outside spectral range of 400 to 950 nm.

Figure 1.

AFM images (10 × 10m scan) of nanohole arrays with 1000 nm periodicity, for which the D/P corresponds to the A) upper and B) lower boundaries of the transition region respectively.

The D/P ratio and the periodicity are two factors that significantly affect the optical properties of nanohole arrays. The excitation wavelength of the surface plasmon³⁴ and the sensitivity to refractive index of nanohole arrays are proportional to the periodicity; higher excitation wavelength and sensitivity are achieved with a larger periodicity.³⁵ Whilst the plasmonic properties can be extended to the IR region,³⁶ this study focuses on the optical properties of nanohole arrays within the visible-near infrared region ranging from 400 to 950 nm, as this region covers the plasmonic properties of Au and Ag and also spans the range of most common Raman systems (e.g. λ = 488, 514, 532, 633, and 785 nm). As expected, the surface plasmons (SPs) of nanotriangle arrays (D/P of 1.0) and of nanohole arrays of larger periodicities (e.g. 1000 and 1500 nm) are excited above λ = 1 μm (Table 1). Indeed, for nanotriangle arrays, decreasing the D/P ratio promotes plasmon coupling, redshifting the plasmonic band to lower energies (higher wavelengths). For nanohole arrays, decreasing the D/P ratio does not significantly influence the excitation wavelength, but increases the intensity of the plasmonic band. The observations noted here have also been reported for other periodicities of nanotriangle and nanohole arrays.^15,16 As for samples with small D/P ratios or short periodicities, a plasmonic band in the visible region of the light spectrum was observed. Hence, the majority of samples prepared using 650 and 820 nm periodicities support a SP in the target spectral region, while the SP of samples with 1000 and 1500 nm periodicities could not be excited under experimental conditions. Samples with lower D/P ratios feature multiple plasmonic bands associated to the several modes excited in the spectral region probed. The sample set was designed to evaluate the influence of the SP excitation wavelength on the Raman properties of nanohole arrays.

Bulk Plasmonic Properties: From Nanotriangle to Nanohole Arrays

The D/P ratio significantly impacts the Raman response of SERS substrates. Importantly, the Raman response reported here is for the illumination of a surface of constant area on the substrates, regardless of the geometrical shape of the substrate, providing a direct comparison of the Raman intensity. The Raman response is normalized to that of nanotriangle array (D/P = 1.00) of the same periodicity for comparison purposes. In the nanohole region, for D/P ratios smaller than 0.60, the Raman response is essentially equivalent to that of nanotriangle arrays. A distinct exception to this observation concerns the nanohole arrays of 650 nm periodicity excited at λ = 785 nm (Figure 2, right). By featuring a strong plasmonic band near λ = 700 nm, the response is amplified to about a factor of 6 in comparison to nanotriangle arrays. Otherwise, for every periodicity and excitation laser (λ = 633 nm and 785 nm), the Raman response is maximal for SERS substrates within the transition region with D/P of 0.75 to 0.6 (Figure 2). Particularly, the largest Raman responses were observed for D/P ratios of 0.60, 0.69, 0.61, and 0.69 for substrates of 650, 820, 1000, and 1500 nm periodicities respectively. The SERS substrates obtained from 650 and 1000 nm periodicities exhibited the highest relative Raman improvement in the transition region. The amplification factor is approximately 3.5 and almost 5 for the excitation wavelengths of 633 and 785 nm respectively. A smaller amplification factor is observed for SERS substrates of 820 and 1500 nm periodicities; a factor of 2.5 to 3 and 1.5 to 2 for excitation wavelengths of 633 and 785 nm was achieved respectively.

Figure 2.

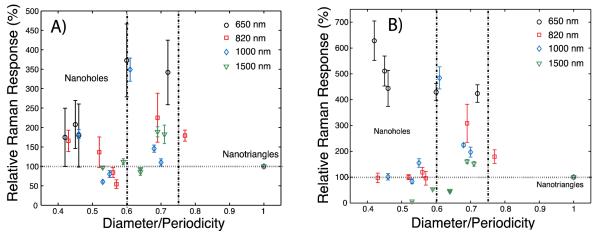
Influence of the diameter/periodicity (D/P) ratio of nanohole arrays on the amplification of the Raman response for an excitation wavelength of A) 633 and B) 785 nm.

The raw intensity of the Raman response for the illumination of a fixed geometrical area of the optimal nanostructure of each periodicity was constant for λ = 633 nm excitation. In contrast, the Raman response at λ = 785 nm was most intense for substrates with 1000 nm periodicity where the response was 50% more intense compared to that of other periodicities. Overall, on our system (Renishaw InVia Raman microscope), we observed a larger raw intensity per unit power for the λ = 633 nm laser. However, the λ = 785 nm Raman laser is available with ten times more intensity, and has the additional advantage of decreasing the fluorescence with longer wavelengths, Therefore, the nanostructures of 1000 nm periodicity with a D/P ratio of 0.69 excited at a 785 nm wavelength yielded the most intense response among the ones tested in this study.

Whilst the Raman response is essentially constant for nanohole arrays (D/P < 0.6), the sensitivity to refractive index is a factor of D/P for these nanostructured substrates. Although the theoretical equations describing the sensitivity of nanohole arrays do not take into consideration the diameter of the holes,³⁵ it was previously reported that the sensitivity is indeed modulated by the diameter of Ag nanoholes with 450 nm periodicity.¹⁶ Here, the sensitivity of Au nanohole arrays of 820 and 1000 nm periodicities also strongly depend on the diameter of the nanoholes within the region of D/P ratios comprised between 0.40 and 0.60. The sensitivity measured with sucrose solutions of RI ranging from 1.33 to 1.37 RIU region varied between 196 nm/RIU and 428 nm/RIU, and reached a maximum for a D/P of 0.44 for nanohole arrays of 820 nm periodicity (Figure 3). For the nanohole arrays of 1000 nm periodicity, the sensitivity increased linearly as a function of D/P to reach a value of 533 nm/RIU for a D/P ratio of 0.6 (Figure 3). The absence of a plasmonic band in the λ = 400 to 950 nm region for larger D/P values prohibited the measurement of sensitivity of these substrates. In comparison, Au exhibited a constant sensitivity for 450 nm periodicity.¹⁶ The various trends resulting from the relationship of the sensitivity as a function of the D/P ratio are not only useful for understanding the plasmonic properties of nanohole arrays, but also for predicting the behavior and analytical properties of these arrays as well.

Figure 3.

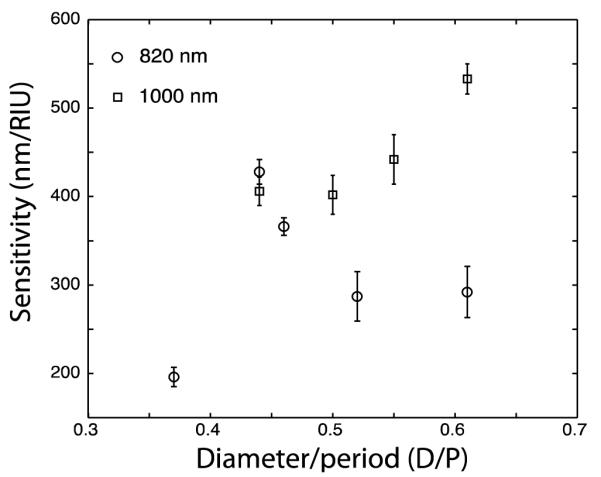
Sensitivity to refractive index of sucrose solutions (RI range: 1.33 to 1.37) measured for nanohole arrays with 820nm (circles) and 1000 nm (squares) periodicities at different D/P ratios in the nanohole region, e.g. D/P < 0.61.

While the sensitivity of SPR sensors with nanohole arrays strongly depends on the D/P ratio and the periodicity, the SERS response follows similar trends for the periodicities and D/P ratios investigated here. By comparing the values in Table 1 with the data plotted in Figure 1, it is possible to argue that the presence of a strong first order SP band is not necessary to achieve an enhanced Raman response especially at the transition region from nanotriangle to nanohole arrays, since Raman lasers are likely to excite higher order plasmon bands on substrates of larger periodicities. Thus, other factors such as plasmonic coupling from tip-to-tip geometry are major contributors to the improvement of the Raman response in the transition region of 0.75 > D/P > 0.60.

Imaging the Hot Spots of Nanotriangle and Nanohole Arrays

Imaging Raman scattering of samples with different periodicities, but similar D/P ratios may provide an overview of the localization of the hot spots on the SERS substrate. The strong correlation between geometrical factors of the samples and the strong Raman response could be explained by the similarities of the hot spots. By measuring high-resolution confocal Raman microscopy images of the SERS substrates, the localization of the enhanced electric field and thus, the identification of the regions with the highest intensity for the Raman response on those nanostructures, can be precisely mapped and correlated to the physical aspects of the SERS substrates. Confocal Raman microscopy allows near diffraction-limited resolution images of the samples. In the case of laser excitation at λ = 532, 633, and 785 nm investigated here, the diffraction limited lateral resolution of the Raman images with a 100X dry objective (NA = 0.9) are 360, 430, and 532 nm respectively. A monolayer of 4-nitrobenzenethiol (4-NBT) uniformly covers the samples to alleviate any surface concentration effect that could have arisen from irregular coating of the SERS substrate with the reporter. As expected, the lateral resolution with the λ = 785 nm laser was inadequate to measure Raman images with sufficient details. Due to their better lateral resolution, Raman images of the SERS substrates with the 532 and 633 nm lasers provide detailed images of the localization of the region of high Raman intensity (Figure 4; complete set is provided in ESI). Four distinct patterns can be observed: (1) islands of high Raman response correlated to the location of the triangles for a D/P of 1.00, (2) a network of high Raman response co-localized with the network of nearly inter-connected triangle arrays at a D/P ratio ranging from 0.74 to 0.63, (3) “donut-shaped” regions of high Raman response around the rim of the nanoholes for 0.63 > D/P > 0.54, and (4) the core area of the nanoholes acts as a point-source of the high Raman response for smaller D/P ratios. It is important to note that the images were acquired with circularly polarized light, explaining the symmetrical nature of the hot spots. By decreasing the periodicity, the quality of the images is lowered due to a poorer ratio of feature size/spatial resolution (Tables S1 and S2 in ESI). Nonetheless, the Raman images revealed that the location of the hot spots is similar for substrates with constant D/P, regardless of the periodicity and the presence or absence of a plasmonic band being excited by the Raman laser.

The highest Raman intensity is observed near the transition between the network of interconnected triangles and the substrates with a high electric field around the rim of the nanoholes. The network of nearly interconnected triangle exhibited a region of high plasmonic coupling,^37,38 due to the presence of a network of dimers. It is expected that the high electric field will lead to significantly improved Raman response at the tip-to-tip region of this substrate. Figure 4 - second panel - presents faint areas near the center of the triangles as well as regions of slightly higher intensity. The contrast is quite poor between these regions, which may be due to the spatial resolution being much larger than the actual hot spots. Nonetheless, this structure of nearly inter-connected nanotriangle arrays (or so-called bowtie arrays) provides significantly improved Raman response in relation to conventional nanotriangle and nanohole arrays.

As expected, the SERS images clearly demonstrate the localized SP excited in nanotriangle arrays. The structure-dependent properties of a nanohole array substrate are evident from the different SERS images obtained depending on the D/P ratio. The delocalization of the region of high Raman response on the metallic network near the transition from nanotriangle to nanohole arrays is characteristic of a propagating SP. We observed in our previous studies that a propagating SP can be excited on the substrate at the transition from nanotriangle to nanohole arrays.¹⁴ In addition, the nanovoid substrates prepared by Kelf et al, which resemble the nanohole arrays, also exhibited a propagating SP at low normalized thickness.²¹ Low normalized thickness corresponds to large D/P ratios. Further decreasing the D/P ratio leads to a localized SP located around the rim of the nanohole, which becomes highly focused inside the nanohole at lower D/P ratios. This transition from propagating to localized SP was also reported in nanovoids substrates. Thus, the plasmonic properties of nanohole arrays are very similar to nanovoids. In summary, the transition from nanotriangle to nanohole arrays is characterized by a localized SP at high D/P for triangle arrays, which propagates near the transition to nanohole array and is localized for nanohole arrays of smaller D/P.

Despite the imperfect nature of NSL for fabricating nanohole arrays, the simplicity of the technique, the low cost of fabrication, and facile tuning of the geometrical parameters of the substrate makes it an interesting alternative to photolithography, E-beam lithography or focused ion beam milling. Most importantly, SERS images demonstrate that the response is relatively homogenous across the sample; a 10 to 30% coefficient of variation was observed on the intensity of the hot spots across the Raman images. This confirms that most of the sample contributes to the overall Raman response, unlike the nanoparticle aggregates for which the majority of the signal may originate from one particular hot spot. Another important observation resides in the intensity observed at the point defects of the samples. The boundary of a dislocation between two regions of different crystalline orientations is more intense than perfectly oriented regions for the triangle arrays (D/P of 1.0). These same boundaries in nanohole arrays exhibit smaller Raman responses, suggesting that the highest Raman response for nanohole arrays will be for samples perfectly oriented.

Correlated AFM and SERS images on the same location of a nanostructured substrate provide valuable insights on the structure-property relationship of these arrays. It was previously reported that for a transition state of nearly-connected nanotriangles for substrates of 820 nm periodicity for a D/P ratio of 0.69, the network of metallic triangle is co-located with the one of intense Raman areas.²⁹ In addition, the point source-like areas of high Raman intensity for nanohole arrays of D/P = 0.43 correlated with the center of the core area of the nanoholes.²⁹ Here, correlated AFM and SERS images confirmed that the “donut-shaped” region of high Raman intensity is perfectly co-localized with the rim of nanohole arrays of 1.5 μm periodicity with a D/P of 0.64 (Figure 5). The dark region of low Raman response at the center of the donut is about 400 nm across for 1500 nm periodicity. This region is close to the diffraction-limited resolution of the λ = 532 and 633 nm lasers, explaining that it was only observed for the 1000 (only with λ = 532 nm) and 1500 nm (with both lasers) periodicities (Tables S1 and S2 in ESI). We anticipate that these regions also exist for nanohole arrays of smaller periodicity, but the spatial resolution of the measurement did not provide direct evidence of this dark core, as it is below the diffraction limit for smaller periodicities.

Figure 5.

Correlated AFM and SERS images of a nanohole array with a D/P ratio of 0.64. The false color Raman image (pink) was acquired at 633 nm, which is delimited by the white boundaries. The ring attributed to the high Raman intensity is co-localized with the rim of the nanohole, which is in agreement with the FDTD calculations.

Finite Difference Time Domain (FDTD) Simulations

Calculations to map the electric field distribution of SERS substrates correlate well with the experimental SERS images (Figure 4 - bottom row; Tables S1 and S2 in ESI). The FDTD simulations were performed with linearly polarized light along the x-axis of the figures. As predicted by numerical simulations,^33,37 the alignment of the areas of high electric field with the orientation of the polarized light is expected. Both simulations at λ = 532 and 633 nm show that the region of high electric field surrounds the nanotriangles for substrates exhibiting a D/P ratio of 1.0, therefore matching with the SERS image showing the triangles as being the regions of high Raman intensity. FDTD simulations are also in strong agreement with the experimental data for the nanohole array substrate with a 0.74 > D/P > 0.63. The SERS image and the FDTD simulation for a 0.63 > D/P > 0.54 demonstrate that the region of high electric field and intense Raman response is located around the rim of the nanoholes. By decreasing the D/P ratio of the FDTD simulations to 0.3, the center of the nanoholes becomes a point-source region of high electric field, fitting very well with the experimental SERS image for smaller D/P.

The slight discrepancy between the experimental and simulated D/P, in particular for smaller D/P values, is due to the imperfect nature of the samples prepared with NSL. Indeed, the experimental D/P measured by AFM and the simulations do not consider the tapered nature of the nanohole wall. In fact, the nanoholes are more bowl-like, instead of cylindrical. Therefore, the apparent D/P for the sample labeled 0.57 > D/P > 0.50 is true for the top of the nanohole, but a SEM image of this sample demonstrates that the bottom of the nanohole had a smaller D/P ratio of approximately 0.3 (Figure S1 in ESI), which is in good agreement with the simulations. Measuring the diameter of the region of high Raman response for the smallest nanohole diameter also results in a D/P of 0.3, once again in agreement with the SEM image and the FDTD simulation. To our knowledge, it is the first time that such result demonstrates that if the nanohole diameter is small in comparison to the periodicity, the region of high electric field is not located at the edge of the rim of the nanohole (so called donut-shape), but rather at the center of the nanohole (typically made of glass, rather than metal), where molecules are not expected to absorb in common biosensing strategies. It also explains the lower Raman intensity measured for these samples, despite the excitation of the plasmonic band. The electric field is concentrated in a region where very few molecules are located, resulting in a lower Raman intensity.

The deviation between the FDTD simulations and the experimental SERS images for a D/P near 0.7 is another example of the influence of the imperfect nature of the samples prepared by NSL. The AFM image of the sample with a 0.77 > D/P > 0.74 shows a lower topography at the tip-to-tip region (Figure 1), due to the shadow effect of the NSL mask during the deposition of the metal layer. This imperfection in the tip-to-tip region may promote high electric field at this region, as observed in the experimental SERS image, instead of the rim of the nanoholes as simulated.

FDTD simulations performed at λ = 532 nm provide images with better lateral resolution than the ones at λ = 633 nm (Tables S1 and S2 in ESI). While this is in agreement with experimental Raman images, FDTD simulations are not diffraction-limited and so this does not explain the poorer definition of the hot spots with the longer wavelength. The simulations were performed with substrates of 1500 nm periodicity, such that there is no presence of plasmonic bands due to periodic hexagonal array of nanoholes (Table 1). Therefore, the influence of the D/P ratio can be clearly seen in the interpretation of the Raman images. One possible explanation involves fringes resulting from the excitation of the substrate. Fringes arise from the excitation of a surface plasmon polariton (SPP) around an individual nanohole by the incident electric field in the zero-order excitation. This SPP propagates radially from the individual nanoholes,^39,40 and an interference pattern is created from the SPP of adjacent nanoholes, which can be observed in the FDTD simulations.

Conclusions

Raman spectroscopy, confocal Raman microscopy, surface plasmon resonance and FDTD simulations have been employed to extensively characterize the transition from nanotriangle to nanohole arrays. For every periodicity sampled (650 to 1500 nm), the largest Raman response was observed at the transition state between nanotriangle and nanohole arrays. This transition occurs within a D/P region ranging from 0.75 (nearly interconnected triangle) to 0.60 (network of nanoholes). The SERS images of the hot spots on the nanostructures vary as the transition from nanotriangle to nanohole occurs. The hot spots were observed to be a delocalized area of high Raman intensity, which perfectly matches the metallic network of the array at a D/P ratio of nearly 0.7 and a donut-shape region of high Raman response (nanohole array), which correlates very well with the edges of the nanoholes. There by, the SERS images demonstrate the presence of a localized SP in nanotriangle arrays, a propagating SP for the substrate at the transition from nanotriangle to nanohole arrays and a localized SP in nanohole arrays. These changes in structure were demonstrated by correlating the AFM results and Raman microscopy images with one another. For the first time to our knowledge, it was observed that by further decreasing the D/P ratio, the region of high electric field for nanohole arrays is positioned at the center of the nanoholes, with a center-to-center spacing perfectly matching the periodicity. This observation has significant implications for biosensing applications in terms of optimal placement of bioanalytes. The experimental SERS images are in good agreement with the FDTD simulations and the outcome provides a comprehensive study of the plasmonic properties of nanohole arrays, from understanding the different locations of the hot spots to demonstrating the largest potential for SERS and SPR sensing applications.