A Mechanistic Model of Ca Regulation of Thin Filaments in Cardiac Muscle

Abstract

We present a model of Ca-regulated thin filaments in cardiac muscle where tropomyosin is treated as a continuous elastic chain confined in the closed position on the actin helix by electrostatic forces. The main distinction from previous works is that the intrinsic stress-free helical shape of the tropomyosin chain was taken into account explicitly. This results in the appearance of a new, to our knowledge, tension-like term in the energy functional and the equilibrium equation. The competitive binding of calcium and the mobile segment of troponin-I to troponin-C were described by a simple kinetic scheme. The values of dimensionless model parameters were estimated from published data. A stochastic Monte Carlo simulation of calcium curves has been performed and its results were compared to published data. The model explains the high cooperativity of calcium response of the regulated thin filaments even in the absence of myosin heads. The binding of myosin heads to actin increases the calcium sensitivity while not affecting its cooperativity significantly. When the presence of calcium-insensitive troponin-C was simulated in the model, both calcium sensitivity and cooperativity decreased. All these features were previously observed experimentally.

Introduction

Muscle contraction is driven by the cyclic interaction of globular heads of myosin molecules with the actin that forms the core of the thin filaments. The actin-myosin interaction is controlled by the regulatory proteins troponin (Tn) and tropomyosin (Tm), which are parts of the thin filaments. The Tm-Tn complex blocks the actin-myosin interaction in the absence of Ca²⁺and enables it when the calcium concentration increases. A coiled-coil Tm molecule binds the next Tm molecule in a head-to-tail manner to form a continuous chain that is complementary to the surface of the 36-nm-long actin helix (1,2). The Tm chain is constrained by electrostatic forces (3) at a particular azimuthal position. This electrostatic interaction involves some conserved residues (4). Mutations of these residues to Ala change the myosin binding to the actin-Tm complex in the absence and presence of Tn (4,5). The actin-Tm constraint, however, is not tough. It allows Tm to oscillate azimuthally with respect to actin with a standard deviation of ∼10° (6). Tn sits on Tm and moves azimuthally together with the Tm chain. In the absence of Ca²⁺, the inhibitory domain of the troponin-I (TnI) readily binds actin. Such binding leads to an azimuthal shift of the whole Tm chain to a state where it covers myosin-binding sites on actin and causes muscle relaxation (7,8).

The Ca-free state corresponds to the Blocked or B-state of the three-state model of McKillop and Geeves (8). The binding of Ca²⁺ to troponin-C (TnC) opens a hydrophobic pocket between the Ca-binding loop and the central α-helix of TnC. The open pocket can bind a labile part of TnI called the “switch domain”, which is located next to the inhibitory domain (9). When this happens, the inhibitory domain of TnI cannot reach its binding site on actin and the whole Tm-Tn complex remains in an actin-free state that corresponds to the Closed or C-state (9). When the regulatory Tm-Tn complex is in the C-state, actin can bind a myosin head. The initial binding is weak, but later some conformational changes occur in myosin and, possibly, actin, so that the binding becomes stronger. A strongly bound myosin head shifts Tm further and exposes myosin-binding sites of neighbor actin monomers. This is the Open or O-state of the Tn-Tm complex (8). Generally speaking, there is a competition between TnC and actin for binding of the mobile segment of TnI: Ca²⁺ favors the TnI binding to TnC and thus promotes its detachment from actin.

The calcium curve that describes the contractile or biochemical response of striated muscles or regulated thin filaments to calcium ions is usually approximated with the Hill equation,

$$V=\frac{{\left[\text{Ca}\right]}^n}{{\left[\text{Ca}\right]}_{50}^n+{\left[\text{Ca}\right]}^n},$$

where V is the normalized response (tension of a muscle cell or a myofibril, i.e., the ATPase rate, a signal that characterizes structural changes in troponin, etc.); [Ca] is the molar Ca²⁺ concentration; [Ca]₅₀ is the Ca²⁺ concentration that gives a half-maximal response; and n is the cooperativity constant, called the Hill coefficient. Because cardiac TnC binds only one Ca²⁺ ion, n is expected to be 1. In reality, n is much higher, ∼2.5–3 or higher (10,11). The high cooperativity is often explained by the shift of the Tm chain by myosin heads that are strongly bound to actin, because myosin head binding facilitates the unbinding of neighbor TnC from actin and opens myosin-binding sites on neighbor actin monomers (7). However, it was shown that an inhibition of the strong actin-myosin interaction with blebbistatin does not reduce the steepness of the calcium curve significantly (10,11). This indicates that the cooperativity is an intrinsic property of the thin filaments themselves (10). The binding of myosin heads to the actin decreases [Ca]₅₀, not affecting n much (10).

Here we describe a mechanistic model that explains the high steepness of the Ca-activation curve in cardiac muscle even in the absence of myosin heads. Our approach is based on works (12–15) where tropomyosin was modeled by a continuous flexible chain in a harmonic potential well on the surface of an actin filament. A new, to our knowledge, expansion of this model is that we have taken into account that the tropomyosin chain has an intrinsic stress-free helical shape. This leads to a change in governing equations and brings new, to our knowledge, features to the system. In addition, for calculating changes in the elastic energy of the Tm chain upon the binding of TnI or myosin head to actin, we exploit a more precise three-point approximation instead of the two-point approximation used in the literature (12–15).

Mathematical Model

Model of the Tm chain

We consider tropomyosin as a continuous semiflexible worm-like chain (12) that runs along the whole thin filament in the groove of the long actin helix. The chain can be pinned to actin by either TnI or a myosin head. The change in the azimuthal angle caused by the pinning is −φ_T or φ_M, respectively, as TnI and a myosin head move Tm to opposite directions (the filament axis is directed toward the pointed end of the actin). In the original model (12–15), the intrinsic helical shape of the tropomyosin was not taken into account, so that changes in the shape of the Tm chain were described by the equation of a straight elastic bar in a harmonic potential well. Here, the stress-free helical shape of tropomyosin is explicitly accounted for. The pitch of the long actin helix is ∼36 nm. An unpinned, i.e., free Tm chain, has twice-longer pitch, ∼72 nm. The helical twist of an unpinned Tm chain is ψ = 2π/72 nm = 0.0873 nm⁻¹ (the 72-nm-long period of the Tm helix is twice as long as that of the long actin helix). The Tm chain is considered inextensible although bendable. It is assumed that, when Tm slides on the actin surface, the axis of the Tm coiled-coil remains on a cylinder of radius a. We introduce Cartesian coordinates so that the radius-vector of a point on the tropomyosin chain (Fig. 1 A) is described by

$$\overrightarrow{r}=\text{acos}\left(\psi z+\phi \left(z\right)\right){\overrightarrow{e}}_1+\text{asin}\left(\psi z+\phi \left(z\right)\right){\overrightarrow{e}}_2+\left(\psi z+u\left(z\right)\right){\overrightarrow{e}}_3.$$ (1)

Here, the unitary vector ${\overrightarrow{e}}_3$ is directed along the thin filament axis (z is the axial coordinate) and ${\overrightarrow{e}}_1$, ${\overrightarrow{e}}_2$ are orthogonal unitary vectors in a cross-section of the filament; u(z) is the axial displacement; and φ(z) is the angular displacement of Tm (Fig. 1, A and B). In the undisturbed C-state, the Tm chain is in an equilibrium stress-free state and forms a helix:

$$\overrightarrow{r}=\text{acos}\left(\psi z\right){\overrightarrow{e}}_1+\text{asin}\left(\psi z\right){\overrightarrow{e}}_2+z{\overrightarrow{e}}_3.$$ (2)

The inextensibility condition means that the length of a tropomyosin segment does not change upon its sliding along the actin surface. This means that (Fig. 1 B)

$$d{s}^2=\left({\left(1+u^{\prime }\left(z\right)\right)}^2+a^2{\left(\psi +{\varphi }^{\prime }\left(z\right)\right)}^2\right)d{z}^2=\left(1+a^2{\psi }^2\right)d{z}^2=d{s}_0^2,$$ (3)

where s and s₀ are the arc lengths along the Tm chain in the bent and undisturbed states, respectively. In Eq. 3 and onward, the prime means a derivative over z. If the axial and angular displacements of the Tm chain are small, one can simplify Eq. 3 by neglecting the terms proportional to the squares of the displacement components. This results in a simple linear relation between the angular and axial component of the displacement:

$$u^{\prime }\left(z\right)+a^2{\psi }^{\prime }\left(z\right)=0.$$

We also assume that Tm is confined in the closed C-state at φ = 0 by the elastic force −αφ, which is determined by electrostatic actin-Tm interactions where α is a constant factor that characterizes the strength of the chain-confining potential. This assumption was suggested earlier (12,13), and more recently supported by an energy computation for the actin-Tm interaction in Eq. 3. It was shown that upon the myosin binding to actin, Tm slides along the actin surface from the closed C-state to the open O-state without rolling (16). The twisting stiffness of Tm was found to be much lower than its bending stiffness (17). These data support the idea (12) that the elastic Tm energy is mainly determined by its bending. For these reasons, we assume that the elastic energy of a segment of the tropomyosin chain between two axial points, b and c, is determined by its bending energy and energy of the actin-Tm interaction:

$$E=\frac{1}{2}\underset{b}{\overset{c}{\int }}\left(\alpha {\left(\varphi \left(z\right)\right)}^2+K\left({\left(\frac{a{\varphi }^{″}\left(z\right)}{\sqrt{g_0}}\right)}^2+{\left(2a\psi {\varphi }^{\prime }\left(z\right)\right)}^2\right)\right)dz.$$ (4)

Here, g₀ = 1 + a²ψ² and K is the bending stiffness that is assumed to be constant along the Tm chain, independent of the direction of bending. The validity of this simplification will be discussed later. Some details of the mathematical treatment are given in Appendix.

Figure 1.

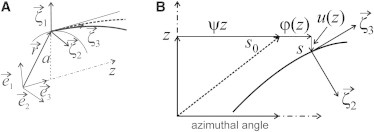
The schematic representation of the Tm chain (thick continuous line) on the cylindrical actin surface. (A) The three-dimensional representation of the Tm chain on the F-actin surface. (B) The involute of the cylindrical actin surface. (Dashed line) The helical Tm shape in the closed C-state. (Dash-dotted line) The actin axis. Other notations are explained in the text.

We introduce a dimensionless axial distance, x = z/ξ, where

$$\xi ={\left(\frac{4K{a}^2}{\alpha \sqrt{g_0}}\right)}^{\frac{1}{4}}$$

is the persistent length of the Tm chain. Then, the energy can be rewritten as

$$E=\frac{\alpha \xi \sqrt{g_0}}{2}\underset{b/\xi }{\overset{c/\xi }{\int }}\left(\frac{1}{4}{\left({\varphi }^{″}\left(x\right)\right)}^2+{\varphi }^2\left(x\right)+\beta {\left({\varphi }^{\prime }\left(x\right)\right)}^2\right)dx,$$ (5)

where $\beta =2a{\psi }^2\sqrt{K{g}_0/\alpha }$ is a dimensionless parameter. It should be noted that the term “persistent length” used here and in the literature (12–15) has different meaning from that used in the worm-like chain theory and Li et al. (17), where L_P = K/k_BT, with k_B as the Boltzmann constant and T as absolute temperature.

The last term in the energy integrals in Eqs. 4 and 5 is similar to the term that appears in the elastic bar theory when the bar is subjected to the tensile force (18). However, here the physical nature of the term that is characterized by the dimensionless parameter β in Eq. 5 is different. It arises from the intrinsic helical shape of Tm, not from the true tensile force.

Because the troponin complex sits on the Tm chain, the binding of the inhibitory domain of TnI to actin pins the chain at a fixed angle −φ_T. Such TnI pinning corresponds to the blocked B-state of the troponin-tropomyosin complex (8).The strong binding of a myosin head to actin forces the Tm chain to move azimuthally to the opposite direction, i.e., pins it to a positive angle φ_M = −χφ_T (here χ is a constant).

Troponin complexes are bound to every Tm molecule in a chain with an axial repeat of c ≈ 38.5 nm that corresponds to seven actin monomers on a strand of the long pseudo-two-strand actin helix. The ratio of the troponin-troponin distance to the persistent length gives one more dimensionless parameter, λ = c/ξ. A myosin head can bind every actin monomer on an actin protofilament except those covered by Tn. The axial distance between the neighbor actins is 5.5 nm.

The Tm chain on a thin filament can be pinned to actin at a number of points by either TnI or myosin heads. When a new pin point is formed due to a protein-protein binding (or another reason), detachment of a myosin head or TnI from actin leads to a change in Tm elastic energy. The probabilities of the binding or unbinding depend on the energy change associated with this event.

The total energy of a Tm chain pinned to the angle −φ_T by a TnI molecule is

$$E_T=\alpha \xi {\varphi }_T^2\sqrt{g_0\left(1+\beta \right)}$$

(calculated from the solution given in Eq. A4). The energy E_T normalized for the thermal energy k_BT gives a dimensionless energy parameter

$$\gamma =\frac{\alpha \xi {\varphi }_T^2\sqrt{g_0\left(1+\beta \right)}}{k_{\text{B}}T}.$$

It is difficult to obtain an explicit general solution for the energy change for a Tm chain with an arbitrary number of pin points. Instead, we calculated the energy of an infinitely long Tm chain for two (E₂) and three (E₃) pin points, either TnI or myosin, assuming that the energy changes caused by pinning or unpinning in the intermediate point are mainly determined by its nearest pinned neighbors on both sides and is not affected significantly by chain pinning outside this interval. The validity of this simplification is discussed in the Supporting Material.

Binding of Ca²⁺ and components of troponin complex to each other and to actin

A kinetic scheme, used to describe the interaction of troponin components, TnI and TnC, with Ca²⁺ and actin, which was based on the structure of the troponin complex (9), is shown in Fig. 2. In the scheme, K_Ca, K_I, and K_A are the equilibrium constants for Ca²⁺ binding to TnC, for binding of the switch segment of TnI to TnC, and for binding of the inhibitory domain of TnI to actin, respectively. The value ε < 1 is a constant (we used ε = 0 for most simulations; the effect of nonzero ε on Ca²⁺ sensitivity in the model of regulated thin filaments is illustrated in Fig. S4 in the Supporting Material).

Figure 2.

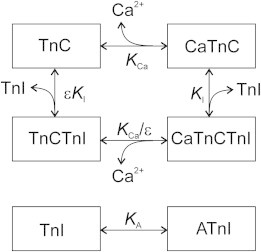
The kinetic scheme of the interaction of the troponin components, TnC and TnI, with Ca²⁺ and actin. Here K_Ca and K_I are the equilibrium constants for the binding of Ca²⁺ and the switch domain of TnI to TnC, respectively; K_A is the equilibrium constant for the TnI binding to actin; and ε < 1 is a constant.

The scheme suggests that only one Ca²⁺ ion can reversibly bind TnC (7). The calcium binding to TnC facilitates TnI binding to the open hydrophobic pocket on TnC and promotes TnI detachment from the actin. Let С = K_Ca[Са²⁺]; ↠ and z are dimensionless or normalized Ca²⁺ concentration and probabilities for TnC and for the inhibitory/switch segment of TnI to be in free or unbound states, respectively. For the steady-state processes, the probabilities of being in states CaTnC, CaTnCTnI, and TnCTnI are Cy, CyzKI, and yεzKI, respectively. Because the sum of the probabilities for TnC and TnI to be in one of the possible states is unity, x, y, and z satisfy the equations

$$\begin{array}{c}y+yC+yCz{K}_I+y\epsilon z{K}_I=1,\\ z+z{K}_A+y\epsilon z{K}_I+yCz{K}_I=1.\end{array}$$ (6)

If the inhibitory domain of TnI is detached from the actin (K_A = 0), the expressions in Eq. 6 can be solved for any given calcium concentration, C. It gives y and z as

$$\begin{array}{cc}y=\frac{\sqrt{{\left(1+C\right)}^2+4K_I\left(\epsilon +C\right)\left(1+C\right)}-\left(1+C\right)}{2K_I\left(\epsilon +C\right)\left(1+C\right)},& z=y\left(1+C\right).\end{array}$$

If TnI is bound to actin and keeps Tm in the blocked B-state, then z = 0 and y = 1/(1 + C).

Binding of myosin heads to regulated thin filament

The binding of myosin heads to regulated thin filaments in contracting muscle has a complicated nature. Initially, a head weakly binds an actin monomer that is not covered by the Tm chain but which should be in the closed C-state, although not in the blocked B-state (19). Some of the weakly bound heads then change their binding mode and become strongly bound. When this happens, the head pins the Tm chain, shifting it to the opened O-state. Instead of considering the two-step binding of myosin heads to actin and their complicated three-dimensional arrangement, we assumed that the weak binding is short-lived and quickly reversible so that the weakly bound heads do not affect the Tm configuration. We substituted the two-step process with a single strong binding step. Although both weak binding and the weak-to-strong transition depend on the configuration of the Tm chain (and on Ca²⁺), the combined step is equivalent to the closed-to-open transition, or pinning of the Tm chain to φ_M.

Myosin heads that bind a particular thin filament originate from three surrounding thick filaments. Their binding has an ∼14.5-nm axial modulation that corresponds to the axial spacing of the crowns of myosin heads on the backbone of the myosin filaments. This modulation results in the appearance of the M3 myosin meridional reflection on the x-ray diffraction pattern of contracting muscle (20). Although we used the simplest assumption that the effective affinity, ρ, of myosin heads to actin is constant along the thin filament, a more realistic assumption that ρ has an axial modulation with a ∼14.5-nm period does not affect the results of our calculations (see Fig. S6).

Change in the energy of the Tm chain: two- and three-pin approximations

We considered a Tm chain on a 1001-nm-long thin filament with 27 troponins (two of which are on the filament ends) and 365 actin monomers. One-half of the total number, or 183 actin monomers, are regulated by Tm chain. Because each troponin complex occupies an actin monomer, 156 = 183 − 27 actin monomers were accessible for myosin heads. Each time TnI binds actin, it pins the chain to a negative angle −φ_T, whereas a strongly bound myosin head pins it to a positive angle φ_M = −χφ_T (Fig. 3).

Figure 3.

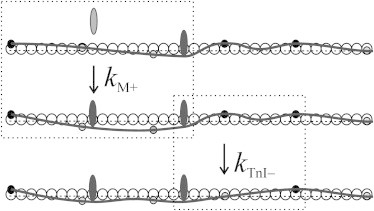
The schematic representation of a fragment of the pinned Tm chain (solid line). (Solid circles) Troponin complexes bound to actin and pin Tm chain; (shaded circles) detached complexes. (Solid ellipses) Actin-bound myosin heads; (shaded ellipses) detached head. (Dotted boxes) A two-pin segment before and after myosin binding to an intermediate actin site (rate constant k_M+) and a three-pin segment before and after TnI detachment from an intermediate actin site (rate constant k_TnI+).

For the steady state of the Tm chain, the ratio of the forward (pinning) and reverse (unpinning) rate constants is determined by the change in the chain energy upon the binding or unbinding of TnI or a myosin head to actin. Because an explicit solution for a chain with an arbitrary number of pin points is difficult to obtain, we used the three-pin approximation that takes into account only the actin site that is probed and its nearest neighbors on both sides. For the ith myosin head, the ratio of the rate constants for the binding to actin and unbinding is given by

$$p_i=\frac{k_{M+}}{k_{M-}}=\rho \text{exp}\left(-\gamma \left(E_3-E_2\right)\right),$$

where ρ is a constant that characterizes the availability of the myosin heads and their affinity for actin. Similarly, the ratio for the rates of the binding of the jth Tn complex to the actin and unbinding from it is given by

$$p_j=\frac{k_{T+}}{k_{T-}}=z{K}_A\text{exp}\left(-\gamma \left(E_3-E_2\right)\right).$$

Here, E₂ and E₃ are dimensionless energies, i.e., energies calculated using Eq. 5 and scaled for E_T. The method for calculating dimensionless energies, E₂, E₃, for different possible configurations and distances between the pins are given in the Appendix and the Supporting Material. Their values were precalculated for all possible types of pin points and distances between them using explicit solutions for an infinitely long Tm chain. These were then saved in computer memory and used for the Monte Carlo simulations.

Monte Carlo simulation

To determine the average equilibrium characteristics of the pinned Tm chain at any calcium concentration, C, and to calculate the average fractions of the actin-bound TnC, CaTnC, and myosin heads, we use the Monte Carlo method. The main difficulty was caused by the high dimension of the phase space: for a chain with 183 actin pin points it is 2¹⁸³, which is too much for using conventional Markov-chain Monte Carlo methods such as the Metropolis-Hastings algorithm. To search such a configuration space of high dimension more effectively, an element subjected to probe for pinning/unpinning was chosen not randomly or consequently, but according to the probability of changing of its status. The idea of the algorithm was to pick up predominantly those elements that are more likely to switch their state—bind to actin, if they are detached, or unbind from it, if they are bound.

More explicitly, the ith actin element was probed for pinning with the probability proportional to (p_i)^1/3, where p_i = zK_A exp(−γ(E₃ – E₂)) for a TnI and p_i = ρ exp(−γ(E₃ – E₂)) for myosin head. For unpinning, the probability of choosing the ith actin monomer was proportional to (p_i)^1/3. After an actin site for the next probe was chosen, the pinning probability was min[1, (p_i)^1/3] and the unpinning probability was min[1, (p_i)^−1/3]. Here, p_i is the ratio of forward (pinning) and reverse (unpinning) rate constants for ith actin site. As a result of such choice of the element and the probability of changing its state, the overall rate of forward (pinning) transition was proportional to (p_i)^1/3 min[1, (p_i)^1/3], whereas the rate of the reverse (unpinning) transition was proportional to (p_i)^−1/3 min[1, (p_i)^−1/3], so that their ratio was p_i as required.

Step by step, the algorithm was as follows: for a given state of the system, the segment [0; 1] was divided into 182 subsegments with their length proportional to (p_i)^1/3, if the ith actin site (i = 1, … 183) was pinned, or to (p_i)^−1/3, if it was not pinned. Then, a random number, a, between 0 and 1 was drawn using a random number generator. If a fell to the ith subsegment, the ith actin site was probed for changing its state. If the probability was 1, the state of the element was changed involuntarily. If not, another random number, b, between 0 and 1 was drawn and compared with P_i, where P_i = min[1, (p_i)^1/3] if the ith actin was pinned or with P_i = min[1, (p_i)^−1/3], if it was unpinned. If b was smaller than P_i, the state of the ith actin was changed. It was pinned by the TnI or by myosin head, if it had been unpinned before, and vice versa. For each calcium concentration C, the choice of an actin site and probe for changing its state were repeated up to 5 × 10⁷ times. The average values for the fractions of CaTn complexes, actin-bound TnI, and myosin heads bound to actin were calculated as a function of the normalized calcium concentration C.

Results

Cooperative Ca activation of the thin filaments without myosin heads

The basic set of dimensionless parameters was chosen as follows: K_I = 1000, K_A = 200, γ = 4, and λ = 2 (this means that persistence length ξ = 19.25 nm), β = 3.5, ε = 0, and χ = 0.4. When ε is nonzero, many TnIs appear to remain in the actin free state even at low Ca²⁺ concentration, so relaxation is incomplete (see Fig. S4). Although the presence of a significant fraction of actin-free Tn in the absence of Ca²⁺ as well as the dependence of Ca²⁺ binding to TnC on the regulatory domain of TnI probably takes place in the regulated thin filaments, here we mainly concentrated on effects of Tm helicity that were not exploited previously and left the effects of nonzero ε for further work.

We tried, but could not obtain, reasonably steep calcium curves in the absence of myosin heads with the parameter γ lower than 3.5. This means that the high cooperativity of the thin filament activation requires a rather high chain-energy cost for the TnI binding to actin. For higher values of the energy parameter, γ, the Ca curves could be even steeper than those reported here (see Fig. S5).

The Ca curves for the fractions of CaTnC and actin-TnI complexes at different values of parameters β and λ are shown in Fig. 4. The model curves with β =3.5 and λ = 2 show the steep and highly cooperative Ca²⁺ activation (the apparent Hill coefficient n ≈ 2.5) in the absence of myosin heads. This agrees with the data of Sun and Irving (10) and Sun et al. (11), who found that the Ca²⁺ binding to TnC is cooperative even in the presence of blebbistatin that blocks the strong myosin binding to actin. An increase in β leads to a decrease in Ca sensitivity and to an increase in the steepness of the Ca curve, i.e., in the apparent Hill coefficient, n (Fig. 4 A).

Figure 4.

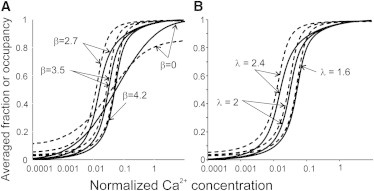
The calculated model Ca curves in the absence of myosin heads for different values of β and λ. (A) The calculations for λ = 2 and β-values shown on the plot. (B) The calculations for β = 3.5 and λ-values shown on the plot. (Dashed lines) Average calculated fractions of actin-unbound TnI. (Continuous lines) Occupancies of TnC sites by Ca²⁺ ions.

At a constant persistence length of the Tm chain (corresponding to the constant bending stiffness and α-parameter), β depends on the helical parameter ψ of the actin helix. In the model described in the literature (12–15), the straight elastic bar theory was used, which corresponds to β = 0. In this case, the cooperativity was lost. Both activation and relaxations at zero and saturating Ca²⁺ concentrations become incomplete at the same values of the other parameters. Higher β that corresponds to the real helicity of F-actin and Tm chain leads to the higher cooperativity of the Ca activation of the thin filaments.

The variation of λ characterizes the change in the tropomyosin bending stiffness, K, and/or in the force constant, α, that constrains tropomyosin in the C-state. An increase in λ leads to a shift of Ca curves to the left, i.e., increases the Ca²⁺-sensitivity and decreases its cooperativity (Fig. 4 B). Because λ is the ratio of the axial distance between neighbor troponins (38.5 nm) to the persistence length of the Tm chain, it increases when the tropomyosin bending stiffness decreases. On the other hand, an increase in the coefficient α that characterizes the actin-myosin electrostatic force, which constrains the Tm chain in the C-state, leads to an increase in λ.

Binding of myosin heads to actin increases Ca sensitivity, but not cooperativity

When myosin heads are able to bind actin, the simulated calcium curves shift to the left, showing an increased sensitivity without a significant increase in the slope of the Ca curves (Figs. 5 and 6). The reason for that is obvious: when a myosin head binds actin strongly, it shifts the tropomyosin chain to the O-state and facilitates the detachment of the neighbor troponins from actin. Sun and Irving (10) monitored the dependence of the faction of the CaTnC complexes on the Ca²⁺concentration in rigor, and found much lower [Ca²⁺]₅₀ than in the presence of ATP. The cooperativity was also absent, n = 1. To simulate the rigor conditions in our model, K_A was set to zero, to disable the TnI binding to actin because it takes place in rigor where Tm is shifted to the angle φ_M by strongly bound myosin heads preventing TnI from reaching its binding site on actin. Modeling results are very similar to what was observed experimentally (Fig. 5): the Ca²⁺ binding was noncooperative (n = 1), and the difference between [Ca²⁺]₅₀ values for the Ca²⁺ binding to TnC in rigor and in the presence of ATP and blebbistatin was ∼1.5 pCa units—very close to what was observed experimentally (10).

Figure 5.

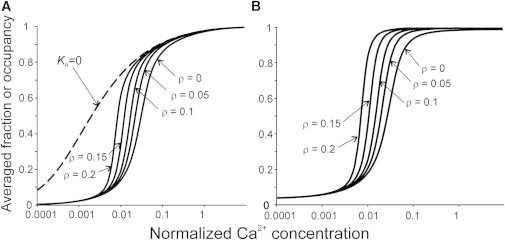
The effect of myosin heads on simulated Ca curves. (A) Averaged occupancy of TnC by Ca²⁺ ions for different affinities of myosin heads to the actin, ρ. (Dashed line) Calculation for K_A = 0 that corresponds to TnC titration with Ca²⁺ ions in rigor. (B) The average fraction of TnI not bound to actin. β = 3.5, λ = 2 for all calculations.

Figure 6.

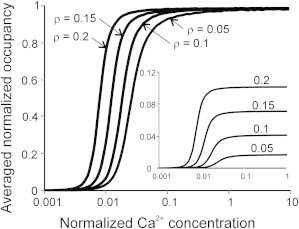
The normalized average actin occupancy by myosin heads versus the normalized Ca²⁺ concentration at different head affinity to actin. (Inset) The nonnormalized actin occupancy for the same conditions (β = 3.5, λ = 2; ρ-values are shown above the lines).

When the affinity of myosin heads to actin was decreased in our model, the Ca sensitivity also decreased significantly with only slight decrease in the slope of the Ca curves (Fig. 6). This agrees well with experiments where the actin-myosin interaction was depressed by blebbistatin (21). The dependence of [CaTnC] and normalized number of actin-bound myosin heads on C were similar to each other, as was observed by simultaneous measurement of tension and conformational change in TnC (10,11).

Effect of Ca-insensitive troponin-C on activation

We also modeled experiments in which a fraction of Ca-insensitive troponins-C molecules was incorporated into the thin filaments of the skinned rat trabeculae from rat hearts (21). We modeled these experiments by random choice of 10, 25, and 40% troponins that were unable to bind Ca²⁺. The results are shown in Fig. 7 as Ca curves for the fraction of CaTnC complexes among those that are able to bind Ca²⁺, TnI-actin complexes, and actin-bound myosin heads. As it was found in experiments (21), an increase in the fraction of Ca-insensitive troponins-C led to a decrease in the amplitude of Ca activation in the model (Fig. 7). This was seen as a decrease in the fraction of actin-detached TnC and of actin-bound myosin heads at a saturating Ca²⁺ concentration. Also, in the presence of Ca-insensitive TnC, [Ca₂₊]₅₀ and the slope of model Ca curves decreased, which was as observed experimentally (21).

Figure 7.

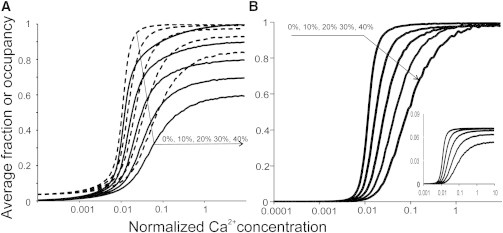
Calcium curves for model simulations of the experiments (21) in which some TnC sites were insensitive to Ca²⁺. (A) Average calculated fractions of actin-unbound TnI (dashed lines) and of CaTnC complexes (continuous lines). The fractions of Ca-insensitive TnC are shown in %. (B) Average normalized fraction of actin-bound myosin heads. (Inset) Occupancy of actin-site myosin heads for the same calculations (β = 3.5, λ = 2, ρ = 0.15).

Discussion

Main findings

The model that treats the tropomyosin chain as an elastic bar, has the intrinsic stress-free helical shape, and slides without an elongation on the surface of the actin filament, describes some essential features of the Ca²⁺ activation of the thin filaments in cardiac muscle. The model presumes that the Tm chain is constrained in the C-state on the actin surface by electrostatic forces. The model explains the highly cooperative Ca²⁺ binding to TnC even in the absence of myosin heads. It also reproduces an increase in Ca sensitivity of the thin filaments by bound myosin heads without a significant increase in the cooperativity. The model also simulates the results of experiments where some troponin-C molecules were substituted with mutants insensitive to Ca²⁺ (21).

Comparison with previous works

Our approach is based on the idea (12–15) that the cooperativity of the thin filaments is caused by the mechanical properties of the tropomyosin chain, which behaves as a continuous semi-flexible worm-like chain that slides on the surface of an actin filament. The shift of the chain from its equilibrium C-state due to its pinning to actin by either troponin or myosin head propagates to the neighbor segment of the chain and results in the cooperativity. The difference between our model and those suggested previously is that we explicitly treat the tropomyosin chain as an elastic bar that has the intrinsic stress-free helical shape. This causes the additional term in the energy functional, and the additional term in the force equilibrium equation (see Appendix). This term is similar to one that arises is the elastic bar theory due to the application of tension (18). In our case, however, this term is not induced by real tension, but results from the intrinsic helical shape of the Tm chain. The presence of this term increases the effective length of the Tm chain segment that is affected by its pinning to actin by either TnI or myosin head, thus increasing the cooperativity of the thin filament (see the Appendix and the Supporting Material).

Model justification and parameter estimations

Although there is evidence of variation of the Tm bending stiffness (17) and its curvature (22) along the tropomyosin molecule, these effects are small, and were neglected for the sake of simplicity. The coiled-coil structure of Tm also suggests that its bending stiffness depends on the direction of the bending. However, the twisting of two α-helices has a pseudo-periodicity of ∼5.5 nm, which is close to the axial distance between neighbor actin monomers. This means that for ranges shorter than 5.5 nm, the Tm bending stiffness is indeed essentially anisotropic. Nevertheless, the characteristic radius of the Tm bending due to pinning to actin by either Tn or myosin head is much longer than 5.5 nm by at least one persistence length. Therefore, the Tm bending is determined by the average bending stiffness over the 5.5 nm coiled-coil axial period, which is independent of the direction.

For most of our calculations, we used λ = 2, which corresponds to the persistence length ξ = 19.25 nm. This figure is very close to that estimated by Geeves et al. (15), and is consistent with contemporary estimates of the tropomyosin bending stiffness K (17) and the constraining constant α (3) obtained using computational approaches. Once ξ and λ are defined, β = 3.5 can be calculated directly using radius of the Tm chain of 4.2 nm (16) and the actin helical twist, ψ. Contemporary estimates of φ_T and φ_M are 25 and 10° (6) giving χ = 0.4. The energy parameter γ = 4, which characterizes the ratio of the Tm chain energy, caused by TnI binding to actin, to the thermal energy k_BT, is somewhat higher than the 1.6 measurement used in Geeves et al. (15). However, for β > 0, the energy of the Tm chain with a single actin-Tn pin of the constant amplitude is proportional to

$$\sqrt{1+\beta }.$$

The presence of the term containing β leads to an increase in the energy by a factor of 2.12 compared to that at β = 0. Therefore, our estimate of γ is not far from that used in Geeves et al. (15). The chain energy associated with a 10° pinning by the myosin head in our model is γχ² = 0.64—that is, slightly higher than one-half of the thermal energy, k_BT. This figure is consistent with a 10° random azimuthal fluctuation in the C-state estimated from x-ray fiber diffraction data (6). Smaller γ-values lead to a decrease in the cooperativity (smaller apparent Hill coefficients, n). With higher γ, one can easily achieve the higher cooperativity with n > 3. The TnC affinity for Ca²⁺, K_Ca, affects only the scaling of the dimensionless Ca concentration, [C]. Our choice of the binding constants of the mobile domains of TnI to actin and TnC, K_A = 200 and K_I = 1000, respectively, provided an effective competition of the mobile domains of TnI for TnC and actin at the chosen γ-value.

Authors in the literature (13–15) used a two-pin approximation. This means that the change in chain energy was calculated using known two-pin solutions (12) for the infinitely long chain with two pin points separated by a certain distance. For the chain that has more pin points, its configuration was approximated by a two-pin solution in each interval between neighbor pin points (13–15). Here we used a more precise three-pin approximation: changes in the energy associated with pinning or unpinning of an actin site were estimated from a comparison of a three-pin solution (where the central point is the one of interest) with the two-pin solution with fixed left and right neighbor pin points. Test calculations (see the Supporting Material) show that the two-pin approximation sometimes gives a significant error in the energy configuration. The energy estimation from the comparison of E₃ and E₂ obtained from the three- and two-pin approximations, respectively, is more accurate. We tested this by a comparison with the four-pin case where an additional pin point was outside the segment of the interest. In this case, the fourth point affected the shape of the chain, but only marginally influenced the change in the chain energy due to the pinning or unpinning (see the Supporting Material).

Explanation of the results and their possible implications

Although the persistence length in our model was only one-half of the distance between neighbor troponins on the Tm chain, the model showed the high cooperativity of a calcium activation. The reason for it is that an increase in β leads to an increase in the length of the Tm segments affected by a single pinning to actin. At β = 3.5, the width of the chain segment where the angular displacement is at least one-half that in the pin point, is 1.5 times higher than at β = 0 (see Fig. S1). The value of the apparent Hill coefficient, n, in the absence of myosin heads was in our simulations (Fig. 4) close to that found by Sun and Irving (10) in the experiments where strong binding of myosin to actin was depressed by blebbistatin.

The binding of a myosin head to actin shifts the Tm chain to the direction opposite to that induced by TnI binding to actin, i.e., toward the open O-state of the thin filament. This explains why the myosin binding facilitates the Ca activation, decreasing the Ca²⁺ concentration that provides a half-maximal response. However, the cooperativity of the calcium curves did not change much, possibly because the absolute value for the angular shift induced by the binding of the myosin head to the actin compared to that of the troponin binding to the actin (10 vs. 25° (6)). The Hill coefficient n increased from n = 2.3 (for CaTn complexes) or n = 2.7(for actin-TnI complexes) in the absence of myosin heads (ρ = 0) to n = 3.5 (CaTn) or n = 4.5 (actin-TnI) at ρ = 0.2. The maximum (saturated) fraction of myosin heads bound to actin at high calcium concentration is proportional to the affinity of myosin heads to actin, ρ.

We also simulated experiments of Farman et al. (21), who used a mutant TnC (DM-TnC) that is incapable of Ca²⁺binding. The more calcium-insensitive TnC molecules were randomly introduced to the model, the less sensitive and less steep was the calcium curve. This is similar to what was observed experimentally: an increase in the fraction of DM-TnC reduced the maximum tension, [Ca²⁺]₅₀, and the steepness of the calcium curve (21).

Appendix: Equilibrium Configuration of Pinned Tm Chain and Energy Calculation

The dimensionless energy of a Tm chain segment between pin-points b and c is given by

$$E=\frac{1}{2}\underset{b}{\overset{c}{\int }}\left(\frac{1}{4}{\left({\varphi }^{″}\left(x\right)\right)}^2+{\varphi }^2\left(x\right)+\beta {\left({\varphi }^{\prime }\left(x\right)\right)}^2\right)dx.$$ (A1)

The equilibrium configuration of the chain between the pins provides the minimum for the energy functional (Eq. A1) and is given by

$${\phi }^{IV}\left(x\right)-4\beta {\phi }^{″}\left(x\right)+4\phi \left(x\right)=0.$$ (A2)

Its general solution is

$$\phi \left(x\right)=A\text{cosh}\left(\sqrt{2\left(\beta +\sqrt{{\beta }^2-1}\right)}\right)+B\text{sinh}\left(\sqrt{2\left(\beta +\sqrt{{\beta }^2-1}\right)}\right)+C\text{cosh}\left(\sqrt{2\left(\beta -\sqrt{{\beta }^2-1}\right)}\right)+D\text{sinh}\left(\sqrt{2\left(\beta -\sqrt{{\beta }^2-1}\right)}\right)$$ (A3)

where A, B, C and D are constants. If the chain is pinned in several points, the following boundary conditions should be satisfied in each of these points, x_i, where the pin angle is φ_i:

$$\phi \left(x_i-0\right)=\phi \left(x_i+0\right)={\phi }_i,$$

$${\phi }^{\prime }\left(x_i-0\right)={\phi }^{\prime }\left(x_i+0\right),$$

$${\phi }^{″}\left(x_i-0\right)={\phi }^{″}\left(x_i+0\right).$$

These conditions mean that the chain angular displacement and its first and second derivatives are continuous functions of the axial coordinate, x. The second of these two conditions means that neither troponin nor myosin binding to actin produce any bending torque of the Tm chain. For an infinitely long Tm chain, the boundary conditions in infinity are

$$\phi \left(x\right)\to 0,{\phi }^{\prime }\left(x\right)\to 0,$$

when x → ∞ or x → −∞.

The explicit solutions of Eq. A2 for an infinitely long chain with arbitrary positions and angles of one, two, three, and four pin points were obtained using a computer program. The total chain energy was then calculated using Eq. A1. For a single pin point, φ(0) = 1, at x = 0 the solution for x > 0 (for negative x, φ(−x) = φ(x), i.e., φ(x) is an even function) is given by

$$\phi \left(x\right)=\frac{\sqrt{2\left(\beta +\sqrt{{\beta }^2-1}\right)}\text{exp}\left(-\sqrt{2\left(\beta -\sqrt{{\beta }^2-1}\right)}x\right)-\sqrt{2\left(\beta -\sqrt{{\beta }^2-1}\right)}\text{exp}\left(-\sqrt{2\left(\beta +\sqrt{{\beta }^2-1}\right)}x\right)}{\sqrt{2\left(\beta +\sqrt{{\beta }^2-1}\right)}-\sqrt{2\left(\beta -\sqrt{{\beta }^2-1}\right)}}.$$ (A4)

Plots of the equilibrium shape of the chain pinned in a single point for different values of β are shown in Fig. S1. The higher the β-value, the wider the segment affected by the pinning. As a result, the pinning of the helical chain affects significantly more actin sites than one would expect from the theory of a straight elastic Tm chain (β = 0) with the same persistence length.

Similarly, E₂ and E₃ for two and three pins, respectively, were precalculated for all possible pin types (troponin or myosin head) and possible distances between them on a 1001-nm-long actin filament and then used for Monte Carlo simulations.