Skip to main content
NCBI home page
The Journal of Neuroscience logoLink to The Journal of Neuroscience
. 2012 Oct 3;32(40):13873–13880a. doi: 10.1523/JNEUROSCI.5644-11.2012

Stochastic Generation of Gamma-Band Activity in Primary Visual Cortex of Awake and Anesthetized Monkeys

Dajun Xing 1,2,✉, Yutai Shen 1, Samuel Burns 2, Chun-I Yeh 2, Robert Shapley 2, Wu Li 1,✉
PMCID: PMC3752128  PMID: 23035096

Abstract

Oscillatory neural activity within the gamma band (25–90 Hz) is generally thought to be able to provide a timing signal for harmonizing neural computations across different brain regions. Using time–frequency analyses of the dynamics of gamma-band activity in the local field potentials recorded from monkey primary visual cortex, we found identical temporal characteristics of gamma activity in both awake and anesthetized brain states, including large variability of peak frequency, brief oscillatory epochs (<100 ms on average), and stochastic statistics of the incidence and duration of oscillatory events. These findings indicate that gamma-band activity is temporally unstructured and is inherently a stochastic signal generated by neural networks. This idea was corroborated further by our neural-network simulations. Our results suggest that gamma-band activity is too random to serve as a clock signal for synchronizing neuronal responses in awake as in anesthetized monkeys. Instead, gamma-band activity is more likely to be filtered neuronal network noise. Its mean frequency changes with global state and is reduced under anesthesia.

Introduction

Stimulus-driven gamma-band activity in the local field potential (LFP) has been found and intensively studied throughout the brain. Gamma activity has been reported to be correlated with perceptual processes (Gray et al., 1989; Buzsáki and Chrobak, 1995; Hopfield, 1995; Singer, 2001; Fries et al., 2007; but see Roelfsema et al., 2004; Ray and Maunsell, 2010) and with cognitive functions such as attention (Fries et al., 2001; Chalk et al., 2010) and memory (Buzsáki and Chrobak, 1995; Lisman and Idiart, 1995; Pesaran et al., 2002), and gamma dysfunction occurs in mental disorders (Wilson et al., 2007; Gonzalez-Burgos and Lewis, 2008). These results led to speculations that gamma activity might be involved in cognition (Fries et al., 2001; Singer, 2001) or consciousness (Uhlhaas et al., 2009).

It has been hypothesized that gamma activity provides phase-locking signals for multiple cortices (Lisman and Idiart, 1995; Jefferys et al., 1996; Fries et al., 2007; Wang, 2010; Buzsáki and Wang, 2012). This hypothesis requires that gamma activity act like a metronome that harmonizes processes between brain areas. However, gamma activity exists not only in the brains of awake animals (Fries et al., 2001; Pesaran et al., 2002; Siegel and Konig, 2003; Gail et al., 2004; Liu and Newsome, 2006; Gieselmann and Thiele, 2008; Wilson et al., 2008; Khawaja et al., 2009; Chalk et al., 2010; Ray and Maunsell, 2010), but also in the anesthetized state (Gray et al., 1989; Gray and McCormick, 1996; Logothetis et al., 2001; Henrie and Shapley, 2005; Jia et al., 2011) and even in brain slices (Whittington et al., 1995; Compte et al., 2008; Cardin et al., 2009).

The aim of this study is to answer whether gamma-band activity is generated by the same mechanism in awake and anesthetized states. One way for gamma activity to serve as a synchronization signal between brain areas is for it to act like a clock; an alternative way is to synchronize brain signals through bursts of gamma power. Our previous studies on anesthetized monkeys suggested that gamma activity was a stochastic process that could provide synchronization only by brief bursts (Burns et al., 2010b, 2011). Therefore, here we are particularly interested in whether the temporal structure of gamma activity is as random in the awake as in the anesthetized state.

We compared the dynamics of gamma-band activity recorded from the primary visual cortex (V1) of awake and anesthetized monkeys. There was higher peak frequency in the awake relative to anesthetized state, but the stochastic character of gamma activity in both brain states was identical: large variability of the peak frequency, short oscillatory epochs, and stochastic statistics of the incidence and duration of oscillatory activity. These stochastic dynamics could be generated by a recurrent network with Poisson-distributed inputs regardless of the mental state. Our results from both experiments and simulations indicate that gamma activity is the noise-driven output from a damped oscillatory system and that gamma-band activity can be used as a measure of the general state of the cortical network.

Materials and Methods

Preparation of awake monkeys.

All procedures were conducted in compliance with the National Institutes of Health Guide for the Care and Use of Laboratory Animals, and were approved by the Institutional Animal Care and Use Committee of Beijing Normal University. Two male adult monkeys (Macaca mulatta) were used. Under general anesthesia induced with ketamine (10 mg · kg−1) and maintained with isoflurane (1.5–2.0%), a titanium post was attached to the skull with bone screws for immobilizing the animal's head during behavioral training. After the animal had been trained in a simple fixation task, two 6 × 8 multielectrode arrays (with electrode length of 0.5–0.6 mm, interelectrode spacing of 0.4 mm, and typical electrode impedances of a few hundred kiloohms at 1 kHz; Blackrock Microsystems) were implanted into V1 corresponding to eccentricities between 2.0° and 5.0° in the lower visual field. The LFPs were recorded at 30 kHz using a 128-channel system (Cerebus; Blackrock Microsystems). Visual stimuli were generated by a stimulus generator (ViSaGe; Cambridge Research Systems) on a 22-inch CRT monitor (Iiyama Vision Master Pro 514, 1200 × 900 at 100 Hz, mean luminance 23.7 cd · m−2) at a viewing distance of 114 cm.

The other stimulus settings were identical to those in anesthetized experiments (see Visual Stimulation, below). A trial began when a lever was pulled by the animal. On each trial, a 0.1° fixation point (FP) was displayed in the CRT center. The animal's eye positions were sampled at 30 Hz by an infrared tracking system (Matsuda et al., 2000), which offered a spatial resolution of up to 0.05°. Within 600 ms after FP presentation, the animal was required to fixate within an invisible circular window of 0.6° in radius around the FP. After the animal maintained its fixation for 200 ms, the stimulus was displayed for 2 s, followed by a blank interval of 200 ms. The FP was then slightly dimmed, and the animal had to release the lever within 600 ms for a drop of juice as reward. A trial was aborted if the animal's fixation was moved outside the fixation window.

Preparation of anesthetized monkeys.

Acute experiments were performed on nine male adult monkeys (Macaca fascicularis). All procedures were in accordance with the guidelines of the U.S. Department of Agriculture and were approved by the University Animal Welfare Committee at the New York University. Under general anesthesia, a craniotomy (∼5 × 7 mm) was made posterior to the lunate sulcus. A small opening in the dura (∼3 × 5 mm) was made to provide access for multiple electrodes. After the surgery and during the experiments, anesthesia was maintained with a continuous intravenous infusion of sufentanil citrate (6–12 μg · kg−1 · h−1), and the animal was paralyzed with verucuronium bromide (0.1 mg · kg−1 · h−1). Vital signs, including heart rate, electroencephalogram, blood pressure, and oxygen level in blood were closely monitored. A matrix of seven electrodes (1–4 MΩ; Thomas Recording) were arranged linearly and 300 μm apart. To keep all electrodes at approximately similar cortical depth, we independently moved each electrode from the surface of V1 until a detectable high-frequency response (hash) driven by the visual stimulus was found, which provided a very good estimation of the upper part of layer 2/3 and allowed us to align all electrodes at a similar cortical depth. Electrical signals were amplified, digitized, and filtered (0.3–10 kHz) with a multichannel recording system (RA16SD; Tucker-Davis Technologies), which was interfaced to a computer running a multichannel version of the OPEQ program (designed by Dr. J.A. Henrie, Center for Neural Science, New York University, New York, NY) to acquire both spike and LFP data. Visual stimuli were generated also using the custom OPEQ program with Open GL optimization. Data collection was synchronized with the screen refresh to a precision of <0.01 ms. Stimuli were displayed on a 20-inch monitor (IIyama HM 204DTA flat Color Graphic Display, 1024 × 768 at 100 Hz, mean luminance 59.1 cd · m−2) with a viewing distance of 114 cm.

Visual stimulation.

Drifting sinusoidal gratings (>90% contrast; spatial frequency, 2 cycle/deg; temporal frequency, 4 Hz) were displayed within a circular patch of 4° visual angle in diameter, covering the visual field locations of all recording sites. The mean luminance within and outside the stimulus patch was identical. The gratings drifted in different directions between 0 and 360°, in 30° steps in a pseudorandom order. The stimulus was presented for 2 or 4 s and repeated 4–30 times.

Time–frequency analysis.

The continuous Gabor transform (CGT) was used for time–frequency analysis. The CGT is a short time or windowed Fourier transform (also called a spectrogram) that retains the time dependence of the spectrum. The continuous transform differs from the discrete version in that the signal is oversampled in time and frequency so that neighboring points are not independent. The complex Gabor filter ψ(t; t0, ω0) we used is a one-dimensional plane wave with frequency ω0 (in Hz) windowed with a Gaussian g(t) centered at t0,

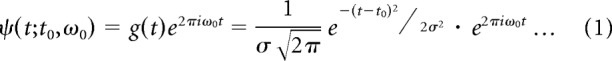graphic file with name zns04012-2589-m01.jpg

The width parameter σ (time window) was chosen to optimize time and frequency resolution (Burns et al., 2010). Here we used σ = 25 ms. The CGT of a single trial LFP, f(t), was computed by convolving the complex Gabor function, ψ(t; t0,ω0) (Eq. 1) with f(t). The result, G(t0, ω0) (Eq. 2), was a complex-valued function that represented the amplitude (R(t0, ω0); Eq. 2) and phase (Φ(t0, ω0), Eq. 2) of the signal f(t) at the frequency ω0 of the Gabor filter as a function of the center time, t0 of the Gabor filter.

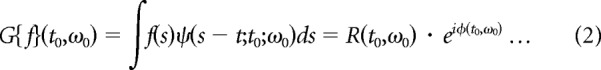graphic file with name zns04012-2589-m02.jpg

The power at a particular time and a particular frequency was |G(t0,ω0)|2. The power spectrum over the stimulus interval was |G(t,ω)|2 integrated over the interval. The time origin of the complex Gabor filter t0 was varied to trace out the entire spectrogram of the signal as in Figure 1, A and B.

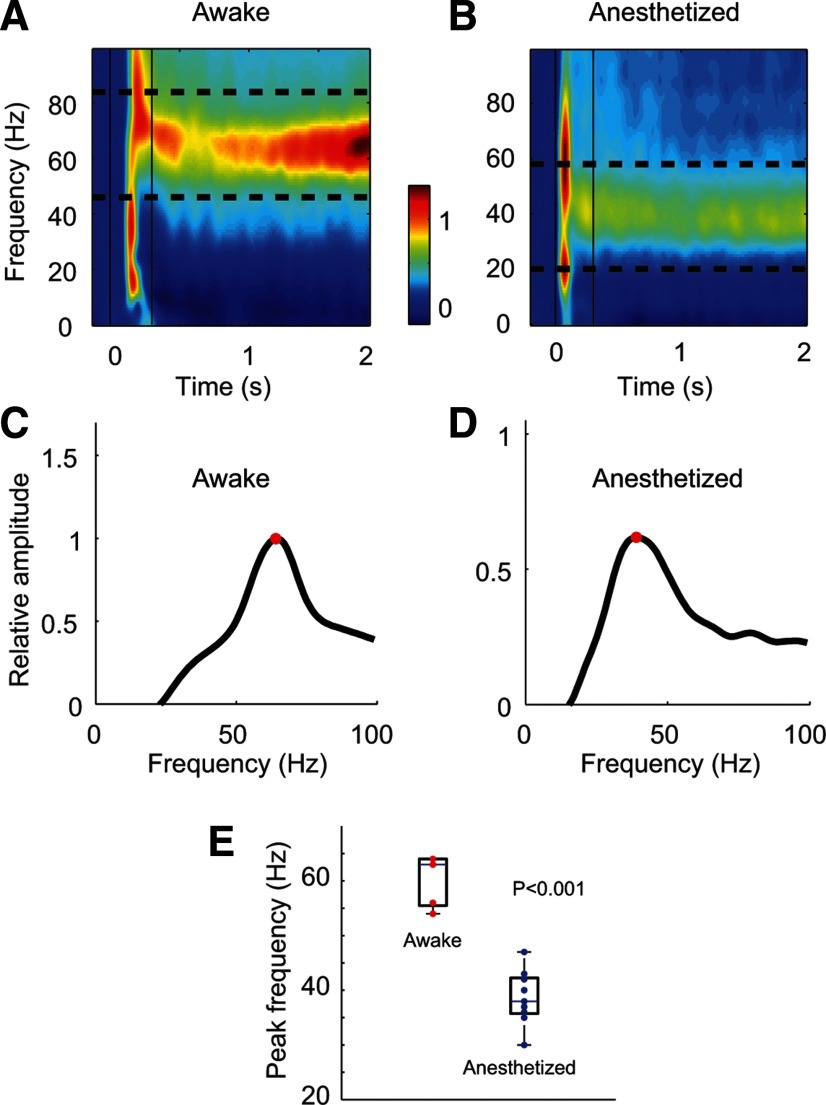
Figure 1.

Figure 1.

Open in a new tab

A comparison of peak gamma frequency in awake and anesthetized monkeys. A, B, Averaged power spectrogram of the LFPs from one awake (n = 39 recording sites, A) and one anesthetized (n = 35 sites, B) monkey. After stimulus onset (time 0), sustained power appeared between 40 and 80 Hz in A, but between 20 and 60 Hz in B. C, D, Power spectrum averaged across the entire stimulation period in A and B, respectively. E, Summary of peak gamma frequency. The upper two and the lower two red points were from the two awake monkeys tested (total sites n = 60), with each red point representing data averaged from different electrodes within 1 d. Each blue point represents data averaged from one anesthetized monkey (total sites n = 387 from 9 animals).

The raw, visually activated LFP power spectrum was converted into a relative power spectrum, normalized by the LFP power in the absence of visual stimulus. That is, the absolute power in the gamma-frequency band during visual stimulation was divided by the absolute power in the corresponding frequency band without any stimulus (background condition), minus 1. Thus R(f) = (GVS(f)/GBG(f)) − 1. The data in the figures in this paper are all presented as relative spectra.

Identifying a gamma-band burst.

To quantify the peak frequency and duration of a gamma-band event in the spectrogram, we first searched for a point in the time–frequency coordinate, during visual stimulation, with spectrogram amplitude at least three times the spontaneous power at any frequency between 25 and 80 Hz. The frequency for this point was defined as f0, and the time for this point as t0. We then searched for the optimal f and t around f0 and t0 (f was within the range of f0 ± 2.5 Hz, and t within the range of t0 ± 0.05 s) by maximizing the duration of an event with maximum phase difference <45° of phase angle. This procedure allowed us to estimate both the time duration and peak frequency of a gamma-burst.

Results

To examine the temporal dynamics of gamma-band activity in two distinct cortical states, we recorded the LFP from V1 of two awake and nine anesthetized monkeys in response to sinusoidal grating patches. The awake animals performed a simple fixation task. Each stimulus display (≥2 s) was preceded by a blank interval (∼0.2 s). The grating stimuli (>90% contrast, 2 cycle/deg spatial frequency, 4 Hz drifting temporal frequency, 4° diameter) were randomly presented at one of 12 evenly spaced movement-directions (0–360°). The stimulus was centered on the cluster of receptive fields mapped by an array of microelectrodes corresponding to 2–5° eccentricity (see Materials and Methods, above).

Stimulus-driven gamma-band activity in awake and anesthetized monkeys

Consistent with many previous studies (Logothetis et al., 2001; Pesaran et al., 2002; Gail et al., 2004; Henrie and Shapley, 2005; Ray and Maunsell, 2010), after stimulus onset we observed a sustained power increase within the gamma band in both awake (Fig. 1A) and anesthetized (Fig. 1B) monkeys. On average, the peak gamma frequency was 60 Hz in the awake (Fig. 1C) and 40 Hz in the anesthetized (Fig. 1D) state; the difference in peak frequency was statistically significant (p < 0.001, independent t test, t = 6.46; Fig. 1E). In agreement with previous observations (Gray et al., 1989; Fries et al., 2007; Montemurro et al., 2008), gamma-band activity in V1 was not phase-locked to the stimulus frequency, which was usually much lower than the gamma-band peak in the LFP power spectrum between 40 and 60 Hz; rather, the gamma-band activity was induced by, but was asynchronous with, the stimulus.

Temporal structure of gamma-band activity in a single trial

To understand gamma-band activity and its functions, it is useful to analyze on a trial-by-trial basis the LFP signal dynamics (Burns et al., 2010b). Time–frequency analysis of single trials showed that the oscillation in the awake animal was faster than in the anesthetized (Fig. 2, compare A with C, top), consistent with the power spectrum analysis (Fig. 1). However, the oscillatory activity was not a continuous signal as suggested in the averaged spectrum (Fig. 1A,B); but rather, the energy within the gamma band appeared as intermittent brief bursts with varied peak frequencies (Fig. 2A,C, bottom, hot spots).

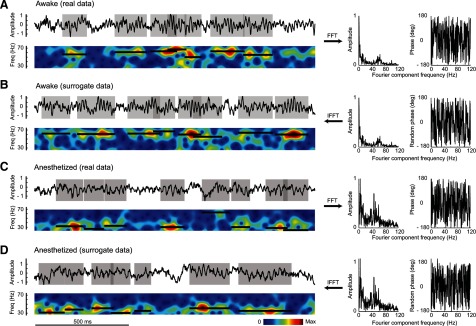
Figure 2.

Figure 2.

Open in a new tab

Temporal dynamics of the gamma-band activity: awake versus anesthetized monkeys and real versus surrogate data. A, Top, Example of the LFP recorded from an awake monkey after stimulus onset; the gray shaded areas are gamma-band bursts detected by our algorithm. Bottom, Power spectrogram of the LFP; each black bar marks the peak frequency (y-axis) and the duration of each gamma-band burst. Right, Amplitudes and phases of the LFP Fourier components. B, An example of surrogate LFP generated from the real LFP in awake monkey by the inverse Fourier transform (IFFT) of the raw amplitudes and randomized phases (drawn between −180° and 180°). C, D, An example of the real and surrogate LFP, respectively, from an anesthetized monkey.

To quantify further the durations and peak frequencies for each gamma-burst event, we selected LFP epochs whose amplitudes were at least three times larger than the burst responses when the monkey viewed a blank screen. The criterion for defining an epoch as a gamma burst was that the range of the phase for a fixed frequency within the epoch was no more than 45° (Fig. 2, black horizontal bars; for detailed algorithm, see Materials and Methods, above). The joint distribution of the peak frequency and duration of the gamma-band bursts in the awake animal (Fig. 3A, top) looks similar to that in the anesthetized (Fig. 3B, top): both showed an almost identical distribution of the gamma-burst durations and a comparable range of peak-frequency variations.

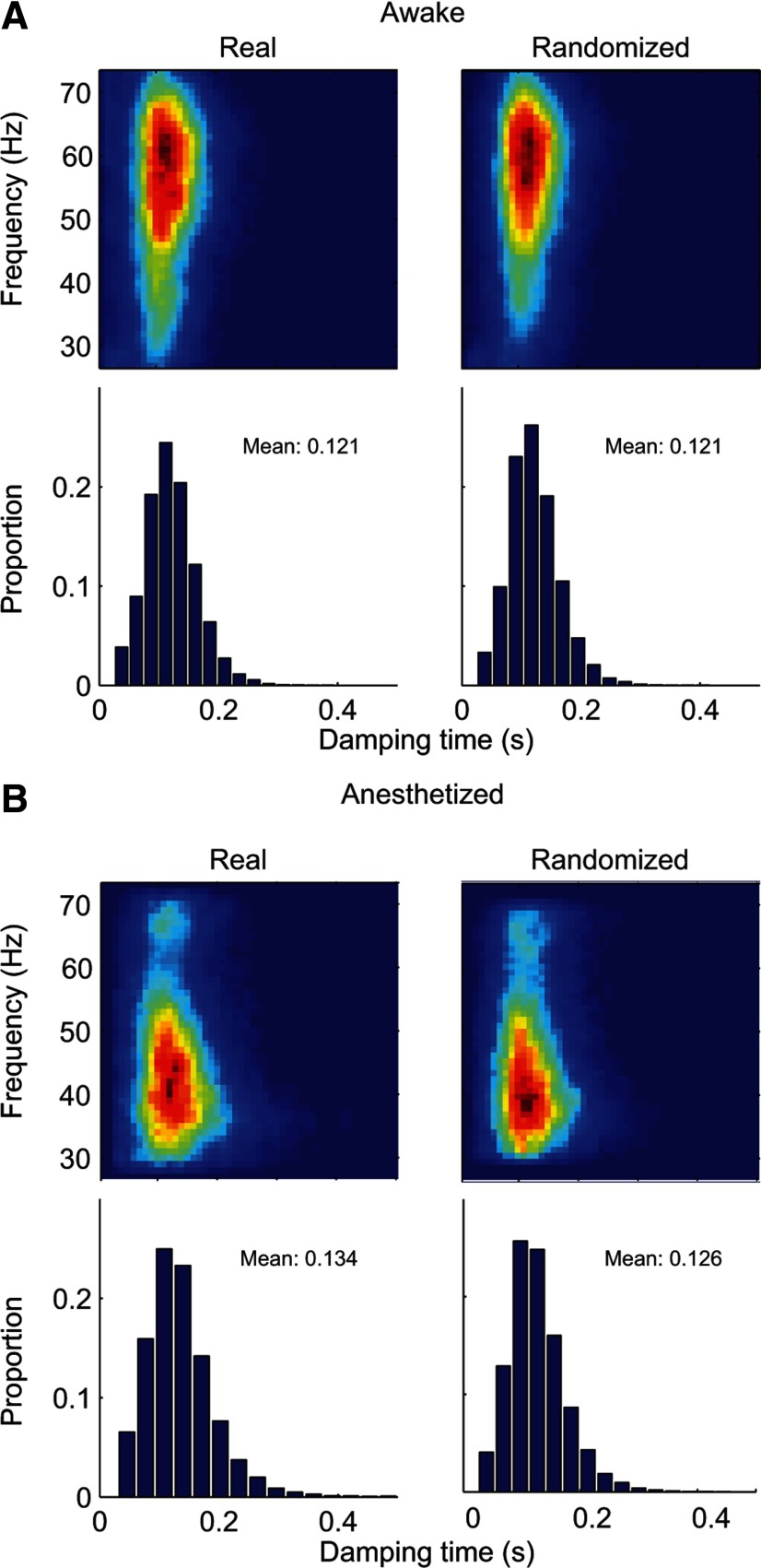
Figure 3.

Figure 3.

Open in a new tab

Joint distribution of the duration and peak frequency of gamma-band bursts: awake versus anesthetized monkeys and real versus surrogate data. A, Top left, Joint distribution of the duration and peak frequency of gamma-band bursts from the LFP recorded in two awake monkeys (total recording sites, n = 60). Bottom left, Marginal distribution of the durations of gamma-band events. Right, Corresponding results from the surrogate LFP. B, Results from nine anesthetized animals (total sites, n = 387).

How long is each gamma-band burst?

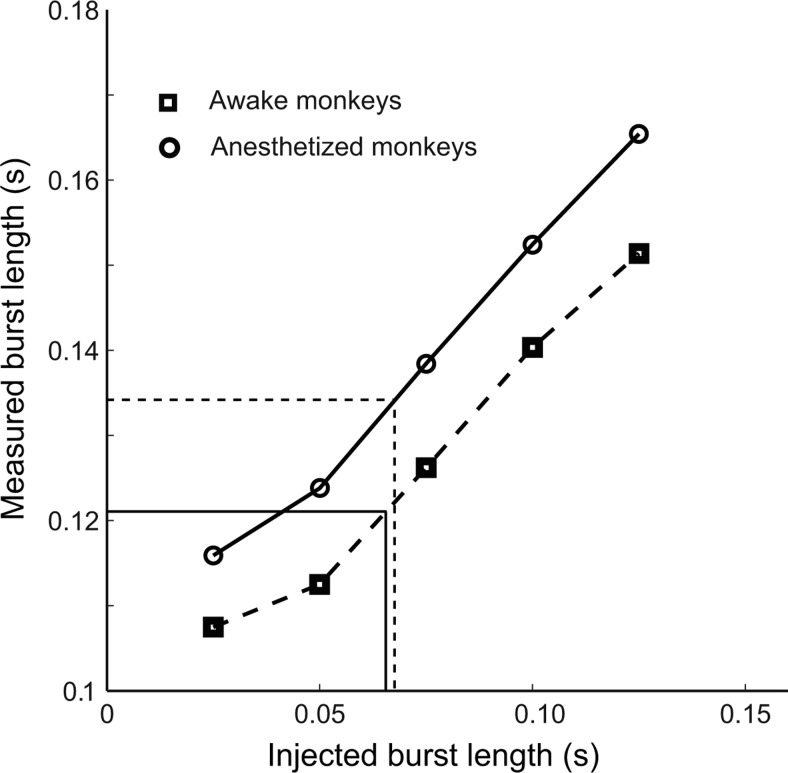
The estimated durations of gamma-band bursts, on average, were short (mean: 0.121 s for awake and 0.134 s for anesthetized; Fig. 3A,B, bottom). Because the Gabor filter used for time–frequency analysis had a certain width (SD = 25 ms) and the LFP was a random process, the raw estimates of gamma-burst durations could deviate from the actual values. A calibration process was performed to get a more accurate estimate of the burst length. We extracted the number of gamma bursts together with their peak frequencies, amplitudes, and onset times in a trial of stimulus-driven LFP (2 s). We then randomly took a trial of LFP recorded without any stimulus (blank LFP) of the same duration (2 s) and added artificial gamma bursts into the blank LFP at the same onset time, with the same peak frequency and amplitude, but with a predefined length. The artificial gamma-band burst was a Gabor function. Two standard deviations of the Gabor function's Gaussian envelope was defined as the burst length. Five predefined lengths were used (2σ = 0.025, 0.050, 0.075, 0.100, and 0.125 s). We used our algorithm to detect the burst length in the simulated LFP for each predefined length. By applying the calibration process to all of the recorded trials, we generated a relationship between the measured mean duration of gamma-burst (Fig. 4, y-axis) and the true length of gamma-bursts (Fig. 4, x-axis). Then we obtained the corrected burst length from the projection of measured burst length onto the x-axis of injected length.

Figure 4.

Figure 4.

Open in a new tab

Calibration of the gamma-band burst length. Artificial gamma bursts were created by Gabor functions. The burst length was 2 SD of the Gabor's Gaussian envelope and the peak frequency was the frequency of the Gabor's sinusoidal carrier. The artificial gamma bursts had a fixed length chosen from one of five levels (2σ = 0.025, 0.050, 0.075, 0.100, 0.125 ms). The artificial bursts of each specified length were synthesized by using the starting times, peak frequencies, and peak amplitudes measured from all gamma-band bursts in the real LFP data. They were injected into the LFP recorded without visual stimulus. We applied the detection algorithm to the simulated LFP and plotted the injected versus the mean measured burst length.

The corrected mean duration of a gamma burst was 62 and 65 ms for awake and anesthetized monkeys, respectively. Under both conditions, the averaged number of gamma cycles in each burst was <4.

How variable is gamma's peak frequency in different bursts?

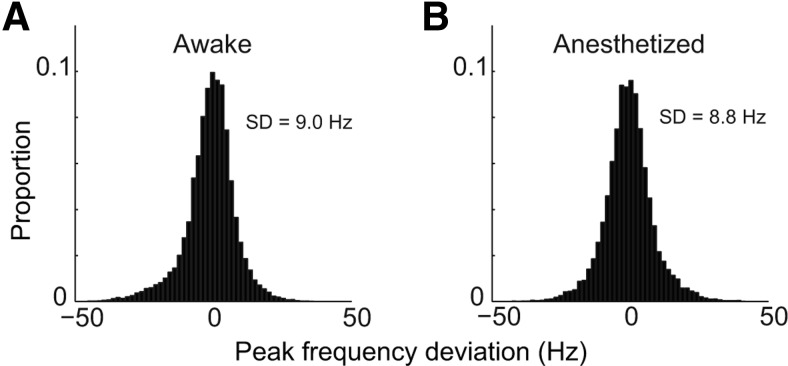
As stated earlier, if a gamma-band burst were used for timing, not only its duration should be long enough, but also its peak frequency should also be approximately constant. To examine the variability of the gamma peak frequency during visual stimulation, we calculated the mean of the peak gamma frequencies averaged across all gamma bursts in each trial, and then subtracted the trial mean from the peak gamma frequency in each burst. This yielded a peak–frequency deviation for each gamma burst within a trial. Then we pooled all trials together to estimate the distribution of peak–frequency deviations across all trials in awake (Fig. 5A) and anesthetized (Fig. 5B) animals. Both distributions were rather broad and very similar (SD = 9.0 Hz for awake, SD = 8.8 Hz for anesthetized). Because of the procedure for constructing the histograms in Figure 5, the estimates of distribution of peak–frequency deviations were not affected by frequency variation between sites or between individual animals. This analysis therefore provides stronger evidence than the joint distributions in Figure 3 that the peak frequencies of the gamma bursts were highly variable, and the variation was of similar magnitude in awake and anesthetized V1.

Figure 5.

Figure 5.

Open in a new tab

Distribution of peak–frequency deviation for each gamma burst in awake and anesthetized monkeys. Relative peak frequency (peak–frequency deviation) for a gamma burst was defined by the difference between absolute peak frequency for the gamma burst and the mean peak gamma frequency averaged across all of the gamma bursts in that trial. The distribution for the relative peak frequency was plotted by pooling all relative peak frequencies from all trials in awake (A) and anesthetized (B) monkeys. Both distributions were rather broad and very similar (SD = 9.0 Hz for awake, SD = 8.8 Hz for anesthetized).

The brevity of gamma bursts and the variability of their peak frequencies suggest that gamma-band activity is unreliable as a pacemaker. Instead, the measured gamma-band activity from both awake and anesthetized monkeys resembled noise-driven signals.

Gamma-band activity is similar to filtered noise

The hypothesis of gamma oscillation as a noisy signal was tested statistically with surrogate LFP signals derived from the LFP recorded from awake and anesthetized monkeys. Based on the real signals, the amplitudes and phases at different frequencies were estimated by Fourier transform (Fig. 2A,C, right). By leaving the amplitudes of Fourier components unchanged while randomizing their phases (Fig. 2B,D, right), we generated surrogate LFPs by inverse Fourier transform (Fig. 2B,D, top). Using the same algorithm as for real LFP data, we detected the gamma bursts in the surrogate signals (Fig. 2B,D, bottom, black bars).

The distributions of the peak frequencies and durations of gamma-band bursts are almost indistinguishable between the real and surrogate data for both awake and anesthetized conditions (Fig. 3A,B, compare left and right). These results, together with the large variation of the peak frequency (Fig. 5) and the short duration of each epoch (Figs. 2–4), strongly suggest that the gamma-band activity is unstructured in nature and is unlikely to serve as a timing signal for cortical computations.

Gamma-band activity from a recurrent excitatory-inhibitory network

To demonstrate further that gamma-band activity could be generated simply by filtered noise, we constructed a simplified neural-network model (Wilson and Cowan, 1972; Tsodyks et al., 1997; Mazzoni et al., 2008; Kang et al., 2010) composed of only two components: excitatory and inhibitory nodes (Eqs. 3, 4, E and I). The two nodes represent the excitatory and inhibitory populations interacting with each other (the interaction types and strengths are denoted by W in Eqs. 3 and 4) and both receive independent Poisson-distributed inputs: InputE and InputI (Eqs. 3, 4; Fig. 6A). The excitatory node connects to the inhibitory one with coupling strength Wie and to itself with Wee; the inhibitory node connects to the excitatory one and to itself with coupling strengths Wei and Wii, respectively. E and I represent the activity of excitatory and inhibitory nodes, respectively. In this model, only the positive parts of E and I affect the interaction between the two nodes, which is described in Equations 3–5, below (with τe and τi representing the synaptic time constants for excitation and inhibition, respectively):

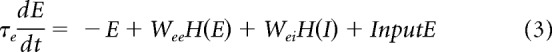graphic file with name zns04012-2589-m03.jpg
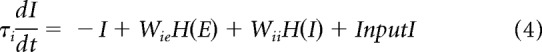graphic file with name zns04012-2589-m04.jpg
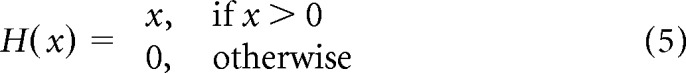graphic file with name zns04012-2589-m05.jpg

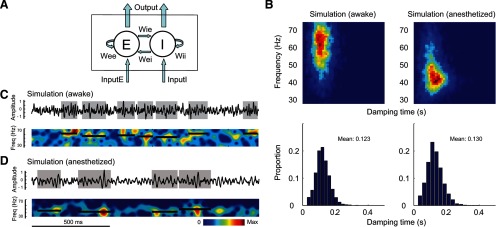
As shown previously (Kang et al., 2010), recurrent excitatory–inhibitory networks like those found in the brain can generate peaked gamma-band activity in the power spectra when driven by random noise. In the simple inhibitory and excitatory model (IE model) described by Equations 3–5, InputE was modeled as a Poisson input with λe = 8.5, and InputI as a Poisson input with λi = 10. When the parameters Wee, Wei, Wie, Wii, τe, τi were set at 1.5, 2.5, 2.85, 4, 4.3, 12, respectively, the simulated output contained gamma-band activity that was similar to that in awake monkeys (Fig. 6C vs Fig. 2A; Fig. 6B, left vs Fig. 3A, left). With these settings, the network was not an oscillator. The dynamic system described by these parameters does not oscillate to a constant input without any noise. It also does not oscillate in the absence of visual stimulation, like the real cortex (Henrie and Shapley, 2005; Burns et al., 2010a; Ray and Maunsell, 2010; Jia et al., 2011). However, when the input noise is increased as during visual stimulation (we model the noise as a Poisson process), the network does generate gamma-band activity. Simply by reducing the coupling strength from the excitatory to the inhibitory node and by increasing the synaptic time constants, for instance, changing Wie, τe, τi from 2.85, 4.3, 12 to 2.25, 6, 18, respectively, while keeping the other parameters unchanged, the simulated gamma-band activity was markedly reduced in peak frequency while the other temporal properties remained unaffected, comparable to gamma-band bursts in anesthetized monkeys (Fig. 6D vs Fig. 2C; Fig. 6B, right vs Fig. 3B, left). Note that in this simulation, the main parameters that determined the peak frequency of the network's gamma-band activity were only the strength of excitatory-to-inhibitory coupling Wie and the synaptic time constants for excitation and inhibition τe, τi.

Figure 6.

Figure 6.

Open in a new tab

Gamma-band activity generated by a recurrent network model. A, The model comprises an excitatory (E) and an inhibitory (I) node that are interconnected with coupling strength Wie, Wee, Wei, and Wii. Both nodes receive independent Poisson-like inputs InputE and InputI, and the synaptic time constants for excitation and inhibition are τe and τi. B, Top left, Joint distribution of the duration and peak frequency for gamma-band bursts from the LFP generated by the excitatory node when the parameters Wee, Wei, Wie, Wii, τe, τi were set at 1.5, 2.5, 2.85, 4, 4.3, 12, respectively. InputE was modeled as a Poisson input with λe = 8.5, and InputI as a Poisson input with λi = 10. Bottom left, Marginal distribution of the durations of gamma-band events. Right, Corresponding results when only Wie, τe, τi were changed from 2.85, 4.3, 12 to 2.25, 6, 18, respectively. Each simulation reiterated 1000 trials of 2.5 s LFP. C, D, An example of simulated LFP and its power spectrogram under the two conditions in B, respectively.

Discussion

Our results indicate that gamma activity could be generated by the same mechanism when the brain is in different states of consciousness. The joint distributions of peak frequency and burst duration, as well as the distribution of peak–frequency deviation from the mean, were similar in V1 of awake and anesthetized monkeys. Moreover, in both brain states, gamma-band activity was temporally unstructured, as proven by the similarities in statistics between real LFPs, phase-randomized surrogate data, and the output of a noise-driven network.

What is the function of gamma-band activity?

Our experimental and modeling results revealed the stochastic nature of gamma-band activity in V1. The word “stochastic” captures the key difference between a clock signal and a non-clock signal—whether the signal is periodic (i.e., sustained in phase and constant in frequency across many cycles) or stochastic (randomly varying in phase and frequency). Based on our results, we conclude that gamma activity in the LFP of V1 cortex is a noisy signal generated by local neural circuitry, and that it cannot be used as a reliable clock because of the brevity and stochastic nature of the oscillatory events. The randomness in gamma-band activity was just as evident in the awake monkeys as in the anesthetized, suggesting that gamma activity is unlikely to be useful for acting as a clock for perceptual and cognitive processes across cortical regions. This idea is consonant with the study by Ray and Maunsell (2010), where they argued that gamma-band activity is not suited for binding visual information within V1. The main supporting evidence of Ray and Maunsell (2010) was that neighboring V1 sites may have different oscillatory frequencies in response to a single Gabor patch in which the luminance contrast varied from the center toward the surround. Our current study provides evidence that gamma-band activity is not a clock signal from a more general perspective—the stochastic nature of the gamma activity.

The stochastic properties of gamma activity, however, do not rule out an alternative hypothesis of gamma-band activity for synchronizing brain signals: the LFP including gamma-band activity could synchronize neuronal assemblies on a short time scale of <100 ms through bursts of power. Because cortical neurons act like coincidence detectors (Koch et al., 1996; Shelley et al., 2002), sporadic gamma bursts could be important in making it possible for a cell assembly to excite postsynaptic cortical neurons by causing the different cells in the assembly to fire presynaptic spikes that are coincident in time (Fries et al., 2007). But these coincident events would be aperiodic and random because of gamma's inherent randomness.

How is gamma-band activity generated?

Based on the popular concept that gamma-band activity is a ‘clock’ for temporal synchronization of spikes, gamma activity has been modeled as sustained oscillations in the LFP (Bressler and Freeman, 1980; Leung, 1982; Wang and Rinzel, 1993; Hopfield, 1995; Lisman and Idiart, 1995; Wang et al., 1995; Gray and McCormick, 1996; Jefferys et al., 1996; Traub et al., 1996, 2001; Wang and Buzsáki, 1996; Kopell et al., 2000; Buzsáki and Draguhn, 2004; Fries et al., 2007). However, our experimental data indicate that gamma-band activity is not generated by an oscillator (or even a small number of oscillators). Therefore, future models of gamma-band activity need to take into account its stochastic behavior.

Based on our real and simulated data, we speculate that gamma-band activity in LFP is generated by a single mechanism: network filtering of broad-band network activity. Our results are consistent with previous work modeling cortical gamma-band activity (Rennie et al., 2000; Mazzoni et al., 2008; Kang et al., 2010). Recurrent excitatory–inhibitory networks acting like tuned filters with realistic time constants and excitatory/inhibitory coupling strength are bound to produce a tuning peak in the gamma band. It has been shown (Kang et al., 2010) that recurrent excitatory–inhibitory networks with the same architecture as those used to account for orientation tuning (Kang et al., 2003; Zhu et al., 2010) also generate narrow-band temporal tuning. Thus, a single network model can emulate two very different cortical functions. There are also other network models for generating gamma-band activity, such as those involving phase-locking of inhibitory interneurons at the gamma-band peak frequency (for example, see Wang and Rinzel, 1993; Traub et al., 2001), but these very nonlinear phase-locking models do not emulate neuronal populations in the cortex in vivo (Burns et al., 2010b).

Sensory input and gamma-band activity

The current study focused on the variation of the peak frequency and active duration for gamma bursts during a period when the input is in a steady state: grating patches drifting at a constant speed and with other stimulus parameters optimized for generating gamma-band activity (Jia et al., 2011). In our experimental condition, the sensory input to visual cortex was constant on average at the population level, and our analysis was restricted to the time period 300 ms after stimulus onset until its offset. During this period, gamma-band activity in V1 is not phase-locked to the temporal frequency of gratings, which is usually much lower than the gamma activity shown between 40 and 60 Hz. Rather, the gamma-band activity is induced by, but is asynchronous with, the stimulus (Gray et al., 1989; Fries et al., 2007; Montemurro et al., 2008). We concluded that, in our experimental paradigm, the gamma-band activity is generated by noise, because of the statistical similarity between real LFP data and surrogate signals (Fig. 3). This conclusion was supported by our model simulation with noisy input to a resonant network (Fig. 6).

It is important to point out that our data do not suggest that gamma-band activity does not carry any information about the visual stimulus. For example, Figure 1 shows that the gamma-band power is much stronger when the grating stimulus is on, compared with the period before the stimulus was on the screen. This result, among many others (Gail et al., 2004; Henrie and Shapley, 2005; Liu and Newsome, 2006; Belitski et al., 2008; Gieselmann and Thiele, 2008; Mazzoni et al., 2008; Khawaja et al., 2009; Ray and Maunsell, 2010; Jia et al., 2011), directly points to the fact that gamma-band activity is modulated by a visual stimulus. However, our study suggests that a key component for generating gamma-band activity is input fluctuation at relatively high frequency because our model does not generate oscillations to a constant input without variation—it needs input variation in time. Such variation can be either noise or signal, but it has to be variable in time. In a realistic situation, both noise and signal in the input will be modulated by a sensory stimulus, and this can explain why gamma-band activity is modulated by but not phase-locked to the visual stimulus. Our result is consistent with recent work on the generation of gamma-band activity to time-varying stimuli (Mazzoni et al., 2008, 2011).

What causes the shift of peak gamma-frequency between awake and anesthetized monkeys?

Ray and Maunsell (2010) have shown that the peak frequency of gamma activity is dependent on stimulus strength, increasing with luminance contrast of grating stimuli. Although the gamma-band activities in the LFPs from both anesthetized and awake monkeys were similar to each other in being temporally unstructured, we did observe a significant increase in peak gamma frequency in the awake relative to the anesthetized state. We provided one possible explanation: the change of peak frequency can be simply explained by changing the time constants of inhibition and excitation. In our simple recurrent model, the time constants are not the same as those of inhibitory and excitatory neurons. Instead, they represent the time constants of the net inhibition and excitation. In more realistic models, the smaller net time constants in the awake state may be explained by the effects of consciousness, such as vigilance or attention. Many studies have shown that V1 is subject to top-down influences (Lamme and Spekreijse, 2000; Lamme et al., 2000; Pack et al., 2001; Li et al., 2008) and that the firing rates in V1 or lateral geniculate nucleus of awake animals are higher than those in anesthetized animals (Li et al., 2008; Chen et al., 2009; Alitto et al., 2011). Such results indicate that the cortical network in the awake V1 might be in a higher conductance state; therefore, the network would have smaller time constants. However, there might be other possible mechanisms underlying the change of peak gamma-frequency (Li, 1998).

Rhythmic gamma-band neural activity has been generally thought to be central to perceptual and cognitive processes that require a close coordination across a large number of neurons in multiple cortical regions. The current study provides compelling evidence that gamma activity could be generated by the same mechanism when the brain is in the anesthetized and in the consciously awake states. In particular, the oscillatory events are temporally unstructured and statistically stochastic, not reliable enough to be a clock for concerted neural computations. The prevailing point of view about the timing function of gamma-band activity in perception and cognition needs reevaluation.

Footnotes

This work was supported by National Basic Research Program of China Grant 2011CBA00405; National Natural Science Foundation of China Grants 30970983 and 31125014; Open Research Fund of the State Key Laboratory of Cognitive Neuroscience and Learning, China; the 111 Project B07008; the Swartz Foundation; NIH Training Grant T32-EY007158; and NIH Grant R01 EY-01472. We thank Dr. J. A. Henrie for software and hardware development of the multielectrode recording system in the anesthetized experiments, and thank X. B. Xu and Y. Yan for technical assistance in the awake experiments. We also thank Patrick Williams and Marianne Maertens for help collecting preliminary data.

The authors declare no financial conflicts of interest.

References

  1. Alitto HJ, Moore BD, 4th, Rathbun DL, Usrey WM. A comparison of visual responses in the lateral geniculate nucleus of alert and anaesthetized macaque monkeys. J Physiol. 2011;589:87–99. doi: 10.1113/jphysiol.2010.190538. [DOI] [PMC free article] [PubMed] [Google Scholar]
  2. Belitski A, Gretton A, Magri C, Murayama Y, Montemurro MA, Logothetis NK, Panzeri S. Low-frequency local field potentials and spikes in primary visual cortex convey independent visual information. J Neurosci. 2008;28:5696–5709. doi: 10.1523/JNEUROSCI.0009-08.2008. [DOI] [PMC free article] [PubMed] [Google Scholar]
  3. Bressler SL, Freeman WJ. Frequency analysis of olfactory system EEG in cat, rabbit, and rat. Electroencephalogr Clin Neurophysiol. 1980;50:19–24. doi: 10.1016/0013-4694(80)90319-3. [DOI] [PubMed] [Google Scholar]
  4. Burns SP, Xing D, Shapley RM. Comparisons of the dynamics of local field potential and multiunit activity signals in macaque visual cortex. J Neurosci. 2010a;30:13739–13749. doi: 10.1523/JNEUROSCI.0743-10.2010. [DOI] [PMC free article] [PubMed] [Google Scholar]
  5. Burns SP, Xing D, Shelley MJ, Shapley RM. Searching for autocoherence in the cortical network with a time-frequency analysis of the local field potential. J Neurosci. 2010b;30:4033–4047. doi: 10.1523/JNEUROSCI.5319-09.2010. [DOI] [PMC free article] [PubMed] [Google Scholar]
  6. Burns SP, Xing D, Shapley RM. Is gamma-band activity in the local field potential of V1 cortex a “clock” or filtered noise? J Neurosci. 2011;31:9658–9664. doi: 10.1523/JNEUROSCI.0660-11.2011. [DOI] [PMC free article] [PubMed] [Google Scholar]
  7. Buzsáki G, Chrobak JJ. Temporal structure in spatially organized neuronal ensembles: a role for interneuronal networks. Curr Opin Neurobiol. 1995;5:504–510. doi: 10.1016/0959-4388(95)80012-3. [DOI] [PubMed] [Google Scholar]
  8. Buzsáki G, Draguhn A. Neuronal oscillations in cortical networks. Science. 2004;304:1926–1929. doi: 10.1126/science.1099745. [DOI] [PubMed] [Google Scholar]
  9. Buzsáki G, Wang XJ. Mechanisms of gamma oscillations. Annu Rev Neurosci. 2012;35:203–225. doi: 10.1146/annurev-neuro-062111-150444. [DOI] [PMC free article] [PubMed] [Google Scholar]
  10. Cardin JA, Carlén M, Meletis K, Knoblich U, Zhang F, Deisseroth K, Tsai LH, Moore CI. Driving fast-spiking cells induces gamma rhythm and controls sensory responses. Nature. 2009;459:663–667. doi: 10.1038/nature08002. [DOI] [PMC free article] [PubMed] [Google Scholar]
  11. Chalk M, Herrero JL, Gieselmann MA, Delicato LS, Gotthardt S, Thiele A. Attention reduces stimulus-driven gamma frequency oscillations and spike field coherence in V1. Neuron. 2010;66:114–125. doi: 10.1016/j.neuron.2010.03.013. [DOI] [PMC free article] [PubMed] [Google Scholar]
  12. Chen Y, Anand S, Martinez-Conde S, Macknik SL, Bereshpolova Y, Swadlow HA, Alonso JM. The linearity and selectivity of neuronal responses in awake visual cortex. J Vis. 2009;9:12.1–17. doi: 10.1167/9.9.12. [DOI] [PMC free article] [PubMed] [Google Scholar]
  13. Compte A, Reig R, Descalzo VF, Harvey MA, Puccini GD, Sanchez-Vives MV. Spontaneous high-frequency (10–80 Hz) oscillations during up states in the cerebral cortex in vitro. J Neurosci. 2008;28:13828–13844. doi: 10.1523/JNEUROSCI.2684-08.2008. [DOI] [PMC free article] [PubMed] [Google Scholar]
  14. Fries P, Reynolds JH, Rorie AE, Desimone R. Modulation of oscillatory neuronal synchronization by selective visual attention. Science. 2001;291:1560–1563. doi: 10.1126/science.1055465. [DOI] [PubMed] [Google Scholar]
  15. Fries P, Nikolić D, Singer W. The gamma cycle. Trends Neurosci. 2007;30:309–316. doi: 10.1016/j.tins.2007.05.005. [DOI] [PubMed] [Google Scholar]
  16. Gail A, Brinksmeyer HJ, Eckhorn R. Perception-related modulations of local field potential power and coherence in primary visual cortex of awake monkey during binocular rivalry. Cereb Cortex. 2004;14:300–313. doi: 10.1093/cercor/bhg129. [DOI] [PubMed] [Google Scholar]
  17. Gieselmann MA, Thiele A. Comparison of spatial integration and surround suppression characteristics in spiking activity and the local field potential in macaque V1. Eur J Neurosci. 2008;28:447–459. doi: 10.1111/j.1460-9568.2008.06358.x. [DOI] [PubMed] [Google Scholar]
  18. Gonzalez-Burgos G, Lewis DA. GABA neurons and the mechanisms of network oscillations: implications for understanding cortical dysfunction in schizophrenia. Schizophr Bull. 2008;34:944–961. doi: 10.1093/schbul/sbn070. [DOI] [PMC free article] [PubMed] [Google Scholar]
  19. Gray CM, McCormick DA. Chattering cells: superficial pyramidal neurons contributing to the generation of synchronous oscillations in the visual cortex. Science. 1996;274:109–113. doi: 10.1126/science.274.5284.109. [DOI] [PubMed] [Google Scholar]
  20. Gray CM, König P, Engel AK, Singer W. Oscillatory responses in cat visual cortex exhibit inter-columnar synchronization which reflects global stimulus properties. Nature. 1989;338:334–337. doi: 10.1038/338334a0. [DOI] [PubMed] [Google Scholar]
  21. Henrie JA, Shapley R. LFP power spectra in V1 cortex: the graded effect of stimulus contrast. J Neurophysiol. 2005;94:479–490. doi: 10.1152/jn.00919.2004. [DOI] [PubMed] [Google Scholar]
  22. Hopfield JJ. Pattern recognition computation using action potential timing for stimulus representation. Nature. 1995;376:33–36. doi: 10.1038/376033a0. [DOI] [PubMed] [Google Scholar]
  23. Jefferys JG, Traub RD, Whittington MA. Neuronal networks for induced ‘40 Hz’ rhythms. Trends Neurosci. 1996;19:202–208. doi: 10.1016/s0166-2236(96)10023-0. [DOI] [PubMed] [Google Scholar]
  24. Jia X, Smith MA, Kohn A. Stimulus selectivity and spatial coherence of gamma components of the local field potential. J Neurosci. 2011;31:9390–9403. doi: 10.1523/JNEUROSCI.0645-11.2011. [DOI] [PMC free article] [PubMed] [Google Scholar]
  25. Kang K, Shelley M, Sompolinsky H. Mexican hats and pinwheels in visual cortex. Proc Natl Acad Sci U S A. 2003;100:2848–2853. doi: 10.1073/pnas.0138051100. [DOI] [PMC free article] [PubMed] [Google Scholar]
  26. Kang K, Shelley M, Henrie JA, Shapley R. LFP spectral peaks in V1 cortex: network resonance and cortico-cortical feedback. J Comput Neurosci. 2010;29:495–507. doi: 10.1007/s10827-009-0190-2. [DOI] [PMC free article] [PubMed] [Google Scholar]
  27. Khawaja FA, Tsui JM, Pack CC. Pattern motion selectivity of spiking outputs and local field potentials in macaque visual cortex. J Neurosci. 2009;29:13702–13709. doi: 10.1523/JNEUROSCI.2844-09.2009. [DOI] [PMC free article] [PubMed] [Google Scholar]
  28. Koch C, Rapp M, Segev I. A brief history of time (constants) Cereb Cortex. 1996;6:93–101. doi: 10.1093/cercor/6.2.93. [DOI] [PubMed] [Google Scholar]
  29. Kopell N, Ermentrout GB, Whittington MA, Traub RD. Gamma rhythms and beta rhythms have different synchronization properties. Proc Natl Acad Sci U S A. 2000;97:1867–1872. doi: 10.1073/pnas.97.4.1867. [DOI] [PMC free article] [PubMed] [Google Scholar]
  30. Lamme VA, Spekreijse H. Modulations of primary visual cortex activity representing attentive and conscious scene perception. Front Biosci. 2000;5:D232–D243. doi: 10.2741/lamme. [DOI] [PubMed] [Google Scholar]
  31. Lamme VA, Supèr H, Landman R, Roelfsema PR, Spekreijse H. The role of primary visual cortex (V1) in visual awareness. Vision Res. 2000;40:1507–1521. doi: 10.1016/s0042-6989(99)00243-6. [DOI] [PubMed] [Google Scholar]
  32. Leung LS. Nonlinear feedback model of neuronal populations in hippocampal CAl region. J Neurophysiol. 1982;47:845–868. doi: 10.1152/jn.1982.47.5.845. [DOI] [PubMed] [Google Scholar]
  33. Li W, Piëch V, Gilbert CD. Learning to link visual contours. Neuron. 2008;57:442–451. doi: 10.1016/j.neuron.2007.12.011. [DOI] [PMC free article] [PubMed] [Google Scholar]
  34. Li Z. A neural model of contour integration in the primary visual cortex. Neural Comput. 1998;10:903–940. doi: 10.1162/089976698300017557. [DOI] [PubMed] [Google Scholar]
  35. Lisman JE, Idiart MA. Storage of 7 ± 2 short-term memories in oscillatory subcycles. Science. 1995;267:1512–1515. doi: 10.1126/science.7878473. [DOI] [PubMed] [Google Scholar]
  36. Liu J, Newsome WT. Local field potential in cortical area MT: stimulus tuning and behavioral correlations. J Neurosci. 2006;26:7779–7790. doi: 10.1523/JNEUROSCI.5052-05.2006. [DOI] [PMC free article] [PubMed] [Google Scholar]
  37. Logothetis NK, Pauls J, Augath M, Trinath T, Oeltermann A. Neurophysiological investigation of the basis of the fMRI signal. Nature. 2001;412:150–157. doi: 10.1038/35084005. [DOI] [PubMed] [Google Scholar]
  38. Matsuda K, Nagami T, Kawano K, Yamane S. A new system for measuring eye position on a personal computer. Soc Neurosci Abstr. 2000;26:744.2. [Google Scholar]
  39. Mazzoni A, Panzeri S, Logothetis NK, Brunel N. Encoding of naturalistic stimuli by local field potential spectra in networks of excitatory and inhibitory neurons. PLoS Comput Biol. 2008;4:e1000239. doi: 10.1371/journal.pcbi.1000239. [DOI] [PMC free article] [PubMed] [Google Scholar]
  40. Mazzoni A, Brunel N, Cavallari S, Logothetis NK, Panzeri S. Cortical dynamics during naturalistic sensory stimulations: experiments and models. J Physiol Paris. 2011;105:2–15. doi: 10.1016/j.jphysparis.2011.07.014. [DOI] [PubMed] [Google Scholar]
  41. Montemurro MA, Rasch MJ, Murayama Y, Logothetis NK, Panzeri S. Phase-of-firing coding of natural visual stimuli in primary visual cortex. Curr Biol. 2008;18:375–380. doi: 10.1016/j.cub.2008.02.023. [DOI] [PubMed] [Google Scholar]
  42. Pack CC, Berezovskii VK, Born RT. Dynamic properties of neurons in cortical area MT in alert and anaesthetized macaque monkeys. Nature. 2001;414:905–908. doi: 10.1038/414905a. [DOI] [PubMed] [Google Scholar]
  43. Pesaran B, Pezaris JS, Sahani M, Mitra PP, Andersen RA. Temporal structure in neuronal activity during working memory in macaque parietal cortex. Nat Neurosci. 2002;5:805–811. doi: 10.1038/nn890. [DOI] [PubMed] [Google Scholar]
  44. Ray S, Maunsell JH. Differences in gamma frequencies across visual cortex restrict their possible use in computation. Neuron. 2010;67:885–896. doi: 10.1016/j.neuron.2010.08.004. [DOI] [PMC free article] [PubMed] [Google Scholar]
  45. Rennie CJ, Wright JJ, Robinson PA. Mechanisms of cortical electrical activity and emergence of gamma rhythm. J Theor Biol. 2000;205:17–35. doi: 10.1006/jtbi.2000.2040. [DOI] [PubMed] [Google Scholar]
  46. Roelfsema PR, Lamme VA, Spekreijse H. Synchrony and covariation of firing rates in the primary visual cortex during contour grouping. Nat Neurosci. 2004;7:982–991. doi: 10.1038/nn1304. [DOI] [PubMed] [Google Scholar]
  47. Shelley M, McLaughlin D, Shapley R, Wielaard J. States of high conductance in a large-scale model of the visual cortex. J Comput Neurosci. 2002;13:93–109. doi: 10.1023/a:1020158106603. [DOI] [PubMed] [Google Scholar]
  48. Siegel M, König P. A functional gamma-band defined by stimulus-dependent synchronization in area 18 of awake behaving cats. J Neurosci. 2003;23:4251–4260. doi: 10.1523/JNEUROSCI.23-10-04251.2003. [DOI] [PMC free article] [PubMed] [Google Scholar]
  49. Singer W. Consciousness and the binding problem. Ann N Y Acad Sci. 2001;929:123–146. doi: 10.1111/j.1749-6632.2001.tb05712.x. [DOI] [PubMed] [Google Scholar]
  50. Traub RD, Whittington MA, Colling SB, Buzsáki G, Jefferys JG. Analysis of gamma rhythms in the rat hippocampus in vitro and in vivo. J Physiol. 1996;493:471–484. doi: 10.1113/jphysiol.1996.sp021397. [DOI] [PMC free article] [PubMed] [Google Scholar]
  51. Traub RD, Kopell N, Bibbig A, Buhl EH, LeBeau FE, Whittington MA. Gap junctions between interneuron dendrites can enhance synchrony of gamma oscillations in distributed networks. J Neurosci. 2001;21:9478–9486. doi: 10.1523/JNEUROSCI.21-23-09478.2001. [DOI] [PMC free article] [PubMed] [Google Scholar]
  52. Tsodyks MV, Skaggs WE, Sejnowski TJ, McNaughton BL. Paradoxical effects of external modulation of inhibitory interneurons. J Neurosci. 1997;17:4382–4388. doi: 10.1523/JNEUROSCI.17-11-04382.1997. [DOI] [PMC free article] [PubMed] [Google Scholar]
  53. Uhlhaas PJ, Pipa G, Lima B, Melloni L, Neuenschwander S, Nikolić D, Singer W. Neural synchrony in cortical networks: history, concept and current status. Front Integr Neurosci. 2009;3:17. doi: 10.3389/neuro.07.017.2009. [DOI] [PMC free article] [PubMed] [Google Scholar]
  54. Wang XJ. Neurophysiological and computational principles of cortical rhythms in cognition. Physiol Rev. 2010;90:1195–1268. doi: 10.1152/physrev.00035.2008. [DOI] [PMC free article] [PubMed] [Google Scholar]
  55. Wang XJ, Buzsáki G. Gamma oscillation by synaptic inhibition in a hippocampal interneuronal network model. J Neurosci. 1996;16:6402–6413. doi: 10.1523/JNEUROSCI.16-20-06402.1996. [DOI] [PMC free article] [PubMed] [Google Scholar]
  56. Wang XJ, Rinzel J. Spindle rhythmicity in the reticularis thalami nucleus: synchronization among mutually inhibitory neurons. Neuroscience. 1993;53:899–904. doi: 10.1016/0306-4522(93)90474-t. [DOI] [PubMed] [Google Scholar]
  57. Wang XJ, Golomb D, Rinzel J. Emergent spindle oscillations and intermittent burst firing in a thalamic model: specific neuronal mechanisms. Proc Natl Acad Sci U S A. 1995;92:5577–5581. doi: 10.1073/pnas.92.12.5577. [DOI] [PMC free article] [PubMed] [Google Scholar]
  58. Whittington MA, Traub RD, Jefferys JG. Synchronized oscillations in interneuron networks driven by metabotropic glutamate receptor activation. Nature. 1995;373:612–615. doi: 10.1038/373612a0. [DOI] [PubMed] [Google Scholar]
  59. Wilson HR, Cowan JD. Excitatory and inhibitory interactions in localized populations of model neurons. Biophys J. 1972;12:1–24. doi: 10.1016/S0006-3495(72)86068-5. [DOI] [PMC free article] [PubMed] [Google Scholar]
  60. Wilson TW, Rojas DC, Reite ML, Teale PD, Rogers SJ. Children and adolescents with autism exhibit reduced MEG steady-state gamma responses. Biol Psychiatry. 2007;62:192–197. doi: 10.1016/j.biopsych.2006.07.002. [DOI] [PMC free article] [PubMed] [Google Scholar]
  61. Wilson TW, Hernandez OO, Asherin RM, Teale PD, Reite ML, Rojas DC. Cortical gamma generators suggest abnormal auditory circuitry in early-onset psychosis. Cereb Cortex. 2008;18:371–378. doi: 10.1093/cercor/bhm062. [DOI] [PMC free article] [PubMed] [Google Scholar]
  62. Zhu W, Xing D, Shelley M, Shapley R. Correlation between spatial frequency and orientation selectivity in V1 cortex: implications of a network model. Vision Res. 2010;50:2261–2273. doi: 10.1016/j.visres.2010.01.007. [DOI] [PMC free article] [PubMed] [Google Scholar]

Articles from The Journal of Neuroscience are provided here courtesy of Society for Neuroscience

RESOURCES