Behavioral diversity in microbes and low-dimensional phenotypic spaces

Abstract

Systematic studies of phenotypic diversity—required for understanding evolution—lag behind investigations of genetic diversity. Here we develop a quantitative approach to studying behavioral diversity, which we apply to swimming of the ciliate Tetrahymena. We measure the full-lifetime behavior of hundreds of individual organisms at high temporal resolution, over several generations and in diverse nutrient conditions. To characterize population diversity and temporal variability we introduce a unique statistical framework grounded in the notion of a phenotypic space of behaviors. We show that this space is effectively low dimensional with dimensions that correlate with a two-state “roaming and dwelling” model of swimming behavior. Temporal variability over the lifetime of an individual is correlated with the fraction of time spent roaming whereas diversity between individuals is correlated with the speed of roaming. Quantifying the dynamics of behavioral variation shows that behavior over the lifetime of an individual is strongly nonstationary. Analysis of behavioral dynamics between generations reveals complex patterns of behavioral heritability that point to the importance of considering correlations beyond mothers and daughters. Our description of a low-dimensional behavioral space should enable the systematic study of the evolutionary and ecological bases of phenotypic constraints. Future experimental and theoretical studies of behavioral diversity will have to account for the possibility of nonstationary and environmentally dependent behavioral dynamics that we observe.

Phenotypic diversity is the substrate on which natural selection acts and therefore plays a defining role in evolution. Recent technological innovations have dramatically improved measurements of genetic diversity; however, our understanding of phenotypic heterogeneity lags far behind, mainly because defining and measuring phenotypes pose a significant challenge.

A quantitative study of phenotypic diversity rests on the construction of phenotypic spaces. To construct a space of phenotypes requires defining phenotypic states and a measure of similarity or distance between those states. Phenotypic spaces have been constructed for morphological phenotypes, where states are quantified as shapes and distances between shapes are measured via spatial transformations (1). Examples of phenotypic spaces for morphologies include bird beaks and feet (2, 3), seashells (4), plants (5), and bat wings (3).

Remarkably, for the small number of morphological phenotypes where phenotypic spaces have been constructed, it has been found that these spaces are frequently low dimensional. For example, within the space of all possible shapes of seashells only a small number actually arise in nature (4). Therefore, low-dimensional phenotypic spaces capture constraints on the diversity of possible phenotypes.

Given the role of phenotypic diversity in evolution, such constraints may reflect the natural history of organisms adapting to their environment (5) such as a Pareto optimal set of solutions corresponding to phenotypic trade-offs between tasks (3). In addition, low-dimensional phenotypic spaces can simplify our understanding of the genetic or epigenetic basis of variation by guiding a systematic search for the genomic basis of variation along specific phenotypic dimensions (5).

Despite the potential for phenotypic spaces to provide general insights into evolution and genetics, few phenotypic spaces, other than those for morphologies, have been constructed (6). This limitation is particularly true for behavioral phenotypes where defining states and measuring variation are difficult.

Behavioral states are often defined by stereotyping, where an organism is observed for a small fraction of its lifetime and behaviors are defined manually. This approach has proved powerful for understanding the mechanistic basis of specific behaviors, for example, runs and tumbles in motile bacteria (7) or omega turns in worms (8). However, full-lifetime measurements of swimming behavior in bacteria have shown that stereotyping often fails to capture the diversity of behaviors exhibited over the lifetime of an individual or between individuals in a population (9, 10). Therefore, to construct a phenotypic space of behaviors requires (i) full-lifetime measurements of behavior for many individuals and (ii) a flexible definition of behavioral states and a measure of similarity between those states.

Here we measure the full-lifetime swimming behavior for hundreds of single Tetrahymena cells. We establish a flexible definition of behavioral states and explicitly construct a phenotypic space of behaviors. Our central findings are, first, that the behavioral space for this organism is effectively low dimensional and that constraints on behavioral diversity emerge within this low-dimensional behavioral space; and, second, the dynamics of behavioral variation within this space are complex, exhibiting nonstationarity over the lifetime of an individual as well as intricate patterns of behavioral heritability between individuals.

Results

Swimming Behavior of Tetrahymena.

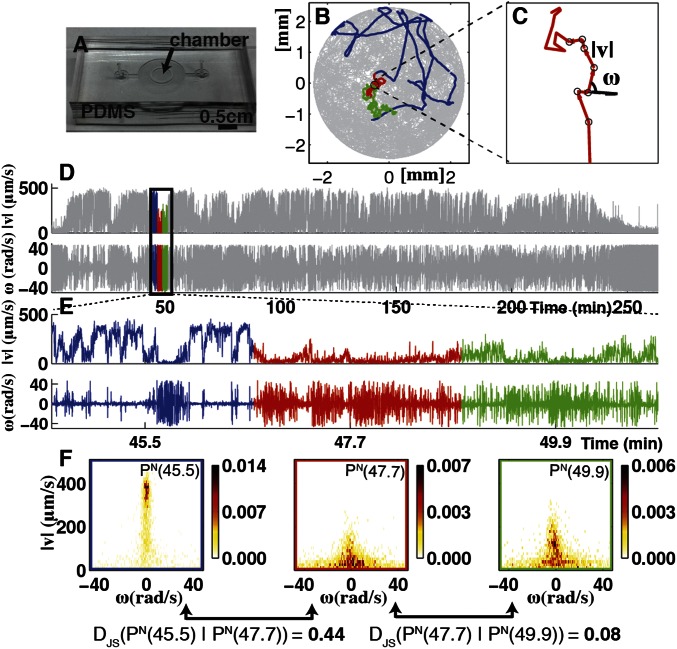
In an experiment, a single Tetrahymena cell is placed in a microfluidic chamber (11) filled with growth medium (Fig. 1A), and its movements are recorded using a custom video microscope (Movies S1 and S2). Our measurements capture swimming behavior through two rounds of division, yielding full-lifetime trajectories for six individuals. We refer to the six individuals arising from a single progenitor as a “family”. The depth of microfluidic chambers is chosen so that the motion of Tetrahymena cells is essentially 2D without impairing motility (Fig. S1). For Tetrahymena the Reynolds number is ∼10⁻³ so viscous effects dominate inertia and all cellular motion is active. An automatic tracking algorithm retains the identity of each cell and the resulting data are 2D trajectories (Fig. 1B). We present behavioral measurements for wild-type (WT) Tetrahymena thermophila in a variety of environmental conditions and Tetrahymena borealis in a single condition.

Fig. 1.

Full-lifetime tracking of swimming behavior in T. thermophila and defining behavioral states. (A) An example of a microfluidic device used in this study. Tetrahymena are loaded into the circular central chamber (Experimental Procedures). (B) The 4-h full-lifetime swimming trajectory of an individual confined to a chamber like the one shown in A is shown in gray, and a 6-min portion is divided into three segments of equal duration (blue, red, green). Full trajectories of (x, y) coordinates (B) are transformed into a time series of speeds and angular velocity 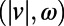. (C) A short segment of trajectory illustrates the calculation of 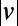and 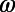. (D) The result of such a transformation for an entire time series. (E) An expanded view of the and 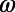time series for the colored segments of the trajectory in B and D. (F) Histograms of 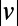and 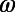for each of the three segments of swimming trajectory in E. The faster, straighter swimming in the blue segment is apparent as the narrow peak of density centered around 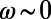(rad/s) and 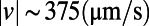. Although the slower, higher tortuosity swimming behavior in the red and green segments is evident as the density below 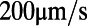with a greater range of 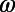. For a segment centered at time t of individual N, its histogram is denoted 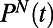. We refer to each histogram as a “behavioral state”. Color bars reflect the density in each histogram. Differences between behavioral states are measured by the Jensen–Shannon divergence, denoted 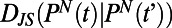. For the dissimilar blue and red segments 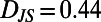whereas for the more similar red and green segments .

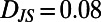Defining Behaviors and a Similarity Measure.

We developed a statistical description of behavior based on minimal assumptions about the structure of behavioral variability. Our method, explained in Fig. 1, is based on distributions of speed 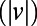and angular velocities (ω) rather than absolute locations because the environment is homogenous and isotropic, excluding the boundaries. We divide full-lifetime trajectories into nonoverlapping windows of length t_w (2–4 min, Fig. S2), and within each window we measure the probability distribution of 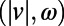pairs. The resulting histograms 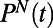(Fig. 1F) represent the behavior of individual N at time t. Constructing histograms is an approximation that allows us to quantify behavior without stereotyping while retaining information about temporal changes of 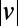and 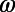on timescales longer than t_w. We define the similarity of two behaviors as the distance between two histograms measured by the Jensen–Shannon divergence 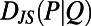(12). The Jensen–Shannon divergence evaluates the overlap between two probability distributions (P and Q) and yields 0 for identical distributions and 1 for distributions that do not overlap.

Measuring Temporal and Population Behavioral Diversity.

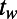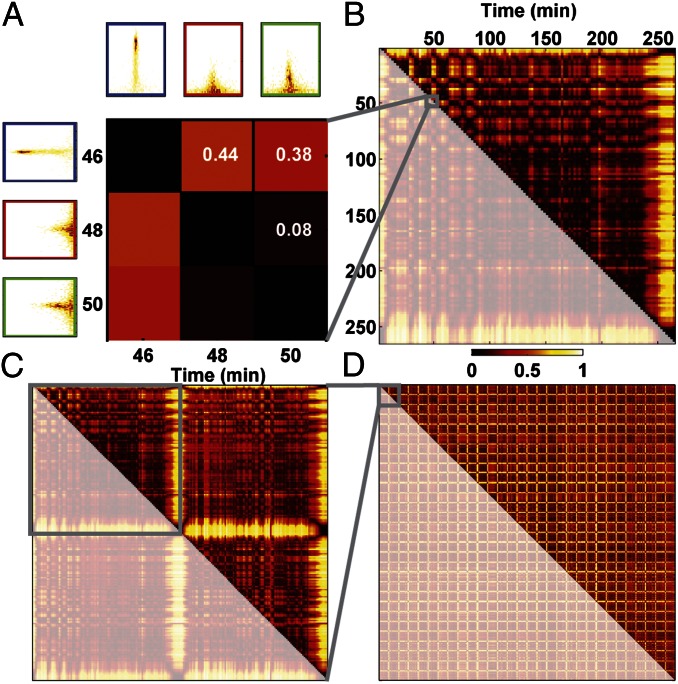
Using our flexible definitions of behaviors and distance 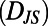, we characterize the diversity of swimming behaviors through time and between individuals. To study behavioral variation in time for one individual we compare all behaviors pairwise throughout the lifetime of an individual (Fig. 2 A and B). Pairwise comparisons between histograms result in a matrix like the one shown in Fig. 2B, which we call a changeability matrix and denote by 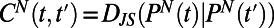. The structure apparent in the changeability matrix in Fig. 2B reflects the variation in behavior over the lifetime of this individual. For example, it is clear that the swimming behaviors just before and after cell division are very different from the behavior during the rest of the lifetime. Indeed, near the beginning and end of its life Tetrahymena swims more slowly than during the rest of its lifetime (Fig. 1D, Upper). Although changes in behavior near division events are the most obvious variation during a lifetime of each individual, a range of variations can be uncovered by analysis of the changeability matrix as we discuss below.

Fig. 2.

Measuring temporal and population-level behavioral diversity. (A) To illustrate the construction of matrices measuring behavioral diversity the three behavioral states from Fig. 1F are reproduced. A 3 × 3 matrix is constructed where each entry of the matrix represents a 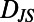measurement between two behavioral states. The corresponding 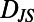values are shown in white and reflected by the color (color bar below B applies to all panels). (B) Constructing 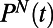histograms from nonoverlapping segments of a full-lifetime trajectory and calculating D_JS between each pair of behavioral states yields a changeability 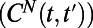matrix that describes temporal diversity over the lifetime of an individual. Note that the 3 × 3 matrix in A is contained within this matrix (gray lines). The redundant entries in the lower triangle of this matrix are opaque. In C we extend the calculation to capture behavioral diversity between two individuals. Each lifetime is divided into a fixed number of behavioral states (n = 100 in this case) by varying t_w for each individual. These states are indexed by s rather than t. With this construction we compute D_JS between behavioral states arising from the same individual, as in A and B, and from different individuals. The resulting individuality matrix, 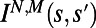for a pair of individuals, is shown in C. Note that the changeability matrix from C resides on the block diagonal of this individuality matrix, highlighted in gray. The upper right block of this matrix is composed of D_JS values computed between behaviors exhibited by different individuals. (D) The calculation is extended to measure individuality for 30 individuals in the same chemical environment (1xR). The box in the upper left indicates the individuality matrix in C.

By measuring 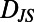for behaviors exhibited by different individuals we capture individuality. To simplify the presentation of individuality we divide each lifetime into a fixed number of behaviors (n) by varying 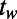between individuals. For the data presented here n = 100 but our results are unchanged for 25 < n < 100 (Fig. S3). We indicate this difference by indexing behaviors by 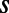rather than 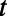with 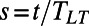, where 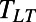is the lifetime. We can thus compare behaviors between individuals N and M by computing an individuality matrix: 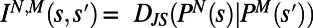. An example of an individuality matrix for two individuals is given in Fig. 2C. Note that for N = M we recapitulate the changeability matrix for individual N (Fig. 2C, gray box). We extend this calculation to construct a large individuality matrix for 30 WT T. thermophila individuals in a rich growth medium environment [1× Rich (1xR), Fig. 2D)]. The matrix in Fig. 2D captures all behavioral diversity present in a population of 30 individuals.

Dimensionality Reduction of Behavioral Space.

The individuality matrix in Fig. 2D describes the space of possible behaviors for members of a population. Here we ask: how many dimensions are needed to adequately capture the behavioral variation in Fig. 2D? We might expect behavioral diversity to be high dimensional, described by many parameters. However, it may be that diverse behaviors are generated in a small number of ways and that the behavioral space is low dimensional.

We ask whether behaviors lie in a low-dimensional space by using metric multidimensional scaling (MDS) (13, 14) to represent behaviors as points in a few dimensions where the Euclidean distances between those points correspond as closely as possible to behavioral distances 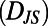. Metric MDS numerically finds a low-dimensional “embedding” of an individuality matrix. The success of an MDS embedding is measured by computing the error incurred by representing behaviors in a few dimensions or the “stress”. Evaluating the dimensionality of an individuality matrix using MDS is accomplished by iteratively embedding the data in an increasing number of dimensions and asking how many dimensions are necessary to obtain a low-stress embedding. Although rigorously determining the intrinsic dimensionality of the data is challenging, a low-stress embedding indicates that the data can reliably be represented in a low-dimensional Euclidean space.

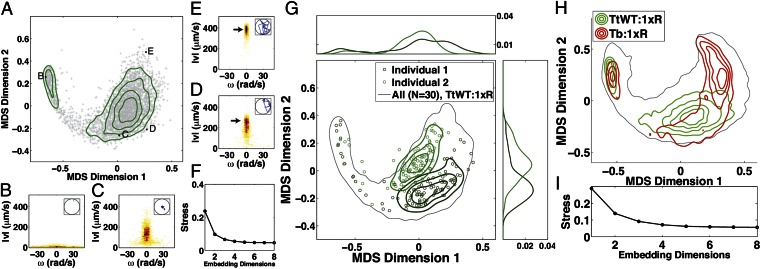
Applying MDS to the individuality matrix shown in Fig. 2D reveals, remarkably, that two dimensions describe the diversity captured by this matrix (Fig. 3 A and F). We conclude the diversity of swimming behavior of WT T. thermophila in rich medium (1xR) as measured by 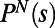is low dimensional. We have shown that the low-dimensional representation of behavioral diversity that we find is not a trivial consequence of our analytical method. For example, we are able to construct artificial trajectories that require many more embedding dimensions (Fig. S4). Similarly, the low dimensionality of the observed diversity of behaviors does not seem to depend on the particular choice of the similarity metric or the MDS embedding method. (Fig. S5 and Table S1).

Fig. 3.

Behavioral diversity is low dimensional with dimensions that correspond to a two-state model of behavior and describe temporal and population diversity, respectively. (A) A multidimensional scaling (MDS) embedding in two dimensions of the individuality matrix for 30 individuals in 1xR (Fig. 2D). Each point in A represents a behavioral state and the Euclidean distances between points approximate the 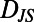values between each state (Fig. 2D). (F) two dimensions are sufficient to make the correspondence between Euclidean distances and 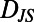a good one. We conclude that behavioral diversity is low dimensional (SI Experimental Procedures). (B–D) Examples of two behavioral states and corresponding trajectories (Insets). B is characteristic of behavior near divisions and the cloud of points in the upper left of A corresponds to division behaviors. (C and D) Behavioral states at low and high values of MDS dimension 1, respectively. C is representative of localized “dwelling” behavior and D shows ballistic “roaming” behavior. MDS dimension 1 therefore corresponds to the fraction of time a given behavioral state spends roaming (SI Experimental Procedures). E shows a behavioral state at high MDS dimension 1 and MDS dimension 2 and corresponds to roaming behavior as well, but with a higher speed than in D (arrows), and thus MDS dimension 2 corresponds to the speed of roaming. G plots 100 behavioral states for two individuals with their marginal distributions above and to the right. The variance along MDS dimension 1 is larger than along MDS dimension 2 for both individuals, indicating that temporal diversity (over a lifetime) occurs primarily in MDS dimension 1. Differences between individuals occur primarily along MDS dimension 2 (compare overlap of marginal distributions). H shows an MDS embedding like the one in A except for 171 individuals, 30 WT T. thermophila (TtWT) individuals in each of five environmental conditions and 21 T. borealis (Tb) individuals in 1xR. TtWT:1xR and Tb:1xR populations are represented by contours; other TtWT populations are included but not shown for clarity. The 95% contour for all 171 individuals is shown in gray. I shows the stress as a function of the number of embedding dimensions.

The basic features of behavior are clear from the embedding shown in Fig. 3A. First, we find two distinct behavioral regions: one corresponding to the slow swimming behavior just before and after cell divisions (upper left) and another corresponding to the rest of the cells’ lifetime (large cloud, center).

Dimensionality Reduction and a Two-State Model of Behavior.

In general there is no systematic way to relate the MDS dimensions to the behavior of Tetrahymena. However, we can look for correlations between the location of a behavior in a given dimension and a parameter of interest. To do this we have examined the properties of behaviors 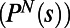as a function of where they lie in the embedding (Fig. 3 B–E). Fig. 3B shows an example of a near division behavior characterized by very slow swimming, whereas Fig. 3 C–E shows examples of nondivision behaviors that occur during the bulk of the lifetime. We find that behaviors characterized by ballistic swimming and rapid explorations of the chamber (“roaming”) have large positive values along MDS dimension 1 (Fig. 3 D and E). Conversely, behaviors that are characterized by slow swimming, sharp turning, and restricted exploration (“dwelling”) reside at large negative values along MDS dimension 1 (Fig. 3C). Variations between behaviors in the speed of roaming are reflected along MDS dimension 2, with faster roaming having larger values (Fig. 3E).

Therefore, with the exception of behaviors associated with division events, MDS dimension 1 correlates with the fraction of time a behavior spends roaming, and MDS dimension 2 correlates with the roaming speed. This suggests that a two-state roaming–dwelling behavioral model applied to other organisms (15) is appropriate for T. thermophila. We classified behaviors, using a mixture model clustering procedure (16) to determine the fraction of each behavior spent roaming and the speed of roaming. With this model we are able to quantitatively demonstrate the correspondence between the two MDS dimensions in Fig. 3A and a dwelling–roaming model of behavior (Table S2 and Fig. S6).

Temporal Diversity and Population Diversity Are Largely in Separate Dimensions.

Fig. 3G shows the 100 points associated with each of two individuals from the population in Fig. 3A. This representation of the data reveals that within each individual variation occurs primarily along MDS dimension 1 and between individuals diversity occurs primarily along MDS dimension 2. We find that this trend is consistent across the whole population of WT T. thermophila individuals in 1xR medium. Thus, the two MDS dimensions are associated with changeability and individuality, respectively, and this correlation is strong (correlation coefficient >0.7) and holds statistically for all individuals in the embedding (Table S2). We conclude that individuals vary over their lifetime primarily in the fraction of time spent roaming and less in the speed with which they roam, whereas variation between individuals arises mainly in the speed of roaming.

Generality of Low-Dimensional Behavioral Diversity.

The low-dimensional representation of behavioral diversity in T. thermophila shown in Fig. 3A motivated us to ask whether behavioral diversity in this organism, and even its close relatives, can be captured in a small number of dimensions. Specifically, does the dimensionality of behavioral diversity increase when cells are subject to different environments? Or is the diversity we observed for WT T. thermophila in the 1xR environment representative of the behavioral repertoire for this organism? To address this we asked whether the low-dimensional representation of behavioral diversity that we found for 30 individuals in a single environment was robust to changes in the environmental conditions and how the dimensionality of behavioral diversity was altered if we included measurements of a closely related species.

We measured the full-lifetime behavior for an additional 120 single cells: 30 WT T. thermophila individuals, five families of six individuals, in each of an additional four conditions. We chose conditions that represent diverse chemical and physical perturbations. First, we doubled the nutrient levels in the rich medium (2xR). Second, for T. thermophila, particulates are important for food vacuole formation and necessary for fast growth (17), so we filtered the 1xR medium of particles larger than 0.2 μm and supplemented it with polymer beads (1xB). Third, because ciliates feed on bacteria, we grew Escherichia coli to high density in 1xR and then sterilized the medium and used this “bacterized” medium (Bac). Finally, we measured 30 individuals in a synthetic medium that supports fast growth [chemically defined medium (CDM)] (18). To assay behavioral diversity more broadly within the genus, we measured 21 T. borealis individuals in the 1xR medium. We chose T. borealis as a representative species of the Tetrahymena genus that was still readily cultured in the laboratory (T. borealis can be grown in 1xR).

From these data we constructed an individuality matrix composed of 171 full lifetimes. This matrix contains all ∼1.4 10⁷ 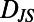measurements between 17,100 behavioral states. We performed dimensionality reduction by MDS on this matrix and found, remarkably, that although new regions of behavioral space are explored, the diversity exhibited by all 171 individuals is also approximately two dimensional (Fig. 3 H and I). Further, the correlation between our low-dimensional representation of diversity and a two-state model of behavior is maintained for individuals in variable environments and T. borealis. We also find that the correspondence between MDS dimension 1 and changeability and MDS dimension 2 and individuality is maintained. We conclude that the low-dimensional behavioral space discovered here applies to diverse environmental conditions and both WT T. thermophila and T. borealis.

Dynamics in Behavioral Space.

Here we explore the dynamics of behavioral variation within the behavioral space in Fig. 3. We study behavioral dynamics within the lifetime of an individual and between individuals in a population.

Nonstationary Behavioral Dynamics.

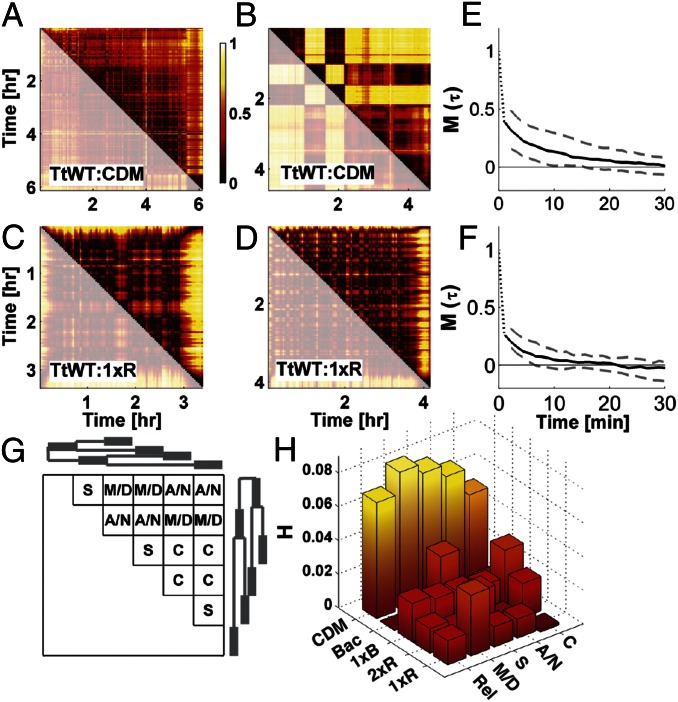
The changeability matrix defines behavioral variation over the lifetime of an individual. In Fig. 4 A–D we show changeability matrices for four WT T. thermophila individuals, two in CDM (Fig. 4 A and B) and two in 1xR (Fig. 4 C and D). The dynamics are strongly heterogeneous and nonstationary, with qualitative changes in behavioral dynamics even for two isogenic individuals in the same chemical environment. The WT T. thermophila:CDM individual in Fig. 4A exhibits slow variation in its behavior over a period of 6 h whereas the individual in Fig. 4B exhibits multiple abrupt behavioral transitions. The examples in Fig. 4 A and B contrast with those in Fig. 4 C and D, where behavioral variation is stochastically variable on a shorter timescale. These examples show that behavioral dynamics over the lifetime of an individual are nonstationary and that this nonstationarity varies with the chemical environment of the cell and the individual observed.

Fig. 4.

Behaviors are dynamically heterogeneous over a lifetime and between generations. (A–D) Examples of changeability matrices from four WT T. thermophila (TtWT) individuals in two conditions—two from CDM and two from 1xR. Color scale for all matrices is shown to the right of A and the dimensions of each matrix are time. Because these matrices are symmetric, redundant data are gray. E and F show the memory 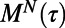, defined in the main text, for populations (30 individuals) in CDM and 1xR, respectively. Black lines indicate the median (across the population) and dashed lines the 0.1 and 0.9 quantiles. Data for a short time before and after divisions are discarded for this calculation. G shows a schematic individuality matrix for a family of six (“related”) individuals arising from a single progenitor. Heritability (H) is defined in the main text as the difference in median individuality between related and unrelated individuals (from different families). The difference between these two quantities is shown in the row labeled “Rel” in H for the five conditions where the TtWT strain was measured. The calculation is repeated, subdividing related individuals into mother–daughter pairs (M/D), sisters (S), aunt–niece (A/N) pairs, and cousins (C). This subdivision is shown schematically in G for a family of six individuals; the phylogeny of a family is shown to the left and above the individuality matrix. Each row of the heritability matrix shown in H corresponds to one such subdivision labeled at the lower right. All measurements of heritability are significant at the 5% level, using a Wilcoxon rank sum test.

Despite the nonstationarity of behavior we can measure a timescale of behavioral variation by computing a quantity analogous to an autocorrelation function, which we term the behavioral memory:

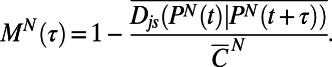Memory measures the timescale over which behaviors become dissimilar. Behavioral memory is plotted in Fig. 4 E and F for all WT T. thermophila:CDM individuals and WT T. thermophila:1xR individuals, respectively. As is evident in Fig. 4 E and F, the timescale of behavioral nonstationarity strongly depends on the environmental condition, and memory quantifies this difference. Indeed, we found that the memory of behavior can vary between 9% and 28% of the lifespan (Table S2). However, despite the dynamic heterogeneity observed between individuals, we find that the memory is consistent within individuals in a given environmental condition—that is, on average WT T. thermophila:CDM individuals exhibit longer memory than WT T. thermophila:1xR individuals (Fig. 4 E and F). Thus, memory quantifies the difference in timescale that is apparent in Fig. 4 A–D.

Heritability.

By comparing dissimilarities between individuals of known relatedness we quantify behavioral variation between generations. Each group of 30 individuals in a given environmental condition is composed of five families of six “related” individuals. All progenitors from the same condition come from the one batch culture, so their relatedness is not known, but with very high probability (>0.999), they are separated by 10 generations—we refer to them as “unrelated” individuals. We define heritability as , where the 〈▪〉 denotes the median behavior for unrelated (N, M) or related (I, J) individuals. Smaller distances between related individuals than between unrelated individuals indicate heritable behavior, and we observe conditions in which swimming behavior is heritable (CDM) and conditions where behavior is not heritable (Bac, “Rel” row in Fig. 4H). Control experiments indicate that swimming in the same chamber does not cause the heritability we observe (Fig. S7).

Heritability is similar to behavioral memory, but it extends the idea to include changes over multiple generations; thus strong heritability indicates that behavioral similarity is slowly lost with successive generations. Conversely, in conditions where heritability is weak (Bac) behaviors can decorrelate, on average, within a single generation.

Closer examination reveals that the structure of behavioral heritability in Tetrahymena is remarkably complex. Within a family of six individuals we distinguish different types of relatedness—“mother”/“daughters” (M/D), “sisters” (S), “cousins” (C), and “aunts”/“nieces” (A/N) (Fig. 4H) (we use anthropomorphic terms for convenience, not to connote their meaning for sexually reproducing organisms). A surprising pattern of heritability emerges if we compare the behavior of different types of related individuals with the behavior of unrelated individuals (Fig. 4H). For instance, in addition to CDM, mother-to-daughter heritability is noticeable in 1xR, but is absent in Bac. In Bac, sisters behave more similarly to each other than to their mothers or unrelated cells (third S row in Fig. 4H). Variation in the structure of the rows of Fig. 4H shows that the transmission of behavior between generations depends on the environment and that heritability can be present in a population as correlations between mothers and daughters as well as cousins or sisters.

Discussion

Measuring and Quantifying Behavioral Diversity.

We have measured swimming behavior for hundreds of individual Tetrahymena and defined behavior using a flexible statistical framework. The underpinnings of our method are (i) a microfluidic-based method for rapidly measuring the full-lifetime behavior of many single cells and (ii) a flexible definition of behavior that allows us to measure similarities (distances) between behaviors.

Our analytical approach allows us to quantitatively characterize the behavioral diversity captured by our measurement. Most previous methods for quantifying behavior are inappropriate for this task because they model motion as a stationary stochastic process (19, 20). Although such models can describe behavior over short timescales or under specific conditions, they cannot capture nonstationary behavior that occurs over longer timescales and for individuals in diverse conditions. However, Gallagher et al. recently studied Caenorhabditis elegans behavior, using hidden Markov models (HMMs), and revealed behavioral variation in worms similar to that described here (21). Our method provides complementary insights while requiring significantly less parameterization. Due to the large number of parameters required for modeling complex behavioral dynamics using HMMs, we found this approach to be unsatisfactory for our data (SI Experimental Procedures).

With our approach, we have revealed two important aspects of behavioral diversity. First, the behavioral diversity in Tetrahymena can be described in a low-dimensional behavioral space. Second, within this space, behavioral dynamics are strongly heterogeneous on timescales from minutes to multiple generations.

The Dimensionality of Behavioral Diversity.

Using dimensionality reduction we found that there are a few biologically relevant dimensions that govern behavioral diversity in a variety of environments and for two species of Tetrahymena. Our statistical framework has permitted us to infer behavioral constraints without a priori choosing the set of behaviors that are observable. Our results provide a striking example of constraints emerging from a statistical description of phenotypic data.

The low-dimensional phenotypic description discovered here might shed light on the origins of phenotypic diversity. Dwelling and roaming behaviors are often associated with “exploration” and “exploitation” of environmental resources, respectively. Our discovery that the speed of roaming varies between individuals but not over the lifetime of one individual might reflect a dispersal strategy in this organism. Although testing such a hypothesis directly is challenging, this aspect of behavior might reflect the natural history of Tetrahymena, a possibility that could be explored by asking whether such constraints apply to similar organisms. Indeed, our data indicate that this constraint is potentially present more broadly in the Tetrahymena genus. Further, similar behavioral states in C. elegans suggest that roaming, dwelling, and slow motility may reflect broadly applicable behavioral constraints (21). Finally, for Tetrahymena, variation in the speed of roaming between individuals might reflect variation in the number of ciliary rows, providing a link between morphological variation and behavioral adaptation.

The microbial context of our study means that the adaptive value of behavioral variation can be studied using experimental evolution. In this context, our approach is equipped to address how behaviors evolve at the individual and population levels. For example, is population-level diversity in the speed of roaming maintained under selection for faster swimming or not? Answering such questions could shed light on the role of constrained behavioral diversity in adaptation.

In addition, it will be intriguing to study the mechanistic implications of these behavioral constraints. With the characterization of phenotypic space provided here, we can now systematically explore how physical, genetic, or epigenetic variation drives behavioral diversity in different directions in behavioral space.

Finally, we note that by representing the phenotypic space of behaviors in a Euclidean space we have assumed that behavioral space is a metric space. However, phenotypic spaces need not be metric (22). Although we cannot explicitly test this assumption, we find that our conclusions are robust to using nonmetric MDS where only rank orders of behavioral similarities are preserved (Table S1 and Fig. S3). Whether the behavioral space is metric remains an interesting avenue for future work.

Behavioral Dynamics.

Within the low-dimensional space of behaviors we have shown that behavioral dynamics over the lifetime of an individual and between individuals are nonstationary. Further, the structure of behavioral nonstationarity is a strong function of the environment (Fig. 4 A–F). This result has important consequences for behavioral measurements and for understanding behavioral adaptation.

Our measurement of behavioral memory provides a first step to quantifying behavioral nonstationarity and sets a lower bound on the duration of measurements required to capture dynamics. More importantly, given the variation in behavioral dynamics we observe with changes in the environment (Fig. 4 A–D), it is clear that an understanding of how organisms alter their behavior in time to respond to the environment requires methods for studying nonstationary dynamics.

Our measurements of heritability extend the notion of complex behavioral dynamics from individuals to populations. As a consequence of our observation that behavioral heritability is complex and strongly environmentally dependent, it is clear that considering correlations between cells of different relatedness, beyond just mothers and daughters, is important for understanding how information transmitted between generations can structure diversity in a population. Previous studies showed that generation times and gene expression levels could be passed between generations in bacterial and mammalian cell lineages (23–25). Our measurement extends these results to behavior in a microbe and demonstrates the environmental contingency of this process. Note that our definition of heritability measures behavioral similarity between individuals in contrast to the common notion of heritability in genetics that captures how much phenotypic variation is explained by genetic variation.

It will be interesting to determine whether the nonstationarity in behavioral dynamics and the complex heritability we observe are selected properties of behavior in Tetrahymena. We expect that a systematic study of behavioral variation with changing environmental parameters will shed light on the role of selection in shaping the dynamics of behavioral variation.

Taken together, our results show that behavioral space can be low dimensional and within that space behavioral dynamics are complex, especially when comparing dynamics in different environments. Our work should enable systematic experimental and theoretical studies of how behavioral diversity permits microbes to adapt their behavior over evolutionary timescales.

Experimental Procedures

Measurement and Tracking.

For 48 h before an experiment Tetrahymena are grown at room temperature in the medium in which their behavior is measured. Cultures were inoculated from long-term soybean stocks. Microfluidic polydimethylsiloxane (PDMS) chambers were constructed using standard soft lithography techniques (Fig. 1A). At the beginning of an experiment a single cell is loaded into a circular chamber that is 240 μm deep and 4.9 mm in diameter. The chamber is illuminated by a light-emitting diode and imaged at 15 frames per second through a relay lens, using a commercial webcam image sensor (Logitech). Five microscopes are operated in parallel, and in each chamber the cells are allowed to complete three rounds of division. The temperature during the experiment was held constant at 23 °C ± 0.02 °C. Because the volume of a cell is 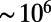times smaller than the volume of the chamber, nutrients are not depleted during the experiment. Tracking is performed after recording using a custom Matlab code, which follows closely previous work (26) (SI Experimental Procedures).

Data Analysis.

All analysis was performed with Matlab.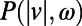 histograms were constructed using an optimal binning method (27) and 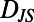estimates were corrected for bias analytically (SI Experimental Procedures). Metric multidimensional scaling results for the embedding studied in Fig. 3 were robust to repeated runs of the gradient descent algorithm with random initial conditions and simulations demonstrating the nontriviality of the low-dimensional embedding (discussed in SI Experimental Procedures). The classification of behavioral states into a two-state model was accomplished by a Gaussian mixture model clustering procedure (SI Experimental Procedures).