Abstract
Background
Modeling of pharmacokinetic parameters and pharmacodynamic actions requires knowledge of the arterial blood concentration. In most cases, experimental measurements are only available for a peripheral vein (usually antecubital) whose concentration may differ significantly from both arterial and central vein concentration.
Methods
A physiologically based pharmacokinetic (PBPK) model for the tissues drained by the antecubital vein (referred to as "arm") is developed. It is assumed that the "arm" is composed of tissues with identical properties (partition coefficient, blood flow/gm) as the whole body tissues plus a new "tissue" representing skin arteriovenous shunts. The antecubital vein concentration depends on the following parameters: the fraction of "arm" blood flow contributed by muscle, skin, adipose, connective tissue and arteriovenous shunts, and the flow per gram of the arteriovenous shunt. The value of these parameters was investigated using simultaneous experimental measurements of arterial and antecubital concentrations for eight solutes: ethanol, thiopental, 99Tcm-diethylene triamine pentaacetate (DTPA), ketamine, D2O, acetone, methylene chloride and toluene. A new procedure is described that can be used to determine the arterial concentration for an arbitrary solute by deconvolution of the antecubital concentration. These procedures are implemented in PKQuest, a general PBPK program that is freely distributed http://www.pkquest.com.
Results
One set of "standard arm" parameters provides an adequate description of the arterial/antecubital vein concentration for ethanol, DTPA, thiopental and ketamine. A significantly different set of "arm" parameters was required to describe the data for D2O, acetone, methylene chloride and toluene – probably because the "arm" is in a different physiological state.
Conclusions
Using the set of "standard arm" parameters, the antecubital vein concentration can be used to determine the whole body PBPK model parameters for an arbitrary solute without any additional adjustable parameters. Also, the antecubital vein concentration can be used to estimate the arterial concentration for an arbitrary input for solutes for which no arterial concentration data is available.
Background
One limitation in interpreting human pharmacokinetic data in terms of physiological parameters is that many pharmacokinetic calculations require knowledge of the arterial blood concentration while in most human studies the blood is sampled from a peripheral vein. The relation between the peripheral vein and arterial blood concentration is a complicated function of the pharmacokinetic distribution of the drug in the organs drained by this vein. In addition, the pharmacodynamic action of most drugs is usually dependent on the arterial concentration and one would like to be able to determine this arterial concentration given the experimentally measured peripheral vein concentration. The problems associated with using peripheral vein blood samples in pharmacokinetic calculations have been discussed in detail by Chiou [1,2].
An area where this sampling problem is particularly important is in the development of physiologically based pharmacokinetic (PBPK) models in which the drug kinetics are described in terms of physiological organ parameters (e.g. organ blood flows, organ partition coefficients, etc.). The values of many of the PBPK parameters, such as organ volumes and blood flows, are fixed and do not depend on the specific solute that is investigated. However, in the PBPK modeling of a new solute there will be some PBPK parameters that are unique to that solute (e.g. liver metabolism, organ partition) and must be experimentally determined. The usual approach in human PBPK investigations is to treat these as adjustable parameters whose values are determined by optimizing the fit to the experimental data. The PBPK model describes the human in terms of a set of organ and blood compartments connected in series and parallel [3]. Two of the compartments in the PBPK model are the arterial and the central vein blood, and the standard approach is to adjust the PBPK parameters to provide an optimal fit between the experimental and model concentrations in one of these blood compartments. Since the peripheral vein concentration may differ significantly from both the central vein and arterial concentration, this procedure will be problematical if only the peripheral vein blood concentration is experimentally measured.
A new approach to overcome this problem is described in this paper. In the great majority of human pharmacokinetic investigations the peripheral site is the antecubital fossa, which will be referred to as the "antecubital vein". The basic idea is to add another organ, the "arm", representing the tissues drained by the antecubital vein. The blood draining this "arm" becomes another PBPK model compartment, and the PBPK parameters can now be adjusted to optimize the fit to this concentration. The most important aspect of this approach is that the PBPK parameters describing the "arm" are chosen in such a way that, once they have been determined, they are applicable to any arbitrary new solute that is investigated and no new additional adjustable parameters are introduced into the PBPK model. For example, suppose that one of the whole human parameters that must be adjusted for a specific solute is the partition coefficient in muscle. Since the "arm" PBPK model depends on exchange in the "arm" muscle and it is assumed that the arm muscle has the same pharmacokinetic properties (partition coefficient, volume of distribution, flow/Kg etc.) as the whole body muscle, adjusting the muscle partition coefficient for the whole body simultaneously modifies the "arm" PBPK parameter. This procedure has been implemented in PKQuest, a general purpose PBPK software routine that has been applied to a large number of solutes [3-7]. The implementation is completely transparent. The user simply chooses "arm" for the sample site and adjusts the PBPK parameters to fit the experimental antecubital vein concentration, just as if the arterial or central vein concentration were available.
Another new feature that has been incorporated into PKQuest is a general procedure for using the antecubital vein blood concentration to estimate the arterial concentration. The unit bolus response function of the "arm" is determined from the PBPK "arm" parameters. This response function is then used to estimate the arterial blood concentration by deconvolution of the antecubital vein concentration. Once the PBPK parameters for the solute have been determined, the user simply inputs the antecubital vein concentrations and PKQuest outputs the corresponding arterial concentration.
The validity of this approach depends on being able to find a set of PBPK "arm" parameters that accurately describe the antecubital vein concentration. In this paper, experimental measurements of simultaneous arterial and antecubital vein concentrations for eight solutes are investigated: ethanol, thiopental, 99Tcm-diethylene triamine pentaacetate (DTPA), ketamine, D2O, acetone, methylene chloride and toluene. This list covers the rather limited experimental data that is available. It will be shown that a single set of "standard arm" parameters provides an adequate description of the more recent pharmacokinetic studies of the four solutes ethanol, thiopental, DTPA and ketamine. However, it is clear that these "standard arm" parameters are not applicable to all human pharmacokinetic studies and they do not describe the results with the other four solutes. This suggests that these "arm" parameters have a strong dependence on the physiological state of the arm and the general applicability of this approach requires the development of a standard protocol for sampling antecubital vein blood.
Methods
Experimental data
All the experimental data was obtained from previous publications. The experimental data points were obtained by using UN-SCAN-IT (Silk Scientific Corporation) to read the data from the published figures. If data was averaged from N subjects, it was assumed that it represented one "average" subject.
The ethanol data was from the paper by Jones et. al. [8]. Simultaneous blood samples were obtained from catheters in the radial artery and "large cubital" vein from 13 healthy men (mean age 31). An ethanol dose of 0.4 gm/kg body weight was given as a constant, 30 minute, intravenous infusion. This data was part of large series in which the A-V difference was determined when the hand was heated or cooled. Only the control data without heating or cooling the hand was used to determine the arm parameters.
Two sets of thiopental data were used. The first set was from the paper by Barratt et. al. [9] that reported the average of simultaneous measurements of arterial and "forearm vein" blood samples from 8 patients. Thiopental was injected at a dose of 5 mg/kg body weight over 30 seconds. Samples were taken for 12 minutes after the injection and then clinical anesthesia was induced. The second data set was from the paper by Stanski et. al. [10]. Simultaneous blood samples were obtained from catheters in the radial artery and "antecubital fossa (basilica vein)". The thiopental was given as a constant 6 minute infusion of 150 mg/min. The data are from one study on a healthy male volunteer. The body weight of this subject was not reported, so the dose/kg could not be determined. A body weight of 65 kg was assumed. Since the main purpose of this investigation is to model the factors determining the arterial/antecubital concentration ratio, small errors in, parameters such as body weight should not be significant since they should cancel out when the ratio is taken.
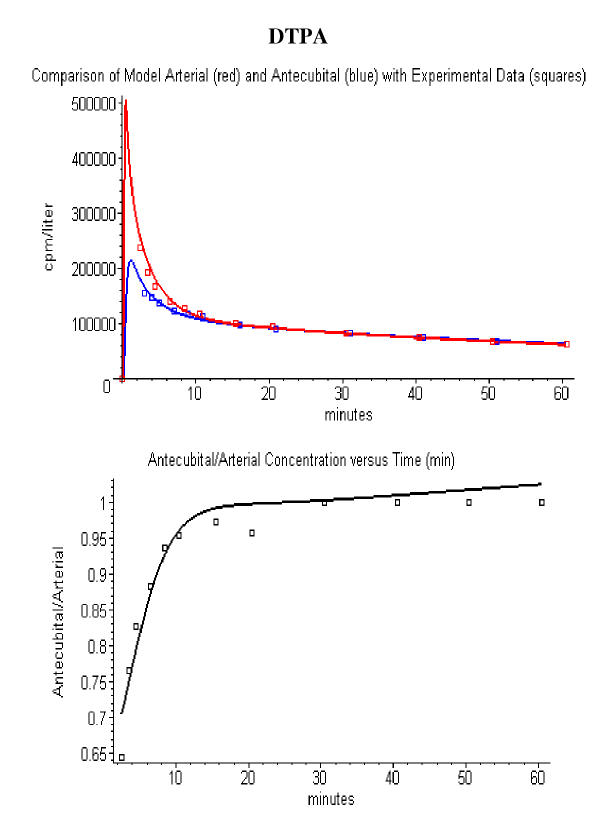
The DTPA data was from the paper by Cousins et. al. [11]. The "antecubital venous" blood samples were obtained 30 s after the arterial samples. A mixture of DTPA and inulin were given as an IV bolus injection (~15 s). Individual data for arterial and AV differences of DTPA and inulin for patients undergoing diagnostic coronary arteriography for chest pain was displayed graphically. The data from subject #2 was used to determine the arm parameters. The time of each data point was increased by 30 s to correct for the time between the IV bolus injection and mixing in the central venous compartment. Since the absolute dose was not reported, the dose was regarded as an adjustable parameter.
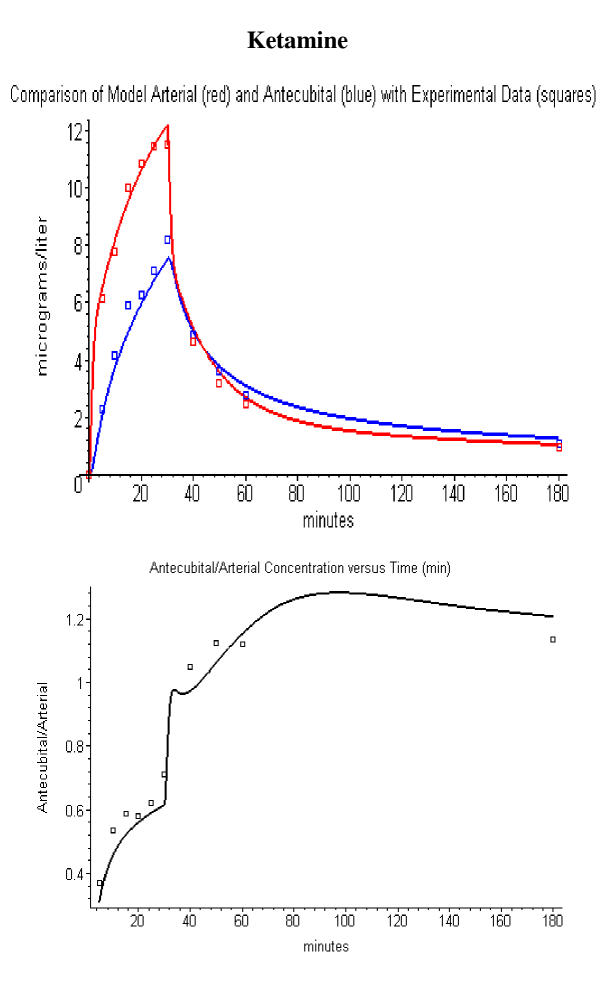
The ketamine data was from the paper by Persson et. al. [12]. Measurements for both the R and S-enantiomer were reported. There were only small differences between the two enantiomers. The R-enantiomer data was used for the modeling except for the last time point (180 min), which was the average of the R and S values because of the large scatter in the values. Varying doses of ketamine were given as a constant 30 minute intravenous infusion and the reported arterial and venous concentration data was scaled and plotted in units of concentration/mg dose. The venous samples were taken from an "indwelling catheter in the arm".
The D2O data was from the paper of Schloerb et. al. [13] and Edelman [14] which describe simultaneous arterial and "antecubital vein" measurements of D2O kinetics. Results were described graphically for 3 different subjects. The data for subject JO [13] was used here.
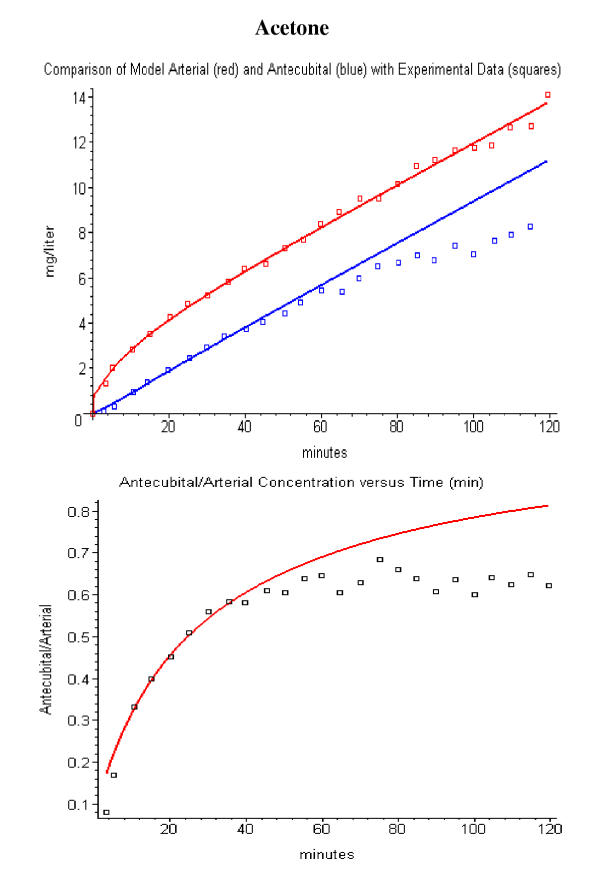
The data for the volatile solutes acetone [15], methylene chloride [16] and toluene [17] were from the set of papers by Carlsson and colleagues. The solutes were input by inhalation and simultaneous measurements of end alveolar, arterial and venous blood concentrations were reported. The venous blood for methylene chloride [16] data was from "a medial cubital vein". Although the site of the venous blood sample for the acetone and toluene data was not reported, it was also assumed to be from an antecubital vein. Data for rest and different work levels were reported. Only the resting data was used. In the methylene chloride study the resting inspired concentration was 870 mg/meter3 for the first 30 minutes, 1740 mg/meter3 for the next 30 minutes followed by periods of work on a bicycle ergometer. Although not stated, the subjects were presumably on the bicycle ergometer during the rest period. The resting inspired concentration was 1309 mg/meter3 in the acetone study and 300 mg/meter3 in the toluene study. The position of the subjects during the resting phase of the acetone and toluene study was not stated.
PBPK model for the "whole body" and the "arm"
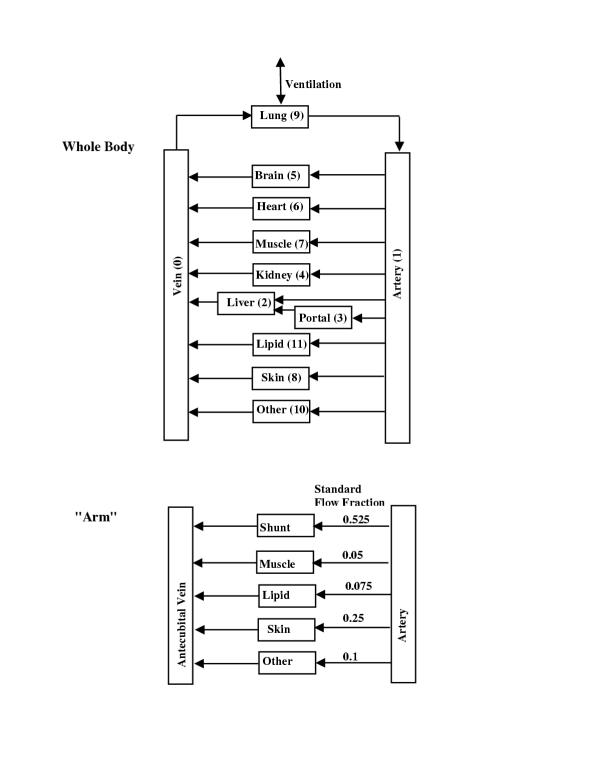
The PBPK model that is used to describe the whole body and the "arm" is shown in figure 1. The PBPK values for organ blood flow and weight are identical to those used previously in PKQuest [18]. The tissue region of each organ is assumed to be well stirred. The term "arm" refers to the tissues that drain into the antecubital vein. It is assumed that the "arm" consists of 5 different tissues (figure 1). Four of these tissues ("skin", "muscle", "adipose" and "other") are assumed to have PBPK parameters (e.g. partition coefficients, blood flow/Kg, etc.) that are identical to the whole body tissues with the same name. (The term "other" refers to subcutaneous and other forms of connective tissue). Thus, the concentration in the blood leaving these arm tissues will be identical to that leaving the whole body tissues, and no new calculation is necessary to determine this concentration. In addition, there is a new "tissue" that is unique to the arm. This tissue, referred to as "shunt", describes the pharmacokinetic exchange that occurs in the arteriovenous anastomoses in the skin of the hand.
Figure 1.
Schematic diagram of the whole body and "arm" PBPK model. The pharmacokinetics of the "arm" organs are identical to the whole body organs with the same name. The "standard" fraction of the antecubital vein blood supplied by the various organs is listed under "Standard flow fraction".
The differential equation describing the free (unbound) concentration (cshunt) in the shunt tissue is described by an equation with the same form as was used for the other tissues in the model ([3], see eq. 4, Appendix I).
![]()
where Vshunt, wfractshunt, fwshunt and Fshunt and are the weight (Kg), water fraction, fraction of solute that is free and blood flow (liters/min), respectively of the shunt organ; wfractB and fwB are the water fraction and fraction free in the blood, and cA is the free arterial concentration (it is assumed that there is no metabolism in this tissue). fclearshunt is the fraction that equilibrates in one pass through the capillary and is related to the capillary permeability. The infinite permeability (flow limited) case corresponds to fclear = 1. It is assumed that the tissue supplied by the shunt has the same pharmacokinetic properties as skin so that wfractshunt, fclearshunt and fwshunt are equal to the skin values. The ratio Vshunt/Fshunt (= vshunt) is introduced as a new parameter. With these assumptions in eq. (1), the concentration in this new tissue is described using only 1 additional parameter (vshunt):
![]()
The free concentration in the vein (cvi) leaving tissue i is related to the tissue concentration ci by ([3], eq. I3):
![]()
If the tissue exchange is flow limited (fcleari = 1) then cvi = ci, the free tissue concentration.
The free concentration in the antecubital vein (carm) is described by the sum of the output from the 5 "arm" tissues:
![]()
where fri is the fraction of the total antecubital vein blood flow contributed by tissue i. The values of cvi for skin, muscle, other, and adipose are identical to the whole body values, and the value of cvshunt is obtained from the solution to the new differential equation 2.
Determination of "whole body" and "arm" PBPK parameters
A unique set of whole body PBPK parameters must be determined for each of the 8 solutes investigated in this paper. This parameter set was determined by optimizing the fit between the experimental arterial data and the concentration in the PBPK "artery" compartment (see fig. 1). The procedure used in PKQuest is to define a "standard human" parameter set that completely describes the pharmacokinetics of a solute such as D2O. Then, the user need only specify the parameters that are unique for the specific solute, such as liver metabolism and tissue/blood partition. The tissue/blood partition coefficient of the different organs is the most problematical and uncertain parameter. PKQuest has a variety of ways to represent this parameter, depending on the properties of the solute.
After the whole body PBPK parameters were determined, the "arm" PBPK parameters were chosen by finding the parameter set that provided the best fit to the experimental antecubital vein concentration. The "arm" is characterized by 5 new parameters: 4 values of fri, the fraction of blood flow to each "arm" organ, (the sum of fr must equal 1) and vshunt (the weight/blood flow ratio for the AV shunt). These 5 parameters depend only on the "physiological state" of the "arm" and they should not be solute dependent. If this approach is going to be applicable to the study of drugs for which arterial data is not available, then it is essential that this same "physiological state" is present in the standard pharmacological investigation. The data from the ethanol, thiopental, DTPA and ketamine studies were all acquired under similar conditions and an attempt was made to find one set of 5 parameters that would provide an adequate description of the experimental arterial/antecubital vein concentration for these 5 solutes. Because of the limited number of these solutes, it is not possible to systematically optimize the 5 parameters. Values were chosen simply by a rough trial and error adjustment. The most important parameter is the value of frmuscle because it has the lowest blood flow/kg and produces the largest difference between the arterial and venous concentration. Figure 7 provides an illustration of the variation in the antecubital vein concentration associated with a range of values of frmuscle. The standard value for vshunt was l liter/kg/min. Once an optimal set of parameters was determined, it was included in the default data set in the "standard human" package of PKQuest so that the user does not need to enter them. This standard set for fri is listed in figure 1. The user can either choose this standard set or, optionally, input arbitrary values for these 5 parameters. This "standard arm" set of PBPK values does not fit the experimental arterial/antecubital vein values for D2O or for the volatile solutes. Presumably, this indicates that the arm is in a different "physiological state" for these solutes. This is discussed in more detail below.
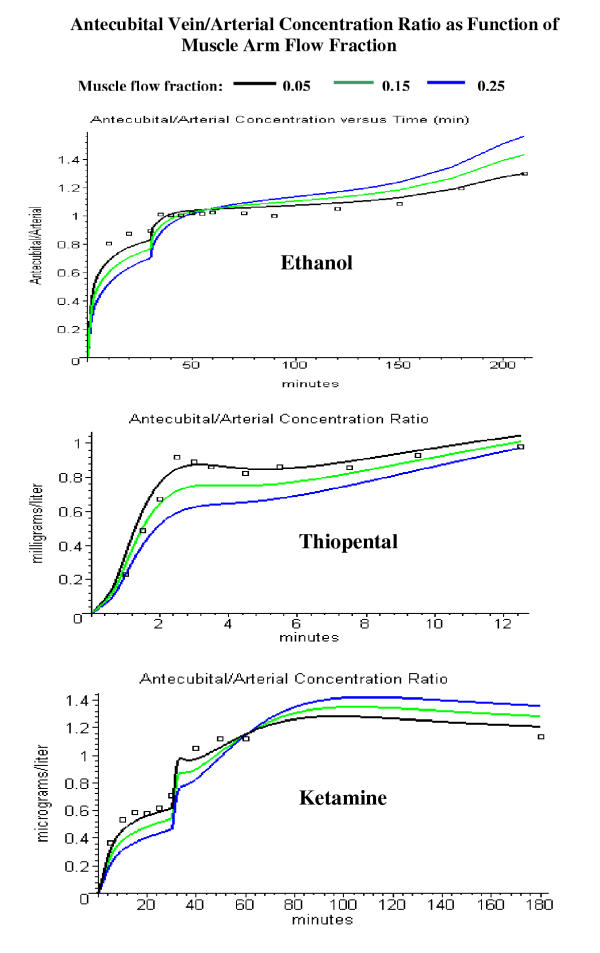
Figure 7.
Comparison of the PBPK model antecubital vein/arterial concentration ratio with the experimental data for different values of muscle flow fraction (frmuscle) for ethanol (top), thiopental (middle) and ketamine (bottom). The model ratio is shown for a fractional muscle flow contribution of 0.05 (black, the "standard" value, used in figs. 2, 3, 4, 5), 0.15 (green) and 0.25 (blue).
The PKQuest worksheet for each solute is listed in the additional file "PKQuest_worksheets.doc". These worksheets completely characterize the PBPK model and list the experimental arterial and venous concentration data that was used. The reader can reproduce all the calculations and figures described in this paper by running PKQuest with these individual worksheets. The main features of the PBPK parameters for the 8 solutes are summarized below.
Ethanol
The PKQuest PBPK model of ethanol has been described in detail previously [6]. It is assumed that ethanol has the same tissue distribution as water (D2O), except for fat for which it has a partition coefficient of 0.051 [19]. Ethanol metabolism is non-linear and the optimal values of Vmax (2.45 millimoles/min/70 kg) and Km (0.096 millimole/liter) were chosen using the non-linear Powell [20] minimization routine that is built into PKQuest. This feature of PKQuest allows the user to minimize the error between the experimental data and the model output for an arbitrary number of parameters just by inputting a list of parameters [3]. The Maple worksheet that completely characterizes the PBPK parameters for ethanol is shown in fig. 2 in order to illustrate how the model is specified in PKQuest. The calls in this worksheet to the routines "defaultpar" and "standardhuman2" define the default and standard human default PBPK parameters that characterize the pharmacokinetics of the standard solute (equivalent to D2O). The default "arm" parameters (fri, etc.) are also determined by standardhuman2. Only three other parameters are required to completely specify the ethanol pharmacokinetics: the Vm and Km for ethanol liver metabolism and the fat/water partition coefficient of ethanol (= 0.051, [19]).
Figure 2.
Maple worksheet for ethanol. The calls to the PKQuest routines "defaultpar()" and "standardhuman2()" set most of the PBPK model parameters. Only the PBPK parameters that are unique for ethanol, along with the experimental data needs to be input.
Thiopental
Since thiopental had not been previously modeled using PKQuest, a new set of PBPK parameters had to be developed to fit the arterial data of Stanski et. al. [10] and Barratt et. al. [9]. Thiopental is highly bound to blood and tissue and the blood/tissue partition coefficients dominate the kinetics. These partition coefficients where chosen based primarily on the rat data of Ebling et. al. [21] and the PBPK model is similar to the human model of Wada et. al. [22]. The tissue/plasma partition coefficient was 6 for adipose tissue, 3 for liver and kidney, 0.8 for muscle and 1 for all other tissues. A fraction free in plasma of 0.15 was used [23-25]. The only parameter that differed in the model fits to the Stanski et. al. [10] and Barratt et. al. [9] data was the value of the thiopental liver clearance, which was adjusted to optimize the fit to the arterial data.
DTPA
DTPA is an extracellular solute that is limited to distribution in the interstitial tissue space. The PBPK parameters used for DTPA were identical to those used in a previous application of PKQuest to EDTA ([18]). The fraction of water that is extracellular in these organs is: muscle (0.15), skin (0.6), adipose (0.2) and other (0.8). (See [18] for a detailed list and discussion of these parameters). The renal clearance was adjusted to fit the arterial plasma data of Cousins et. al. ([11], subject 2). This is the only adjustable PBPK parameter for DTPA. All the other parameters correspond to the default standard human parameters for an extracellular solute.
Ketamine
Because there are no PBPK models available for ketamine, a new set of PBPK parameters had to be developed. Although there have been four measurements of tissue/plasma ketamine partition coefficients [26-29], these studies are limited because they were not obtained at steady state plasma values. The following values represent a composite of the results in these four publications, with most weight given to the intraperitoneal input data [29] which most closely approximates the steady state: tissue/plasma partition coefficient: 20 (kidney); 10 (adipose); 2 (muscle); and 4 (all other tissues). A plasma protein binding fraction of 0.6 [30] was used. Liver clearance was adjusted to optimize the fit to the arterial data.
D20
Since D2O is the "standard" solute in PKQuest, it is described simple by the call to "standardhuman2".
Volatile solutes (toluene, methylene chloride and acetone)
The modeling of these solutes presents a special problem because they were administered in the inspired air so that the exact systemic input is not known. As reviewed by Johanson [31], the kinetics of uptake and washout of volatile solutes with high water/air partition coefficients have a complicated dependence on the exchange that occurs in the large airways of the respiratory tract ("washin-washout effect"). This was discussed previously in the application of PKQuest to methoxyflurane and toluene [5]. Because of this complication, accurate PBPK modeling of the uptake of these solutes requires detailed modeling of the large airways [31,32], a feature that is not incorporated into the current version of PKQuest. However, since uptake can be estimated from the difference between the inspired and the expired (end alveolar) concentration, the following empirical approach could be used to determine the input for these 3 volatile solutes. The water/air partition coefficient is small enough for methylene chloride (5.96, [33]) and toluene (1.75, [33]) that the rate of uptake can be approximated by using an empirical blood/air partition coefficient equal to the measured arterial blood/end alveolar partition during uptake. In contrast, acetone has such a large water/air partition coefficient (395, [34]) that the uptake is dominated by exchange with the large airways and the end alveolar concentration is uncoupled from the arterial concentration. During the uptake experiments [15] the end alveolar concentration is nearly constant so that it can be assumed that there is a constant uptake rate equal to the inspired minus end alveolar gas concentration.
As described previously in the application of PKQuest to toluene and the anesthetic gases [5], a new PBPK approach is used for modeling the blood/tissue partition coefficient. It is assume that the blood/tissue partition is completely determined by the lipid/water partition coefficient, along with a set of values for the fraction of lipid in blood and the different tissues. With this assumption, the PBPK model is completely specified by just the physical values of the water/air and fat/water partition coefficient. In addition, if the blood/air partition coefficient is known, then this can be used to calculate the equivalent lipid content of blood that would yield this value of the blood/air partition. The values used for the 3 solutes are: 1) methylene chloride: Kbair = 11, Kfair = 130 and Kwair = 6; 2) toluene: Kbair = 9, Kfair= 1470 and Kwair = 2.2; 3) acetone: Kbair = 300, Kfair = 80 [34], Kwair = 344. Acetone is relatively insoluble in lipid, with a lipid/water partition coefficient of 0.23 [34] and the blood/air partition coefficient is dominated by the water/air partition. The resultant blood/tissue partition coefficients are similar to those that have been used in previous PBPK modeling of the human pharmacokinetics of methylene chloride [35,36], toluene [37,38] and acetone [32].
The major emphasis of this paper is an analysis of the factors that determine the arterial – antecubital vein concentration difference. Small errors in the PBPK model should not be important, as long as the model arterial concentration is a good approximation to the experimental arterial data.
Determination of PBPK parameters using antecubital vein experimental data
As described in the Introduction, the standard approach for optimizing the parameters is to adjust them to provide a good fit to experimental measurements of either the central vein or arterial blood concentration. Since the antecubital vein concentration differs significantly from both the arterial and central vein concentrations, this presents a serious limitation in the application of the PBPK approach. As described above, if the "arm" parameters are known then one can also relate the antecubital vein concentration to the whole body PBPK parameter set. In the implementation in PKQuest, the use of the antecubital vein to determine PBPK parameters is completely transparent: The user simply chooses "arm" for the sample site and adjusts the PBPK parameters to fit the experimental antecubital vein concentration, just as if the arterial or central vein concentrations were available.
Determination of arterial blood concentration by deconvolution of the antecubital vein concentration
A new procedure has been developed and incorporated into PKQuest to use the antecubital vein concentration to estimate the corresponding arterial concentration. For the special case where the "arm" tissue solute exchange is flow limited and there is no metabolism in the well-stirred "arm" tissues, the contribution of tissue i to the antecubital vein concentration (cδi) after a bolus (delta function) arterial input is described by a single exponential:
![]()
where the parameters Ai and bi depend on the flow/volume ratio of the tissue, the partition coefficient of the solute in blood and tissue and fri. This special case applies to most solutes, including all the solutes studied in this paper. The unit bolus response function describing the antecubital vein concentration is then obtained by summing of these exponentials over all the "arm" tissues:
![]()
The "arm" concentration (carm(t)) for an arbitrary input is then equal to the convolution of this response function with the arterial concentration (cart(t)):
![]()
If the "arm" concentration is known, the arterial concentration can then be determined by deconvolution of eq. (7).
Four different deconvolution algorithms are implemented in PKQuest and have been described previously [7]. Although any of these algorithms could be used to solve eq. (7) for cart(t), the following default procedure seems to work well in most cases. Deconvolution used the cubic spline technique of Verotta [39,40]. The position of the break points is chosen as quantiles of the experimental data points and the user selects the number of breakpoints. Once the PBPK parameters have been determined, the arterial concentration is output by entering a one-line command into PKQuest:
findartery: = table([armconc = vein_data, nbreakpoints = 8]);
where vein_data is a table of the antecubital vein experimental data points. This input produces two graphical plots: 1) a plot of cart(t) and 2) a plot of a comparison of the experimental values of the antecubital vein concentration and the function carm(t) obtained from convolution of this cart(t) (eq. 7). This second curve provides a check on the accuracy of the deconvolution procedure. Several other optional parameters can be entered into the "findartery" Maple table: 1) For the case where there is a discontinuity in the input (e.g. fixed length constant venous infusion) then it is useful to force the spline fit to have a breakpoint at this discontinuity, which is indicated by setting the parameter "fixtimebreak" to the time of the discontinuity. 2) The user can also vary the spline "smoothing parameter", although the default option (= 1) works well in most cases. Pitsiu et. al. [41] recommend varying the number of breakpoints and using some statistical procedure to determine the optimum number. However, by looking at the graphical outputs for different values of nbreakpoints, the user can usually select the best value.
Results
Ethanol, thiopental, DTPA and ketamine
The arterial – antecubital vein concentration relationship is characterized by five parameters: the fractional contribution of blood flow (fri) from "skin", "muscle", "adipose" and "other" to the antecubital vein blood and the weight/blood flow ratio (vshunt) of the "shunt" tissue. (The sum of the fractional flows must equal 1, which determines the value of frshunt). If these parameters are known, then one can use the antecubital vein concentration to estimate the arterial concentration. These parameters depend only on the "physiological state" of the arm and should be independent of the specific solute properties, such as the blood/tissue partition coefficient. Although it was initially hoped that there would be one "standard" physiological state that was generally applicable, this was overly optimistic. However, it was possible to find a "standard arm" PBPK parameter set that provided an adequate description of the simultaneous arterial and antecubital vein pharmacokinetic measurements for the four solutes described in this section.
The set of "standard arm" PBPK parameters that provides the best fit to the data for these four solutes is: flow fraction (fri) = 0.05 (muscle), 0.25(skin), 0.075 (adipose), 0.1 (other), 0.525 (shunt); and vshunt = 1 ml/min/gm. A comparison between the experimental arterial (red) and antecubital vein (blue) data and the PBPK model concentrations using this parameter set is shown in figs. 3, 4, 5, 6 for ethanol, thiopental, DTPA and ketamine. The best indicator of the accuracy of the arm parameters is the plot of the antecubital/arterial concentration ratio (bottom row in figs. 3, 4, 5, 6) since small absolute errors in the whole human PBPK parameters would be expected to cancel out in this ratio. For example, although the absolute concentration is critically dependent on the values of the liver and renal clearance, the relationship between the arterial and antecubital vein concentration should not depend on these parameters.
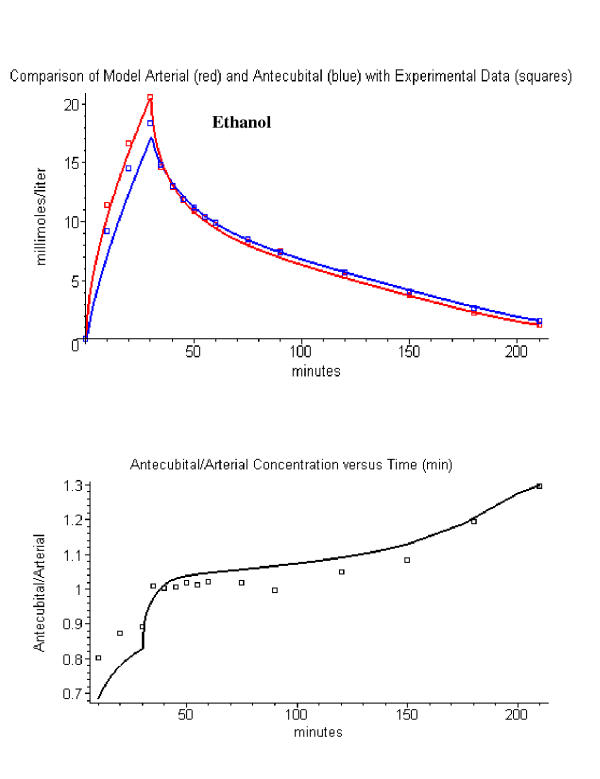
Figure 3.
The top panel shows a comparison of the ethanol PBPK model arterial (red line) and antecubital vein (blue line) with the experimental data (squares) of Jones et. al. [8]. The bottom panel compares the model antecubital vein/arterial concentration ratio (black line) versus the experimental values (squares). Using a fractional contribution of muscle to antecubital vein blood of 0.05.
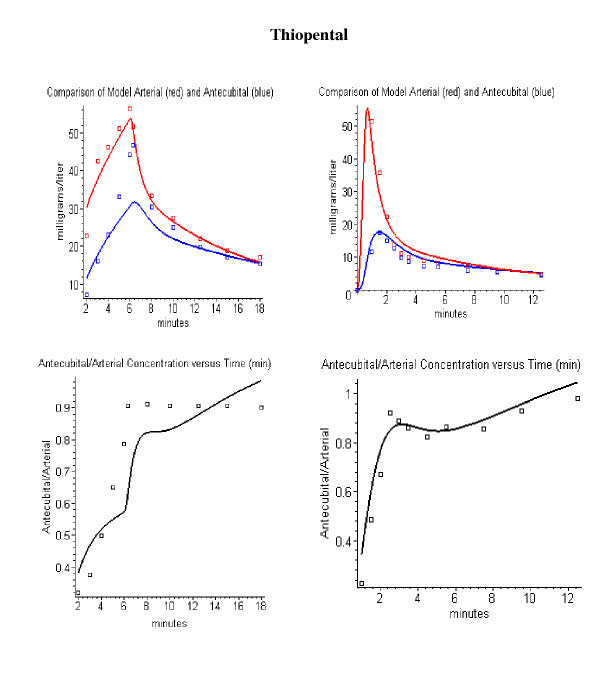
Figure 4.
Comparison of thiopental PBPK model with the experimental data of Stanski et. al. [10] (left column) and Barratt et. al. [9] (right column). The top panels compare the model arterial (red) and antecubital vein (blue) concentration with the experimental data (squares). The bottom panels compare the model antecubital vein/arterial concentration ratio (black line) versus the experimental values (squares). Using a fractional contribution of muscle to antecubital vein blood of 0.05.
Figure 5.
Comparison of DTPA PBPK model arterial (red line) and antecubital vein (blue line) concentrations with the experimental data (squares) of Cousins et. al. [10] (top panel). The bottom panel compares the model antecubital vein/arterial concentration ratio (black line) versus the experimental values (squares). Using a fractional contribution of muscle to antecubital vein blood of 0.05.
Figure 6.
Comparison of ketamine PBPK model arterial (red) and antecubital vein (blue) concentrations with the experimental data (squares) of Persson et. al. [12] (top panel). The bottom panel compares the model antecubital vein/arterial concentration ratio (black line) versus the experimental values (squares). Using a fractional contribution of muscle to antecubital vein blood of 0.05.
The parameter frmuscle (the fraction of antecubital vein blood that drains muscle) has the strongest influence on the antecubital vein concentration because muscle has the lowest value of flow/kg. The "standard arm" data set that was used in figs. 3, 4, 5, 6 has a very small value of frmuscle (0.05) and a corresponding large value for frshunt (0.525). The sensitivity of the results to small changes in frmuscle is shown in fig. 7, which plots the ratio of the antecubital/arterial concentration for an frmuscle of 0.05 (black line, the "standard" value), 0.15 (green) and 0.25 (blue) for ethanol, thiopental and ketamine. It can be seen that an increase in frmuscle by just 10% (from 0.05 to 0.15) leads to a significantly poorer fit to the antecubital vein blood concentration.
D2O and the volatile solutes (acetone, methylene chloride and toluene)
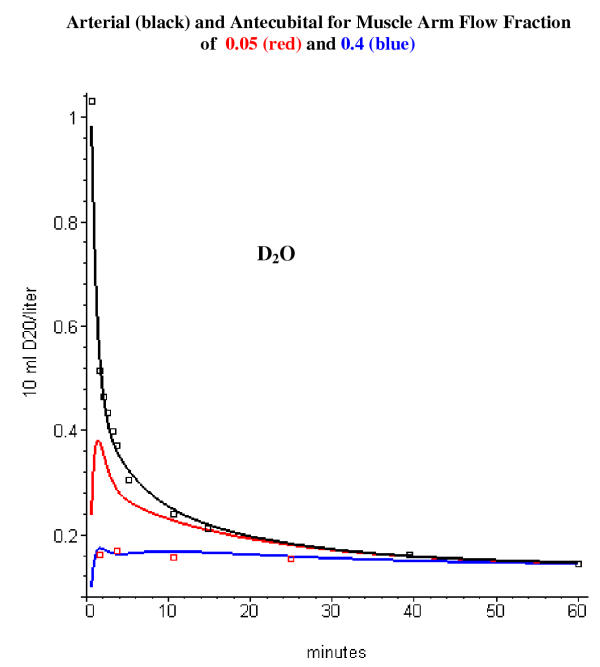
A much larger value of frmuscle is required to describe the antecubital vein concentration for these four solutes. Figure 8 shows a comparison of the model and experimental antecubital vein blood concentration for the D2O data of Schloerb et. al. [13]. It can be seen that using the "standard" value of frmuscle of 0.05 (red line) provides a very poor fit to the experimental antecubital vein data (red squares). In order to fit the antecubital vein data, a frmuscle of about 0.4 is required (blue line). (As the value of frmuscle is increased, the value of frshunt is correspondingly decreased.)
Figure 8.
Comparison of D2O PBPK model arterial (black line) and antecubital vein concentrations with the experimental arterial (black squares) and antecubital (red squares) data of Schloerb et. al. [13]. The red line shows the predicted model antecubital vein concentration using the "standard" arm parameters used in figs. 2, 3, 4, 5 (muscle arm flow fraction = 0.05). The blue line shows the model antecubital vein concentration with the fractional muscle arm blood flow contribution increased to 0.4.
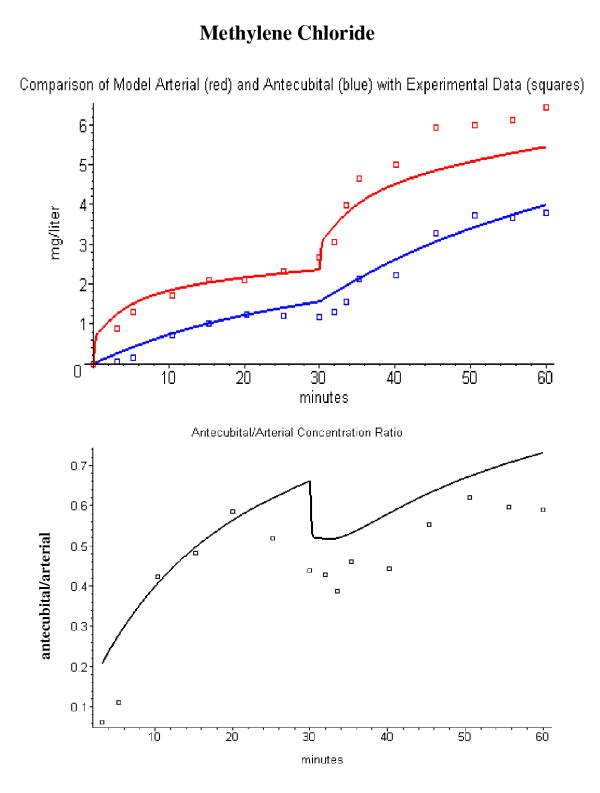
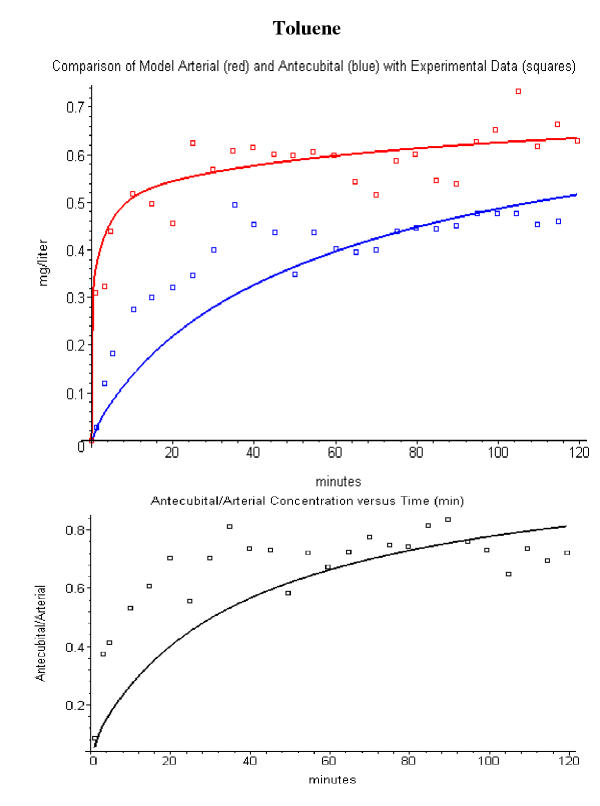
A value of frmuscle of 0.4 to 0.5 is also required to describe to describe the antecubital vein concentration data for the volatile solutes. Figures 9, 10, 11 shows the results of the PBPK model analysis using a value of frmuscle of 0.5 (and frshunt of 0.075) for acetone, methylene chloride and toluene. This large muscle (and negligible shunt) contribution to antecubital vein blood is consistent with the previous PBPK modeling of Johanson and Naslund [36] of the arterial and antecubital vein concentrations for volatile solutes. They were able to describe the experimental data assuming that the antecubital vein blood was supplied entirely by muscle and skin. The fit at long times in fig. 9 is poor for the acetone data. Wigaeus et. al. [15] commented in the original paper that there was something anomalous about the acetone data at long times because the venous concentration remained lower than the arterial concentration for the entire 2 hour washout period. This is very difficult to explain and would be consistent with a direct loss of acetone from the tissues of the hand and arm.
Figure 9.
Comparison of acetone PBPK model arterial (red line) and antecubital vein (blue line) concentrations with the experimental data (squares) of Wigaeus et. al. [15] (top panel). The bottom panel compares the model antecubital vein/arterial concentration ratio (red line) versus the experimental values (squares). Using a fractional contribution of muscle to antecubital vein blood of 0.5.
Figure 10.
Comparison of methylene chloride PBPK model arterial (red line) and antecubital vein (blue line) concentrations with the experimental data (squares) of Astrand et. al. [16] (top panel). The bottom panel compares the model antecubital vein/arterial concentration ratio (black line) versus the experimental values (squares). Using a fractional contribution of muscle to antecubital vein blood of 0.5.
Figure 11.
Comparison of toluene PBPK model arterial (red line) and antecubital vein (blue line) concentrations with the experimental data (squares) of Carlsson et. al. [17] (top panel). The bottom panel compares the model antecubital vein/arterial concentration ratio (black line) versus the experimental values (squares). Using a fractional contribution of muscle to antecubital vein blood of 0.5.
Determination of arterial concentration by deconvolution of the antecubital vein concentration
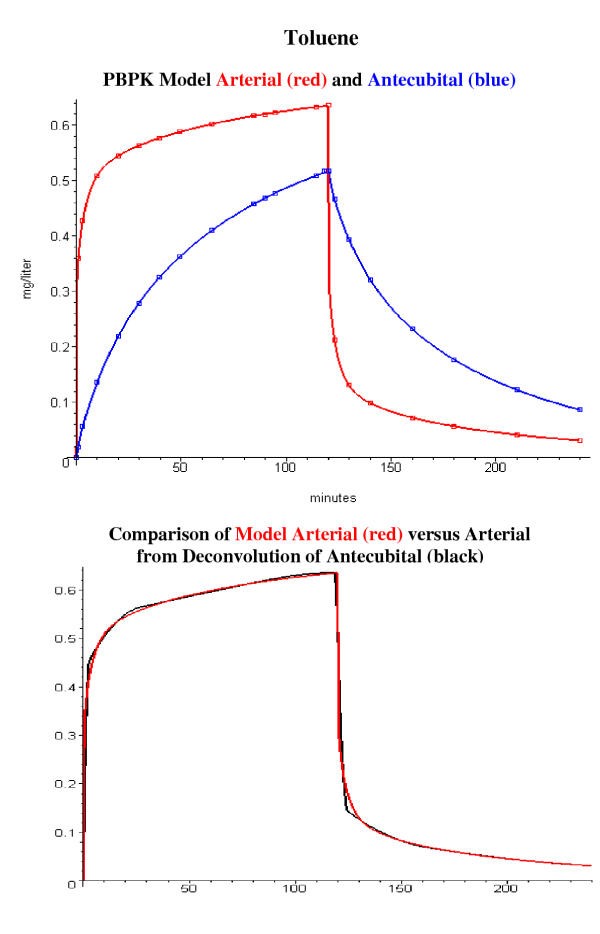
This section describes the results of two tests of validity of the new deconvolution procedure of using the antecubital vein concentration to determine the corresponding arterial concentration. Figure 12 describes the application of the deconvolution method to error free model data generated using PKQuest. The top panel shows the PBPK model arterial and antecubital vein ("arm") concentration generated using the toluene PBPK parameter set for a 120 minute constant inhalation (frmuscle = 0.5). The deconvolution procedure was then applied to the antecubital vein model data sampled at the positions indicated by the blue squares in the top panel. The bottom panel compares the arterial concentration determined by this deconvolution approach (black) with the true model arterial concentration (red). This deconvolution used the default smoothing parameter and a set of breakpoints at 0, 2.84, 27, 59, 92, 118, 120, 124, 162, and 240 minutes. Not surprisingly, given the error free data and the correct set of whole body and "arm" PBPK parameters, the agreement is nearly perfect. The agreement can be further improved if a smaller smoothing parameter is used.
Figure 12.
Determination of arterial concentration by deconvolution of the model antecubital vein concentration data. The top panel shows the model arterial (red) and antecubital (blue) concentration determined using the toluene PBPK model and a value of frmuscle = 0.5. The bottom panel compares the arterial concentration (black line, bottom panel) determined by deconvolution of the antecubital vein discrete data (blue squares, top panel) with the true model arterial concentration (red line, bottom panel).
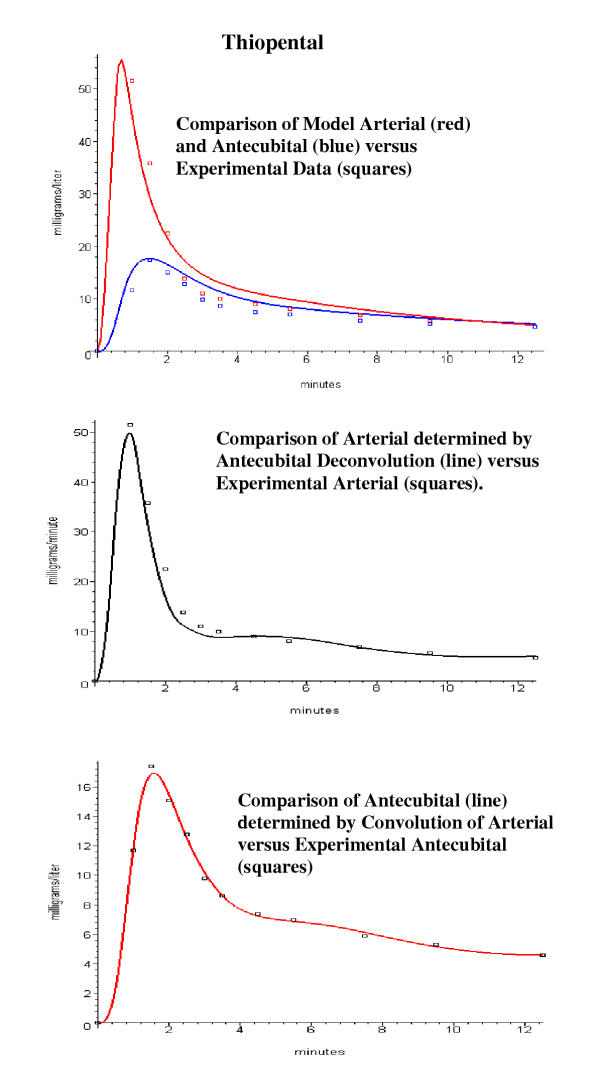
Figure 13 illustrates the application of this technique to the experimental thiopental data of Barratt et. al. [9] and should be representative of the use of PKQuest to estimate the arterial concentration given experimental values for the antecubital vein concentration. It is assumed that the "arm" is described by the "standard arm" PBPK set (flow fraction (fri) = 0.05 (muscle), 0.25(skin), 0.075 (adipose), 0.1 (other), 0.525 (shunt); and vshunt = 1 ml/min/gm). The first step is to determine the whole body PBPK parameters using just the antecubital vein concentration by optimizing the fit between the experimental and model antecubital vein concentration (top panel, fig. 13). The next step is to use these whole body PBPK parameters and the "standard arm" parameters to estimate the arterial concentration by deconvolution of the experimental antecubital vein data (middle panel, fig. 13). As a check on the accuracy of the deconvolution, the lower panel shows the antecubital vein concentration (red line) obtained by convolution (eq. (7)) of the response function (r(t)) and this arterial concentration (cart, black line, middle panel). The default smoothing parameter was used with a set of 6 breakpoints at 0, 0.5. 1.2, 2.4, 3.7, 6.7 and 12.5 minutes. These figures are taken directly from the PKQuest run and represent the standard PKQuest output.
Figure 13.
Determination of arterial concentration by deconvolution of the experimental antecubital vein concentration data for thiopental. The top panel shows the experimental arterial and antecubital vein data (squares) of Barrett et. al. [9] and the model predictions using the whole body and "arm" PBPK parameters described in fig. 4 (using frmuscle = 0.05). The middle panel compares the arterial concentration (black line) determined by deconvolution of the antecubital vein experimental data (blue squares, top panel) versus the experimental arterial data (black squares). The bottom panel compares the antecubital concentration (red line) determined by convolution of the arterial concentration (black line, middle panel) versus the experimental antecubital data (black squares).
Discussion
PBPK "arm" parameters
The values of the PBPK "arm" parameters that characterize the blood flow to the organs drained by the antecubital vein were determined by modeling the experimental simultaneous measurements of the arterial and antecubital vein concentration. In order to compare the model predictions to the experimental data, the following three conditions are required: 1) Simultaneous measurements of human arterial and antecubital vein concentration at relatively early times (<10 minutes) before equilibration occurs; 2) An intravenous input so that the time course of the systemic input is known; and 3) No metabolism in the "arm" tissues, which implies no blood or peripheral (non-liver) metabolism. (Condition #2 was relaxed slightly for the volatile solutes for which uptake could be estimated from the inhaled minus end alveolar concentration difference.) Unfortunately, only a limited number of pharmacokinetic studies have been published that meet these three criteria. Chiou [1] reviewed the literature up to 1989 and I have reviewed the more recent literature. The eight solutes investigated in this paper are a nearly complete list. (Although nicotine experiments [42] satisfied these conditions, it was not possible to develop a satisfactory PBPK model that fit the arterial data points using the published rat tissue/plasma partition coefficients [43], possibly because of the changes in resting skin and muscle arm blood flow produced by nicotine [44,45]).
The arterial – antecubital vein concentration difference for the four solutes ethanol, thiopental, DTPA and ketamine are adequately fit (figs. 3, 4, 5, 6) by a set of arm parameters in which the skeletal muscle contributes only about 5% to the total antecubital vein ("arm") flow (frmuscle = 0.05) and there is a corresponding large contribution by the AV shunt flow (52.5 % of total "arm" flow). As shown in fig. 7, these fits are quite sensitive to the value of the muscle contribution, and increasing frmuscle to just 15% (and decreasing the AV shunt to 42.5%) produces a significantly poorer fit.
These four solutes have a wide range of pharmacokinetic properties that should be representative of most pharmacologic agents. Ethanol distributes freely in the body water space while the distribution of DTPA is limited to the extracellular space. Thiopental and ketamine have large fat/blood and tissue/blood partition coefficients. Although the agreement between the experimental data and model results shown in figs. 3, 4, 5, 6 is clearly not perfect, the model values of the antecubital vein/arterial concentration ratio provide a good first approximation to the experimental values.
In sharp contrast, fitting the data for D2O (fig. 8) and the volatile solutes (figs. 9, 10, 11) requires a much larger muscle contribution, in the range of 40 to 50% (and a corresponding AV shunt contribution of 7.5 to 17.5 %). This difference cannot be explained by differences in the properties of the solutes. Ethanol and D2O have nearly identical pharmacokinetics. In addition, acetone, although volatile, has a relatively small lipid/water partition (0.23) and its pharmacokinetics should also be similar to ethanol. The most obvious explanation of this surprisingly large variation in frmuscle is that the "arm" is in a different "physiological states" for the two data sets. In particular, in the methylene chloride study the collection of the resting data (used in fig. 10) was immediately followed by data collected while exercising on a bicycle ergometer, suggesting that the subjects were also on the ergometer during the resting period. One would expect this experimental condition would lead to increased arm muscle blood flow. The other volatile solute data was collected by the same set of investigators under similar conditions. The only obvious methodological difference in the D2O studies was that the venous blood samples "... were collected by repeat puncture and were drawn from the antecubital vein" while in the other studies, the blood was drawn from an indwelling catheter. It is possible that this method sampled superficial vein blood that had a smaller contribution from hand blood flow. Another possibility is that the repeat punctures were associated with arm movements and increased muscle blood flow.
Whatever the explanation for this variation, it is clear that there can be large variations in the value of the arm parameters and that this must be recognized if one wishes to predict the arterial concentration using antecubital vein blood samples. The fact that the four, more recent, pharmacokinetic investigations of ethanol, thiopental, DTPA and ketamine can be described by a single set of "arm" parameters suggest that this set might be regarded as a "standard" set that can be applied to other pharmacokinetic investigations in the literature. However, support for this conclusion will require additional pharmacokinetic studies, specifically designed to look at the factors that influence the arterial – antecubital vein concentration difference. These results also suggest that efforts should be directed at establishing a standard set of conditions for collecting antecubital vein blood (ambient air temperature, arm position, etc.).
Arteriovenous anastomotic "arm" blood flow
The main feature of the "standard arm" PBPK parameter set used for ethanol, thiopental, DTPA and ketamine is that 55% of the antecubital vein blood comes from the very high flow AV shunt (1 ml/min/gm) and another 20% from the relatively high flow skin (0.1 ml/min/gm) with only about 5% being contributed by the skeletal muscle. There is direct experimental evidence that the skin and AV anastomoses of the hand can contribute a large fraction to the antecubital vein blood flow. Plethysmographic measurements of forearm blood flow with and without wrist cuff inflation indicate that about 50% of the blood flow entering the forearm goes to the hand [46,47], and, presumably, most of the hand blood flow is to skin and arteriovenous anastomoses.
Another indication of the importance of the AV anastomotic blood flow is provided by ultrasound measurements of flow velocities in the arteries of the arm and leg [48]. These studies indicate that there are large, spontaneous variations in the blood flow in these arteries with time constants of about 20 seconds. The fluctuations in the arms and legs are synchronized, indicating a centrally mediated sympathetic temperature regulation mechanism. The fluctuations are also correlated with changes in heart rate and cardiac output. It is estimated that 5 to 10% of the cardiac output of resting subjects is through these arteriovenous anastomoses [48]. The very large amplitude of the fluctuations in ulnar artery velocity suggests that 50% or more of ulnar artery blood flow is associated with arteriovenous anastomoses. This fluctuating AV blood flow pattern is found only in the skin of the hands, feet and face [49,50].
Given that hand blood flow (which is primarily AV anastomotic flow) represents about 50% of total forearm flow, and that the antecubital vein drains primarily the hand and the superficial layers of the forearm [51-53], this 55% AV shunt contribution is not surprising. This large contribution of high flow AV shunt and skin blood to the antecubital vein has not been generally recognized in the pharmacokinetic literature. For example, in the theoretical modeling of the antecubital vein blood by Tuk et. al. [54], it was assumed that the tissue drained by the antecubital vein was mostly muscle with a blood flow of 0.045 ml/min/gm.
The other PBPK parameter that characterizes this AV blood flow is the local flow/kg through the "shunt" tissue (vshunt). Midttun et. al. [55] measured a local AV flow rate of 1 to 1.4 ml/min/gm using a heat washout method. This is in the same range as the value of 1 ml/min/gm that was used to model the data in figs. 3, 4, 5, 6, 7, 8, 9, 10, 11. Another major assumption in the PBPK "arm" model is that the "arm" pharmacokinetics can be modeled in terms of a number of tissues (skin, muscle, adipose, etc.) whose pharmacokinetics are identical to the average PBPK values for the whole human. Elia et. al. [56]measured human forearm muscle blood flow using 133Xe washout and found values of 1.6 to 1.8 ml/min/100 gm, similar to the PKQuest PBPK value of 2.2. Weber et. al. [57] obtained a higher value for forearm muscle blood flow (4 ml/min/100 gm) using two site plethysmography. Blaak et. al. estimated a forearm adipose blood flow of about 2 ml/min/100 gm using 133Xe washout, about 60% of the value of the whole body PBPK value of 3.5. Given the limitations in these methods and the range of results obtained, the validity of the model assumption seems reasonable, at least as a first approximation.
Use of antecubital vein blood samples to estimate the arterial concentration
Since the pharmacodynamic action of most drugs is dependent on the arterial concentration, it is important to be able to estimate the arterial concentration given experimental measurements of the antecubital concentration. Pitsiu et. al. [41] have recently presented a general approach for modeling the relationship between the arterial and peripheral vein concentration for linear systems. Using simultaneous measurements of arterial and antecubital vein concentrations, they develop a multi-exponential system response function (transfer function) that relates the experimental peripheral vein data to the arterial data. Using deconvolution (see eq. (7)), this response function can then be used to predict the arterial concentration given the peripheral vein concentration for arbitrary input regimens of this solute. The disadvantage of this approach is that it requires simultaneous experimental arterial and peripheral vein data for each solute that is investigated.
The PBPK method described here provides an alternative approach to predicting the arterial concentration for an arbitrary input. This procedure is illustrated in fig. 13 for the experimental thiopental data of Barratt et. al. [9] The first step is to determine the whole body PBPK parameters using the antecubital vein concentration data for a known systemic (e.g. intravenous) input. In the top panel of fig. 13, the rate of thiopental liver metabolism was adjusted in order to fit the model antecubital vein concentration (blue line) to the experimental data. In the implementation in PKQuest, the user simply inputs "arm" in order to indicate that the experimental data corresponds to antecubital vein blood samples. Once these whole body PBPK parameters have been determine, the system response function can then be directly determined from the PBPK model (see Methods). The arterial concentration can then be determined by deconvolution of this response function with the antecubital vein concentration data (see eq. (7)). The results of this deconvolution calculation are illustrated in the second and third panels of fig. 13.
This procedure is critically dependent on knowledge of the "standard arm" parameters that describe the fraction of the antecubital vein blood that is supplied by the different organs (i.e. skin, muscle, AVshunt, etc.). Although this new PBPK approach to estimating the arterial concentration is less accurate than the approach of Pitsiu et. al. [41], it has the important advantage that once the "standard arm" PBPK parameters have been determined they should be applicable to all other solutes. This means that the analysis can be applied to solute data in the literature for which no arterial measurements are available.
The complete PKQuest program is freely distributed at http://www.pkquest.com.
Competing Interests
None declared.
Pre-publication history
The pre-publication history for this paper can be accessed here:
Supplementary Material
Contains the complete PKQuest Maple worksheets used in this paper.
References
- Chiou WL. The phenomenon and rationale of marked dependence of drug concentration on blood sampling site. Implications in pharmacokinetics, pharmacodynamics, toxicology and therapeutics (Part I) Clin Pharmacokinet. 1989;17:175–199. doi: 10.2165/00003088-198917030-00004. [DOI] [PubMed] [Google Scholar]
- Chiou WL. The phenomenon and rationale of marked dependence of drug concentration on blood sampling site. Implications in pharmacokinetics, pharmacodynamics, toxicology and therapeutics (Part II) Clin Pharmacokinet. 1989;17:275–290. doi: 10.2165/00003088-198917040-00005. [DOI] [PubMed] [Google Scholar]
- Levitt DG. PKQuest: a general physiologically based pharmacokinetic model. Introduction and application to propranolol. BMC Clin Pharmacol. 2002;2:5. doi: 10.1186/1472-6904-2-5. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Levitt DG. PKQuest: capillary permeability limitation and plasma protein binding - application to human inulin, dicloxacillin and ceftriaxone pharmacokinetics. BMC Clin Pharmacol. 2002;2:7. doi: 10.1186/1472-6904-2-7. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Levitt DG. PKQuest: volatile solutes - application to enflurane, nitrous oxide, halothane, methoxyflurane and toluene pharmacokinetics. BMC Anesthesiol. 2002;2:5. doi: 10.1186/1471-2253-2-5. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Levitt DG. PKQuest: measurement of intestinal absorption and first pass metabolism - application to human ethanol pharmacokinetics. BMC Clin Pharmacol. 2002;2:4. doi: 10.1186/1472-6904-2-4. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Levitt DG. The use of a physiologically based pharmacokinetic model to evaluate deconvolution measurements of systemic absorption. BMC Clin Pharmacol. 2003;3:1. doi: 10.1186/1472-6904-3-1. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Jones AW, Norberg A, Hahn RG. Concentration-time profiles of ethanol in arterial and venous blood and end-expired breath during and after intravenous infusion. J Forensic Sci. 1997;42:1088–1094. [PubMed] [Google Scholar]
- Barratt RL, Graham GG, Torda TA. Kinetics of thiopentone in relation to the site of sampling. Br J Anaesth. 1984;56:1385–1391. doi: 10.1093/bja/56.12.1385. [DOI] [PubMed] [Google Scholar]
- Stanski DR, Hudson RJ, Homer TD, Saidman LJ, Meathe E. Pharmacodynamic modeling of thiopental anesthesia. J Pharmacokinet Biopharm. 1984;12:223–240. doi: 10.1007/BF01059279. [DOI] [PubMed] [Google Scholar]
- Cousins C, Mohammadtaghi S, Mubashar M, Strong R, Gunasekera RD, Myers MJ, Peters AM. Clearance kinetics of solutes used to measure glomerular filtration rate. Nucl Med Commun. 1999;20:1047–1054. doi: 10.1097/00006231-199911000-00010. [DOI] [PubMed] [Google Scholar]
- Persson J, Hasselstrom J, Maurset A, Oye I, Svensson JO, Almqvist O, Scheinin H, Gustafsson LL. Pharmacokinetics and non-analgesic effects of S- and R-ketamines in healthy volunteers with normal and reduced metabolic capacity. Eur J Clin Pharmacol. 2002;57:869–875. doi: 10.1007/s002280100353. [DOI] [PubMed] [Google Scholar]
- Schloerb PR, Friis-Hansen BJ, Edelman IS, Solomon AK, Moore FD. The measurement of total body water in the human subject by deuterium oxide dilution. J Clin Invest. 1950;29:1296–1310. doi: 10.1172/JCI102366. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Edelman IS. Exchange of water between blood and tissues. Characteristics of deuterium oxide equilibrium in body water. Amer J Physiol. 1952;171:279–296. doi: 10.1152/ajplegacy.1952.171.2.279. [DOI] [PubMed] [Google Scholar]
- Wigaeus E, Holm S, Astrand I. Exposure to acetone. Uptake and elimination in man. Scand J Work Environ Health. 1981;7:84–94. doi: 10.5271/sjweh.2561. [DOI] [PubMed] [Google Scholar]
- Astrand I, Ovrum P, Carlsson A. Exposure to methylene chloride. I Its concentration in alveolar air and blood during rest and exercise and its metabolism. Scand J Work Environ Health. 1975;1:78–94. doi: 10.5271/sjweh.2852. [DOI] [PubMed] [Google Scholar]
- Carlsson A. Exposure to toluene: uptake, distribution and elimination in man. Scand J Work Environ Health. 1982;8:43–55. doi: 10.5271/sjweh.2497. [DOI] [PubMed] [Google Scholar]
- Levitt DG. The pharmacokinetics of the interstitial space in humans. BMC Clin Pharmacol. 2003;3:3. doi: 10.1186/1472-6904-3-3. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kaneko T, Wang PY, Sato A. Partition coefficients of some acetate esters and alcohols in water, blood, olive oil, and rat tissues. Occup Environ Med. 1994;51:68–72. doi: 10.1136/oem.51.1.68. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Press WH, Teukolsky SA, Vetterling WT, Flannery BP. Numerical Recipes in C. Second. Cambridge, Cambridge University Press; 1992. pp. 412–420. [Google Scholar]
- Ebling WF, Wada DR, Stanski DR. From piecewise to full physiologic pharmacokinetic modeling: applied to thiopental disposition in the rat. J Pharmacokinet Biopharm. 1994;22:259–292. doi: 10.1007/BF02353622. [DOI] [PubMed] [Google Scholar]
- Wada DR, Bjorkman S, Ebling WF, Harashima H, Harapat SR, Stanski DR. Computer simulation of the effects of alterations in blood flows and body composition on thiopental pharmacokinetics in humans. Anesthesiology. 1997;87:884–899. doi: 10.1097/00000542-199710000-00024. [DOI] [PubMed] [Google Scholar]
- Christensen JH, Andreasen F, Jensen EB. The binding of thiopental to human serum albumin at variable pH and temperature. Acta Pharmacol Toxicol (Copenh) 1983;52:364–370. doi: 10.1111/j.1600-0773.1983.tb01116.x. [DOI] [PubMed] [Google Scholar]
- Ho ST, Hu OY, Pao LH, Ho W, Lee SC. The mechanism of reducing thiopentone dose in elderly patients undergoing surgery. Proc Natl Sci Counc Repub China B. 1988;12:1–8. [PubMed] [Google Scholar]
- Burch PG, Stanski DR. The role of metabolism and protein binding in thiopental anesthesia. Anesthesiology. 1983;58:146–152. doi: 10.1097/00000542-198302000-00008. [DOI] [PubMed] [Google Scholar]
- Edwards SR, Mather LE. Tissue uptake of ketamine and norketamine enantiomers in the rat: indirect evidence for extrahepatic metabolic inversion. Life Sci. 2001;69:2051–2066. doi: 10.1016/S0024-3205(01)01287-5. [DOI] [PubMed] [Google Scholar]
- Edwards SR, Minto CF, Mather LE. Concurrent ketamine and alfentanil administration: pharmacokinetic considerations. Br J Anaesth. 2002;88:94–100. doi: 10.1093/bja/88.1.94. [DOI] [PubMed] [Google Scholar]
- Marietta MP, White PF, Pudwill CR, Way WL, Trevor AJ. Biodisposition of ketamine in the rat: self-induction of metabolism. J Pharmacol Exp Ther. 1976;196:536–544. [PubMed] [Google Scholar]
- White PF, Marietta MP, Pudwill CR, Way WL, Trevor AJ. Effects of halothane anesthesia on the biodisposition of ketamine in rats. J Pharmacol Exp Ther. 1976;196:545–555. [PubMed] [Google Scholar]
- Hijazi Y, Boulieu R. Protein binding of ketamine and its active metabolites to human serum. Eur J Clin Pharmacol. 2002;58:37–40. doi: 10.1007/s00228-002-0439-4. [DOI] [PubMed] [Google Scholar]
- Johanson G. Modelling of respiratory exchange of polar solvents. Ann Occup Hyg. 1991;35:323–339. doi: 10.1093/annhyg/35.3.323. [DOI] [PubMed] [Google Scholar]
- Kumagai S, Matsunaga I. Physiologically based pharmacokinetic model for acetone. Occup Environ Med. 1995;52:344–352. doi: 10.1136/oem.52.5.344. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gargas ML, Burgess RJ, Voisard DE, Cason GH, Andersen ME. Partition coefficients of low-molecular-weight volatile chemicals in various liquids and tissues. Toxicol Appl Pharmacol. 1989;98:87–99. doi: 10.1016/0041-008x(89)90137-3. [DOI] [PubMed] [Google Scholar]
- Sato A, Nakajima T. Partition coefficients of some aromatic hydrocarbons and ketones in water, blood and oil. Br J Ind Med. 1979;36:231–234. doi: 10.1136/oem.36.3.231. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Andersen ME, Clewell H. J., 3rd, Gargas ML, Smith FA, Reitz RH. Physiologically based pharmacokinetics and the risk assessment process for methylene chloride. Toxicol Appl Pharmacol. 1987;87:185–205. doi: 10.1016/0041-008x(87)90281-x. [DOI] [PubMed] [Google Scholar]
- Johanson G, Naslund PH. Spreadsheet programming--a new approach in physiologically based modeling of solvent toxicokinetics. Toxicol Lett. 1988;41:115–127. doi: 10.1016/0378-4274(88)90085-9. [DOI] [PubMed] [Google Scholar]
- Pierce CH, Dills RL, Morgan MS, Nothstein GL, Shen DD, Kalman DA. Interindividual differences in 2H8-toluene toxicokinetics assessed by semiempirical physiologically based model. Toxicol Appl Pharmacol. 1996;139:49–61. doi: 10.1006/taap.1996.0142. [DOI] [PubMed] [Google Scholar]
- Jonsson F, Johanson G. Bayesian estimation of variability in adipose tissue blood flow in man by physiologically based pharmacokinetic modeling of inhalation exposure to toluene. Toxicology. 2001;157:177–193. doi: 10.1016/S0300-483X(00)00356-5. [DOI] [PubMed] [Google Scholar]
- Verotta D. Estimation and model selection in constrained deconvolution. Ann Biomed Eng. 1993;21:605–620. doi: 10.1007/BF02368641. [DOI] [PubMed] [Google Scholar]
- Verotta D. Concepts, properties, and applications of linear systems to describe distribution, identify input, and control endogenous substances and drugs in biological systems. Crit Rev Biomed Eng. 1996;24:73–139. doi: 10.1615/critrevbiomedeng.v24.i2-3.10. [DOI] [PubMed] [Google Scholar]
- Pitsiu M, Gries JM, Benowitz N, Gourlay SG, Verotta D. Modeling nicotine arterial-venous differences to predict arterial concentrations and input based on venous measurements: application to smokeless tobacco and nicotine gum. J Pharmacokinet Pharmacodyn. 2002;29:383–402. doi: 10.1023/A:1020957208071. [DOI] [PubMed] [Google Scholar]
- Gourlay SG, Benowitz NL. Arteriovenous differences in plasma concentration of nicotine and catecholamines and related cardiovascular effects after smoking, nicotine nasal spray, and intravenous nicotine. Clin Pharmacol Ther. 1997;62:453–463. doi: 10.1016/S0009-9236(97)90124-7. [DOI] [PubMed] [Google Scholar]
- Plowchalk DR, Andersen ME, deBethizy JD. A physiologically based pharmacokinetic model for nicotine disposition in the Sprague-Dawley rat. Toxicol Appl Pharmacol. 1992;116:177–188. doi: 10.1016/0041-008x(92)90297-6. [DOI] [PubMed] [Google Scholar]
- Benowitz NL, Jacob P., 3rd, Olsson P, Johansson CJ. Intravenous nicotine retards transdermal absorption of nicotine: evidence of blood flow--limited percutaneous absorption. Clin Pharmacol Ther. 1992;52:223–230. doi: 10.1038/clpt.1992.134. [DOI] [PubMed] [Google Scholar]
- Fewings JD, Rand MJ, Scroop GC, Whelan RF. The action of nicotine on the blood vessels of the hand and forearm in man. Br J Pharmacol. 1966;26:567–579. doi: 10.1111/j.1476-5381.1966.tb01837.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lenders J, Janssen GJ, Smits P, Thien T. Role of the wrist cuff in forearm plethysmography. Clin Sci (Lond) 1991;80:413–417. doi: 10.1042/cs0800413. [DOI] [PubMed] [Google Scholar]
- Williams CA, Lind AR. Measurement of forearm blood flow by venous occlusion plethysmography: influence of hand blood flow during sustained and intermittent isometric exercise. Eur J Appl Physiol Occup Physiol. 1979;42:141–149. doi: 10.1007/BF00431020. [DOI] [PubMed] [Google Scholar]
- Lossius K, Eriksen M, Walloe L. Fluctuations in blood flow to acral skin in humans: connection with heart rate and blood pressure variability. J Physiol. 1993;460:641–655. doi: 10.1113/jphysiol.1993.sp019491. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bergersen TK. A search for arteriovenous anastomoses in human skin using ultrasound Doppler. Acta Physiol Scand. 1993;147:195–201. doi: 10.1111/j.1748-1716.1993.tb09489.x. [DOI] [PubMed] [Google Scholar]
- Coles DR, Cooper KE, Mottram RF, Occleshar JV. The source of blood samples withdrawn from deep forearm veins via catheters passed upstream from the median cubital vein. J Physiol. 1958;142:323–328. doi: 10.1113/jphysiol.1958.sp006019. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Imanishi N, Nakajima H, Aiso S. Anatomic study of the venous drainage architecture of the forearm skin and subcutaneous tissue. Plast Reconstr Surg. 2000;106:1287–1294. doi: 10.1097/00006534-200011000-00008. [DOI] [PubMed] [Google Scholar]
- Gray H. In: Anatomy of the Human Body. 27. Goss C M, editor. Philadelphia, Lea and Febiger; 1959. [Google Scholar]
- Tuk B, Danhof M, Mandema JW. The impact of arteriovenous concentration differences on pharmacodynamic parameter estimates. J Pharmacokinet Biopharm. 1997;25:39–62. doi: 10.1023/A:1025767710234. [DOI] [PubMed] [Google Scholar]
- Midttun M, Sejrsen P, Colding-Jorgensen M. Heat-washout: a new method for measuring cutaneous blood flow rate in areas with and without arteriovenous anastomoses. Clin Physiol. 1996;16:259–274. doi: 10.1111/j.1475-097x.1996.tb00573.x. [DOI] [PubMed] [Google Scholar]
- Elia M, Kurpad A. What is the blood flow to resting human muscle? Clin Sci (Lond) 1993;84:559–563. doi: 10.1042/cs0840559. [DOI] [PubMed] [Google Scholar]
- Weber F, Anlauf M, Serdarevic M. Noninvasive, quantitative determination of muscle blood flow in man by a combination of venous-occlusion plethysmography and computed tomography. Basic Res Cardiol. 1988;83:327–341. doi: 10.1007/BF01907366. [DOI] [PubMed] [Google Scholar]
- Blaak EE, van Baak MA, Kemerink GJ, Pakbiers MT, Heidendal GA, Saris WH. Total forearm blood flow as an indicator of skeletal muscle blood flow: effect of subcutaneous adipose tissue blood flow. Clin Sci (Lond) 1994;87:559–566. doi: 10.1042/cs0870559. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Contains the complete PKQuest Maple worksheets used in this paper.