Abstract
Recent proteomic studies have identified proteins related to specific phenotypes. In addition to marginal association analysis for individual proteins, analyzing pathways (functionally related sets of proteins) may yield additional valuable insights. Identifying pathways that differ between phenotypes can be conceptualized as a multivariate hypothesis testing problem: whether the mean vector μ of a p-dimensional random vector X is μ0. Proteins within the same biological pathway may correlate with one another in a complicated way, and type I error rates can be inflated if such correlations are incorrectly assumed to be absent. The inflation tends to be more pronounced when the sample size is very small or there is a large amount of missingness in the data, as is frequently the case in proteomic discovery studies. To tackle these challenges, we propose a regularized Hotelling’s T2 (RHT) statistic together with a non-parametric testing procedure, which effectively controls the type I error rate and maintains good power in the presence of complex correlation structures and missing data patterns. We investigate asymptotic properties of the RHT statistic under pertinent assumptions and compare the test performance with four existing methods through simulation examples. We apply the RHT test to a hormone therapy proteomics data set, and identify several interesting biological pathways for which blood serum concentrations changed following hormone therapy initiation.
Keywords: proteomics, pathway analysis, regularization, Hotelling’s T2
1 INTRODUCTION
Proteins participate in virtually every process within cells, and they are essential parts of organisms. Proteomics technology allow us to measure protein abundance in a high dimensional fashion. Though antibody array-based approaches could conceptually generate data analogous to microarray data, such platforms are still at an early stage of development. Mass spectrometry(MS)-based platforms remain the workhorse for proteomic research. The resulting data could provide insight into biological systems relevant to a disease or treatment and lead to the identification of related mediating variables or biomarkers.
Proteins work independently and interactively to perform various biological functions. Thus, in addition to association analyses for individual proteins, there is an interest in pathway analyses. Here, pathways refer to sets of proteins that are relevant to specific biological functions, without regard to the state of knowledge concerning the interplay among such proteins. Pathway analyses aim to detect a priori defined sets of proteins that are associated with phenotypes of interest. Several informatics databases (Ashburner et al. 2000; Kanehisa 2002; Subramanian et al. 2005) provide protein functional pathway classifications. Pathway analyses complement the marginal analyses for individual proteins and support further exploration of information in the data. Proteins in each pathway are related by a priori information on biological function, and thus they may lead to valuable insight into the disease etiology or treatment effect and could inform clinical decisions concerning disease prevention or therapeutic maneuvers. Furthermore, when multiple proteins from a same pathway show concerted signals, there may be enhanced power for detecting a group association, compared to that for each separately.
Various methods have been proposed for pathway analysis (or gene set analysis) in microarray studies (Mootha et al. 2003; Subramanian et al. 2005; Tian et al. 2005; Dinu et al. 2007; Efron and Tibshirani 2007). In other related works, Lu et al. (2005) proposed a multiple forward search algorithm for selecting a subset of genes whose expressions differ most between groups; Shojaie and Michailidis (2009) made explicit usage of the regulatory relationships among genes in pathways to detect differentially expressed subnetworks; and Wu et al. (2009) implemented a sparse linear-discriminant-analysis method to test the significance of pathways and at the same time to select subsets of genes that drive the significant pathway effect. More recently, pathway analysis has also been pursued in genome-wide association studies (Wang et al. 2007; Chen et al. 2010).
However, studies of high-dimensional protein expression typically involve quite different technologies than do microarray or genetic association studies, with corresponding major differences in pertinent data analysis methods. Specifically, since proteins of interest may be quite large, MS platforms typically enzymatically digest proteins into peptides, and identify peptides by peaks at their molecular mass in a mass spectrum, with peptide concentration proportional to peak size. Because of run-to-run variations in peak sizes from the same specimen, some of the stronger proteomic platforms focus on concentration ratios for samples to be compared, for example, pre- versus post-treatment specimens, from the same study subject, or specimens from cases which developed a study disease versus corresponding matched controls. Particularly, the members of such a pair are labeled with isotopes having known molecular weight and the ratio of peptide peak sizes, that are separated by the difference in molecular weight of the two labels, provide estimates of peptide concentration ratios. Such ratios, for a set of uniquely determining peptides then yield concentration ratio estimates for the proteins from which they arise. In addition, proteins may vary in abundance over several orders of magnitude, and specimens may be highly fractionated, prior to peptide digestion and liquid chromatography-tandem mass spectrometry within each fraction, to facilitate reliable protein identification. See Eckel-passow et al. (2009) for further detail on mass spectrometry-based proteomic assessment.
As a result of these rather complex assessment procedures, the proteomic profiles that motivate this work consist of estimated concentration ratios for a few hundred proteins. Since these determinations are time consuming and expensive, specimens from several study subjects are typically pooled prior to proteomic analysis, and the number of paired samples to be contrasted may be quite small (10 pooled samples in our application). Also, the mass spectrometer sampling of peaks is dynamic, so that there may be a concentration ratio estimate for a particular protein from one sample pair, but the corresponding data may be missing from the next pair. These features imply the need for novel data analytic methods for paired sample comparisons. Furthermore, proteins having related functions may well yield correlated concentration ratios and act in a concerted fashion (Alon et al. 1999), and ignoring such correlation could lead to inflated type I error rates (Tian et al. 2005; Dinu et al. 2007).
Denote the log 2 ratios between two phenotypes (for example, cases versus controls or baseline versus 1-year after treatment) for proteins in a pathway by Xp×n = {x1,…, xn}. Suppose {xi} are n independently identically distributed samples from a multivariate distribution, whose mean is μ and covariance matrix is Σp×p, consider a test of the hypothesis, H0 : μ = μ0. A classical tool to this multivariate hypothesis testing problem is the Hotelling’s T2 (HT) test. The HT statistic is given by
| (1) |
where is the sample mean vector, and is the sample covariance matrix (m = n − 1). Under a multivariate normality assumption, when p < n, the HT statistic is invariant under linear transformations and the distribution of this test statistic does not depend on the covariance matrix Σ. Under the null, HT follows a Fp,m−p+1 distribution. However, the HT test has very poor performance when p is close to n; and is ill-defined when p equals or exceeds n. This is because the test statistic relies on the inverse of sample covariance matrix , which has large variation when p is close to n and does not exist when p ≥ n. To address this limitation, Dempster (1958) and Dempster (1960) proposed a non-exact test based on a χ2 approximation. Bai and Saranadasa (1996) proposed a simplified test that has equivalent asymptotic power to Dempster’s test. Srivastava (2007) proposed a generalized Hotelling’s T2 statistic, denoted as F+, which converges to a normal distribution with a suitable standardization. A few other test statistics have also been proposed for the p ≥ n scenario, including Fujikoshi et al. (2004), Bai and Silverstein (2004), Schott (2007), Srivastava and Du (2008), Pan and Zhou (2008), Liang and Tang (2009) and Chen and Qing (2010). In most of these methods, asymptotic approximations are used for deriving the significance levels of the test statistics under the null. However, when sample size is small and/or the data has a high rate of missingness, the null distributions of the test statistics may differ substantially from their asymptotic approximations. Hence, we instead use a non-parametric approach to derive the significance levels for the proposed test statistic.
In this paper, we propose a regularized Hotelling’s T2 (RHT) test for both p < n and p ≥ n scenarios. The idea is to employ regularization techniques in the nonparametric testing context. Specifically, regularization is introduced to stabilize the inverse of the sample covariance matrix in (1) giving, for λ > 0,
| (2) |
Note, similar regularization procedures on the sample covariance matrix have been used in the literature in other contexts such as estimation and prediction (Lin and Perlman 1985; Ledoit and Wolf 2004; Schafer and Strimmer 2007). Compared to the test statistics proposed by Dempster (1958) and Dempster (1960), Bai and Saranadasa (1996) and the others mentioned earlier, RHT has a simpler form, and appears to be comparatively more robust to complex missing data patterns. Recently, Yates and Reimers (2009) independently proposed a similar test statistics to (2) under a rather different scenario, where the authors aim to perform two-sample pathway analysis in large microarray studies and derive the p-values based on permuting the group labels. However, permutation is not feasible in the proteomics studies we considered in this paper – the observed data are protein concentration ratios between two different groups and the sample sizes are usually extremely small (n = 10 in our example). Although for such one-sample (ratio of two groups) data, flipping the signs of ratios is analogous to permuting the group labels, this strategy for generating null distributions does not work under the small sample size setting, as we conferred through simulation studies. Hence, we propose a resampling scheme to estimate p-values, in which we implement an objective approach to selecting the regularization parameter. This testing procedure takes advantage of the asymptotic distribution theory for RHT which we establish in this manuscript. Specifically, we derive an asymptotic null distribution of the RHT test statistic as both n and p increase to infinity at a comparable rate, which then leads to an asymptotic cut-off value of the test that is completely data driven. We also quantify the power of the test and provide sufficient conditions for consistency of the RHT test. These theoretical results are helpful in understanding scenarios under which the RHT statistics may or may not perform well. The proposed testing procedure is specifically designed to handle limited sample sizes and missingness in the data, assuming missing completely at random (see Section 4 for the justification of this assumption in our application).
We now use a simple simulated example to further motivate the RHT statistic.
Example A. First, we set n = 10 and p = 8 to mimic the dimension of our proteomic study. We sample X from a multivariate normal distribution N(μ, Σp×p), and consider three different settings:
Independent Null: μ1 = ⋯ = μ8 = 0; Σ = I;
Dependent Null:μ1 = ⋯ = μ8 = 0; Σ = Σ1 with σii = 1 and σij = 0.5 for i ≠ j;
Dependent Alternative: μ1 = ⋯ = μ4 = 1, μ5 = ⋯ = μ8 = 0; Σ = Σ1.
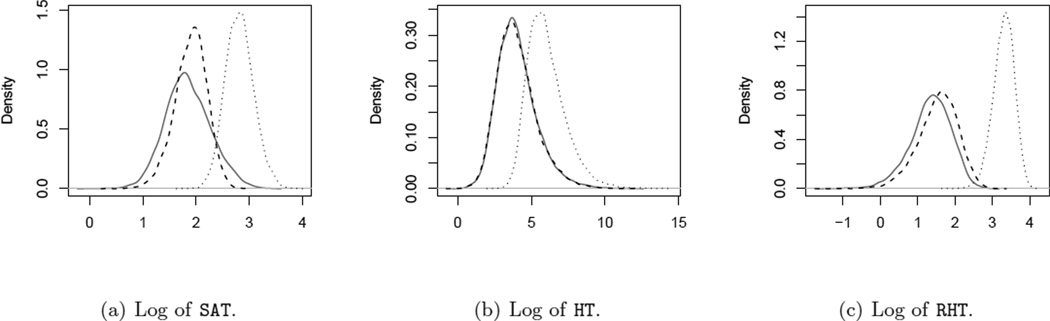
Figure 1 shows the distribution of the following statistics: RHT, HT and the sum of absolute t-statistic (SAT), i.e. the sum of absolute values of t-statistics from each of the p variables (Ackermann and Strimmer 2009). In pathway analysis, because the true Σp×p is usually unknown, the Independent Null (IN, solid curves) obtained by resampling is often used to derive significance levels of test statistics. For SAT, since the correlation among the p variables is ignored, its distribution under IN is much more spread than its distribution under Dependent Null (DN), which may induce inflated type I error rate. On the other hand, for HT and RHT, the distributions under IN are either identical to or stochastically greater than that under DN, suggesting the type I error rate can be properly controlled. In addition, the greater the deviation between the null (dashed curves) and the alternative (dotted curves), the more powerful is the test. In this sense, HT has a larger overlap between the null and the alternative than RHT, suggesting lesser power compared to RHT. In Supplementary Information, we also examine the performance of a few other test statistics, including Dempster’s test, Bai and Saranadasa’s test, and the F+ test. These test statistics also suffer from inflated type I error rates, when resampling based procedures are used.
Figure 1.
Distribution of various test statistics on a simulated example with p = 8, N = 10. The dashed curves are the densities of the test statistics from Independent Null. The solid curves are the densities under Dependent Null. And the dotted curves are the densities under Dependent Alternative. Please see the text for more details.
The remainder of the paper is organized as follows: In Section 2, we present the test statistic, its asymptotic properties, and a non-parametric testing procedure. In Section 3, we compare the performance of RHT with four other existing test statistics on simulated examples. In Section 4, we apply the test to our motivating proteomic study and identify pathways related to postmenopausal hormone therapy. The theoretical proofs are provided in Section 5, and we conclude the paper in Section 6.
2 METHODS
2.1 RHT test statistics and its asymptotic properties
For ease of presentation, we assume μ0 = 0. When p < n, Hotelling’s T2 (HT) statistic is a classical tool for testing μ = 0. However, as noted above, HT has poor power when p is close to n, and is ill-defined when p ≥ n. To avoid these limitations, we impose regularization on the sample covariance matrix and propose a regularized Hotelling’s T2 statistics (RHT)
| (3) |
Here λ is a positive parameter. RHT can also be viewed as a union intersection test (UIT) statistic: For a ∈ Rp, define ya = aTx ~ N(aTμ, aTΣa). Denote the F-statistic for testing H0a : E(ya) = 0 as . Then, HT = maxa≠0ta, a UIT statistic for testing H0 = ∩a H0a : μ = 0. If we replace the sample variance in the denominator of ta with aT (Sn + λI)a, a regularized estimate of the variance of ya, we get another UIT statistic , which is exactly our RHT.
In the presence of missingness, and are defined as
where NA denotes ‘not measured’. We assume here that observations are missing completely at random (Little and Rubin 1987).
The ridge-like regularization in (3) resolves the singularity problem for computing , so that RHT can be calculated for both p < n and p ≥ n cases. The regularization also helps to stabilize the inverse of the sample covariance matrix, thus RHT is expected to enjoy superior power compared to HT when p is close to n. We illustrate this point by characterizing the asymptotic power of the two test statistics under pertinent assumptions.
Suppose that {xi} ~i.i.d. N(μ, Σp) and there is no missingness. We make the following assumptions:
A1: Σp is a p × p positive definite matrix.
A2: p, n → ∞ such that p/n → γ ∈ (0, ∞) and .
A3: Let τ1,p ≥ ⋯ ≥ τp,p > 0 be the eigenvalues of Σp. Then the empirical spectral distribution (ESD) of Σp, defined by , converges as p → ∞ to a probability distribution function H(τ) at every point of continuity of H, whose support, supp(H), is included in a compact set [h1, h2] with 0 < h1 ≤ h2 < ∞.
A4: lim supp→∞ τ1,p < ∞ and lim infp→∞ τp,p > 0.
Note that A3 does not imply A4, since there can be a small number (o(p), to be precise) of eigenvalues of Σp that can either diverge to infinity or converge to zero, even though A3 is satisfied.
Variants of conditions A1–A4 constitute fairly standard regularity conditions in the context of analysis of the empirical spectral distribution (ESD) of a high-dimensional sample covariance matrix. Conditions A1 and A4 appear, e.g. in Bai and Silverstein (2004) and Karoui (2007). Our setting is most closely related to the problem studied in Ledoit and Péché (2010) and except for the additional requirement that (needed for proving the asymptotic normality of the RHT statistic), our conditions match with conditions H2 to H4 in that paper.
With assumptions A1–A4, we derive Theorem 1 to characterize the asymptotic distribution of RHT(λ) under the null. First, we introduce some notations used in the theorem. For z ∈ ℂ, denote mF (z) as the Stieltjes transform of the limiting ESD of Sn, viz. , where d1 ≥ ⋯ ≥ dp are the eigenvalues of Sn. In other words, mF (z) is the pointwise a.s. limit of
| (4) |
Also, mF (z) is the solution of the following equation (Marcenko and Pastur 1967):
| (5) |
as is used in Theorem 1.
Theorem 1 Let λ > 0 be fixed, under H0 and assumptions A1–A4, we have
| (6) |
| (7) |
| (8) |
Remark 1 i) When γ < 1, (6) holds even with λ = 0, and in that case, we have Θ1(0, γ) = 1/(1 − γ) and Θ2(0, γ) = 1/(1 − γ)3, which gives the asymptotic null distribution of HT statistics as stated on page 314 of Bai and Saranadasa (1996).
ii) When Σp = Ip, mF (−λ) has a simple analytical form, and the corresponding Θ1(λ, γ) and Θ2(λ, γ) can be written out explicitly (see equations (13) and (14) below).
In practice we estimate mF (−λ), Θ1(λ, γ) and Θ2(λ, γ) by mFn,p(−λ), Θ̂1,n(λ) and Θ̂2,n(λ), respectively, where mFn,p(·) is given by (4), and Θ̂j,n(λ), j = 1, 2 are obtained by substituting in (7) and (8), γ by p/n, mF (−λ) by mFn,p(−λ) and by where . The following result proves the consistency of the estimators.
Proposition 1 Under the assumptions of Theorem 1, as n → ∞,
| (9) |
| (10) |
By virtue of Proposition 1, we have the following corollary of Theorem 1.
Corollary 1 Under the assumptions of Theorem 1, we have
| (11) |
Observe that Corollary 1 gives a practical and efficient way of determining the asymptotic cut-offs for the RHT test. Note that, the quantities Θ̂1,n(λ) and Θ̂2,n(λ) are completely data-driven, and their computation does not require any knowledge of the true covariance matrix Σ beyond its positive definiteness.
The next two results characterize the asymptotic power of the proposed test.
Theorem 2 Suppose that λ > 0, assumptions A1–A4 hold, and the “effect size” ‖δn‖= cn−θ for some positive constant c and θ ∈ (0, 1/4), where and μp is the true mean. Denote the power of RHT(λ) as βn(δn) ≔ Pδn (RHT(λ) > ξp,γ,λ(1 − α)), where ξp,γ,λ(1 − α) is the (1 − α) quantile of the asymptotic distribution of RHT(λ) under H0. Then, βn(δn) → 1 as n → ∞.
Proposition 2 Suppose that λ > 0, Σp = Ip, assumption A2 holds, and n1/4 ‖δn‖→ c > 0 as n → ∞. Then, the power of RHT(λ) satisfies
| (12) |
where Φ denotes the c.d.f. of N(0, 1),
| (13) |
| (14) |
To facilitate the flow of the paper, we defer the proofs of the above theoretical results to Section 5. Noted that the proof of Theorem 1 (specifically, Lemma 2 in Section 5) employs a novel technique following Ledoit and Péché (2010), based on the Stieltjes transform of the empirical spectral measure of a random matrix. This technique, useful in proving certain limit theorems in random matrix theory, essentially reduces the problem of deriving the asymptotic distribution of the RHT statistic to that of proving the asymptotic convergence of certain quadratic forms involving the sample covariance matrix. We deem this as a theoretical contribution of the paper.
Unlike the classical Hotelling’s T2 test, the power function of the RHT test cannot be expressed in a simple form when λ > 0. As can be seen from the expansion (26) of the normalized RHT statistic in Section 5, when μ ≠ 0, the main contribution to the power of the RHT test comes from the quantity , where Λn is distributed as the inverse of Wn +λΣ−1 and (n − 1)Wn has the p-dimensional Wishart distribution with n − 1 degrees of freedom. If the spectral norm of Σ and Σ−1 are bounded above, the same is true for Λn and . In that setting, the power of the RHT test primarily depends on the norm of the vector δn. The structure of δn shows that, if μ is aligned to the direction of the smallest eigenvectors of Σ, then the power will tend to be large; while if μ is aligned to the eigenvectors associated with the leading eigenvalues of Σ, then the power can deteriorate somewhat. However, unless the covariance matrix Σ is badly conditioned, the power will depend mainly on the l2 norm of μ and not much on the structure of Σ. In the end, it is worth pointing out that, when γ ≥ 1, Theorem 2 and Proposition 2 do not hold for λ = 0 (see Simulation 1 in Section 5). This suggests that RHT(λ) for λ > 0 and HT (=RHT(0)) are intrinsically different, and the former is more suitable if p ≈ n or p ≥ n.
2.2 A testing procedure based on resampling
Proteomics data may have substantial missingness and small sample sizes, and thus the asymptotic null may not well approximate the empirical null for RHT statistic. In this section, we propose a non-parametric approach to estimate the p-values. The idea is to use Independent Null, which can be characterized through resampling, to approximate the Dependent Null (the true null). Specifically, we propose to select the tuning parameter λ through minimizing the difference between the asymptotic (1 − α)-quantile of the Independent Null and the asymptotic (1 − α)-quantile of the Dependent Null, where α is the target significance level; then based on the selected λ, the (1 − α) quantile of the empirical Independent Null from resampled data is used as the critical cutoff value. We describe the details of these steps below.
Step 1. Resampling. In the proteomics data, the proportion of missingness among proteins can be highly variable due to the dynamic nature of the mass spectrometer sampling, and different missingness patterns may affect the test statistics. Hence, we choose to preserve the same missing data pattern and proceed with the resampling procedure as follows. Denote the pool of non-missing measurements (concentration log ratios) of all proteins in all samples as Ω. Usually, Ω has been standardized to zero sample mean and unit sample standard deviation in the preprocessing normalization step. In each resampling iteration, we first randomly sample p × n numbers from Ω without replacement and record them in a matrix X̃p×n. We preserve the same missing pattern in X̃ as the observed data by setting x̃ij = NA for those {(i, j) : xij = NA}. In this resampling procedure, the log ratios within each random set are nearly independent, and hence can be viewed as having zero mean and identity covariance matrix. We will refer to the null distribution of the RHT statistics based on the resampled data as Independent Null (IN), while the null distribution of the RHT statistic based on the observed data as Dependent Null (DN).
Step 2. Choosing λ. We use the asymptotic approximation to choose the degree of regularization (λ), such that the tail of the IN well approximates the tail of the DN. The former is then used to derive the critical value of the test statistics in Step 3. Specifically, for each λ, we first calculate (Θ̂1,n(λ), Θ̂2,n(λ)) based on the observed data Xp×n, and based on resampled data X̃p×n. Then for a target significant level α, we calculate the difference between the asymptotic (1 − α) quantile of DN and IN:
| (15) |
where ξ1−α is the (1 − α) quantile of standard normal N(0, 1). We then select λ as:
| (16) |
where Λ is a prespecified selecting range for λ, and δ is a small positive value. Here Γ is the collection of λ values, based on which the tail of IN is rather close to the tail of the DN. In Simulations and Application sections, we set Λ = [0.01, 10] and δ = 0.5 to ensure Γ ≠ ∅. We then choose to be conservative on the regularization level by selecting the minimum value of Γ, which further helps to control the type I error rate. Note that when λ = 0, the RHT statistic becomes the HT statistic, which is invariant to correlation structure in the data. Consequently, DN is stochastically the same as the IN when λ = 0, which suggests E(Dα(0)) = 0. On the other hand, when λ → ∞, RHT statistic does not make use of the correlation structure among X and becomes rather similar to the SAT statistic, which could have inflated type I error rate when correlation is present. In some sense, RHT statistic is between HT and SAT, aiming to achieve a better balance between type I error rate and power.
The calculation of Dα(λ) takes the eigenvalues of sample covariance matrix from IN and DN as input, where the latter comes from observed data. To obtain the eigenvalues from IN, we independently resample the observed pathway data 100 times, and derive the corresponding . The median of this set is selected to be the final .
Step 3. Calculating p-value. Once λ̂sel is chosen, the empirical distribution of the test statistics derived from the resampled data can be used to calculate the p-value. Particularly, let RHT(λ̂sel) denote the test statistics calculated from the observed data Xp×n; and denote the test statistics calculated from M independent resampled data sets . The p-value is then calculated as
| (17) |
2.3 Modified RHT using Bootstrap
When γ = p/n value is large, the estimates Θ̂1,n(λ) and Θ̂2,n(λ) tend to have large variance, which sometimes hurts the power of the proposed test, especially when the signal size is small or moderate (Figure S3). To circumvent this problem, we introduce a modified ‘bootstrap-like’ statistic, RHTBootstrap, for large pathways. The idea is to first focus on small pathway subsets, for which signals can be efficiently captured by RHT statistics; and then average the information across all subsets. The detailed procedure is as follows:
Sample without replacement B subsets of variables, so that the bth subset harbors pb features;
Calculate RHTb for each subset;
Report the average .
Here, if pb is small, RHTBootstrap behaves similarly to SAT and may not take adequate account of the correlation among variables. Furthermore, in Theorem 2, we have shown that, unlike the HT test, the power of the RHT test converges to 1 even when p/n is close to 1. Therefore, choosing a pb as large as possible while γb = pb/n < 1 is expected to maintain good power, while guarding against inflated type I error rates and taking maximal advantage of correlation among variables. We used pb = n−2 in Simulations and Application sections. Meanwhile, a convenient choice of λ for RHTBootstrap is , where λ̂b is the selected tuning parameter for the bth subset according to equation (16). The advantage of RHTBootstrap versus RHT is illustrated with simulation examples in Supplementary Information.
We summarize the procedures of the proposed test in the following two algorithms.
3 SIMULATIONS
We compare the performance of the proposed RHT and RHTBootstrap tests with several other alternatives: (1) HT test; (2) HTBootstrap (similar to RHTBootstrap); (3) SAT; (4) Maxmean statistic (Efron and Tibshirani 2007); (5) TD test (Dempster 1958; Dempster 1960); (6) TBS test (Bai and Saranadasa 1996); and (7) F+ test (Srivastava 2007). The HT test is only performed for p < n cases; while RHTBootstrap, HTBootstrap and F+ are only performed for p ≥ n cases. For RHT, RHTBootstrap(p > n), HTBootstrap(p > n), SAT, and Maxmean, we calculate the p-values using the resampling procedure described in Section 2.2. For HT, TD, TBS, and F+, we use their asymptotic distributions to obtain the corresponding significance levels (see Section 1 of Supplementary Information for details of these statistics and their asymptotic approximations). Note that with missingness, those asymptotic distributions can be far from the empirical null distributions, especially with limited sample size. We see from the following simulations that the tests based on these asymptotic distributions often cannot control type I error rate.
Algorithm 1.
A regularized Hotelling’s T2 test
|
Algorithm 2.
A regularized Hotelling’s T2 test with Bootstrap
|
Simulation 1: Impact of sample size when p < n and p/n → 1.
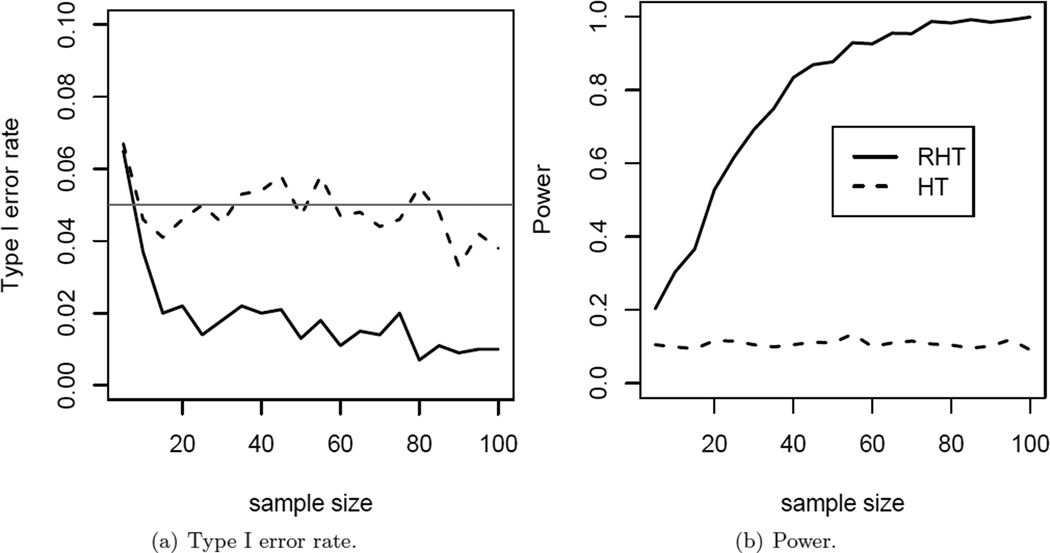
In this simulation, we compare the performance of the proposed RHT test with that of the HT test under p/n → 1 scenario. Specifically, for each n ∈ {5, 10, 15, …, 100}, we set p = n−2 and simulate X ~ N(μ, Σ), where μ = (0.5, …, 0.5)T, σii = 1 and σij = 0.2 (i ≠ j). The type I error rate and power of the two tests are calculated based on 1000 simulations. The results are illustrated in Figure 2. HT test controls the type I error rate properly, while the proposed RHT test tends to be slightly conservative. When power is considered, HT test performs extremely poorly, which is consistent with the theoretical result in Bai and Saranadasa (1996), while the power of RHT test increases to 1 with increasing sample size, consistent with our Theorem 2 in Section 2.1. This suggests that the regularization employed in RHT statistics is much preferred for handling data with p close to n.
Figure 2.
Impact of sample size when p = n − 1. (a): Type I error. The horizontal black line indicates the targeted significance level of 0.05. (b): Power at alternative μ = (0.5,‖,0.5)T.
Simulation 2: Impact of correlation and missingness when p < n.
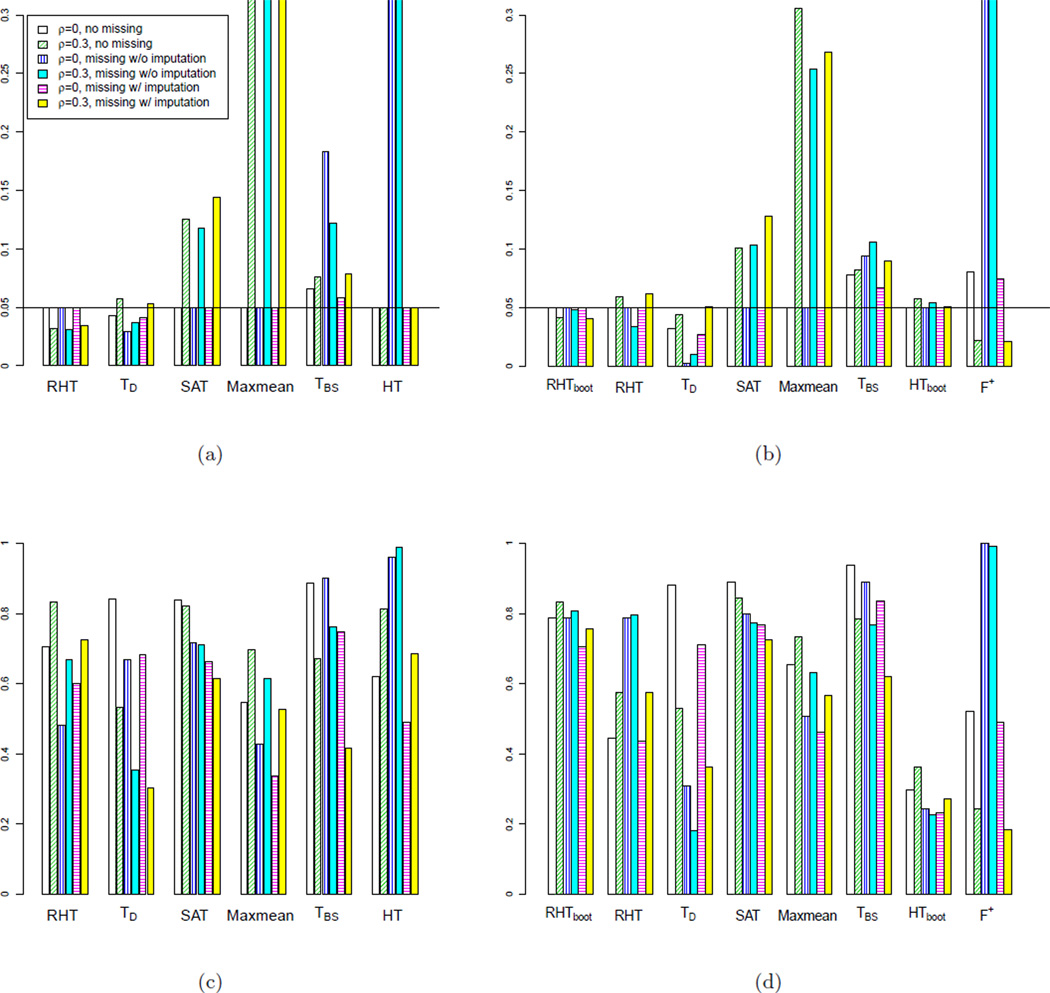
In this simulation, we consider a traditional setting with p < n (p = 20 and n = 50), and evaluate the impact of correlation and missingness on the performances of various tests. Specifically, we simulate X ~ N(μ, Σ), with μ = 0 under the null and {μ1 = … = μ10 = 0, μ11 = … = μ15 = 0.2, μ16 = … = μ20 = −0.2} under the alternative; σii = 1 and σij = ρ for i ≠ j. We consider two different correlation settings: completely independent (ρ = 0) and moderately pair-wise correlated (ρ = 0.3). For each ρ, we generate data in three ways: (1) without missingness; (2) with 20% missing completely at random (MCAR) (in our proteomics data, the missingness rate is about 25%); and (3) with 20% MCAR and apply a k-nearest neighbors (KNN) imputation method (Troyanskaya et al. 2001) to impute the missing values. This results in six different settings.
We simulate 1000 independent data sets for each setting, and evaluate the type I error rate and power of the competing tests at 0.05 p-value cutoff. The results are illustrated in Figure 3 (a) and (c). SAT and Maxmean could induce inflated type I error rates when correlations are present. TBS and HT tests fail to control type I error rates when missingness is not imputed. Only RHT and TD manage to control the type I error rates under all settings. In fact, with missingness, the asymptotic null distributions for HT, TBS and TD can substantially deviate from the corresponding empirical null distributions, resulting inaccurate significance level approximations. The deviation can depend on the pattern and extent of missing data. Concerning power, when correlations are present, RHT has better power than TD. In addition, for both ρ = 0 and ρ = 0.3, the presence of missingness decreases the power of both RHT and TD. On the other hand, regardless of missing data, the presence of correlation slightly increases the power of RHT. This suggests that making use of correlations among variables in a proper way may enhance the power of pathway analyses.
Figure 3.
Comparing type I error rates (a),(b) and power (c),(d) of competing tests at 0.05 p-value cutoff. (a) and (c) are for Simulation 2: p = 20, n = 50. (b) and (d) are for Simulation 3: p = 20, n = 10. In both Simulation 2 and 3, the correlation matrix Σ has diagonal elements: σii = 1, and off diagonal elements: σij = ρ (i, j = 1,…,p).
Simulation 3: Impact of correlation and missingness when p > n.
In this simulation, we set p = 20 and n = 10 to mimic the dimensionality of our real application. We simulate the data in the same way as described in Simulation 2. In addition, here, we evaluate three additional tests, F+, RHTBootstrap and HTBootstrap. Note the parametric HT test is ill-positioned when p > n and is not compared. The results are shown in Figure 3 (b) and (d). RHT, RHTBootstrap, HTBootstrap and TD evidently control type I error rates. Among those, RHTBootstrap is the most powerful under all settings. The presence of missingness dramatically decreases the power of TD, but has much less effect on the power of RHT and RHTBootstrap.
In both Simulation 2 and 3, the performances of RHT test (or RHTBootstrap) with and without imputation are similar. Imputation helps HT and F+ tests to control type I error rate when there is missingness in the data, and imputation increases the power of TD test. However, even with imputation, when there is correlation, the performance of RHT test when p < n or RHTBootstrap when p > n remains the best.
In Supplementary Information, we compare the performance of RHT test with and without bootstrap on simulated examples, and demonstrate that the former has superior power than the latter when γ = p/n is large. Thus, to avoid confusion, for p > n scenarios, we will only consider RHTBootstrap statistic in the following simulations.
Simulation 4: Impact of complicated correlation structure.
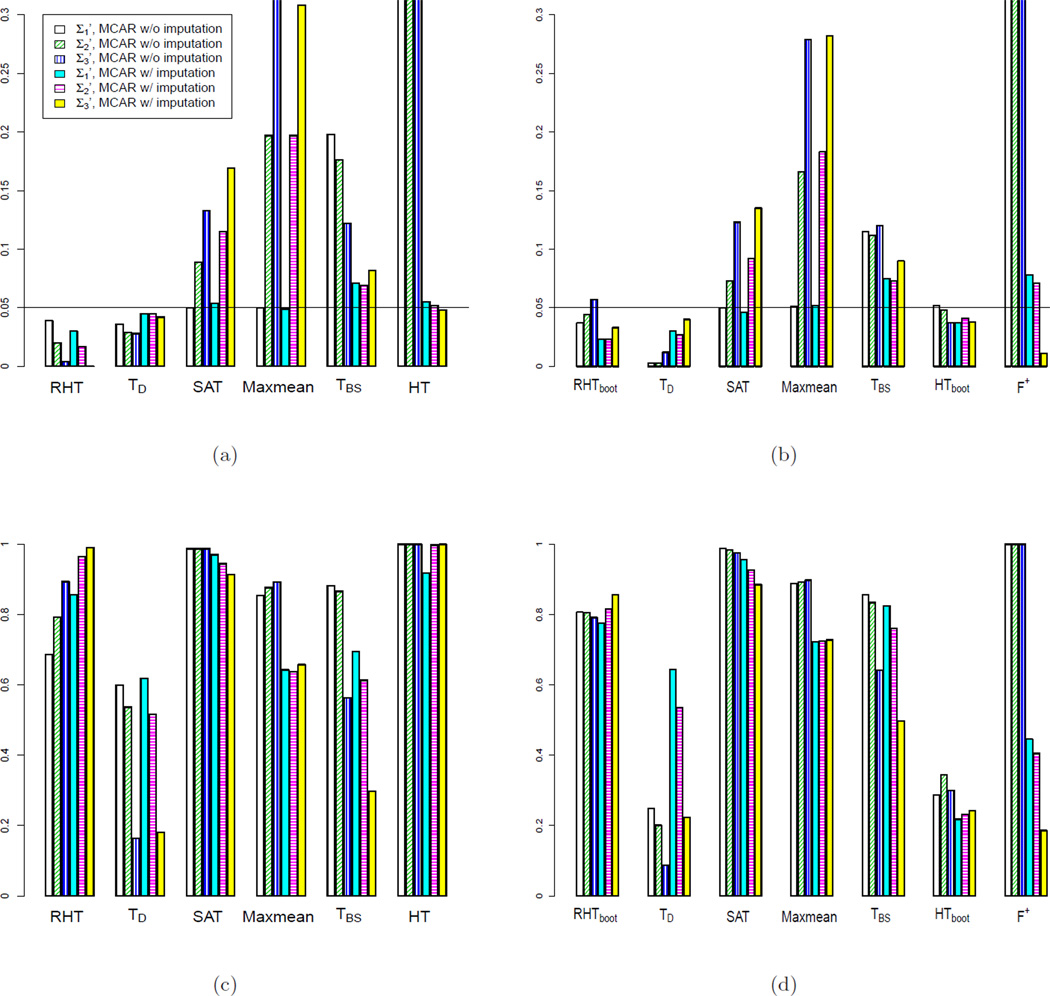
We also perform simulations using more complicated correlation structures. Specifically, is defined as a diagonal matrix with . For , the off diagonal elements are set to be , where ; and the diagonal elements are set to be the same as . In addition, we define with off diagonal elements and the same diagonal elements as .
We set p = 20 and consider two different sample sizes n = 50 and 10. We generate missingness completely at random as in Simulation 2 and 3, and impute the missing values using KNN imputation. The results, which are shown in Figure 4, lead to the same conclusion that RHT and RHTBootstrap perform the best among the competing tests in terms of type I error rate and power. This suggests that the proposed test works well even when the variables in the pathway have somewhat different variances. Note that under complex correlation patterns, correlation does not necessarily increase type I error rates. Ignoring correlation structure may also result in overall reduction in both type I error rate and power.
Figure 4.
Comparing type I error rates (a),(b) and power (c),(d) of the competing tests at 0.05 p-value cutoff, with complex correlation patterns. For (a) and (c), p = 20, n = 50. For (b) and (d), p = 20, n = 10. For the three types of correlations, . For . For , and . For .
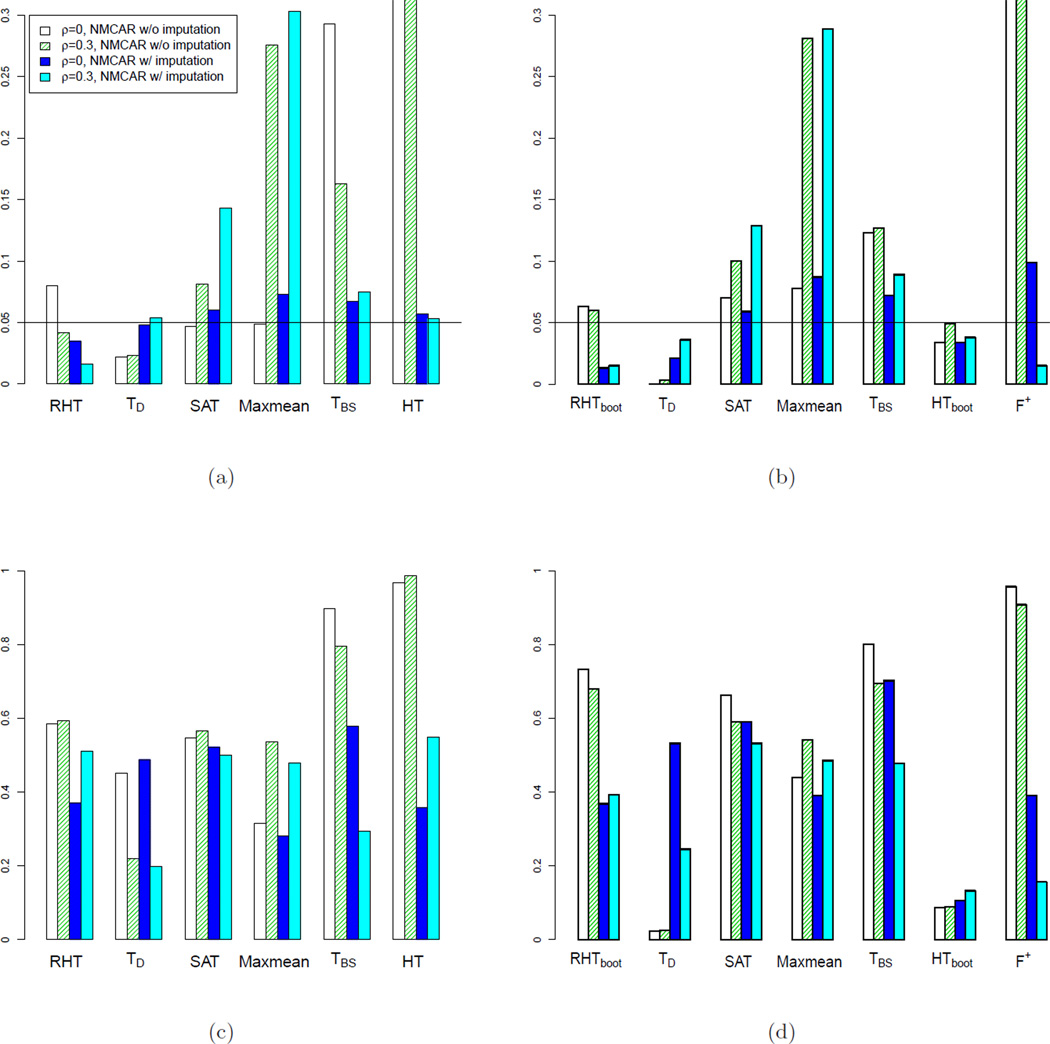
Simulation 5: Impact of missing not completely at random and imputation.
We further simulate data with not-missing-completely-at-random (not-MCAR) and compare competing tests without and with imputation. The missing probabilities, which range from 20% to 40%, are simulated to be positively correlated with the absolute values of the ratios, such that extreme ratios have higher probabilities to be missing. Figure 5 shows the results of competing tests on not-MCAR data with possible correlations for p < n (p = 20, n = 50) and p > n (p = 20, n = 10). With not-MCAR data, SAT, Maxmean, TBS, HT and F+ tests still could not control type I error rates. KNN-imputation could potentially further increase the type I error rates for SAT, Maxmean, HT and F+. On the other hand, due to the conservative design of RHT test, even when data are not-MCAR, the proposed RHTBootstrap test could still control the type I error rates within a reasonable range, and it is substantially more powerful than TD or HTBootstrap tests.
Figure 5.
Comparing type I error rates (a),(b) and power (c),(d) of competing tests at 0.05 p-value cutoff, with not-missing-completely-at-random (NMCAR). For (a) and (c), p = 20, n = 50. For (b) and (d), p = 20, n = 10. In both simulations, the correlation matrix Σ has diagonal elements: σii = 1, and off diagonal elements: σij = ρ (i, j = 1,…,p).
In summary, SAT test could not control type I error rate when correlation is present. Maxmean behaves similarly as or worse than SAT. HT and HTBootstrap have very poor performance when p is close to or greater than n, due to the intrinsic limitation of HT statistics. The other few tests, TD, TBS, and F+ are all parametric tests and are based on asymptotic theories derived under non-missing settings. However, when missingness is present, the distribution of these test statistics vary a lot with the degree and pattern of missingness. Moreover, the calculation of TD, TBS, and F+ statistics involves the estimation of S2, which could be highly non-robust when missing data is present. Furthermore, the sample size in our problem is relatively small. Thus, the asymptotic distributional approximations to these parametric tests do not hold well, and then, not surprisingly, their performances are less competitive. In contrast, for RHT, we employ a resampling-based testing procedure, in which the pattern of missingness is explicitly accounted for, and the cut-off values are obtained empirically, as opposed to relying entirely on the asymptotic theory for the complete data scenario. Thus, RHT performs more favorably with MCAR data. We recommend using RHT test when p < n and RHTBootstrap for p > n. Also, the proposed resampling test strategy will not apply to TD, TBS, or F+. This is because these statistics are not invariant to Σ, while the resampling can approximate only the null distribution under Σ = I. In contrast, for RHT, by changing the regularization parameter λ, we are able to identify a resampling distribution that well approximates the tail of the true null distribution under the same regularization level, and hence properly control the type-I error rate of the test.
We also perform simulations for two-sample testing and get similar conclusions (see Supplementary Information).
4 APPLICATION
Postmenopausal hormones have been widely used in the United States and elsewhere, for the control of vasomotor and other menopausal symptoms. Following some years of observational epidemiologic study, the health benefits and risks of two widely used hormone therapy regimens were more formally tested during 1993–2005 in randomized controlled trials among more than 27,000 healthy U.S. postmenopausal women, as a part of the Women’s Health Initiative (WHI). The estrogen plus progestin regimen studied in a trial of 16,608 postmenopausal women with uterus stopped early in 2002 when health risks were judged to exceed benefits (Rossouw et al. 2002). The risks included elevations in breast cancer, stroke, coronary heart disease, and venous thromboembolism, while fracture reduction was a noteworthy benefit. The estrogen-alone trial among 10,739 women who were post-hysterectomy was stopped early in 2004 (Anderson et al. 2004), primarily because of a stroke elevation of similar magnitude to that seen for estrogen plus progestin. See Prentice and Anderson (2007) for further details. A nested case-control study, involving candidate blood biomarkers of inflammation, coagulation, and lipids, was carried out in an attempt to elucidate cardiovascular aspects of these findings, but failed to identify important mediators of the observed clinical effects (Kooperberg et al. 2007; Rossouw et al. 2008).
Proteomic discovery work was initiated soon thereafter. The application considered here is one component of this proteomic initiative. This component sought circulating proteins, and protein pathways, for which the concentrations changed following the initiation of hormone therapy. Specifically, this proteomic discovery project involved the comparison of serum protein concentrations one year after randomization to corresponding pre-randomization concentrations for 100 women who adhered to their assigned active regimens during the first year of hormone therapy trial participation. The research agenda for the overall initiative also involved proteomic case-control comparisons for coronary heart disease, stroke, and breast cancer using the same proteomic platform. Novel proteins, and protein pathways, that changed concentration following hormone therapy, and that were associated with the risk of study diseases, are being studied further as potential mediators of hormone therapy clinical effects. This ongoing research involves assessing the concentrations of proteins of interest in individual cases and controls in the hormone therapy trial cohorts. Some results from this research strategy have recently been reported (Prentice et al. 2010).
The 100 women in this proteomic study component included 50 who were randomly selected from among women assigned to active estrogen plus progestin and adhered (80% or more pills taken) to their assigned treatment during the first year following randomization, and a corresponding 50 assigned to active estrogen-alone. An Intact Protein Analysis System (IPAS) platform (Faca et al. 2006) was used in these studies. The 1-year and baseline serum specimens were labeled with either a heavy or a light acrylamide, and combined. Because the IPAS measurement process is rather time-consuming and expensive, serum samples were pooled to form 10 specimen pool pairs. Each pool is formed from an equal volume of serum from 10 women, resulting 5 pool pairs for estrogen plus progestin and 5 for estrogen-alone (Pitteri et al. 2009). Serum samples were obtained from fasting blood samples according to a standard protocol, and stored at −80 degree until needed for analysis. Baseline and 1-year pool pairs, from randomly selected sets of 10 women from the regimen-specific sets, were formed on the day needed for mass spectrometry analyses. Peptide concentration ratios were extracted as the ratio of areas under mass spectrum peaks separated by the mass difference between heavy and light acrylamide, and protein concentration ratios were estimated by reconstructing proteins from their peptide signatures. Missing data may arise if mass spectrum peaks are not clearly above background, or if quantified peptides do not identify the protein from which they derive with certainty.
The result of estimated protein concentration ratios can be displayed as a matrix Xp×n, where n = 10 is the number of pool pairs, and p = 369 is the total number of proteins having relative concentration ratios estimated, and the (i, j) element of the matrix is the log2 ratio of protein concentration at 1-year compared to baseline for the i-th protein in the j-th serum pool pair.
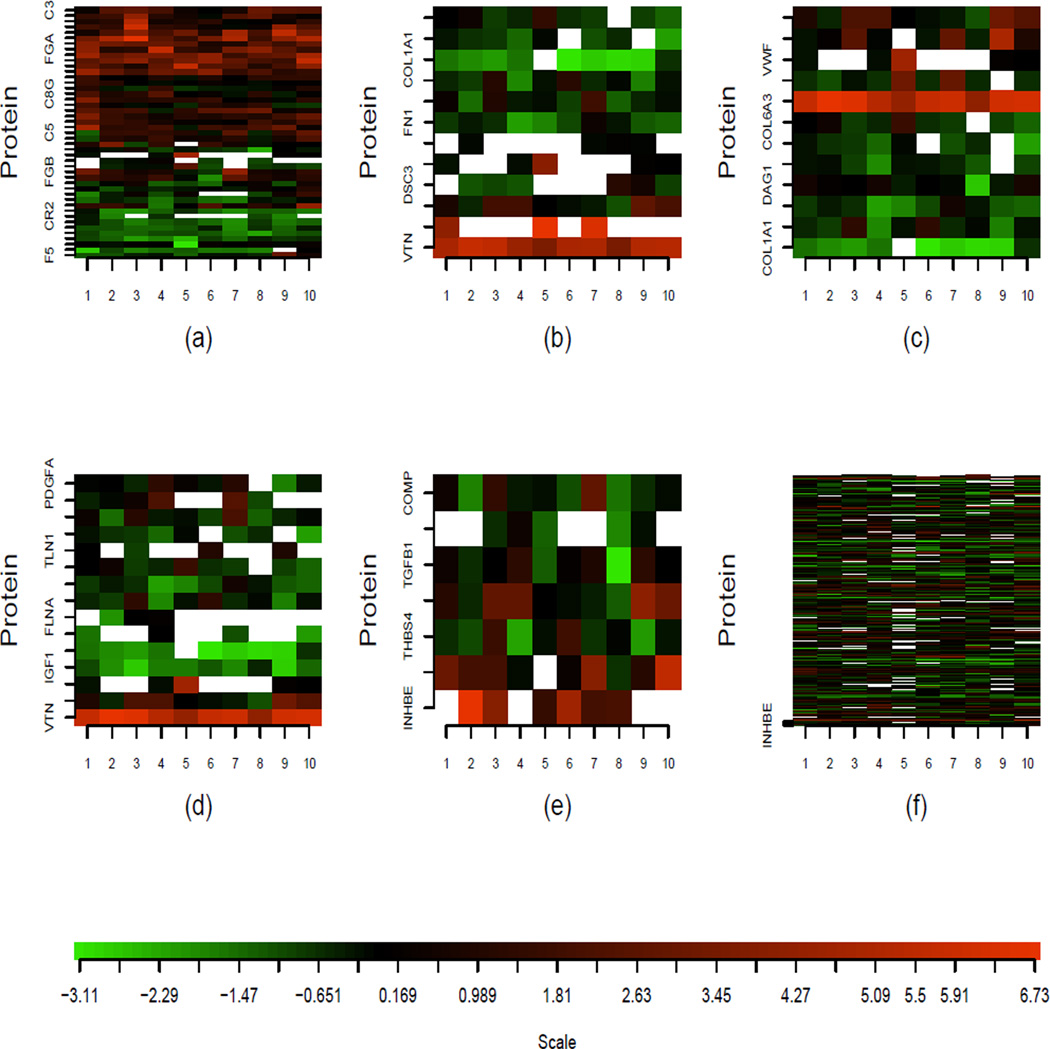
The probability of missingness for a given protein may depend on abundance level in the generating pools, on the protein sequence (e.g., acrylamide binds to cysteine residues, so only proteins containing such residues will have concentration ratio estimated) and protein mass. However, missingness rates for proteins quantified is not expected to depend on the value of the 1-year to baseline concentration ratio; nor is it expected to depend on the concentration ratios for other quantified proteins. Hence, a missing completely at random assumption seems plausible in this context. We note that the MCAR assumption may not be satisfied for some proteomics studies, especially when protein abundance level instead of ratio is measured for each protein. It would be beneficial to check the MCAR assumption before applying the proposed method. For this application, Figure S5 in Supplementary Information shows the boxplots of pooled absolute protein log2 ratios stratified by # missing observations, for the 369 quantified proteins. We do not observe a clear trend between the absolute log 2 ratios and missingness rate. Figure 6(f) also provides a visualization of the missing patterns of a few example pathways and of all the proteins in the data set (roughly 25% of the data are missing).
Figure 6.
Heatmaps of protein log concentration ratios from the five significant pathways and from all proteins in the data set. Each row represents the ratios from a protein and each column represents one IPAS experiment. Missing values are displayed in white. Positive, zero and negative log concentration ratios are shown in red, black, and green. (a)–(e) are the heatmaps of complement and coagulation cascades, cell communication, ECM receptor interaction, focal adhesion and TGF-beta signaling pathways, respectively. (f) is the heatmap of all proteins in the data.
We apply the proposed RHT test to 18 KEGG human disease pathways (Kanehisa 2002) having 5 or more proteins quantified in our dataset. Our goal is to detect whether any of the pathways show concerted differential abundance between baseline and 1-year. Before we perform the test of μ = 0 for the log ratios, we first scale the log ratios for each protein by its estimated standard deviation plus a constant (= 0.17, which is the 10% quantile of all estimated standard deviations). For pathways having fewer than 9 proteins, we use RHT statistics; while for pathways having 9 or more proteins, we use RHTBootstrap statistics with . P-values were calculated based on 10,000 resamplings. Considering that pathways might have overlapping proteins and are not completely independent, Bonferroni correction for controlling 5% family-wise error rate (FWER) might be too conservative. Thus we choose a relatively loose FWER, 10%, which corresponds to a stringent 1% false discovery rate (FDR) (Benjamini and Hochberg 1995). At this cutoff, there are five significant pathways: complement and coagulation cascades, cell to cell communication, extracellular matrix (ECM) receptor interaction, focal adhesion and TGF-beta signaling pathways (see Table 1 for details). Figure 6(a)–(e) display the heatmaps of these five pathways. For comparison, the heatmap of all proteins in the data is shown in Figure 6(f). From the heatmaps we can see that, the five pathways we identified each has multiple proteins showing consistent patterns of red or green across experiments, corresponding to evidence of increased or decreased concentration after randomization. Specifically, by testing each protein in the selected pathway individually, we find that about 28.6%–60.0% proteins in each selected pathway have nominal p-value<0.05, suggesting the significant pathways are not wholly due to one or two proteins.
Table 1.
Significant KEGG pathways at FDR 1% and FWER of 10% (p-value cutoff = 0.1/18= 0.0056 by Bonferroni correction), identified from a postmenopausal hormone therapy proteomic study of the Women Health Initiative. P-values were calculated based on 10,000 resamplings.
| Pathway names | # non-missing protein |
P-value of RHT |
P-value of SAT |
P-value of HT/GHT |
P-value of TD |
P-value of TBS |
% significant proteins* |
|---|---|---|---|---|---|---|---|
| Complement and coagulation cascades | 45 | 0 | 0 | 0 | 0.002 | 0 | 22.2 |
| Cell communication | 12 | 0 | 0.001 | 0 | 0 | 0 | 16.7 |
| Extracellular matrix receptor interaction | 12 | 0 | 0 | 0 | 0 | 0 | 16.7 |
| Focal adhesion | 15 | 0 | 0 | 0 | 0 | 0 | 20.0 |
| TGF-beta signaling | 7 | 0.005 | 0.003 | 0.057 | 0.072 | 0 | 0.0 |
% of proteins with significant nominal p-value at 0.10 FWER (protein p-value cutoff of 0.10/369).
Related to this, one can ask whether these pathways may have otherwise emerged as hormone therapy-related by virtue of several individual proteins having concentration changes that meet multiple testing criteria. This is likely the case for the complement and coagulation cascade pathway, which includes multiple proteins (22.2%) showing strong evidence of differential abundance, i.e., with nominal protein p-value significant at 0.10 FWER (p-value below 0.1/369). In comparison, 11.4% of the proteins in the data passed this nominal p-value cutoff. The next three pathways, extracellular receptor, cell communication and focal adhesion pathways, which are substantially overlapping with 8 common proteins, each includes a higher than random percentage of proteins with nominal p-value significant at FWER 10%. These three pathways are closely related proceses with possible co-functioning (see Supplementary Figure S6 from KEGG website). On the other hand, besides the 8 common proteins, each pathway also has some unique proteins with suggestive significant p-values. For example, the focal adhesion pathway has the protein IGF1 with nominal p-value of 4.4e-05. The pathway TGF-beta signaling does not include any proteins meeting the FWER criterion (0.1/369). In fact, this pathway appears to be a novel and important finding that derives from correlated effects on several pathway proteins. The TGF-beta signaling pathway is commonly altered in human cancers (Pasche 2001). The pathway signals through the TGF-beta serine or threonine kinase receptors and downstream intercellular proteins of the SMAD transcription factor family to inhibit cell proliferation and induce apoptosis; the pathway also induces tumor progression via cell differentiation, migration, and adhesion. Much of the significance of the TGF-beta pathway derives (Figure 6(e)) from deviators in the beta E chain (INHBE) or the beta C chain (INHBC) of inhibin. Inhibins inhibit follicle stimulating hormone secretion; and inhibin secretion is enhanced by insulin-like growth factor 1, which is also elevated by post menopausal hormone therapy (Pitteri et al. 2009). Though speculative at this time, the observed effects on TGF-beta superfamily signaling could help to provide a unifying theme toward understanding hormone therapy effects on breast cancer, and possibly on observed hormone therapy effects more generally. The list of proteins in each of the five significant pathways is given in Supplementary Information.
For comparison, we also applied SAT, HT/F+, TD and TBS tests to this data set. Table S1 in Supplementary Information shows the number of significant pathways at FWER of 0.05 and 0.10 by Bonferroni correction for all the five tests including RHT. We can see that SAT, HT/F+ and TBS tests each yields many ‘significant’ pathways. Since we have shown in simulations that those four tests often cannot control type I error rate under missingness and correlation, it is reasonable to suspect that many of the ‘significant’ pathways based on these tests are false positives. Among the 6 pathways identified by TD test at FWER of 0.10, four overlap with the results of RHT test. However, TD failed to identify the TGF-beta signaling pathway, and the other two pathways TD identified, cell adhesion molecules and regulation of actin cytoskeleton pathways, seem less interpretable.
5 PROOFS
In this section, we prove the two theorems using a series of Lemmas. The proofs of the Lemmas are then outlined in the subsections while more technical details are provided in Supplementary Information. However, due to space limitations, we omit the proofs of Proposition 1, 2 and Corollary 1, which are either straightforward extensions of literature results or rather similar to the proofs of the two theorems.
5.1 Proof of Theorem 1
Under the null, and is independent of Sn. Let , then Z ~ Np(0, Ip) and is independent of Sn. It follows . With Lemma 1 and 2, Theorem 1 follows immediately. The proofs of the following Lemmas are provided in sections 5.4–5.5.
Lemma 1 Under the same condition as Theorem 1, we have
| (18) |
Lemma 2 Under the same condition as Theorem 1, we have
| (19) |
| (20) |
5.2 Proof of Theorem 2
Let Z ~ N(0, Ip) and be independent of Sn. Under the alternative,
| (21) |
Let . Then (n − 1)Wn, which is independent of Z, has a Wishart distribution with dimension p and degrees of freedom n − 1. Further define
Consider the eigen-decomposition of Λn = QTLQ, where Q is an orthogonal matrix and L is a diagonal matrix with positive diagonal elements ζn, 1 ≥ ζn, 2 ≥ … ≥ ζn, p.
Lemma 3 Under assumptions A1–A4, {ζn, i} are bounded away from both zero and infinity asymptotically: ∃ and satisfying
| (22) |
| (23) |
Based on Lemma 3, we have
| (24) |
since as n → ∞. Next, conditionally on Wn, . Then according to (23), it is easy to see . It follows that
| (25) |
Then, using (21), we have the expansion
| (26) |
The first term on the right hand side of (26) converges in distribution to N(0, 1) by Theorem 1, the second term converges to 0 in probability by (25), and the third term diverges to infinity in probability by (24). Therefore, Theorem 2 follows.
5.3 Proof of Lemma 3
We first prove Lemma 3, which will then be used to prove Lemma 1. Denote the eigenvalues of Wn as ηn,1 ≥ ηn,2 ≥ ⋯ ≥ ηn,p. First,
It follows that ζn,p ≥ 1/(ηn,1 + λ/τp,p). In addition, since {τj,p} are bounded away from zero and infinity, and as n → ∞ (Geman 1980), we shall have a.s. for some . On the other hand,
It follows that a.s. for some .
5.4 Proof of Lemma 1
Recall that . Decompose Λn as QTLQ, where Q is an orthogonal matrix and L is a diagonal matrix with positive diagonal elements ζn,1 ≥ ζn,2 ≥ … ≥ ζn,p. Then we have under the null, , where are i.i.d. χ2 random variables with 1 degree of freedom, and Z̃ = QZ.
Let Tp,i = ζn,i(wn,i−1), , and . It is easy to see that . Conditional on Θ = {ζn,i}n,i, we have , and . It follows that
Here E(x; a, b) denotes the expected value of x with respect to condition a and b. The last inequality holds as {ζn,i}i are bounded away from both zero and infinity asymptotically (Lemma 3). Then, according to Lindeberg-Feller theorem (Lindeberg 1922; Feller 1971), we have . It follows , based on the following:
Lemma 4 are random variables. gn(xn, yn) is a real function of xn and yn. If gn|yn → D Z, where Z is independent of {yn}, then we have gn → D Z.
The proof of Lemma 4 is straightforward and is provided in the Supplementary Information.
5.5 Proof of Lemma 2
Proof of Lemma 2 is based on the ideas developed in (Ledoit and Péché 2010).
Proof of (19): Denote the resolvent of Sn by Rn(z) = (Sn−zIp)−1. Note that, where . Hence, for any j ∈ {1, …, n},
| (27) |
where . Observe that Yj and are independent for all z ∈ ℂ.
Post-multiplying both sides of the identity (Sn − zIp) + zIp = Sn by Rn(z), we have
| (28) |
Now, letting z = −λ (for which Rn(z) is well defined). Taking trace on both sides of (28), dividing both sides by p, and using (27), we have
| (29) |
for appropriate residual terms and . Also, define
| (30) |
We claim that (proved in Supplementary Information)
| (31) |
Define . Then, from (29) and (30) we can express
The second equality is using (7) and the last equality is by (31) and assumption A2.
Proof of (20): Post-multiplying the identity (28) (with z = −λ) by ΣpRn(−λ), taking trace, dividing by p, and using (27), we have
| (32) |
for appropriate residuals and . Define
| (33) |
We claim that (proved in Supplementary Information)
| (34) |
It then follows from (29), (31), (32), (34) and (8) that
6 SUMMARY
Pathway analysis is a useful tool for genomics or proteomics array studies. By combining information of multiple genes or proteins from the same functional group, pathway analysis may achieve better power for detecting meaningful biological signals and the result may augment the interpretation provided by univariate analyses.
Many methods have been proposed for pathway (or gene-set) analysis in the literature, mostly for microarray gene expression studies and for genome-wide association studies. Proteomics, as an emerging technology, has distinctive features compared to other ‘omics’ studies. Proteomics data may have complicated correlation structure, substantial missingness and small sample size. Furthermore, depending on the proteomic platform, the proteomic data may consist of concentration ratios rather than abundant concentrations. These factors limit the suitability of existing statistical methods.
When considering multiple proteins together, some multivariate tests can be used to handle correlation. However, when the sample size is small, and is close to or less than the number of proteins considered, these tests experience difficulty. Some novel tests have been proposed for the p ≥ n scenarios, but they rely on asymptotic theory and evidently require a relatively large sample size for good performance. In addition, missing data further complicates the use of these tests. In this work, we propose a new RHT test, in which we design the test statistics using regularization techniques, and propose a non-parametric testing procedure to conservatively control the type I error rate. The regularization parameter is adaptively selected based on the data, thereby enhancing the robustness of the proposed method.
Another contribution of the paper is to establish the asymptotic theory for the proposed RHT statistics under a diverging dimension regime, such that p/n → γ ∈ (0,∞). These results provide useful insights on the properties of the test statistics, and suggest that RHT has intrinsic advantages over the original HT in terms of power when p is close to or greater than n. In the extensive simulation studies, we further demonstrate that RHT has favorable performance compared to existing methods, especially when missing data and/or correlations are present.
Our nonparametric testing procedure based on resampling makes a missing completely at random assumption. MCAR is a reasonable working assumption for this application. However, the pattern of missingness can be due to many complicated factors in mass spectrometry experiments, and MCAR may not apply for mass spectrometry based data more generally. Further developments to relax the missing data assumption will be useful and additional research is underway. On the other hand, even under the MCAR assumption, the missing data raises challenges for statistical analysis. Particularly, for test statistics in complicated forms (e.g. TD, TBS and F+ tests), their distributions vary substantially according to the degrees and the patterns of missingness, and thus tend to be less robust in application. On the other hand, the simple quadratic form of the proposed RHT makes its performance less affected by various missing data patterns. In addition, we develop a resampling-based testing procedure for RHT, in which the pattern of missingness is explicitly accounted for, and the cut-off values are obtained empirically, as opposed to relying entirely on the asymptotic theory for the complete data scenario.
We apply the RHT test to a hormone therapy proteomic study and identify five pathways whose protein serum concentrations changed after one year of hormone therapy treatment. These findings may provide additional insight for understanding the biological processes mediating the clinical effects of hormone therapy treatment (Pitteri et al. 2009).
The R package RHT is available from the authors upon request. It will be made available through CRAN shortly.
Supplementary Material
Acknowledgments
This work was partially supported by grant CA53996 from the National Cancer Institute, grant R01GM082802 from the National Institute of General Medical Sciences, and grant DMS1106690 from the National Science Foundation. The proteomics data were generated in the laboratories of Drs. Sam Hanash and Martin McIntosh with support from Women’s Health Initiative “core” funds via contract N01-WH22110 from the National Heart, Lung and Blood Institute. The authors would like to thank the editor, the associate editor and the anonymous reviewers for many helpful and insightful suggestions. The authors would also like to thank Women’s Health Initiative investigators for permission to use the hormone therapy proteomics data in the manuscript. Moreover, the authors are grateful to Drs. Michael Perlman and Li Hsu for their insightful suggestions on the manuscript, and Drs. Sharon J. Pitteri and Carolyn M. Hutter for helpful discussions and suggestions on the interpretation of the biological results.
References
- Ackermann M, Strimmer M. A general modular framework for gene set enrichment analysis. BMC Bioinformatics. 2009;10:47. doi: 10.1186/1471-2105-10-47. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Alon U, Barkai N, Notterman DA, Gish K, Ybarra S, Mack D, Levine AJ. Broad patterns of gene expression revealed by clustering analysis of tumor and normal colon tissues probed by oligonucleotide arrays. Proc. Nat. Acad. Sci. 1999;96(12):6745–6750. doi: 10.1073/pnas.96.12.6745. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Anderson GL, Limacher M, Assaf AR, et al. the Women’s Health Initiative Steering Committee. Effects of conjugated equine estrogen in postmenopausal women with hysterectomy: The women’s health initiative randomized controlled trial. JAMA. 2004;291(14):1701–1712. doi: 10.1001/jama.291.14.1701. [DOI] [PubMed] [Google Scholar]
- Ashburner M, Ball CA, Blake JA, Botstein D, Butler H, et al. Gene ontology: Tool for the unification of biology. the gene ontology consortium. Nature Genetics. 2000;25:25–29. doi: 10.1038/75556. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bai Z, Saranadasa H. Effect of high dimension: by an example of a two sample problem. Statistica Sinica. 1996;6:311–329. [Google Scholar]
- Bai ZD, Silverstein JW. Clt for linear spectral statistics of large-dimensional sample covariance matrices. Ann. Probab. 2004;32(1A):553–605. [Google Scholar]
- Benjamini Y, Hochberg Y. Controlling the false discovery rate: a practical and powerful approach to multiple testing. JRSSB. 1995;57(1):289–300. [Google Scholar]
- Chen LS, Hutter CM, Potter JD, Liu Y, Prentice RL, Peters U, Hsu L. Insights into colon cancer etiology via a regularized approach to gene set analysis of gwas data. The American Journal of Human Genetics. 2010;86:860–871. doi: 10.1016/j.ajhg.2010.04.014. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chen SX, Qing YL. A two sample test for high dimensional data with application to gene-set testing. 2010 In press. [Google Scholar]
- Dempster AP. A high dimensional two sample significance test. Ann. Math. Statist. 1958;29:995–1010. [Google Scholar]
- Dempster AP. A significance test for the separation of two highly multivariate small samples. Biometrics. 1960;16:41–50. [Google Scholar]
- Dinu I, Potter JD, Mueller T, Liu Q, Adewale AJ, et al. Improving gene set analysis of microarray data by SAM-GS. BMC Bioinformatics. 2007;8:242. doi: 10.1186/1471-2105-8-242. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Eckel-passow JE, Oberg AL, Therneau TM. An insight into high-resolution mass-spectrometry data. Biostatistics. 2009;10(3):481–500. doi: 10.1093/biostatistics/kxp006. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Efron B, Tibshirani R. On testing the significance of sets of genes. Annals of Applied Statistics. 2007;1:107–129. [Google Scholar]
- Faca V, Coram M, Phanstiel D, Glukhova V, Zhang Q, Fitzgibbon M, McIntosh M, Hanash S. Quantitative analysis of acrylamide labeled serum proteins by LC-MS/MS. J. Proteome Res. 2006;5(8):2009–2018. doi: 10.1021/pr060102+. [DOI] [PubMed] [Google Scholar]
- Feller W. An Introduction to Probability Theory and Its Applications. 3rd ed. Volume 2. New York: Wiley; 1971. [Google Scholar]
- Fujikoshi Y, Himeno T, Wakaki H. Asymptotic results of a high dimensional manova test and power comparison when the dimension is large compared to the sample size. J. Japanese Statist. Soc. 2004;34:19–26. [Google Scholar]
- Geman S. A limit theorem for the norm of random matrices. Ann. Probab. 1980;8:252–261. [Google Scholar]
- Kanehisa M. the KEGG database. Novartis Found Symp. 2002;247:91–101. [PubMed] [Google Scholar]
- Karoui N. Tracy-widom limit for the largest eigenvalue of a large class of complex sample covariance matrices. Annals of Probability. 2007;35(2):663–714. [Google Scholar]
- Kooperberg C, Cushman M, Hsia J, Robinson JG, Aragaki AK, et al. Can biomarkers identify women at increased stroke risk? the women’s health initiative hormone trials. PLoS Clin Trials. 2007;2(6):e28. doi: 10.1371/journal.pctr.0020028. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ledoit O, Péché S. Eigenvectors of some large sample covariance matrix ensembles. Probability Theory and Related Fields. 2010 [Google Scholar]
- Ledoit O, Wolf M. A well-conditioned estimator for large-dimensional covariance matrices. J. Multivariate Analysis. 2004;99:365–411. [Google Scholar]
- Liang J, Tang M. Generalize F-tests for the multivariate normal mean. Comp. Statist. and Data Analysis. 2009;53:1177–1190. [Google Scholar]
- Lin S, Perlman M. A monte carlo comparison of four estimators of a covariance matrix. In: Krishnaiah PR, editor. Multivariate analysis–VI: Proceedings of the Sixth International Symposium on Multivariate Analysis. 1985. pp. 411–429. [Google Scholar]
- Lindeberg JW. Eine neue herleitung des exponential-gesetzes in der wahrscheinlichkeitsrechnung. Math Zeit. 1922;15:211–235. [Google Scholar]
- Little RJA, Rubin DB. Statistical Analysis with Missing Data. New York: Wiley; 1987. [Google Scholar]
- Lu Y, Liu P, Xiao P, Deng H. Hotelling’s t2 multivariate profiling for detecting differential expression in microarrays. Bioinformatics. 2005;21(14):3105–13. doi: 10.1093/bioinformatics/bti496. [DOI] [PubMed] [Google Scholar]
- Marcenko V, Pastur L. Distribution of eigenvalues in certain sets of random matrices. Mat. Sb. (N.S.) 1967;72(114):507–536. [Google Scholar]
- Mootha VK, Lindgren CM, Eriksson KF, Subramanian A, Sihag S, et al. PGC-1-responsive genes involved in oxidative phosphorylation are coordinately downregulated in human diabetes. Nat. Genet. 2003;34:267–273. doi: 10.1038/ng1180. [DOI] [PubMed] [Google Scholar]
- Pan GM, Zhou W. Central limit theorem for signal-to-interference ratio of reduced rank linear receiver. Annals of Applied Probability. 2008;18:1232–1270. [Google Scholar]
- Pasche B. Role of transforming growth factor beta in cancer. Journal of Cellular Physiology. 2001;186(2):153–168. doi: 10.1002/1097-4652(200002)186:2<153::AID-JCP1016>3.0.CO;2-J. [DOI] [PubMed] [Google Scholar]
- Pitteri SJ, Hanash SM, Aragaki A, Amon L, Chen L, et al. Postmenopausal estrogen and progestin effects on the serum proteome. Genome Medicine. 2009;1:121. doi: 10.1186/gm121. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Prentice R, Paczesny S, Aragaki A, Amon L, Chen L, Pitteri S, McIntosh M, Wang P, Buson B, Hsia J, Jackson R, Rossouw J, Manson J, Johnson K, Eaton C, Hanash S. Novel proteins associated with risk for coronary heart disease or stroke among postmenopausal women identified by in-depth plasma proteome profiling. Genome Med. 2010;2(7):48–60. doi: 10.1186/gm169. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Prentice RL, Anderson GL. The women’s health initiative: Lessons learned. Annu. Rev. Public Health. 2007;29:131–150. doi: 10.1146/annurev.publhealth.29.020907.090947. [DOI] [PubMed] [Google Scholar]
- Rossouw JE, Anderson GL, Prentice RL, et al. the Writing Group for the Women’s Health Initiative Investigators. Risks and benefits of estrogen plus progestin in healthy post-menopausal women: principal results from the women’s health initiative randomized controlled trial. JAMA. 2002;288(3):321–333. doi: 10.1001/jama.288.3.321. [DOI] [PubMed] [Google Scholar]
- Rossouw JE, Cushman M, Greenland P, Lloyd-Jones DM, Bray P, et al. Inflammatory, lipid, thrombotic, and genetic markers of coronary heart disease risk in the womens health initiative trials of hormone therapy. Arch Intern Med. 2008;168(20):2245–2253. doi: 10.1001/archinte.168.20.2245. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Schafer J, Strimmer K. A shrinkage approach to large-scale covariance matrix estimation and implications for functional genomics. Statistical Applications in Genetics and Molecular Biology. 2007;4(1) doi: 10.2202/1544-6115.1175. [DOI] [PubMed] [Google Scholar]
- Schott J. Some high-dimensional tests for a one-way MANOVA. J. Multivariate Analysis. 2007;98:1825–1839. [Google Scholar]
- Shojaie A, Michailidis G. Analysis of gene sets based on the underlying regulatory network. Journal of Computational Biology. 2009;16(3):407–426. doi: 10.1089/cmb.2008.0081. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Srivastava M, Du M. A test for the mean vector with fewer observations than the dimension. J. Multivariate Analysis. 2008;99:386–402. [Google Scholar]
- Srivastava MS. Multivariate theory for analyzing high dimensional data. Journal of the Japan Statistical Society. 2007:53–86. [Google Scholar]
- Subramanian A, Tamayo P, Mootha VK, Mukherjee S, Ebert BL, et al. Gene set enrichment analysis: A knowledge-based approach for interpreting genome-wide expression profiles. Proc. Natl. Acad. Sci. USA. 2005;102:15545–15505. doi: 10.1073/pnas.0506580102. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tian L, Greenberg SA, Kong SW, Altschuler J, Kohane IS, Park PJ. Discovering statistically significant pathways in expression profiling studies. Proc. Natl. Acad. Sci. USA. 2005;102:13544–13549. doi: 10.1073/pnas.0506577102. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Troyanskaya O, Cantor M, Sherlock G, Brown P, Hastie T, Tibshirani R, Botstein D, Altman RB. Missing value estimation methods for dna microarrays. Bioinformatics. 2001;17(6):520–525. doi: 10.1093/bioinformatics/17.6.520. [DOI] [PubMed] [Google Scholar]
- Wang K, Li M, Bucan M. Pathway-based approaches for analysis of genomewide association studies. The American Journal of Human Genetics. 2007;81(6):1278–1283. doi: 10.1086/522374. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wu M, Zhang L, Wang Z, Christiani D, Lin X. Sparse linear discriminant analysis for simultaneous testing for the significance of a gene set/pathway and gene selection. Bioinformatics. 2009;25(9):1145–1151. doi: 10.1093/bioinformatics/btp019. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Yates PD, Reimers MA. Rcmat: a regularized covariance matrix approach to testing gene sets. BMC Bioinformatics. 2009;10:300. doi: 10.1186/1471-2105-10-300. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.