Non-transcriptional regulatory processes shape transcriptional network dynamics

Preface

Information about the extra- or intracellular environment is often captured as biochemical signals propagating through regulatory networks. These signals eventually drive phenotypic changes, typically by altering gene expression programs in the cell. Reconstruction of transcriptional regulatory networks has given a compelling picture of bacterial physiology, but transcriptional network maps alone often fail to describe phenotypes. In many cases, the dynamical performance of transcriptional regulatory networks depends on post-transcriptional or post-translational regulation and pleiotropic effects. Cellular response dynamics are ultimately determined by interactions between transcriptional and non-transcriptional networks with dramatic implications for physiology and evolution. Here, we provide an overview of non-transcriptional interactions that can affect the performance of natural and synthetic bacterial regulatory networks.

Introduction

Regulatory networks determine how cells adapt to the extra- or intracellular environment. In a typical network, a sensor detects a physical or chemical stimulus and transmits that information into the network as a biochemical signal. Networks are composed of a series of interconnected nodes, or signal-processing molecules (Figure 1A). Each node receives an input signal from an upstream node and sends an output signal to a downstream node in response.

Figure 1.

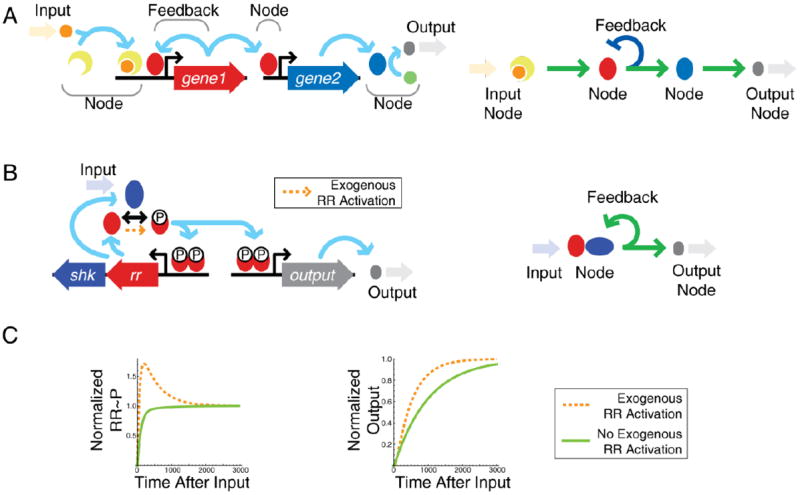
Information flow in signaling networks can strongly depend on non-transcriptional details with important physiological consequences. (A). Illustration of components in a transcriptional network. Input signals transfer information via nodes to create a physiological output. Right panel – transcriptional network diagram corresponding to detailed network on the left. C. A typical two-component system gene circuit is positively autoregulated by phosphorylated response regulator (RR). Right panel – simplified transcriptional network diagram corresponding to detailed network on the left. C. The system can exhibit feedback-induced overshoot (surge) kinetics if there is a small amount of regulator phosphorylation from an exogenous source (orange arrow and dashed line) in addition to sensor phosphorylation. In the absence of exogenous phosphorylation, induction is monotonic (solid green line). Overshoot of RR phosphorylation speeds induction of downstream genes (Normalized Output).

Signals often flow through hierarchically structured transcriptional networks where each node is a transcription factor^{1, 2},. The final output of the network is a set of induced or repressed genes that determine the phenotype of the cell in response to information flowing through the network. Within these networks are many smaller modules with some overrepresented structural motifs such as feedback or feedforward loops that may carry specific physiological functions^3,4. Despite thorough studies on the properties of transcriptional regulatory motifs^5-8, connectivity maps of transcriptional networks alone are often insufficient to explain the dynamical response of a cell to a given stimulus. A wide range of non-transcriptional interactions—post-transcriptional, post-translational, and pleiotropic processes—significantly affect the functionality of transcriptional networks. Indeed, non-transcriptional signal processing can result in a complex network diagram even when only one or a handful of genes are involved. Only by viewing transcriptional networks along with the mechanistic details of non-transcriptional processes can we arrive at a complete understanding of cellular regulation.

Non-transcriptional processes like phosphorylation, methylation, regulated protein/mRNA degradation and sequestration can have unexpected consequences in regulatory networks. Consider a bacterial two-component system (Figure 1B). A bifunctional sensor with both kinase and phosphatase activity senses an environmental stimulus and modulates the fraction of activated response regulator, which in turn modulates transcription of a downstream regulon⁹. The transcriptional network diagram of a typical two-component system is simple (Figure 1B, right panel): the sensor and response regulator genes are expressed from a positively autoregulated operon¹⁰. However, an apparently minor non-transcriptional detail—whether the response regulator undergoes a low level of non-cognate sensor kinase-mediated phosphorylation—can drastically alter the effect of the feedback on the dynamic response (Figure 1C)¹¹. Such non-cognate phosphorylation can come either from crosstalk with other sensor kinases or from phosphotransfer from small molecules. This effect constitutes a small fraction of the total phosphorylation flux when the system is activated, and is buffered by sensor phosphatase activity against activating the system in the absence of signal input¹¹. Yet this slight difference changes the dynamic behavior of the system in an important way. With the interaction, phosphorylated response regulator levels overshoot and settle to a steady state after signal onset, unlike the monotonic response expected in the absence of the interaction (Figure 1C, left panel)¹¹. This dynamic is computationally predicted to arise from a negative feedback loop that emerges in the system¹¹ (see also Supplemental Box). Such overshoot kinetics can speed the induction time of downstream genes (Figure 1C, right panel) and has profound physiological consequences. In the Salmonella enterica, serovar Typhimurium PhoPQ signaling system, overshoot is necessary for virulence¹². Wild-type bacteria are virulent and kill mice within ten days. However, removing the overshoot with a feedback-disabling promoter modification decreases virulence such that Salmonella-injected mice survive indefinitely¹².

Deducing relationships between physiological function, dynamical response and underlying molecular mechanisms is key to generalizing the current handful of laboratory model systems to new, medically important, or unculturable bacterial species. Characterization of metabolic, protein-protein-interaction and gene regulatory networks has broadened our understanding of their underlying structures⁴. Nevertheless, true understanding of the regulatory properties of networks requires that we discover relationships between mechanistic details and dynamics. These relationships, known as evolutionary design principles^4,13, are formulated by conducting detailed measurements of dynamics, constructing synthetic gene networks, and using mathematical models. Defining the principles that underlie biological regulation will not only facilitate our interpretation of natural networks but will also improve our ability to engineer microorganisms to have robust synthetic behaviors with widespread medical and industrial importance. In this Review we describe the effects of non-transcriptional regulatory processes such as ultrasensitivity, implicit and interacting feedback loops, and spatiotemporal localization of molecules on transcriptional networks using examples from both natural and engineered bacterial systems.

The ultrasensitive genetic switch

The ability of a biochemical network to respond to an input signal can be characterized by its signal-response curve or transfer function (Box 1). For transcriptional regulatory networks such curves show how the expression of downstream genes change as a function of transcription factor concentration or activation signals. For transcription factors acting as monomers, the expected dependence resembles Michaelis-Menten kinetics: linear at low signal concentrations and saturated at high¹⁴. Multimeric transcription factors with cooperativity can produce sigmoidal response curves typically captured with Hill kinetics, but the effective cooperativity (i.e. the Hill coefficient) is restricted to a low integer number¹⁵ reflecting the number of subunits present in a complex¹⁶. On the other hand, post-translational signal-response curves are capable of attaining much higher effective cooperativities.

Box 1.

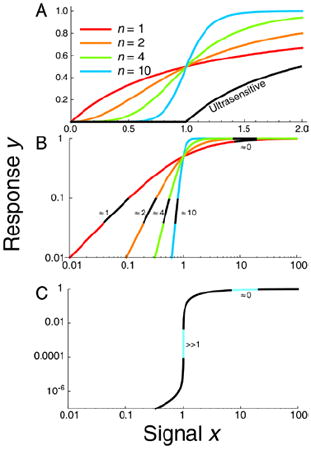
Signal-response systems are quantified with the mathematical approach of sensitivity analysis. The sensitivity is typically quantified as the derivative, or slope, of the curve on a log-log scale. With nth order Hill kinetics, the sensitivity decreases from the value of the Hill coefficient n at small signal to zero near saturation (large signal). In gene regulation, the Hill coefficient is usually limited by a small integer values (curves with n = 1, 2 or 4 in A and B). Post-translational interactions can increase the kinetic order to much higher levels (e.g. n = 10; blue curves in A and B). In ultrasensitive regimes, low and high signals have smaller kinetic orders while a discrete intermediate signal has a very high kinetic order (n = 20, 40 or higher), corresponding to a signal-response threshold (Panel C).

Signal-responses with high effective cooperativities are usually referred to as ultrasensitive¹⁷. They are characterized by a sharp transition threshold between off and on states (Box 1). The system output will be relatively insensitive to changes in signal either below or above the threshold, remaining unambiguously off or on. Sub-threshold signals are absorbed like a small amount of water in a sponge while above-threshold signal is akin to a large quantity of water saturating the sponge and spilling out. Ultrasensitivity to signals in the intermediate range can regulate costly processes requiring a decisive response, or program cells to ignore small or transient signals when the activation of output genes is not advantageous.

Several different molecular mechanisms related to saturation can allow biochemical ultrasensitivity. In the classical covalent modification mechanism, a protein can be activated (e.g. by phosphorylation) and deactivated by two competing enzymes near saturation¹⁷. Ultrasensitivity in covalent modification systems is important in development, especially in eukaryotes, for creating irreversible lineage commitment^18-20. Ultrasensitivity also plays a role in bacterial systems, for example in the E. coli chemotactic response²¹ or in regulation of metabolic enzyme activity²². Regulated degradation²³ and stoichiometric sequestration²⁴ (i.e. molecular titration, discussed below) can also give rise to ultrasensitivity in bacteria.

Ultrasensitivity from stoichiometric sequestration

Ultrasensitivity can arise from stoichiometric sequestration, where a protein is kept inactive via strong binding to a specific antagonist²⁴. In bacterial transcriptional regulation, alternative sigma factors are often sequestered by anti-sigma factors. Free of sequestration, the alternative sigma factor stimulates binding of RNA polymerase to condition-specific promoters. However, if concentrations of sigma and anti-sigma are independently regulated, the transcriptional response will be ultrasensitive to the ratio of their concentration.

For example, the global stress response regulator σ^E in Mycobacterium tuberculosis exhibits ultrasensitivity due to sequestration by the anti-sigma RseA²⁵. The fraction of active (free) σ^E changes with the level of total σ^E in an ultrasensitive fashion. When the concentration of RseA exceeds σ^E, most σ^E will be bound and there will be little free sigma factor (region 1 in Figure 2A). When the concentration of σ^E reaches that of RseA (region 2), most of σ^E is still sequestered. However, once σ^E abundance surpasses that of RseA (region 3 in Figure 2A), free sigma factor concentration sharply increases. Once abundant, the alternative sigma factor effectively binds the RNA polymerase core, causing a global shift in gene expression. As a result of the ultrasensitive switch, the anti-sigma factor RseA buffers the effects of σ^E changes until a critical stress threshold is reached. A directly analogous situation arises when a constitutively transcribed small RNA (sRNA, Figure 2B) binds to a target mRNA, preventing translation until the sRNA is saturated, determining a precise threshold for protein production.^{26, 27} In both examples the existence of ultrasensitivity crucially depends on the strength of sequestration interaction – with the increased binding (decrease in dissociation constant) we expect an increase in the effective cooperativity (curves in Figure 2A).

Figure 2.

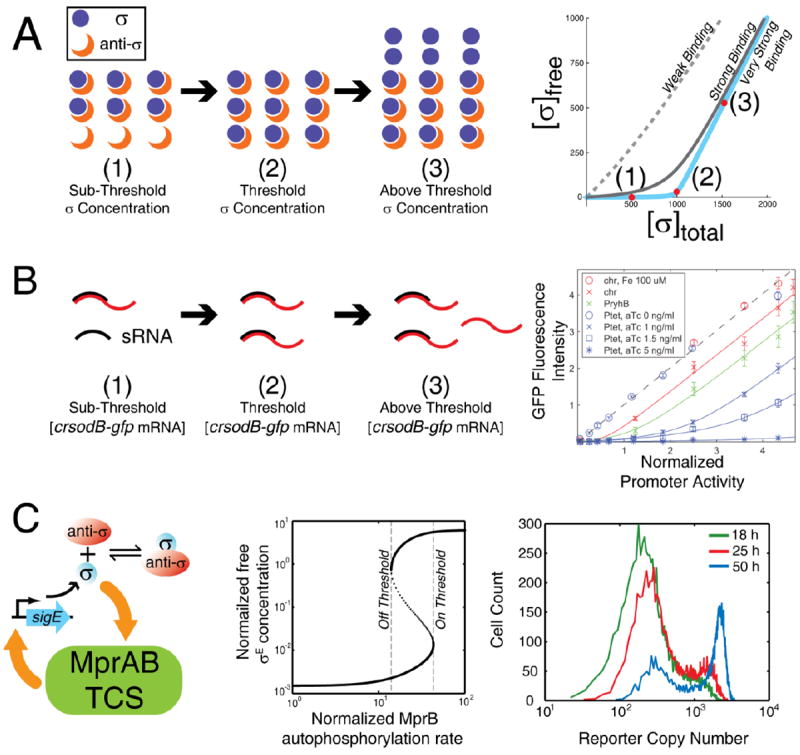
Saturation creates an ultrasensitive switch. A. As total sigma factor concentration increases, anti-σ sequesters it until the critical point is reached, determined by the concentration of anti- σ and the affinity of the σ -anti- σ interaction. The resulting quantitative effect is a titration curve for free σ that crosses a steep transition into the range where the sigma factor has high concentrations. Comparing responses for different binding affiinities shows that strong binding is necessary for the effect. B. An analogous threshold arises when a small RNA (sRNA) prevents translation. After mRNA concentration exceeds a threshold determined by sRNA concentration (due to sufficient stress signals level), translation of unsequestered mRNA proceeds. Points in the graph represent experimental data from expressing GFP fused with the crsodB sRNA recognition sequence in the 5’-UTR under various sRNA induction conditions; solid curves are model predictions²⁶. Each line corresponds to a different sRNA concentration. C. In Mycobacterium tuberculosis, σ^E upregulates MprAB, a two-component system (TCS) that regulates stress responses. Positive feedback from the TCS combined with an ultrasensitive σ-anti-σ interaction enables a bistable signal-response from MprAB with two ultrasensitive thresholds as demonstrated by signal-response curve(middle panel). Right panel shows that simulated single cell distributions of σ^E activity reporter are bimodal with a growing fraction of cells inducing σ^E after stress intiation. [Graph in part B copied directly from Levine et al 2007.]

Ultrasensitivity coupled to positive feedback

Positive autoregulation can further increase effective cooperativity²⁸. The combination of ultrasensitivity and positive feedback can thus create signal-response curves characteristic of a bistable switch²⁸. Bistable switches have two ultrasensitive thresholds – one for transitioning from the “off” to “on”, and the other moving from “on” to “off”. These signal-response curves are not only ultrasensitive but also hysteretic – the response of the network to intermediate signal levels differs depending on history; whether the cell was previously exposed to high or low signal concentrations (Figure 2C). With two thresholds the signal-response is similar to a ratchet, turning on or off irreversibly in the absence of a decisive change in signal level. The σ^E/RseA pair in mycobacteria exhibits just such an effect through a feedback loop via the MprAB two-component system (Figure 2C). Stress-responsive MprA becomes phosphorylated to activate transcription of σ^E. With a sudden sharp increase in σ^E, signaling via MprAB is sharply increased, creating a hysteretic switch²⁵. Ultrasensitivity resulting from sequestration is essential for attaining bistability²⁴. This bistability may enable “bet hedging” in a population of M. tuberculosis invading a host during transition to dormancy^{25, 29}: noise in the network disperses the signal level around the switch point, causing subsets of the population to be active and inactive for stress-response signaling.

Single-cell ultrasensitivity

In the tiny (femtolitre) volumes of microbial cells, stochastic effects of small numbers of interacting molecules are unavoidable. On the level of cell populations, noise can reduce the apparent effects of ultrasensitivity or bistability³⁰. What looks like a discrete switch in a single cell appears to be “averaged out” over the population. Ultrasensitivity can therefore often be present, with important implications for cellular physiology, but be difficult to detect at the population level. Single-cell measurements are therefore a very useful experimental tool for detecting ultrasensitive behaviors.

Implicit feedback loops

Pleiotropic and post-translational effects can also result in unexpected and indirect interactions between network components. For instance, feedback loops can occur because of subtle or indirect interactions between biochemical reactions^31-34 These effects can be quantified with appropriate mathematical methods (Box 2). However, their detection requires detailed experimental data, which is often lacking because the important components are not known in advance. A synergistic combination of mathematical modeling and mechanistic experimental studies can therefore elucidate non-obvious regulatory processes in biological networks.

Box 2.

In a chemical reaction network with established rates of production and degradation of each species, feedback loops can still be difficult to determine by examination. Mathematical tools adapted from chemical engineering can assist in their analysis. One approach, chemical reaction network theory¹⁰⁵, exploits topological features of post-translational networks to predict bistability³³, absolute concentration robustness¹⁰⁶ (e.g. robustness of regulation by bifunctional two-component systems to the expression level of their proteins ^{107, 108}), and other dynamic properties of networks.

Another approach is to write each molecular subspecies as a system of differential equations and exploit dynamical systems theory. For example, one can detect implicit feedback loops using a matrix that captures the local sensitivity of all molecular species to each other using partial derivatives, known mathematically as the Jacobian matrix³⁴. The Jacobian reveals to what extent fluxes that produce and degrade one variable depend on others. We may find that variable A depends on C, which in turn depends on B, which in turn depends on A, so that we have a feedback loop A → B → C → A. To be sure that all feedback loops are detected, all significant interactions between species (both direct and pleiotropic) should be present in the Jacobian matrix. This task is often challenging due to subtle physical effects that may need to be determined experimentally.

A simple model for a two-species network where one species has a ubiquitous inhibitory effect on growth can be diagrammed with each reaction and regulatory interaction, and represented as a set of differential equations where x′ and y′ are the rates of each variable:

The regulator x induces production of y, which inhibits growth-mediated protein degradation (via dilution). Here, the network Jacobian is:

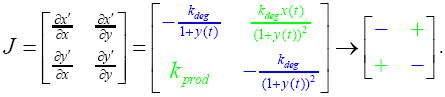
A mathematical expression for each matrix entry tells us the sign of each effective interaction. With dependencies within the network determined by the entries in the Jacobian matrix, a circuit diagram of off-diagonal elements simplifies the picture and shows the effects of growth inhibition manifesting as a positive feedback loop:

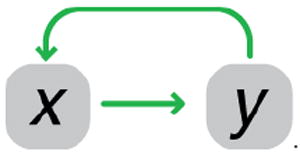
Growth rate modulation as an implicit feedback loop

Transcription, gene dosage, and protein dilution are affected by cellular growth rates³⁵. If the level of the expressed protein changes the growth rate, production and/or decay rates also change and an implicit feedback loop arises^{35, 36}. For example, most proteins in bacteria are quite stable: the dominant force of decay in their concentrations is cell growth and division. At a constant rate of exponential growth, a given protein effectively undergoes first-order degradation. When growth slows down, protein dilution is reduced. During prolonged stress or in stationary phase, induced proteolytic enzymes may degrade proteins³⁷. A stable protein, however, can undergo a sharp increase in concentration during growth arrest. If this protein or its metabolic product, imposes a burden on growth, a positive feedback loop in protein abundance can arise³⁵ (Figure 3).

Figure 3.

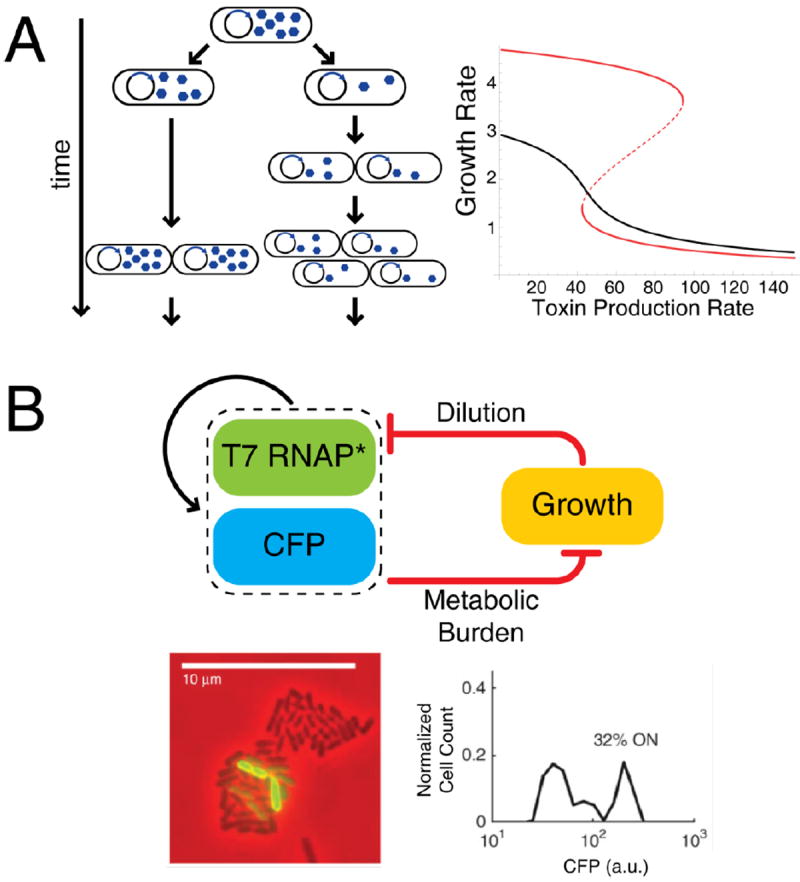
Modulation of growth rate can create an implicit feedback loop with two resulting subpopulations of microbes. A. A toxin expressed from a plasmid is unequally partitioned into two daughter cells. With higher toxin, there is slower growth, allowing, in turn, more toxin buildup. The result of the feedback loop is a non-linear relationship between toxin promoter strength and growth rate. A mathematical model predicts two resulting subpopulations of cells growing at different rates for some conditions (red curve; dashed portion represents unstable intermediate steady state) and unimodal populations with nonlinear toxin response in other conditions (black curve) ³⁵. B. A synthetic system in E. coli with autoregulating T7 RNA polymerase that also upregulates a fluorescent protein (CFP) as a readout. A second, implicit feedback loop arises from the metabolic burden of gene expression. Microcolonies of the synthetic strain exhibit bimodal fluorescence (visible as both dark and green cells) as a result of bistability³⁶. [Part B copied directly from Tan et al.]

One predicted consequence of growth-modulated feedback is the bistable phenotype that may be relevant for antibiotic persistence: a toxin-antitoxin system with toxin above a certain threshold results in a slow- or non-growing subset of persister cells^{38, 39} as a result of growth-inhibiting toxin production³⁵. During cell division, parental toxin is partitioned according to a binomial distribution into two daughter cells; one daughter cell may receive much more parental toxin than the other (Figure 3A). Because growth rate decreases as a function of toxin abundance, intermediate levels of toxin production may drive an otherwise identical bacterial population to have two distinct growth rates.

Even if growth rate feedback itself does not result in bistability, it can change critical parameters in an otherwise non-bistable network, inducing bistability. Such a system was recently constructed in E. coli using an autoregulating T7 RNA polymerase (Figure 3B)³⁶. In this system T7 RNA polymerase has a non-cooperative positive feedback effect that alone is incapable of inducing bistability. However, the expression of T7 imposes a metabolic burden on the cell, slowing cell growth and resulting in an implicit positive feedback loop. Together, the two loops create a bistable switch. As with the bistable σ^E/MprAB system above, noise disperses the gene expression level to the two stable states simultaneously in the same population. This can be observed as two distinct subpopulations of cells with low and high T7 reporter expression (Figure 3B).

Implicit feedback arising from enzymatic interactions

In addition to growth rate-dependent pleiotropic effects, implicit feedback can arise from modulation of catalytic reactions by substrates, products or cofactors³³. For example, substrate inhibition⁴⁰ can lead to a non-monotonic dose-response in enzyme catalysis, resulting in a feedback loop that allows bistability: more substrate inhibits conversion of substrate to product resulting in more substrate⁴¹. An implicit positive feedback loop can also be induced if interacting proteins form a long-lived, catalytically inactive “dead-end” complex^{31, 32, 42}. For example, in the partner-switching network controlling the activity of sigma factor σ^F in B. subtilis^{31, 32}, formation of inactive ADP-associated SpoIIAB-AA complex is self-enhancing: the inactive complex sequesters SpoIIAB from activity, increasing the fraction of unphosphorylated AA to bind to ADP-associated SpoIIAB. This feedback loop irreversibly commits the pre-spore compartment to sporulation.

Untangling coupled feedback loops

Simple model systems of single feedback loops have provided critical insight into biological network dynamics. However, natural networks often contain a complex mesh of gene regulation and biochemical interactions⁴³. Even after identifying implicit feedback loops, ultrasensitive switches, and other non-linearities, coupled feedback loops and biochemical interactions can add another level of sophistication to physiological responses. The resulting dynamics may depend on mechanistic details: extrinsic inputs, transcription rates, and binding constants. A single, sufficiently complex network architecture can perform many different dynamical functions; this multifunctionality has been linked to evolvability⁶ and may thus result in selection for network complexity. Complex network architectures can also arise from evolutionary drift with no particular selective pressure^{44, 45}.

How do we determine the physiological relevance of a complex network architecture? One answer is to use network component perturbations or deletions to systematically characterize interconnections. For instance, one can break a feedback loop and compare dynamical performance to the intact network or use steady state properties to infer feedback effects. Experimentally, transcriptional feedback can be broken by replacing a feedback-modulated promoter with a constitutive or inducible promoter⁴⁶ or by deleting genes in the network. Similarly, networks can be rewired in silico using mathematical models (Supplemental Box) ^{11, 47}. Measurements of the open-loop gain—the response of a network output to changes in the level of inducer—can then allow determination the effective sign of feedback (i.e. taking into account both positive and negative interactions). For some networks, characterization of the open-loop response reveals if the network can be bistable (Supplemental Box). However, gene deletions risk of complicating fine-tuned control of the system and moving away from the steady state of the intact system.

Systematic experimental perturbation of feedback

Recent studies of the glutamate-dependent acid response (AR2) in E. coli^{48, 49} used a combination of feedback loop deletions and systematic network perturbations to decrypt elements responsible for its complex dynamic response. When an E. coli culture is exposed to low pH, the acid-responsive two-component system EvgAS becomes activated. Among the operons in the phospho-EvgA regulon is b1500-ydeO; B1500 (a.k.a. SafA) forms a negative feedback loop with the PhoPQ two-component system while YdeO upregulates, directly and indirectly, glutamic acid decarboxylase operons gadE and gadB-gadC (Figure 4A-B). This subnetwork induces a fast immediate response with an overshoot, as measured by promoter-luciferase reporter fusions (p-Lux; first 60 minutes in Figure 4C)⁴⁹. Phosphorylated PhoP also induces IraM transcription⁴⁸, activating RpoS when the stress is persistent, ultimately upregulating the gadE and gadB-gadC operons (after 60 minutes in Figure 4C). Burton et al⁴⁹ systematically compared wild-type responses to open-loop dynamics created by deletion of phoP, ydeO, and rpoS (Figure 4C). Using these results, accounting for non-transcriptional interactions, and reconstructing the underlying circuit diagram gives clues into the function of the acid response network. This network employs a biphasic dynamic with a fast initial response and a persistent, high-expression phase for when the stress is ongoing. The first phase is mediated by negative feedback, long known for speeding induction dynamics⁵⁰. The second phase involves a feedforward loop to the output stress response genes, known to cause signal delays in a sign-sensitive manner (here, delaying gene expression deactivation but not activation, due the gabBC promoter acting as an OR gate)^{5, 8}. Interleaved architecture makes initial responses fast and decisive, while persistent responses maintain high expression for long time periods. The result of this complex network architecture is more effective survival in acidic environments (Figure 4C, AR2 Phenotypes)⁴⁹.

Figure 4.

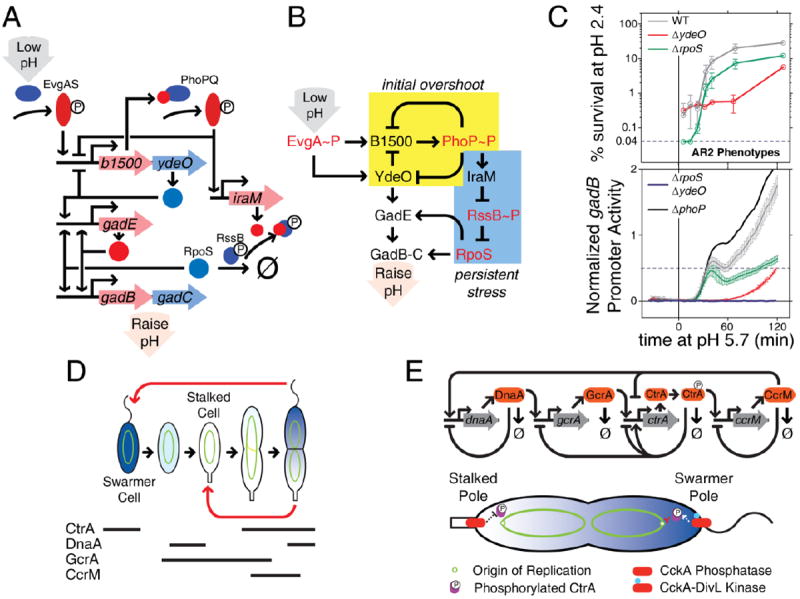
Complex feedback architecture with non-transcriptional interactions enables complex dynamic responses. A. The E. coli AR2 acid response system is a complex network with interleaved transcriptional-post-translational interactions that responds to acid stress on two timescales: initial low pH feeding into the EvgAS two-component system, and upregulation of alternative sigma factor RpoS in response to persistent stress^{48, 49}. B. A circuit diagram reveals a negative feedback architecture for early responses (pre-60 minutes) and a coherent feedforward loop under persistent stress. C. High temporal resolution measurement of promoter kinetics in the AR2 system shows two response phases: a fast, overshooting response from the negative feedback loop, and a persistent high-expression response imparted by the RpoS-Gad feedforward loop⁴⁹. Losses of dynamical characteristics in systematic deletions show the role of each feedback loop in the emergent AR2 biphasic system response. D. The Caulobacter crescentus cell cycle has evolved to deterministically produce daughter cells at two different developmental stages: a transient swarming cell type that and a mature stalk cell type. Each cell cycle stage has characteristic expression of core genetic circuitry components. E. The core genetic program is a feedback circuit that depends on regulated degradation to attain oscillatory behavior. A spatial gradient of CtrA phosphorylation mediated by polar localization of kinase and phosphatase activities suppresses chromosome replication in the swarmer pole but not in the stalked pole.

Feedback architectures for complex dynamic responses

Mounting evidence suggests that biphasic responses are a general survival strategy in bacteria that emerges from complex feedback architecture. An important example is the stringent response during which amino acid starvation is sensed during translation by a ribosome-associated protein, RelA, that produces ppGpp as an activator of amino acid biosynthesis. Biosynthesis of amino acids relieves starvation, acting as a negative feedback loop that prevents induction of the generalized stress response⁵¹. However, if biosynthesis is unsuccessful, sufficient ppGpp accumulates to induce the RpoS-mediated stress response and prepare the cell for long-term survival⁵¹. Similarly, autoregulated two-component systems in the presence of an exogenous source of response regulator phosphorylation are predicted to exhibit either negative feedback (initial induction with fast responses) or positive feedback (persistent stress response with high expression), depending on signal strength (Box 3)¹¹. Negative feedback is associated with overshoot kinetics (Figure 1), while positive feedback confers a robustness to transient signal interruptions^{3, 4, 52}.

The biphasic dynamics arising from complex feedback architecture can also manifest as two subsets of a bacterial population simultaneously exhibiting different phenotypes. Several examples exist with coupled positive feedback loops. In Bacillus subtilis, positive feedback in several steps of the Spo0A sporulation phosphorelay generates noise, increasing the variability of phospho-Spo0A levels in the population⁵³. As a result, a fraction of the cells exceed the downstream threshold for sporulation entry, and both vegetative and sporulating subpopulations co-exist in a bet-hedging strategy. The Spo0A system is an integrated part of a larger network that appears to ratiometrically integrate quorum sensing signals along with stress⁵⁴ and interacts with competence regulation⁵⁵, showing that population structure and cell-to-cell communication can become a part of the decision circuit. Multiple positive feedback loops also occur in gram-negative bacteria: in Salmonella, the SPI1 type III secretion system is controlled by a coupled set of transcription factors that positively regulate one another to both impose a discrete threshold on SPI1 gene expression and increase expression levels when induced⁵⁶.

Coupled negative feedback loops have important physiological consequences as well. They relate to dynamic properties of the network, and their effects typically depend on details such as delays between the signal and response caused by signal processing steps: transcription, translation, protein folding, multimerization, etc. While negative feedback without delay improves induction response times⁵⁰ and reduces noise⁵⁷, persistent oscillations and increased noise can arise with delays in the response^{58, 59} or consumption of end products in metabolic pathways^{58, 60}. Multiple negative feedback loops stabilize the system and improve homeostasis by eliminating these effects⁶¹.

Non-transcriptional cell cycle control

The Gram-negative bacterium Caulobacter crescentus is a model bacterium in which coupled networks of post-translational spatiotemporal control regulate the cell cycle⁶². Each division in C. crescentus is a finely orchestrated process resulting in the simultaneous production of two distinct daughter cells – a swarmer cell and a stalked cell (Figure 4D). The swarmer cell undergoes a brief motile stage before maturing to the stalked phenotype, attaching to a surface, and resuming asymmetrical cell division. Unlike in bet-hedging cases (such as in B. subtilis described above), these two cell types are maintained deterministically: every mother cell cycle produces one stalk and one swarmer daughter.

The core regulatory circuit consists of four genes expressed at specific points during the cell cycle (Figure 4D). Each gene product regulates multiple downstream cell cycle-specific genes. In one model, the four gene products form a positive feedback loop. Within the larger positive loop, the phosphorylated form of master regulator CtrA is at the center of two negative loops, one with GcrA and one with CcrM (Figure 4E). Repeated expression of the same genes in the same order, over many consecutive cell cycles, depends on fast, regulated turnover of the protein products via proteolytic degradation⁶³ (Figure 4E). For stable proteins, signal loss depends on dilution via cell growth and division, a much slower process than is needed for brief expression during a short fraction of a cell cycle. So, with induced degradation of each gene product, the core cell cycle genes are expressed in distinct pulses for discrete periods, forming an oscillator⁶³. Such oscillatory dynamics prevent competition between signals for different stages in the cell cycle.

The asymmetric character of C. crescentus cell division depends on a spatial signaling gradient in the master regulator CtrA and maintenance of the chromosome in a polarized physical orientation⁶⁴, with the origin of replication at the stalked pole before replication initiation. The critical parameter is the amount of phosphorylated CtrA. The bifunctional kinase/phosphatase CckA modulates CtrA phosphorylation and is under feedback control by CtrA~P itself^{65, 66}. When CtrA is phosphorylated, CckA is largely localized to the stalked and swarmer polar regions of the pre-divisional cell. The stalked pole CckA has CtrA phosphatase activity while swarmer pole CckA exhibits kinase activity via interaction with DivL⁶⁷. A recent study coupled mathematical analysis with experimental, spatially-resolved measurements of CtrA-regulated DNA replication initiation⁶⁷ to elegantly demonstrate phosphorylation control that allows replicative asymmetry⁶⁷. Nevertheless, the gradient in total CtrA likely contributes to the cell cycle: perturbations in CtrA proteolysis and CckA activity buffer one another⁶². This type of partial redundancy of non-transcriptional processes ensures that the cell cycle proceeds robustly in the presence of noise. The complexity of the C. crescentus cell-cycle control network, combining transcriptional and non-transcriptional interactions, may therefore have evolved in response to selective pressure for a robust phenotype.

Spatial gradients and oscillatory cell cycle regulation dynamics also appear in other bacterial species. CtrA-modulated cell cycle regulation is conserved in α-proteobacteria⁶⁸. Studies have shown that a stalk cell undergoes aging, with decreasing reproduction associated with a specific stalk pole⁶⁹, an effect that has been generalized to the morphologically symmetric γ-proteobacterium E. coli⁷⁰.

Mechanistic synthetic biology

Non-transcriptional non-linearities, implicit interactions, and overall complexity underscore the challenges of studying natural networks. Improved knowledge of, and control over, network architectures is essential for a better understanding of their function. These issues have driven researchers to construct synthetic biological networks that function as tractable laboratory models and allow a more thorough understanding of phenotype at the level of genotype⁷¹.

Challenges in constructing synthetic gene networks

In early synthetic biological networks, signals were often encoded as the number of protein transcription factors in a cell^72-76. In this type of network, the precision of signal transmission is limited by gene expression noise. Random production and degradation of mRNAs⁷⁷ and proteins⁷⁸, transmitted fluctuations from other molecules in the network^{78, 79}, and variations in global factors such as polymerases and ribosomes⁸⁰, reduce the precision with which a given protein can be expressed. Indeed, the standard deviation in protein abundance across a population of cells is often 10-50% of the mean⁸¹. Because many transcription factors bind strongly to their promoters, small changes in transcription factor concentration can significantly change promoter activity. In such circumstances fluctuations can lead to signal degradation in an individual cell and dramatic differences in behaviors of networks between neighboring cells. These fluctuations can in turn result in breakdown in the function of the synthetic network⁷⁵.

Signal matching is another difficulty that arises in the construction of synthetic gene networks. The range of output signal produced by a given node can be improperly matched with the range of signal to which another node can respond. For example, if two promoters are connected in series, leaky expression of a transcription factor from the first promoter may be sufficient to strongly activate or repress the second^{76, 82}. In such a case the downstream node promoter effectively becomes ‘deaf’ to information coming from the upstream node promoter and the network can lose dynamic range of response, or become non-functional^{76, 82, 83}.

Control of translation rate

Various methods have been used to match signal strengths in synthetic gene networks^{73, 76, 83-85}, with modification of translation initiation rates being a particularly successful approach. For a given protein, the mRNA sequence surrounding the start codon regulates total abundance in the cell. Among other parameters, the distance of the ribosome binding site (RBS) from the start codon and the degree of base pairing with 16s ribosomal RNA controls the rate of translation, and thereby concentration. RBS swapping⁷³ and directed evolution⁸³ have been used to tune the abundances of signal-carrying proteins in transcriptional networks. Recently, thermodynamic models that allow the de novo design of RBS sequences with desired translation rates have been developed^{85, 86}. New DNA assembly methods make it possible to place a synthetic RBS sequence in front of any open reading frame without leaving scars from restriction enzyme sites⁸⁷. This type of seamless sequence replacment is important when cloning RBSs, as their activity is strongly dependent on adjacent nucleotide sequences⁸⁵.

Robust oscillations via post-translational control

A goal of synthetic biology is to engineer networks capable of generating robust, dynamic cellular behaviors. A particularly challenging behavior is that of persistent oscillations. The first attempt to construct an oscillator used three transcriptional repressors organized in a ring topology, known as the repressilator⁷⁵. If any repressor achieved high concentration, it would repress the next member of the network. The third repressor would then increase in abundance, subsequently repressing the first. Though this topology gave rise to oscillations, they were short-lived and unstable, unlike the robust natural oscillations in organisms such as C. crescentus. Because signal is carried as transcription factor abundance, gene expression noise is thought to compromise the performance of the repressilator^{75, 81}.

Recently, Hasty and colleagues demonstrated that non-transcriptional effects can play an important role in the performance of transcriptional oscillatory networks^{88, 89}. In one engineered network, the arabinose-dependent transcription factor AraC was engineered to activate its own transcription and transcription of the lac repressor protein LacI⁸⁸. In this way, when arabinose is present, both AraC and LacI rise in abundance. After accumulating to a significant level, LacI dominantly represses new AraC transcription. Both transcription factors were tagged for proteolytic degradation, causing their abundances to decrease rapidly when AraC is not being actively produced. A mathematical model of the network suggests that delays in the LacI-mediated negative feedback step arising from transcription, translation, protein folding, multimerization, and DNA binding are crucial for robust oscillations. Indeed, the longer the negative feedback delay, the more robust the oscillations are to changes in network parameters⁹⁰. Though the general properties of negative feedback driven oscillatory networks have long been known, the construction of this synthetic network highlighted the impact that these more subtle processes can have on the performance of gene networks.

In a follow up study, the performance of engineered oscillators was further improved by employing a cell membrane diffusible acyl-homoserine lactone (AHL) signaling molecule from the Vibrio fischeri quorum sensing system⁸⁹. In this network, the AHL signal activates its own production and that of the enzyme AiiA, which degrades it. AHL is also a ligand for the transcription factor LuxR, acting much like arabinose in the previous oscillator. Here, the concentration of AHL is proportional to the abundance of enzymes producing and degrading it, and it likely serves to average out the noise in the expression of these proteins. The membrane diffusibility of AHL also drives neighboring cells to occupy the same signaling state at the same time. Beyond driving the bacteria to oscillate in synchrony, this type of population averaging also improves the robustness of the network in any individual cell. Any cell that begins to drift from the synchronized signal range is drawn back into the oscillatory regime by the influence of neighboring cells.

Physical colocalization improves signal flow

Signal flow through a network can also be regulated by controlling physical interactions between signaling nodes⁹¹. Keasling and co-workers recently demonstrated that metabolite flux through a carbon catabolic pathway can be dramatically improved by scaffolding otherwise freely-diffusing metabolic enzymes into a multi-protein complex^{92, 93}. The group began by introducing two S. cerevisiae enzymes into E. coli to generate mevalonate, a precursor to the anti-malarial compound Artemisinin⁹⁴. It was found that a major performance limitation of this pathway was the proper matching of the three nodes. In the first design, the upstream enzymes in the pathway (AtoB and HMGS) generated a large amount of metabolic product, while a comparatively slow third enzyme (HMGR) produced a bottleneck. Overexpression of HMGR failed to significantly alleviate the problem due to the growth burden of its production in the E. coli host cell. The problem was solved by tethering different numbers of the three enzymes together on a synthetic protein scaffold constructed from a translational fusion of three mammalian protein-protein interaction domains (SH3, PDZ, and GDB)⁹³. Scaffolding two HMGS and two HMGR to a single AtoB enzyme resulted in a nearly 80-fold increase in yield over the unscaffolded system, while other stoichiometries were less efficient. The large increase in yield occurred at very low absolute enzyme abundance, decreasing the overall metabolic burden imposed on the host cell.

Improvements arising from scaffolding are likely due to higher local concentrations of pathway intermediates, reduction of the accumulation of toxic intermediates throughout the cell, and proper input-output matching of nodes with different enzymatic rates. From a design perspective, input-output matching by scaffolding is analogous to tuning ribosome binding sites for diffusible signal carriers: total strength of a given node can be raised or lowered by engineering the efficiency of the node.

New inspiration for the biological network designer

Not surprisingly, physical interactions underlie signal processing in natural systems as well. One remarkable example is the stressosome, a 1.8MDa protein complex in B. subtilis that contains a symmetrical core structure reminiscent of a viral capsid, decorated with an array of outward-facing sensor proteins. The sensors appear to detect a variety of stresses such as UV light, pH fluctuations, and ethanol⁹⁵. Each sensor is oriented to transmit a detected signal detected from the outside inward, as a phosphorylation event within the stressosome core. Phosphorylation results in the release of an enzyme activating the alternative sigma factor σ^{B 96}. Most early synthetic biological networks were inspired by the circuits of electrical engineering. Systems such as the stressosome, however, demonstrate that biology can process signals using approaches that a mechanical engineer might envision as well. Though we are far from being able to design macromolecular structures this sophisticated, we will be well served to take inspiration from biological networks in all of their varied forms.

Concluding remarks

The rise of genomics and systems biology has greatly enhanced our understanding of the molecular organization of life, particularly microbial life. Recent studies, highlighted here, demonstrate that broad systems-level analysis must be deepened with consideration of molecular mechanisms and non-transcriptional effects. Mechanistic details such as growth rates, spatial gradients, implicit feedback loops, and others can alter the properties of gene expression programs. The ability to deeply understand life, and to engineer it for useful purposes, requires accounting for these effects.

The mechanistic approach to understanding biological networks has important implications for the uses of mathematical models and their relation to experiment. The theoretical foundation of biology is not networks themselves, but their underlying physics. Relevant models, conceptual and mathematical, must reflect the chemical physics of matter: atoms and molecules interacting in space. It is from these interactions that sophisticated gene expression programs arise. Physics has constrained evolution, and must be remembered when building a model, performing an experiment, or designing a synthetic network.

The importance of mechanism—evolutionary and physical—underscores the importance of quantitative experiments. Microbiologists are moving toward an experimental approach guided by, and guiding, theory. Such complementary approaches are necessary for the next generation of life sciences. The quantitative effects of ultrasensitivity, implicit and complex feedback networks, and spatiotemporal organization of genetic programs covered in this review exemplify the importance of non-transcriptional processes. Many other quantitative processes and characteristics outside the scope of this review are known to exist: transcriptional coupling⁹⁷, DNA-mediated interactions such as promoter cooperativity⁹⁸, and multicellular effects⁹⁹. Yet other examples likely await discovery.

Synthetic network design has benefitted from the combined use of transcriptional and non-transcriptional interactions. The fact that synthetic networks are subject to the same mechanistic rigors and challenges as a natural system makes them an important scientific tool: they enable the comprehensive quantitative experiments needed to deepen our biological understanding. Indeed, characterization of these networks in living cells has revealed subtle physical effects, the impacts of which were not widely appreciated a priori. Feedback between synthetic and systems biology will pave the way toward important medical and industrial applications that will arise from our deepened understanding of biological networks. The complementary approach of synthetic network construction alongside quantitative network analysis stands to contribute, perhaps more than any other single approach, to our understanding of the organizing principles of biology.

Figure 5.

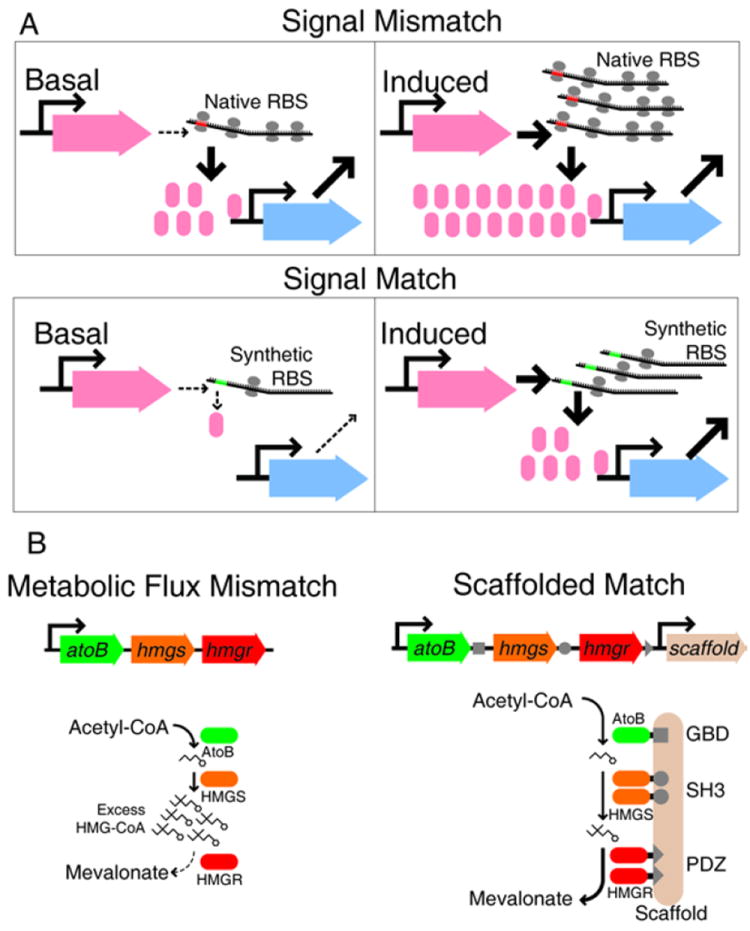
Engineering non-transcriptional processes for synthetic biology. A. ‘Leaky’ transcription can produce sufficient signal to flood downstream nodes. Signal matching can be achieved by engineering the ribosome binding site (RBS) to prevent low-level transcription from causing extraneous downstream signaling⁸⁵. B. A similar mismatch occurs in a synthetic metabolic pathway for mevalonate production. A physical scaffold prevents accumulation of undesired intermediate HMG-CoA, reducing host cell toxicity and greatly increasing mevalonate product yield^{92, 93}.

Online summary.

• The performance of bacterial transcriptional regulatory networks is often affected by post-transcriptional, post-translational, and pleiotropic effects.

• Despite their importance, non-transcriptional effects are often obscure or difficult to characterize without quantitative analytical techniques.

• Feedback loops can arise via non-transcriptional interactions and these have important effects on signal processing.

• Stress-response networks, cell-cycle regulators, and sRNA-mediated gene expression are examples of bacterial signaling networks that depend strongly on non-transcriptional interactions.

• Mathematical network analysis techniques used in combination with quantitative experimental approaches can reveal how non-transcriptional processes contribute to complex dynamic phenotypes.

• Synthetic biological networks are a powerful tool for studying the role of non-transcriptional effects in natural networks. Synthetic networks are well-defined and easily manipulated. Recent advances in synthetic network design underscore the importance of non-transcriptional effects.

• Synthetic network construction complemented by quantitative network analysis will speed discovery and deepen our understanding of the fundamental organizing principles of biology.

Glossary

network

Set of biochemical reactions or interactions employed for cellular information processing. The term network can refer either to either interactions on whole-cell level or smaller circuits - subsystems of the larger network

non-transcriptional

A combination of post-transcriptional, post-translational and pleiotropic effects

coupled feedback loops

Multiple feedback loops that interact in some way, such as being nested, or resulting from a single regulatory event that modulates multiple transcriptionally coupled genes

bet-hedging

An evolved phenotype that employs heterogeneity to ensure that distinct subsets of a cellular population are adapted to different outcomes of an unpredictable future environment

implicit feedback loop

A feedback loop whose existence is not obvious, but emerges from non-transcriptional interactions

biphasic

A response composed of two distinct, characteristic types of dynamics separated in time, such as initial transient phase and a long-term persistent phase

signal

Biological signals can take a wide variety of forms. In the context of this review, signal refers to the information that flows through a biological network

signal matching

Adjusting the amount of signal produced by an upstream node so that it is within the range to which a downstream node is responsive (unsaturated)

node

A molecular entity that takes in a signal and outputs a signal in response, such as a transcription factor or allosterically regulated enzyme. Upstream or downstream nodes refer to their order in the information flow

ultrasensitivity

A type of signal-response curve characterized by a very high slope in the responsive range

oscillator

A network architecture that results in periodic oscillations of some output

Jacobian matrix

A matrix whose entries quantitate the sensitivity of each variable (often corresponding to chemical species) to each other variable

effective cooperativity

A concept representing sensitivity, or how much one molecular species affects production of another. A phenomenological generalization of cooperativity, where binding of one molecule to another increases the affinity of further copies of one of the molecules to bind

bistability

A feature of a system where there are two stable steady states under the same conditions. Which state the system adopts in practice depends on initial conditions and noise. A bistable switch has a signal-response curve with two stable steady states

robustness

The term has taken many, subtly different meanings in the field of systems biology. For the purposes of this review, we take robustness to mean insensitivity of dynamic performance to small parameter perturbations that would arise from intrinsic or extrinic noise, slight enivronmental variations, etc

Michaelis-Menten kinetics

A model of enzyme kinetics often used to mathematically represent first-order saturation processes where the flux $V=V_{\mathit{max}}\frac{x}{K_m+x}$ for substrate or regulator x, maximum flux rate V_max, and Michaelis-Menten constant K_m

Hill kinetics

A generalization of Michaelis-Menten kinetics that allows mathematical representation of higher-order, or cooperative, processes where flux $V=V_{\mathit{max}}\frac{x^n}{K_m^n+x^n}$ has n^th-order effective cooperativity

pleiotropic

A type of interaction where one component or effect simultaneously affects many targets

toxin-antitoxin system

A small gene network that typically includes one gene encoding a toxin and another encoding a neutralizing antitoxin

dynamical performance

The characteristics of a response to a signal over time

noise

Variability in signals and responses from cell to cell that arise either intrinsically from the nature of the physico-chemical processes or from extrinsic variability such as randomness in ribosome inheritance

Biographies

J. Christian J. Ray is a former post-doctoral fellow with OAI, studying the dynamic consequences of bacterial chromosome organization using mathematical models and bioinformatic approaches. He is now working with Gábor Balázsi at M. D. Anderson using a theory-driven experimental approach to understand the relationship between network dynamics and evolution.

Jeffrey J. Tabor is an Assistant Professor in the Department of Bioengineering at Rice University. He engineers synthetic sensing and signal transduction networks to study cellular decision-making and coordinated multicellular behaviors.

Oleg A. Igoshin is an Assistant Professor in the Department of Bioengineering at Rice University. He specializes in computational systems biology with emphasis on cellular differentiation and decision-making, on evolutionary design principles of biochemical networks and on self-organization and pattern formation in bacterial biofilms.