A comparison of methods using optical coherence tomography to detect demineralized regions in teeth

Abstract

Optical coherence tomography (OCT) is a three- dimensional optical imaging technique that can be used to identify areas of early caries formation in dental enamel. The OCT signal at 850 nm back-reflected from sound enamel is attenuated stronger than the signal back-reflected from demineralized regions. To quantify this observation, the OCT signal as a function of depth into the enamel (also known as the A-scan intensity), the histogram of the A-scan intensities and three summary parameters derived from the A-scan are defined and their diagnostic potential compared. A total of 754 OCT A-scans were analyzed. The three summary parameters derived from the A-scans, the OCT attenuation coefficient as well as the mean and standard deviation of the lognormal fit to the histogram of the A-scan ensemble show statistically significant differences (p < 0.01) when comparing parameters from sound enamel and caries. Furthermore, these parameters only show a modest correlation. Based on the area under the curve (AUC) of the receiver operating characteristics (ROC) plot, the OCT attenuation coefficient shows higher discriminatory capacity (AUC=0.98) compared to the parameters derived from the lognormal fit to the histogram of the A-scan. However, direct analysis of the A-scans or the histogram of A-scan intensities using linear support vector machine classification shows diagnostic discrimination (AUC = 0.96) comparable to that achieved using the attenuation coefficient. These findings suggest that either direct analysis of the A-scan, its intensity histogram or the attenuation coefficient derived from the descending slope of the OCT A-scan have high capacity to discriminate between regions of caries and sound enamel.

I. Introduction

Preventive dentistry places emphasis on the non-surgical management of dental decay by treating lesions with agents such as fluoride to arrest decay, remineralize the site and restore the enamel integrity before it cavitates. A central requirement for this strategy to be effective is a means to detect early lesions and monitor their status. Clinical radiography shows poor sensitivity for detecting early, shallow lesions [1] therefore clinical inspection based on visual examination and probing with a sharp dental explorer is generally relied upon. The subjectivity of clinical inspection has led to an intense effort to develop objective detection techniques [2], [3]. Optical coherence tomography (OCT) is one of the candidate methods being developed for the non-subjective detection of early caries [4]-[11]. The method is based on quantitative measurements of the back-scattered light intensity as a function of depth into the enamel layer. OCT can probe the enamel subsurface of the tooth with a spatial resolution in the micrometer range. Previous OCT investigations at 1310 nm have involved the use of polarization-sensitive OCT to remove the strong surface reflection to allow imaging of early caries [6-7]. In this study we have used an 850-nm as the probing wavelength of our OCT system. This wavelength was used as it is how our commercially available system (Humphrey OCT-2000 system, Humphrey Systems, Dublin, CA, USA) is configured. Studies in the literature have successfully used OCT in the 800 nm range to investigate biological tissues including ocular [12] and dental tissues [5, 8]. It is widely known that shorter wavelengths (i.e. 850 nm) are more strongly scattered within biological tissues than light with longer wavelengths (i.e. 1310 nm). This fact ensures a maximum probing depth of only 1-2 mm’s within the dental tissue for the former but demineralization appears and develops within the first 300-400 micrometers of the enamel, region well within the probing capabilities of an 850-nm OCT system. The enhanced scattering corresponding to the 850-nm probing beam could provide better sensitivity to demineralization-induced changes of the optical properties in enamel. Previously we observed that the OCT signal at 850 nm was more highly attenuated in healthy enamel than in carious lesions, and the measured OCT attenuation coefficients from the two groups formed distinct statistical populations [4], [8]. A similar approach of looking at the shape of the decending A-scan signal was used by Mujat et al. who used optical path-length spectroscopy to investigate incipient lesions [8]. Other groups have examined the OCT reflective loss of in regions of demineralization and correlated the observations with quantitative light-induced fluorescence [9].

While the OCT attenuation coefficient appears to have good discriminatory power for detecting incipient caries, the descending slope of the OCT A-scan needs to be selected and then fit to provide an attenuation coefficient. In the presence of noise there can be ambiguity over which region of the OCT A-scan to select for the fitting. This introduces uncertainty in the calculation of the attenuation coefficient. In this article we compare the discriminatory power of the attenuation coefficient derived from the descending slope of the OCT A-scan with parameters that summarize the shape of the complete A-scan. In addition we examine the potential of using a multivariate classification strategy that directly exploits the entire A-scan or histograms of the A-scans as input information. These latter methods do not require user intervention to select the descending slope of the A-scan which makes them more amendable to automation. The diagnostic potential of these methods are tested on a set of extracted teeth that have been inspected by dental practitioners.

II. EXPERIMENTAL

A. Tooth samples & Clinical Assessment

Human molars and premolars (n=21) were acquired from consenting patients at the University of Manitoba Dental Clinics who were undergoing extractions for orthodontic reasons. Any remaining soft tissue on the teeth was removed by scaling and the teeth were preserved in sterile filtered de-ionized water in order to prevent desiccation. Each ex vivo tooth was independently assessed by two dental clinical investigators. Samples were grouped into two categories: 1) caries-free samples were ones which had no visible decalcification or demineralization; 2) teeth with early carious lesions had regions of decalcification with intact surfaces and opacity of enamel that appeared as white spots when teeth surfaces were dry. All samples were used for OCT measurements without further treatment.

B. Optical coherence tomography system

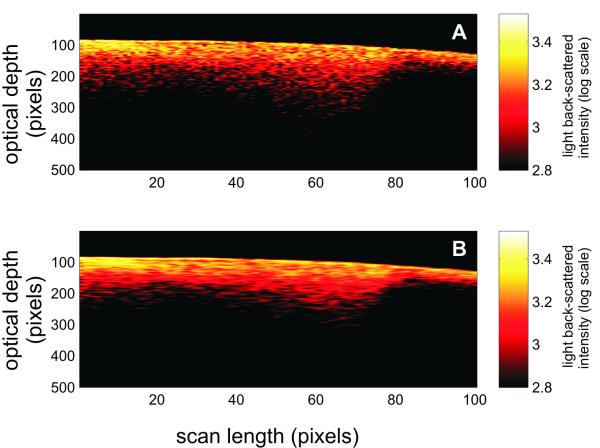
OCT images were recorded as described previously in [4] and [11] with a Humphrey OCT-2000 system (Humphrey Systems, Dublin, CA, USA). The system uses a super-luminescent light emitting diode with a central wavelength at 850 nm. The coherence length of the source when measured in free-space was ~15 μm. This value has a role in determining the axial resolution of the OCT system while the transverse resolution of this system was ~10 μm and is determined by the smallest rotation angle of the galvanometric mirror setup. The embedded galvanometric mirror laterally moves the light beam from one point to the next, steering the light beam to provide a succession of adjacent A-scans (depth scans). Two-dimensional depth images (also known as B-scans) were formed by a straight-line collection of adjacent A-scans. Each OCT image (or B-scan) consisted of 100 A-scans with each A-scan being 500 pixels deep with a measured spatial resolution of 5.5×10⁻³ mm/pixel. Each A-scan corresponds to one position of the focused beam on the tooth surface and the distance between adjacent A-scans was 20 μm resulting in B-scans that were 2 mm wide. An example of such an OCT image acquired from the distal surface of a tooth with a demineralized area is presented in fig. 1A. Prior to starting the image acquisition, the light beam was focused to the thinnest possible line on the sample surface with the samples positioned such that the beam was nearly perpendicular to the surface across the width of the scanned region, i.e. 2 mm. The total optical power on the sample was 750 μW. Samples were imaged in an upright position by securing the apical root portion of the tooth to a substrate with dental rope wax.

Fig. 1.

A) A representative two-dimensional OCT image (B-scan) at 850 nm showing part of the distal region of a tooth with incipient demineralization. B) Result of applying an adaptive Frost filter with a 1×5 exponentially damped convolution kernel for smoothing the speckle noise of the B-scan shown in (A).

C. OCT image acquisition and data processing

OCT images were collected from regions of healthy enamel and regions of incipient (non-cavitated) carious lesions. Images were acquired from the proximal surfaces (distal and mesial surfaces) which are found between adjacent teeth. Because the focal depth of the sample beam was almost an order of magnitude greater than the distances (generally less than 2 mm) probed within the teeth, the OCT beam could be regarded as being collimated along the extent of each individual A-scan. This experimental setup minimized the effect focusing could have on the OCT signal intensity recorded as a function of optical distance within the sample.

A standardized procedure was established in order to ensure experimental repeatability of the OCT measurements. This procedure included fixing OCT system parameters, sample positioning as well as ensuring normality of the probe beam to the scanned tooth surface. From each tooth surface, triplicate sets of images were obtained.

The acquired OCT images were corrected for the inherent curvature of the tooth surface by aligning the reflection peak from the enamel/air interface in each A-scan along the same horizontal pixel line in the two-dimensional image. Having aligned images enable the use of various filtering methods to improve the image quality. The spotty pattern observed across the B-scan shown in fig. 1A is due in part to coherent speckle noise. This type of noise is inherent to all interferometric imaging methods. In the present study, multiple scattering within the tooth matrix generates speckle in the corresponding OCT image as a result of part of the detected light experiencing changes in travel distance relative to the ballistic path as it interacts with the tooth matrix [13], [14]. Quenching speckle noise is necessary in order for OCT images to provide a reliable morphological representation of a highly scattering matrix [15], [16]. An adaptive Frost filter [17] with a 1×5 exponentially damped convolution kernel was used on all OCT images acquired for this study in order to reduce the coherent speckle noise. The filtering was conducted along the horizontal direction, i.e. parallel to the tooth surface. The filter smoothes the image by adapting itself to local statistics without removing existing edges or sharp features. This method involves computing a set of weight values for each pixel within the filter window surrounding each pixel. The effect of this smoothing technique on OCT images can be observed in fig. 1B where the speckle intensity is reduced and the extent of the carious lesion can be better visualized in comparison to fig. 1A, which shows the raw OCT image.

D. A-scans and derived summary parameters

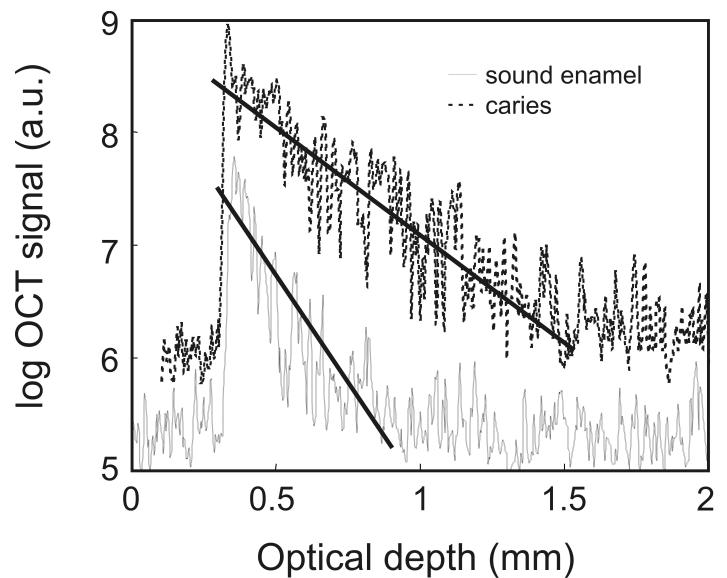
Fig. 2A exemplifies two individual A-scans selected from a filtered image. Prior to analyzing these signals, the A-scans were scaled to have intensity values ranging from 0 to 1. The intensity normalized A-scans were analyzed directly and compared to two other approaches, where parameters were derived directly from the A-scans. One procedure (fig. 2A) involves fitting an exponential function to the descending tail of the OCT A-scan [4]. The attenuation coefficient (α) corresponding to the exponential fit (i.e. the slope of the A-scan represented on a logarithmic scale) can be evaluated and comparisons can be made between values corresponding to OCT signal attenuation in sound and demineralized enamel.

Fig. 2.

A) Representative A-scan depth profiles from regions of sound enamel and carious enamel. The fitting the exponential decaying slope of the OCT A-scans to derive the optical attenuation coefficient parameter (α) are illustrated with the solid lines. (a.u. = arbitrary units)

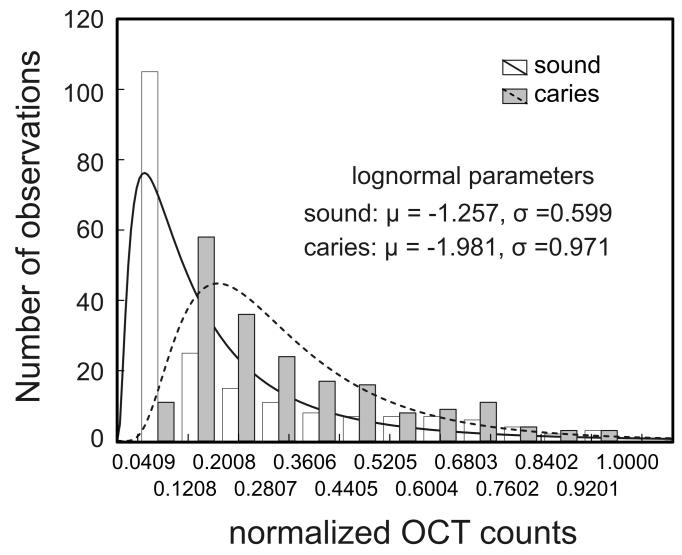
B) Histograms of the A-scan signal from sound and carious enamel along with the lognormal fit to the histogram.

The rate of the decaying OCT signal is one of the parameters also reflected in the histogram of the A-scan signal. Each histogram was determined by binning the intensity values from the first 200 points of the normalized OCT A-scan into 12 bins spanning the intensity range from 0 to 1. Histograms were generated by the Matlab function, hist (http://www.mathworks.com). As an asymmetric, unimodal distribution, the lognormal distribution provides a simple functional form that suitably fits the histograms obtained from the A-scans probing enamel (see fig. 2B).

$$K\left(x\right)\approx \frac{1}{x\sigma \sqrt{2\pi }}{e}^{\frac{-{\left(\ln \right(x)-\mu )}^2}{2{\sigma }^2}}$$ (1)

The lognormal fit to the counts, K(x), of the histogram of an OCT A-scan summarizes the distribution of the signal in terms of a mean (μ) and standard deviation (σ). The lognormal mean of the histogram increases for a more slowly decaying OCT A-scan while for a given mean, the skewness of the histogram increases with σ and reflects the shape of the distribution. The mean (μ) and the standard deviation (σ) of lognormal fit to the histogram of the A-scan provides two summary parameters that we investigated as diagnostic markers for the presence of caries.

The Matlab function, lognfit, was used to return maximum likelihood estimates of the mean (μ) and standard deviation (σ) of the lognormal fit to the histogram. The chi-square goodness-of-fit test was used to establish if the histograms obtained from OCT A-scans could be adequately represented by a lognormal distribution. Chi-square test statistic was generally less than the threshold chi-square value of the 0.05 significance level, χ²(0.05, 9) = 16.9, and always less than the threshold value for the 0.01 significance level, χ²(0.01, 9) = 21.7, suggesting that the lognormal distribution modeled the histograms reasonably well.

E. Simulated A-scans for testing repeatability and susceptibility to noise

Monte Carlo methods were used to generate simulated OCT A-scans free from speckle noise. The freely available MPI (message passing interface – Intel) library was used on a Linux cluster for our Monte Carlo simulations. A C++ implementation of the Mersenne Twister with a period length of (2^19337) −1 provided pseudo-random numbers for launch, scattering and displacement operation. The random number generator for each process was seeded with a unique value based on the rank of the process. A total of eighteen CPU’s (AMD Opteron Processor 250) were used in our Monte Carlo simulations.

A-scans from semi-infinite homogeneous isotropic (g = 0) and strongly forward (g= 0.9) directed scattering media with a scattering coefficient of μ_s = 50 cm⁻¹ were simulated. Each photon ray was launched from a circular aperture whose radius corresponded to the physical dimension of the focused beam of the OCT system used in our studies. Photons were launched with spatial uniform density from the aperture and were given initial direction cosines values of (0,0,1) - the axis system was arranged so that the x-y plane lies in the source plane (i.e. parallel to the sample surface) and the positive z-axis is perpendicular to this plane, along the propagation direction of the probe beam. The photons counted as being detected were back-reflected and exited the scattering medium through the same circular aperture that defined the photon source. To obtain a simulation of an A-scan, the number of photons detected was binned as a function of distance traveled in the scattering medium. The maximum of the resulting unimodal distribution was normalized to have a value of one.

In order to test the repeatability of the procedure to extract the summary parameters from OCT A-scans with noise, varying levels (mean = 0, standard deviation = 0.1, 0.15 and 0.2) of random Gaussian noise were added to the Monte Carlo-simulated A-scans. The attenuation coefficient (α), the mean (μ) and the standard deviation (σ) of the lognormal fit to the histogram were compared for the simulated A-scans with varying levels of Gaussian noise.

F. Statistical analysis

Matched OCT attenuation coefficients and lognormal fit parameters were obtained from a total of 754 A-scans, with 555 A-scans from regions of sound enamel while 199 were from sites identified as having an incipient caries lesion. Scatter plots and Pearson product-moment correlation coefficients were used to examine the strength of the linear relationship between the three summary parameters.

Student’s t-tests were performed to test the null hypothesis that the means of the summary parameters were equal for healthy and carious regions of enamel. A p<0.05 was used to reject the null hypothesis.

Receiver operating characteristics (ROC) curves and the area under the curves (AUC) were used to compare the discriminatory capacity of the summary parameters as well as multivariate classification approaches using the normalized A-scan directly and the histogram of the OCT A-scan. ROC curves are a graphical method that summarizes the diagnostic capacity of a marker to distinguish between two sample populations [18]-[20]. The sensitivity and specificity of a diagnostic marker is often cited as a quality measure of the marker. In order to calculate the sensitivity and the specificity for a test, a decision threshold must first be specified. The ROC curve is an extension of this procedure where the sensitivity and specificity of the marker is calculated as the decision threshold is varied between −∞ to ∞. The ROC curve plots the sensitivity of the test (true positive fraction) versus the 1 – specificity (false positive fraction). The area under the ROC curve, usually abbreviated AUC, provides a measure of the diagnostic discrimination of a diagnostic test. The ROC curve for a test with no discriminatory power lies along the diagonal plot and has an AUC = 0.5. A perfect test has an AUC=1. The greater the AUC, the better overall discriminatory capacity of the test. Therefore the AUC is often used to indicate the quality of a marker for a diagnostic test. Nonparametric ROC curves were generated using a linear scan algorithm [21] and nonparametric AUC was calculated using the Mann-Whitney U test [18]-[20].

When determining the discriminatory capacity of the individual summary parameters, attenuation coefficient (α) of the A-scan as well as the mean (μ) and standard deviation (σ) of lognormal fit to the histogram of the A-scan, the classification models are univariate with no adjustable model parameters. However, the classification models directly using the A-scans or the histogram of A-scan intensities or a combination of summary parameters are multivariate in nature and require training to optimize model parameters followed by testing of the model to ascertain the diagnostic value of the trained model. Support vector machines (SVM), regularized linear classifiers that try to find a hyperplane that separates two classes with widest margin [22], were used for multivariate classification. Linear SVM, as implemented in a Matlab toolbox OSU-SVM (http://svm.sourceforge.net), was used for two-class multivariate classification. A-scans, histograms of A-scans or a combination of the summary parameters derived from A-scans labeled as arising from healthy enamel or a region of carious enamel were used to train SVM models as well as for testing the predictive ability of the models. A sample-out bootstrap cross validation strategy was used to train and test SVM models. This strategy randomly selects data from a subset of the teeth investigated and develops a surrogate classification model from this subset of data. The predictive ability of this surrogate model was tested using the data from the teeth that were excluded from building the surrogate model. A total of 2000 sample-out bootstrap samples were generated and the general performance of the model is inferred by summing the test performance over the surrogate models. Nonparametric ROC curves and AUC values were determined from the test set samples ranked according to SVM prediction values. This cross-validation procedure ensures that all the data is used for both training and testing of the model but each surrogate model has an independent test and training data set thereby providing a nearly unbiased estimate of the classifier error. The method also ensures that data from each tooth exclusively appears in the test or training set over the various iterations of cross-validation. For each of the multivariate models the mean AUC and the corresponding 95% confidence intervals of the AUC were determined using the AUCs calculated over the 2000 test partitions. For comparison with the multivariate models, percentile bootstrap confidence intervals were calculated each of the univariate models again using 2000 bootstrap samples.

III. RESULTS AND DISCUSSION

A. Diagnostic value of OCT A-scans and parameters derived from A-scans

Fig.1A is a representative image of an OCT 2-dimensional depth B-scan taken across a region of carious enamel surrounded by sound enamel. In addition to the back-scattering of light at the air-enamel interface there is significant subsurface light back-scattering at the lesion site compared to the back-scattering occurring in sound enamel (see right edge of the figure). Although there is visual detail in the morphological information obtained from this image, from a clinical perspective it is useful to have parameters that can be used to non-subjectively discriminate sound enamel from early incipient caries. Fig. 2A presents two representative OCT A-scans at 850 nm with one A-scan obtained from a sound region and the second A-scan from a site with incipient caries. There are distinct differences between depth scans crossing sound and scans crossing demineralized regions. Compared to the sound region, there is significant OCT signal penetrating further into the tooth matrix in demineralized enamel with the A-scan showing a lower rate of attenuation with optical depth. This translates into a smaller slope for the exponential fit of the descending portion of the A-scan (fig. 2A) as well as a wider histogram of the A-scan profile (fig. 2B). The form of the A-scan or the histogram of the A-scan can be investigated directly. In addition, the difference in signal attenuation as captured by the attenuation coefficient (α) or wider histogram of the A-scan as captured by the mean (μ) and standard deviation (σ) of the lognormal fit to the histogram can potentially be used to identify incipient demineralized regions beneath otherwise intact tooth surfaces.

The population means between the sound and carious regions of enamel are statistically significantly different at p<0.01 for all three summary parameters (α, μ, σ) of the OCT A-scan. The linear relationship between these summary parameters was examined using the Pearson product-moment correlation coefficient (see Table 1). None of the summary parameters are highly correlated, with the attenuation coefficient and the mean of the lognormal fit to the histogram having the highest absolute correlation (ρ = −0.53). The modest correlation between the summary parameters suggests that they may each have a different capacity to act as diagnostic markers for detection of demineralized regions.

Table 1.

Pearson product moment correlation coefficients Pearson product moment correlation coefficients between three summary parameters, the attenuation coefficient (α) as well as the mean (μ) and standard deviation (σ) of the lognormal fit to the histogram of the A-scan derived from 850 nm OCT A-scans of human dental enamel.

	μ	Σ	α
μ		0.24	−0.53
σ	0.24		−0.26
α	−0.53	−0.26

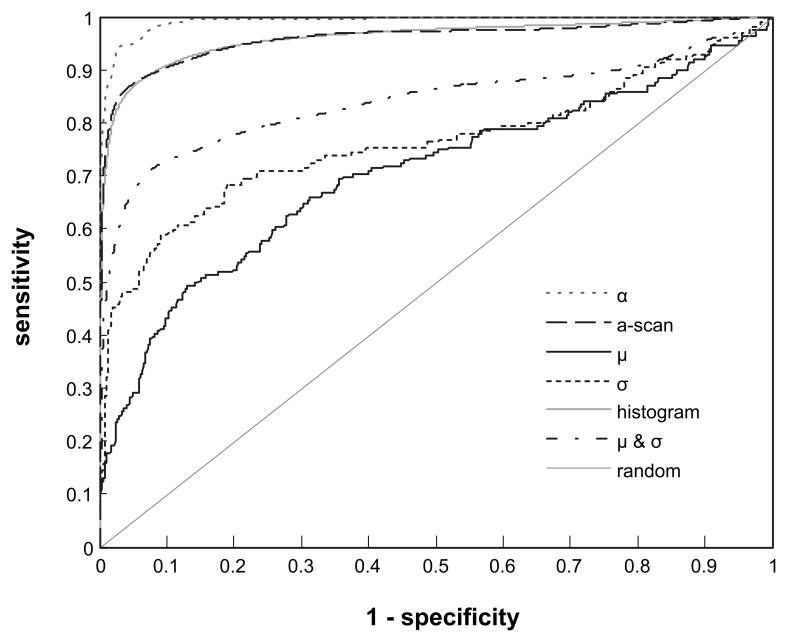
Fig. 4 plots the non-parametric ROC curves for the three summary parameters derived from the OCT A-scans acquired at 850 nm as well as the ROC curves for three multivariate classification models: a) where the mean (μ) and standard deviation (σ) of the lognormal fit to the histogram are considered in concert, b) where the histogram vector of the normalized A-scan is used as input to the classification, and c) where the normalized A-scan is directly classified. The AUCs for the various ROC curves are listed in Table 2. For comparison the diagonal line on the ROC plot represents the ROC curve for a random diagnostic test, i.e. one of no diagnostic utility (AUC=0.5). The ROC curves for all summary parameters are to the left of the diagonal line and have an AUC > 0.5 indicating that they are better than random classifiers. The ROC curve for the attenuation coefficient is closest to the left and top borders of the plot with an AUC=0.992 suggesting that for this parameter the distributions for caries and sound enamel are particularly well separated.

Fig. 4.

Receiver operating characteristics (ROC) curves showing the capacity of using the OCT A-scan and various parameters derived from the A-scan to discriminate between regions of healthy and carious enamel.

Table 2.

Area under the curve (AUC) of the receiver operating characteristics (ROC) curve for the OCT A-scan and various parameters derived from the A-scan to discriminate between regions of healthy and carious enamel. Percentile bootstrap 95% confidence interval (CI) reported.

Model parameter(s)	Model dimension	AUC	Lower 95% CI	Upper 95% CI
α	1	0.992	0.985	0.996
μ	1	0.760	0.713	0.807
σ	1	0.703	0.655	0.747
μ and σ	2	0.841	0.752	0.925
histogram	12	0.961	0.924	0.990
A-scan	200	0.962	0.910	0.980

Taken individually, the summary parameters extracted from the lognormal fit to the histogram show a much poorer capacity to discriminate between healthy and carious lesions compared to the attenuation coefficient. The mean (μ) and standard deviation (σ) of the lognormal fit have AUCs of 0.760 and 0.703, respectively. When combined, the diagnostic capacity of the lognormal fit parameters improves considerably, AUC=0.841, but does not attain the discriminatory capacity of the attenuation coefficient. The skew to the left upper quadrant of the ROC curves associated with the parameters from the lognormal fit, individually or in combination, indicate that they have the potential to be sensitive indicators of caries but offer poor specificity.

Using the binned intensity values of the histogram directly as input to the classifier shows a significant improvement in the discrimination (AUC=0.961) of caries from healthy enamel compared to the use of the summary parameters derived from the lognormal fit to the histogram. The ROC curve also shows that the classifier based on the A-scan histograms is capable of being both highly sensitive and specific. For example, selecting a threshold that gives 97% sensitivity for detecting caries, the classifier is 84.5% specific. These results suggest that diagnostic information on the state of the enamel is latent within the histogram of A-scan intensities but that the parameters derived from the lognormal fit to the histogram only poorly capture this diagnostic information. Fitting the histograms with a more complex distribution may provide summary parameters with better capacity to discriminate between healthy and carious enamel. However, using the histogram vector as input to a multivariate classifier appears to be a suitable and simple alternative.

Similarly, classifying the normalized A-scans directly appears to be a plausible strategy that yields the same diagnostic performance as using the histograms of the A-scans. The two ROC curves are virtually superimposible with nearly the same AUC

B. Noise impunity of summary parameters derived from OCT A-scans

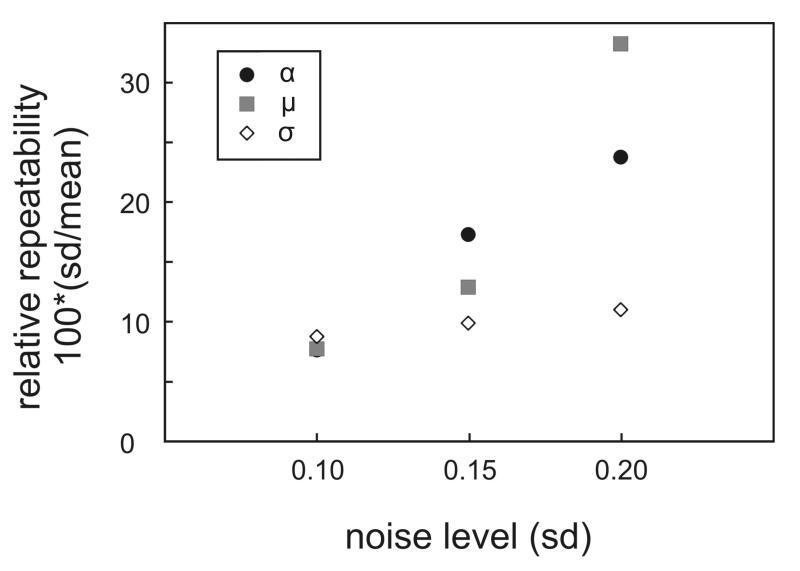
As discussed above, it appears that various parameters can potentially serve as diagnostic markers that can be extracted from the OCT images for distinguishing sound enamel from demineralized regions. We explored the possible advantages and limitations that would guide the choice for the most suitable parameter. One possible factor is the noise level of the OCT A-scans. Fig. 3 displays the variation in the OCT attenuation coefficient (α) as well as the mean (μ) and standard deviation (σ) of the lognormal fit to the histogram of the OCT A-scans where varying levels (using standard deviations of 0.1, 0.15 and 0.2) of random Gaussian noise were added to simulated A-scans. In order to compare the noise characteristics of the three summary parameters, the standard deviation was expressed as a percentage of the mean value of the summary parameter for a particular level of added noise. The OCT attenuation coefficient as well as the mean (μ) of the lognormal fit to the histogram show a greater sensitivity to noise compared to the parameter σ that summarizes the width of the histogram fit to the A-scan. In addition, on average, the μ parameter increases with increasing A-scan noise. These simulation results suggest that attenuation coefficient and μ summary parameters derived from OCT A-scans are less robust to noise compared to the standard deviation (σ) of the lognormal fit to the histogram of the OCT A-scans.

Fig. 3.

Analysis of the sensitivity of the summary parameters (α, μ, σ) to noise in the OCT A-scan. Random Gaussian noise (standard deviations of 0.1, 0.15 and 0.2) was added to simulated A-scans and the relative repeatability of OCT attenuation coefficient (α) as well as the mean (u) and standard deviation (σ) of the lognormal fit to the histogram of the OCT A-scan were determined.

IV. Conclusion

OCT imaging at 850 nm is being explored as a method for detecting early caries. When visually comparing OCT images (B-scans) of enamel, the OCT signal is highly attenuated in regions of sound enamel while there is significantly more subsurface OCT back-scattered signal from demineralized regions. We attribute this to the higher porosity of demineralized enamel [23]. To quantify this observation we have analyzed the OCT signal as a function of depth into the enamel. The diagnostic potential of using the A-scan vector, the histogram of the A-scan intensities and three summary parameters (α, μ, σ) derived from the A-scan were compared. Our studies also examine the descending A-scan profile to derive the attenuation coefficient of the OCT signal that quantifies the OCT signal as a function of depth into the enamel subsurface. We observe that this value is higher in sound enamel since the intact tissue quenches the OCT signal, bringing it to the noise floor, within a shorter depth when compared to the OCT signal from more porous demineralized regions. Mujat et al. also observed that deeper lesions have greater optical path-length as compared to shallow lesions [8]. However, in contrast, they found that sound enamel had an even larger optical path-length. It is unclear why their trend was observed given their explanation for the slower decay in deeper lesions. Thus our results might seem contradictory to those reported by Mujat et al. One possible source for this discrepancy is the different wavelengths used in the studies. Mujat et al’s study used a low coherence interferometer operating at 1300 nm while our study used a 830 nm source. The optical properties of enamel will differ between these two wavelength ranges. Furthermore, it should be highlighted that the OCT attenuation coefficient parameter, used in our study should not to be confused with the scattering coefficient of the tissue.

The OCT attenuation coefficient derived from the descending slope of the A-scan has an excellent capacity to discriminate between caries and healthy enamel and has a moderate sensitivity to the level of noise of the A-scan. The noise sensitivity seems related to the consistency in selecting the starting and ending points of the descending slope of the A-scan for the fit. The parameters that characterize the lognormal fit to the histogram of the A-scan intensities have the potential of being sensitive indicators for caries but convey poor specificity. In addition reliably extracting the mean parameter for the lognormal fit from noisy A-scans is problematic. These features detract from the utility of using the lognormal parameters of the A-scan histogram or their combination as sensitive and specific markers for early caries.

An alternative and promising strategy uses the histograms of the normalized A-scans or the normalized A-scans directly as inputs to a multivariate classifier. These approaches have comparable diagnostic performance but show a marginally inferior diagnostic performance compared to the attenuation coefficient.

Our results indicate that when carefully chosen, the attenuation coefficient has excellent capacity to discriminate between sound and carious regions of human dental enamel. However, determining the attenuation coefficient requires that the descending slope of the A-scan must be first selected and then fitted thereby imparting a degree of subjectivity in determining its value particularly when faced with noisy A-scans. Thus corroboration of the diagnosis by the direct analysis of the A-scan or its intensity histogram may be beneficial and more amenable to automation.