The range of interaction between DNA-bending proteins is controlled by the second-longest correlation length for bending fluctuations

Abstract

When a DNA molecule is stretched, the zero-force correlation length for its bending fluctuations – the persistence length A – bifurcates into two different correlation lengths - the shorter “longitudinal” correlation length ξ_‖(f) and the longer “transverse” correlation length ξ_⊥(f). In the high-force limit, ${\xi }_{\Vert }(f)={\xi }_{\perp }(f)/2=\sqrt{k_{B}TA/f}/2$. When DNA-bending proteins bind to the DNA molecule, there is an effective interaction between the protein-generated bends mediated by DNA elasticity and bending fluctuations. Surprisingly, the range of this interaction is not the longest correlation length associated with transverse fluctuations of the tangent vector along the polymer, but instead is the second longest longitudinal correlation length ξ_‖ (f, μ). The effect arises from the protein-bend contribution to the Hamiltonian having an axial rotational symmetry which eliminates its coupling to the transverse fluctuations.

In living cells, binding of proteins to DNA controls gene expression and packaging of the genome [1–3], requiring DNA-binding proteins to communicate and cooperate over a wide range of length scales. Many DNA-binding proteins distort the double helix, which has led to development of micromechanical methods for analyis of protein-DNA interactions [4–7]. Notably, tension along DNA molecules can induce cooperative interactions between distant DNA-bending proteins [8–10]. Numerical analysis of a semiflexible “worm-like chain” (WLC) showed the force-generated interaction range between two quenched bends (corresponding to bound proteins) to be $\xi (f)\approx \sqrt{A/\beta f}/2$ [10], in the high-force range f > k_BT/A ≈ 0.1 pN. The dominant (longest) correlation length for the WLC is that for bending fluctuations, ${\xi }_{\perp }(f)\approx \sqrt{A/\beta f}$ [11]. Surprisingly, the protein-induced bends have an interaction range exactly half of ξ_⊥(f). Here we show that this arises from the rotational symmetry of the part of the energy describing the protein-DNA interaction. We will illustrate this for a specific model, but we will also argue that our results are general for a wide class of similar models of proteins interacting with DNA.

To investigate the force-dependent interactions between DNA-binding proteins we use a discretized WLC model including protein-binding effects [10] (essentially the model of Refs. [12] and [13]). The DNA is treated as a chain of N links each of length b, with each link able to point in any direction with a Boltzmann weight that depends on the angle between adjacent links. This form of the model allows it to be treated by “transfer matrix” [14] methods, whereby summation over individual link degrees of freedom can be reduced to matrix multiplications. This method has a long history of use in biopolymer physics, from early studies of the helix-coil transition [15], to recent studies of semiflexible polymer elasticity [16, 17].

In our model, proteins are taken to bind “nonspecifi-cally” (with no sequence-dependent affinity) to the nodes between adjacent links. The DNA-protein complex energy is a sum over the links,

$$\beta E=\sum _{i=1}^N\{\frac{a}{2}|{\widehat{t}}_{i+1}-{\widehat{t}}_i{|}^2(1-n_i)+[\frac{a\prime }{2}{({\widehat{t}}_{i+1}·{\widehat{t}}_i-\gamma )}^2-\mu ]n_i-\beta bf{\widehat{t}}_i·\widehat{z}-\eta n_i{n}_{i+1}\},$$ (1)

where t̂_i is an unit vector which describes the direction of each link, the dimensionless parameter a (= A/b) is the naked DNA bending rigidity, a′ is the rigidity of a protein-occupied node, and n_i is the protein occupation degree of freedom for the i-th node (n_i = 0 for an unoccupied node, or 1 for a protein-bound node). Protein binding is controlled by the chemical potential μ which is a function of bulk protein concentration c (μ = ln[c/c₀] where c₀ is a protein-dependent constant determining the binding affinity), and the bends induced by protein binding are described by γ = cosθ, where θ is the preferred angle between adjacent links resulting from protein binding. The DNA-protein complex is stretched by the applied force in the ẑ direction. Finally, η is the intrinsic binding cooperativity, describing the strength of direct interaction between adjacent bound proteins.

This model describes a variety of DNA-binding proteins [10, 12, 18], depending on the various parameter values chosen. For most situations of interest, the total DNA contour length L (= Nb) can be taken to be much bigger than the link length b, and a periodic boundary condition can be used (t̂_N = t̂₀). We compute the equilibrium partition function Z = Tr(T^N) following the method of Ref. [10], where T is the transfer matrix for a link

$$\mathbf{T}=\left(\begin{array}{cc}(\langle {\widehat{t}}_i,1|\mathbf{T}|{\widehat{t}}_{i+1},1\rangle )\hfill & (\langle {\widehat{t}}_i,1|\mathbf{T}|{\widehat{t}}_{i+1},0\rangle )\hfill \\ (\langle {\widehat{t}}_i,0|\mathbf{T}|{\widehat{t}}_{i+1},1\rangle )\hfill & (\langle {\widehat{t}}_i,0|\mathbf{T}|{\widehat{t}}_{i+1},0\rangle )\hfill \end{array}\right)=\left(\begin{array}{cc}\mathbf{A}{e}^{\mu +\eta }\hfill & \mathbf{A}{e}^{\mu }\hfill \\ \mathbf{B}\hfill & \mathbf{B}\hfill \end{array}\right).$$ (2)

Here A and B are matrices with elements $\langle \widehat{t}|\mathbf{A}|\widehat{t}\prime \rangle =e^{-\frac{a\prime }{2}{(\widehat{t}·\widehat{t}\prime -\gamma )}^2+\beta bf\widehat{t}·\widehat{z}}$ and $\langle \widehat{t}|\mathbf{B}|\widehat{t}\prime \rangle =e^{-\frac{a}{2}|\widehat{t}\prime -\widehat{t}{|}^2+\beta bf\widehat{t}·\widehat{z}}$.

The matrices may be expressed in terms of spherical harmonics, i.e.,

$$\langle lm|\mathbf{A}|l\prime m\prime \rangle \equiv \int d\widehat{t}\int d\widehat{t}\prime Y_{lm}^{*}(\widehat{t})\langle \widehat{t}|\mathbf{A}|\widehat{t}\prime \rangle Y_{l\prime m\prime }(\widehat{t}\prime ),$$ (3)

where the integrals are on the unit sphere. Due to axial symmetry around the stretching (z) direction, the matrix elements are diagonal in m, i.e., Eq. 3 is proportional to δ_mm′. Closed-form expressions for the matrix elements of A and B can be found in Sec. S1 of Supplemental Material [19].

Protein occupation at any node along the chain can be computed in this transfer matrix framework using the “operators” 〈t̂, n|n̂|t̂′, n′〉 = δ_t̂t̂′, δ_nn′ n, or

$$\widehat{\mathbf{n}}=\left(\begin{array}{cc}1\hfill & 0\hfill \\ 0\hfill & 0\hfill \end{array}\right),$$ (4)

where 1 and 0 stand for the unit matrix and zero matrix in the {|l,m〉} space, respectively. The average and two-point correlations for the occupation variables are

$$\langle n_i\rangle =\text{Tr}(\widehat{\mathbf{n}}{\mathbf{T}}^N)/\text{Tr}({\mathbf{T}}^N),\langle n_i{n}_{i+j}\rangle =\text{Tr}(\widehat{\mathbf{n}}{\mathbf{T}}^j\widehat{\mathbf{n}}{\mathbf{T}}^{N-j})/\text{Tr}({\mathbf{T}}^N),G^{\widehat{\mathbf{n}}}(r,f)\equiv \langle n_i{n}_{i+j}\rangle -\langle n_i\rangle \langle n_{i+j}\rangle ,$$ (5)

where G^n̂(r, f) is the protein occupation correlation function for two DNA-binding proteins separated by contour length r = jb.

The three components of the tangent vector can also be expressed as “operators”: 〈t̂, n|t̂ⁱ|t̂′, n′〉 = δ_t̂t̂′δ_nn′tⁱ, i = x,y, or z. It will be useful to express t̂^x and t̂^y in terms of raising and lowering operators t̂^± = t̂^x ± it̂^y. Matrix elements of these operators in the {|l,m〉} basis are straightforward to compute (Sec. S2 of Supplemental Material [19]).

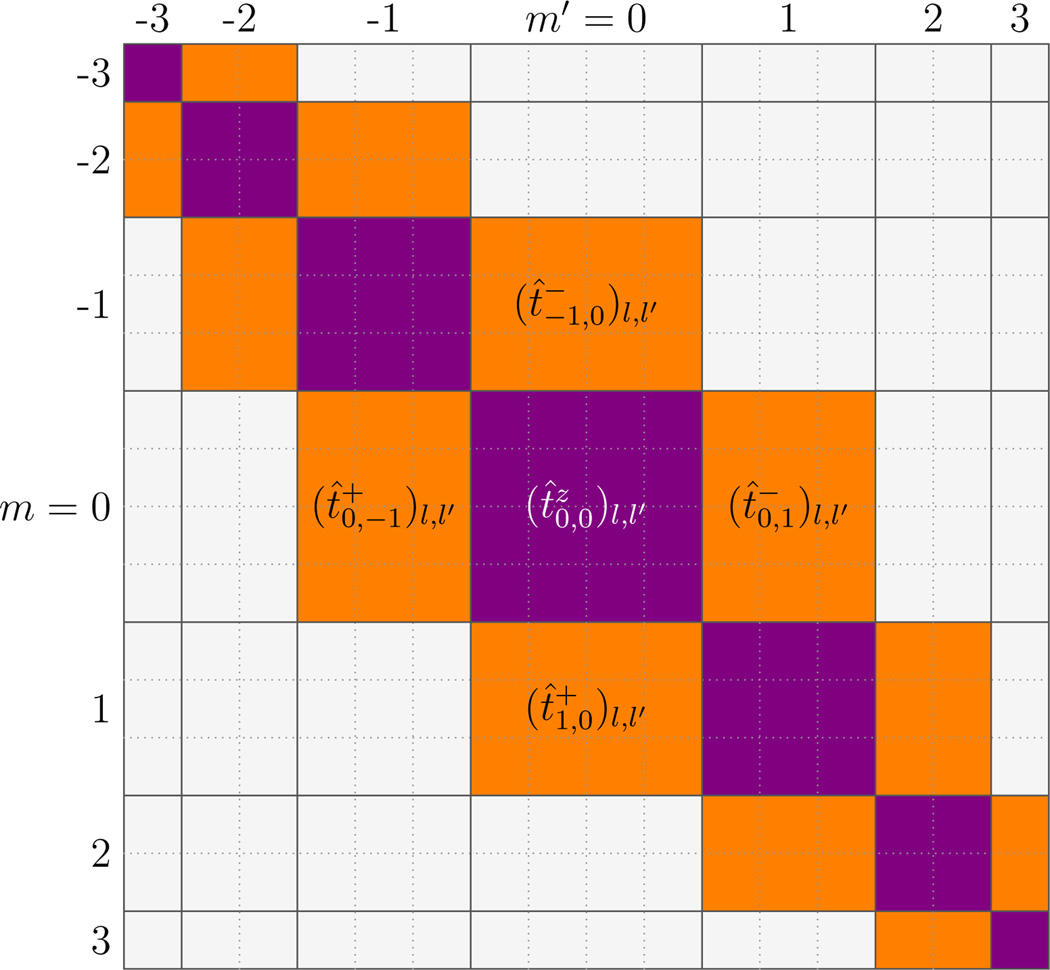
These matrices have some important symmetries; t̂^± and t̂^z are diagonal in n (for the moment we suppress the simple n-dependence of these operators). Second, t̂^z is diagonal in m due to rotational symmetry around the z direction; in the {|l,m〉} space with an appropriate order of basis vectors, t̂^z is block-diagonal (nonzero entries shown as purple or dark gray entries of Fig. 1 for l, l′ ≤ 3). On the other hand, in this basis the raising (lowering) operator t̂⁺ (t̂⁻) is a block lower (upper) next-to-diagonal matrix [nonzero entries indicated as the orange or light gray lower (upper) next-to-diagonal elements in Fig. 1].

FIG. 1.

(color online) Structure of the three tangent component operators t̂^z, t̂⁺, and t̂⁻ in {|l, m〉} space for the case l,l′ ≤ 3 (ignoring the n-dependence). For matrix t̂^z, only matrix elements along the main diagonal blocks are possibly non-zero (purple or dark gray); all other matrix elements are zero. For matrix t̂⁺ (t̂⁻, only matrix elements in the lower (upper) next-to-diagonal blocks are possibly non-zero (orange or light gray); all other matrix elements are zero.

The raising and lowering operators also have some key symmetries in the {|l,m〉} basis:

$$\begin{array}{c}\underset{\Vert }{{\widehat{\mathbf{t}}}_{l,m,n;l\prime ,m-1,n}^{+}}=-\underset{\Vert }{{\widehat{\mathbf{t}}}_{l\prime ,1-m,n;l,-m,n}^{+}}\hfill \\ {\widehat{\mathbf{t}}}_{l\prime ,m-1,n;l,m,n}^{-}=-{\widehat{\mathbf{t}}}_{l,-m,n;l\prime ,1-m,n}^{-}\hfill \end{array}.$$ (6)

The average z-component of the tangent vector is

$$\langle t_i^z\rangle =\text{Tr}({\widehat{\mathbf{t}}}^z{\mathbf{T}}^N)/\text{Tr}({\mathbf{T}}^N),$$ (7)

which also equals the molecule end-to-end extension as a fraction of total contour length. The transverse components of the tangent vector average to zero by symmetry: $\langle t_i^x\rangle =\langle t_i^y\rangle =0$.

The longitudinal correlations are

$$G^{{\widehat{\mathbf{t}}}^z}(r,f)\equiv \langle t_i^z{t}_{i+j}^z\rangle -\langle t_i^z\rangle \langle t_{i+j}^z\rangle ,\langle t_i^z{t}_{i+j}^z\rangle =\text{Tr}({\widehat{\mathbf{t}}}^z{\mathbf{T}}^j{\widehat{\mathbf{t}}}^z{\mathbf{T}}^{N-j})/\text{Tr}({\mathbf{T}}^N),$$ (8)

and the transverse correlations are

$$G^{{\widehat{\mathbf{t}}}^x}(r,f)\equiv \langle t_i^x{t}_{i+j}^x\rangle =\langle t_i^{+}{t}_{i+j}^{-}\rangle /2=G^{{\widehat{\mathbf{t}}}^y}(r,f),\langle t_i^{+}{t}_{i+j}^{-}\rangle =\text{Tr}({\widehat{\mathbf{t}}}^{+}{\mathbf{T}}^j{\widehat{\mathbf{t}}}^{-}{\mathbf{T}}^{N-j})/\text{Tr}({\mathbf{T}}^N).$$ (9)

Before studying force-generated protein-protein interactions, we examine the bending correlation lengths for naked DNA. In the absence of protein (μ = −∞, driving n_i = 0), Eq. 1 becomes a 1-d Heisenberg model. We use a segment size b = 5 nm (approximately 15 bp) and DNA bending stiffness a = 10 corresponding to persistence length A = ab = 50 nm. We consider the long-DNA limit L ≫ A for all computations, and a cutoff on l is chosen to obtain ten-digit numerical precision (typically l_max = 14). The averages of the z-component of the tangent vector 〈t̂^z〉 and the tangent vector correlation functions G^t̂z (r, f) and G^t̂x (r, f) are computed from Eqs. 7, 8 and 9 (Sec. S3 of Supplemental Material [19]). For large j, we extract correlation lengths from the expected asymptotic form of the correlation functions:

$$G^{{\widehat{\mathbf{t}}}^z}(r,f)=C_{\Vert }(f)e^{-r/{\xi }_{\Vert }(f)},$$ (10)

where ξ_‖ (f) and C_‖ (f) are the longitudinal correlation length and amplitude. Similarly, we extracted the transverse correlation length ξ_⊥(f) and amplitude C_⊥(f).

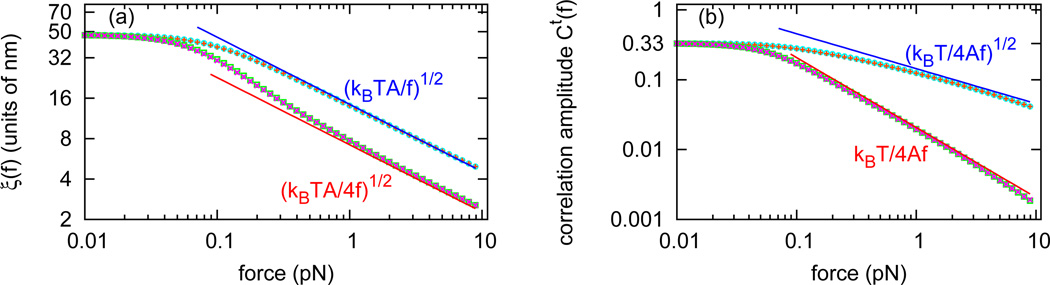
Fig. 2(a) shows ξ_‖(f) (bottom pink crosses) and ξ_⊥(f) (top orange pluses) as a function of force. For small forces, the two correlation lengths approach the same limit ξ_‖(f) ≈ ξ_⊥(f) ≈ 50 nm, the persistence length for a dsDNA. However, as force is increased, the two correlation lengths vary differently. As one enters the high-force range (f > k_BT/A ≈ 0.1 pN) the correlation lengths bifurcate into two curves, both ∼ f^−1/2 but with different coefficients: ${\xi }_{\perp }=2{\xi }_{\Vert }=\sqrt{k_{B}TA/f}$. ξ_‖(f) approaches (numerically) exactly half of ξ_⊥(f) for large forces.

FIG. 2.

(color online) Tangent vector correlation lengths and amplitudes for naked DNA. (a) The longitudinal correlation length ξ_‖(f) calculated by three different methods: by Eq. 10 (bottom pink crosses), by Eq. 11 (bottom red line), and by Eq. 13 (bottom green squares, overlapping with bottom pink crosses). The transverse correlation length ξ_⊥(f) calculated by three different methods: by Eq. 10 (top orange pluses), by Eq. 11 (top blue line), and by Eq. 13 (top aqua circles, overlapping with top orange pluses). In high-force range, ${\xi }_{\perp }(f)=2{\xi }_{\Vert }(f)=\sqrt{k_{B}TA/f}$. (b) The longitudinal correlation function amplitude C_‖(f) calculated by Eq. 10 (bottom pink crosses), agreeing with G^t̂z (0, f) (bottom green squares) and the high-force limit from Eq. 11 (bottom red line). The transverse correlation function amplitude C_⊥(f) calculated by Eq. 10 (top orange pluses), agreeing with G^t̂x (0, f) (top aqua circles) and the high-force limit from Eq. 11 (top blue line).

Fig. 2(b) shows the longitudinal correlation function amplitude C_‖ (f) (bottom pink crosses), the zero-distance correlation function G^t̂z (0, f) (bottom green squares), the transverse correlation function amplitude C_⊥(f) (top orange pluses ), and the zero-distance correlation function G^t̂x (0, f) (top aqua circles). The longitudinal amplitude is (numerically) the square of the transverse correlation function amplitude for large forces.

To analytically understand the relationship between the transverse and longitudinal correlation functions for naked DNA, we consider the high-force limit (f ≫ k_BT/A) of the continuous WLC model where a Gaussian approximation for tangent vector fluctuations becomes appropriate [11]. In this limit, since t̂ fluctuates only slightly around ẑ, then t_x and t_y are small quantities, and $t_z=1-(t_x^2+t_y^2)/2+𝒪(t_x^4+t_y^4)$. Following Ref. [11] (Sec. S4 of Supplemental Material [19]),

$$G^{{\widehat{\mathbf{t}}}^x}(r,f)=\sqrt{k_{B}T/4Af}{e}^{-r/\sqrt{k_{B}TA/f}}+\cdots ,G^{{\widehat{\mathbf{t}}}^z}(r,f)=(k_{B}T/4Af)e^{-r/\sqrt{k_{B}TA/4f}}+\cdots .$$ (11)

Therefore, the longitudinal correlation function is essentially the square of the transverse correlation function in the large force limit, indicating that ${\xi }_{\Vert }(f)=\sqrt{k_{B}TA/4f}={\xi }_{\perp }(f)/2$ and $C_{\Vert }(f)=k_{B}TA/4Af=C_{\perp }^2(f)$. Fig. 2 includes analytic results for ξ_‖(f) (Fig. 2(a), bottom red line), ξ_⊥(f) (Fig. 2(a), top blue line), C_‖(f) (Fig. 2(b), bottom red line) and C_⊥(f) (Fig. 2(b), top blue line). In the high-force range, the analytic results match our numerical calculation.

The asymptotic behaviors of the transverse and longitudinal correlation functions can also be obtained from the discrete WLC transfer matrices, using G^t̂z (r, f) and G^t̂x (r, f) defined in Eq. 8 and Eq. 9, respectively. In the large-N limit (Sec. S5 of Supplemental Material [19]),

$$G^{{\widehat{\mathbf{t}}}^z}(r,f)=\sum _{k=1}{({\mathbf{t}}_0^z)}_{0,k}{({\mathbf{t}}_0^z)}_{k,0}{\left(\frac{{\lambda }_k^0}{{\lambda }_0^0}\right)}^j,G^{{\widehat{\mathbf{t}}}^z}(r,f)=\frac{1}{2}\sum _{k=1}{({\mathbf{t}}_{0,-1}^{+})}_{0,k}{({\mathbf{t}}_{-1,0}^{-})}_{k,0}{\left(\frac{{\lambda }_k^1}{{\lambda }_0^0}\right)}^j,$$ (12)

where the ${\lambda }_k^m(m=0,\pm 1,\pm 2,\cdots ;k=|m|,|m|+1,|m|+2,\cdots )$ are the eigenvalues of the m-th diagonal block of the “naked DNA” matrix B and ${\lambda }_{|m|}^m>{\lambda }_{|m|+1}^m>{\lambda }_{|m|+2}^m>\cdots$. Sec. S6 of the Supplemental Material [19] shows how applied force f affects the eigenvalues $\{{\lambda }_k^m\}$, i.e., the transfer matrix spectrum of naked DNA.

${({\mathbf{t}}_m^z)}_{k_1,k_2}$ is the matrix element of the m-th diagonal block of the matrix t̂^z (ignoring n-dependence) expressed by taking the eigenvectors of the m-th diagonal block of the naked matrix B $(\{|{\lambda }_k^m\rangle \})$ as the basis, ${({\mathbf{t}}_m^z)}_{k_1,k_2}=\langle {\lambda }_{k_1}^m|{\widehat{\mathbf{t}}}_m^z|{\lambda }_{k_2}^m\rangle$ Similarly, ${({\mathbf{t}}_{m,m-1}^{+})}_{k_1,k_2}=\langle {\lambda }_{k_1}^m|{\widehat{\mathbf{t}}}_{m,m-1}^{+}|{\lambda }_{k_2}^{m-1}\rangle$ and ${({\mathbf{t}}_{m,m-1}^{-})}_{k_1,k_2}=\langle {\lambda }_{k_1}^{m-1}|{\widehat{\mathbf{t}}}_{m-1,m}^{-}|{\lambda }_{k_2}^m\rangle$.

For large distances (large j) the correlation functions (12) is dominated by the k = 1 contributions, giving

$${\xi }_{\Vert }(f)=\frac{b}{\text{ln}({\lambda }_0^0/{\lambda }_1^0)},{\xi }_{\perp }(f)=\frac{b}{\text{ln}({\lambda }_0^0/{\lambda }_1^1)}.$$ (13)

We have verified that the calculated results of ξ_‖ (f) and ξ_⊥(f) by Eq. 13 computed by matrix diagonalization [bottom green squares and top aqua circles in Fig. 2(a)] match the result computed directly from the multiplication of matrices [compare to bottom pink crosses and top orange pluses in Fig. 2(a)].

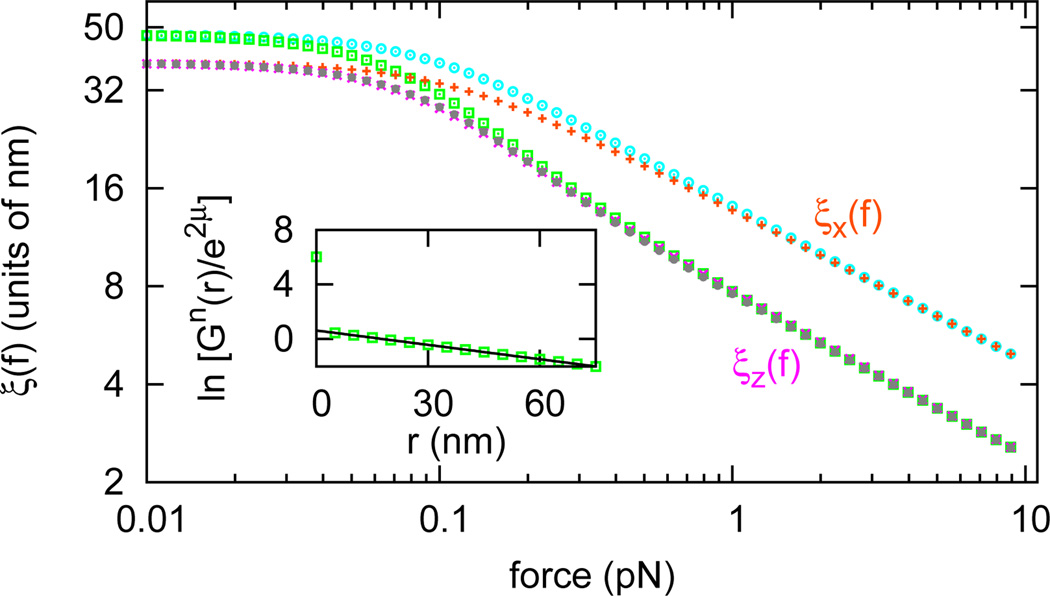
We now consider the interaction between DNA-bending proteins. We computed the protein occupation correlation function G^n̂ (r, f) along a DNA in dilute protein solution, the decay of which provides the correlation length for the inter-protein interaction, for the case γ = 0 and a′ = 50, corresponding to a rather stiff protein-DNA complex with a preferred bend angle of 90°. We extract the protein occupancy correlation length, just as in Eq. 10; the result for μ = −5 and η = 0 is shown in Fig. 3 (bottom grey filled circles; also see Sec. S7 of Supplemental Material [19]). For comparison, in Fig. 3 we also show the tangent vector correlation lengths of protein-bound DNA (bottom pink crosses and top orange pluses) and those of naked DNA (bottom green squares and top aqua circles).

FIG. 3.

(color online) Protein occupation correlation length along DNA (bottom grey filled circles) in dilute protein solution (μ = −5, η = 0, γ = 0, a′ = 50). For reference, the tangent vector correlation lengths along DNA in the same solution (bottom pink crosses and top orange pluses) and those along a naked DNA (bottom green squares and top aqua circles) are shown. Inset shows ln[G^n̂(r)/e^2μ] vs. distance at f = 0.1 pN (green squares) and a linear fit of it (black line).

Fig. 3 reveals that the protein occupancy correlation length is equal to the longitudinal tangent vector correlation length ξ_‖(f, μ). This can be understood from the diagonal-in-m form (Fig. 1) of the protein occupancy matrix n̂, which is shared by A, t̂^z, and B reflecting their axial rotational symmetry. For the protein occupancy correlation function, just as for G^t̂z (r, f), blocks of different m are decoupled, leading to the correlation function decay being determined by the largest two eigenvalues of the (m = 0)th diagonal blocks of transfer matrix T, which has the largest eigenvalue of T. Thus, the correlation function of the protein occupation degrees of freedom have a decay length of ξ_‖ (f,μ). For large forces, this is exactly half of the longest correlation length in the problem, that of ξ_⊥(f, μ); this longer transverse correlation length arises from the off-block-diagonal structure of t̂^± which allows selection of the two largest eigenvalues from any two adjacent diagonal blocks of T. The protein occupancy operator n̂ has higher symmetry (Eq. 4), which makes $\langle n_i^2\rangle =\langle n_i\rangle$ and explains the jump of protein occupation correlation function at r = 0.

Our main result, namely ξ_‖ being the range of protein-protein interactions mediated by bending fluctuations along a stretched DNA, follows from the rotational symmetry of the protein-DNA interaction operator A. This result is general for proteins which distort DNA structure as long as the distortions are isotropically distributed around the double helix axis (the same result follows for other values of γ, a′ and μ, Sec. S8 of Supplemental Material [19]). For non-sequence-specific binding this will be the case since two proteins may bind in essentially any relative axial orientation by shifting their binding positions over a 10.5 base-pair range (the h ≈ 3.6 nm helix repeat for dsDNA), a length scale small relative to the inter-protein separations we are considering. Twist fluctuations of inter-protein DNA will further randomize the relative axial orientation of pairs of DNA-bound proteins. Of course, for very large forces where ξ_‖ becomes comparable to h, a more detailed model taking into account the helix structure would need to be employed, but in that regime, with ξ_‖ comparable in size to a typical DNA-binding protein, one would expect direct interactions between adjacent proteins to dominate (Sec. S7 of Supplemental Material [19]).

One might ask whether the longer ξ_⊥ can ever be the protein-protein interaction range. This would require the relative angular orientations of the two proteins around the axial (stretching) direction to be fixed: one might imagine using a sequence-specific DNA-binding protein and binding sites “phased” to be at the same orientation around the double helix (spaced multiples of 10.5 bp) in an attempt to do this. However, since angular (twist) fluctuations between the two sites will increase with in-terprotein distance, one would expect to see an interaction decaying with the longer ξ_⊥only at short distances, with the shorter ξ_‖ dominating at longer distances.

Finally we note that while the individual protein-generated distortions considered here are isotropically distributed around the double helix axis, the relative orientation of two nearby bends can be expected to be angularly correlated. This arises from the fact that two oppositely-directed bends of the double helix compensate one another’s distortion [8–10]. Therefore one can expect force on a DNA to direct the self-organization of DNA-bending-proteins into clusters (via the interaction we have analyzed) with correlated bend directions. If the bends are chiral (the general case since DNA and proteins are both chiral), nearby proteins will be chirally organized, i.e. forming locally helical DNA-protein complexes. An important case is that of nucleosomes, which have well-defined entry/exit angles for the DNA bound to them, with broken chiral symmetry; moderate applied tension can be expected to drive the packing and helical organization of adjacent nucleosomes in chromatin.