The Nuisance of Nuisance Regression: Spectral Misspecification in a Common Approach to Resting-State fMRI Preprocessing Reintroduces Noise and Obscures Functional Connectivity

Abstract

Recent resting-state functional connectivity fMRI (RS-fcMRI) research has demonstrated that head motion during fMRI acquisition systematically influences connectivity estimates despite bandpass filtering and nuisance regression, which are intended to reduce such nuisance variability. We provide evidence that the effects of head motion and other nuisance signals are poorly controlled when the fMRI time series are bandpass-filtered but the regressors are unfiltered, resulting in the inadvertent reintroduction of nuisance-related variation into frequencies previously suppressed by the bandpass filter, as well as suboptimal correction for noise signals in the frequencies of interest. This is important because many RS-fcMRI studies, including some focusing on motion-related artifacts, have applied this approach. In two cohorts of individuals (n = 117 and 22) who completed resting-state fMRI scans, we found that the bandpass-regress approach consistently overestimated functional connectivity across the brain, typically on the order of r = .10 – .35, relative to a simultaneous bandpass filtering and nuisance regression approach. Inflated correlations under the bandpass-regress approach were associated with head motion and cardiac artifacts. Furthermore, distance-related differences in the association of head motion and connectivity estimates were much weaker for the simultaneous filtering approach. We recommend that future RS-fcMRI studies ensure that the frequencies of nuisance regressors and fMRI data match prior to nuisance regression, and we advocate a simultaneous bandpass filtering and nuisance regression strategy that better controls nuisance-related variability.

1. Introduction

Resting-state functional connectivity magnetic resonance imaging (RS-fcMRI) is a dominant method for characterizing the human functional connectome (Cole et al., 2010; Van Essen and Ugurbil, 2012). In RS-fcMRI, the blood-oxygen-level-dependent (BOLD) contrast is measured for several minutes in an MR scanner while the subject remains passive (Biswal et al., 2010). The BOLD signal measures metabolic changes that result from neural activity (Magri et al., 2012), and during resting-state fMRI, BOLD fluctuations reflect spontaneous neural activity, which are strongest in the .009 Hz – .08 Hz frequency range (He et al., 2008; Schölvinck et al., 2010). Correlations of RS-fcMRI time series across brain regions reflect intrinsic functional connectivity (i.e., interactivity among functionally related populations of neurons; Van Dijk et al., 2010), and numerous studies on this topic have contributed greatly to the elucidation of the functional architecture of the human brain (Bucker et al., 2011; Fair et al., 2007; Fox et al., 2005). The RS-fcMRI method has also stimulated research investigating the development of brain networks in children and adolescents (Dosenbach et al., 2010; Fair et al., 2007; Stevens et al., 2009; Supekar et al., 2009), as well as potentially maladaptive network differences in individuals with psychiatric disorders (Church et al., 2009; Cole et al., 2011; Seeley et al., 2009).

Relative to task-based fMRI studies, signal processing in seed-based correlation analyses of resting-state fMRI data typically includes two additional steps: 1) bandpass filtering of voxel time series into the low-frequency range, typically 0.009–0.08 Hz (but see Jo et al., 2010); and 2) regression of additional sources of noise, including estimates of individual head motion, average BOLD signals in the white matter and ventricles, and controversially, the average BOLD signal across all brain voxels (Murphy et al., 2009). These steps are often performed in the above order and are intended to reduce or eliminate temporally synchronous artifacts in resting-state fMRI time series that could be mistaken for neural activation and functional coupling. Nuisance regression seeks to attenuate non-neural BOLD fluctuations from measurable noise sources such as scanner drift and head motion, as well as periodic physiological signals (e.g., heartbeat and respiration; Birn et al., 2008; Chang et al., 2009), whereas bandpass filtering suppresses all variability in a range of frequencies that are a priori not of interest.

Relatively little research has explored the optimal approach for applying bandpass filtering and nuisance regression to RS-fcMRI data (cf. Weissenbacher et al., 2009). In our study, we considered three possibilities: 1) bandpass filtering followed by nuisance regression (BpReg); 2) regression followed by bandpass filtering (RegBp); and 3) simultaneous bandpass filtering and regression (Simult). Bandpass filtering and nuisance regression can both be conceptualized as linear filters of the data—that is, the filtered signal, y, is a linear transformation of the original signal, x: y_t = J_t{x}, where the transformation operator J linearly maps every value of x to a transformed value of y at each time t. When two linear filters are orthogonal to each other, the output signal is the same regardless of which filter is applied first (Jenkins and Watts, 1968). Nuisance regressors (e.g., motion parameters) and bandpass filter coefficients, however, are unlikely to be orthogonal because noise sources typically include power at frequencies in the stopband (i.e., the frequencies to be suppressed), leading to statistical dependency between the spectral filter and nuisance regressors. Thus, the manner in which bandpass filtering and nuisance regression are applied to RS-fcMRI data may affect the quality of noise in RS-fcMRI data, as well as estimates of functional connectivity.

Using simultated time series and empirical RS-fcMRI data, we demonstrate that the nuisance regression model is misspecified in the frequency domain when the fMRI time series are bandpass filtered but one or more regressors are unfiltered, resulting in the reintrouduction of temporally synchronous nuisance-related variation into frequencies previously suppressed by the bandpass filter, as well as suboptimal correction for nuisance signals in the frequencies of interest. This paradoxical reintroduction of nuisance variation is contrary to the underlying goal of the regression, yet our review of the RS-fcMRI literature below indicates that the bandpass-regress (BpReg) approach is common, although not universal. By contrast, there is no frequency mismatch in the nuisance regression for bandpass filtering after regression (RegBp) and simultaneous filtering (Simult), so these approaches do not suffer from the same flaw.

The potential for ill effects of nuisance regression on connectivity estimates is topical in light of compelling evidence from three contemporaneous papers demonstrating that head motion during RS-fcMRI acquisition confounds estimates of functional connectivity (Van Dijk et al., 2012; Power et al., 2012a; Satterthwaite et al., 2012). Specifically, the relationship between head motion magnitude and connectivity estimates was spatially structured such that greater head motion was associated with increased estimates of short-range connectivity and potentially suppressed estimates of long-range connectivity. However, two of these studies used the BpReg approach for the head motion regressors such that the fMRI data were bandpass filtered, whereas motion parameters were not (K. Van Dijk, personal communication, December 18, 2012; Van Dijk et al., 2012; J. D. Power, personal communication, June 26, 2012; Power et al., 2012a); the other report conducted nuisance regression prior to bandpass filtering (i.e., RegBp; T. Satterthwaite, personal communication, November 13, 2012; Satterthwaite et al., 2012). This raises the possibility that the effects of head motion on connectivity estimates may partially reflect nuisance variability reintroduced by BpReg.

In addition, Power and colleagues observed that motion-related fluctuations in the overall BOLD signal contaminated RS-fcMRI time series despite bandpass filtering and nuisance regression (also see Friston et al., 1996), potentially biasing connectivity estimates. To attenuate motion-related artifacts, they suggested censoring volumes surrounding periods of large head motion prior to computing correlations among brain regions. As our results suggest, however, motion-related fluctuations using the BpReg approach may reflect the inadvertent reintroduction of nuisance variation into the RS-fcMRI time series by the BpReg approach. Conversely, the appropriate application of bandpass filtering and nuisance regression using the RegBp or Simult approaches may help to mitigate motion-related artifacts.

Out study sought to characterize the effects of bandpass filtering and nuisance regression on estimates of functional connectivity using seed-based correlational analyses, as well as differences among processing approaches in the quality and magnitude of noise in RS-fcMRI signals, particularly motion-related artifacts. In order to develop best-practice recommendations and to quantify the prevalence of the BpReg approach, we also reviewed the use of bandpass filtering and nuisance regression in a subset of RS-fcMRI studies. A secondary goal was to characterize whether the distance-connectivity association differed between the Simult and BpReg approaches. To address these questions, we analyzed resting state fMRI data from two cohorts: one collected at the University of Pittsburgh that included children, adolescents, and young adults; and a smaller cohort of children collected at Washington University in which motion-related changes in connectivity estimates were previously described by Power and colleagues (2012a).

2. Methods

2.1. Data Acquisition

2.1.1. University of Pittsburgh cohort (UPitt)

Participants in the University of Pittsburgh cohort were 117 normally developing individuals (M age = 15.4, SD = 2.96, range = 10.11 – 20.01). Experimental procedures for this study complied with the Code of Ethics of the World Medical Association (1964 Declaration of Helsinki) and the Institutional Review Board at the University of Pittsburgh. Subjects or their guardians provided informed consent and subjects were paid for their participation.

Participants completed a single five-minute resting-state fMRI scan (200 volumes) acquired in a Siemens (Erlangen, Germany) 3T Tim Trio MR scanner. During the resting-state scan, which occurred after a task-related acquisition for a separate study, participants were asked to close their eyes and relax, but not to fall asleep. Prior to scanning, all participants spent 15 minutes in a mock MRI scanner to acclimate them to the MR environment before entering the research scanner. Structural images were acquired using a sagittal magnetization-prepared rapid gradient-echo (MP-RAGE) sequence (TR = 1570 ms, TE = 3.04 ms, flip angle = 8°, TI = 800 ms, voxel size = .78125 × .78125 × l mm). Functional images were acquired using an echo-planar sequence sensitive to the blood oxygen level dependent (BOLD) contrast [T2*] (TR=1.5 s, TE = 29 ms, flip angle = 70°, voxel size = 3.125 × 3.125 mm in-plane resolution, 29 contiguous 4-mm axial slices). During fMRI acquisition, heartbeat was continuously recorded using a pulse oximeter attached to the left index finger. Due to equipment malfunction in eight individuals, heartbeat data were successfully recorded in 109 participants.

As is typical of developmental studies (e.g., Satterthwaite et al., 2012), younger participants in this cohort exhibited greater head movement than older participants. The correlation between overall head movement and age was r(115) = −.35, p = .0001).

2.1.2. Washington University cohort (WashU)

Participants in the Washington University cohort were 22 subjects aged 7 to 9 years, previously described as “cohort 1” in an article by Power and colleagues (2012a). These data were collected at Washington University in St. Louis using a Siemens 3T Tim Trio scanner (for additional details, see Power et al., 2012a). Physiological signals were not recorded for this cohort. These data were generously provided to the scientific community by Power and colleagues and are publicly available at http://fcon_1000.projects.nitrc.org/.

2.2. Data Analyses

2.2.1. fMRI data preprocessing

Imaging data were preprocessed using AFNI (Analysis of Functional Neuro-Images) (Cox, 1996) and FSL (Smith et al. 2004). The following conventional fMRI preprocessing steps were applied: 1) Slice-timing correction using quintic interpolation (AFNI 3dTshift); 2) Alignment between the structural image and the third functional volume, using six-parameter rigid body transformation (AFNI @auto_tlrc); 3) estimation of six rigid body motion correction parameters (translation and rotation parameters in the x, y, and z dimensions) that co-register each functional volume to a reference volume (AFNI 3dvolreg using the third volume as the registration target); 4) Estimation of a 12-parameter affine transformation to warp the structural image to the Montreal Neurological Institute (MNI)-152 template (AFNI @auto_tlrc using the template distributed with FSL software version 4.1.9); 5) Combination of motion correction parameters and atlas transformation matrix into a single interpolation step, and resampling all functional volumes into the atlas space using sinc interpolation (AFNI 3dAllineate); 6) Scaling of each voxel time series to a mean value of 1000 (AFNI 3dTstat and 3dcalc); and 7) Spatial smoothing using 6 mm full width at half maximum kernel (AFNI 3dBlurInMask).

2.2.2 RS-fcMRI data preprocessing

The magnitude of participant head motion was quantified by computing the average relative root mean squared deviation (measured in mm), representing the average total displacement from one frame to the next (integrating the rotational and translational parameters; Jenkinson, 1999), and average framewise displacement (FD), which also integrates rotational and translational motion by converting rotational motion into a displacement value by projecting onto a 50mm sphere (Power et al., 2012a). The framewise change in the global BOLD signal for all brain voxels was computed as the average root mean square variance across voxels of the temporal derivative of the fMRI time series (DVARS; Power et al., 2012a). Descriptive statistics for head motion in the two cohorts are reported in Table 1.

Table 1.

Average magnitude of head motion for the sample

Cohort		n	Mean RMS Deviation (SD)	Mean FD (SD)
UPitt	Children (10 – 12)	33	.149 (.108)	.265 (.195)
	Adolescents (13 – 17)	57	.107 (.094)	.195 (.163)
	Adults (18–20)	27	.081 (.032)	.152 (.060)
	Entire Sample	117	0.112 (.072)	.204 (.160)
WashU		22	.133 (.071)	.292 (.150)

Note. FD = Framewise Displacement.

To reduce the impact of non-neural noise sources on estimates of resting-state functional connectivity, RS-fcMRI time series were bandpass filtered (.009 – .08 Hz) and multiple nuisance sources were removed from the RS-fcMRI voxel time series using ordinary least squares regression (Weissenbacher et al., 2009). To obtain regressors for non-neural noise sources, Freesurfer software (version 5.1; Fischl et al., 2002) was used to segment structural MRI scans into gray matter, white matter, ventricle, and non-brain tissues for each subject. Masks for white matter and ventricle tissue were derived from the Freesurfer parcellation, and to reduce the risk of partial volume effects, these masks were eroded twice to ensure that only deep white matter and ventricle voxels were retained. Nuisance variables included the white matter BOLD signal averaged from deep cerebral white matter voxels; the ventricle BOLD signal averaged from the ventricle mask; the whole-brain signal averaged computed as the mean of all brain voxels; six motion parameters; and the derivatives of all these repressors (a total of 18 regressors). In order to investigate the optimal approach for applying bandpass filtering and nuisance regression to RS-fcMRI data, we varied the order of these steps. For the BpReg approach, functional imaging data were bandpass filtered before multiple regression, whereas nuisance regressors were not bandpass filtered. For the RegBp approach, nuisance regression was performed on preprocessed functional data, and the residuals from the regression model were bandpass filtered. For the Simult approach, both the fMRI data and 18 nuisance regressors were filtered into the .009–.08 Hz range prior to nuisance regression. This approach was accomplished by the 3dBandpass program in AFNI (Cox, 1996), which converts each time series into the frequency domain using the fast Fourier transform (FFT), suppresses fluctuations at the stopband frequencies, and reconstructs the filtered signal using the inverse FFT. More specifically, for our data, the 3dBandpass filter was a finite impulse response filter based on a 200-point FFT transform of the voxel time series with a 5% taper of the data at the high- and low-frequency cutoffs. To mitigate possible ringing artifacts (Carp, in press), prior to bandpass filtering, spikes in voxel time series were reduced by interpolating extreme values using information from temporally proximate volumes by the AFNI program 3dDespike.

2.2.3. Simultaneous bandpass filtering and nuisance regression (Simult)

Spectral filtering and nuisance regression can be combined into a single filter within a multiple regression framework where the regressors include non-neural sources of noise (e.g., the average cerebrospinal fluid signal), as well as sinusoidal components at the frequencies to be suppressed (see online supplement S1 for an explanation of the mathematical underpinnings). A numerically equivalent and computationally faster approach to simultaneous filtering is to bandpass filter both the fMRI time series and nuisance regressors to the same frequency range, then to regress the filtered fMRI time series on the filtered regressors, and this was the approach taken for the analyses in our study (using the AFNI program 3dBandpass). The equivalence of these approaches inheres from the fact that parameter estimates in multiple regression represent partial coefficients, where each coefficient is the increment in the dependent variable for a one unit change in a given independent variable, holding constant all other independent variables (i.e., its unique contribution). In effect, by removing statistical dependency among all independent variables in the model, the multiple regression approach bandpass filters both the fMRI data and the regressors (see online supplement S1 for more detail).

2.2.4. Statistical analyses

To provide a comprehensive sampling of functional brain regions, 264 regions of interest (ROIs) were derived from previous meta-analyses of task and resting-state fMRI data (Power et al., 2010; Table S1). Each ROI was defined by a 5mm radius sphere centered at published peak coordinates in the MNI-152 stereotactic space. For the UPitt cohort, 20 ROIs from the original set of 264 regions (Power et al., 2012a) were excluded because of poor coverage by our EPI sequence (especially of inferior cerebellar ROIs), leaving 244 ROIs. Estimates of auto-spectrum and cross-spectrum power for fMRI and nuisance regressor time series were computed using five orthogonal discrete prolate spheroidal sequence tapers (Percival and Walden, 1993). Spectral estimates were computed for each ROI and were divided into 200 frequency bins (where each bin had a resolution of approximately 0.0033 Hz).

Frequency and ROI were crossed random effects nested within subject such that all subjects had spectral estimates for all ROIs, but the ROIs and frequencies sampled are a random subset of possible brain regions and frequency bins that could be interrogated. Given this data structure, linear mixed models were optimal for analyzing the large number of clustered observations (Snijders and Bosker, 1999). One advantage of mixed models is that the empirical best linear unbiased predictors (EBLUPs) for each of the random effects can be derived, which provide estimates of spectral density variability for each subject, ROI, or frequency. Mixed models of auto- and cross-spectrum power were computed using the lme4 (Bates et al., 2011) package for R (R Development Core Team, 2011). Because the number of parameters and the computation of degrees of freedom for hypothesis tests in mixed models is not well-defined (Baayen et al., 2008), and to control for familywise error, a single general linear hypothesis test was computed for each model using the multivariate distribution of the coefficients of interest. Adjused p-values are reported such that the Type I familywise error rate is less than.05 per model (Hothorn et al., 2008; Westfall, 1997).

Heartbeat signals collected for the UPitt cohort were used to create RETROICOR regressors for each axial slice that represented cardiac-related fluctuations in the fMRI time series at the time of image acquisition. The RETROICOR approach models physiological fluctuations using a low-order Fourier series that quantifies the phase of the BOLD signal relative to the cardiac cycle (Glover et al., 2000). Because our study was specifically interested in characterizing the types of noise that are evident in RS-fcMRI time series, we did not use the RETROICOR regression approach to mitigate cardiac artifacts. Rather, RETROICOR data were used to characterize whether the strength of cardiac artifacts in RS-fcMRI time series differed among preprocessing approaches. Thus, for most primary analyses, results are reported for all 117 participants, whereas for cardiac-connectivity results, only 109 participants were available.

To quantify the association between head motion and average functional connectivity strength, for analyses of BpReg and Simult data, we computed the correlations between head motion (average framewise displacement per subject) and functional connectivity for each of the pairwise functional connections (cf. Satterthwaite et al., 2012). This analysis yielded a single 264×264 correlation matrix per approach where each value represented the strength of association between motion and a given pairwise connection. Because this matrix was generated by correlating the vector of per-subject average FD values with pairwise connectivity estimates across subjects, there is a potential for bias in the mean of motion–connectivity estimates that could be attributable to covariance among the connectivity estimates. To mitigate this concern, we tested the statistical significance of mean motion-connectivity correlations using nonparametric permutation tests. More specifically, for each approach, we randomly permuted the per-subject average FD vector 10,000 times and computed the mean of the permuted FD–pairwise connectivity absolute correlations for each permutation. These estimates formed an empirically derived null distribution that was used to test the significance of the observed motion–connectivity means. Because no alterations were made to the mean or covariance structure of the connectivity estimates, any source of bias due to the non-independent correlations of mean FD with pairwise connectivity strength across subjects would have been equivalent across permutations and between approaches. In a similar fashion, to test for differences in the strength of motion–connectivity associations between BpReg and Simult, for each permutation of the mean FD vector, we computed the average difference in motion–connectivity estimates between BpReg and Simult.

2.3. RS-fcMRI preprocessing literature review

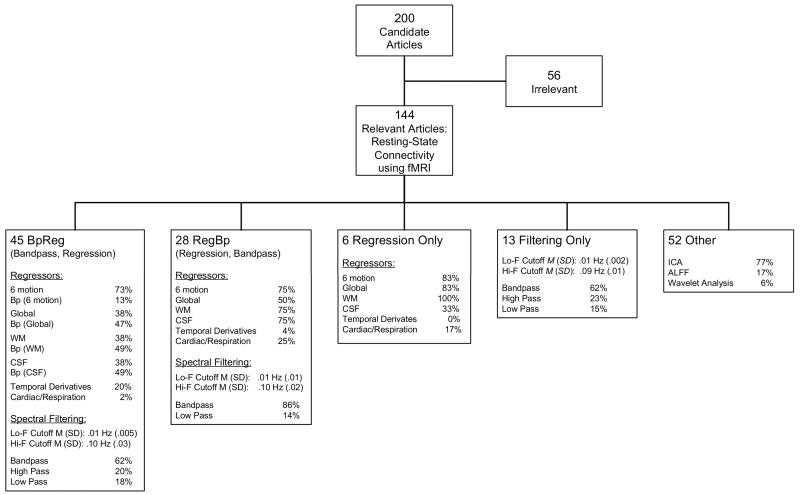
In order to characterize preprocessing practices in RS-fcMRI research, we conducted a literature search for relevant studies using the PubMed database (http://www.ncbi.nlm.nih.gov/pubmed) on August 27^th, 2012. Specifically, the query “resting state”[Title/Abstract] OR resting[Title/Abstract]) AND (connectivity[Title/Abstract] OR correlation[Title/Abstract] OR network[Title/Abstract]) was used to identify studies that might be relevant to resting-state brain connectivity research. This query resulted in 1415 candidate articles. To reduce the burden associated with reviewing each of these manuscripts while still pursuing an accurate summary of preprocessing practices in RS-fcMRI research, we randomly sampled 200 articles from this list and reviewed their content and methods. To be eligible for inclusion in the review, studies had to meet the following criteria: 1) primary empirical source; 2) use fMRI as the imaging modality; 3) report analyses of resting-state fMRI scans; and 4) include a focus on brain networks or connectivity in the title or abstract. On the basis of these criteria, 56 of the possible articles were excluded from consideration¹. In addition, because our study focused on the use of bandpass filtering and nuisance regression in seed-based correlation analyses, we categorized, other popular analytic methods for RS-fcMRI data, such as independent components analysis (ICA; Calhoun et al., 2009), as “Other,” and did not report preprocessing details here.

In cases where the preprocessing steps were not clearly explicated in the manuscript, primary authors were contacted by email to clarify their approach. Also, because studies that conducted nuisance regression after bandpass filtering of fMRI data (i.e., BpReg) may also have bandpass filtered the regressors, but not reported this in the manuscript, all authors of BpReg articles were contacted to verify the frequencies represented in the nuisance regression, as well as the order of the preprocessing steps. Twenty-nine authors (62%) replied to our email inquiry.

3. Results

3.1. Proof of concept: BpReg reintroduces nuisance variation into stopband frequencies and poorly attenuates nuisance variation in the passband

To illustrate the key point that the regression of a bandpass-filtered fMRI time series on full-spectrum nuisance regressors (BpReg) results in considerable distortion of the fMRI signal, we begin with a toy example of two simple periodic time series. First, consider a contrived resting-state fMRI time series, X, sampled for 200s with a TR of 1s. The series is composed of four sinusoidal components at .02, .035, .11, and .25 Hz and is displayed in Figure 1:

$$X=\sum _{t=1}^n\sin \left(2\pi t\frac{4}{n}\right)+\sin \left(2\pi t\frac{7}{n}\right)+\cos \left(2\pi t\frac{22}{n}\right)+\cos \left(2\pi t\frac{50}{n}\right)$$

where n = 200. The raw periodogram of this series has four peaks at the expected frequencies and no sinusoidal components at other frequencies (Figure 1, X). Conventional RS-fcMRI signal processing approaches would suppress the two high-frequency components of X using a bandpass filter, 0.009 HZ < f < 0.08 Hz, which would retain the two low-frequency components of the original signal at .02 and .035 Hz (Figure 1, X_low).

Figure 1.

The effects of bandpass filtering and nuisance regression on the spectral composition of simulated time series. The left panel depicts the simulated time series, X and C, over time, as well as X following different approaches to bandpass regression and nuisance regression. The right panel depicts the spectral power of the series, and vertical gray rectangles denote the nuisance frequencies present in C that one wishes to suppress. Xlow contains the low frequency components of X after bandpass filtering, .009 Hz < f < .08 Hz. RegBp = nuisance regression, then bandpass filtering; Simult = simultaneous bandpass filtering and nuisance regression; BpReg = bandpass filtering, then nuisance regression.

Next, consider a periodic signal, M, representing participant motion during the 200s fMRI acquisition, composed of sinusoidal frequencies at 0.06, 0.2, 0.3, and 0.4 Hz, depicted in Figure 1:

$$M=\sum _{t=1}^n\cos \left(2\pi t\frac{12}{n}\right)+\cos \left(2\pi t\frac{40}{n}\right)+\sin \left(2\pi t\frac{60}{n}\right)+\cos \left(2\pi t\frac{80}{n}\right)$$

The motion signal was mixed with the original fMRI signal, X, to yield a motion-corrupted fMRI signal,

$$C=X+.8M_{.06Hz}+.6M_{.2Hz}+.4M_{.3Hz}+.2M_{.4Hz}$$

Here, the relationship between the motion signal, M, and corrupted fMRI signal, C, followed a gradient such that lower-frequency components were associated with larger signal fluctuations. This scaling helped to differentiate among the approaches described below and crudely represents the possibility that the effects of motion on the MR signal vary across the spectrum (cf. Figures S2 and S3 in the online supplement). In this circumstance, because M is composed of four sinusoidal components of equal amplitude, the expected linear relationship between C and M is the average of the weights used to combine M with X: E(β) = (0.8 + 0.6 + 0.4 + 0.2)/4 = 0.5. The periodogram of the corrupted MR signal, C, depicts the four MR periodicities in X, as well as the four motion frequencies in M (Figure 1). The motion-corrupted signal, C, was intended to represent what would be observed in empirical RS-fcMRI data tha have motion-related intensity fluctuations.

To eliminate the bivariate association between M and C, we used ordinary least squares linear regression, which is conventional in RS-fcMRI:

$${\mathbf{Y}}_t={\mathbf{X}}_{t\times p}{\beta }_{p\times 1}+{\epsilon }_t$$

where there are t times of observation, p nuisance signals, and the residual represents the discrepancy between the model estimate of Y_t and its observed value: ${\epsilon }_t={\mathbf{Y}}_t-{\widehat{\mathbf{Y}}}_t$.

Three approaches to bandpass filtering the nuisance regression were tested : 1) bandpass filtering of C followed by regression on M, (BpReg); 2) regression of C on M followed by bandpass filtering (RegBp); and 3) simultaneous regression and bandpass filtering (Simult). For clarity, the following notation is used. Application of a bandpass filter .009 Hz < f < .08 Hz is denoted: B(X). Regression of the corrupted MR signal on the motion regressor is denoted C ~ M, and the residuals of the regression are denoted R(C ~ M). We also compared these filtering approaches to the RS-fcMRI signal prior to bandpass filtering and nuisance regression (Raw), but after slice timing correction, motion correction, intensity normalization, and spatial smoothing.

3.1.1. BpReg: bandpass filter, then nuisance regression, R(B(C)~ M)

First, we computed the regression of B(C) on M, which is the predominant convention in RS-fcMRI research. The estimate of the motion effect was: $\widehat{\beta }=.20$, t(198) = 3.49, p = .0006, model R² = 0.06. This parameter estimate does not follow intuitively from the simulation of the time series and suggests that the model is misspecified. As shown above, the expected relationship between C and M at .06 Hz is 0.8 (the mixing weight). No relationship can exist between B(C) and M at 0.2, 0.3, or 0.4 Hz because these frequencies have been removed from C by the bandpass filter. Thus, the parameter estimate of 0.2 reflects the average relationship between B(C) and M at each of the frequencies present in M: (0.8 + 0.0 + 0.0 + 0.0)/4 = 0.2. This is a form of model misspecification in the frequency domain where the relationship between the dependent variable, B(C), and the independent variable, M, is non-constant across the spectrum (Eagle, 1974).

The BpReg signal is a poor approximation of the target MR signal, X_low, r = 0.65. Also troubling is that the variance explained by nuisance regression for the bandpass-regress approach is approximately half that explained under the Simult approach (see 3.1.3), suggesting soboptimal attenuation of the motion signal by BpReg. Indeed, the 0.6 Hz component of the BpReg signal is only reduced by a factor of 1.87 relative to C (i.e., a decrease of 2.71dB). In addition, the periodogram of the BpReg signal has spectral power not only at .06 Hz, but also at 0.2, 0.3 and 0.4 Hz, the high-frequency components of M, and this high-frequency fluctuation is visually evident in the signal (Figure 1, BpReg). Thus, the nuisance regression reintroduces high-frequency variability into the MR signal previously suppressed by the bandpass filter, effectively “leaking” spectral power precisely at the frequencies present in the original motion signal, M.

In time series regression, parameter estimates tend to be dominated by the strongest frequency components present in the series because these are associated with the greatest variability (Engle, 1974). Consequently, the estimated association between B(C) and M is influenced by the .06 Hz component, and although there can be no association between B(C) and M at 0.2, 0.3, or 0.4 Hz, these frequencies are introduced into the residuals from the regression. The introduction of leaked frequencies reflects the fact that in conventional time series regression, the frequencies of a regressor are considered together such that a single regression line is obtained that best represents the association between the dependent and independent variables at all frequencies. If the association varies considerably across frequencies, then spectrally structured noise is present in the residuals.

3.1.2. RegBp: nuisance regression, then bandpass filter, B(R(C ~ M))

A simple linear regression of C on M was computed prior to bandpass filtering. The estimate of the motion effect precisely matched the mixing weights of M into $C:\widehat{\beta }=0.5$, t(198) = 6.87, p > .0001, model R² = 0.19. The residuals of this regression were then bandpass filtered .009-.08Hz, resulting in the signal depicted in Figure 1, RegBp. The resulting signal is a reasonable reconstruction of the bandpass filtered MR signal, X_low, and approaches perfect correlation, r = 0.98. The periodogram for the RegBp approach indicates that the low-frequency component of M at .06 Hz is attenuated, but still present, in the residuals. This resulted from the weighted mixing of the frequency components of M with X whereas the component amplitudes of M were equal, a subtle model misspecifrication. Nevertheless, the power of the .06 Hz band was substantially reduced from 15.09 dB in C to 6.35 dB in the RegBp signal, a factor of 7.48.

3.1.3. Simult: simultaneous bandpass filtering and regression

When simultaneous bandpass and nuisance regression was performed on our toy time series, the parameter estimate for M was $\widehat{\beta }=0.8$, t(198) = 3.05, p = .005, semipartial r² = 0.12. This coefficient is precisely the mixing weight of the .06 Hz component of M into C, which is the only component of M within the passband of the spectral filter. This illustrates a key difference from the RegBp approach: under Simult, the nuisance regression attenuates nuisance-related variation within the passband and the bandpass filter suppresses all variation outside of the passband. This can be conceptualized as a type of band-spectrum regression, where the nuisance regression model is applied only inside the passband (Engle, 1974). The residuals of the simultaneous approach precisely reconstructed the low-frequency MR signal X_low, r = 1.00, and the periodogram indicates a perfect match between X_low and Simult. Further, the power of the .06 Hz component is attenuated to −13.48dB, which is 719.77 times weaker than the original signal, C.

3.1.4. Conclusions from the proof of concept

The above example illustrates the costs of performing nuisance regression after bandpass filtering when the regressors retain their original spectral characteristics, which is a common approach used in RS-fcMRI studies. Under the BpReg approach, the power of the .06 Hz nuisance component was 4.01 times stronger than the RegBp signal, and 385.75 times stronger than the Simult signal. Furthermore, BpReg systematically under-corrected for the nuisance regressor, M, because a conventional regression estimate captures the average association across all frequencies, yet the MR-noise association is constrained to be zero at the filtered frequencies of the bandpass-filtered MR signal, B(C). It follows that greater spectral power in the nuisance signal at frequencies outside of the passband will result in poorer adjustment for the nuisance signal by BpReg at frequencies in the passband. In addition to under-correcting for nuisance variation, BpReg introduced spectral power into the MR signal at previously suppressed frequencies. The leaked power occurred precisely at those frequencies in the nuisance regressor that were not present in the MR signal (i.e., those outside of the passband), and the variability introduced was perfectly associated with the nuisance regressor (i.e., the spectral coherence approached 1.0). Furthermore, the magnitude of power at frequencies introduced by the mismatched regression is proportionate to the strength of the association between the MR and nuisance signals inside the passband.

These findings highlight that BpReg under-corrects for nuisance variation in the frequencies of interest (.009-.08 Hz) and introduces temporally synchronous nuisance variation into the MR signal at frequencies that were previously bandpass filtered. By contrast, the RegBp and Simult filtering approaches were not associated with the introduction of nuisance artifacts and did not suffer from the same suboptimal attenuation of nuisance variation. Using empirical data, we demonstrate below that Simult performs as well as or better than RegBp for removing nuisance variation within passband frequencies. Our simulation illustrates the basis of this finding: Simult outperforms RegBp because it optimizes its fit within the passband frequencies, thereby reducing the range of frequencies over which a single nuisance-MR parameter estimate is assumed to be invariant, while the bandpass filter suppresses all stopband frequencies. By contrast, the RegBp approach must optimize the fit of its regression model over all frequencies present in the signals, and our results indicate that nuisance signals give rise to differing degrees of variation in the MR signal over the frequency spectrum, degrading the removal of nuisance variation within the passband for RegBp relative to Simult.²

With these findings in mind, we explored the effects of spectral misspecification by BpReg on empirical RS-fcMRI data, focusing especially on the degree of noise evident in the data and the effects of nuisance variability on estimates of connectivity.

3.2. Preprocessing practices in RS-fcMRI research

As shown in Figure 2, 92 (64%) of the 144 relevant RS-fcMRI articles reviewed used a seed-based correlation analyses to characterize functional connectivity. Of these studies, 49% used the BpReg approach that is potentially associated with the reintroduction of nuisance variability, as demonstrated above. The large majority of these articles (86%) included the six motion parameters in the nuisance regression, yet only six studies out of the 45 reviewed (13%) bandpass filtered the head motion data. In five of the articles where both fMRI time series and motion parameters were similarly filtered, this reflected a high-pass filter (e.g., f > .01 Hz) conducted as part of a general linear model approach using FSL or SPM software, which apply the same filtering operations to both fMRI data and regressors (Kiebel and Holmes, 2006). Among the BpReg articles that applied a more conventional bandpass filter (e.g., 009 – .08 Hz), only one filtered the motion regressors, and this was identified only by contacting the author, not on the basis of the article itself. Many of the BpReg articles included the average white matter, CSF, and/or global signal as nuisance regressors. In a majority of cases, these signals were similarly filtered because they were acquired after the fMRI data were bandpass filtered, but this detail was identified primarily through correspondence, as the published articles were typically ambiguous in this regard. In addition, based on correspondence with authors, five articles initially identified as BpReg were moved to the RegBp category.

Figure 2.

Bandpass filtering and nuisance regression approaches used in 144 resting-state fMRI functional connectivity studies drawn from 200 randomly sampled studies. For approaches that applied spectral filtering (BpReg, RegBp, Filtering Only), mean values and standard deviations for the low-frequency and high-frequency cutoffs for the filter are reported, as is the relative frequency of bandpass, high-pass, and low-pass filtering. For the BpReg approach, studies that spectrally filtered a given nuisance regressor to match the filtered fMRI data and denoted Bp (Signal).

Altogether, 80% of the BpReg studies contained at least one unfiltered nuisance regressor that did not match of fMRI data in the frequency domain. The most common unfiltered nuisance regressors were motion parameters (73%), suggesting that the modal source of reintroduced nuisance variation using the BpReg approach would be motion-related artifacts. In some cases, this flaw appeared to stem from the use of RS-fcMRI prepocessing software that applied a BpReg approach where the motion regressors were unfiltered (e.g., DPARSF/REST: http://www.restfmri.net/forum/DPARSF or some of the scripts distributed with the 1000 Functional Connectomes Project: http://fcon_1000.projects.nitric.org).

3.3. The effects of bandpass filtering and nuisance regression on empirical RS-fcMRI time series

3.3.1. BpReg systematically under-corrects for nuisance signals of RS-fcMRI time series

3.3.1.1. UPitt Cohort

To test for under-correction of nuisance signals due to a misspecified regression model, we computed the total variance explained in the RS-fcMRI time series explained by the nuisance regressors (i.e., the model R²). For BpReg, the average R² was 0.47 (SD = .18); RegBp mean R² = 0.55 (SD = 0.17); and Simult mean R² = 0.73 (SD = 0.14). A mixed model of the Simult versus BpReg R² difference, allowing for random effects of ROI and subject, was highly significant, t = 283.28, p < .0001, corroborating the hypothesis that BpReg does a poor job of removing nuisance variability relative to Simult. The RegBp approach accounted for significantly more variance than BpReg (t = 77.60, p <. 0001) and less variance than Simult (t = 205.7, p <. 0001).³

3.3.1.2. WashU Cohort

The magnitude of under-correction of nuisance signals was similar in the WashU cohort. For BpReg, mean R² = 0.36 (SD = 0.14), RegBp mean R² = 0.54 (SD = .16); and Simult mean R² = .61 (SD = 0.17). The difference in variance explained between Simult and Bpreg was highly significant, t = 111.73, p < .0001. Also, RegBp accounted for more overall variance than BpReg, t = 77.54, p < .0001, but less variance than Simult, t = 34.20, p < .0001.

3.3.2. Bandpass filtering is corrupted by BpReg

3.3.2.1. UPitt Cohort

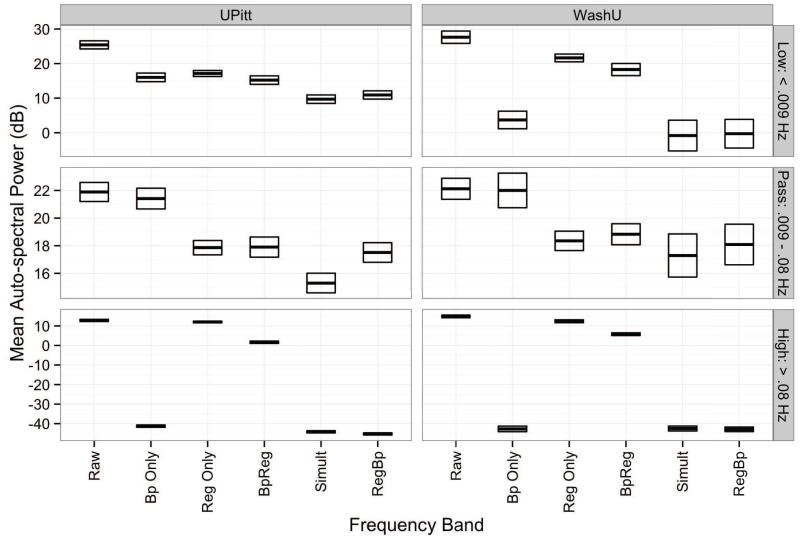
The BpReg approach also reintroduced considerable variability into the stopband frequencies (f < .009 Hz and f > .08 Hz) previsouly suppressed by bandpass filtering, whereas RegBp and Simult RS-fcMRI time series had minimal spectral power in these frequencies (Figure 3). Power in the high-frequency stopband (f < .08 Hz) was significantly higher for BpReg than RegBp or Simult, z = 68.55, adj. p < .0001, although weaker than the time series without bandpass filtering and regression (Raw), z = 14.62, adj. p < .0001. Similarly, in the low-frequency stopband (f < .009 Hz), spectral power was significantly greater for BpReg relative to RegBp and Simult, z = 3.30, adj. p = .006, but low-frequency fluctuations for BpReg were not as high as the Raw series, z = 6.05, adj. p < .0001.

Figure 3.

Mean auto-spectral power of RS-fcMRI time series in the low-frequency stopband (f < .009 Hz), passband (.009 – .08 Hz), and high-frequency stopband (f < .08 Hz) ranges. Darkened lines denote the mean power estimate, and the bounds of the boxes indicate one standard error above and below the mean. Raw = fMRI time series prior to bandpass filtering and nuisance regression; Bp Only = Bandpass filtering without nuisance regression; Reg Only = Regression alone without bandpass filtering; BpReg = bandpass filtering of fMRI data, then nuisance regression; Simult = simultaneous bandpass filtering and nuisance regression; RegBp = nuisance regression, then bandpass filtering.

Within the passband, spectral power was significantly lower for Simult than BpReg, z = 2.61, adj. p = .04, whereas RegBp was marginally lower than BpReg, z = 2.25, adj. p = .11. All three approaches, however, had significantly less power in the passband frequencies relative to Raw, z = 6.35, adj. p < .0001, reflecting the reduction of variability due to the nuisance regression.

3.3.2.2. WashU Cohort

In the WashU cohort, spectral power in the high-frequency stopband (f > .08 Hz) was significantly higher for BpReg than RegBp or Simult, z = 48.44, adj. p < .0001, but weaker than the Raw series, z = 13.79, adj. p < .0001 (Figure 3). Similarly, in the low-frequency stopband (f < .009 Hz), spectral power was significantly greater for the BpReg relative to RegBp and Simult, z = 5.43, adj. p < .0001, but low-frequency fluctuations for BpReg were not as high as Raw, z = 3.88, adj. p = .0006. Power within the passband did not differ significantly across approaches (z = 1.15, adj. p = .84), but was significantly lower than the Raw series (z = 4.06, adj. p < .0001).

3.3.3. Variability reintroduced by BpReg is associated with nuisance signals

To test the assertion that a spectrally misspecified nuisance regression (BpReg) introduces variation into the resting-state MR time series that is temporally synchronous with the nuisance regressors (white matter, motion regressors, etc.), we computed the cross-spectral power of the processed MR signal with each of the 18 nuisance regressors for each of the possible approaches (BpReg, RegBp, and Simult, as well as RS-fcMRI time series using bandpass filtering alone [Bp Only], regression alone [Reg Only], or neither of these teps [Raw]). These cross-spectra quantify the degree of covariation between the MR signal and nuisance signals across the range of observed frequencies. A mixed model of the cross-spectral power was computed, averaging across nuisance regressors, where frequency band (pass, high-filtered, and low-filtered) and processing approach were fixed effects, and ROI and frequency were random effects nested within subject. More detailed depictions of cross-spectral power across the frequency spectrum are provided in the online supplement, Figures S2 and S3.

3.3.3.1. UPitt Cohort

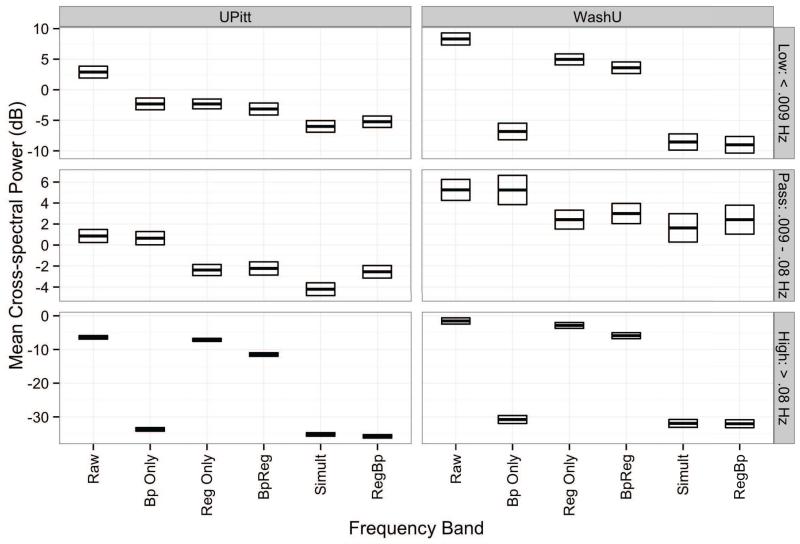
As displayed in Figure 4 (left panel), high-frequency covariation between nuisance signals and MR time series for BpReg was significantly higher than RegBp and Simult, z = 48.03, adj. p < .0001. This difference in cross-spectral power was approximately 2.5 orders of magnitude, a marked increase in nuisance-related fluctuations in the high-frequency stopband. Nevertheless, and covariation between BpReg time series and nuisance signals was 5.11 dB lower than the Raw data, z = 8,78, p < .0001. There was no significant difference between RegBp and Simult in the high-frequency stopband, z = 1.00, p = .98. In the low-frequency stopband (f < .009 Hz), MR-nuisance covariation was significantly higher for BpReg than for Simult and RegBp (z = 2.22, p = 05), whereas Simult and RegBp did not differ from each other, z = 77, p = .78. There were also MR-nuisance cross-spectral differences within the passband frequencies (.009–.08 Hz): cross-spectral power was significantly lower for Simult than BpReg, z = 2.68, adj. p = 03. And cross-spectral power was significantly lower for Simult than RegBp inside the passband, z = 2.31, adj. p = .05, whereas RegBp and BpReg did not differ significantly from each other, z = 0.45, ajd. p = .78. Thus, the association of nuisance signals with RS-fcMRI time series was best controlled in the passband frequencies by the Simult approach. In addition, as shown in Figure 4, MR-nuisance covariation in the stopband was much lower for Bp Only than BpReg, corroborating that BpReg reintroduces nuisance-related variability.

Figure 4.

Mean cross-spectral power of RS-fcMRI time series with the 18 nuisance regressors. Estimates reflect average cross-spectral power across the 18 regressors in the low-frequency stopband (f < .009 Hz), passband (.009 – .08 Hz), and high-frequency stopband (f < .08 Hz) ranges. Darkened lines denote the mean power estimate, and the bounds of the boxes indicate one standard error above the below the mean. Raw = fMRI time series prior to bandpass filtering and nuisance regression; Bp Only = Bandpass filtering without nuisance regression; Reg Only = Regression alone without bandpass filtering; BpReg = bandpass filteirng of fMRI data, then nuisance regression; Simult = simultaneous bandpass filtering and nuisance regression; RegBp = nuisance regression, then bandpass filtering.

To determne whether between-subjects variability in the power of the nuisance-MR cross-spectra was significantly associated with head motion, we extracted the EBLUP for the random effect of subject from a cross-spectrum MLM using the Raw RS-fcMRI time series. This value represented the subject-specific difference in the magnitude of temporally synchronous MR-nuisance fluctuations relative to the overall sample, and values ranged from −6.79 dB to 10.68 dB (SD = 3.61). We then correlated the subject cross-spectrum EBLUP with the cumulative framewise displacement for each subject across the resting-state acquisition (FD was log-transformed to normalize high positive skew). There was a remarkably high correlation between MR-nuisance cross-spectral power and cumulative FD, r = .94, t(115) = 29.02, p < .0001, with cross-spectral power increasing. 09 dB for every 1mm framewise displacement that occurred cumulatively over the acquisition. In our sample, cumulative FD ranged from 10.76mm – 219.05mm (M = 42.19, SD = 35.78).

3.3.3.2. WashU Cohort

In the WashU cohort, nuisane regressors and RS-fcMRI time series were also much more temporally synchronous for the BpReg approach than the Simult and RegBp approaches (Figure 4, right panel). In the high-frequency range (f > .08Hz), MR–nuisance covariation was significantly higher for BpReg relative to RegBp and Simult, z = 35.39, adj. p < .0001, and the magnitude of this cross-amplitude difference was 26.09 dB (Figure 4, right panel). For very low frequencies (f < .009 Hz), cross-spectral power for BpReg was 12.38 dB greater than Simult and RegBp, z = 13.48, adj. p < .0001. Finally, within the passband (.009 – .08 Hz), we failed to find a significant difference for BpReg relative to Simult and RegBp, z = 1.03, adj. p = 68, although the direction of power differences matched the UPitt cohort (i.e., Simult had the lowest cross-spectral power, whereas BpReg and RegBp were relatively similar).

3.3.4. Large-amplitude global signal changes at the times of head motion are evident for BpReg but are largely controlled by RegBp and Simult

Power and colleagues (2012a) found that bandpass filtering and nuisane regression (using BpReg) did not eliminate large-amplitude changes in the average BOLD signal across the brain that result from head motion (Friston et al., 1996). Such motion-related fluctuations in the global signal may dwarf neurally driven components of the BOLD response and bias connectivity estimates. Given that spectral filtering can be viewed as a form of smoothing (Jenkins and Watts, 1968), however, it is plausible that a bandpass filter might help to smooth over transient signal spikes less than 12.5s in duration (i.e., the upper cutoff frequency of a filter at. 08Hz), and the regression of motion parameters may further attenuate motion-related BOLD fluctuations. Our results above demonstrated that the BpReg approach reintroduced nuisance-related fluctuations into the signal, and such fluctuations are likely temporally synchronous with head motion since motion parameters were among the nuisance regressors.

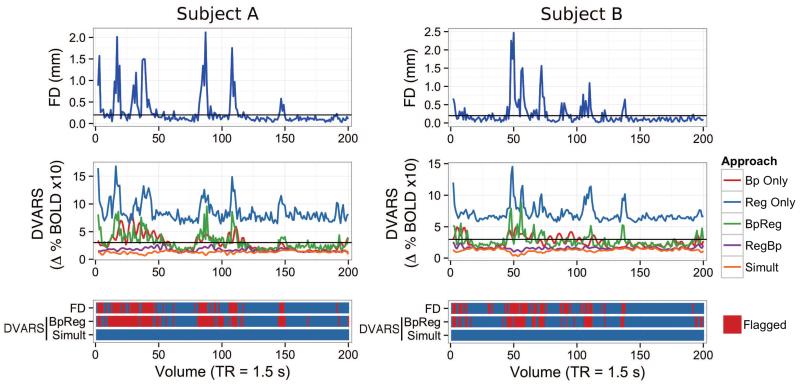
To visualize the association between global changes in the BOLD signal and head motion, we plotted FD (a framewise summary of head motion) and DVARS (a framewise summary of global BOLD signal changes) over the RS-fcMRI scan for each participant (building on the approach of Power et al., 2012a). In order to explore whether the association between head motion and DVARS varied among the preprocessing approaches considered here, DVARS was computed for each approach separately, as well as for bandpass filtering alone and nuisance regression alone. Prototypical plots for two participants are displayed in Figure 5, where FD and DVARS are temporally aligned in order to show the degree of their correspondence over the RS-fcMRI scan. Volumes with FD > 0.2mm or DVARS > 3 in the UPitt cohort were flagged as potentially contaminated by head motion (these more stringent thresholds were suggested by Power et al., 2012b).

Figure 5.

Temporal correspondence of head movement (FD) and global BOLD signal fluctuation (DVARS) for two prototypical subjects from the UPitt cohort, using different preprocessing approaches. Framewise displacement (top panel, FD) summarizes the magnitude of rotational and translational head movement between volumes. The framewise change in the global BOLD signal for all brain voxels (middle panel, DVARS) was computed as the average root mean square variance across voxels of the temporal derivative of the fMRI time series (Power et al., 2012a). DVARS was computed separately for five preprocessing appraoches: 1) bandpass filtering alone (Bp Only); 2) nuisance regression alone (Reg Only); 3) bandpass filtering of fMRI data followed by nuisance regression of unfiltered signals, including motion parameters (BpReg); 4) nuisance regression of unfiltered signals followed by bandpass filtering of fMRI data (RegBp); and 5) simultaneous filtering of nuisance frequencies and nuisance regressors using a multiple regression framework (Simult). The bottom panel shows the correspondence of head movement (FD) and residual fluctuations in the BOLD signal (DVARS) for the BpReg and Simult approaches. Volumes exceeding FD > 0.2mm or DVARS > 3 are marked in red as potentially contaminated by motion, per the suggestion of Power and colleagues (Power et al., 2012b).

We observed four patterns in the plots of subjects’ FD and DVARS data. First, large motion-related fluctuations in the BOLD signal were evident when regression of movement parameters and their derivatives (as well as WM, CSF, and the global signal) was performed without bandpass filtering (Figure 5, Reg Only). This suggests that nuisance regression alone is insufficient to control the large BOLD signal fluctuations induced by head motion. Second, bandpass filtering of the fMRI time series without nuisance regression attenuated motion-related BOLD fluctuation to some degree, but also appeared to spread the deleterious effects of motion in time. This ringing artifact is attributable to bandpass filtering and was identified in a recent paper by Carp (in press), who proposed that motion-contaminated volumes be imputed using nearest neighbor interpolation of the uncontaminated volumes. Thus, bandpass filtering alone may inadvertently spread motion-related contamination throughout the fMRI time series, making it particularly difficult to assess and remove. Third, DVARS and FD were well aligned using the BpReg approach and closely resembled the regression only DVARS plots, suggesting that motion-related BOLD fluctuations remained problematic despite bandpass filtering the fMRI data, then regressing out unfiltered nuisance signals. Fourth, for RegBp and Simult, there was very little temporal correspondence between DVARS and FD and none of the volumes exceeded the DVARS > 3 criterion indicating large global shifts in the BOLD signal.

In addition, for each subject, we plotted the BOLD signal for each ROI over time alongside participants’ FD values, which summarize head motion. Figure 6 depicts global signal change across ROIs for a prototypical subject (right panel): vertical banding is evident at times of large head motion for BpReg (cf. Power et al., 2012a), indicating large-magnitude global signal changes that are temporally synchronous with head motion, but vertical banding is not evident for RegBp or Simult. Furthermore, large-amplitude BOLD signal fluctuations across the brain, often in opposite directions, are evident for BpReg at the time of large movements (Figure 6, left panel), whereas the RegBp and Simult BOLD signal is much smoother across the brain and there is little evidence of a bifurcation of positive and negative BOLD changes.

Figure 6.

Temporally synchronous global signal fluctiations are evident for the bandpass-regress order, but not for regress-bandpass or simultaneous filtering. The right panel depicts the framewise change in the BOLD signal for each of the 244 ROIs over time for a prototypical subject. Framewise head displacement is depicted in the bottom panel, where black denotes the absence of motion and white denotes large head movement. The point in time marked by the arrow represents a high motion frame, and axial brain images of the change in BOLD signal at this time are displayed on the left (scaling equal across images). Only for the bandpass-regress approach are rapid, temporally synchronous fluctuations evident at times of high motion (vertical bands in the right panel).

To corroborate the visual inspection of these fMRI time series, DVARS, and FD plots, we compared the DVARS values for high- versus low-motion volumes across preprocessing approaches. In addition, to rule out the possibility that the choice of an FD threshold for identifying motion contamination may have influenced DVARS comparisons, we also correlated FD and DVARS for each subject using each approach to see whether RegBp and Simult minimized the correspondence of head motion and global BOLD signal fluctuation⁴.

3.2.4.1. UPitt Cohort

We identified motion-contaminated brain volumes using a stringent guideline proposed by Power and colleagues (2012b) in a follow-up commentary on this topic: volumes with FD > 0.2mm were flagged as contaminated, as were the preceding and two succeeding volumes. Across 117 subjects, 42.6% of all volumes were flagged at this threshold, with a per-subject average of 42.7% (SD = 28.9%). We then tested whether DVARS values differed across approaches as a function of motion contamination (Table 2). For BpReg, DVARS was significantly higher for contaminated than uncontaminated volumes, z = 19.45, adj. p < .0001, whereas there was a marginal difference between contaminated and uncontaminated volumes for RegBp, z = 1.98, adj. p = .07. For Simult, DVARS was slightly lower for contaminated frames than uncontaminated frames, z = −2.65, adj. p = .01, which may reflect the greater suppression of the global signal at times of head motion due to the stronger fit of motion estimates by the Simult nuisance regression. Regardless, the Simult approach best controlled motion-related BOLD fluctuation. Also, the maximum DVARS value did not exceed 5 (a threshold initially suggested by Power and colleagues to identify motion-contaminated frames) for any subject or frame for the RegBp and Simult approaches.

Table 2.

Average DVARS values for contaminated and uncontaminated frames and correlations between FD and DVARs

Cohort	Approach	DVARS						FD-DVARS correlation (r)	95% CI
		Uncontaminated			Contaminated
		M	SD	Max	M	SD	Max
UPitt	BpReg	2.21	0.62	8.49	3.04	1.40	22.57	.33	.28 – .36
	Simult	1.33	0.28	2.95	1.23	0.45	4.59	−.13	−.18 – −.09
	RegBp	1.56	0.28	3.22	1.63	0.49	4.66	.09	.05 – .14
WashU	BpReg	5.48	1.63	19.05	9.03	5.38	77.40	.39	.28 – .49
	Simult	3.68	1.23	16.02	4.20	2.55	22.99	.08	−.04 – .20
	RegBp	4.11	1.11	15.47	5.28	2.67	25.03	.24	.12 – .35

Note. For the UPitt cohort, a threshold of FD > 0.2mm was used to identify motion-contaminated volumes, whereas the threshold was FD > 0.3mm for the WashU cohort. In both datasets, for each volume exceeding the FD threshold, the preceding frame and two succeeding frames were also identified as contaminated (Power et al., 2012).

Consistent with these results, the correlation between DVARS and FD (see Table 2) was significantly higher for BpReg than Simult and RegBp, z = 14.88, adj. p < .0001. Moreover, the DVARS-FD correlations for Simult and RegBp were near zero, whereas the effect size for BpReg was moderate. Thus, the large-magnitude changes in the global signal previously reported appear to be largely a function of motion-related artifacts re-introduced by the BpReg approach that are adequately controlled by RegBp and Simult.

WashU Cohort

As described above (Table 1), the WashU cohort included a higher average level of head motion relative to the UPitt cohort, likely because the WashU participants were all children. Thus, to explore whether DVARS differed for high-motion versus low-motion volumes in this sample, we set a threshold of FD > 0.3mm, which lies between the conservative FD > 0.2mm threshold (Power et al., 2012b) and the earlier recommendation FD > 0.5mm (Power et al., 2012a). This threshold was chosen in order to flag a similar number of volumes as motion-contaminated relative to the UPitt cohort. At a threshold of FD > 0.3mm (along with the preceding and two succeeding frames, as above), 42.8% of frames were identified as contaminated, with a per-subject average of 41.4% (SD = 22.5%). For BpReg, DVARS was significantly higher for contaminated than uncontaminated volumes, z = 3.54, adj. p < .001. We also observed a smaller, but significant, increase in DVARS for contaminated volumes under RegBp relative to uncontaminated frames, z = 2.48, adj. p = .02. For Simult, we did not observe significant DVARS differences between contaminated and uncontaminated volumes, z = 1.12, adj. p = .31 (see Table 2).

As with the UPitt cohort, the DVARS-FD correlation for BpReg was much higher than RegBp (z = 4.67, adj. p < .001) or Simult (z = 9.12, adj. p < .001). Of note, whereas the correlation for RegBp was significantly positive (adj. p < .001), the correlation for Simult was not significantly different from zero (adj. p = .56). This difference in the strength of DVARS-FD correlation between Simult and RegBp was significant, z = 4. 45, adj. p < .001, suggesting the motion-related global fluctuations in the BOLD signal were best attenuated by the Simult approach.

3.2.5. The association between head motion and connectivity estimates is much stronger for the BpReg approach relative to Simult

In order to understand whether the negative effects of head motion on estimates of functional connectivity were exacerbated by the reintroduction of nuisance variability using the BpReg approach, we computed the between-subjects correlation of average head motion (mean FD per subject) and connectivity strength for each of the pairwise connections among all ROIs (cf. Satterthwaite et al., 2012). We also explored whether motion–connectivity differences between BpReg and Simult varied as a function of the distance between ROIs by dividing functional connections into 10mm bins from 10-170mm and simultaneously testing these differences in a linear mixed model. Although we found no evidence that the RegBp approach induced nuisance-related fluctuations into the RS-fcMRI time series, our findings above showed that the Simult approach better attenuates nuisance variability within the frequencies of interest in resting-state fMRI studies. Thus, for brevity, most of the analyses below compare Simult versus BpReg⁵.

3.2.5.1. UPitt Cohort

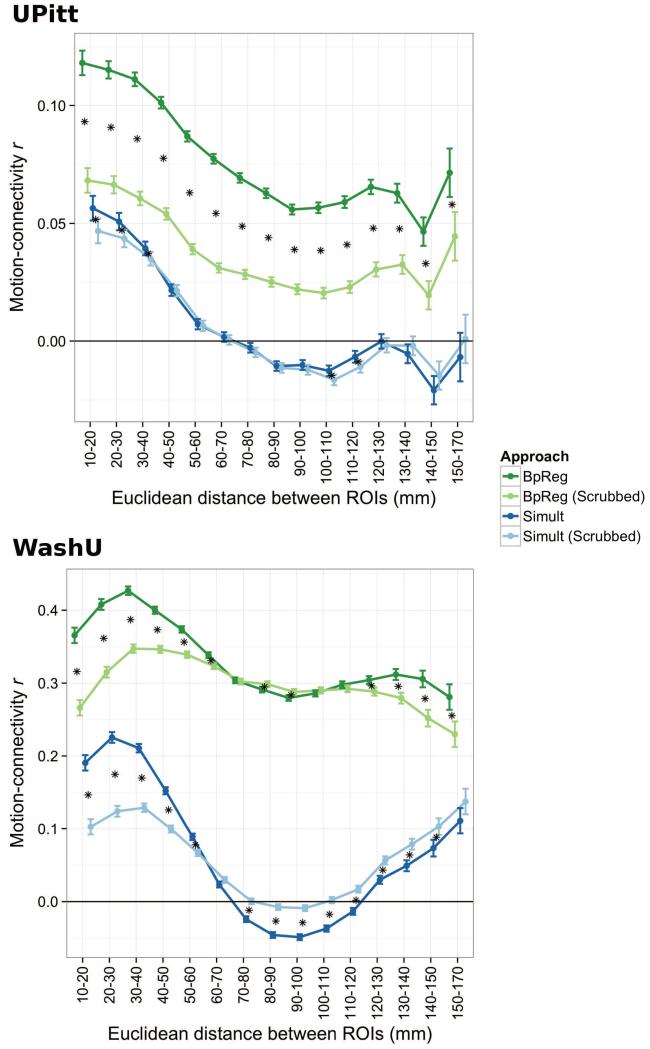
Across all pairwise functional connections, we found a small association between head motion and functional connectivity strength for the BpReg approach, average |r| = .12 (SD = .09), p < .0001. For BpReg, consistent with previous reports (Van Dijk et al., 2012; Satterthwaite et al., 2012), head motion was associated with larger functional connectivity estimates for short-range connections (see Figure 7, top panel), although the motion–connectivity association was significantly positive regardless of distance (adj. ps < .0001). For Simult, the motion-connectivity association was generally weak, average |r| = .09 (SD = .07), p < .0001, with regions less than 60mm apart having small positive correlations (adj. ps < .001), whereas head motion was negatively associated with connectivity estimates for regions 80-120mm apart (adj. ps < .001) and 140-150mm apart (adj. p < .0001). The absolute motion-connectivity association was significantly greater for BpReg than Simult, average Δ|r| = .04, p = .002, d = .46. Although the motion-connectivity difference for BpReg versus Simult differed somewhat as a function of distance (χ[14] = 45.09, p < .0001), distance-related differences between approaches were small, ranging from Δr = .062–.08.

Figure 7.

The association between head motion and functional connectivity estimates differs as a function of interregional distance, preprocessing approach, and motion scrubbing. Darkened circles denote estimated means, whereas vertical bars denote standard errors. For both cohorts, the motion-connectivity association was significantly lower for Simult than BpReg, reardless of interregional distance, adj. ps < .0001. Motion scrubbing (Power et al., 2012a) was applied to the UPitt and WashU cohorts based on the intersection of FD and DVARS. For UPitt, volumes where DVARS (under BpReg) exceeded 3 and FD exceeded 0.2mm were discarded, as were the preceding and two succeeding volumes, prior to computing connectivity estimates. For WashU, scrubbing thresholds were chosen to maximize comparability of our findings with a previous report of these data (Power et al., 2012a): DVARS > 5 and FD > 0.5mm. For UPitt, 25.6% of volumes per subject were discarded, on average (SD = 24.4%). For WashU, 25.3% of volumes were discarded per subject (SD = 18.8%). Asterisks denote significant shifts in the motion-connectivity association between scrubbed and unscrubbed data, adj. ps < .05.

3.2.5.2. WashU Cohort

In the WashU sample, the motion-connectivity association for the BpReg approach was considerably greater, mean |r| = .36 (SD = .20), p < .0001, and was particularly high for short-range connections (Figure 7, bottom panel). For the Simult approach, the motion-connectivity association was somewhat weaker, mean |^r| = .23 (SD = .16), p < .0001. Short-range (10-70mm) and long-range connections (120-170mm) tended to show weak positive correlations with motion (adj. ps < .0001), whereas head motion and connectivity estimates were negatively correlated for connections 70-110mm apart, adj. ps < .0001. The motion-connectivity association was significantly greater for BpReg than Simult, p = .003, d = .73, representing an average increase of Δ|r| = .13 for BpReg, although the magnitude of this effect was qualified by interrregional distance, χ(14) = 1444.4, p < .0001. Differences in the motion-connectivity association between BpReg and Simult were greatest for connections between 60 and 120mm apart and smallest for short-range connections (10-30mm) and long-range connections (150-170mm).

3.2.6. Censoring high-motion volumes (motion “scrubbing”) modestly reduces motion-connectivity association for BpReg, but has less effect for Simult

Power and colleagues (2012a) recommended that high-motion frames be censored (“scrubbing”) prior to computing correlations in order to mitigate the influence of head motion on functional connectivity estimates. To the extent that this procedure is effective, it should attenuate the correlation between head motion and functional connectivity strength. To explore this possibility, we computed functional connectivity estimates after motion scrubbing, which were then correlated with per-subject mean FD, as above. We also tested whether the effect of scrubbing on motion-connectivity association differed as a function of interregional distance.

3.2.6.1. UPitt Cohort

To implement motion scrubbing, volumes where DVARS (under BpReg) exceeded 3 and FD exceeded 0.2mm were discarded, as were the preceding and two succeeding volumes, prior to computing connectivity estimates. The DVARS threshold of 3.0 was chosen for three reasons: 1) it was well above the typical values observed in subjects who moved very little; 2) it corresponded to the 75^th percentile of DVARS values in the UPitt cohort, suggesting relatively high fluctuations in the BOLD signal; and 3) it was suggested in a recent commentary by Power and colleagues (2012b) as a more stringent DVARS threshold. On average, 25.6% of frames were discarded per subject (SD = 24.4%).

Scrubbing significantly attenuated the head motion-connectivity association for the BpReg approach, mean Δ|r| (scrubbed – unscrubbed) = −.02, (SD = .07), p = .0005, d = .22 (Figure 7, top panel). For the Simult approach, scrubbing modestly increased the average absolute motion-connectivity association, Δ|r| (scrubbed – unscrubbed) = .002 (SD = .05), p = .02, d = .04. Notably, the motion-connectivity association for the unscrubbed Simult data was still significantly lower than the scrubbed BpReg data, Δ|r| = −.02, p = .01, d = .24, regardless of interregional distance, suggesting that optimal preprocessing may better reduce the effects of head motion on connectivity estimates than censoring high-motion volumes.

For BpReg, scrubbing reduced the motion-connectivity association most for shorter-range connections and least for longer-range connections, linear trend contrast z = 10.81, p < .0001. For Simult, scrubbing reduced the motion-connectivity association for connections between 10 and 40mm apart, but this effect was small in magnitude (Δr = −.004 to −.01) relative to scrubbing-related changes for BpReg. Interestingly, scrubbing the Simult data magnified the negative motion-connectivity association for connections from 100-120mm apart, adj. ps < .001, albeit slightly (average |Δr = .004).

3.2.6.2. WashU Cohort

Motion scrubbing thresholds were chosen to maximize comparability of our findings with a previous report of these data (Power et al., 2012a): DVARS > 5 and FD > 0.5mm. At these thresholds, on average, 25.3% of volumes were discarded per subject (SD = 18.78%), resulting in a similar level of censoring compared to the UPitt cohort. We failed to find a significant reduction of the average absolute motion-connectivity association after scrubbing the BpReg data, Δ|r| = −.02, p = .23, d = .10. Of note, however, the effects of scrubbing for BpReg differed as a function of interregional distance (Figure 7, bottom panel), χ(14) = 2356.70, p < .0001, such that motion-connectivity was significantly reduced for connections 10-50mm apart (M Δr = −.08, adj. ps < .001) and produced smaller reductions for connections 50-70mm and 120-170mm apart (M Δr = −.03). Scrubbing the BpReg data increased the motion-connectivity correlation slightly for connections 80-100mm apart (M Δr = .008).

For Simult, scrubbing modestly improved the absolute motion-connectivity association, on average, Δ|r| = −.02, p = .001, d = .13. But the effects of scrubbing depended on the interregional distance, such that scrubbling significantly reduced motion-connectivity association for connections 10-60mm apart (M Δr = −.07, adj. ps < .001), but increased this correlation for connections 70-150mm apart (M Δr = .03).

In line with the UPitt cohort, the average absolute motion-connectivity association for the unscrubbed Simult data was much lower than the scrubbed BpReg data, Δ|r| = −.11, p = .006, d = .66, regardless of interregional distance. In short, for the WashU cohort, we found that the BpReg approach led to an average motion-connectivity association over 50% stronger than for Simult. Motion scrubbing attenuated this effect modestly for both BpReg and Simult, particularly for short-range connections. For the Simult approach, scrubbing attenuated the motion-connectivity association for short-range functional connections, but it also increased this association for long-range connections. Finally, in both cohorts, even after motion scrubbing, the motion-connectivity association was still highest for short-range connections and the distance-dependent associations of motion with connectivity estimates were qualitatively similar before and after motion scrubbing, particularly for Simult (Figure 7). Additional analyses comparing the effects of scrubbing versus use of the Simult approach on functional connectivity estimates are reported in the online supplement, section S3.

3.3. Spectral misspecification by the BpReg approach influences connectivity estimates and the parcellation of brain regions into functional networks

Although the above findings are striking in their magnitude, they do not elucidate how artifacts re-introduced by the spectrally misspecified nuisance regression adversely affect estimates of functional connectivity. Thus, we conducted additional analyses to demonstrate that the BpReg approach systematically overestimates correlations among brain regions and that this inflation reflects greater noise-related variability relative to Simult. Using a community detection approach (Lancichinetti and Fortunato, 2009), we also explored how the parcellation of brain regions into functional networks differed between Simult and BpReg (see online supplement S2 for results).

3.3.1. Functional connectivity is systematically overestimated by the BpReg approach

3.3.1.1. UPitt Cohort

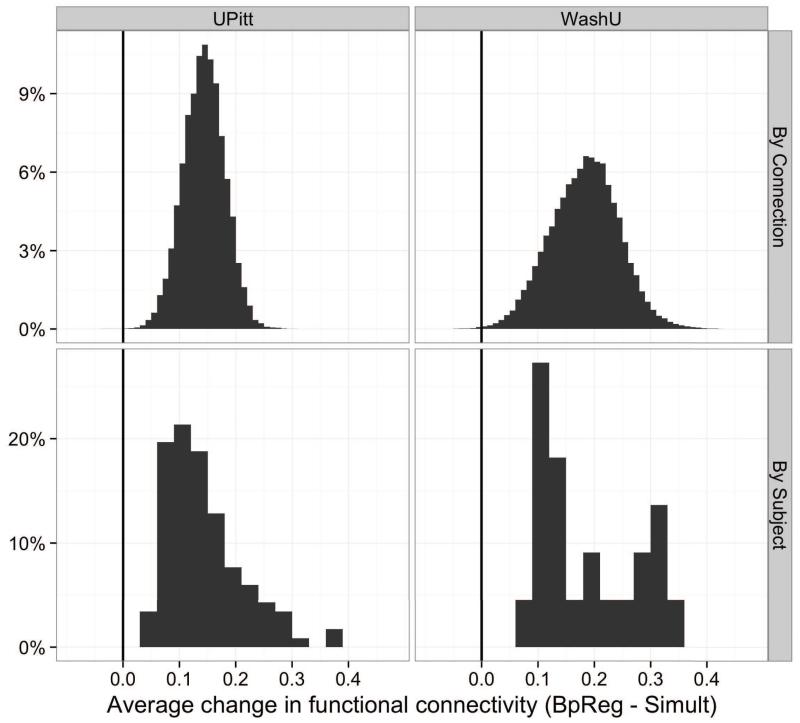
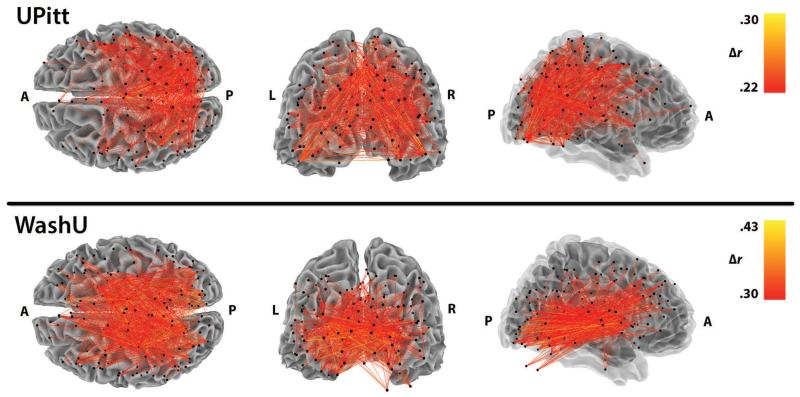
In the UPitt cohort, functional connectivity estimates for BpReg were consistently and significantly higher than Simult across subjects, M Δr = .14, SD = .07, range = .03 – .37, t(116) = 23.08, p < .0001, d = 3.0 (Figure 8, lower left panel). Averaging over subjects, functional connectivity estimates among the 244 ROIs were also significantly higher for BpReg than Simult: M Δr = .14, SD = .04, range = −.03 – .31, t(29645) = 669.06, p < .0001, p = 1.23 (Figure 8, upper left panel). By contrast, the per-subject mean correlation difference between RegBp and Simult was only .003 (SD = .004). Connectivity differences between BpReg and Simult were greatest for ROIs near the center of the brain, including many parietal and occipital cortical regions, as well as insula, hippocampus, and the supplementary motor area (Figure 9, top panel). Relatedly, connectivity differences between approaches were largest for regions 40-70mm apart (Figure S4). BpReg-Simult differences were generally weaker for ROIs that were more distant from the geometric center of the brain (approximately 0, −22, 10 in MNI coordinates), r = −.22, t(242) = −3.43, p = .0008.

Figure 8.

Differences in correlation estimates between the BpReg and Simult approaches, averaging across connections and subjects. Pairwise connectivity estimates were computed for each subject across all regions of interest. The top row represents the average correlation change per interregional connection, averaging across subjects (BpReg - Simult). The bottom row represents the average correlation change per subject, averaging across all connections.

Figure 9.

The spatial distribution of functional connectivity differences between BpReg and Simult. Displayed is the top 2.5% of functional connectivity estimates that differed most between BpReg and Simult, averaging across subjects. Correlation change estimates represent the difference between approaches, BpReg - Simult.

3.3.1.2. WashU Cohort

Per-subject average functional connectivity estimates in the WashU cohort were also inflated for BpReg relative to Simult, M Δr = .19, SD = .09, range = .08 – .33, t(21) = 9.64, p < .0001, d = 2.67 (Figure 8, lower right panel). Averaging across subjects, connectivity estimates among the 264 ROIs were significantly higher for BpReg than Simult: M Δr = .18, SD = .06, range = −.04 – .43, t(34715) = 559.21, p < .0001, d = 1.48. As with the UPitt cohort, we observed virtually no differences in the per-subject mean correlation between RegBp and Simult, M Δr = .008, SD = .009. Similar to the UPitt cohort, connectivity differences between BpReg and Simult were most pronounced for interior ROIs such as insula, thalamus, putamen, and cerebellum (Figure 9, bottom panel); and connectivity estimate differences were greatest for regions 40-80mm apart (Figure S4). The magnitude of BpReg-Simult connectivity differences was negatively associated with distance from the center of the brain, r = −.50, t(262) = −9.41, p < .0001.

3.4. The degree to which correlation estimates are overestimated by BpReg is positively associated with nuisance signals

Correlation differences between BpReg and Simult were directly associated with nuisance signals, including head motion, reflecting the reintroduction of temporally synchronous nuisance variation by the BpReg approach. In the UPitt cohort, the average per-subject inflation of functional connectivity estimates by BpReg (relative to Simult) was significantly related to mean FD, r(115) = .28 [95% CI = .03–.38] p = .002. Employing the scrubbing procedures described above (FD > 0.2mm and DVARS > 3) modestly attenuated this association, r(115) = .17 [95% CI = −.02–.34], p = .07. The connectivity inflation-head motion correlation was considerably larger in the WashU cohort, r(20) = .67 [95% CI = .34–.85], p = .0006, and this was not substantially attenuated by scrubbing, r(20) = .62 [95% CI = .26–.82], p = .002. Thus, in both cohorts, greater head movement was associated with greater inflation of functional connectivity estimates for BpReg relative to Simult.

Cardiac artifacts are another known source of variability in RS-fcMRI data (Chang et al., 2009) that can lead to nuisance fluctuations over a broad range of frequencies due to aliasing (Lund et al., 2006). In the UPitt cohort, the average amplitude of cardiac artifacts in the RS-fMRI data, based on the RETROICOR method (Glover et al., 2000), was significantly correlated with the average connectivity difference between BpReg and Simult, r = .21, t(107) = 2.22, p = 03. Thus, stronger cardiac artifacts were significantly associated with greater inflation of functional connectivity estimates under the BpReg approach relative to Simult, consistent with the above evidence that spectrally misspecified regression reintroduces artifacts into the data.

4. Discussion

Our study sought to investigate how bandpass filtering and nuisance regression affect the integrity of RS-fcMRI connectivity estimates and to explore the degree to which noise-related variability is attenuated by these techniques. In particular, we compared a common preprocessing approach, where unfiltered nuisance signals such as head motion estimates are regressed out of RS-fcMRI time series after voxelwise bandpass filtering (BpReg), with bandpass filtering after regression (RegBp) and simultaneous filtering (Simult). Our results indicate that the BpReg approach had unintended negative effects: by bandpass filtering the fMRI time series, but not the noise signals, the regression model is misspecified in the frequency domain such that nuisance variability is systematically under-controlled. This occurs because standard regression methods optimize the fit of two time series across all frequencies present in both signals (Engle, 1974), yet the fluctuations in the stopband frequencies have been suppressed from the fMRI signals but not the nuisance regressors. Consequently, the fit of the regression (and the variance explained) is shifted toward zero. Moreover, the misspecified regression under the BpReg approach reintroduces temporally synchronous nuisance fluctations into RS-fcMRI time series at frequencies previously suppressed by the bandpass filter (typically f < .009 Hz and f > .08 Hz). The inadvertent retention of nuisance variability by BpReg resulted in systematically inflated functional connectivity estimates, often on the order of Δr = .10 – .30 or higher for many subjects in both RS-fcMRI datasets. In addition, the parcellation of brain regions into functionally connected networks differed somewhat between BpReg and Simult, and these differences were likely attributable to the greater inclusion of noise by BpReg.

We found that the degree to which connectivity estimates were inflated by the BpReg approach was associated with the severity of participant head motion during the fMRI acquisition and with the magnitude of the cardiac-related BOLD fluctuations. One negative consequence of BpReg is that individuals who had greater levels of head movement would also tend to have higher estmates of connectivity. This finding may be particularly relevant to developmental studies because youth tend to move more in the MR scanner than adults (Power et al., 2012a; Satterthwaite et al., 2012), confounding conclusions about age-related differences in connectivity strength. More broadly, connectivity comparisons on any stable individual characteristic that is associated with level of head motion, such as sex (Van Dijk et al., 2012), would be particularly difficult to interpret using the BpReg approach because mean connectivity differences may reflect head movement per se, not the factor of interest.

Head motion and cardiac artifacts are only two of the many possible sources of noise in the MR environment that may influence fMRI time series, and the general point is that whatever nuisance-related fluctuations were represented in the regression model would be reintroduced as brain-wide temporally synchronous artifacts by the BpReg approach. This is disconcerting because the inclusion of white matter, cerebrospinal fluid, and global signals as nuisance regressors is intended to mitigate an unknown mixture of non-neural BOLD fluctuations that may be attributable to head motion, respiration, heartbeat, scanner artifacts, and other unmeasured noise sources (Birn et al., 2006; Windischberger et al., 2002). Yet our results suggest the paradoxical conclusion that using unfiltered noise signals with the BpReg approach may in fact contribute to nuisance-related fluctuations in the final RS-fcMRI time series.

By contrast, the nuisance regression model for the RegBp and Simult approaches is appropriately specified and is not associated with poor attenuation of nuisance signals or the nuisance-related inflation of connectivity estimates. Although differences between RegBp and Simult were relatively subtle, we found that simultaneous filtering was significantly better at reducing nuisance-related variability in the resting-state frequencies of interest (.009 – .08 Hz) compared to the regression-bandpass approach. In addition, residual fluctuations in the global BOLD signal attributable to head motion were largely eliminated by the Simult approach, whereas weak residual motion-related fluctuations were evident for RegBp. These differences reflect the fact that for each nuisance regressor, the RegBp regression optimizes a single parameter estimate that captures the association of an fMRI signal and a given nuisance signal across all observed frequencies, yet the fMRI–nuisance relationship is often heterogeneous across the spectrum (cf. Figures 4, S2, S3), degrading the performance of RegBp. Simultaneous filtering, however, fits the nuisance regression model within the passband frequencies, and because this is a smaller range, it is more likely that the fMRI–noise association will be similar across these frequencies, facilitating noise removal relative to RegBp. Substantive differences in connectivity results between RegBp and Simult probably reflect the relatively greater removal of noise by Simult, yet we found in practice that connectivity estimates for these approaches were often very similar.

4.1. Distance-dependent differences in the association of head motion and connectivity estimates are much lower for Simult than BpReg

Several recent studies have documented that head motion may bias RS-fcMRI connectivity estimates (Van Dijk et al., 2012; Power et al., 2012a; Satterthwaite et al., 2012), increasing correlations for short-range connections and potentially suppressing connectivity among more distal brain regions. In our study, this source of bias was much weaker for the Simult approach than BpReg (Figure 7), reflecting the motion-related variability that inadvertently contaminates RS-fcMRI time series under BpReg. In the UPitt cohort, variability in connectivity estimates attributable to head motion was 94% lower for Simult than BpReg, on average; in the WashU cohort (Power et al., 2012), motion-related variance in connectivity estimates was 91% lower for Simult than BpReg.

Even for simultaneous filtering, however, we found that connectivity estimates for short-range connections were higher among individuals who moved more during RS-fMRI acquisition, whereas motion was weakly negatively correlated with functional connectivity for medium-to-long-range connections. This aligns with the results of Satterthwaite and colleagues (2012), who found similar distance-dependent effects of head motion on functional connectivity estimates using the RegBp approach, which does not suffer from the flaws inherent to BpReg. Moreover, Power and colleagues (2012a) conducted a careful analysis to determine whether one or more nuisance regressors might be introducing spatially structured noise into the data, and they concluded that the nuisance regression was not responsible for the distance-dependent effects of head motion on connectivity estimates. Consistent with this, our findings suggest that distance-related effects of head motion on connectivity are not caused by an error in preprocessing per se, but that their magnitude is magnified by the BpReg approach, which poorly controls for motion-related variability in the RS-fcMRI time series. Thus, the severity of motion-related effects on connectivity estimates may have been inadvertently exacerbated by using the BpReg approach in two of the published papers on this topic (Van Dijk et al., 2012; Power et al., 2012a).

4.2. Motion scribbing attenuates the association between head motion and connectivity estimates, but is potentially less effective for the Simult approach

To reduce the bias of functional connectivity estimates by head motion, Power and colleagues (2012a) proposed that motion-contaminated volumes be censored (i.e., motion “scrubbing”) prior to estimating connecivity. We found that motion scrubbing reduced the overall motion-connectivity association more for BpReg than Simult, consistent with the greater magnitude of motion-related artifacts in the BpReg data. Scrubbing tended to reduce the motion-connectivity association most for short-range connections (10-50mm apart) and had more heterogeneous effects on longer-range connections. In the UPitt cohort, the effects of scrubbing on data processed using Simult were minimal, reducing motion-connectivity association for short-range connections by only r = −.005, on average. In the WashU cohort, scrubbing the Simult data actually increased the motion-connectivity association for connections more than 100mm apart.

Critically, differences between BpReg and Simult in the strength of the motion-connectivity association were much larger in magnitude than the effects of scrubbing, which were small by conventional standards (Cohen, 1988). Thus, we found that simultaneous bandpass filtering and nuisance regression (Simult) more robustly attenuated the effects of head motion on connectivity estimates than did motion scrubbing. Furthermore, distance-dependent differences in the motion-connectivity relationship were not qualitatively improved by motion scrubbing (Figure 7), although it was relatively effective for mitigating the motion-related increases of short-range connectivity estimates in the WashU cohort. Given that roughly one-quarter of the data were discarded by motion scrubbing in both cohorts, our results suggest that researchers may want verify that scrubbing effectively reduces the motion-connectivity correlation for data processed using the Simult approach to justify its cost in terms of data loss. We found that the effects of motion scrubbing and preprocessing approach were relatively independent, so there may be datasets in which both scrubbing and use of the Simult approach are indicated to attenuate the motion-connectivity association.

4.3. Motion-related BOLD fluctuations are poorly controlled by BpReg, but largely attenuated by Simult and RegBp

Power and colleagues (2012a) found that large-amplitude brain-wide fluctuations in the BOLD signal surrounding periods oflarge head motion persisted in RS-fcMRI data despite bandpass filtering and nuisance regression (using BpReg). Using a measure of change in the global BOLD signal from one volume to the next, DVARS, we investigated whether such motion-related fluctuations represented the poor control of motion-related variability by BpReg. We found a strong correspondence between DVARS and head motion for data preprocessed using BpReg, but that preprocessing using RegBp or Simult largely controlled motion-related fluctuations in the global BOLD signal (Figure 5).

Thus, although there is compelling evidence that head motion induces BOLD signal fluctuations (Friston et al., 1996), our study suggests that the proper application of bandpass filtering and nuisance regression may sufficiently mitigate this in RS-fcMRI data. Moreover, our analyses raise questions about the utility of the DVARS metric to identify motion-contaminated volumes. When computed after bandpass filtering and nuisance regression, this measure may provide more information about the magnitude of temporally synchronous nuisance-related variability reintroduced by BpReg than it does about the magnitude of motion-related fluctuations. As such, computing DVARS prior to bandpass filtering and nuisance regression may provide more useful information that could be used to develop corresponding thresholds to identify motion contamination since large-amplitude motion-related fluctuations are often evident in data prior to these preprocessing steps (Power et al., 2012b).

4.4. Recommendations for bandpass filtering and nuisance regression in RS-fcMRI preprocessing

In order to establish best practices for preprocessing resting-state fMRI data, it is important to explore which techniques minimize noise in the data and provide the most accurate estimates of functional connectivity. Our review of RS-fcMRI studies found that 40% used the BpReg approach, and the most common frequency mismatch between the fMRI data and nuisance regressors was for head motion parameters. Thus, motion-related nuisance variability is likely the greatest source of nuisance variability that has inadvertently been poorly controlled in RS-fcMRI studies using BpReg.

Altogether, we found that both bandpass filtering and nuisance regression were important steps in the preprocessing pipeline that helped to reduce motion-related variability. Nuisance regression alone was insufficient to attenuate motion-related spikes in the global signal (Figure 5), whereas bandpass filtering alone tended to spread motion artifacts in time (see also Carp, in press). Simultaneous filtering was the approach that best attenuated nuisance-related variability in RS-fcMRI time series and largely removed motion-related fluctuations in the BOLD signal. Thus, we recommend that this approach be used in future seed-based correlation analyses of RS-fcMRI data. As described above, simultaneous filtering is most straightforwardly implemented by bandpass filtering the fMRI data and all nuisance regressors (including motion parameters) prior to nuisance regression. We note that simultaneous filtering is applied by the AFNI program 3dBandpass (specially using the –ort option for nuisance regressors), and we encourage researchers to utilize this tool. We also hope that developers of fMRI software, RS-fcMRI toolboxes, or publicly released processing scripts will provide an option to use the Simult approach and that they advocate its use in software documentation. Moreover, providing simultaneous filtering as the default in established RS-fcMRI processing pipelines (e.g., DPARSF/REST) will be important to ensure that best practices are implemented by applied researchers who may be less familiar with signal processing.

Our review of the RS-fcMRI literature revealed considerable heterogeneity in the preprocessing procedures applied to resting-state data (Figure 2). Moreoever, in many articles, the sequence and details of RS-fcMRI preprocessing, particularly bandpass filtering and nuisance regression, were unclear (cf. Carp, 2012). Thus, we recommend that more explicit details be provided about 1) the sequence of preprocessing steps, 2) the spectral frequencies of the fMRI data and each of the nuisance regressors at the time of the regression, and 3) the logic behind preprocessing decisions, such as whether to include temporal derivatives in the regression model or not to temporaly filter the fMRI data. The most critical point, as demonstrated in our study, is to ensure that none of the nuisance regressors include frequencies that are not part of the frequency spectrum of the fMRI data, as this will poorly correct for noise, and this detail should be provided clearly in future RS-fcMRI papers.

4.5. Caveats and Limitations

Weissenbacher and colleagues (2009) found that bandpass filtering after regression (RegBp) resulted in slightly better connectivity specificity (i.e., the strength of connectivity between two regions of interest relative to connection strength with truly unconnected regions) relative to simultaneous filtering, although the basis for this difference was not explored. Although RegBp may increase the specificity of connectivity estimates relative to Simult, our findings suggest that this potential enhancement may come at the cost of higher nuisance-related variability within the frequencies of interest (.009 – .08 Hz) and larger motion-related residual fluctuations in the global BOLD signal after preprocessing.

Although our findings that spectral misspecification seriously corrupts connectivity estimates under BpReg are strong, we are less snaguine that simultaneous filtering alone provides sufficient control for nuisance variability in RS-fcMRI data. Indeed, Simult did not completely eliminate distance-dependent differences in the association between head motion and functional connectivity estimates, although their magnitude was much smaller relative to BpReg. This finding is illustrative of a deeper point in RS-fcMRI research that the true strength of interregional connectivity is unknown and the field is still struggling to develop a coherent model of noise in resting-state data (Behzadi et al., 2007; Birn et al., 2006). Thus, we view simultaneous filtering as an important step forward in improving the standards for RS-fcMRI preprocessing, but we acknowledge that the improvements are relative to the BpReg approach and that the separation of the neural component of RS-fcMRI time series from measured and unmeasured noise sources remains an open and important field of inquiry. Many other approaches to refining RS-fcMRI analyses are likely to be important in solving motion-related problems, such as motion scrubbing (Power et al., 2012a), correction for ringing artifacts (Carp, in press) and physiological noise (Birn et al., 2008); optimal statistical methods for modeling noise (Behzadi et al., 2007); time series prewhitening (Christova et al., 2011); and controlling for local variation in the MR signal (Jo et al., 2010). Moreover, a recent paper by Satterthwaite and colleagues (2013) found that using a voxelwise high-parameter motion regression model that included motion spikes, temporal derivatives, and quadratic terms reduced, but did not eliminate, the influence of head motion on connectivity estimates.

4.6. Conclusions

Altogether, our study provides compelling evidence that a conventional approach to preprocessing RS-fcMRI data for seed-based correlation analysis, where bandpass filtering is followed by nuisance regression of unfiltered signals, results in a misspecified regression model that systematically inflates estimates of functional connectivity. This inflation reflects two related phenomena: nuisance variation in the frequencies of interest (.009 – .08 Hz) is under-controlled, and nuisance variation in frequencies previously suppressed is reintroduced in a brain-wide temporally synchronous fashion by the regression. The degree to which BpReg inflates connectivity reflects the reintroduction of noise signals including head motion and cardiac artifact. These findings have potentially significant implications for studies where nuisance variability is expected to differ between groups of interest, such as head motion differences between children and adults. We propose a simultaneous bandpass filtering and nuisance regression approach that provides better control of nuisance variability and is a well-specified model. Some of the functional relationships and network parcellations previously observed in RS-fcMRI studies using the BpReg approach may be substantially different when reexamined using simultaneous filtering, and such differences would likely reflect the greater inclusion of nuisance variability by BpReg. Nevertheless, because the true strength of functional connectivity is not known in empirical data, simultaneous filtering may be only one of many improvements needed to achieve unbiased estimates of connectivity, and further simulation research in this domain is needed. We hope that our results encourage RS-fcMRI researchers to apply simultaneous filtering and to explore the effects of this approach on their scientific conclusions about functional brain networks.

Highlights.

• Bandpass filtering and nuisance regression are intended to reduce noise in RS-fMRI.

• When RS-fMRI data are filtered, but regressors are not, noise is poorly controlled.

• In addition, this approach reintroduces synchronous noise into fMRI data that exacerbate motion- and cardiac-related artifacts.

• Such noise leads to systematically inflated estimates of functional connectivity.

• Simultaneous bandpass filtering and regression eliminates this source of bias is eliminated.