Acid-base and Electrochemical Properties of Manganese meso(ortho- and meta-ethylpyridyl)porphyrins: Potentiometric, Spectrophotometric and Spectroelectrochemical Study of Protolytic and Redox Equilibria

Abstract

The difference in electrostatics and reduction potentials between manganese ortho-tetrakis(N-ethylpyridinium-2-yl)porphyrin (MnTE-2-PyP) and manganese meta-tetrakis(N-ethylpyridinium-2-yl)porphyrin (MnTE-3-PyP) is a challenging topic, particularly because of the high likelihood for their clinical development. Hence, a detailed study of the protolytic and electrochemical speciation of Mn^II–IVTE-2-PyP and Mn^II-IVTE-3-PyP in a broad pH range has been performed using the combined spectrophotometric and potentiometric methods. The results reveal that in aqueous solutions within the pH range ~2–13 the following species exist: (H₂O)Mn^IITE-m-PyP⁴⁺, (HO)Mn^IITE-m-PyP³⁺, (H₂O)₂Mn^IIITE-m-PyP⁵⁺, (H₂O)(HO)Mn^IIITE-m-PyP⁴⁺, (H₂O)(O=)Mn^IIITE-m-PyP³⁺, (H₂O)(O=)Mn^IVTE-m-PyP⁴⁺ and (HO)(O=)Mn^IVTE-m-PyP³⁺ (m = 2, 3). All the protolytic equilibrium constants that include the accessible species as well as the thermodynamic parameters for each particular protolytic equilibrium have been determined. The corresponding formal reduction potentials related to the reduction of the above species and the thermodynamic parameters describing the accessible reduction couples were calculated as well.

INTRODUCTION

Over the last decade, there has been a great deal of interest in manganese porphyrins (MnPs) because of their unique electronic properties - robustness as oxidation catalysts. Based on structure-activity relationship where metal-centred reduction potential, E_1/2, was related to ability to disproportionate/dismute superoxide, the ortho Mn(III) N-alkylpyridylporphyrins were identified as most potent SOD mimics.¹ We have recently shown that the water-exchange rates at Mn(III) in this type of MnPs is fast enough not to interfere with their high rates of the O₂^•− dismutation.² Furthermore, based on their ability to easily donate or accept electrons, efficacious MnP-based SOD mimics proved to be excellent scavengers of peroxynitrite and most efficacious in favourably affecting cellular transcription activities, resolving the excessive inflammatory and immune response.^3,4,5 Mn(III) N-alkylpyridylporphyrins posses 5 positive charges in the proximity of the metal site and thus afford both thermodynamic and electrostatic facilitation for the reaction with anionic superoxide and peroxynitrite. Thus they proved remarkable efficacy in ameliorating diseases that have oxidative stress in common, such as central nervous system disorders, diabetes, cancer radiation injuries, etc. The rate of O₂^•− dismutation, k_cat, can conveniently be taken as an indicator of their potential as therapeutics. In addition to the ability to affect redox-based processes, their efficacy in vivo is affected by their bioavailability. This in turn is affected by their lipophilicity, shape, size, rotational flexibility, etc. The comprehensive study on SOD-deficient E. coli shows that meta isomer, MnTE-3-PyP⁵⁺, is 10-fold more lipophilic than ortho analogue and accumulates 10-fold more in E. coli. Thus both ortho and meta isomers of N-ethylpyridylporphyrin, as well as other substituted pyridylporphyrins, may be considered perspective therapeutics. While the O₂^•− dismutation involves the Mn^IIIP/Mn^IIP redox-couple, the removal of peroxonitrite (ONOO⁻ is widely considered as a major damaging species in vivo) occurs through its binding to the Mn(III) site followed by its one-electron reduction to NO₂^• radical (a highly damaging species in its own right) along with oxidation of Mn^IIIP to Mn^IVP.⁶

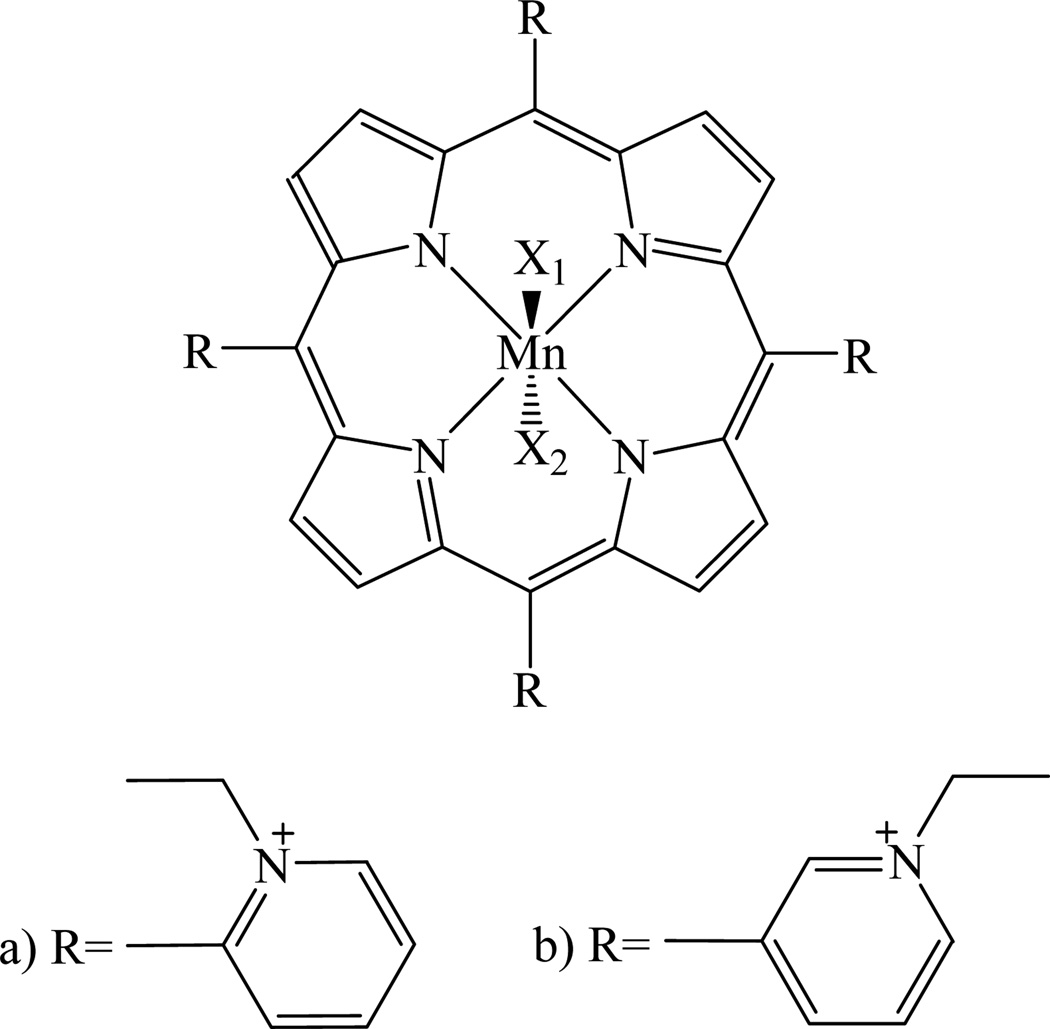
Hence, the basic chemistry of manganese(II-IV) ortho-tetrakis(N-ethylpyridinium-2-yl)porphyrin and meta-tetrakis(N-ethylpyridinium-3-yl)porphyrin (Figures 1a and 1b), related to the Mn site which is responsible for their ability to affect redox-based cellular signalling processes, is addressed in this study.

Figure 1.

a)Manganese ortho-tetrakis(N-ethylpyridinium-2-yl)porphyrin ≡ MnTE-2-PyP. b) Manganese meta-tetrakis(N-ethylpyridinium-2-yl)porphyrin ≡ MnTE-3-PyP. X₁ and X₂ stand for the aqua, hydroxo, or/and oxo ligand(s), with X₂ not necessarily included.

Although biological relevance of MnPs was the primary reason for conducting this study, an additional reason to undertake it was the observation of a strong effect of a slight positional change of ethylpyridinium substituents on the lipophilicity and the metal-centered formal reduction potential of the studied MnPs. The reduction potentials for diaqua Mn^IIIP/Mn^IIP and Mn^IVP/Mn^IIIP couples have been reported, ^7,8,9 but several reports differ in the identities of all relevant species, or the data have been collected under different experimental conditions. A great variety of different complex species have been proposed so far, as for instance (O=)₂Mn^IVP, (OH)(O=)Mn^IIIP and Mn^IIP^•,¹⁰ (H₂O)₂Mn^IVP and (H₂O)(OH)Mn^IVP,^11,12 as well as (H₂O)(HO=)Mn^IVP species.⁹ However, none of the papers report the ionic strength, which has been shown to affect the proton dissociation of the complexes to a great extent.¹³ On the other hand, the obtained thermodynamic parameters of manganese ortho-tetrakis(N-n-butylpyridinium-2-yl)porphyrin (MnTnBu-2-PyP) deprotonation have not supported the identification of (H₂O)(O=)Mn^IVP complex as the “fully” protonated Mn^IVP species in an aqueous solution 4 < pH < 13.¹³

In order to improve our understanding of a rather complex behaviour of MnPs, in this work we report the results of a detailed study of the protolytic and electrochemical speciation of Mn^II-IVTE-2- PyP and Mn^IIIVTE-3-PyP in a broad pH range. The difference in electrostatics and reduction potentials of these two isomers is a challenging topic, particularly because of the high likelihood for their clinical development.

EXPERIMENTAL

Throughout the experiments, double distilled water and the highest purity chemicals were used. The measurements were performed under the N₂ or Ar atmosphere. The buffers used were prepared from CH₃COONa (Sigma), Na₂B₄O₇·10H₂O (Riedel-de Haën), CAPS (N-cyclohexyl-3-aminopropanesulfonic acid) (Sigma), Na₂HPO₄·2H₂O (Merck) and NaH₂PO₄ (Merck). The pH of aqueous solutions was determined on a Mettler DL50 titrator with a Mettler DG111-SC glass electrode and a thermostatted titration vessel. The pH electrode was calibrated by titration of a strong acid with a strong base in 2M NaClO₄.

The investigated metalloporphyrins, Mn^IIITE-2-PyPCl₅ and Mn^IIITE-3-PyPCl₅, were synthesized according to the published procedures.^{14, 15} Mn^IIPs were prepared by the reduction of Mn^IIIPs with ascorbic acid (Fluka), whereas the oxidation of Mn^IIIPs was performed by K₃[Mo(CN)₈] prepared according to published procedure^{16, 17} immediately before the experimental measurements. An equimolar solution of octacyanomolybdate(V/IV) was prepared by oxidation of K₄[Mo(CN)₈] with KMnO₄ in perchloric acid and the formed Mn²⁺(aq) was quantitatively removed by filtration of precipitated Mn(OH)₂ formed upon the addition of 0.1 M NaOH. The concentration of K₃[Mo(CN)₈] was determined spectrophotometrically (ε₃₈₈ = 1360 M⁻¹ cm⁻¹).¹⁸

The UV-Vis spectra were recorded on a Cary 50 spectrophotometer equipped with an optic fiber immersion probe and a thermostatted titration vessel or a thermostatted cell holder.

BASi SEC-C thin layer quartz glass spectroelectrochemical cell with 1mm light path and Princeton Applied Research PAR-273A potentiostat were used for spectroelectrochemical measurements (SEC). As the working, reference, and auxiliary electrode an 80-mesh Pt-gauze, the Ag/AgCl standard electrode (3M NaCl) and a platinum wire were used, respectively. The potentials are reported vs. Standard hydrogen electrode (SHE, referring to the hydrogen pressure of 1 bar).

RESULTS

ACID-BASE PROPERTIES OF MnTE-m-PyP (m = 2, 3) COMPLEXES

Deprotonation of Mn^IIITE-m-PyP

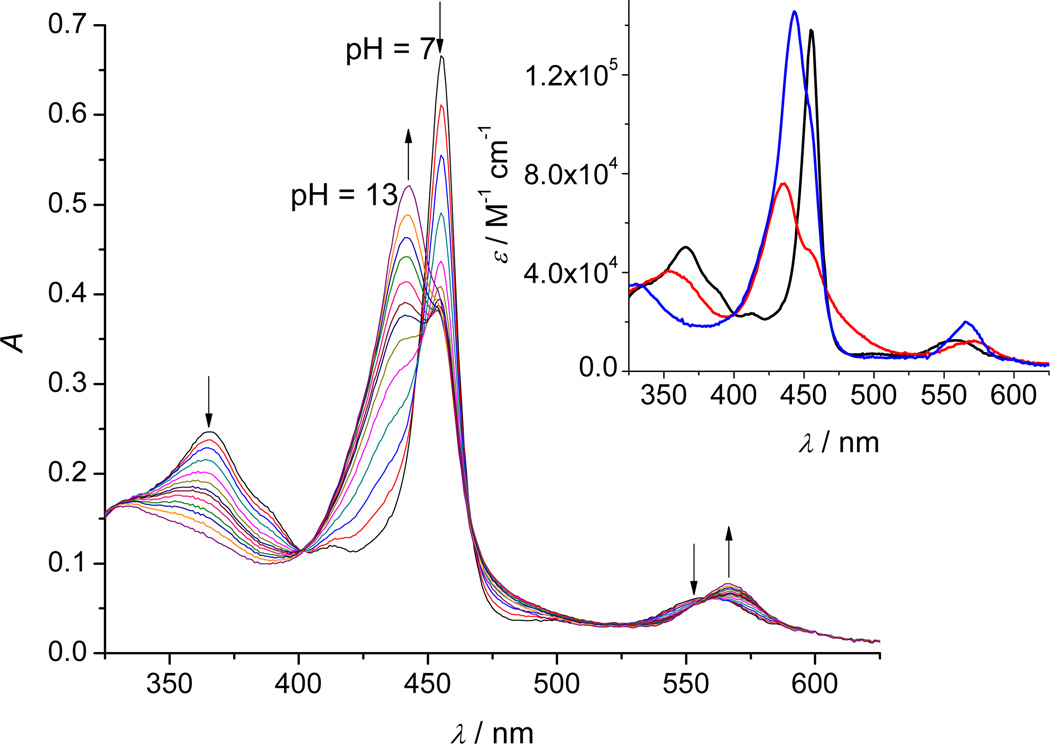
In an aqueous solution, MnPs can axially coordinate water molecules, which can deprotonate to hydroxo- and/or oxo-complexes, depending on the oxidation state and pH. Such deprotonation is usually associated with an immediate spectral change observable in the UV-Vis spectral region. The observed spectral change of the Mn^IIITE-2-PyP in an aqueous solution as function of pH is shown in Figure 2. Since no spectral change has been observed from pH 7 down to pH 1.5, these spectra are not shown in the figure.

Figure 2.

A typical titration profile of 4.8 µM Mn^IIITE-2-PyP in 2 M NaClO₄ with 0.2 M NaOH (θ = 25 °C, l = 1 cm). The pH values of the solution were varied within the pH-range 7–13 (for the sake of clarity not all measured spectra are shown). Inset: The theoretical spectra of the protonated (), mono-deprotonated (), and double-deprotonated () species.

An absence of isosbestic points during the titration clearly indicates an involved equilibrium that includes at least three absorbing species. Indeed, the spectral analysis by the SPECFIT^19,20,21 program confirmed three relevant absorbing species related through the acid-base equilibrium defined by two pK_a-s. Fitting such a reaction model to the experimental data resulted in the following values: pK_a1 = 10.89 ± 0.01 and pK_a2 = 11.62 ± 0.02. The inset of Figure 2 illustrates the theoretical spectra of the relevant species predicted from the fit.

A similar spectral change as function of pH in an aqueous solution was observed for Mn^IIITE-3-PyP and is shown in Figure S1. Fitting the model to the experimental data resulted in the following values: pK_a1 = 11.57 ± 0.01 and pK_a2 = 12.70 ± 0.09.

Deprotonation of Mn^IITE-m-PyP

Since in acidic medium Mn^IIPs decompose to free metal ions and the porphyrin ligand,²² it was necessary to determine the acidity range in which the Mn^IIPs were stable enough to perform the titrations. Hence, an aqueous solution of each MnP was adjusted to a particular pH, purged with argon in a SEC UV-Vis cell and a negative potential of ca. −250 mV vs. the formal potential of a particular MnP has been applied to the Pt-electrodes inserted in the solution. The time-dependent spectral changes observed for both Mn^IIIPs, continuously monitored for ca. 30 minutes in an anaerobic cell at constant pH (Figures S2 and S3, respectively), confirm the thermodynamic lability of both Mn^IIPs. After the initial reduction at pH ≤ 2, an “irreversible” decomposition of the formed Mn^IITE-2-PyP was observed, characterized by the formation of a species with an absorbance maximum characteristic of the free porphyrin (H₂TE-2-PyP, λ_max = 415 nm). The observed spectral changes at pH 4 and 8 are similar, except that at pH 4 the formed product cannot be quantitatively re-oxidized to Mn^IIITE-2-PyP. This is an indication of the proton-concentration dependence of the decomposition rate. Mn^IITE-3-PyP was found to be even more unstable, since the extensive decomposition of this complex to the free metal ion and the porphyrin ligand was observed already at pH 4. Therefore, the “safe” acidity ranges for the acid-base titrations of both Mn^IIPs were established at pH > 7.

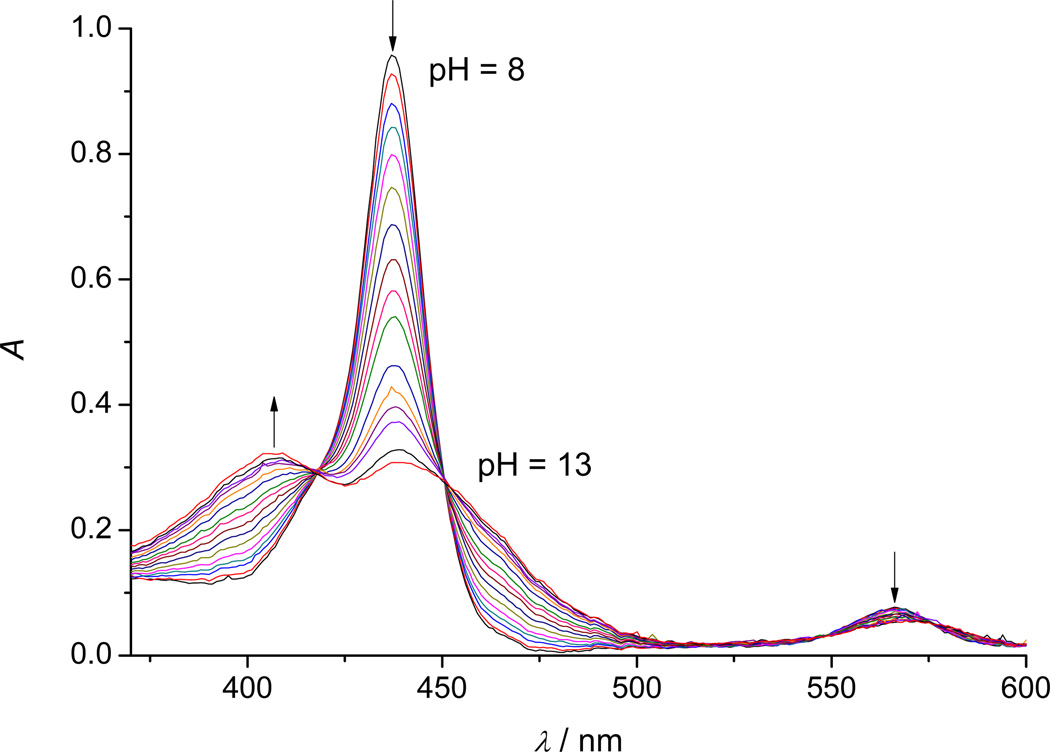
Maintenance of the total MnTE-2-PyP in reduced form was accomplished by the addition of 1 mM ascorbic acid and by keeping aqueous solutions under purified argon. The observed spectral change of Mn^IITE-2-PyP in an aqueous solution in the presence of ascorbic acid as a function of pH is shown in Figure 3.

Figure 3.

A typical titration profile of 5 µM Mn^IITE-2-PyP in 2 M NaClO₄ with 0.2 M NaOH, (θ= 25 °C, l = 1 cm). The pH values of the solution were varied within the pH-range 8–13 (for the sake of clarity not all measured spectra are shown). Spectra obtained at pH < 8 are shown in Figure 5.

The SPECFIT factor analysis reveals two relevant absorbing species present in the solution, but the existence of the third one could not be definitively ruled out. Therefore, the observed spectral data were fitted to two different models, one affording two spectral species and one pK_a value and another one affording three spectral species and two pK_a-s. Fitting the former model to the experimental spectral data resulted in the value of pK_a = 11.75 ± 0.01, whereas fitting the latter model to the same experimental data resulted in pK_a1 = 9.7 ± 0.2 and pK_a2 = 11.76 ± 0.01.

The 3-species model for Mn^IITE-2-PyP deprotonation produces a slightly better fit, which can be expected due to more degrees of freedom. Standard deviation for that model is only slightly better than the one for the 2-species model (σ = 1.8 × 10⁻³vs. σ = 2.1 × 10⁻³) and the residuals of spectral data are very similar for both models. However, the theoretical spectra of the fully protonated and monodeprotonated species of Mn^IITE-2-PyP in the 3-species model are practically identical (Figure S4), and the calculated pK_a1 value has a ten times larger standard deviation than pK_a2. Furthermore, the pK_a value for the 2-species model is remarkably similar to pK_a2 for the 3-species model. In conclusion, our result on the acid-base equilibrium of Mn^IITE-2-PyP confirms only one pK_a with certainty, while the other one is not supported by the current experimental data.

The observed visible spectral change of the Mn^IITE-3-PyP in the presence of ascorbic acid as a function of pH is similar to the one obtained for Mn^IITE-2-PyP and is shown in Figure S5, but to maintain the total MnTE-3-PyP in its reduced form, an addition of 10 mM ascorbic acid was necessary. Fitting the 2-species model including a single-proton dissociation to the experimental data resulted in the value of pK_a = 12.04 ± 0.03. The theoretical spectra of the involved species (inset of Figure S5) reveal the similarity of the two studied Mn^IIPs. It is worth noting that the spectra of Mn^IITE-3-PyP obtained by either the electrochemical reduction or the chemical reduction with ascorbic acid, match each other more than satisfactorily (Figure S6).

Deprotonation of Mn^IVTE-m-PyP

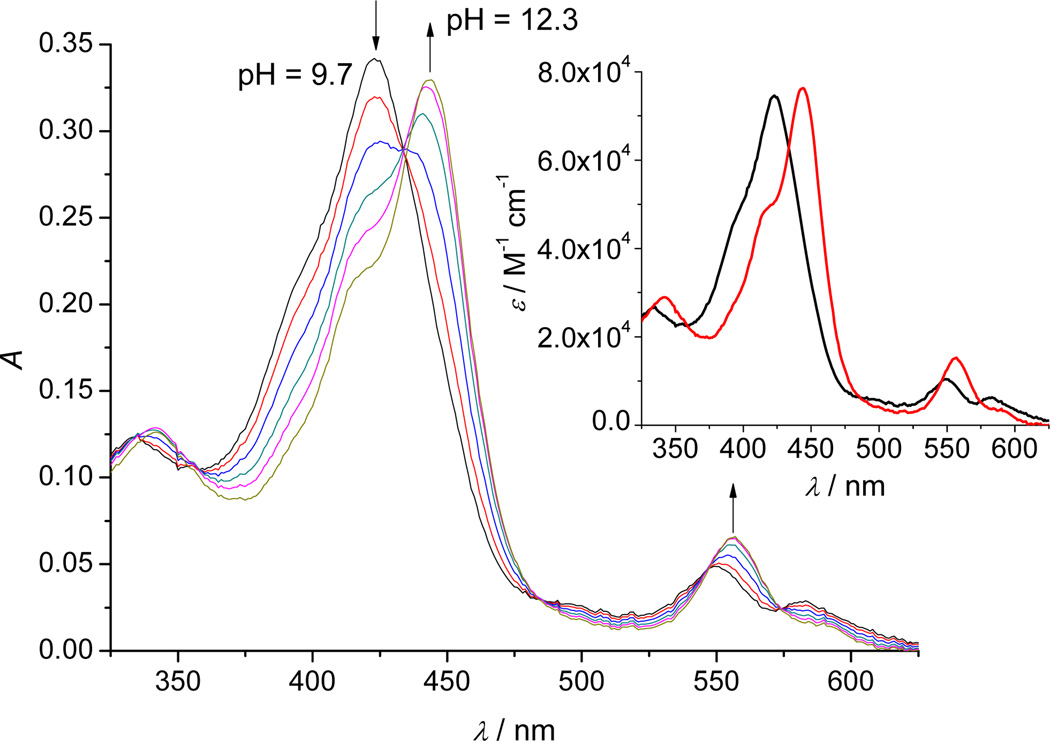
In order to determine the deprotonation patterns of the Mn^IVPs, the spectrophotometric pH-titrations were performed under purified argon in the presence of an efficient oxidant. Maintenance of the total MnTE-2-PyP in oxidized form in mildly basic conditions was achieved with 0.1 mM [Mo(CN)₈]³⁻. Dependence of the observed visible spectrum of Mn^IVTE-2-PyP in an aqueous solution on pH is shown in Figure 4. Above pH 12.3 no further spectral change has been observed and these data are not shown in the figure.

Figure 4.

A typical titration profile of 4.6 µM Mn^IVTE-2-PyP in 2 M NaClO₄ with 0.2 M NaOH (θ = 25 °C, l = 1 cm), in the presence of 0.1 mM [Mo(CN)₈]³⁻. The pH values of the solution were varied within the pH-range 9.7–12.3 (for the sake of clarity not all measured spectra are shown). Inset: The theoretical spectra of protonated () and deprotonated () species.

The spectral analysis revealed two relevant absorbing species related through a single-proton exchange. Fitting the model to the experimental data resulted in the value of pK_a = 11.14 ± 0.02. The predicted theoretical spectra of relevant species are shown as an inset in Figure 4. Below pH 9.7 the reduced form of the complex is extremely stabilized and a possible deprotonation constant in that pH range was inaccessible by the presented type of experiments.

The titration of Mn^IVTE-3-PyP was carried out under very similar experimental conditions as described for Mn^IVTE-2-PyP, and the observed spectral change is similar as well (Figure S7). The spectral analysis using the SPECFIT program again revealed only two relevant absorbing species and fitting this model to the experimental data resulted in a single value of pK_a = 11.99 ± 0.04.

ELECTROCHEMICAL PROPERTIES OF MnTE-m-PyP (m = 2, 3) COMPLEXES

As presented above, the deprotonations of each Mn^IIP and Mn^IVP were found to be characterized by only one pK_a. Based on these results alone, structures of the species linked by a single proton exchange cannot be distinguished. In order to resolve this ambiguity we set up a new series of experiments including pH-spectrophotometric titrations of both MnPs in the presence of either ascorbic acid or octacyanomolybdate(V) but with the particular MnP present in two oxidation states. The obtained results allow relating the thermodynamic parameters of the investigated acid-base equilibria to the formal reduction potentials of each couple, as well as the number of transferred electrons to the number of protons transferred in the equilibria involved.

Reduction of Mn^IIIPs with ascorbate

In order to determine the values of the formal reduction potential for the studied Mn^IIIP/Mn^IIP couples, the spectrophotometric titrations were performed in the presence of ascorbic acid, with respect to the “safe” acidity range. The spectral data reveal a gradual reduction of both MnPs with ascorbic acid upon addition of NaOH to the solutions.

The oxidation of ascorbate, Asc²⁻, proceeds through two distinct steps. The first-step formation of a free-radical anion, Asc^•−, is followed by a very fast disproportionation of the formed radical yielding ascorbate dianion and dehydroascorbic acid: 2Asc^•− ⇆ Asc²⁻ + D.²³ Dehydroascorbic acid is further transformed to the final product by a relatively slow but irreversible reaction.²⁴ Therefore, in order to maintain the “reversibility” of the studied redox reactions during the spectrophotometric titrations, each spectrum has been measured immediately after mixing the reactants at the appropriate pH, thus avoiding the degradation of both Mn^IIPs and dehydroascorbic acid.

Figures 5 and S8 show the spectral changes of Mn^IIITE-2-PyP and Mn^IIITE-3-PyP in the presence of a large molar excess of ascorbic acid upon addition of NaOH, respectively. In both experiments the concentration of dehydroascorbic acid was maintained constant and in a large molar excess over MnPs by the initial addition of ferricyanide to oxidize a part of ascorbate according to the reaction: 2[Fe(CN)₆]³⁺ + Asc²⁻ ⇆ 2[Fe(CN)₆]²⁺ + D.

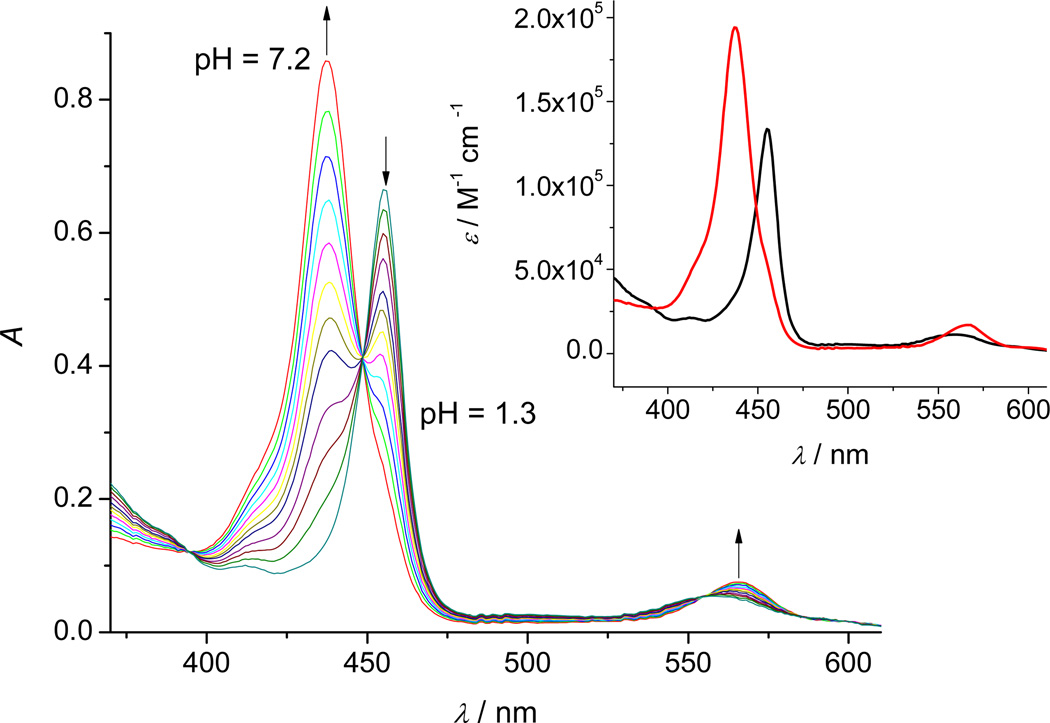
Figure 5.

A typical titration profile of (4.9 µM Mn^IIITE-2-PyP + 20 mM ascorbic acid + 0.5 mM [Fe(CN)₆]³⁻) in 2 M NaClO₄ with 0.2 M NaOH (θ = 25 °C, l = 1 cm). The pH values were varied within the pH-range 1.3–7.2 (for the sake of clarity not all measured spectra are shown). Inset: The theoretical spectra of Mn^IIITE-2-PyP⁵⁺ () and Mn^IITE-2-PyP⁴⁺ ().

The spectral analyses of the data indicate two absorbing species for each MnP, related through a proton dissociation reaction: Mn^IIITE-m-PyP ⁿ⁺ ⇆ Mn^IITE-m-PyP ⁽ⁿ⁻¹⁾⁺ + H+, with the apparent reaction equilibrium constant defined as:

$$K_{\text{red.}}=\frac{[({\mathrm{H}}_2\mathrm{O})\mathrm{M}{\mathrm{n}}^{\text{II}}\mathrm{T}\mathrm{E}-m-{\text{PyP}}^{4+}]\left[{\mathrm{H}}^{+}\right]}{[{({\mathrm{H}}_2\mathrm{O})}_2{\text{Mn}}^{\text{III}}\text{TE}-m-{\text{PyP}}^{5+}]}.$$ (1)

The data shown in Figures 5 and S8 were fitted in order to determine the half-reduction points, i.e. the pH values at which [Mn^IITE-m-PyP ]/[Mn^IIITE-m-PyP] = 1. For Mn^IIITE-2-PyP and Mn^IIITE-3-PyP the calculated half-reductions are found at pH = p K_red = 3.21 ± 0.02 and pH = p K_red = 8.84 ± 0.04, respectively. The theoretical spectra shown in the insets of these two figures are in excellent agreement with the theoretical spectra of the same species obtained by the separate spectrophotometric pH-titrations of each MnP: Mn^IIITE-2-PyP⁵⁺ (Figure 2), Mn^IITE-2-PyP⁴⁺ (Figure 3), Mn^IIITE-3-PyP⁵⁺ (Figure S1) and Mn^IITE-3-PyP⁴⁺ (Figure S5).

The formal reduction potential of ascorbic acid, $E_{\mathrm{D},{\mathrm{H}}^{+}/{\mathrm{H}}_2\mathrm{A}\mathrm{s}\mathrm{c}}^0=+390\mathrm{m}\mathrm{V}$,²⁵ is pH-dependent due to the deprotonations of H₂Asc. Our potentiometric titration of ascorbic acid in 2 M NaClO₄ at 25 °C afforded the values of pK_a1A = 4.21 ± 0.03 and pK_a2A = 11.13 ± 0.05. The Nernst equation for the potential of D, H+/H₂Asc couple expressed in terms of total concentrations of both ascorbic acid and dehydroascorbic acid at 25 °C is therefore:

$$E=E_{\mathrm{D},{\mathrm{H}}^{+}/{\mathrm{H}}_2\mathrm{A}\mathrm{s}\mathrm{c}}^0-\frac{0.0591}{2}\text{log}\frac{{\left[\mathrm{A}\mathrm{s}\mathrm{c}\right]}_{\text{tot}}}{({\left[{\mathrm{H}}^{+}\right]}^2+[{\mathrm{H}}^{+}]K_{\mathrm{a}1\mathrm{A}}+K_{\mathrm{a}1\mathrm{A}}{K}_{\mathrm{a}2\mathrm{A}}){\left[\mathrm{D}\right]}_{\text{tot}}}$$ (2)

Using eq. (2), the potentials of the 0.25 mM dehydroascorbic acid/19.75 mM ascorbic acid couple at pH = 8.84 and pH = 3.21 can be calculated as −52 mV and +145 mV, respectively. Since the reaction solutions were left to equilibrate at each point of the titration, the calculated potentials equal the formal reduction potentials of fully protonated Mn^IIIP/Mn^IIP couples.

Oxidation of Mn^IIIPs with octacyanomolybdate(V)

Below pH 10, in the presence of octacyanomolybdate(V), the investigated porphyrin complexes were mixtures of Mn(III)/(IV) oxidation states. The reactions of both Mn^IIIPs with octacyanomolybdate(V) can be written as: Mn^IIITE-m-PyP⁵⁺ + [Mo^V(CN)₈]³⁻ ⇆ Mn^IVTE-m-PyP⁶⁺ + [Mo^IV(CN)₈]⁴⁻. By a gradual increase of pH from neutral up to 10, a 0.1 mM [Mo(CN)₈]³⁻ gradually oxidizes either of the Mn^IIIPs in solution. The spectral changes caused by the addition of NaOH to the neutral solutions of MnTE-2-PyP and MnTE-3-PyP in the presence of equimolar octacyanomolybdate(V/IV) are shown in Figures 6 and S9, respectively.

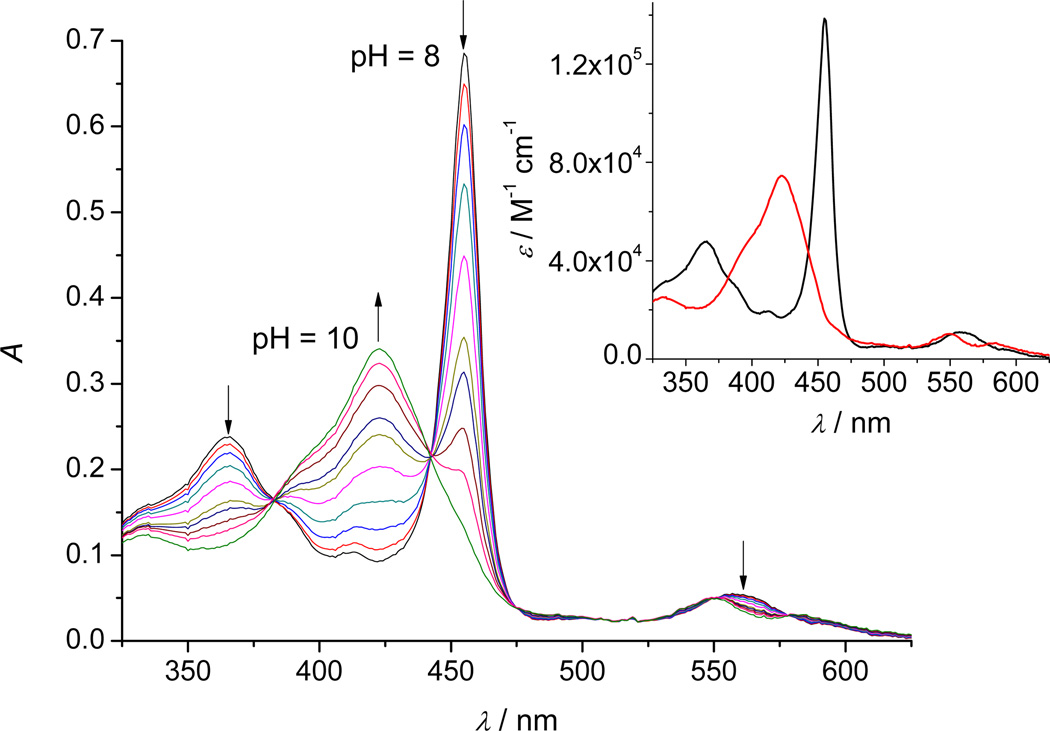
Figure 6.

A typical titration profile of 5 µ Mn^IIITE-2-PyP in 2 M NaClO₄ with 0.2 M NaOH (θ = 25 °C, l = 1 cm) in the presence of 0.1 mM [Mo(CN)₈]³⁻ and 0.1 mM [Mo(CN)₈]⁴⁻. The pH values of the solution were varied within the pH-range 8–10 (for the sake of clarity not all measured spectra are shown). Inset: The theoretical spectra of the reduced () and oxidized forms of MnTE-2-PyP ().

For each MnP, the SPECFIT spectral analyses indicate two absorbing species related through the simultaneous dissociation of two protons. The formal reduction potential of octacyanomolybdate has been determined as $E_{{\left[\mathrm{M}\mathrm{o}{(\mathrm{C}\mathrm{N})}_8\right]}^{4-}/{\left[\mathrm{M}\mathrm{o}{(\mathrm{C}\mathrm{N})}_8\right]}^{3-}}^{0\text{'}}=+870\mathrm{m}\mathrm{V}$ by CV experiments in 2 M NaClO₄. Within the studied pH range, this formal reduction potential is pH-independent and the observed pH-dependence of measured spectra must be a consequence of the MnPs’ deprotonation. Furthermore, as the above presented results on the proton dissociation reveal that within the used pH range both Mn^IIIPs deprotonate negligibly, the observed proton dependence must be attributed solely to a double deprotonation of Mn^IVPs species. Therefore, an oxidation half-reaction suitable to the observed spectral changes can be written as: (H₂O)₂Mn^IIITE-m-PyP⁵⁺ ⇆ (O)(H₂O)Mn^IVTE-m-PyP⁴⁺ + 2H⁺+ e⁻, characterized by the following apparent equilibrium constant:

$$K_{\text{app.}}=\frac{[(\mathrm{O})({\mathrm{H}}_2\mathrm{O})\mathrm{M}{n}^{\text{IV}}\text{TE}-m-{\text{PyP}}^{4+}]{\left[{\mathrm{H}}^{+}\right]}^2}{[{({\mathrm{H}}_2\mathrm{O})}_2{\text{Mn}}^{\text{III}}\text{TE}-m-{\text{PyPH}}^{5+}]}.$$ (3)

Fitting the proposed model to the experimental data resulted in the value of pK_app = 17.71 ± 0.02 and pK_app = 17.85 ± 0.01 for (H₂O)₂Mn^IIITE-2-PyP⁵⁺ and (H₂O)₂Mn^IIITE-3-PyP⁵⁺, respectively. The theoretical spectra shown in the inset of these two figures are again in excellent agreement with the theoretical spectra of the same species obtained by the separate spectrophotometric pH-titrations of each MnP: Mn^IIITE-2-PyP⁵⁺ (Figure 2), Mn^IVTE-2-PyP⁴⁺ (Figure 4), Mn^IIITE-3-PyP⁵⁺ (Figure S1) and Mn^IVTE-3-PyP⁴⁺ (Figure S7).

Taking the above mentioned into account, the experimental data should be fully depicted by the redox reaction: (H₂O)₂Mn^IIITE-m-PyP⁵⁺ + [Mo(CN)₈]³⁻ ⇆ (O)(H₂O)Mn^IVTE-m-PyP⁴⁺ + [Mo(CN)₈]⁴⁻ + 2H⁺, and the equilibrium constant given by equation (4).

$$K_{\text{OX.}}=\frac{[(\mathrm{O})({\mathrm{H}}_2\mathrm{O}){\text{Mn}}^{\text{IV}}\text{TE}-m-{\text{PyP}}^{4+}]\left[{\left[\mathrm{M}\mathrm{o}{(\text{CN})}_8\right]}^{4-}\right]{\left[{\mathrm{H}}^{+}\right]}^2}{[{({\mathrm{H}}_2\mathrm{O})}_2{\text{Mn}}^{\text{III}}\text{TE}-m-{\text{PyP}}^{5+}]\left[{\left[\mathrm{M}\mathrm{o}{(\text{CN})}_8\right]}^{3-}\right]}$$ (4)

Considering that the concentrations of [Mo(CN)₈]³⁻ and [Mo(CN)₈]⁴⁻ were practically equal during the entire titrations (the total octacyanomolybdate is in a very large molar excess over MnPs), the calculated values of K_ox. for the two MnPs numerically equal the corresponding values of K_app given above. From the values of K_ox. and the deprotonation constants listed in Table 1 for the two MnPs, the values of the formal reduction potentials of individual species were easily calculated from Nernst equation and are listed in Table 2.

Table 1.

Thermodynamic data and deprotonation constants at 25 °C, I = 2 M NaClO₄ (assigned as in Scheme 1) of manganese alkylpyridyl complexes.

Species	pKa1 ±σ	Δa1Ha ±σ	Δa1Sb ±σ	pKa2 ±σ	Δa2H ±σ	Δa2S ±σ	pKa3 ±σ	Δa3H ±σ	Δa3S ±σ	Ref.
MnIITE-2-PyP	11.75 ± 0.01	-	-	-	-	-	-	-	-	This work
MnIITE-3-PyP	12.04 ± 0.03	-	-	-	-	-	-	-	-	This work
MnIITnBu-2-PyP	11.99 ± 0.03	59 ± 2	−32 ± 7	-	-	-	-	-	-	31
MnIIITE-2-PyP	10.89 ± 0.01	49 ± 1	−44 ± 3	11.62 ± 0.02	48 ± 3	−62 ± 11	-	-	-	This work
MnIIITE-3-PyP	11.57 ± 0.01	51 ± 3	−51 ± 9	12.70 ± 0.09	51 ± 3	−72 ± 11	-	-	-	This work
MnIIITnBu-2-PyP	11.36 ± 0.01	60 ± 2	−16 ± 8	12.33 ± 0.01	49 ± 3	−67 ± 8	-	-	-	31
MnIVTE-2-PyP	-	-	-	-	-	-	11.14 ± 0.02	52 ± 3	−37 ± 11	This work
MnIVTE-3-PyP	-	-	-	-	-	-	11.99 ± 0.04	50 ± 6	−59 ± 19	This work
MnIVTnBu-2-PyP	-	-	-	-	-	-	11.78 ± 0.02	48 ± 2	−63 ± 7	31

^aReaction enthalpies are given in kJ mol⁻¹.

^bReaction entropies are given in J K⁻¹ mol⁻¹.

Table 2.

The formal reduction potentials for the one-electron couples obtained by the spectrophotometric pH titrations at θ = 25 °C, I = 2 M (NaClO₄), assigned as in Scheme 1

Formal potential	MnTE-3-PyP (E0’ ± σ)/V	MnTE-2-PyP (E0’ ± σ)/V	MnTnBu-2-PyP (E0’ ± σ)/Va
E10’	−0.052 ± 0.001	+0.145 ± 0.001	+0.203
E20’	−0.080 ± 0.001	+0.094 ± 0.001	+0.191
E60’	+0.479 ± 0.001	+0.578 ± 0.001	+0.399

^aValues taken from reference 13.

Thermodynamics of deprotonation of Mn^XTE-m-PyP (X = III, IV; m = 2, 3) complexes

In an attempt to identify the species of MnPs involved in the reaction with octacyanomolybdate(V) (Figures 6 and S9), we have performed additional pH-spectrophotometric titrations of both MnPs in the temperature range from 15 °C to 35 °C. The variations of the observed ionization constants of Mn^IIIPs and Mn^IVPs with temperature are presented in Figures S10 and S11, respectively. An excellent linearity of the van’t Hoff plots was obtained with the correlation coefficients 0.947 < R < 0.992. From the intercepts and slopes of van’t Hoff plots, the reaction enthalpies and entropies were calculated and are given in Table 1.

Thermodynamics of oxidation of Mn^XTE-m-PyP (X = III, IV; m = 2, 3) complexes with octacyanomolybdate(V)

In order to evaluate the thermodynamic parameters for the Mn^IV/IIIPs electron-transfer reactions, the temperature dependences of K_app defined by equation (3) were also examined in the temperature range from 15 °C to 35 °C. The values of K_app. determined at different temperatures and the measured temperature dependence of the formal reduction potential of octacyanomolybdate (Figure S12) combined with the reported value of absolute reduction potential of hydrogen gas electrode (+4.44 V)²⁶ enabled the construction of plots for the temperature dependence of both the formal and the absolute reduction potentials of (O)(H₂O)Mn^IVTE-m-PyP⁴⁺,2H⁺/(H₂O)₂Mn^IIITE-m-PyP⁵⁺ redox couples (Figures S13 and S14). Omitting the variation in heat capacity in the temperature interval from 288.15 K to 303.15 K, the thermodynamic parameters can be calculated from the slopes of E^0' vs. T and E^0* vs. T (ΔS = n F ΔE/ΔT and ΔH = –n F E + T ΔS), resulting in the values given in Tables 3 and S1.

Table 3.

Thermodynamic data for the accessible redox couples of the studied manganese porphyrin complexes obtained in 2 M NaClO₄. The values were calculated from formal redox potentials vs. SHE.

Couple	Parametera,b
	ΔH0’ ± σ	ΔS0’ ± σ
(O)(H2O)MnIVTE-2-PyP4+ + 2H+ + e− → (H2O)2MnIIITE-2-PyP5+	−182 ± 5	+8 ± 18
(O)(H2O)MnIVTE-2-PyP4+ + H+ + e− → (OH)(H2O)MnIIITE-2-PyP4+	−133 ± 8	−36 ± 21
(O)(H2O)MnIVTE-2-PyP4+ + e− → (O)(H2O)MnIIITE-2-PyP3+	−85 ± 11	−98 ± 32
(O)(OH)MnIVTE-2-PyP4+ + 2H+ + e− → (OH)(H2O)MnIIITE-2-PyP5+	−185 ± 11	+1 ± 32
(O)(H2O)MnIVTE-3-PyP4+ + 2H+ + e− → (H2O)2MnIIITE-3-PyP5+	−174 ± 5	+37 ± 16
(O)(H2O)MnIVTE-3-PyP4+ + H+ + e− → (OH)(H2O)MnIIITE-3-PyP4+	−123 ± 8	−14 ± 25
(O)(H2O)MnIVTE-3-PyP4+ + e− → (O)(H2O)MnIIITE-3-PyP3+	−72 ± 11	−86 ± 36
(O)(OH)MnIVTE-3-PyP4+ + 2H+ + e− → (OH)(H2O)MnIIITE-3-PyP5+	−173 ± 14	+45 ± 44

^aReaction enthalpies are given in kJ mol⁻¹.

^bReaction entropies are given in J K⁻¹ mol⁻¹.

DISCUSSION

The equilibrium spectrophotometric measurements reveal three forms of Mn^IIIPs within the studied pH range (1.5 < pH < 13). Considering the different experimental conditions used, the obtained values of the deprotonation constants of Mn^IIIPs are quite close to the ones reported for similar complexes, e.g. the methyl analogues of the studied porphyrins (pK_a1(Mn^IIITM-2-PyP) = 10.5, pK_a2(Mn^IIITM-2-PyP) = 11.4, pK_a1(Mn^IIITM-3-PyP) = 11.5, and pK_a2(Mn^IIITM-3-PyP) = 13.2, pK_a1(Mn^IIITnBu-2-PyP) = 10.3, pK_a2(Mn^IIITnBu-2-PyP) = 11.2).^6,27,28 Since the titrations were carried out down to pH 1.5, it can be safely assumed that the observed fully deprotonated species of both Mn^IIIPs are diaqua complexes, with two axially coordinated water molecules.

On the other hand, only two forms of Mn^IIPs could be experimentally identified. The question that arises is which species is experimentally inaccessible. This dilemma was resolved by combining the results of acid/base titrations when total MnPs were reduced, with the results of the titrations when the manganese in MnPs existed in both +2 and +3 oxidation states. When Mn^IIIPs were titrated with NaOH in the presence of ascorbic acid in the pH region where only their fully protonated (diaqua species) complexes exist, the redox reactions were accomplished by no proton exchange on the MnPs. Obviously, the experimentally accessible Mn^IIPs species are the fully protonated and the mono-deprotonated ones.

The inability to detect fully deprotonated Mn^IIPs came rather as a surprise, considering that during the titrations the pH of the solutions was increased up to 13. However, in contrast to the Mn^IIIPs and the Mn^IVPs, the Mn^IIPs coordinate only one axial water molecule²⁹ because of an increase of the manganese ion radius upon its reduction. In turn, manganese is inserted slightly above the porphyrin plane, one of the coordinated water is driven away, the thermodynamic stability is decreased and the kinetic inertness of Mn^IIPs in acidic medium is lost, leading to the observed decomposition of the complexes (Figures S2 and S3).

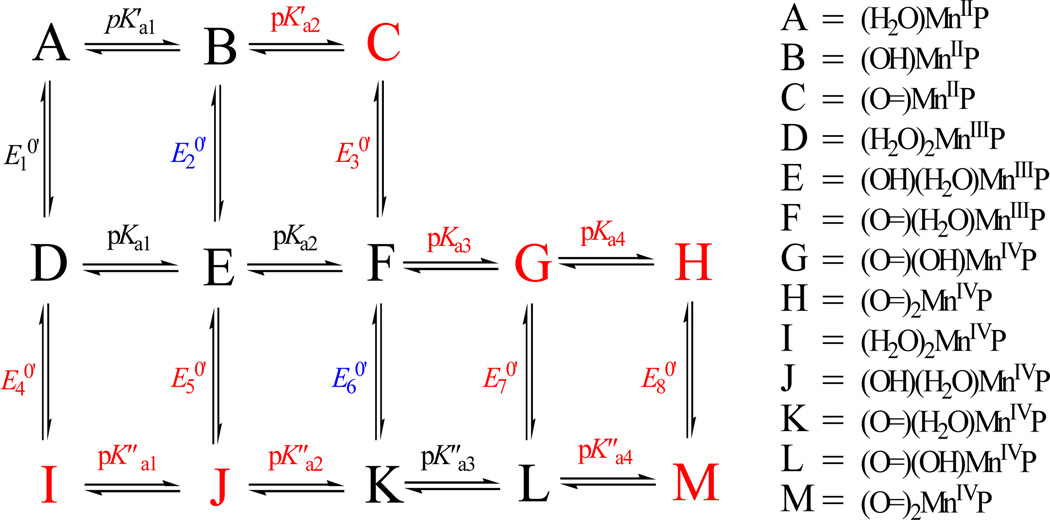
For the same reason, the species that would form upon a full deprotonation of Mn^IITE-2-PyP must coordinate only an oxo-ligand. Such a complex may be destabilized by the unfavourable solvent reorganizations caused both by the overall charge decrease of the complex and a charge redistribution within the complex species induced by a strong π-bonding of oxo-ligand to the central Mn(II) ion. A plausible model for the deprotonation and redox reactions of Mn^III/IIPs, based on the above mentioned arguments, is depicted by the reaction Scheme 1 and the values of the deprotonation constants obtained according to this model are listed in Table 1.

Scheme 1.

The equilibria describing the observed behaviour of MnPs in aqueous solutions. The directly determined equilibrium constants and the species involved are coloured black, the indirectly determined equilibrium constants are coloured blue and the experimentally inaccessible equilibria and the species involved are given in red.

Based on the fitting procedure, only two forms of Mn^IVPs were identified in aqueous solutions. It should be noted that the inability to detect more protolytically related species is a consequence of our inability to maintain total MnPs in the +4 oxidation state below pH 10, which limited the pH range of titrations. It has been shown that Mn^IVPs are unstable, particularly at a low pH, reacting with water to regenerate Mn^IIIPs.¹² Hence, though we could have chosen a much stronger oxidant than octacyanomolybdate, a possible interference of the water oxidation prevented such an option.

Besides the question of identification of the experimentally inaccessible species, an additional question is whether the observed deprotonated complexes have coordinated water molecule(s) at all. An increase of positive charge on the manganese is expected to increase the acidity of the coordinated water molecules.³⁰ According to Scheme 1, the oxidation of (H₂O)₂Mn^IIIP⁵⁺ could be accompanied by the observed double-deprotonation only if pK”_a2 < 9. This implies at least a four-units decrease of pK_a upon oxidation of Mn(III) to Mn(IV). Therefore, it appears that under the studied experimental conditions for both Mn^IVPs the experimentally inaccessible species are the diaqua-, hydroxoaqua-, and dioxo-complexes.

On the basis of the obtained results, Scheme 1 is proposed to depict all of the reactions involved in the equilibrium embedding all the relevant complex species. The vertically presented reactions are more conveniently characterized by the formal reduction potentials, as shown in Table 2, rather than by the pK values. The combination of the calculated values of K_ox. with the reported $E_{{\left[\text{Mo}{(\text{CN})}_8\right]}^{4-}/{\left[\text{Mo}{(\text{CN})}_8\right]}^{3-}}^0$, as well as the calculated values of K_red. with the reported $E_{\mathrm{D},{\mathrm{H}}^{+}/{\mathrm{H}}_2\mathrm{A}\mathrm{s}\mathrm{c}}^0$ afforded the calculation of the relevant formal reduction potentials E₁^0,, E₂^0, and E₆^0, given in Table 2, along with the potentials recalculated for MnTnBu-2-PyP complex¹³ according to the model given in Scheme 1. The most convenient way of navigating through the Scheme 1 is to calculate the corresponding values of ΔG_a^0’ = − R T lnK_a or ΔG^0’ = − v F E^0’, allowing simple calculation of the formal redox potentials. For instance, E₆^0’ = ΔG(F⇆K)/F = {ΔG^0’ (D⇆K+2H⁺) + ΔG^0’ (D⇆E+H⁺) + ΔG^0’ (E⇆F+H⁺)}/F (the formal redox potentials for all experimentally available redox transitions are given in Table S2).

The values shown in Table 1 reveal a gradual decrease of pK_a1 values of MnTE-2-PyP upon the increase of oxidation number of the coordinated manganese ion. The increased acidity of the coordinated water molecule is very probably caused by the strengthening of the Mn–O bond and consequent weakening of the O–H bond upon the building up of positive charge on the central metal ion. Rather small differences between pK_a1 of the reduced and oxidized forms of MnPs are probably caused by the additional coordination of a water molecule in the latter forms. The lower pK_a for the ortho than meta derivatives is attributed to the proximity, and hence stronger electron-withdrawing effect of the pyridyl positive charges to the porphyrin ring.

The obtained thermodynamic parameters reveal that all the deprotonation reactions are accomplished by a significant decrease of entropy. The reported value of proton hydration entropy (ΔS(H⁺) = −87.6 J K⁻¹ mol⁻¹)³¹ clearly shows that the overall reaction entropies are dominated mainly by the hydration entropy of the released proton, whereas the entropy changes related to the individual MnP moieties are all positive ranging from ca. +7 J K⁻¹ mol⁻¹ up to +72 J K⁻¹ mol⁻¹. This can be explained by the weakened hydration of the deprotonated MnPs caused by a decrease of their overall charge upon the dissociation of one proton. As in case of MnTnBu-2-PyP,¹³ the obtained reaction enthalpies for the deprotonation of Mn^IVPs are indeed very close to the enthalpies for the second deprotonation of Mn^IIIPs. However, all the enthalpy values obtained in this work, including the enthalpies for the first deprotonation of Mn^IIIPs, are within the limits of experimental errors, making this thermodynamic parameter indecisive regarding the assignation of the Mn^IVPs deprotonation processes to the diaqua or aquaoxo species.

The calculated values in Table 2 differ somewhat from the previously published potentials determined by cyclic voltammetry.⁷ The differences in E^0'vs. SHE are due to the differences in methodology and electrode calibration. Yet, importantly, the differences in E_1/2 among members of Mn(III) N-alkylpyridylporphyrin series remain and thus all relationships that have been based on E_1/2 are also correct.

It is interesting to inspect the values of the formal reduction potentials shown in Table 2. While the formal reduction potentials for the Mn^IVPs/Mn^IIIPs couples are all exergonic, the formal reduction potentials of the Mn^IIIPs/Mn^IIPs couples for both ortho-MnPs are still exergonic, though less positive, whereas for the meta-MnPs they switch to the endergonic (i.e. negative). This phenomenon is a consequence of a larger separation between the electron-withdrawing positive charges on the pyridinium substituent and the central Mn ion in the meta complexes, which decreases the Mn-site electron deficiency making Mn less apt to accept electrons. The results are consistent with the reported observation for MnTMPyP complexes, which show that the “ortho effect” observed for the Mn(III)/Mn(II) couple is greatly diminished in the case of the high-valent Mn(IV)/Mn(III) couple due to the mutual cancelation with the effect of pK_a1 and pK_a2 changes.⁶

Additionally, it is interesting to make a short inspection of the thermodynamic data collected in this work regarding the electron transfer processes. All the accessible couples that involve the double protonation are characterised by a positive entropy change. Its origin must be in the dehydration of the proton since the positive entropy changes diminish in the reductions linked to the dissociations of only one proton and, even more so, in the reductions with no proton dissociation at all. Furthermore, at the ambient temperature, the main driving force of the reduction is the enthalpy change. Taking into account the convention by which the formation enthalpies of H⁺(aq) and e⁻ equal zero at all temperatures, the calculated reaction enthalpies correspond to the transformation of related complex species. Therefore, the enthalpy decrease must be due either to the exothermic binding of proton(s) to the oxo ligand, or to the increased hydration of the complex species which undergoes the increase of charge from +4 to +5. The thermodynamics of proton binding can be circumvented by considering the reactions; (O)(H₂O)Mn^IVTE-2-PyP⁴⁺(aq) + e⁻ → (O(H₂O)Mn^IIITE-2-PyP³⁺(aq) and (O)(H₂O)Mn^IVTE-3-PyP⁴⁺(aq) + e⁻ → (O(H₂O)Mn^IIITE-3-PyP³⁺(aq). The calculated relative thermodynamic parameters are ΔH^0’ = −85 kJ mol⁻¹, ΔS^0’ = −98 J K⁻¹ mol⁻¹, and ΔH^0’= −72 kJ mol⁻¹, ΔS⁰’ = −86 J K⁻¹ mol⁻¹, respectively (Table 3). The entropy changes oppose the spontaneity of these two reductions, but the increase in enthalpies, caused by a decrease of the hydration of complex species as their positive charge is reduced, is by far exceeded by the exothermal electron affinity of these two Mn(IV) complex cations.

The electron affinities, i.e., their opposites, the ionisation potentials, (which in turn can be compared to the ionisation potential of Mn³⁺) can be calculated for (O)(H₂O)Mn^IVTE-m-PyP⁴⁺(aq) species as a difference between the calculated absolute enthalpy changes (Table S1) and the hydration enthalpy changes caused by the reduction of these two ions. The hydration enthalpy changes for (O)(H₂O)Mn^IVTE-m-PyP⁴⁺(aq) species have been calculated by means of a slightly modified Born equation,^32,33 using the values of the aqueous cavity radii of (O)(H₂O)Mn^IIITE-2-PyP⁴⁺(aq) and (O)(H₂O)Mn^IIITE-3-PyP⁴⁺(aq) obtained by the preliminary chronocoulometric measurements (r = 18.5 Å and r = 22.3 Å, respectively), and assuming in the first approximation that the rigidity of the porphyrin ring prevents a significant change of the cavity radius upon the oxidation/reduction. The calculated hydration enthalpy changes caused by the reduction of coordinated manganese from +4 to +3 are ca. 88 kJ mol⁻¹ and 73 kJ mol⁻¹, respectively. This value approximates the electroaffinity to ~600 kJ mol⁻¹, which is close to the first ionisation energy of manganese (717.4 kJ/mol³⁴). This may indicate that the positive charge on the manganese in (O)(H₂O)Mn^IVTE-m-PyP⁴⁺(aq) is indeed mostly neutralized by the coordinated oxo and porphyrinato ligands.

All the MnTE-m-PyP complexes exhibit an intense Soret band between 407 and 455 nm, but the hydroxo-complexes display an additional strong peak or shoulder in that spectral region (Table 4). It is not clear whether or not the space orientation of the hydroxo ligand itself could cause such a molecular symmetry decrease in these complexes, since such an effect is not observed for the (HO)(O=)Mn^IVTE-m-PyP³⁺. If the space orientation of the hydroxo ligand causes such an effect, the spectra of double-deprotonated complex species would all indicate a preference for the oxo- over dihydroxo prototropic structures.

Table 4.

The spectral characteristics of various MnP species obtained by the spectrophotometric pH titrations θ = 25 °C, I = 2 M (NaClO₄).

Species	m = 2		m = 3
	λmax/nm	ε/105 M−1cm−1	λmax/nm	ε/105 M−1cm−1
(H2O)MnIITE-m-PyP4+	437	2.021	441	2.601
(HO)MnIITE-m-PyP3+	407 449	0.702 0.587	408 455	0.795 1.064
(H2O)2MnIIITE-m-PyP5+	455	1.384	462	1.549
(H2O)(HO)MnIIITE-m-PyP4+	435 453(sh)	0.766	440 456(sh)	0.923
(H2O)(O=)MnIIITE-m-PyP3+	443	1.300	446	1.562
(H2O)(O=)MnIVTE-m-PyP4+	423	0.738	425	0.996
(HO)(O=)MnIVTE-m-PyP3+	444	0.755	427	0.849

The UV peaks of all aqua-Mn^IIPs show red shift upon the manganese oxidation to Mn(III) ion, possibly due to the electron-withdrawing nature of the central metal ion in the higher oxidation state which caused the electronic density on the porphyrin macrocycle to decrease to a certain degree. This in turn decreases the conjugation throughout the ring and causes the reduction of the electron transition energy of the porphyrin macrocycle, accounting for the red shift in its UV absorption peak. An opposite direction peak-shift is caused by the deprotonation of the aqua MnPs, by which the electron density in the porphyrin ring is increased, increasing the conjugation and in turn the electron transition energies as well. Upon the oxidation of manganese in (H₂O)(O=)Mn^IIITE-m-PyP³⁺, a blue shift was also observed, indicating that besides the decreasing electronic density of the central metal ion, there are additional factors having a considerable role in the processes controlling the energy gap between the porphyrins’ HOMO and LUMO. The similar spectral characteristics are exhibited by the butyl derivative as well,¹³ showing that the length of the side chains has little effect on the spectral shapes and peak positions of the MnP complexes.

In conclusion, our results reveal that in aqueous solutions in the pH range ~2–13 the following accessible species exist: (H₂O)Mn^IITE-m-PyP⁴⁺, (HO)Mn^IITE-m-PyP³⁺, (H₂O)₂Mn^IIITE-m-PyP⁵⁺, (H₂O)(HO)Mn^IIITE-m-PyP⁴⁺, (H₂O)(O=)Mn^IIITE-m-PyP³⁺, (H₂O)(O=)Mn^IVTE-m-PyP⁴⁺ and (HO)(O=)Mn^IVTE-m-PyP³⁺. We have determined all the protolytic equilibrium constants that include these species as well as the thermodynamic parameters of the relevant protolysis reactions. The corresponding formal reduction potentials related to the reduction of the above species and the thermodynamic parameters describing the accessible reduction couples were calculated as well.

While for the speciation of Mn^IITE-m-PyPs the obtained results entirely confirm the reaction model proposed for the Mn^IITnBu-2-PyP, the previous attribution of the observed species for Mn^IVTnBu-2-PyP, based on the thermodynamic parameters alone, proposed (H₂O)(OH)Mn^IVTnBu-2-PyP⁵⁺ as one of the experimentally accessible species.¹³ Therefore, the presented results proved that the derivation of a correct reaction model based only on the thermodynamic data could be rather misleading, indicating the necessity of a more comprehensive approach presented in this work, including the thorough investigation of electrochemical properties of MnP complexes as well.