Development of Dimethyl Sulfoxide Solubility Models Using 163 000 Molecules: Using a Domain Applicability Metric to Select More Reliable Predictions

Abstract

The dimethyl sulfoxide (DMSO) solubility data from Enamine and two UCB pharma compound collections were analyzed using 8 different machine learning methods and 12 descriptor sets. The analyzed data sets were highly imbalanced with 1.7–5.8% nonsoluble compounds. The libraries’ enrichment by soluble molecules from the set of 10% of the most reliable predictions was used to compare prediction performances of the methods. The highest accuracies were calculated using a C4.5 decision classification tree, random forest, and associative neural networks. The performances of the methods developed were estimated on individual data sets and their combinations. The developed models provided on average a 2-fold decrease of the number of nonsoluble compounds amid all compounds predicted as soluble in DMSO. However, a 4–9-fold enrichment was observed if only 10% of the most reliable predictions were considered. The structural features influencing compounds to be soluble or nonsoluble in DMSO were also determined. The best models developed with the publicly available Enamine data set are freely available online at http://ochem.eu/article/33409.

Introduction

Solubility in dimethyl sulfoxide (DMSO) is one of the important parameters considered by pharmaceutical companies during early drug discovery.^1,2 The compounds that are nonsoluble cannot be used in automatized high-throughput-screening (HTS) and are thus lost for experimental measurements. Moreover, they may have low water solubility and thus be nonbioavailable. Therefore, companies try to minimize the number of such molecules when acquiring new collections.

There have been only a few studies in which machine learning methods were used for the classification of molecules as soluble and nonsoluble in DMSO.^3,4 The problem of model development for this property is directly connected to the limited availability of experimental data. While industry routinely screens hundreds of thousands of molecules, these data are usually not publicly available.

The number of molecules that are nonsoluble in DMSO is usually only a small fraction of the soluble ones, i.e. the data are highly imbalanced. The problem of imbalanced data learning is well-known in the machine learning literature.⁵ It is also frequently faced in the chemoinformatics field, in particular in HTS virtual screening experiments. Indeed, in the latter cases only a tiny fraction of molecules is detected as active ones and the developments are targeted to extend the hits with new chemical scaffolds. The problem of prediction of solubility in DMSO is to some extent an opposite one: instead of maximizing the number of samples from the under-represented class of nonsoluble molecules, the goal is to further decrease it.

In this study, we used a battery of machine learning methods and descriptors to develop new models for prediction of solubility in DMSO and to compare their performances. We show that the frequently reported performance measures of the prediction performance (such as total accuracy, Matthews correlation coefficient, balanced accuracy), which are reported for the whole data set, are not sufficient for practical applications of methods for screening of new molecules. We show that the use of a positive predictive value within a specified coverage provides the appropriate measure to compare predictive models for filtering molecules that are not soluble in DMSO.

We also address the problem of the prediction accuracy by developing models using data from separate companies as well as by combining them. We show that collaborative efforts are beneficial to all partners contributing the data.

Data

Compound Libraries

The DMSO solubility data (solubility in 100% DMSO) were collected from UCB (UCB Pharma S.A., http://www.ucb.com) and Enamine Ltd. (http://www.enamine.net) companies. All data were available in SDF format. They were standardized, stripped of salts, and neutralized using ChemAxon tools⁶ that are integrated in the OCHEM⁷ model development workflow.⁸

Both companies used the same threshold of 10 mM to separate soluble and nonsoluble molecules and thus the data sets could be merged seamlessly. More specifically, the following steps were used at the UCB

• (1)Add DMSO volume upon solid to get the theoretical 10 mM solution
• (2)Orbital shaking (2000 rpm) at room temperature during 30 min
• (3)Visual inspection: look through the vial in front of a light source with several bottom-up cycles to check for turbidity or solid deposits

Enamine used the same procedure with the exception of the second step, which used multicycle pipetting at room temperature. The first UCB data set (UCB1) contained 72 999 molecules including 1294 (1.7%) nonsoluble ones. The Enamine data set, after filtering of duplicates, comprised 50 620 molecules with 2681 (5.3%) nonsoluble ones.

The low percentage of nonsoluble molecules in the UCB collection may reflect the strategy of the company to focus on central nervous system (CNS) active compounds. This CNS focus biases the molecule selection toward particular physicochemical windows (LogD, pK_a, MW), which induce improved solubility. The Enamine data has the ratio of nonsoluble/soluble compounds that could be expected in typical screening libraries.

Additionally, we analyzed a third data set, UCB2, of 39 470 molecules (5.8% nonsoluble), which corresponded to the recent acquisitions and measurements performed at UCB. This set was composed of all insoluble and a diverse selection of soluble molecules. It was used to evaluate performances of algorithms developed in this study. The final model was developed using all molecules.

Since in the current study only solubility in DMSO is considered, we will refer to soluble and nonsoluble in DMSO molecules as “soluble” or “nonsoluble” ones by skipping mentioning “in DMSO”.

Evaluation of Intrinsic Noise

The measurements of DMSO solubility can be subjected to experimental errors, in particular if molecules are on the borderline of solubility.

Insolubility might be associated with one or several of the following events. From the kinetic point of view, the initial solid compound might dissolve at a different speed depending on its intrinsic solubility as well as its solid form. Solubilized compounds might even sometimes reprecipitate due to recrystallization under a new, much less soluble solid form. From the reactivity point of view, some compounds might react with the DMSO, dissolved oxygen, or residual solvent water. These reactions (hydrolysis, oxidation, etc.) could lead to compound decomposition, which might generate insoluble species or cause precipitation of the parent molecule. Also, some acids can cause decomposition of DMSO through the Pummerer rearrangement⁹ with formation of formaldehyde and methylmercaptan, which can further react with solutes and cause their precipitation.

A previous estimation of inconsistencies in DMSO solubility measurements has been reported by the ChemDiv company: a random re-evaluation of their data revealed a 1% error rate.² The initial Enamine data set contained 50 907 molecules. This number comprised 279 duplicates: 273 pairs of molecules within one solubility class and 7 duplicates within two different solubility classes, thus providing an estimation of the error rate of about 2%, that is the ratio of pairs of duplicated molecules having different classes of solubility to those that have the same solubility.

Methods

Machine Learning Methods

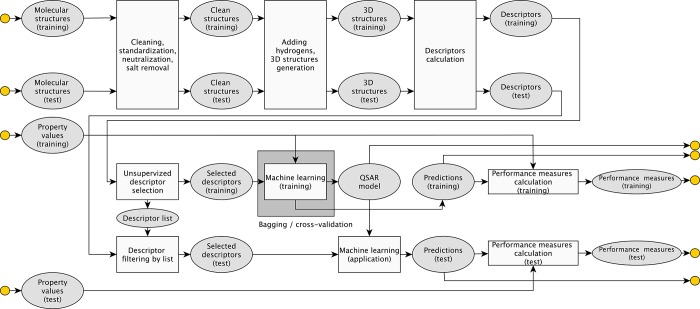
The model for DMSO solubility was developed using a number of classification machine learning approaches available at the OCHEM site.⁸ The workflow for model development is shown in Figure 1. Below, we briefly overview them and full details can be found in the cited references:

Figure 1.

Basic steps of model development and analysis using OCHEM.

k Nearest Neighbors (kNN) predicts a property for a compound using the consensus voting of k compounds from the training set that are nearest to it according to some distance metric. We used the Euclidean distance calculated using normalized descriptors (mean 0 and standard deviation 1). The number of nearest neighbors that provided the highest accuracy of classification was calculated following a systematic search in the range (0, 100).

Associative Neural Network (ASNN) uses the correlation between ensemble responses as a measure of distance amid the analyzed cases for the nearest neighbor technique.^10,11 Thus ASNN performs kNN in the space of ensemble predictions. This provides an improved prediction by the bias correction of the neural network ensemble. The configurable options are the following: the number of neurons in the hidden layer, the number of iterations, the size of the model ensemble, and the method of neural network training. The default values provided at the OCHEM Web site were used.

Fast Stagewise Multivariate Linear Regression (FSMLR) is a procedure for stagewise building of linear regression models by means of greedy descriptor selection.¹²

Partial Least Squares (PLS). The number of latent variables was optimized automatically using 5-fold cross-validation on the training set.

Multiple Linear Regression Analysis (MLRA) uses stepwise variable selection. The method eliminates on each step one variable that has a regression coefficient nonsignificantly different from zero (according to the t-test). Thus MLRA has only one parameter, ALPHA, which corresponds to the p-value of variables to be kept for the regression. ALPHA = 0.05 was used.

Support Vector Machine (SVM) uses the LibSVM program.⁹ The SVM method has two important configurable options: the SVM type (ε-SVR and μ-SVR) and the kernel type (linear, polynomial, radial basis function, and sigmoid). Classic ε-SVR and radial basis function kernels were used. The other SVM parameters, namely cost C and width of the RBF kernel, were optimized using default grid search, which was performed according to the LibSVM manual.

J48andRF are Java implementations of WEKA¹³ C4.5 decision tree and Random Forest, respectively. The default parameters provided by WEKA were selected and thus there was no optimization. Each RF model was built using 10 trees.

Molecular Descriptors

The online chemical database and modeling environment (OCHEM) Web site offers a large selection of descriptors, which were contributed by different academic groups and commercial enterprises. Their list and brief description can be found elsewhere.^8,14 For this study, we considered each block as a separate set; that is, we did not combine descriptor types from different vendors. Below we briefly list them and provide links and references to detailed descriptions. The information whether descriptors in the block are based on 2D or also require 3D structures is also specified.

ADRIANA.Code (3D) comprises 211 molecular descriptors based on a sound geometric and physicochemical basis. The classes of descriptors cover global molecular descriptors, shape and size descriptors, topological, and 3D property-weighted autocorrelation descriptors.¹⁵

CDK (3D) included topological, geometrical, constitutional, electronic, and hybrid descriptors.¹⁶ In total, 274 descriptors were calculated.

ChemAxon 499 descriptors (3D) included elemental analysis, charge, geometry, partitioning, protonation, isomers, and “other” descriptors.⁸

Dragon6 (3D) represented the largest pool, which included 4885 descriptors grouped in 29 different blocks.¹⁷

E-state indices^18,19 (2D) were calculated using E-state program, which was used to predict logP and water solubility in the ALOGPS program.²⁰ The logP and logS values calculated using ALOGPS 2.1 version were also included.

ISIDA Fragmentor (2D)²¹ was used to calculate augmented atoms of length 3 to 5.

GSFrag (2D) included descriptors based on fragments that contain a labeled vertex, allowing one to capture the effect of heteroatoms.²²

Inductive descriptors (3D), which are based on LFER (Linear Free Energy Relationships) equations for inductive and steric substituent constants, were implemented according to ref (23). These descriptors were used for modeling of different physicochemical and biological properties²⁴ and thus were also expected to be relevant for the analysis of DMSO solubility.

Mera (3D) included geometrical, energy characteristics, and physicochemical descriptors.²⁵ In this set we also included MERSY (MERA Symmetry), which estimates molecular symmetry and chirality.

Shape Signatures (3D) encoded spatial shape characteristics of molecules using ray tracing, which explores volume enclosed by the solvent accessible surface of a molecule.²⁶

Spectrophores fingerprints²⁷ (3D) are calculated as one-dimensional compression of molecular properties fields surrounding molecules.

Extended-connectivity fingerprints (2D)²⁸ with diameter 4 and vector length 1024 (ECFP4) were calculated using ChemAxon tools.⁶ These descriptors, and in particular ECFP4,²⁸ are frequently used for similarity searching. We used these descriptors to compare performances of different approaches to define molecular similarities.

Filtering of Descriptors

Before development of models, all descriptors were filtered. The almost constant descriptors that had two or less different values were eliminated. We also deleted highly correlated descriptors (R > 0.95) as well as those that had standard deviation less than 0.01. These are the standard filters used in the OCHEM workflow (Figure 1).

Bagging

Bagging is an ensemble modeling approach that calculates several (usually tens to hundreds) models and averages them to produce the final model.²⁹ For our analysis, we used ensembles of N = 64 models. The use of larger numbers of models per ensemble (i.e., 128, 256, 512 and 1024) did not provide a significant increase of the balanced accuracy of models but required more computational power.

The traditional bagging creates multiple replicas of the initial training set by randomly selecting molecules for replacement from the initial set. On each run, about 33% of the molecules are not selected by bagging and form “out-of-the-bag” sets, which are used to test the performance of models. When creating training and test sets, we initialized a random generator using the same number and, thus, all methods used the same data.

To address the problem with unequal distribution of samples between classes of active and inactive molecules, we used so-called stratified bagging.⁵ In this analysis, we created the balanced training data sets by limiting the number of soluble molecules to be the same as that of the nonsoluble ones. Thus, the sizes of the bagging training sets were double the number of the nonsoluble molecules. Therefore, only about 4–11% of the compounds from UCB and Enamine data sets were used to build each individual bagging model. However, since data sets for each model were generated randomly, the majority of molecules contributed to the bagging procedure.

Since we used balanced training sets, the total (ACC) and balanced accuracies (BAC) measures for the training sets were identical (see Table 1). The parameters of methods (e.g., number of nearest neighbors in kNN, parameters of SVM, etc.) were optimized to provide the lowest error for the training sets using different procedures implemented for each method (e.g., leave-one-out for kNN; 5-fold internal cross-validation for SVM; hold-out procedure for ASNN, etc.). Each of these procedures introduced a different degree of fit. Therefore, the fitting results for the training sets were not reported in this article. The performance of the developed models was compared using molecules that were not selected for the respective training sets. These “out-of-the-bag” molecules were predicted only after the models were built.

Table 1. Performance Measures Frequently Used to Compare Classification Models.

		experimental measurements
		soluble	nonsoluble
predicted solubility	soluble	true positive (TP)	false positive (FP)	positive predictive value PPV = TP/(TP + FP)
	nonsoluble	false negative (FN)	true negative (TN)	negative predictive value NPV = TN/(TN + FN)
		sensitivity = TP/(TP + FN)	specificity = TN/(TN + FP)

accuracy (ACC) = (TP + TN)/(TP + FP + FN + TN)

balanced accuracy (BAC) = 0.5(sensitivity + specificity)

Matthews correlation coefficient (MCC) = (TP × TN – FP × FN)/[(TP + FP)(TP + FN)(TN + FP)(TN + FN)]1/2

The training of models using balanced sets of molecules is considered as one of the most successful strategies to address the problem of imbalanced data sets.⁵ The bagging approach was also important to provide the reference method to estimate the accuracy of predictions, as described in the next paragraph.

Estimation of the Prediction Accuracy

One of the goals of this study was to develop a strategy to enrich the molecule selection with soluble molecules. The use of the most accurate predictions was important for such a selection. The accuracy of predictions of models was estimated based on the concept of the distance to model.³⁰⁻³³ The distance to model (abbreviated as DM) could be algorithm- and data-specific. In our previous studies, we have shown that the deviation of predictions in an ensemble of models was one of the most accurate DM to separate reliable and nonreliable predictions.³¹ Indeed, the deviation of the ensemble of models accounts both for used descriptors and the modeled property and corresponds to one of the “property-based similarities” as defined elsewhere.³²

The standard deviation of predictions within bagging ensembles (BAGGING-STD) provided a convenient way to provide a uniform measure across different methods analyzed in this study. Following development of models, their prediction variances were used to order molecules from most reliable (smallest BAGGING-STD) to least reliable (largest BAGGING-STD) predictions. For the majority of studies, as described below, only the 10% of molecules with the lowest BAGGING-STD values were considered. The selection of 10% was based on the assumption that the selection of compounds is usually performed from redundant libraries having tens to hundreds of molecules. Thus, the 10% threshold was selected to identify a reasonable number of molecules that could be used for further filtering with other filters.

Estimation of the Performance of Methods

Several measures were analyzed to estimate the accuracy of models. The total accuracy (ACC), balanced accuracy (BAC), Matthews correlation coefficient (MCC), positive predictive value (PPV), sensitivity, and specificity were considered (see Table 1). In addition to measures defined for the whole set, one can also consider their performance for a subset of, e.g. most reliable predictions, i.e. PPV_10% would refer to the PPV for the 10% of molecules with the lowest BAGGING-STD values.

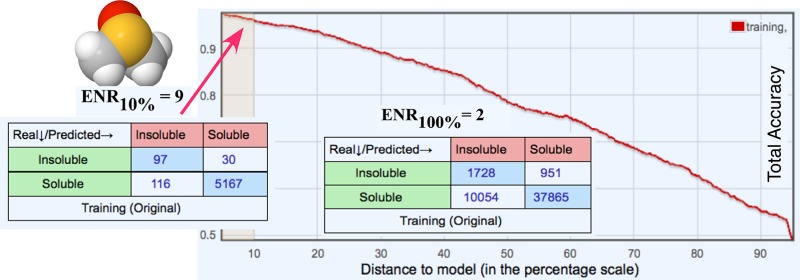
One more measure, enrichment of the soluble molecules, defined as a ratio of the percentage of nonsoluble molecules within the whole analyzed set to the percentage of insoluble compounds predicted as soluble ones within PPV_10% molecules (i.e., 100%-PPV_10%)

1

was used. This number was also compared to ENR_100% calculated as

2

i.e., to the average enrichment of models when ignoring the accuracy of predictions.

Exclusion of Duplicates

The duplicates within each data set were eliminated in the data preparation process, i.e., during data upload to the database. OCHEM used InChi hash-keys³⁴ to automatically detect duplicates (stereochemistry is also considered) during the data upload process. The molecules that had the same reported type of solubility were automatically marked as “internal duplicates” and were not uploaded to the database (but were used to perform analysis described in section Evaluation of Intrinsic Noise). However, it could appear that some molecules have exactly the same descriptors despite their chemical structures being different. We automatically identified such groups of molecules and used each group either in the respective training set or in the out-of-the-bag set. Thus, if some molecule were a duplicate in the Enamine and in one of the UCB sets, our procedure would always assign it either to training or out-of-the-bag set, but not to two sets simultaneously.

Results and Discussion

Overview of Analyzed Data Sets

Table 2 indicates distribution of average properties between soluble and nonsoluble molecules.

Table 2. Average Properties of Molecules from Analyzed Data Sets^a.

	UCB1			UCB2			Enamine			all
property	sol	insol	delta%	sol	insol	delta%	sol	insol	delta%	sol	insol	delta%
N	71705	1294		37182	2288		47939	2681		156826	6263
MW	321	347	7.8	295	368	22	358	389	8.3	336	372	10.2
NA	22.5	24.6	8.9	21	25.8	20.5	24.7	27	8.9	23.5	26	10.1
PSA	61	70.6	14.6	65.6	70.5	7.2	66.6	69.7	4.5	63.2	69.9	10.1
acceptors	3.76	4.3	13.4	4	4.7	16.1	4.5	5.7	23.5	4.03	5.03	22.1
donors	1.08	1.22	12.2	1.2	1.04	–14.3	0.92	0.56	–49	1.05	0.83	–23
rotatable bonds	4.4	4.26	–3.2	4.4	4.1	–7.1	5.1	4.8	–6.1	4.61	4.5	–2.4
log P	2.8	2.82	0.7	2.94	3.23	9.4	2.98	3.19	6.8	2.88	3.13	8.3
log S	–3.76	–3.88	–3.1	–3.85	–4.23	–9.4	–4.04	–4.2	–3.9	–3.87	–4.15	–7

^aN is the number of molecules in the data set; MW—molecular weight; NA—number of nonhydrogen atoms; PSA—polar surface area; log P and log S are calculated using the ALOGPS 2.1 program.²⁰

Previous work conducted to estimate aqueous solubility from molecular structure showed that models based on parameters such as clogP (calculated octanol/water partition coefficient, log P), molecular weight, and the number of rotatable bonds could lead to solubility in DMSO predictions with satisfactory levels of accuracy and precision to be useful in the drug design process.³⁵ In the three data sets used in the study, although insoluble compounds have, on average, higher molecular weight (MW), higher log P, smaller solubility, and less rotatable bonds, the property variations are small.

In terms of properties such as partial surface area (PSA) and H-bond acceptors and donors (HBA and HBD), these are closely associated to solubility but their net impact is hard to predict. Indeed, H-bonding is favorable to solubility in the case of solute–solvent interactions but unfavorable in the case of solute–solute interaction (increase of solid crystal lattice).³⁶ In all three data sets, HBD/HBA have the largest variation between solubility classes. If the average number of HBA is always increasing for insoluble compounds, the average number of HBD is decreasing, except for the UCB1 data set.

An analysis of an overrepresentation of chemical functional groups within soluble and nonsoluble compounds was performed using the SetCompare utility of OCHEM. The functional groups were calculate using the ToxAlerts utility³⁷ which uses SMARTS to recognize important chemical groups (e.g., toxicophores, structural alerts, functional groups). For this analysis we used SMILES arbitrary target specification (SMARTS) patterns for about 580 functional groups. Around 250 of these groups were initially proposed by Haider.³⁸ Miss E. Salmina, who was a FP7MC ITN ECO project fellow in the laboratory of IVT, extended these groups (in collaboration with Prof. N. Haider) during her stay. The over- and underrepresented functional groups are available as ref (39). For each group, we listed the number of appearances within both soluble and nonsoluble molecules as well as p-values to observe such differences by chance. The significance values were calculated using a hypergeometric distribution.

The most significant functional groups, which contribute to low solubility, are aromatic six-membered heterocyclic compounds with two heteroatoms. Indeed, 42% of all nonsoluble molecules have this structural feature while only less than 16% of soluble compounds have it. The heterocyclic compounds with only one heteroatom were also overrepresented (but to a lesser extent, i.e. 22% vs 13%) within the set of nonsoluble molecules. Oxohetarenes were also 2.7 times (37% vs 14%) overrepresented within the nonsoluble set. The other overrepresented groups in the set of nonsoluble compounds included aromatic heterocyclic groups, five-membered heterocycles, tertiary aliphatic amines, etc. A presence of carboxylic acid derivatives (in particular amides), carbonic derivatives, nonfused benzene rings, ureas, and halogen derivatives was associated with increased solubility.

We also used the ScaffoldHunter software⁴⁰ to detect over- and underrepresented individual chemical scaffolds determining DMSO solubility.³⁹ The majority of overrepresented scaffolds were detected for nonsoluble molecules. They could be used to identify potential problems with DMSO solubility for new molecules.

Outlook of Model Development

The models were calculated using the UCB1, the Enamine, and the combination of both data sets using OCHEM.⁸ OCHEM is a public, free online tool for web users.⁷ It is backed up with more than 600 central processing unit (CPU) servers thus allowing it to solve quantitative structure–property relationship (QSPR) problems of high complexity. A number of calculations, e.g. Shape Signatures, 3D conversion of molecules using Corina, and Adriana.code descriptors, are performed at the partners’ Web sites.⁸

Because of confidentiality issues, UCB molecules could not be used for the online calculations at the OCHEM Web site. While OCHEM was provided as a standalone version to UCB, calculation of models using bagging methods required significant computational resources, which were not available for the software provided to the company. Molecular descriptors were calculated at UCB locally and molecular structures were kept private using an OCHEM built-in descriptor shuffle key.

Therefore, for the purposes of the current study, we first evaluated all sets of descriptors and methods using the public version of OCHEM for the Enamine data set. In total, 96 models were calculated. After their analysis, we identified several combinations of methods and descriptors to develop final models using the individual and the combination of the UCB and the Enamine data sets.

Traditional Accuracy Assessment

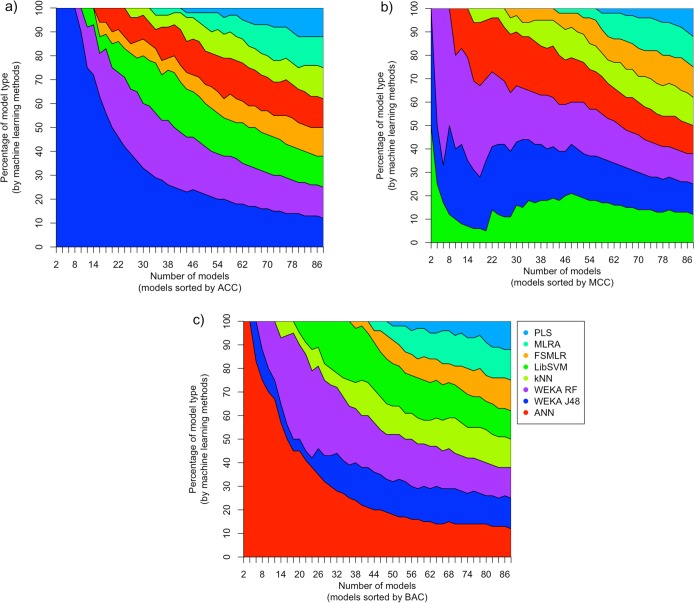
Since the DMSO data set was highly imbalanced, the use of traditional accuracy measures provided rather inconsistent results. Figure 2 demonstrates the shares of models with the highest accuracy according to different accuracy measures among top-performing models. It is clear that decision tree J48 approach dominates (Figure 2A) if we use the total accuracy as the criterion of the model performance. The LibSVM method provides an equal contribution with decision trees and random forest for the 4–8 best performing models using the Matthews correlation coefficient (MCC) (Figure 2B). ASNN clearly dominates and provides the largest number of top-performing models (Figure 2C) if we consider balanced accuracy (BAC).

Figure 2.

Percentage of models contributed by different methods (y-axis) as a function of the number of n top-ranked models (x-axis) selected according to accuracy (ACC), Mathew correlation coefficient (MCC), and balanced accuracy (BAC).

Thus, depending on the used measure of the accuracy of models, we can draw quite different conclusions about their performances. The first measure, total accuracy, can be hardly considered appropriate for the unbalanced data sets, and its results were reported only for illustration purposes. The two other measures, BAC and MCC, are frequently used for analysis of unbalanced sets. As we can see, their results are also quite incompatible. Thus, one should carefully consider and select a performance measure for imbalanced data sets depending on the practical requirements to the models in question. The choice of the performance measure can strongly influence the conclusions of the study.

Analysis of the experimental accuracy of DMSO models for soluble and nonsoluble compounds as a function of the estimated accuracy of predictions (BAGGING-STD) allows better understanding of the results (Figure 3). First, the accuracies of prediction of either soluble (sensitivity) or nonsoluble (specificity) molecules gradually decrease with the increase of the BAGGING-STD distance. Second, there are different patterns in the performances of the models, which depend on the method and descriptors used. All models have higher sensitivity and thus higher accuracy of predictions of soluble molecules. The ASNN provides similar accuracies for both soluble and nonsoluble molecules.

Figure 3.

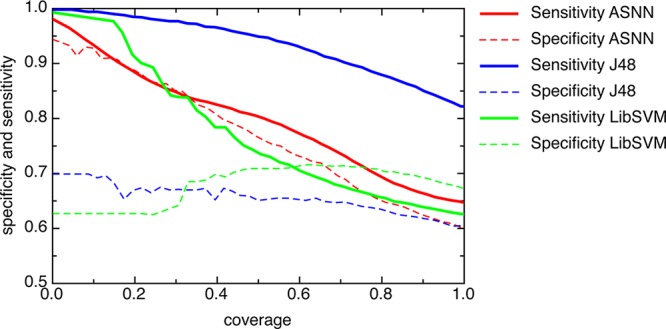
Specificities and sensitivities of different methods versus coverage. The predictions were ordered according to the increasing values of the BAGGING-STD distance to models. ASNN results were calculated using E-state indices and provided the highest balanced accuracy. J48 results were calculated using CDK descriptors and provided the highest total accuracy. LibSVM using inductive descriptors calculated the model with highest Mathew correlation coefficient. The sensitivity and specificity of models decreases with increasing values of BAGGING-STD and thus with increasing the coverage.

Performance Comparison for the Most Reliable Predictions

In order to better understand which measure should be more appropriate for our analysis, let us consider a typical use-case for a DMSO solubility model. When acquiring a new molecule collection, the pharmaceutical company may need to select only a tiny portion of molecules from the chemical provider’s library. Indeed, the most typical strategy is to acquire a “diverse set of compounds” for HTS screening in order to identify some new promising chemical series that could be active against potential targets. The selection of the diversity set can be also based on the QSPR models and/or additional filters, such as Lipinski’s “rule of 5”. In any case, the researchers typically face the problem to identify a small subset of molecules, 1–10% or even less, out of a large set of possible candidates. Thus, in principle, a high accuracy of models could be required just for a subset of all molecules.

Table 3 shows models that achieved the PPV_10% ≥ 99% (and thus lowest percentage of nonsoluble compounds) for 10% of compounds with the highest accuracy of predictions. As it was mentioned in the Data section, the Enamine training set contained 5.3% of nonsoluble compounds. As indicated by ENR_100%, the acquisition of molecules amid those predicted as soluble for the whole set would decrease the number of nonsoluble molecules by 1.8–2.6-fold. The same procedure applied to molecules that had the highest accuracy of prediction within 10% coverage could decrease the number of nonsoluble compounds by 5–9-fold. For example, the highest balanced accuracy of the models for the total data set, 73.3%, was calculated using the ASNN method applied for ISIDA Fragmentor²¹ descriptors. This model has PPV_100% = 97.9%. The use of this model provided only a 2.5 fold enrichment for the whole set. This enrichment was three times lower compared to 7.6 fold when considering only the 10% compounds with the most accurate predictions. As it was mentioned before, prediction of solubility for 1–10% of compounds would be sufficient for most of practical applications. Thus the ability of models to differentiate reliable versus nonreliable predictions and provide high enrichment of the selected data set with soluble compounds determined the real practical value of the models. Conversely, the traditional measures such as ACC, BAC, and MCC would not be important in practice.

Table 3. Top-Performing Models for DMSO Solubility Prediction Developed with Enamine Data Set within the Whole Data Set and 10% Coverage^a.

method	descriptors	number of descriptorsb	BAC100%	PPV100%	ENR100%	PPV10%	ENR10%	BAC10%	SENS10%	SPEC10%	NSOL10%
J48	CDK	175	71.8	97.5	2.2	99.4	8.8	87.1	97.8	76.4	2.3
ASNN	E-state	205	73.1	97.9	2.6	99.4	8.8	92	96	88	4.7
ASNN	Dragon6	1929	73.2	97.9	2.5	99.4	8.8	92.2	97	87.4	3.7
ASNN	Fragmentor	872	73.3	97.9	2.5	99.3	7.6	90.2	95.8	84.6	4.3
ASNN	ChemAxon	134	72.8	97.9	2.5	99.3	7.6	91.2	92.4	89.9	5.8
J48	E-state	205	71	97.3	2	99.2	7.6	77.5	99.4	55.6	1.7
ASNN	CDK	175	73.2	97.9	2.5	99.2	6.6	91	94.8	87.2	5.3
J48	Dragon6	1929	71	97.3	2	99.2	6.6	88.8	97	80.6	4
J48	Fragmentor	872	71	97.3	2	99.1	5.9	82.2	98	66.4	2.5
ASNN	Mera	259	70.9	97.7	2.3	99.1	5.9	88.3	96.2	80.4	4.2
ASNN	Adriana	119	72.9	97.9	2.5	99	5.3	86	82.2	89.8	7.8
J48	Adriana	119	69	97.1	1.8	99	5.3	79.4	98.8	60	2.5
RF	Fragmentor	872	72	97.6	2.2	99	5.3	88.3	97.4	79.1	4.7
ASNN	GSFrag	314	71.9	97.8	2.4	99	5.3	87.6	85.5	89.7	7.5
J48	GSFrag	314	69	97.1	1.8	99	5.3	83	98.8	67.1	2.9
RF	E-state	205	73	97.8	2.4	99	5.3	88.5	96.3	80.6	5.1
RF	inductive	38	67	97.2	1.9	99	5.3	84.9	94.8	74.9	3.5
consensus	all		74.2	97.9	2.5	99.6	13	87.5	98	77	1.2

^aModels with PPV_10% ≥ 99% were selected.

^bAfter filtering, see Methods section. NSOL_10% is the percentage of nonsoluble molecules within 10% coverage of the most highly accurate predictions.

Therefore, in this study we used PPV_10% as the accuracy measure for the comparison of the performances of the models. We will refer to PPV, sensitivity, and specificity values calculated for the 10% of compounds with the highest accuracy of predictions as PPV_10%, SENS_10%, and SPEC_10%, respectively. We also noticed that for the majority of models PPV values were stable for 5–15% of molecules before starting to decrease, i.e., the change of the PPV threshold in this range would not significantly affect the results reported in this study.

Overview of Top-Ranked Methods and Descriptors

Only 2 out of 12 analyzed descriptors sets, namely Spectrophores and Shape Signatures, did not contribute to the top-ranked models (Figure 4). For these descriptors, the best result (PPV_10% of 98.8% and 98.1% for ShapeSignatures and Spectrophores, respectively) was calculated using the random forest method (RF). We also investigated whether combinations of descriptors could further improve the results. Considering the limitation on the number of descriptors per molecule that we currently had in our system, we decided to consider only CDK, E-state, ChemAxon descriptors, MERA, Adriana, and GSFrag. Their descriptors were joined in one set and were used to developed new models. The models calculated using ASNN and WEKA J48 had a PPV_10% of 99.0% while other approaches had even lower accuracy. Thus, combination of descriptors did not improve the accuracy of predictions.

Figure 4.

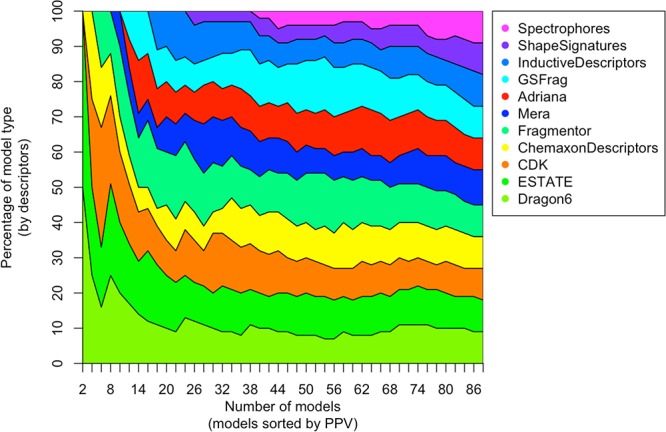
Percentage of models calculated using different descriptors (y-axis) as a function of the number of n top-ranked models (x-axis) for PPV_10% measure. Dragon, E-state, and CDK descriptors contribute the largest share, 75%, of 10 top-ranked models.

All top-ranked models were contributed by three methods: ASNN, J48, and RF. ASNN and J48 methods accounted for about 80% of the top-ranked models, by contributing 8 and 6 models, respectively. RF contributed the remaining models. These three methods were considered for the further analysis.

All methods had higher sensitivity than specificity (with exception of ASNN developed with GSFrag, Adriana, and Dragon6 descriptors). These values were approximately the same for all methods and were larger than 92%, with the exception of the ASNN–Adriana and ASNN–Dragon6 models. The specificity values were lower and ranged from 56% to 95%. Thus, the nonsoluble compounds were more difficult to predict and, on average, were predicted with higher errors compared to the soluble ones.

Considering that all the sensitivity values of methods were rather high and similar, one could expect that specificity (accuracy of prediction of nonsoluble compounds) would determine the PPV values. However, there was a very small Pearson correlation coefficient (R = 0.29) between SPEC_10% and PPV_10%. Actually, the PPV is not deterministically determined by sensitivity and specificity only. It also depends on the percentage of molecules from the nonsoluble class within 10% coverage. As we can see in Table 3, different approaches identified different percentages of nonsoluble molecules as reliably predicted within the 10% interval. The number of false positive (FP) predictions inside of the same interval (calculated as (100%-SPEC_10%)*NSOL_10%) had much a higher correlation R = −0.91 with the PPV. A negative value of the correlation coefficient indicates that increase of the number of FP predictions decreases the PPV.

As we can see in Table 3, the percentage of nonsoluble molecules within 10% coverage of reliable predictions, NSOL_10%, strongly varied depending on the method. On average, there were 4.6% of nonsoluble molecules within this range. This number was lower as compared to the overall percentage of nonsoluble molecules in the whole data set, which was 5.3%.

The appearance of the molecules within 10% of the most reliable predictions reflects the degree of their ease of classification on the classes. Indeed, these compounds all had the lowest BAGGING-STD and thus the majority of models provided the same prediction of their membership class. The under-representation of molecules within this interval shows that the class of nonsoluble molecules was more difficult to predict compared to the soluble ones. This result also correlates with the lower specificity rate observed for nonsoluble molecules in Table 3.

The maximum PPV_10% value was 99.4% for this set. It provided a lower estimation of experimental error, 0.6%, as compared to the experimental error rate of 2% estimated in the Methods section. Both these results, however, do not contradict each other. As was mentioned before, the experimental errors on solubility could be strongly related to some particular molecular properties, e.g. initial crystal packing (strong H packing) or instability. Thus, compounds having some specific features could contribute to the high error rate, since their solubility can change with time. Definitely, such compounds will contribute to both soluble and nonsoluble predictions thus causing a high uncertainty with their predictions. Unsurprisingly, these compounds would not appear amid the most confident prediction.

The remaining rate of 0.5% may correspond to the other measurements’ errors as well as uncertainties in solubility determination.

Importance of Stratified Learning

We investigated whether better models could be achieved using all data. The models were developed using E-state indices and all machine learning methods described in the Methods section. All the models had a BAC = 50% by predicting all compounds as soluble, i.e. failed to separate both classes of compounds.

Comparison of Models Using 2D and 3D Descriptors

This analysis was performed using subsets of 2D and 3D Dragon and CDK descriptors, which required and did not require 3D structures of molecules, respectively. The models calculated using 2D descriptors had similar performances compared to those calculated using all descriptors. Contrary to that, models calculated only with 3D descriptors had on average lower performances. This result can be also attributed to the absence of stereochemistry for the chemical structures in the Enamine data set.

Consensus Modeling

We verified whether a consensus model based on models from Table 4 would offer additional advantages compared to the individual models. The PPV_10% of this model was 99.6% and thus was higher than that of any individual model. We also built a consensus model by combing RF, J48, and ASNN models developed using the E-state descriptors. The PPV_10% of this model was 99.3% and thus did not increase compared to the individual models. Thus, the higher accuracy of the larger consensus model was presumably due to the different representation of molecules with descriptor packages. Conversely, the models developed using the same set of descriptors were based on the same representation of molecules and thus their consensus did not improve the performance.

Table 4. Statistical Parameters of Models Developed for UCB1 Data Set Using E-State Indices.

method	PPV10%	ENR10%	SENS10%	SPEC10%
RF	99.5	3.4	96.9	78.7
J48	99.5	3.4	98	74.1
ASNN	99.4	2.9	94.2	76.9

The E-state descriptors participated in 3 out of 17 top-performing models. Moreover, they provided the smallest set of descriptors for the analysis. Because of the size of this data set as well as problems to run a large computational analysis at UCB, we decided to use only E-state for the further analysis.

Comparison of “Structure-Based” and “Property-Based” Similarities

It was previously demonstrated that the use of property-based similarities³² based on a disagreement of models provides better separation of molecules with reliable and nonreliable predictions compared to the traditional one based on, e.g. Leverage.^30,31,41,42 Cumulative PPV values calculated for the Consensus model when using both types of similarities are shown in Figure 5. Since the performance of the same model was analyzed, PPV_100% is exactly the same, 97.9%. If we limit our analysis to a subset of molecules with the highest accuracy of prediction, property-based similarities, e.g. Consensus STD, calculate higher intermediate PPV values compared to Leverage. Thus, the property-based similarities provide better identification of molecules with correct predictions thus confirming our previous results.

Figure 5.

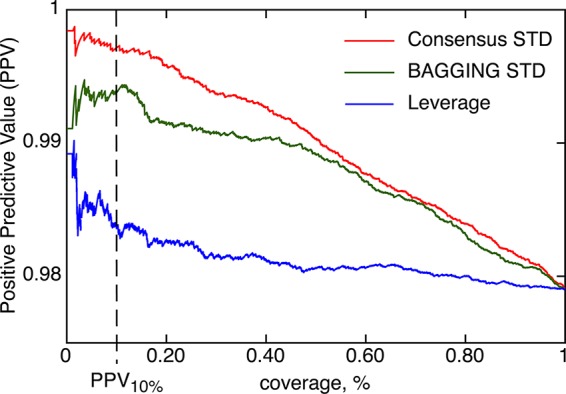
Cumulative positive predictive values (PPVs) are shown as a function of distance to models (DMs) using two property-based similarities³² (Consensus and Bagging STD) and Leverage, which was calculated using ECFP4 descriptors.²⁸ The same Consensus model was analyzed and thus PPV_100% values are identical for all three plots. The PPV values for the first 500 compounds were averaged to decrease chance fluctuations due to a small sampling size. All plots demonstrate that the accuracy of predictions decreases for molecules with large DMs. The property-based similarities better identify molecules with correct predictions and thus higher PPVs compared to Leverage. Thus, the acquisition of molecules selected from regions with most accurate predictions, e.g. 10% of compounds, would provide a smaller fraction of insoluble molecules when using property-based similarities compared to that based on Leverage.

Analysis of the UCB1 Data Set

The results calculated using different methods and E-state indices are summarized in Table 5. This data set contained only 1.7% of nonsoluble molecules, and thus, a random selection of molecules would contribute PPV = 98.3%. Therefore, the enrichment by an application of models developed with this set were smaller, e.g. the top performing RF model provided only about a 3.4 fold decrease in the number of nonsoluble molecules compared to an 8.8 fold decrease observed for molecules from the Enamine set.

Table 5. Validation of Models Using the UCB2 Data Set.

	training data set		UCB2 data set
training data set/model	PPV10%	ENR10%	PPV10%	ENR10%	PPV100%	ENR100%
Enamine/RF	99	5.3	97.9	2.3	96.1	1.5
Enamine/J48	99.2	7.6	98.2	2.8	95.8	1.4
Enamine/ASNN	99.4	8.8	98.4	3.2	96.6	1.7
UCB1/RF	99.5	3.4	99.1	5.9	97.6	2.4
UCB1/J48	99.5	3.4	98.9	4.8	96.8	1.8
UCB1/ASNN	99.4	2.9	98.4	3.2	97.4	2.2
Enamine + UCB1/RF	99.5	10	99.2	7	97.1	2
Enamine + UCB1/J48	99.4	7.8	99.2	7	96.7	1.8
Enamine + UCB1/ASNN	99.4	5.2	98.5	3.8	97.4	2.2

Prediction of the UCB2 Data Set

The models developed using UCB1, Enamine, and UCB1 + Enamine data were used to predict a new data set of compounds that were recently acquired and measured at the company. The accuracies of predictions are reported in Table 5. The prediction of the UCB2 set was a difficult task. The enrichments, when considering all molecules (ENR_100%), were rather low and ranged from 1.4- to 2.4-fold. At the same time, the enrichments ENR_10% for 10% of coverage were on average 2–3 times higher and provided much better filtering of nonsoluble molecules.

The models developed using the Enamine set provided the lowest enrichments. This result is clearly understandable considering different diversity of chemical compounds in the libraries of chemical providers and those of chemical companies. The models developed using UCB1 had a higher accuracy while the highest accuracies were achieved for models developed by a set, which combined the Enamine and UCB1 sets. It is interesting that an increase of the training set sizes had practically no impact on the ENR_100%, which only slightly increased. However, the number of nonsoluble compounds dramatically decreased within the 10% coverage for larger data sets. Importantly, a combination of data from both companies achieved models with the highest ENR_10% values thus indicating advantages of collaboration efforts.

Development of Models Using All Data

The final models were developed using 3 analyzed methods, and the total set of 163 089 molecules, which included 6263 nonsoluble (3.84%) compounds. The PPV_10% of the models ranged from 99% (RF) to 99.3% (J48) and 99.4% (ASNN). As in the previous analyses, these values were higher than PPV_100%, which ranged from 98.1% (J48), 98.2, (RF) to 98.4% (ASNN). Thus, the developed models could decrease the number of insoluble molecules 2–2.4-fold when applied to the whole set of molecules and 3.8–6.4 times when considering only 10% of the most reliable predictions. This result again confirms that taking into consideration only the most reliable predictions allows significantly better filtering of nonsoluble compounds.

Models and Data Availability

The developed models are available as a web reference.³⁹ The readers can open models, access, and analyze their statistics and applicability domain plots as well as apply the models to new compounds using the “Apply the model to new compounds” link at the bottom of the selected model. This page also contains SetCompare results with lists of significant groups and fragments identified for soluble and insoluble compounds. The article profile provides also access to data that were used for model development. The data can be visualized in the browser and downloaded in SDF, Excel, or in comma separated value (CSV) formats using the “Export this basket” link provided for each data set.

Conclusions

We developed and analyzed QSPR models to predict DMSO solubility of chemical compounds using several large data sets. When applied to the whole sets, the developed models allowed to decrease the number of nonsoluble compounds by about 1.4–2.7 times. By considering only 10% of the most reliable predictions, one could achieve usually 2–3-fold enrichment and thus decrease the number of nonsoluble compounds 3–9-fold. This result indicates the importance of accounting for the prediction accuracy. The consideration of only the fraction of (the most accurately) predicted molecules corresponded to the typical use-case scenarios for the developed DMSO models. Indeed, these models are typically used to prescreen large chemical libraries and to purchase only a small subset of molecules with the most favorable properties. Therefore, the ability of the developed models to reliably predict only a small faction of the chemical library does not limit the scope of these models.

J48, RF, and ASNN provided higher accuracy of predictions than the other analyzed methods, such as libSVM, kNN, MLRA, FSMLR, and PLS. It is remarkable that simple classification algorithms such as J48 and RF achieved a very high accuracy of predictions when using the bagging approach. All three analyzed methods, J48, RF, and ASNN, provided similar results for different sets of molecules. From a practical point of view, the J48 and RF methods were faster to calculate and required a smaller size to store the models.

The structural analysis of sets of soluble and nonsoluble molecules identified functional groups and chemical scaffolds that are likely to contribute to low solubility of molecules. The results of this analysis can be important for planning and development of new chemical series that should be soluble or/and modification of the existing series in order to increase their solubility.

The combination of data from both companies provided an increase of the accuracy of prediction of the developed models for the UCB2 set. This result indicates the importance to promote collaborative studies and to develop models for precompetitive absorption, distribution, metabolism, elimination, and toxicology (ADMETox) properties by joining efforts of different stakeholders.

We also showed that consensus modeling by merging models developed with different descriptors could increase the accuracy of the models thus confirming results of our previous studies.⁴³ However, if the same descriptors are used, the consensus modeling may not provide additional advantages.

The ASNN-Estate and the consensus model based on all models from Table 4 were made publicly and freely available at the OCHEM Web site.³⁹ These models allow Web users to predict the solubility in DMSO of new molecules even before they are synthesized or acquired, thus avoiding acquisition of nonsoluble molecules and facilitating interpretation of HTS experiments and speeding up the drug discovery process. To our knowledge, these are the first public and freely accessible models for the solubility in DMSO predictions. The availability of public models, as those developed in the current study, is expected to dramatically shape the future of computational chemistry research during the coming years.⁴⁴

The authors declare the following competing financial interest(s): The authors are the employees of the respective companies.