Abstract
Genetic adaptation to external stimuli occurs through the combined action of mutation and selection. A central problem in genetics is to identify loci responsive to specific selective constraints. Many tests have been proposed to identify the genomic signatures of natural selection by quantifying the skew in the site frequency spectrum (SFS) under selection relative to neutrality. We build upon recent work that connects many of these tests under a common framework, by describing how selective sweeps affect the scaled SFS. We show that the specific skew depends on many attributes of the sweep, including the selection coefficient and the time under selection. Using supervised learning on extensive simulated data, we characterize the features of the scaled SFS that best separate different types of selective sweeps from neutrality. We develop a test, SFselect, that consistently outperforms many existing tests over a wide range of selective sweeps. We apply SFselect to polymorphism data from a laboratory evolution experiment of Drosophila melanogaster adapted to hypoxia and identify loci that strengthen the role of the Notch pathway in hypoxia tolerance, but were missed by previous approaches. We further apply our test to human data and identify regions that are in agreement with earlier studies, as well as many novel regions.
Keywords: natural selection, supervised learning, site frequency spectrum
NATURAL selection works by preferentially favoring carriers of beneficial (fit) alleles. At the genetic level, the increased fitness may stem from two sources: either a de novo mutation that is beneficial in the current environment or new environmental stress leading to increased relative fitness of an existing allele. Over time, haplotypes carrying such variants start to dominate the population, causing reduced genetic diversity. This process, known as a selective sweep, is mitigated by recombination and can therefore be observed mostly in the vicinity of the beneficial allele. Improving our ability to detect the genomic signatures of selection is crucial for shedding light on genes responsible for adaptation to environmental stress, including disease.
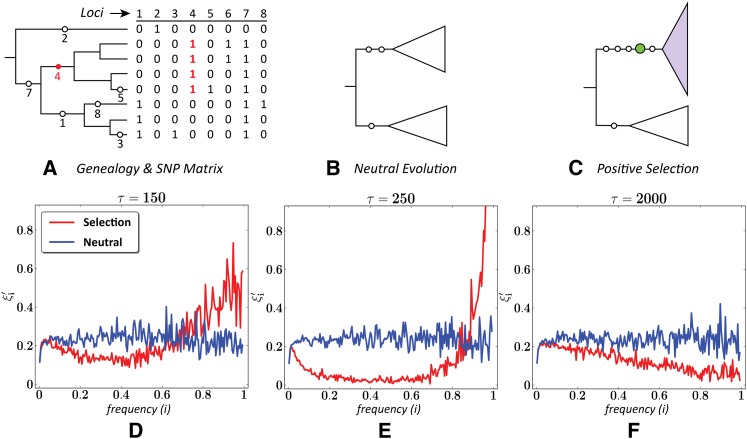
Many tests of neutrality have been proposed based on the site frequency spectrum (Tajima 1989; Fay and Wu 2000; Zeng et al. 2006; Chen et al. 2010; Udpa et al. 2011). We start by describing these tests in a common framework delineated by Achaz (2009). The data, namely genetic variants from a population sample, is typically represented as a matrix with m columns corresponding to segregating sites, and n rows corresponding to individual chromosomes. The sample is chosen from a much larger population of N diploid individuals, where chromosomes are connected by a (hidden) genealogy and mutations occurring in a certain lineage are inherited by all of its descendants (Figure 1A). Thus, in the example shown in Figure 1A, the mutation at locus 4 appears in four chromosomes from the sample, or 0.5 frequency. Following Fu (1995), let ξi denote the number of polymorphic sites at frequency i/n in a sample of size n. The site frequency spectrum (SFS) vector ξ and the scaled SFS vector ξ′ are defined as
| (1) |
Thus, in Figure 1A, we have
| (2) |
Figure 1.
Impact of a selective sweep on the scaled SFS. (A) The genealogy of eight chromosomes with eight polymorphic sites falling on different branches, and the corresponding SNP matrix. (B) Two populations diverged from a source population under neutral evolution, or (C) with one under selection. (D–F) The mean scaled SFS of 500 simulated samples from populations evolving neutrally or under selection (s = 0.08), sampled at τ = 150 (D), 250 (E), and 2000 (F) generations under selection (see Methods for simulation details).
In a constant-sized population evolving neutrally, the branch lengths of various lineages (Kingman 1982), the number of mutations on each lineage (Tajima 1989), and the observed SFS (Fu 1995) are all tightly connected to the population-scaled mutation rate θ (= 4Nμ) by coalescent theory. Specifically, E(ξi) = θ/i for all i = (1, …, n − 1). This implies that each is an unbiased estimator of θ (Fu 1995) and that the scaled SFS ξ′ is uniform in expectation (as illustrated by the neutral curves in Figure 1).
However, this is not the case for populations evolving under positive selection. We consider the case of a selective sweep, where a single (de novo) mutation confers increased fitness. Individuals carrying the mutation preferentially procreate with probability ∝ 1 + s, where s is the selection coefficient. As a result, the frequency of the favored allele and of those linked to it rises exponentially with parameter s, eventually reaching fixation at a rate dependent on s. Not surprisingly, selective sweeps have a dramatic effect on the scaled SFS. Near the point of fixation, the scaled SFS is characterized by an abundance of very high-frequency alleles and a near absence of intermediate frequency alleles (Figure 1E). Importantly, the scaled SFS of regions evolving under selective sweeps differs even in the prefixation and postfixation regimes from that of regions evolving neutrally (Figure 1, D and F).
To a first approximation, all tests of neutrality operate by quantifying the “skew” in the SFS of a given population sample, relative to that expected under neutral conditions. A subset of these tests do so by comparing different estimators of θ. Following Achaz (2009), we note that any weighted linear combination of ξ′ yields an unbiased estimator:
| (3) |
Thus, known estimators of θ can be rederived simply by choosing appropriate weights wi. For instance,
| (4) |
| (5) |
| (6) |
Since different estimators of θ are affected to varying extents by selective sweeps, many tests of neutrality are based on taking the difference between two estimators. These, also, can be defined as weighted linear combinations of ξ′. For example (see Figure 2),
| (7) |
| (8) |
In practice, d is normalized by its standard deviation, and the normalized version is denoted D. The expected value of both (D, H) equals 0 under neutral evolution, but < 0 for populations evolving under selection. A potential caveat of these tests is that although the scaled SFS changes considerably with time (τ) under selection (Figure 1), selection coefficient (s), and demographic history, the test statistic consists of a single fixed-weight function. It is therefore not surprising that the performance of these tests varies widely depending on the values of these parameters.
Figure 2.
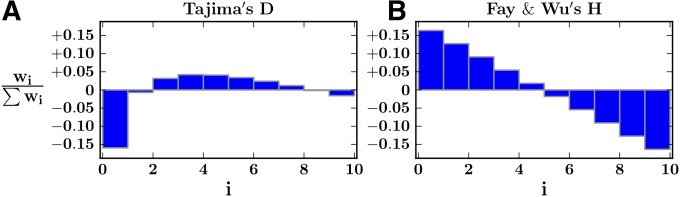
Weights (normalized wi) for two common neutrality tests based on the difference between θ estimators. (A) Tajima’s D weights, consisting of the difference between the normalized weights of and . (B) Fay and Wu’s H weights, consisting of the difference between the normalized weights of and . Shown for n = 10 haplotypes.
Additionally, naturally evolving populations may be subject to multiple selective forces, affecting many unlinked loci. To limit the search to selective pressures acting on a specific phenotype, cross-population tests are commonly used. These tests are applied simultaneously to a population under selection and to a genetically similar control population that is not subject to the specific selection pressure. Some common cross-population tests include XP-CLR (Chen et al. 2010), XP-EHH (Sabeti et al. 2007), LSBL (Shriver et al. 2004), Fst (Hudson et al. 1992), and Sf (Udpa et al. 2011). These tests can also be interpreted in the context of the scaled SFS. For example, the EHH test considers the change in frequency of a single haplotype (Sabeti et al. 2002). This is especially effective in the early stages of a sweep, when the haplotype carrying the beneficial allele increases in frequency while remaining largely intact.
Here, rather than inferring selection using fixed summary statistics (such as θ-based tests) of the scaled SFS, we propose inferring it directly using supervised learning. Specifically, we use support vector machines (SVMs) trained on data from extensive population simulations under various parameters. We consider the relative importance of features in the scaled SFS for classifying neutrality from various types of selective sweeps and find commonalities in these features across the parameter space.
Although there have been recent applications of machine learning to SFS- and LD-based summary statistics for inferring selection (Pavlidis et al. 2010; Lin et al. 2011), to the best of our knowledge, this study represents the first attempt to apply supervised learning directly to the scaled SFS to this end. In addition, whereas most supervised learning approaches are inherently specific to parameters of the training data, here we propose a way to overcome this by leveraging common attributes in the learned models of selection.
We develop an algorithmic framework, SFselect, which can be applied in two ways. If the parameters of a sweep (selective pressure, time under selection, etc.) are given, a model of the scaled SFS can be trained to yield very high sensitivity. We also consider the general, and more common, case in which this information is unknown. Our results suggest that there are distinct similarities in the trained models of prefixation and postfixation regimes (of the beneficial allele) and that these are maintained over a wide range of selection coefficients. We leverage this to generate a discriminative model that is robust over a wide range of values for two parameters: selection coefficient and time since selection. Further results point to the robustness of our test under a (plausible) demographic history of two extant human populations. In addition, we develop a similar approach (XP-SFselect) for cross-population testing based on the two-dimensional SFS (Sawyer and Hartl 1992; Chen et al. 2007; Gutenkunst et al. 2009; Nielsen et al. 2009). A software package implementing our approach is available online at http://bioinf.ucsd.edu/~rronen/sfselect.html.
To validate the utility of our framework, we applied XP-SFselect to genetic variation data from two sources. The first was a laboratory evolution experiment (Zhou et al. 2011) where pooled sequencing was conducted on populations of Drosophila melanogaster evolved under conditions of low (4%) oxygen. We further applied XP-SFselect to data from two human populations sequenced by the 1000 Genomes Project (Abecasis et al. 2010): Northern European individuals from Utah (CEU) and Yoruba individuals from Ibadan, Nigeria (YRI). While many of our identified regions agree with those of previous studies in these populations, we also identify many novel regions.
Methods
Population simulations
We simulated populations using the forward simulator mpop (Pickrell et al. 2009). Each simulation instance was initialized with a source population of size Ne = 1000 diploids from a neutral coalescent using Hudson’s ms (Hudson 2002). By randomly sampling from the source, we created three separate populations of size Ne each, labeled selected, neutral1, and neutral2. From this point, we evolved the populations separately, introducing a single beneficial locus in the selected population. Individuals carrying the advantageous allele had higher likelihood to reproduce at each generation (∝ 1 + 0.5s for heterozygous carriers, and ∝ 1 + s for homozygous carriers). After τ generations, we sampled (n = 100 diploids) from each population and applied tests of neutrality.
We simulated genomic regions of size 50 kbp, with mutation and recombination occurring at rates of μ = 2.4 × 10−7 and r = 3.784 × 10−8/base/generation. We note that these rates are higher than realistic in humans (Nachman and Crowell 2000; Campbell et al. 2012). For considerations of space and time, we simulated populations with effective size Ne = 1000 rather than Ne = 10,000, as considered more realistic in humans. We therefore scaled μ and r to obtain appropriate values of θ = 4 Neμ and ρ = 4 Ner. We simulated the beneficial allele under selection coefficient s ∈ {0.005, 0.01, 0.02, 0.04, 0.08}, or {10, 20, 40, 80, 160} in units of 2Nes, and sampled the populations after τ ∈ {0, 100, 200, …, 4000} generations under selection, or {0, 0.05, 0.1, …, 2} in units of 2Ne. For each of the 200 combinations of (s, τ), we simulated 500 instances of the source, selected, neutral1, and neutral2.
Binning, rescaling, and extending the SFS
For the scaled SFS vectors of unevenly sized population samples to be directly comparable, we rescale and bin frequencies in each sample to a fixed range [0, 1]. Empirically, the best results were obtained using relatively few (≈10) bins, as this reduced the variance per bin. Additionally, variants that have reached fixation in a given population are not informative in the context of that population, but may be informative across populations. We thus retain fixed variants unless fixed across all considered populations and extend ξ (ξ′) with an additional entry ξn (nξn) dedicated to these variants. Note, however, that the result from Fu (1995) showing that E(ξi) = θ/i does not hold for i = n.
For a cross-population test, we use the joint frequency spectrum of two populations, referred to as the cross-population SFS, or XP-SFS (Sawyer and Hartl 1992; Chen et al. 2007; Gutenkunst et al. 2009; Nielsen et al. 2009). Given two population samples of size n and m, the XP-SFS is defined as a n × m matrix ξ, where the ξij entry represents the number of polymorphic sites at frequency i/n in the first sample, and j/m in the second sample. As in the single-population case, we obtained the best results using few (≈8 × 8) bins, due to lower per-bin variance.
Support vector classification
We train SVMs on normalized scaled SFS vectors (also denoted by ), derived from simulated populations evolving both neutrally and under selection. Let us denote class labels as yi ∈ {−1, 1} for selected and neutral, respectively. Given a set of training data , the linear (soft-margin) SVM returns a maximum margin separating hyperplane w and an offset β0 using
where w are feature weights representing the hyperplane, εi ≥ 0 are slack variables designed to allow a data point to be misclassified (εi > 1) or in the margin 0 < εi ≤ 1, and C is the penalty constant for misclassification. To classify new data points using empirical FPR cutoffs, we use class probabilities (Wu et al. 2004; Chang and Lin 2011) rather than the binary decision function. For more detail on SVM implementation, see Supporting Information, File S1.
Finally, we use a linear kernel function so that the learned weights are directly applicable to the scaled SFS, and are thus more readily interpreted. We note the similarity of the SVM decision function given learned weights w = (w1, …, wn), to a weighted linear combination of ξ′ given weights (w1, …, wn−1) as in Tajima’s D or Fay and Wu’s H. This will enable a qualitative comparison of weights obtained from supervised learning to those of existing tests.
Results
Specific SVM tests (SFselect-s)
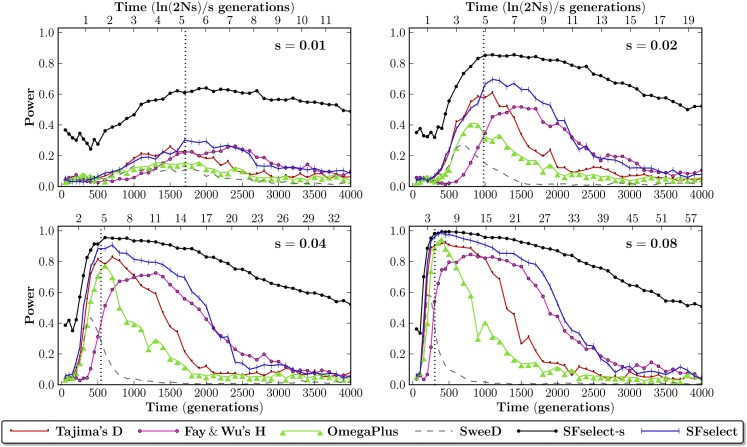
Initially, we assume prior knowledge of the time under selection (τ) and the selection coefficient (s). Under these assumptions (later relaxed), we trained 200 different SVMs on data corresponding to all combinations of (s, τ) simulated. We then applied each SVM to data simulated under the corresponding parameters and evaluated power as compared to several existing methods (Figure 3 and Figure S1). For further details on power estimation, see File S1. We compared our single-population SVMs to Tajima’s D (Tajima 1989) and Fay and Wu’s H (Fay and Wu 2000), which are based on weighted linear combinations of the scaled SFS, but also to the SweepFinder (Nielsen et al. 2005) and ω-statistic (Kim and Nielsen 2004) algorithms (as implemented in SweeD) (P. Pavlidis, personal communication) and OmegaPlus (Alachiotis et al. 2012)). We compared our cross-population SVMs to XP-CLR (Chen et al. 2010), XP-EHH (Sabeti et al. 2007), and Fst (Hudson et al. 1992).
Figure 3.
Power (5% FPR) of the SVM test compared to other single-population tests of neutrality. Shown for 200 data sets representing selective sweeps with selective coefficients s ∈ [0.01, 0.08], sampled at τ ∈ [0, 4000] generations under selection. SFselect-s (black) assumes knowledge of (τ, s), while SFselect (blue) assumes no prior knowledge of these parameters. Time is shown in generations (bottom axes), and ln(2Ns)/s generations (top axes). Dotted vertical lines show the mean time to fixation of the beneficial allele, which occurs at ≈ 5 ln(2Ns)/s generations.
We make a number of observations: (i) power changes proportionately to s for all tests, (ii) time to fixation of the beneficial allele scales as ln(2Ns)/s (Campbell 2007), and (iii) all tests reach peak power following fixation and decay in the prefixation and postfixation regimes. We also note that Tajima’s D performs better prefixation, due to the negative weights (expected inflation) assigned to low frequencies and the positive weights (expected depletion) assigned to intermediate frequencies (Figure 2), while Fay and Wu’s H performs better postfixation, due to the relatively high weights assigned to low- and intermediate-frequency variants.
Invariably, our parameter-specific SVMs (SFselect-s) exhibit higher power compared to the other tests across the wide range of (s) and (τ) combinations considered, remaining powerful throughout much of the postfixation regime. For example, at s = 0.08 the SVM shows 87% power after 2000 generations, vs. 42% for the next best method. Likewise, at s = 0.02, we see 85% power for the SVM at generation 1000 vs. 57% for the next best method. These results demonstrate the potential of statistical learning of weight functions for the scaled SFS. We next consider several models of the scaled SFS learned by our parameter-specific SVMs.
Comparison with existing weighted linear combinations
We consider the feature weights learned by several of our parameter-specific SVMs, compared with weight functions of existing tests. Tajima’s D and Fay and Wu’s H (among other tests) apply a weighted linear combination to the scaled SFS and are thus conceptually similar to trained (linear) SVMs. Differently put, both types of test represent linear models of the scaled SFS under nonneutral evolution.
For several reasons, only qualitative comparisons can be made. First, we use a rescaled and binned version of the SFS. Unlike existing scaled SFS tests (such as D and H) that consider all allele frequencies between 1 and n − 1, where n is the sample size, we rescale sample frequencies to (0, 1] and bin them into n = 10 frequency bins (see Methods). Second, while tests based on estimators of θ consider frequencies up to n − 1, we extend the scaled SFS with an additional bin representing fixed differences (see Methods). Finally, the rescaled, binned, and extended scaled SFS vectors are normalized prior to learning and classification. Hence, although absolute values of the learned weights cannot be directly compared, we nevertheless gain insight from a qualitative comparison with existing scaled SFS tests.
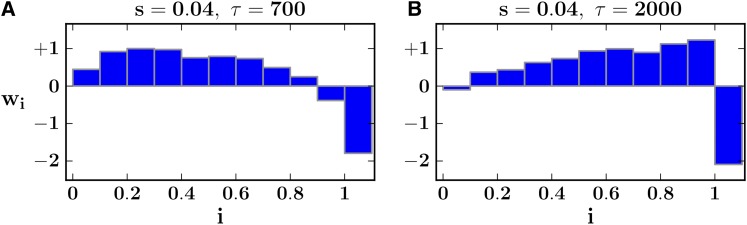
In Figure 4 we consider models learned by our specific SVMs (SFselect-s) from data sets simulated under relatively strong selection (s = 0.04), sampled at times where D or H show high sensitivity. We consider differences and similarities between these models and the weighted linear combinations applied by D and H (Figure 2). For D, peak power occurs near the mean time of fixation (e.g., τ = 700 generations). We observe that the weights learned from this data set do indeed bear some resemblance to those of Tajima’s D. Both have moderately positive weights in the intermediate frequency range, which gradually decay toward the higher and lower frequencies (Figures 4A and 2A). However, the models differ in their weight of the lowest frequency bin, which is highly negative in Tajima’s D.
Figure 4.
Feature weights learned by parameter-specific SVMs. (A) Feature weights of the SVM trained on (s = 0.04, τ = 700), a regime in which Tajima’s D is sensitive. (B) Feature weights of the SVM trained on (s = 0.04, τ = 2000), a regime in which Fay and Wu’s H is sensitive. We note that the rightmost feature (representing fixed differences) has no equivalent in D or H.
At τ = 2000 generations, H shows higher sensitivity compared to D. This is because unlike Tajima’s D, Fay and Wu’s H does not consider an inflation of low-frequency alleles as indicative of nonneutral evolution (Figure 2B). This helps because after fixation, lower-frequency alleles are first to be restored to neutral levels via de novo mutation. In contrast, the weights learned from this data set are quite different from those of H (Figures 4B and 2B), which was designed to capture an excess in high-frequency alleles (Fay and Wu 2000). Specifically, we see positive linearly increasing weights toward the higher frequencies. This is effective because de novo mutation takes longer to drift to higher frequencies.
As stated previously, our fixed differences bin (rightmost) has no equivalent in Tajima’s D or Fay and Wu’s H. It is negatively weighted in both models shown because the beneficial allele (as well as hitchhiking alleles) has fixed, leading to many differentially fixed variants.
Comparison with previous learning-based methods
We further compared our results with two recent tests based on supervised learning of summary statistics. The first, by Pavlidis et al. (2010), applies SVMs to values of two tests: the ω-statistic (Kim and Nielsen 2004), which is based on LD information, and the SweepFinder Λ-statistic (Nielsen et al. 2005), which is based on the SFS. Additionally, the correlation between the genomic positions yielding maximal values of these tests is also used as a feature for learning. We used improved implementations of these algorithms, namely SweeD (P. Pavlidis, personal communication) for SweepFinder and OmegaPlus (Alachiotis et al. 2012) for the ω-statistic. The second approach we compare to, by Lin et al. (2011), applies boosting to weak logistic regression classifiers learned from LD- and SFS-based summary statistics computed within a region. Namely, θπ (Tajima 1989), θH (Fay and Wu 2000), θW (Watterson 1975), Tajima’s D (Tajima 1989), Fay and Wu’s H (Fay and Wu 2000), and iHH (Sabeti et al. 2002).
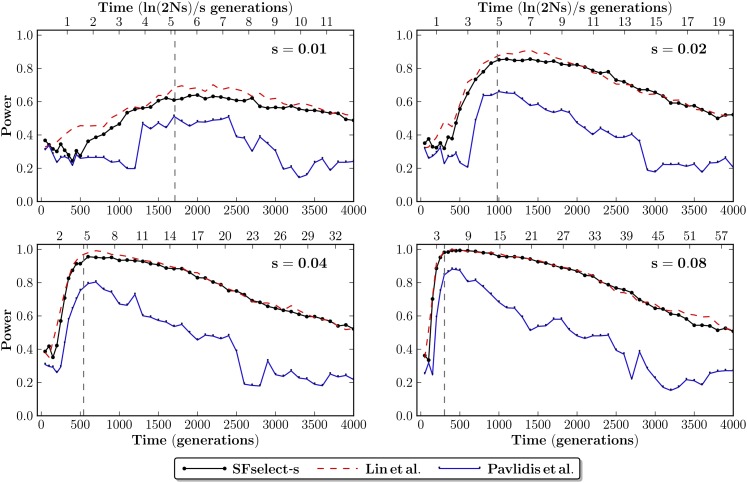
In Figure 5 we show the power of SFselect-s compared to Pavlidis et al. (2010) and Lin et al. (2011) under different sweep parameters. Both SFselect-s and Lin et al. (2011) show higher power compared to Pavlidis et al. (2010) across the sweep types considered. In addition, we observe that overall SFselect-s and Lin et al. (2011) show similar power, apart from a slight advantage to Lin et al. (2011) in a number of time points under weaker selection (s = 0.01, 0.02).
Figure 5.
Power (0.05 FPR) of SFselect-s compared to tests based on supervised learning of summary statistics. We compare to Pavlidis et al. (2010) and Lin et al. (2011). Shown for 200 data sets representing selective sweeps with selective coefficients s ∈ [0.01, 0.08], sampled at τ ∈ [0, 4000] generations under selection. Time shown in generations (bottom axes), and ln(2Ns)/s generations (top axes). The dashed vertical lines (gray) show the mean time to fixation of the beneficial allele, which occurs at ≈5 ln(2Ns)/s generations.
We note that our feature set bears some conceptual similarity to that of Lin et al. (2011). With the exception of the iHH features, Lin et al. (2011) effectively learn from a small set of weighted linear combinations of the scaled SFS. Our framework demonstrates that similar power can be achieved by learning directly from the scaled SFS. In fact, our analysis shows that the small difference in observed power is explained by the iHH features (Figure S4). Furthermore, the fundamental nature of our feature set enables our framework to potentially learn linear combinations that are not captured by the set used in Lin et al. (2011). In addition, we emphasize that although SFselect-s and Lin et al. (2011) show similar power in the parameter-specific case, in practice the parameters of a selective sweep are seldom known. Next, we develop a generalized test that can be applied without a priori knowledge of these parameters.
Generalized SVM test (SFselect)
Learning-based approaches, by definition, require training data. In the context of selection, this typically implies simulating populations undergoing a selective sweep. As a result, the parameters used in the simulation process are inevitably reflected in the trained models. Previous implementations of learning-based approaches have been geared toward specific sweep parameters (Pavlidis et al. 2010; Lin et al. 2011; as well as SFselect-s). Although we are able to learn powerful models (and thus, tests) using this framework, such models are difficult to apply in practice. This is because in most cases, the parameters (s, τ) of a sweep are unknown.
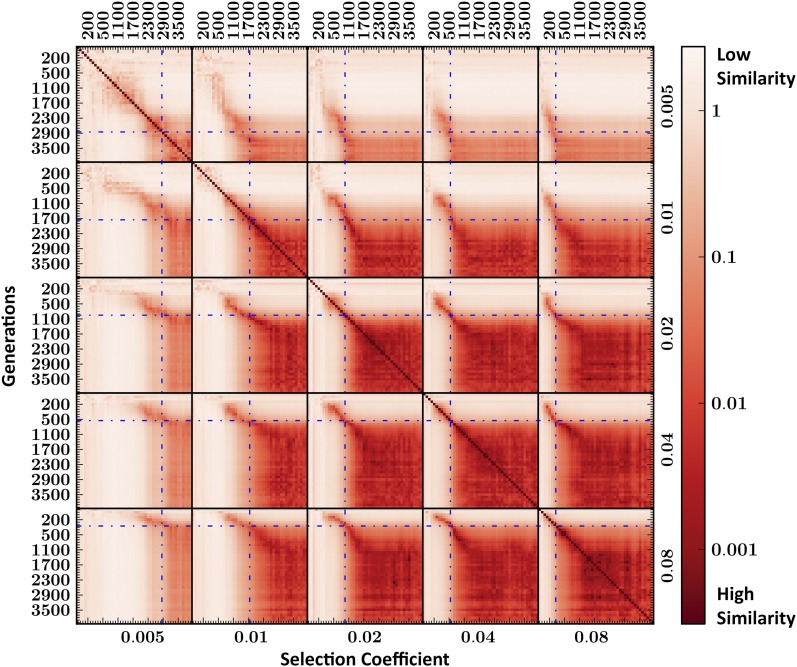
To develop a test that performs well in practice, we must either estimate these parameters or design a test that is robust to them. As a first step, we compare the feature weights learned by parameter-specific SVMs across different values of (s, τ). In Figure 6, we show the cosine distance between all (≈20,000) pairs (wi, wj), defined as
| (9) |
Remarkably, we see two strong similarity blocks across all selection coefficients, partitioned roughly at the time of fixation: a near-fixation similarity block encompassing time points close to (before and including) fixation of the beneficial allele, and a post-fixation similarity block encompassing the later time points. Importantly, the similarity is transitive across selection coefficients, meaning that trained SVMs in a given block are similar not only to each other, but also to SVMs in corresponding blocks of other selection coefficients. For instance, members of the near-fixation block in s = 0.01 (spanning times τ ∈ [700, 1800]) show high similarity to members of the near-fixation block of s = 0.04 (spanning times τ ∈ [200, 500]). In the weaker selective pressures (s = 0.005,0.01), transitions between the two regimes are not as stark, due to the increased variance in fixation times (Durrett 2002). This pairwise similarity structure is generally maintained in cross-population SVMs as well (Figure S2).
Figure 6.
Pairwise cosine distance between 200 trained SVMs. SVMs were trained on data simulated under different selection pressures s ∈ [0.01, 0.08], sampled at different times under selection τ ∈ [0, 4000] generations. Boundaries between selection pressures are denoted by black lines and mean times to fixation by blue dashed lines. We observe two similarity blocks at each selection pressure, corresponding to “near fixation”and “postfixation” of the beneficial allele. The stronger the selection (e.g., bottom right) the earlier/shorter the near-fixation stage, and vice versa.
Based on these findings, we retrained exactly two regime-specific SVMs denoted wnear and wpost. We trained these SVMs on data corresponding to the observed similarity blocks, aggregated over the relevant time points of selection coefficients s ∈ [0.02, 0.08]. For a given point ξ′, we use the estimated class probabilities from these SVMs to define our test score simply as
| (10) |
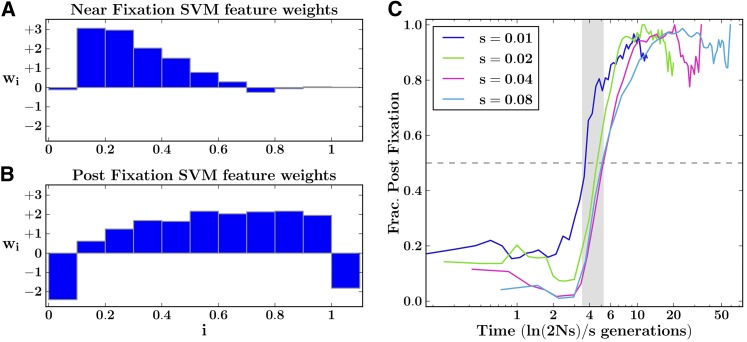
In Figure 7 we show the feature weights learned by these general SVMs (see Figure S3 for feature weights of the corresponding cross-population SVMs). As expected when requiring less knowledge apriori, the general two-stage SVM has less power to detect selective sweeps compared to the parameter-specific SVMs. Nevertheless, it dominates over existing methods across much of the (s, τ) parameter space (Figure 3), most notably so in the time points following fixation of the beneficial allele. In certain regimes, D or H perform similarly to our general model. This is in part because the feature weights are somewhat similar. Particularly, we note the similarity between the near-fixation SVM weights and D (Figure 2). For a corresponding analysis of power of the general cross-population SVM test (XP-SFselect), see Figure S1.
Figure 7.
Feature weights of the two generalized regime SVMs and regime inference rates. (A) Weights learned by the near-fixation SVM. (B) Weights learned by the postfixation SVM. Minor allele frequencies were distributed to n = 11 bins, with the last bin dedicated to fixed differences. (C) Fraction of true positives with postfixation class probability greater than that of near fixation, as function of time. Due to lower absolute number of true positives in the weaker selection pressures (s = 0.01, 0.02), we observe increased variance. The shaded region surrounding 4ln(2Ns)/s generations contains the mean times to fixation of the beneficial alleles.
Finally, the class probabilities returned from wnear and wpost also carry information on whether a given data point is in the prefixation or postfixation regime. By simply considering the maximum of the two values, we were able to infer the regime with >70% accuracy across times and selection pressures, excluding only those surrounding regime transitions, which are inherently unclear (Figure 7C).
Fly models of hypoxia adaptation
We applied XP-SFselect to polymorphism frequency data from pooled whole-genome sequencing of D. melanogaster (Zhou et al. 2011). In this study, fly populations evolved for many generations (≈200) in increasing levels of hypoxia (eventually reaching 4% O2), while genetically similar controls were kept in room air (21% O2) for cross-population analysis. The hypoxic stress was so strong that no wild-type fly survives in the final stage. Consequently, for a subset of adaptive variants needed to survive under such conditions, the population under selection had likely reached a postfixation regime. At the same time, selective sweeps may be ongoing for other variants. In that study, we used a log-ratio statistic (Sf) that applies fixed weights to the scaled SFS and is sensitive to postfixation signal (Udpa et al. 2011).
Applying a 1% genomic control FDR (see, for instance, Chen et al. 2010) in overlapping windows, and collapsing significant windows within 100 kbp of each other, we found 17 significant regions using Sf. At the same time, XP-SFselect identified 25 significant regions (Table S1, Figure S5, Figure S6, Figure S7, and Figure S8) including 11/17 (65%) of the Sf regions. Many of the strongest candidates identified in Zhou et al. (2011), including HDAC4 and hang, were also found by XP-SFselect. In addition, XP-SFselect identified 14 unique regions as significant. For a breakdown of significant windows by regime, see Table 1.
Table 1. Regime of selection as determined by SVM.
| Near-fixation regime | Postfixation regime | |
|---|---|---|
| XP-SFselect and Sf windows | 75 | 274 |
| XP-SFselect-only windows | 211 | 8 |
The number of genomic windows found significant under XP-SFselect (568 overall) with higher class probabilities for the near-fixation, or the post-fixation regime. Showing windows found only by XP-SFselect, as well those identified by both XP-SFselect and Sf. These results imply that while Sf is sensitive to the post-fixation regime, XP-SFselect captures both types of selection.
There is some evidence that XP-SFselect is more robust than Sf. For instance, one region deemed significant by Sf, but not XP-SFselect, appears to be an artifact. This region (chrX:14.61–14.85 Mb) is significant under Sf due to little haplotype diversity in the adapted population, caused by a large block of fixed SNPs. Importantly, the control population also shows reduced diversity in this region, with the same block present at ≈80% frequency. This is likely the result of an event prior to population divergence and, thus, not caused by the hypoxic stress. Sf correctly identified low diversity in the adapted population, but weighed the high-frequency (nonfixed) alleles in controls as evidence of increased diversity instead (Udpa et al. 2011). In contrast, XP-SFselect correctly identifies the frequency difference of 20% as uninteresting genome wide.
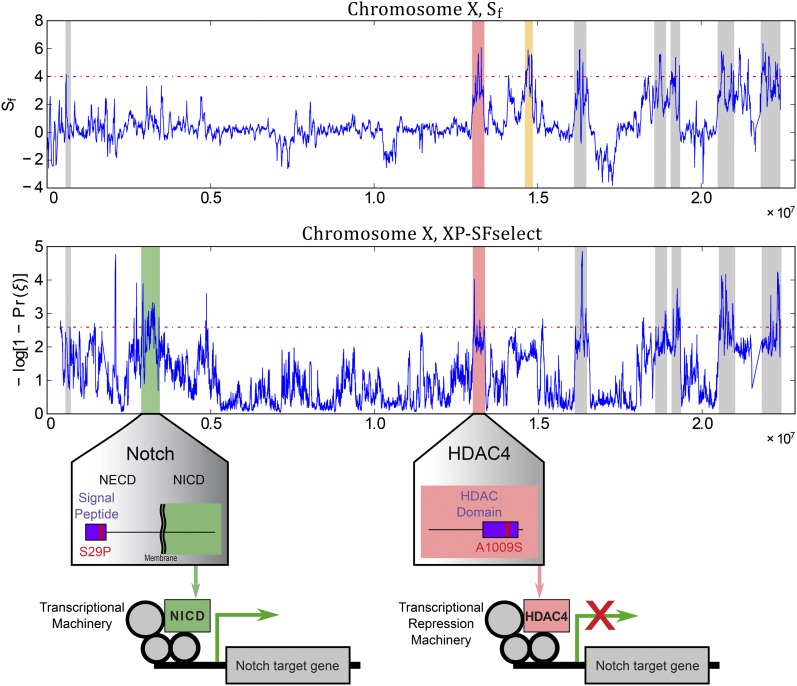
XP-SFselect may also be more sensitive. The main conclusion of Zhou et al. (2011) was that the Notch pathway is genetically involved in hypoxia tolerance, based on the presence of two Notch inhibitory genes (HDAC4 and Hairless) in significant regions. We confirmed these with XP-SFselect but also identified another significant region (chrX:2.87–3.44 Mb) containing a third component of the Notch pathway—the Notch gene itself (Figure 8). Upon further inspection, the Notch gene shows an interesting profile. We see very little diversity in the adapted population (mean coding SNP frequency, 0.99), while corresponding control frequencies are low (mean, 0.26). These include a nonsynonymous SNP (S29P) fixed in the adapted population and completely absent in controls. This serine is located in the N-terminal signal peptide, important for moving Notch to the membrane, where activation can occur. A key feature of the signal peptide is a long stretch of hydrophobic residues that stabilize by forming a helical structure. The serine at position 29 is in the middle of this stretch, and is hydrophilic, potentially impairing the ability of the signal peptide to form the helix. Replacing the serine with a hydrophobic proline may increase the stability (and thus efficiency) of the signal peptide in guiding Notch to the membrane.
Figure 8.
Signatures of selective sweeps affecting Notch pathway in hypoxia tolerant flies. XP-SFselect and Sf on fly chromosome X. The regions highlighted in gray were found significant by both Sf and XP-SFselect. The region highlighted in yellow is an artifactual region deemed significant under Sf, but not under XP-SFselect. The region highlighted in green contains the Notch gene, which activates the Notch signaling pathway. The mutation S29P may enhance the activity of Notch by improving the stability of the signal peptide domain. The region highlighted in red contains the HDAC4 gene, including the mutation A1009S near the active site of the protein, which may reduce its ability to affect Notch gene targets. Both of these mutations are consistent with hypoxia-tolerant flies genetically activating the Notch pathway as a mechanism of adaptation.
Models of human demography
To assess the ability of our framework to detect selection under complex demographic scenarios, as in many extant human populations, we simulated data under a more involved model. A strength of our framework is that if the demographic history is well characterized, a specific model of the SFS that is fine-tuned to that history can be learned. Focusing on the recent demographic histories of Northern Europeans and Western Africans, we note that multiple models can potentially explain the observed patterns of polymorphism (Schaffner et al. 2005; Voight et al. 2005; Fagundes et al. 2007) and that a clear consensus has not yet been reached.
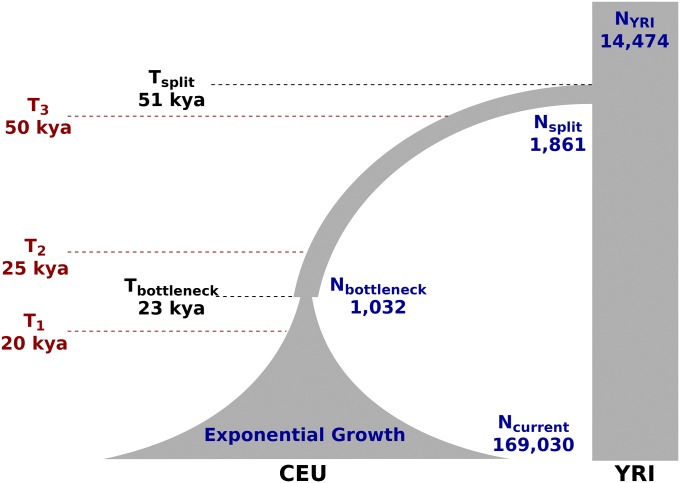
We use a model described recently by Gravel et al. (2011), with two instantaneous bottlenecks followed by a period of exponential growth in the European population (Figure 9). In this demographic scenario, we simulated a beneficial (s = 0.02, 0.005) allele in the European population, introduced at various time points [20, 25, and 50 thousand years ago (kya)]. In our simulations, we assume neutral evolution prior to the populations separating. As a result, we do not expect cross-population tests to have a distinct advantage, as their main strength is to decrease the effect of shared selection in the ancestral population.
Figure 9.
The demographic model used to simulate the CEU and YRI populations. The model is shown with time flowing downward. Model parameters are as described by Gravel et al. (2011), including a growth rate of 0.48% per generation in the European expansion period. We simulated an allele under positive selection (s = 0.02, 0.005) introduced 20, 25, and 50 kya (assuming 25 years per generation).
We evaluated the power of single- and cross-population SVMs trained on the simulated data to detect selection. Table 2 shows power of the SVMs at various time points, compared with other tests. As in constant-sized populations, we observe that Fay and Wu’s H is less powerful except in the late stages (e.g., 50 kya for s = 0.02) and that among the cross-population tests, XP-CLR is generally more powerful than XP-EHH. Additionally, we note that both the single- and cross-population SVMs show significantly higher power than all other tests. Finally, as postulated, we did not observe a consistent advantage for cross-population over single-population tests.
Table 2. Power (0.05 FPR) of different tests on data simulated under a demographic model.
| s | kya | D | H | XP-CLR | XP-EHH | SFselect-s | XP-SFselect-s | |||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 20 | 0.64 | 0.05 | 0.58 | 0.22 | 0.85 | 0.80 | ||||||||
| 0.02 | 25 | 0.82 | 0.22 | 0.77 | 0.28 | 0.89 | 0.88 | |||||||
| 50 | 0.97 | 0.95 | 0.99 | 0.40 | 0.99 | 0.99 | ||||||||
| 20 | 0.04 | 0.04 | 0.06 | 0.06 | 0.29 | 0.40 | ||||||||
| 0.005 | 25 | 0.05 | 0.03 | 0.04 | 0.05 | 0.23 | 0.48 | |||||||
| 50 | 0.45 | 0.11 | 0.41 | 0.25 | 0.71 | 0.66 |
The beneficial allele was simulated in the Northern European population (CEU), while the Western African population (YRI) evolved neutrally and was used as control for the cross-population tests.
Application to human populations
As no clear consensus exists on the demographic history of any human population, we applied our general SVM test (XP-SFselect) to data from two human populations sequenced by the 1000 Genomes Project (Abecasis et al. 2010): individuals of Northern European descent from Utah (CEU, 88 individuals) and Yoruban individuals from Nigeria (YRI, 85 individuals). These populations have been considered in several studies of selection (Frazer et al. 2007; Sabeti et al. 2007; Pickrell et al. 2009; Chen et al. 2010); thus we expected our results to overlap with previously reported regions. Using a 0.2% genomic control FDR in overlapping windows, and collapsing significant windows within 100 kbp of each other, we identified 339 distinct regions, of which 217 overlap known genes. As expected, several of the regions we find have been previously reported. We do, however, find signal in regions that have not so far been reported and may be of phenotypic interest. In Table S2, we list 40 regions showing the strongest signal of selective sweep using XP-SFselect. We used SnpEff (Cingolani et al. 2012) to annotate the functional impact of mutations and extracted all high-impact (splice or nonsense) mutations as well as all nonsynonymous mutations deemed damaging by SIFT (Kumar et al. 2009). In Table S3 we list the subset of these SNPs that fall within significant regions and show a high-frequency differential (≥30%) between the two populations (we find 11 such SNPs genome wide).
Known regions identified by XP-SFselect:
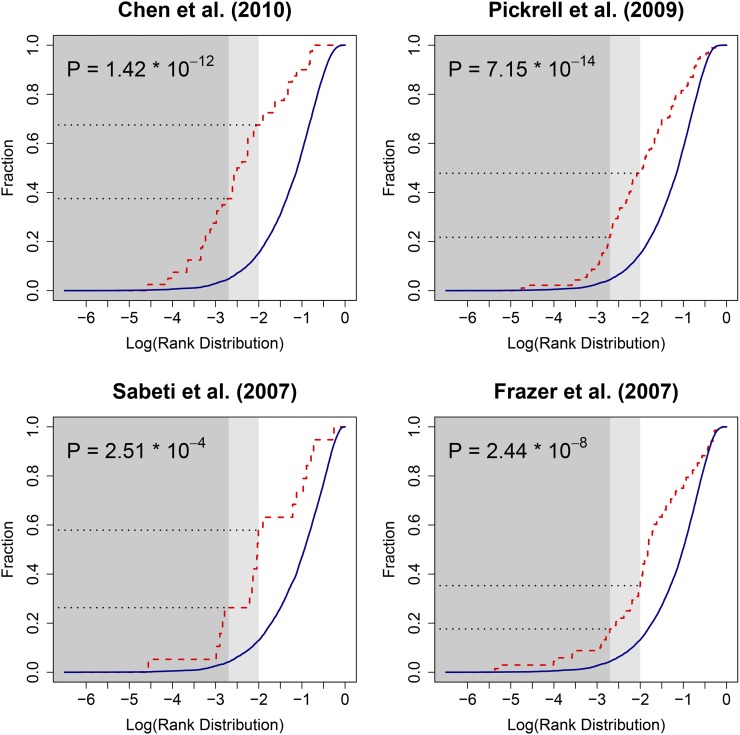
We compared the significant regions found by XP-SFselect to the top regions identified in four previous studies of the same populations: Chen et al. (2010), Pickrell et al. (2009), Frazer et al. (2007), and Sabeti et al. (2007). Of the 339 regions, 36 were reported in these studies (8 of top 40). This partial overlap likely stems from the considerable difference in density between the genotyping data used in the previous studies and that of whole-genome sequencing. When considering the top 1% of our results, however, the overlap becomes substantial (see Figure 10). Specifically, the overlap was 35.3% for Frazer et al. (2007), 47.8% for Pickrell et al. (2009), 57.9% for Sabeti et al. (2007), and 67.5% for Chen et al. (2010).
Figure 10.
Cumulative rank distribution of the top regions reported by previous studies, in the results of XP-SFselect. Rank distributions of previous studies are shown in red and those of 1000 identically sized sets of regions (per study) sampled at random from the genome are shown in blue. We see a significant enrichment of the regions from previous studies among the top 0.2% (dark shading) and 1% (light shading) of XP-SFselect results. The P-values shown are for a Mann–Whitney U-test with null hypothesis of equality between the rank distribution of a given study and that of the corresponding random samples. The studies compared to were: Chen et al. (2010), Pickrell et al. (2009), Sabeti et al. (2007), and Frazer et al. (2007).
Of the previously reported regions, particularly noteworthy are the genomic regions of KITLG (12q21.32) and SLC24A5 (15q21.1), found at 0.002 and 0.1% of the genome wide distribution, respectively. Variation in these genes has been associated with skin pigmentation and was reported to show evidence of selection (Pickrell et al. 2009). Additionally, we found the region containing the lactase gene (LCT) significant at 0.16% genome wide. Several studies have reported this gene as showing evidence of selection in Northern European populations (Bersaglieri et al. 2004; Chen et al. 2010).
Novel regions identified by XP-SFselect:
We identified a region (1q44) significant at 0.01% genome wide, containing a cluster of olfactory receptor (OR) genes: OR2T8, OR2L13, OR2L8, OR2AK2, and OR2L1P. Notably, the subregion containing OR2L8, OR2L13, and OR2AK2 has particularly low diversity in Northern Europeans, with a dense block of 97 nearly fixed SNPs (mean frequency, 0.95) in comparison to the same block in Western Africans (mean frequency, 0.24). This block also includes six nonsynonymous SNPs, of which two were deemed damaging (rs10888281 and rs4478844; see Table S3). Olfactory receptors make up the largest gene family, containing several hundreds of genes, many of which are pseudogenes. It has been suggested that a subset of (intact) OR genes are subject to selection in several human populations (Gilad et al. 2003; Pickrell et al. 2009), but to the best of our knowledge this OR cluster has not been identified as under selection in Northern European or Western African populations.
Additionally, the regions containing MSR1 (macrophage scavenger receptor 1) and MASP2 (mannan-binding lectin serine protease 2) were found significant at 0.07% and 0.09% of the genome wide distribution, respectively. These genes also contained 2 of the 11 variants with high-frequency differential between the populations that were deemed damaging (rs435815 and rs12711521; see Table S3). Interestingly, the ortholog of MSR1 has been shown to confer a protective effect from malaria infection in a recent study on mice (Rosanas-Urgell et al. 2012). At the same time, it has been shown to have a strong signal of balancing selection in African primate populations (Tung et al. 2009). Likewise, MASP2 has been associated with immune response to several diseases, including Chagas disease (Boldt et al. 2011), hepatitis C (Tulio et al. 2011), and placental malaria (Holmberg et al. 2012). Mutations in this gene (including rs12711521 (Boldt et al. 2011), see Table S3) have been linked to both the activity (Thiel et al. 2009) and expression levels (Thiel et al. 2007) of the protein. Such a sharp signal at these loci may imply a differential disease landscape between the two populations. For instance, it is conceivable that the YRI population has had to adapt at these loci to deal effectively with malaria, whereas CEU individuals have not had this stress.
Computational considerations
Our approach is composed of three main steps: data simulation, model training, and region classification. The first step, simulation, is performed with external tools and is therefore outside the scope of this article. For training and classification, there are two options. One may use our pretrained general model for classifying genomic regions as selected or neutral. This approach is very fast: a complete cross-population scan of the human genome (of the CEU and YRI populations) completed in under 2 hr on a standard desktop with 4 GB RAM. We note that this was done on whole-genome sequencing data, with considerably more variants than genotyping.
Another option is to train on data simulated under a specific model (e.g., given a known demographic scenario). The computational space and time required for training strongly depend on the size of the training data. In our experience, training a specific model (≈1000 training examples) required under 1 min, while training the general model (≈90,000 training examples) required close to 2 hr.
It should also be noted that training can potentially be faster. We used the LIBSVM implementation (Graf et al. 2003; Chang and Lin 2011; Pedregosa et al. 2011) due to its capability to calculate class probabilities, which enabled better control of FPR. A strictly linear SVM implementation, such as the one used by LIBLINEAR (Fan et al. 2008), will yield much better scaling of training times.
Discussion
The site frequency spectrum is heavily skewed under positive selection. Using supervised learning, we sought to develop a test that would yield not only improved power to detect a sweep, but also insight into the behavior of the SFS under various sweep types. The scaled SFS, being uniform in expectation under neutrality, provided a natural choice of features to learn from. Rather than a fixed weight function that performs well only under certain regimes, we were able to learn multiple weight functions of the scaled SFS, each providing optimal performance in its respective regime. When combined, these resulted in a usable test that improves over existing methods for both simulated and real data.
Although SVMs are standard practice in supervised learning, other classification methods are also applicable. A popular alternative is logistic regression, with optional (L1 or L2 norm) regularization of the model. While logistic regression has the advantage of providing a naturally continuous output, it proved less effective for our purposes. The two methods performed similarly in the single-population test, but we observed a noticeable decrease in power of the cross-population test (Figure S9 and Figure S10). This is likely due to the difference in loss function. While SVMs use a one-sided hinge loss, with no penalty for well-classified points outside the classification margin, logistic regression minimizes the log loss. Here, correctly classified points—including those outside the SVM margin—incur a (small) penalty. This may have a significant impact if the data are dense near the margins, which is likely the case for the XP-SFS vectors.
Given prior information on a population’s history and mode of selection, one may wish to apply weights to the regime SVMs, thereby increasing the sensitivity of the test. In our fly data, we can safely assume a postfixation regime for those loci most (and earliest) affected by selection, due to the high selective stress and relatively long time (≈200 generations). Thus, we can increase the sensitivity in those regions by weighting down the probabilities returned from the near-fixation SVM. Of course, this will decrease the sensitivity for regions in near-fixation regime. When applying no such bias to the regime of selection, our results indicate that SFselect can identify both types of selection, while previous methods were limited to specific regimes (Table 1).
Finally, although SFselect has high power in the near-fixation and postfixation regimes, there may be room for improvement in early selection. We note that tests based on haplotype diversity, such as iHH (Sabeti et al. 2002), are considered advantageous in this regime. To increase sensitivity in this regime, one might incorporate frequencies of dominant haplotypes as additional features. Moreover, although here we considered only the hard sweep model of positive selection, one might use a similar framework to investigate more complex scenarios, including the soft sweep model. Our results suggest that applying statistical learning directly to the scaled SFS can provide valuable insights for detecting nonneutral evolutionary processes.
Supplementary Material
Acknowledgments
We thank Efrat Golan for technical assistance, as well as Yaniv Erlich, Matan Hofree, Boyko Kakaradov, and two anonymous reviewers for valuable suggestions. We also thank Noah Rosenberg for comments on the manuscript and Pavlos Pavlidis for sharing instructions and code of OmegaPlus and SweeD. R.R. and N.U. were supported by National Science Foundation (NSF) grant CCF-1115206. E.H. is a faculty fellow of the Edmond J. Safra Program at Tel Aviv University and was supported in part by the German Israeli Foundation (grant 0603806851). V.B. was supported by National Institutes of Health (NIH) grant 5RO1-HG004962.
Footnotes
Communicating editor: W. Stephan
Literature Cited
- Abecasis G. R., Altshuler D., Auton A., Brooks L. D., Durbin R. M., et al. , 2010. A map of human genome variation from population-scale sequencing. Nature 467: 1061–1073. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Achaz G., 2009. Frequency spectrum neutrality tests: one for all and all for one. Genetics 183: 249–258. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Alachiotis N., Stamatakis A., Pavlidis P., 2012. OmegaPlus: a scalable tool for rapid detection of selective sweeps in whole-genome datasets. Bioinformatics 28: 2274–2275. [DOI] [PubMed] [Google Scholar]
- Bersaglieri T., Sabeti P. C., Patterson N., Vanderploeg T., Schaffner S. F., et al. , 2004. Genetic signatures of strong recent positive selection at the lactase gene. Am. J. Hum. Genet. 74: 1111–1120. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Boldt A. B., Luz P. R., Messias-Reason I. J., 2011. MASP2 haplotypes are associated with high risk of cardiomyopathy in chronic Chagas disease. Clin. Immunol. 140: 63–70. [DOI] [PubMed] [Google Scholar]
- Campbell C. D., Chong J. X., Malig M., Ko A., Dumont B. L., et al. , 2012. Estimating the human mutation rate using autozygosity in a founder population. Nat. Genet. 44: 1277–1281. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Campbell R., 2007. Coalescent size vs. coalescent time with strong selection. Bull. Math. Biol. 69: 2249–2259. [DOI] [PubMed] [Google Scholar]
- Chang C. C., Lin C. J., 2011. LIBSVM: a library for support vector machines. ACM Trans. Intell. Syst. Technol. 2: 27:1–27:27. [Google Scholar]
- Chen H., Green R. E., Paabo S., Slatkin M., 2007. The joint allele-frequency spectrum in closely related species. Genetics 177: 387–398. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chen H., Patterson N., Reich D., 2010. Population differentiation as a test for selective sweeps. Genome Res. 20: 393–402. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cingolani P., Platts A., Coon M., Nguyen T., Wang L., et al. , 2012. A program for annotating and predicting the effects of single nucleotide polymorphisms, SnpEff: SNPs in the genome of Drosophila melanogaster strain w1118; iso-2; iso-3. Fly 6: 80–92. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Durrett R., 2002. Probability Models for DNA Sequence Evolution, Ed. 2 Springer-Verlag, New York. [Google Scholar]
- Fagundes N. J. R., Ray N., Beaumont M., Neuenschwander S., Salzano F. M., et al. , 2007. Statistical evaluation of alternative models of human evolution. Proc. Natl. Acad. Sci. USA 104: 17614–17619. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fan R.-E., Chang K.-W., Hsieh C.-J., Wang X.-R., Lin C.-J., 2008. LIBLINEAR: a library for large linear classification. J. Mach. Learn. Res. 9: 1871–1874. [Google Scholar]
- Fay J. C., Wu C. I., 2000. Hitchhiking under positive Darwinian selection. Genetics 155: 1405–1413. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Frazer K. A., Ballinger D. G., Cox D. R., Hinds D. A., Stuve L. L., et al. , 2007. A second generation human haplotype map of over 3.1 million SNPs. Nature 449: 851–861. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fu Y. X., 1995. Statistical properties of segregating sites. Theor. Popul. Biol. 48: 172–197. [DOI] [PubMed] [Google Scholar]
- Gilad Y., Bustamante C. D., Lancet D., Paabo S., 2003. Natural selection on the olfactory receptor gene family in humans and chimpanzees. Am. J. Hum. Genet. 73: 489–501. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Graf A., Smola A., Borer S., 2003. Classification in a normalized feature space using support vector machines. IEEE Trans. Neural Networks 14: 597–605. [DOI] [PubMed] [Google Scholar]
- Gravel S., Henn B. M., Gutenkunst R. N., Indap A. R., Marth G. T., et al. , 2011. Demographic history and rare allele sharing among human populations. Proc. Natl. Acad. Sci. USA 108: 11983–11988. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gutenkunst R. N., Hernandez R. D., Williamson S. H., Bustamante C. D., 2009. Inferring the joint demographic history of multiple populations from multidimensional SNP frequency data. PLoS Genet. 5: e1000695. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Holmberg V., Onkamo P., Lahtela E., Lahermo P., Bedu-Addo G., et al. , 2012. Mutations of complement lectin pathway genes MBL2 and MASP2 associated with placental malaria. Malar. J. 11: 61. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hudson R. R., 2002. Generating samples under a Wright–Fisher neutral model of genetic variation. Bioinformatics 18: 337–338. [DOI] [PubMed] [Google Scholar]
- Hudson R. R., Slatkin M., Maddison W. P., 1992. Estimation of levels of gene flow from DNA sequence data. Genetics 132: 583–589. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kim Y., Nielsen R., 2004. Linkage disequilibrium as a signature of selective sweeps. Genetics 167: 1513–1524. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kingman J. F. C., 1982. On the genealogy of large populations. J. Appl. Probab. 19: 27–43. [Google Scholar]
- Kumar P., Henikoff S., Ng P. C., 2009. Predicting the effects of coding non-synonymous variants on protein function using the SIFT algorithm. Nat. Protoc. 4: 1073–1081. [DOI] [PubMed] [Google Scholar]
- Lin K., Li H., Schltterer C., Futschik A., 2011. Distinguishing positive selection from neutral evolution: boosting the performance of summary statistics. Genetics 187: 229–244. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Nachman M. W., Crowell S. L., 2000. Estimate of the mutation rate per nucleotide in humans. Genetics 156: 297–304. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Nielsen R., Williamson S., Kim Y., Hubisz M. J., Clark A. G., et al. , 2005. Genomic scans for selective sweeps using SNP data. Genome Res. 15: 1566–1575. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Nielsen R., Hubisz M. J., Hellmann I., Torgerson D., Andres A. M., et al. , 2009. Darwinian and demographic forces affecting human protein coding genes. Genome Res. 19: 838–849. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Pavlidis P., Jensen J. D., Stephan W., 2010. Searching for footprints of positive selection in whole-genome snp data from nonequilibrium populations. Genetics 185: 907–922. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Pedregosa F., Varoquaux G., Gramfort A., Michel V., Thirion B., et al. , 2011. Scikit-learn: machine learning in python. J. Mach. Learn. Res. 12: 2825–2830. [Google Scholar]
- Pickrell J. K., Coop G., Novembre J., Kudaravalli S., Li J. Z., et al. , 2009. Signals of recent positive selection in a worldwide sample of human populations. Genome Res. 19: 826–837. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rosanas-Urgell A., Martin-Jaular L., Ricarte-Filho J., Ferrer M., Kalko S., et al. , 2012. Expression of non-TLR pattern recognition receptors in the spleen of BALB/c mice infected with Plasmodium yoelii and Plasmodium chabaudi chabaudi AS. Mem. Inst. Oswaldo Cruz 107: 410–415. [DOI] [PubMed] [Google Scholar]
- Sabeti P. C., Reich D. E., Higgins J. M., Levine H. Z., Richter D. J., et al. , 2002. Detecting recent positive selection in the human genome from haplotype structure. Nature 419: 832–837. [DOI] [PubMed] [Google Scholar]
- Sabeti P. C., Varilly P., Fry B., Lohmueller J., Hostetter E., et al. , 2007. Genome-wide detection and characterization of positive selection in human populations. Nature 449: 913–918. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sawyer S. A., Hartl D. L., 1992. Population genetics of polymorphism and divergence. Genetics 132: 1161–1176. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Schaffner S. F., Foo C., Gabriel S., Reich D., Daly M. J., et al. , 2005. Calibrating a coalescent simulation of human genome sequence variation. Genome Res. 15: 1576–1583. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Shriver M. D., Kennedy G. C., Parra E. J., Lawson H. A., Sonpar V., et al. , 2004. The genomic distribution of population substructure in four populations using 8,525 autosomal SNPs. Hum. Genomics 1: 274–286. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tajima F., 1989. Statistical method for testing the neutral mutation hypothesis by DNA polymorphism. Genetics 123: 585–595. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Thiel S., Steffensen R., Christensen I. J., Ip W. K., Lau Y. L., et al. , 2007. Deficiency of mannan-binding lectin associated serine protease-2 due to missense polymorphisms. Genes Immun. 8: 154–163. [DOI] [PubMed] [Google Scholar]
- Thiel S., Kolev M., Degn S., Steffensen R., Hansen A. G., et al. , 2009. Polymorphisms in mannan-binding lectin (MBL)-associated serine protease 2 affect stability, binding to MBL, and enzymatic activity. J. Immunol. 182: 2939–2947. [DOI] [PubMed] [Google Scholar]
- Tulio S., Faucz F. R., Werneck R. I., Olandoski M., Alexandre R. B., et al. , 2011. MASP2 gene polymorphism is associated with susceptibility to hepatitis C virus infection. Hum. Immunol. 72: 912–915. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tung J., Primus A., Bouley A. J., Severson T. F., Alberts S. C., et al. , 2009. Evolution of a malaria resistance gene in wild primates. Nature 460: 388–391. [DOI] [PubMed] [Google Scholar]
- Udpa N., Zhou D., Haddad G. G., Bafna V., 2011. Tests of selection in pooled case-control data: an empirical study. Front. Genet. 2: 83. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Voight B. F., Adams A. M., Frisse L. A., Qian Y., Hudson R. R., et al. , 2005. Interrogating multiple aspects of variation in a full resequencing data set to infer human population size changes. Proc. Natl. Acad. Sci. USA 102: 18508–18513. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Watterson G., 1975. On the number of segregating sites in genetical models without recombination. Theor. Popul. Biol. 7: 256–276. [DOI] [PubMed] [Google Scholar]
- Wu T. F., Lin C. J., Weng R. C., 2004. Probability estimates for multi-class classification by pairwise coupling. J. Mach. Learn. Res. 5: 975–1005. [Google Scholar]
- Zeng K., Fu Y.-X., Shi S., Wu C.-I., 2006. Statistical tests for detecting positive selection by utilizing high-frequency variants. Genetics 174: 1431–1439. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zhou D., Udpa N., Gersten M., Visk D. W., Bashir A., et al. , 2011. Experimental selection of hypoxia-tolerant Drosophila melanogaster. Proc. Natl. Acad. Sci. USA 108: 2349–2354. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.