Knots and nonorientable surfaces in chiral nematics

Abstract

Knots and knotted fields enrich physical phenomena ranging from DNA and molecular chemistry to the vortices of fluid flows and textures of ordered media. Liquid crystals provide an ideal setting for exploring such topological phenomena through control of their characteristic defects. The use of colloids in generating defects and knotted configurations in liquid crystals has been demonstrated for spherical and toroidal particles and shows promise for the development of novel photonic devices. Extending this existing work, we describe the full topological implications of colloids representing nonorientable surfaces and use it to construct torus knots and links of type (p,2) around multiply twisted Möbius strips.

Controlling and designing complex 3D textures in ordered media is central to the development of advanced materials, photonic crystals, tunable devices or sensors, and metamaterials (1–10), as well as to furthering our basic understanding of mesophases (11–13). Topological concepts, in particular, have come to play an increasingly significant role in characterizing materials across a diverse range of topics from helicity in fluid flows (14, 15) and transitions in soap films (16) to molecular chemistry (17), knots in DNA (18), defects in ordered media (19, 20), quantum computation (21, 22), and topological insulators (23). Topological properties are robust, because they are protected against all continuous deformations, and yet flexible for the same reason, allowing for tunability without loss of functionality.

Some of the most intricate and interesting textures in ordered media involve knots. Originating with Lord Kelvin’s celebrated “vortex atom” theory (24), the idea of encoding knotted structures in continuous fields has continued in magnetohydrodynamics (25), fluid dynamics (15), high-energy physics (26–28), and electromagnetic fields (29, 30), and has seen recent experimental realizations in optics (31), liquid crystals (32), and fluid vortices (33). Tying knots in a continuous field involves a much greater level of complexity than in a necktie, or rope, or even a polymer or strand of DNA. In a field, the knot is surrounded by material that has to be precisely configured so as to be compatible with the knotted curve. However, this complexity brings its own benefits, for the full richness of the mathematical theory of knots is naturally expressed in terms of the properties of the knot complement: everything that is not the knot. In this sense, knotted fields are ideally suited to directly incorporate and experimentally realize the full scope of modern knot theory.

Liquid crystals are orientationally ordered mesophases, whose unique blend of soft elasticity, optical activity, and fluid nature offers a fertile setting for the development of novel metamaterials and the study of low-dimensional topology in ordered media. Much of the current focus centers on colloidal systems––colloidal particles dispersed in a liquid crystal host––which have a dual character. On the one hand, the liquid crystal mediates long-range elastic interactions between colloids, furnishing the mechanism for formation of colloidal structures and metamaterials (1–3, 10). On the other hand, the colloids, through anchoring conditions imposed by their surfaces, generate defects in the liquid crystal and so serve to induce and manipulate its topological properties. For instance, multiple colloids exhibit a variety of entangled defect configurations (34, 35), equally interesting states without defects (36), and can even be manipulated so as to form arbitrary knots and links (32, 37). More recently, a significant advance has seen the fabrication of colloids with different topology (38)––tori up to genus five––verifying experimentally the relation between particle topology and accompanying defect charge, and advancing a program to obtain topological control of materials through topological design. Although the phenomena displayed by these systems are indeed rich, as surfaces these colloids (spheres, tori, etc.) all represent closed, orientable surfaces.

In this article we extend these ideas to provide a complete topological characterization of all compact colloidal surfaces in a liquid crystal host. Nonorientable surfaces fully exploit the nonorientable nature of liquid crystalline order (39). On all nonorientable surfaces there are, by necessity, closed paths around which the surface normal reverses its orientation. For surfaces with normal anchoring this imprints a corresponding reversal in the director field, the telltale signature of a disclination line. In this way nonorientable surfaces enforce the creation of topologically protected dislcination lines. By varying the embeddings of the surface we exploit this topology to create metastable disclination loops in the shape of 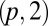torus knots and links, for any p, around multiply twisted Möbius bands. Through this combination of geometry and topology we elucidate a natural setting for the creation and control of complex knotted fields and the integration of mathematical knot theory into experimental science.

Colloids, Surfaces, and Topology

Liquid crystals are typically composed of long, thin, rod-like molecules, which align in the nematic state along a common direction n called the director. This orientation is line-like rather than vectorial, meaning 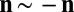and the local orientation takes values in the real projective plane 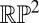, the ground-state manifold for nematics (19, 20). The director field varies smoothly everywhere except on points or lines of discontinuity, known as topological defects, whose nature is captured by the way the order changes in their vicinity. Line defects, called disclinations, are characterized by the behavior on small loops around the singular line and so may be classified by the fundamental group of the ground-state manifold 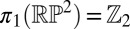. Unique to liquid crystals, these defects reflect the nonorientability of nematic order with the molecules undergoing a π-rotation upon encircling the disclination. Similarly, point defects, referred to colloquially as hedgehogs, are classified by the second homotopy group 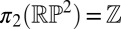. This simple classification is augmented by the topological content of interactions between defects [characterized in terms of the action of 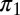on the higher homotopy groups, or by various Whitehead products (40)] so that, in particular, point defects of equal but opposite strength are equivalent (meaning freely homotopic) in the presence of a disclination and, whereas there is only one nontrivial element of 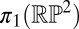, disclinations that close up into loops fall into four distinct homotopy classes (41). Loosely, these may be thought of as corresponding to whether the linking number with other defects is even or odd and whether the loop carries an even or odd hedgehog charge (20).

Defects can be induced and manipulated by immersing colloidal particles in the liquid crystal. This arises through the incompatibility of anchoring conditions on the particle surfaces with the alignment imposed by the cell boundaries, or at large distances. The topological type of this incompatibility, or obstruction, can be associated with elements of the homotopy groups 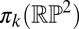so that different surfaces can (loosely) be thought of as generating different types of defects. The nature of the obstruction depends on the anchoring conditions at the surface, but in the most common case of normal, or homeotropic, anchoring (as we consider here) it depends only on the topology of the colloid’s surface. The classification theorem of surfaces (42) is a classic result of 2D topology, which states that any compact surface can be classified up to homeomorphism by its genus, orientability, and number of boundary components. The genus is equal to the number of holes or handlebodies possessed by a surface; for example, a torus has genus one and a sphere genus zero. Orientability implies a consistent choice of normal vector can be made on a surface. The one-sided Möbius strip is the classic nonorientable surface; any normal vector on the strip will be flipped by going around the strip once, forbidding a consistent choice of surface normal. Finally, the number of boundary components is simply the number of distinct connected components in the surface boundary, e.g., a disk has one boundary component and a torus has none.

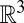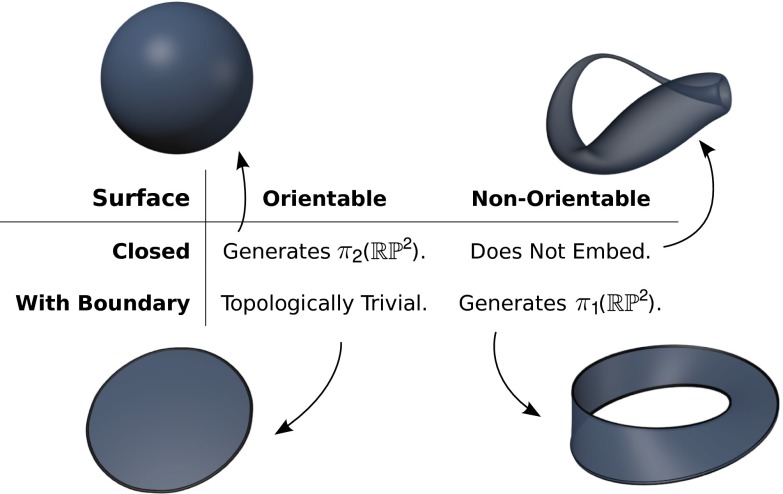
Whereas this is a complete topological classification of surfaces in an abstract setting, for applications they must also be embedded (no self-intersections) into ordinary 3D space, . Different embeddings are interesting in their own right––the whole of knot theory concerns embeddings of a circle into 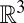––but they do not affect the homotopy class of the defect necessitated in the bulk, which we focus on first. Thus, with the classification of surfaces in mind, it is natural to ask what topological implications each type of surface has for accompanying defects in the surrounding liquid crystal. The complete classification, summarized in Fig. 1, naturally separates into four classes of surfaces: orientable or nonorientable and closed or with boundary.

Fig. 1.

Topological characterization of compact surfaces with homeotropic boundary conditions, embedded in a 3D, nematic liquid crystal. Closed orientable surfaces generate elements of 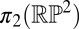, equal to 1 minus the genus of the surface. Nonorientable surfaces with boundary generate the nontrivial element of 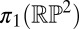, which forces the nucleation of disclination lines in the bulk.

Closed, orientable surfaces are known to induce defects corresponding to the element 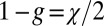of 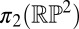, where g is the genus of the surface and χ is the Euler characteristic (38, 43, 44). Briefly, this relation comes through computing the degree of the Gauss map of the surface. The Gauss map 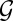of a surface X is a map 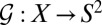that sends every point of the surface to the direction of the surface normal at that point. For orientable surfaces with normal anchoring, the director can be given the orientation of the Gauss map, so that 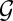describes precisely the molecular orientation at the surface. The degree of this map––the number of times every point on 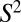is visited, counted with sign––is a homotopy invariant (43) characterizing the type of defect that the surface generates (38, 44). Although experimentally the same surface can produce seemingly different defects, they are always characterized by this same element of 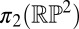. For instance, spherical colloids can nucleate either a point defect (1) or disclination loop (45) but the loop can always be shrunk continuously into a point (46), so that it is more properly classified by 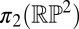. More generally, orientable surfaces can never generate elements of 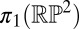, i.e., disclinations, as a topological requirement. Their orientability ensures that any disclination loops formed can always be removed in pairs or shrunk into points.

Closed, nonorientable surfaces cannot be embedded in 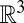without self-intersection, meaning that a true representation of any of these (e.g., the real projective plane or the Klein bottle) in a liquid crystal is not possible. For this reason, we do not consider closed, nonorientable surfaces any further.

Orientable surfaces with boundaries have trivial topological implications for the surrounding liquid crystal. Their orientability, as in the closed case, forbids them from generating elements of 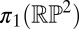as a topological necessity. In addition, because they have a boundary, they cannot generate any elements of 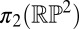. We argue as follows. Closed, orientable surfaces separate space into an inside and an outside and they generate point defects in both regions. If one cuts a hole in the surface, creating a boundary component, then these defects can be combined to leave a defect-free texture. Cutting more holes in the surface will not change things as one could always make the texture on the new hole identical to the surface normal that was removed.

Nonorientable surfaces with boundary necessarily generate a nontrivial element of 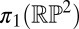. A generalization of the Gauss map to nonorientable surfaces 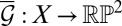assigns to every point of the surface the line element (point in 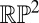) corresponding to the direction of the (unoriented) surface normal. [It is more common, and more useful in general, to think of the nonorientable version of the Gauss map as a map to the Grassmannian 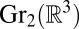––e.g., ref. 47––but because is canonically homeomorphic to 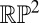there is no loss in our discussion.] Now consider the loop space of our surface 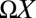. Composition with the nonorientable Gauss map 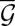creates a set of representatives of 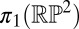. If X is nonorientable then there must be at least one map in this set which represents the nontrivial element (and generates a disclination). Suppose there was no such map, then every map in 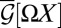could be lifted from 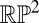to 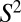and we would have created an orientable Gauss map 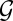, implying the surface is orientable, a contradiction. The disclinations created in this way must entangle the surface, because any disk spanning a nonorientable loop on the surface must be pierced by the defect.

With closed, orientable surfaces, different elements of 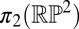could be generated according to the genus of the surface. In the same way, we might ask if different nonorientable surfaces with boundary can act to generate different kinds of disclination loops in the bulk liquid crystal. Although there is only one nontrivial element of 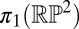, there are four distinct homotopy classes of disclination loops (20, 41) (the four types may be thought of as corresponding to even/odd linking number with other disclinations and even/odd hedgehog charge). We must, therefore, determine which of these is generated by the surface. We cannot force the existence of linked loops in a path-connected domain. If we have a connected domain then a single disclination loop can go through all of the nontrivial cycles created by the surface. Because we will then have only one disclination, it cannot be linked. Furthermore, it must have zero hedgehog charge. The surface simply acts to smoothly align the director field in some region of space so that the texture is equivalent to one containing a lone disclination loop, without the colloid but with the same director orientation in its place, which must have zero charge. Thus, all nonorientable surfaces with boundary, independent of their topological type, have the same topological implication for the liquid crystal, in contrast with the closed, orientable case. These four classifications are summarized in Fig. 1.

Möbius Strips and Knotted Defects

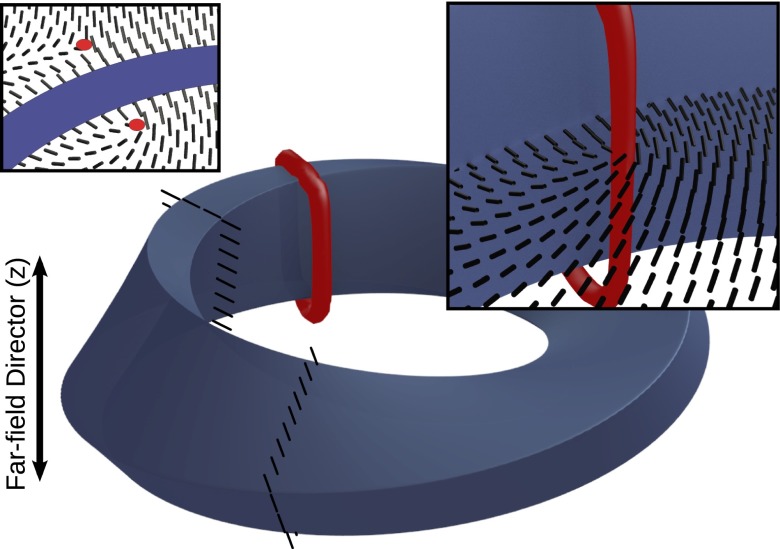
Nonorientability of the surface enforces the existence of a disclination loop but it leaves open the precise form of the defects and their equilibrium configuration. These are determined by energetics and by the nature of the embedding of the surface. Whereas surfaces with boundary are unavoidably 2D, experimentally realizable, but topologically equivalent, surfaces may be constructed by using thin material with homeotropic boundary conditions on the faces and planar anchoring on the thin edges, as shown schematically in Fig. 2. In this way a colloid with varying surface anchoring conditions can be made to faithfully represent a 2D surface. Such boundary conditions are essential to mimic nonorientable surfaces and ensure the topological properties we describe––fully homeotropic boundary conditions simply replicate an orientable torus. Modern fabrication techniques allow for the manufacture of such exotic surfaces (38).

Fig. 2.

Simulation results of a Möbius strip with homeotropic boundary conditions on the flat faces, shown schematically in black along the strip. Note the planar anchoring on the short edge required to correctly represent a 2D surface. The 2D surface can then be thought of as living in the center of the strip. The defect line (red) is clearly visible entangling the strip, as predicted by [1]. (Insets) Local director profile near the defect, showing the +1/2 twist disclination on the inside of the strip; there is a corresponding −1/2 twist profile on the outside.

As the Möbius strip is the prototypical nonorientable surface––all nonorientable surfaces contain the Möbius strip as a subset––it serves as an elementary guide to the behavior of nonorientable surfaces in liquid crystals. A Möbius strip with homeotropic boundary conditions will generate a nontrivial element of 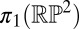as one passes around the strip and hence must be threaded by a disclination loop of zero hedgehog charge, entangling the surface. The shape of disclination loops around colloidal particles is governed largely by the requirement to minimize the distortion energy of the surrounding director field. A simple heuristic for this can be constructed as follows. As one passes through a disclination line a rotation of approximately 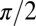is induced in the director. This rotation mediates the transition from the surface normal orientation to that of the far field and will best minimize the distortion in the director field when it is concentrated along those parts of the surface where the local anchoring and far-field directions are perpendicular. Because we consider colloids with homeotropic anchoring, this simply gives the requirement that

along the disclination, where 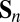is the surface normal and 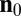is the far-field director. For a spherical particle in a uniform far field, this predicts that the disclination will lie on a great circle in a plane perpendicular to this far-field direction, which is the observed position of Saturn ring defects (45). Likewise the twisted shape of disclinations around spherical colloids in a cholesteric (37, 48) is correctly predicted by the same heuristic.

The preferred defect configuration for a Möbius strip can be found by numerical simulation using continuum Landau–de Gennes modeling (Materials and Methods). As shown in Fig. 2, the minimum energy configuration is a single disclination loop entangling the strip, in the location predicted by [1]. Of course, the precise configuration depends on the strip’s orientation relative to the far field, but we have found that the orientation shown, with the strip’s centerline in a plane perpendicular to the far-field orientation, has the lowest observed energy. The cross-section of the disclination loop shows a twisted 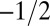profile on the outside of the strip and a 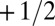twisted profile on the inside, as it has to in order to carry no hedgehog charge (49). This hedgehog charge may be computed by several methods. The recently developed Pontryagin–Thom construction (13) and methods related to disclination profile switching (49) both assert that the charge of the disclination is zero, as required on topological grounds.

Perhaps the simplest generalization of the Möbius strip topology is to vary its embedding in 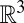. Different embeddings can be obtained by changing the number p of half-twists that the strip contains. The “canonical” Möbius strip has one half-twist 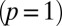, but more generally if p is odd then the surface is still nonorientable and has the same topology as the Möbius strip. When p is even the surface is orientable and has the topology of an annulus. Nonetheless, the embeddings are distinct and carry their own topological embellishments. The boundary of a Möbius strip is a circle. For a single half-twist this is a simple unknot, but for p half-twists it is a 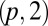torus knot (p odd) or link (p even). To see this, note that the boundary of a p-twisted strip (p odd) lives on a torus whose major radius is that of the strip and whose minor radius is half the strip width. The curve the boundary draws on this torus goes round the meridional cycle p times––once for each half-twist––while traversing the longitudinal cycle twice, which is the definition of a 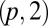torus knot. The story is the same for orientable strips with p even, except that there are two components to the boundary and they form a link.

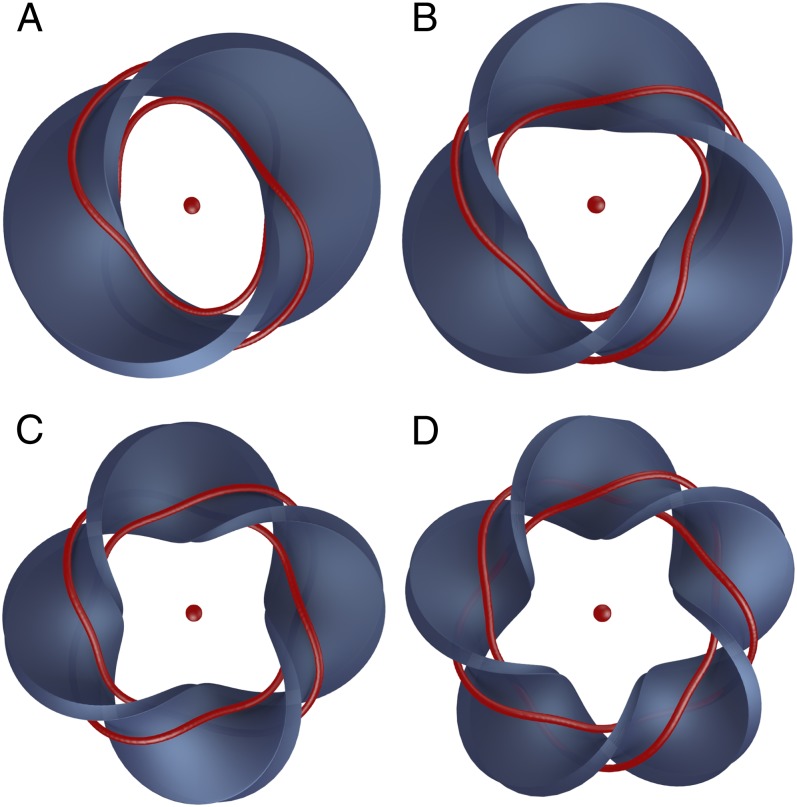
Can this structure, coming from the nature of the embedding, be exploited to controllably produce knotted and linked disclination loops in liquid crystals? Disclination lines that follow the surface of such a multiply twisted Möbius strip will have the same shape and properties as the colloid boundary, yielding precisely constructed knots and links. Here we show that such configurations can be stabilized in chiral nematics; examples for doubly-, triply-, quadruply-, and quintuply twisted strips are shown in Fig. 3. They produce the 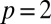Hopf link, the 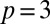trefoil knot, the 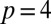Solomon’s knot, and the 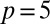cinquefoil knot, respectively. All these knots and links obey the topological requirements set out in the previous section; the strips with an even number of twists are topologically trivial and the strip is entangled by an even number of disclinations, those with an odd number of twists are nonorientable and so enclose an odd number of disclinations.

Fig. 3.

Knotted and linked disclinations in chiral nematics stabilized by the presence of twisted surfaces with homeotropic boundary conditions on the flat faces, and planar on the thin edges. They are torus knots and links of the form 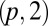. Shown are (A) 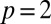Hopf link, (B) 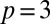trefoil knot, (C) 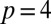Solomon’s knot, and (D) 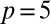cinquefoil knot. The defects in the center are hedgehogs, existing in pairs above and below the strip.

The stabilization of these knotted structures is not just a question of topology; energetics also comes into play. In this regard, the chirality (inverse pitch) of the system has an important role in the stability of these configurations. Indeed it is generally true that chiral systems allow for more exotic structures (4, 37). In the achiral nematic system, the knotted defects are unstable and the liquid crystal assumes a ground-state configuration consisting of p small disclination loops entangling the strip along the contours where , as predicted by [1]. A similar configuration, with slightly twisted loops (Fig. 4), is also the ground state in cholesterics––the knots are metastable––although the difference in energies is small (of order 1–2%) and decreases both with increasing chirality and knot complexity p. The behavior with increasing p can be understood in terms of the total length of disclination line, which scales as p for the isolated loops and as 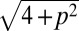for the knots. If the chirality is increased such that the pitch becomes smaller than the width of the colloid, then the disclinations develop twists analogous to those around spherical colloids (37, 48).

Fig. 4.

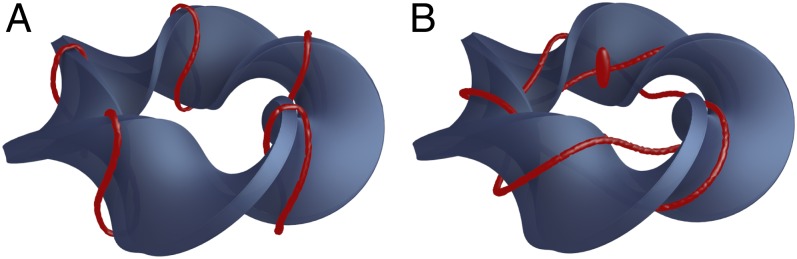
Comparison of configurations for a quintuply twisted strip. (A) Ground-state configuration consisting of five small disclinations loops at the locations predicted by [1]. They have a slightly twisted profile, caused by both the twisting of the strip and the chiral nature of the system. (B) A 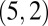torus knot entangling the strip, with two hyperbolic hedgehogs nucleated above and below. The energy difference between these configurations is ∼1.2%.

Like cholesterics, torus knots have a handedness––the 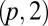and 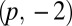knots are mirror pairs––and it is not surprising to find that the relative handedness influences the stability of the textures. The handedness of the knot is set by the shape of the colloid, and if this matches that of the cholesteric then knotted textures are stable, otherwise the system tries to expel the reverse twist in the configuration, resulting in an unstable knot.

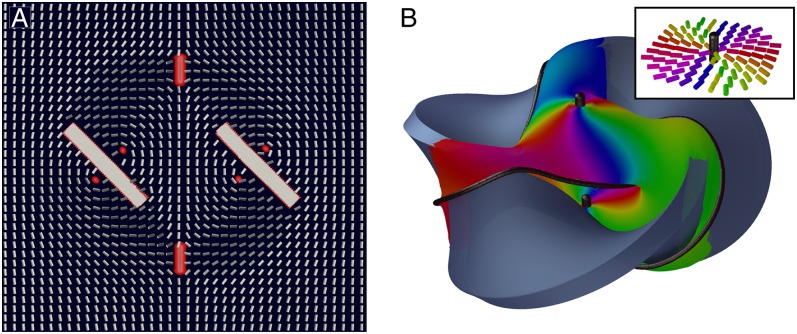
The disclination lines themselves represent just a small portion of the entire system. Their knottedness imprints a complex orientational order on everything that is not the knot. Fig. 5A shows a slice through the director field of a quintuply twisted Möbius strip in a cell with fixed normal boundary conditions. To match the boundary conditions of the cell, the knotted disclination is accompanied by two hyperbolic hedgehogs, expanded into small loops, above and below the strip. The disclination–colloid pair has a constant profile that simply rotates uniformly as one moves around the strip; qualitatively, this structure does not depend on p, the number of half-twists. The cross-section through the colloid has a profile reminiscent of a double-twist cylinder (50), split apart by the colloid into two separate 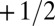twist disclinations.

Fig. 5.

Field structure. (A) Director field profile of a 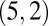torus knot and the two accompanying hyperbolic hedgehogs, opened up into small rings, above and below the strip, with disclinations bound to the colloid’s surface. Local disclination–colloid profile is largely constant up to a rotation as one moves around the strip. Although this profile is for a 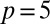configuration, qualitatively the director field does not change as one varies p. The far-field director is fixed to be vertical on the boundary of the cell. (B) Pontryagin–Thom surface (13) for the trefoil knot–colloid pair. The surface is constructed by considering all points where the director field is perpendicular to the far field. The surface is then colored with the remaining 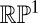degree of freedom (Inset). Defects, disclination line, and two accompanying hedgehogs are shown in black. The color winding around the hedgehogs establishes them as unit charge defects. The surface can be patched by removing the hedgehogs, and allowing the surface to pass through the colloid. One then obtains a Seifert surface for the knot, composed of two disks (top and bottom) connected by three (generally p) twisted bands. It is readily verified that this surface has genus 1 [generally 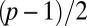, for p odd], the genus of the trefoil knot. Although there is also a color winding around the disclination, this is a fourfold winding, giving the disclination even (equivalent to zero) hedgehog charge, as required.

These configurations bear a striking similarity to the recently discovered “toron” textures (4). Torons come in several flavors, but the ones that concern us have two hyperbolic defects above and below a double-twist torus; that is, a double-twist cylinder, the building block of blue phases (50), bent around such that it forms a torus. Like the knots of Fig. 3, these textures are stabilized in thin cells of chiral nematics, with uniform alignment at large distances. More than a superficial similarity, the knotted field configurations we present here can be thought of as the result of expanding the central part of a toron locally into two 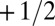twisted defects, which then rotate to form knots. The whole configuration is then stabilized by the colloid; indeed, if the colloid is artificially removed from the simulation after equilibration, the configuration collapses into a toron. This connection may provide a potential route for the production of these textures using Laguerre–Gaussian polarizing beams.

A more quantitative investigation of the texture can be made through use of the Pontryagin–Thom (PT) construction (13), allowing us to examine the full topology of the field structure and even perform rudimentary “experimental knot theory;” we can use the texture around the knot to compute the knot genus, a classical knot invariant (51). The PT construction involves drawing the surfaces on which the director field is perpendicular to a given direction: such a surface is shown in Fig. 5B. Surfaces constructed this way must end either on topological defects or, as in our case, colloids. For a knotted disclination, this PT construction then yields a Seifert surface for the knot, and it is a classic result that the minimal genus over all possible Seifert surfaces is a knot invariant for the given knot (52). To obtain a proper Seifert surface, the PT surface must be continued through the colloid and the points corresponding to the hedgehogs filled in. (Alternatively, because the hedgehogs are actually small loops in the simulations, an equivalent procedure is to take those loops as additional boundaries of a Seifert surface for the link consisting of the torus knot and two unlinked unknots. The genus of this Seifert surface is the same as that of the other one.) Since our disclinations are torus knots, they have genus 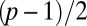for p odd and 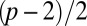for p even (52). Whereas, in principle, the genus of the PT surfaces is only bounded from below by this number, in the simulations presented here the limit is always reached, and we may read off the correct genus.

In conclusion, we have demonstrated the design and construction of elegant knotted and linked disclinations in liquid crystals, exploiting natural embeddings of twisted strips and a complete classification of the topological implications of homeotropic colloids. These knotted disclinations impose a complex structure on the director field, allowing knot invariants to be computed from the texture and facilitating the full introduction of knot theory into experimental soft matter systems. The configurations themselves are intimately related to the recently discovered toron textures, suggesting a route for experimental realization. Future work will further explore the value of knot theory in understanding the subtleties of knotted fields and their potential for novel devices.

Materials and Methods

To simulate the twisted strip colloids we use the standard Landau–de Gennes Q-tensor formalism. The liquid crystal order parameter is taken to be a traceless, symmetric tensor field 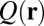. The free energy of the system F is then given as

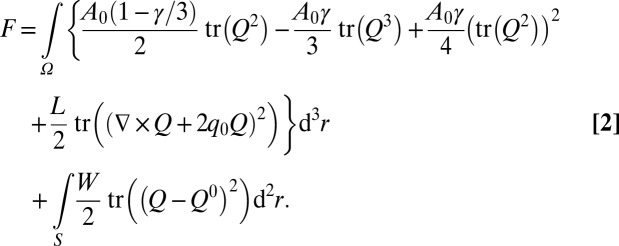The domain 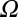is the volume of the liquid crystal, and S is the surface of the colloid. The constant 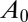defines the bulk energy scale of the material and γ represents an effective temperature. L, the elastic constant, controls elastic distortions in the director field. 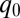is the chirality of the liquid crystal and is equal to 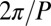, where P is the cholesteric pitch. 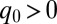denotes a right-handed material and the pitch was set to be of the order of the colloid diameter, although the configurations were found to be stable at higher chiralities. Finally, W controls the strength of the anchoring on the colloid surface, with the preferred orientation given by 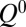. The free energy is minimized by evolving the Q tensor according to Landau–Ginzburg relaxational dynamics. These equations are then solved using finite-difference methods on a cubic mesh of size 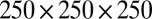or 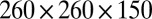grid points. Simulation parameters 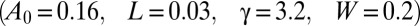were chosen to match typical values for a cholesteric liquid crystal with pitch comparable to the colloid radius (varied between 1 and 2 times this) and strong surface anchoring.