Abstract
Recent single-molecule experiments have observed that formation of a plectonemically super-coiled region in a stretched, twisted DNA proceeds via abrupt formation of a small plectonemic “bubble”. A detailed mesoscopic model is presented for the formation of plectonemic domains, including their positional entropy, and the influence of small chiral loops or “curls” along the extended DNA. Curls begin to appear just before plectoneme formation, and are more numerous at low salt concentrations (< 20 mM univalent ions) and at low forces (< 0.5 pN). However, plectonemic domains quickly become far more stable slightly beyond the transition to supercoiling at moderate forces and physiological salt conditions. At the supercoiling transition, for shorter DNAs (2 kb) only one supercoiled domain appears, but for longer DNAs at lower forces (< 0.5 pN) positional entropy favors formation of more than one plectonemic domain; a similar effect occurs for low salt. Although they are not the prevalent mode of supercoiling, curls are a natural transition state for binding of DNA-loop-trapping enzymes; we show how addition of loop-trapping enzymes can modify the supercoiling transition. The behavior of DNA torque is also discussed, including the effect of the measurement apparatus torque stiffness, which can play a role in determining how large the torque “overshoot” is at the buckling transition.
I. INTRODUCTION
When a DNA double helix is subjected to sufficient torsional stress, it responds by “super-coiling” to form a self-wrapped “plectonemic” structure. This response can be understood in terms of minimization of free energy, and is driven largely by the transfer of the change in linking number from twist (torsional distortion) of DNA, to “writhe”, which requires only mild bending distortion of the double helix [1, 2]. Supercoiling is biologically important since torsionally distorted DNA is at least transiently present in all cells as a result of transcription, replication and other processive enzyme activities. In bacteria, DNA is maintained in a state of quite high torsional stress, with supercoiling known to play an important role in chromosome organization, [3, 4], as well as in processes where DNA strand separation is important, such as initiation of gene transcription [5].
Single-DNA micromanipulation experiments have been able to sensitively probe DNA supercoiling under conditions where a single DNA is stretched by forces in the piconewton (pN) range [6–10]. In this situation, for zero torsional stress, the DNA molecule is extended by the force, but as torsional stress is increased (by increase of DNA linking number corresponding to the number of rotations of the end of the molecule), the double helix first responds by developing chiral fluctuations along its length [11] and then by undergoing “buckling” to form plectonemic interwound supercoils. This can be treated as a problem of phase coexistence, where extended and plectonemic regions of DNA behave as coexisting “phases” [2, 12].
At the onset of formation of plectonemic supercoils, a “buckling” transition has been observed [8, 10], where the extension of the molecule is observed to switch abruptly between an extended state, and a state with a small number of supercoils. The jumps are observed to be between 50 and 100 nm in size, becoming smaller as force is increased. The discontinuous nature of this transition has been attributed to the necessity to form a loop at the end of each plectonemic domain, which introduces a force-dependent free energy barrier to plectoneme formation [10, 13, 14].
This paper is concerned with two main issues. The first is development of a model based on established mesoscopic descriptions of DNA bending and twisting that describes the buckling transition and formation of plectonemic supercoils in finite-length molecules, including electrostatic effects. The second question concerns the number of plectonemic domains that are likely to form as linking number is increased past the initial buckling transition, for DNA lengths typically studied experimentally. Given that a single twisted DNA molecule is a one-dimensional system (although the linking number topological invariant introduces long-ranged interactions, those interactions contribute only
 (L) contributions to the free energy) one expects positional entropy to drive formation of multiple plectonemic domains for sufficiently long molecules [1].
(L) contributions to the free energy) one expects positional entropy to drive formation of multiple plectonemic domains for sufficiently long molecules [1].
Below we describe a model that address these two questions, based on previously developed models of plectonemic supercoiling [1, 2, 15–17], but now including the free energy cost of the plectoneme end-loops and tails, and including plectoneme length and position fluctuations (Sec. II). We also consider small chiral loop, or “curl” excitations, which occur in elastic theories of supercoiling as minima distinct from plectonemic domains. Curls have been argued to be important in determining the extension of twisted DNA prior to the onset of plectonemic interwinding [18].
Sec. III presents results for the theory, with a focus on two lengths of DNA used rather widely in single-molecule twisting-stretching experiments. Short (2200 base-pairs, or 2.2 kb) DNA is considered where it is found that the number of plectonemic domains that can form is severely limited by the molecule length. A longer 10 kb case also considered, for which formation of multiple supercoiled domains is more likely.
Curl fluctuations are found to have energies competitive with plectonemic domains near the buckling transition. Curls become more probable at low forces, and for low-ionic-strength conditions where Coulomb repulsions suppress formation of tightly interwound DNA double helices (Sec. IV). However, we find that the supercoiling buckling transition is, over a broad range of forces and ionic conditions, dominated by formation of plectonemic domains. The effect of proteins that stabilize curl formation (i.e., loop-trapping proteins) is also examined (Sec. IV) where it is found that moderate binding free energies of such proteins stabilize curls, and delay plectoneme formation.
Experimental methods have now been developed to measure torques in twisted DNAs [8, 9, 19], and one of the outputs of the theory are predictions for torque versus linking number curves. Two questions concerning such experiments are discussed in Sec. V. First, the model of this paper, like other recent calculations [10] shows non-monotonic torque variation (“torque overshoots”) as linking number is increased through the buckling transition. We briefly discuss the distinction between the fixed linking number ensemble, where such overshoots can occur in thermal equilibrium, and the fixed-torque ensemble, where equilibrium non-monotonicities of the response of linking number to torque are forbidden. We also discuss the issue of how small the torsional spring constant for an experimental setup needs to be in order to affect observation of the torque overshoots expected in an experiment carried out at fixed linking number.
II. MODEL
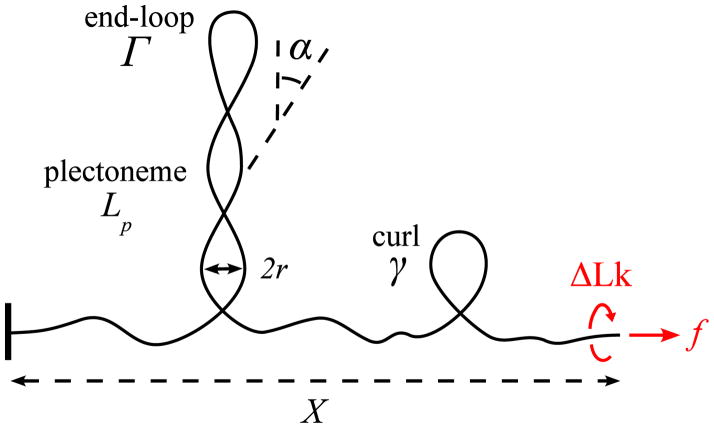
We construct a free energy model for a DNA molecule of length L subjected to applied force f and fixed linking number ΔLk by decomposing the molecule into three types of regions: stretched twisted DNA of length Ls, m domains of plectonemically helically interwound DNA of total molecule length Lp, and n small chiral curls (Fig. 1). The total molecule length is therefore partitioned as L = Ls + Lp + mΓ + nγ, where Γ is the molecule length involved in the junction “tail” plus the loop-shaped “end” of each plectonemic bubble, while γ is the molecule length involved in each chiral curl.
FIG. 1.
(Color online) Sketch of a conformation of an extended DNA with a plectonemic domain, and a chiral curl.
Linking number is similarly partitioned into contributions from the different regions
| (1) |
where ΔLkp includes linking number contributions from the m end loop and tail regions as described below.
The molecule free energy is expressed as a sum of contributions from these three components, plus an entropic mixing term that accounts for positioning of the plectonemic domains and curls randomly along the extended part of the molecule:
| (2) |
The first three terms of this free energy associated with stretched, plectonemic and curled DNA, respectively, each depend on DNA length and linking number associated with each region. All terms are functions of force f which is considered to be under experimental control; total molecule linking number is constrained to be ΔLk. The ensemble of fixed f and ΔLk is that encountered in “magnetic tweezer” experiments [9, 10] as well as in force-and angle-clamped optical trapping experiments [8].
The stretched DNA free energy Fs is proportional to only the DNA length that is not in the plectonemic (including tail-loop) and curl regions. DNA length adsorbed into the plectoneme tail-loop and curl regions is included through plectonemic and curl free energies Fp and Fc.
A. Curls
Curls, or small chiral loops, contribute a free energy cost associated with work done against applied force pulling length into them, plus bending energy; they are stabilized by the free energy gain associated with relaxation of twist energy through their writhe. The basic physics associated with formation of such a loop is illuminated by considering a circular loop model, where a DNA length ℓ is formed into a circle; the bending energy is 2π2kBTA/ℓ while the work done against the external force is fℓ, and where the DNA persistence length is A ≈ 50 nm. Optimizing the sum of these two energies gives where and the optimal .
More sophisticated calculations for a slightly more optimal teardrop-shaped loop give an energy and length which scale with A and f in the same way, but with slightly smaller value of k ≈ 8 (the bending energy prefactor is altered from 2π2 = 19.73 · · · to 15.32 · · · for the “teardrop” loop of elasticity theory, see e.g., [20]). The writhe associated with a curl is near unity, reflecting the single crossing shape.
Below we use and writhe wc as the energy of a single curl, with dimensionless force-dependent prefactors εc ≈ 8 and wc ≈ 1 determined from numerical elasticity analysis (see Appendix Sec. 2). Finally we need an estimate for the DNA contour length involved in a single curl. We take this to be (see Appendix Sec. 5). This is roughly twice the size of the DNA length between the crossings, large enough to avoid strong interaction between adjacent curls. The model is not strongly sensitive to the precise value of γ used, as it enters into the theory logarithmically in the curl positional entropy.
B. Plectonemically supercoiled DNA
The plectonemic domains consist of helically wrapped regions containing DNA length Lp, plus additional DNA length in the m end loops and tail attachments to the stretched portion of the molecule. The helical interwound regions are described by two geometrical parameters: their radius r, and the angle between the tangent to the molecule and the plectonemic axis, α (Fig. 1). These two parameters must be determined by free energy minimization [1, 2, 16, 17].
Linking number inside the plectonemic regions is partitioned into twist and writhe using the usual Fuller-White formula, ΔLkp = Wrp + ΔTwp. The total writhe of the plectonemic regions is
| (3) |
where the first term is the result for a long, regular plectonemic superhelix, and where the final term is the end correction obtained from numerical analysis of elastic equilibria of short plectonemic domains. The number wp is dependent on force and the geometry of the plectoneme, but is numerically close to 1, reflecting out-of-plane chiral bending and the crossings associated with the loop and tail regions. Computation of wp is described in Appendix Sec. 3.
Bending energy of the DNA in the regular interwound helix of the plectonemic region is kBTA(sin α)4/(2r2) per length. Electrostatic repulsion per length of DNA inside the helical region plus entropic confinement free energy is given by [2, 21]
| (4) |
where ℓB = 0.7 nm is the Bjerrum length, the Debye length ( for 150 mM univalent salt and T=296.5 Kelvin), K0 is the modified Bessel function of 0th order, and β = 1/(kBT). Effective charge ν and values of bending persistence length used in this paper are listed in Table I. Values of ν are obtained as in Ref. [17], following Refs. [22, 23]. The persistence length values represent a summary of the gradual reduction in A with increasing salt reported in a number of single-DNA micromechanical studies [8, 9, 24, 25].
TABLE I.
Persistence length and electrostatic parameters used in computations for 1:1 salt concentrations between 10 and 500 mM.
| Salt concentration (mM) | Persistence length A (nm) | Effective charge ν (nm−1) |
|---|---|---|
|
| ||
| 10 | 53 | 2.8186 |
| 50 | 48 | 4.9842 |
| 150 | 45 | 8.8558 |
| 500 | 43 | 23.669 |
The loop and tail regions contribute a positive cost to the free energy, through work done against the external force, and through bending energy. This takes the form of a correction to the plectoneme free energy of where the force-dependent dimensionless factor εp is computed from numerical analysis of elastic equilibria of short plectonemic regions (see Appendix Sec. 3).
We also need an estimate of the size of the end-loop and tail regions of the plectoneme regions. As for the curls, the plectoneme end/tail structure has a length that scales . We use , the same form used for the chiral loops. As for the curls, the precise value for Γ does not strongly influence the results of the model, but a rough estimate is necessary for computing the positional entropy of the plectonemic domains.
Adding together these contributions gives a plectonemic DNA free energy, including end-loop and tail contributions, of
| (5) |
where Wrp is given by (3). For a given force, plectoneme length Lp, and plectoneme linking number ΔLkp, the radius r and plectoneme angle α are determined by minimization of Fp. Here we do not need to include an additional hard-core interaction term as all the plectoneme radii are larger than the hard-core size of the double helix (2 nm), but this can easily be added.
C. Stretched twisted DNA
Finally, the extended twisted DNA is described by a free energy of the form
| (6) |
where Cs = C [1 − (C/4A)/(βAf)1/2] is the effective twist persistence length (the twist modulus divided by kBT), including the effect of softening of the bare twist rigidity C by chiral fluctuations [11].
The function g(f) is the free energy per length of untwisted stretched DNA, and is well approximated in the force regime of interest here by the free energy of a semiflexible polymer, which has the form g = f − (kBTf/A)1/2 + · · · as an expansion in inverse powers of force. We will use the first two terms of this expansion which are sufficient for describing DNA over the force range of 0.2 to 10 pN relevant to this paper and to most experiments (more precise polymer elasticity free energy forms are easily incorporated). The length associated with the extended portion of the DNA is the total length L, less the portion Lp associated with the helical part of the plectonemic regions, as the contribution to the free energy for the additional extension losses associated with the end-loop and junction portions of the plectonemes, and the curls, have already been taken into account in Fc and Fp.
D. Positional “mixing” entropy of curls and loops
To count the number of positional arrangements of n curls and m plectoneme domains, we may consider each domain to be a hard particle of size γ, located somewhere along the extended portion of the DNA. Since DNA length Lp is “lost” to the cylindrically interwound parts of the plectoneme domains, we can consider the free length available to place the plectoneme end-loops and curls to be L − Lp. Each loop and curl requires a DNA length of .
The n + m “defect” regions can be regarded as particles of length γ, able to slide around in a one-dimensional box of length L − Lp. The Tonks one-dimensional hard core gas partition function can be used to estimate the number of distinct configurations associated with the sliding of a given sequence of loop and plectoneme regions as [{(L − Lp − (n + m)γ)/D}n+m]/[(n + m)!] where D is a length defining distinguishable sliding states. Taking into account all reorderings of the two types of domains multiplies this by a factor of (n + m)!/(n!m!). Finally, if there is at least one plectonemic domain (m ≥ 1), there is an additional factor accounting for all partitions of the length Lp between the m plectonemic domains (again using the length D to define distiguishable states), of (Lp/D)m−1/(m − 1)!.
The net positional mixing entropy is given by the logarithm of the product of these terms:
| (7) |
We take the distinguishable state length to be D = A1/4 (kBT/f)3/4, the transverse amplitude of fluctuation of the stretched semiflexible polymer that occurs over one bending correlation length [24]. This distance describes the precision to which the crossing point of the loop can be located, given thermal fluctuations, and is on the order of 5 nm in the ≈ pN force range of interest here. The precise value of D is not critical since it will appear only in logarithmic terms in the free energy.
E. Configuration free energy, linking number partition, and torque
Now we can write the complete free energy for the mixture of extended, plectonemic and curl regions (Eq. 2), combining the energy of n curls, Fc = nEc, with Eqs. 5, 6, and 7:
| (8) |
Using the constraint (1) to eliminate ΔLks from Fs, the balance of linking number between the curl and plectoneme regions follows via minimization of F with respect to undetermined linking numbers ΔLkp and ΔLkc:
| (9) |
This amounts to equating the torque τ in the three different regions
| (10) |
where the final term gives the explicit result for the torque. The free energy then becomes
| (11) |
Plugging in the torque (10) yields:
| (12) |
F. Partition function
We use Eq. (12) to compute the free energy F(n, m, Lp) of a state with n curls and m plectonemic regions of length Lp. Computation of Fp requires minimization of Eq. (5) to determine the plectonemic radius r and the pitch angle α. Then, we sum over all states to compute the total partition function
| (13) |
The first sum takes into account straight DNA with curl fluctuations along it; the second multiple sum accounts for variable numbers of plectonemic domains. The sum over Lp is carried out with a mesh size d = 1 nm, making it essentially an integral; the factor of D accounts for indistinguishability of plectoneme states that differ by less than D in length. All the sums are subject to the constraint that nγ + mΓ + Lp ≤ L, i.e., the molecule length involved in curls and plectonemes should not exceed the total length L.
The average extension, torque, number of curls, number of plectonemes, and DNA length per plectoneme are computed using:
| (14a) |
| (14b) |
| (14c) |
| (14d) |
| (14e) |
where the average extension of each state is
| (15) |
and where the average torque of each state τnmLP is given by (10).
G. Extension distribution
Experimentally, one can observe switching events between states of different extension, and one can analyze the histogram of extension fluctuations [8, 10], so computation of the distribution of extension is of interest. Extension fluctuations in each of the states (n, m, Lp) are small so we can simplify their computation by approximating them to be Gaussian. However, differences in extension between different states can be large, and will lead to bimodal distributions as observed experimentally [8, 10]. In addition to the mean extension (15), we need the fluctuation
| (16) |
Given this, extension fluctuations for each state may be approximated by Gaussian distributions
| (17) |
If desired, this Gaussian approximation can be systematically improved, but the well-defined extension of each state makes this unnecessary here.
The full extension distribution is simply computed from the extension distributions of the individual states. We will consider contributions to this distribution from extended DNA with no curls or plectonemes, DNA with curls but no plectonemes, and DNA with plectonemic regions:
| (18) |
The limits on the sums are the same as those in Eq. 13. The distribution of torque (which is also narrowly distributed in each state) can be computed in the same way.
III. BUCKLING TRANSITION AND FORMATION OF SUPERCOILING
We now move to results of the model. First, we show how the appearance (“buckling”) and then development of supercoiled domains proceeds for two lengths of DNA commonly studied in single-DNA experiments, “short” (≈ 2 kb) and “long” (≈ 10 kb). We use T = 296.5 K throughout for all computations.
A. Short DNA (2.2 kb)
We first consider the case of a relatively short 2.2 kb DNA molecule (total contour length ≈ 748 nm). similar to that studied by Wang et al. [8] (and with similar results, by Brutzer et al. [10]). In this case the molecule is short enough that the buckling transition is relatively abrupt, thanks to the limited range of conformational fluctuations possible for the short molecule.
1. Free energies for states with different n and m
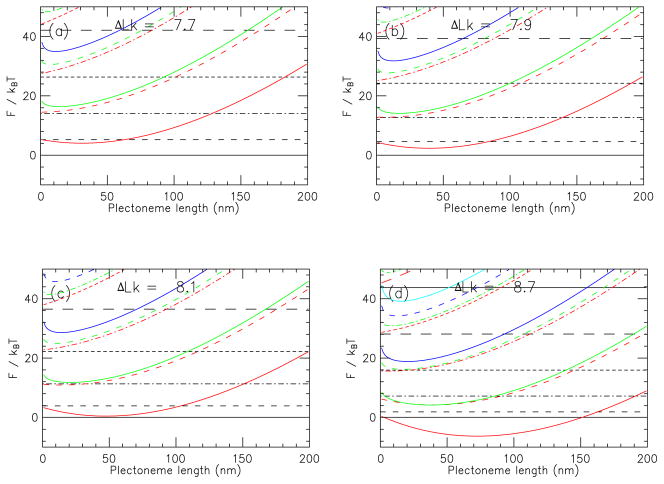
Free energies of the the (n, m) states were computed as per Eq. 12; for m ≠ 0, the free energies are also a function of the total length of interwound plectonemic region Lp. To give an idea of the free energies and free energy differences between different states, Fig. 2 shows free energies for a 2.2 kb molecule under 2 pN force, near the buckling transition in 150 mM NaCl buffer. The zero of free energy is the unbuckled state (no curls or plectonemes, i.e., (n, m) = (0, 0)), and is indicated by a horizontal solid line. The dashed horizontal lines indicate the low-lying curl-only states (denoted below by (n, m) = (n, 0)); near the buckling transition states with successively more curls are successively higher in free energy. As ΔLk is increased, the (1, 0) state is the first curl-only state to have a free energy that equals that of the (0, 0) state.
FIG. 2.
(Color online) Free energies of states with different (n, m) and Lp near buckling transition for 2.2 kb molecule in 150 mM Na+ buffer subject to 2 pN force. Free energies are measured relative to that of the n = 0, m = 0 state. Horizontal black lines indicate straight DNA with different numbers of chiral curls and no plectonemic domains (m = 0): solid, n = 0; dashed, n = 1; dot-dashed, n = 2; short dashed, n = 3; long dashed, n = 4. Curves indicate free energy as function of length of interwound plectonemic region for states with successively larger numbers of plectonemic regions: the line dash style indicates the number of curls in that state, following the same labeling as the straight-curl states. Plectonemic states with m = 1, 2, 3 and 4 for each value of n (each dash type) have free energies which increase with m for each value of plectoneme length (m = 1, 2, 3 and 4 are shown in red, green, blue and cyan, respectively). Parts (a), (b), (c) and (d) show the free energies for successively larger linking numbers passing through the buckling transition. The uppermost solid line in (d) shows the (5, 0) state.
However, the plectonemic states (parabolic colored curves) are also near to the unbuckled (0, 0) state; these states are shown in Fig. 2 as a function of Lp, the DNA length in the interwound region. The lowest-lying state in this case is the (0, 1) state (lowest solid red curve) with about 50 nm (150 bp) of interwound plectoneme, which is slightly lower in free energy than the (1, 0) state near buckling. The next highest plectoneme-containing state is (1, 1) (lowest dashed curve, red), followed closely by (0, 2) (2nd lowest solid curve, green). Plectoneme-containing states with successively more plectonemic end-loops are found at higher free energies; the gaps between successive states correspond roughly to the energy associated with the bending-force loop energy. For example, for Lp = 100 nm, we find β(F(n = 1, m = 0) − F(n = 0, m = 0)) = 5.240, and β(F(n = 0, m = 1) − F(n = 0, m = 0)) = 9.304.
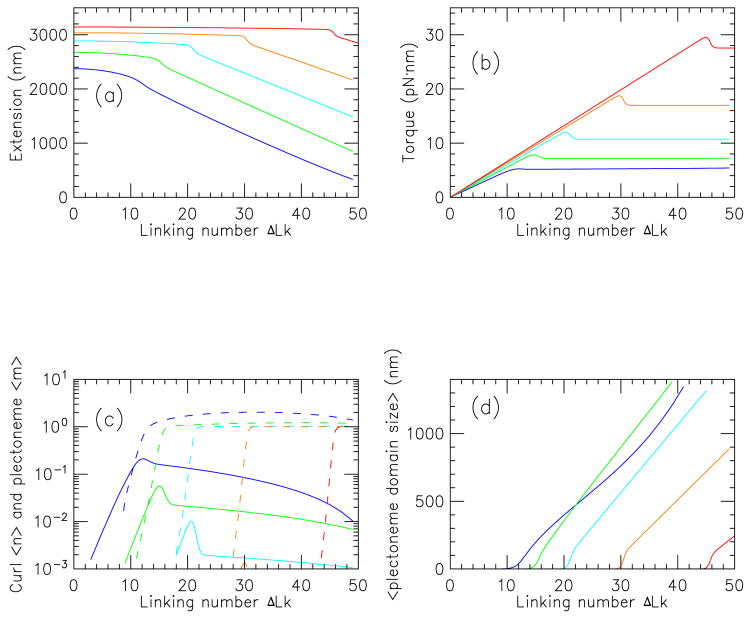
2. Average extension, torque, and numbers of curls and plectonemes
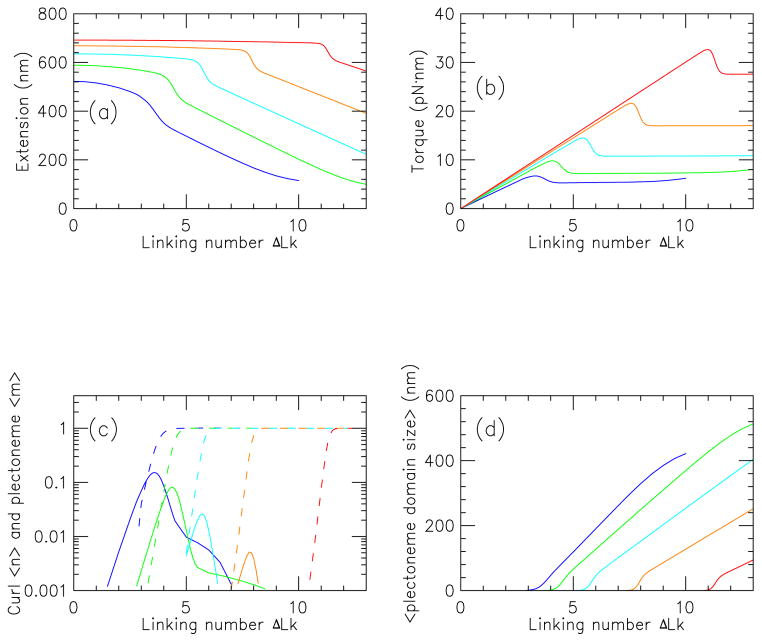
Average extension and torque are computed by summing over all states according to Eqs. (14). Results for extension and torque as a function of ΔLk for f = 0.25 (blue), 0.5 (green), 1 (cyan), 2 (orange) and 4 pN (red) for a 2.2 kb molecule in 150 mM NaCl buffer are shown in Fig. 3 (a) and (b). Increasing forces correspond to higher extensions and torques. There are three regimes apparent. First, for low linking number, the extension drops slowly, and quadratically, while the torque increases nearly linearly with linking number; in this regime the (0, 0) state dominates, and twist increases nearly linearly with ΔLk.
FIG. 3.
(Color online) Properties of stretched twisted DNA as a function of linking number, for a 2.2 kb molecule in 150 mM Na+ buffer, for forces of 0.25 (blue), 0.5 (green), 1 (cyan) 2 (orange) and 4 pN (red).
(a) Extension versus linking number (curves show results for successively higher forces from bottom to top).
(b) Torque versus linking number (curves show results for successively higher forces from bottom to top).
(c) Average number of plectonemic (〈m〉, dashed) and curl ( 〈n〉, solid) regions (solid curves show 〈n〉 values for successively higher forces from left to right for 0.25 to 2 pN, with the 4 pN results too small to appear on this plot; dashed curves show 〈m〉 values for successively higher forces from left to right).
(d) Mean plectoneme domain size (〈Lp/m〉) for states containing interwound plectonemic regions (curves show results for successively higher forces from left to right).
Following the first regime, a rapid decrease of extension occurs. This corresponds to the “buckling transition”, where in this case, the (1, 0) and (0, 1) states become probable. The creation of the plectonemic domain causes the rapid drop in extension. In the torque curves, an “overshoot” is observed, corresponding to the free energy barrier associated with creating the end-loop of the plectonemic state. The torque overshoot ranges from about 2 pN·nm (≈ 0.5kBT) for 0.25 pN, to about 5 pN·nm (≈ 1.25kBT) for 4 pN. The overshoots are rounded by fluctuations.
Finally, following buckling, the extension drops nearly linearly with linking number, as more turns are put into the plectoneme; in this regime the torque is nearly constant. For larger forces, the buckling transition occurs at successively higher values of linking number. Notably, it is somewhat difficult to define exactly where the buckling transition occurs from examination of extension or torque curves. One can see that as force is increased, there is a gradual decrease in the extension change associated with buckling, and a gradual increase in the amount of torque overshoot, in accord with experiment.
Fig. 3(c) shows the average values of curl number n (solid lines) and plectoneme domain number m (dashed lines) as a function of ΔLk, corresponding to the extension and torque curves of (a) and (b). In the first regime, both 〈n〉 and 〈m〉 are zero, and as the buckling transition is approached, they both come up. For f = 0.25 pN, the curl number goes through a maximum of about 〈n〉 ≈ 0.1 near the buckling transition, and then the plectoneme number rises to 〈m〉 ≈ 1. A similar pattern is seen for higher forces, but with a lower peak value of 〈n〉. Thus, for the 2.2 kb molecule in 150 mM NaCl, the buckling transition is dominated by the (0, 0) and (1, 0) states.
Fig. 3(d) shows the average plectonemic interwound region size (Lp/m averaged over states with m ≠ 0) for the four different forces studied in (a)–(c). After the buckling transition, the plectonemic regions gradually increase in size as linking number is added; a roughly linear increase of domain size with linking number occurs.
3. Extension distribution near buckling point
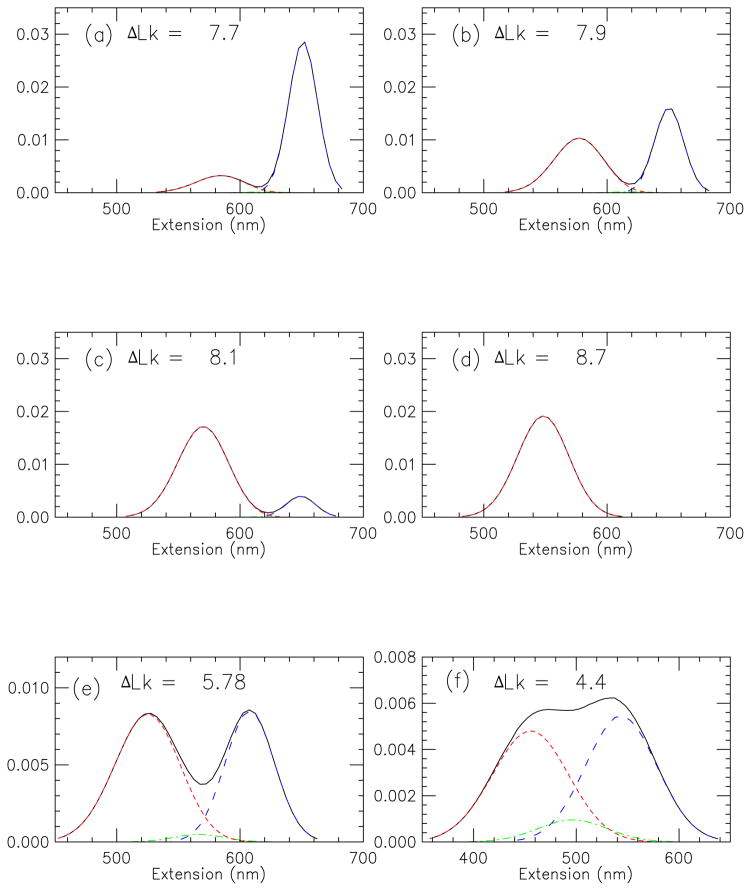
Extension distributions were computed according to Eq. 18; these are shown in Fig. 4 for a 2.2 kb DNA in 150 mM salt, under 2 pN force, for the ΔLk sequence of Fig. 2(a)–(d). Just below buckling (Fig. 4(a)) the bulk of the weight of P (X) (solid line) is made up by the (0, 0) extended state contribution Pext(X) (long dashed curve, blue) peaked at about 650 nm. In Fig. 4(a), states containing plectonemes (Psc(X), short dashed curve, red) are just starting to generate a 2nd peak in the extension distribution centered at around 580 nm. The curl-only contribution Pcurl(X) (dot-dashed curve, green) generates only a small contribution to P (X) peaked at about 620 nm, not easily visible on this graph.
FIG. 4.
(previous page) (Color online) (a)–(d) Extension distribution near buckling transition for 2.2 kb DNA, 150 mM Na+ buffer, corresponding to curves shown in Fig. 2. (f = 2 pN, ΔLk as indicated in panels). Contributions from extended DNA without plectonemic or curl domains (blue, long dashed, peak to right), states with plectonemically supercoiled DNA (red short dashed, peak to left), and states with chiral curls and no plectonemes (green dot-dashed, low peak in middle) and their sum (black solid) are shown. As the buckling transition is approached by gradually increasing linking number, the extension distribution changes from being dominated by the extended state to being dominated by plectonemes; a double-peak distribution is obtained at the buckling point. Near the buckling point only a small number of chiral curls appear.
(e)–(f) Extension distribution at buckling transition for 2.2 kb DNA, 150 mM Na+ buffer, ΔLk as indicated in panels, for (e) f = 1 pN, and (f) f = 0.5 pN. For these lower forces the extension histogram loses its bimodal shape, and the contribution from curl fluctuations becomes larger (dot-dashed line, green)
In Fig. 4(b), the plectoneme (short dashed, red) contribution has grown to be roughly the same contribution to the extension distribution as the extended state (long dashed, blue), yielding a bimodal P (X) (solid line). For slightly larger ΔLk (Fig. 4(c)) the plectoneme distribution (short dashed, red) becomes the dominant contribution to P (X). Thus, for the 2.2 kb short DNA, the extension distribution is dominated by formation of a single plectonemic domain. As ΔLk is increased further, the peak of P (X) moves to progressively lower extensions as more plectonemic state is generated. It is worth nothing that the plectonemic distribution is appreciably broader than the extended-state distribution, due to fluctuations in plectoneme length.
In the 2 pN results for Fig. 4(a)–(d) there is a well-defined bimodal distribution near the buckling point, with only a low level of curls. Fig. 4 (e) and (f), which show extension distributions for the same conditions as for panels (a)–(d) show how the bimodal exclusion of curls starts to go away as force is decreased. Fig. 4(e) shows distributions for 1 pN, where the valley between the extended and plectonemic states is partially filled in by extension fluctuations; in addition the contribution of curls can now be seen (dot-dashed green curve). Fig. 4(f) shows distributions for 0.5 pN, for which the bimodal shape of the extension distribution is nearly eliminated, with an increased contribution from curl states.
B. Longer DNA (10 kb)
Many DNA twisting-pulling experiments are carried out on ≈ 10 kb molecules. This is an important length as it is the typical size of a moderately large circular plasmid from E. coli (small plasmids are closer to the ≈ 2 kb size discussed in Sec. III A), and is also about the size of the independent supercoiled domains of the E. coli chromosome [3].
Fig. 5(a)–(d) shows the average extension, torque, curl and plectoneme numbers, and plectonemic domain size for a 10 kb (L = 3400 nm) DNA subject to the same set of forces discussed for the 2.2 kb molecule in Sec. III A, f = 0.25 (blue, lowest extension and torque), 0.5 (green), 1 (cyan), 2 (orange) and 4 pN (red, highest extension and torque).
FIG. 5.
(Color online) Properties of stretched twisted DNA as a function of linking number, for a 10 kb molecule in 150 mM Na+ buffer, for forces of 0.25 (blue), 0.5 (green), 1 (cyan), 2 (orange) and 4 pN (red).
(a) Extension versus linking number (curves show successively higher forces from left to right).
(b) Torque versus linking number (curves show successively higher forces from bottom to top).
(c) Average numbers of plectonemic regions (〈m〉, dashed; curves show successively higher forces, from left to right) and curls (〈n〉, solid; curves show successively higher forces from left to right).
(d) Mean plectoneme domain size (〈Lp/m〉) for states containing interwound plectonemic regions (curves with successively higher forces have starting points at zero domain size that are located at successively larger linking number values).
Fig. 5(a) shows the extension for the 10 kb case, and in comparison to the extension for the 2.2 kb case (Fig. 3(a)), it is immediately apparent that the larger range of conformational fluctuations plus the overall larger range of extension change tend to wash out the extension “jump” associated with the buckling transition. Furthermore, at low forces (f = 0.25 pN, lowest curve), the overall curve tends towards a bell-like shape similar to that observed experimentally.
The torques (Fig. 5(b)) show a corresponding smoothing of the overshoot behavior seen in the 2.2 kb case. For 10 kb, no overshoot is observed at all for 0.25 pN, and the 0.5 pN overshoot is so small as to likely be unobservable in current experiments.
Average plectoneme and curl numbers are shown in Fig. 5(c). Again, at forces of 0.5 pN and up, the transition is essentially one from extended DNA to a single plectonemic domain. At larger forces, there are even fewer curls found than for shorter molecules (for 2 and 4 pN 〈n〉 ≲ 10−3 in Fig. 5(c), compare with Fig. 3(c)), a phenomenon which is due to suppression of formation of plectonemes in the short 2.2 kb case. However, for the 10 kb case at 0.25 pN force, there is a background of curl fluctuations (about 10% of the time a curl is present) near the buckling transition, and curls continue to be found well into the plectonemic regime. Also, more than one plectoneme appears after buckling for 0.25 pN, with a peak of about 2 plectonemes present at ΔLk ≈ 30. One can expect that for longer molecules and lower forces one will observe larger numbers of plectonemic domains.
The size of plectonemic domains is shown in Fig. 5(d), where it can be seen that for the larger forces (curves leaving x-axis at right), the plectonemic regions appear at a well-defined value of ΔLk, and then increase in size roughly linearly with further increase in ΔLk. The lowest force of 0.25 pN (leftmost curve, blue) shows nonlinear behavior.
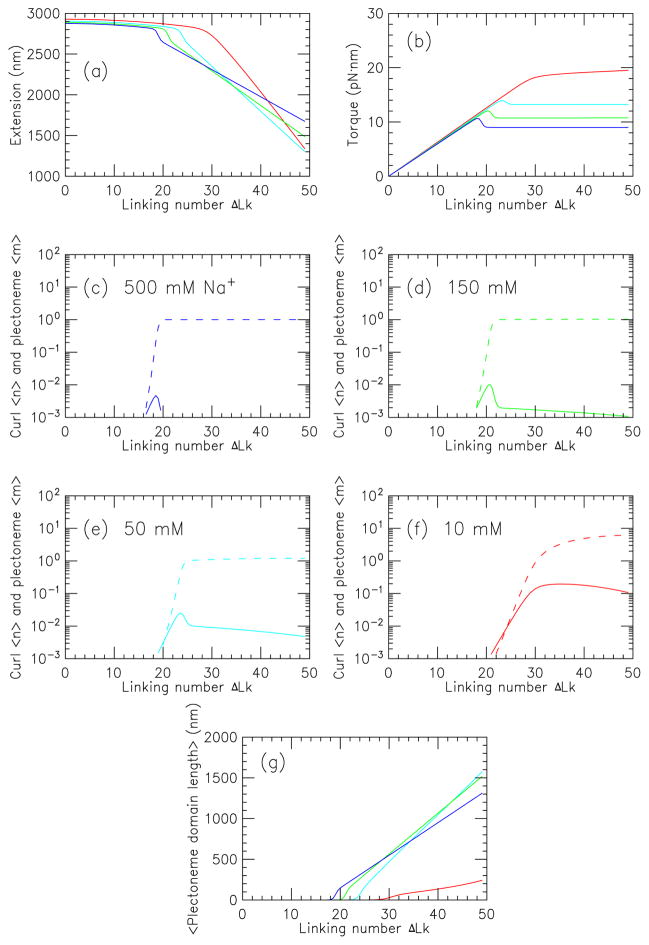
C. Effect of salt concentration
The previous section showed that the transition to supercoiling was controlled mainly by the crossing of free energies of the extended and plectonemic states for 150 mM univalent salt, which provides a level of electrostatic screening generally thought to be representative of that found in living cells. However, the free energies of the curl states are quite close to those of the plectoneme near buckling: a small free energy shift could make the curl states more dominant. This can in fact be accomplished by changing the univalent salt concentration. Decreased salt will destabilize the plectonemic state, since it involves closely interwound double helices; increased salt can be expected to stabilize plectonemic interwinding.
The mechanical propeties of the DNA double helix also depend on salt. Here the twist persistence length C is held fixed at 95 nm as there are no clear experimental data indicating its salt dependence. As salt concentration is increased, there is known to be a gradual decrease in bending persistence length (see Table I).
Fig. 6 illustrates salt effects for a 10 kb DNA under a fixed force of 1 pN. Fig. 6(a) shows extension as a function of linking number for a series of 1:1 salt concentrations, 500 mM (blue), 150 mM (green), 50 mM (cyan) and 10 mM (red). As salt is reduced from 500 mM to 50 mM, the buckling value of ΔLk increases, the transition rounds, and the slope of the post-buckling extension with ΔLk increases. For 10 mM, buckling is strongly delayed, there is no remnant of the buckling extension “jump”, and the post-buckling slope is largest.
FIG. 6.
(previous page) (Color online) Salt dependence of properties of a stretched twisted DNA, as a function of linking number, for a 10 kb molecule for Na+ concentrations of 10 mM (red), 50 mM (cyan), 150 mM (green) and 500 mM (blue), for a force of 1 pN.
(a) Extension versus linking number; curves at ΔLk = 20 run from top to bottom with increasing salt concentration.
(b) Torque versus linking number; curves show results for successively higher salt concentrations from top to bottom.
(c)–(f) Average number of plectonemic (dashed) and curl (solid) regions for (c) 500 mM, (d) 150 mM, (e) 50 mM, and (f) 10 mM.
(g) Mean plectoneme domain size (〈Lp/m〉) for states containing interwound plectonemic regions (curves with successively higher salt have starting points at zero domain size that are located at successively smaller linking number values).
Fig. 6(b) shows the corresponding results for the torque with increasing torques showing results for the same set of salt concentrations as in 6 (a). Again, for 500 mM, 150 mM and 50 mM, one sees a similar torque increase to buckling and then a plateau; the lower-salt cases have less torque overshoot. But, the 10 mM case is qualitatively different, with a gradual increase of the torque after buckling.
Fig. 6(c)–(f) show the evolution of curl number 〈n〉 (solid curves) and plectoneme number 〈m〉 (dashed curves) with ΔLk for 500 mM, 150 mM, 50 mM and 10 mM, respectively. For high salt ((c), 500 mM) buckling occurs as a rather sharp transition to the m = 1 state, with only a low curl density. For 150 mM salt (roughly physiological salt concentration), (d), the buckling transition is sharp, but with an increased amount of curl fluctuations; this trend continues to lower salt (panels (e) and (f)). In the low-salt 10 mM univalent salt case, the curl probability is highest (〈n〉 peaks at around 10%), and there is a proliferation of small plectonemic domains, with 10 small domains appearing for ΔLk ≈ 40.
Panel (g) shows the average interwound length per plectoneme (〈Lp/m〉 averaged over states with m ≠ 0). The higher curves (500 mM blue, 150 mM green, 50 mM cyan) show a nearly linear increase of interwound domain size consistent with the 〈m〉 ≈ 1 associated with supercoiling in those cases (see panels (c)–(f)). In the low-salt (red, 10 mM) case, however, the plectoneme domains are much smaller, corresponding to the appearance of many plectonemic domains as ΔLk is increased (panel (f)). The origin of this effect is in the increased DNA-DNA electrostatic repulsion at low salt, which shifts the free energy balance in favor of formation of many small plectonemic domains. However, curls with their lower writhe are still higher in free energy than plectonemes.
D. Analytical formula for ΔLk at transition
It is useful to have an analytical determination of the critical linking number ΔLk = ΔLk★ at which supercoiling occurs, as a function of DNA length, salt concentration, and applied force. In order to analytically understand ΔLk★, we use several approximations: (i) we approximate the (n = 0, m = 1) mixing entropy Sm/kB ≃ ln[L/D] since Lp and γ are small compared to L; (ii) we set Cs = C and we use Cs since most of the molecule is in the extended phase; (iii) we approximate ΔLk* with , the link value for which the free energy of the extended twisted state βF(0, 0, 0) is equal to the free energy of the m = 1 plectonemic state βF(0, 1, Lp); and (iv) we only consider the minimum plectonemic state, for which ∂F(0, 1, Lp)/∂Lp = 0. This is appropriate for cases where the transition is mainly between (0, 0) and (0, 1) states, as is the case in Figs. 3 and 5.
We solve for and satisfying
| (19) |
where is given by (3) with and m = 1. The requirement that ∂F(0, 1, Lp)/∂Lp = 0 yields (using (3)):
| (20) |
Then using Lk = Tw + Wr to eliminate Wrp in favor of βτ = 2π(Cs/L) Tw, we obtain
| (21) |
| (22) |
The value of τ given by Eq. (10) depends on ΔLk. In order to have (21) explicit in ΔLk we consider the equilibrium value of the torque when Lp is large, τ = τ∞, an approximation of which is given by Eq.(17) of [17]. The linking number at the supercoiling transition mainly scales linearly with molecule length L, but there is a correction in which might be experimentally observable, and which gradually fades away for large molecule length L. For large L the term in the square brackets in (22) will eventually reach zero, and in this case (this continues to be the case when the interior of the square bracket is negative since we have the physical constraint Lp ≥ 0). In such cases βF(0, 0, 0) = βF(0, 1, Lp) for:
| (23) |
The same computations can be done to analyze competition between the one-curl and extended states, by solving for the value at which βF(1, 0, 0) becomes smaller than βF(0, 0, 0). Using the same approximations we arrive at
| (24) |
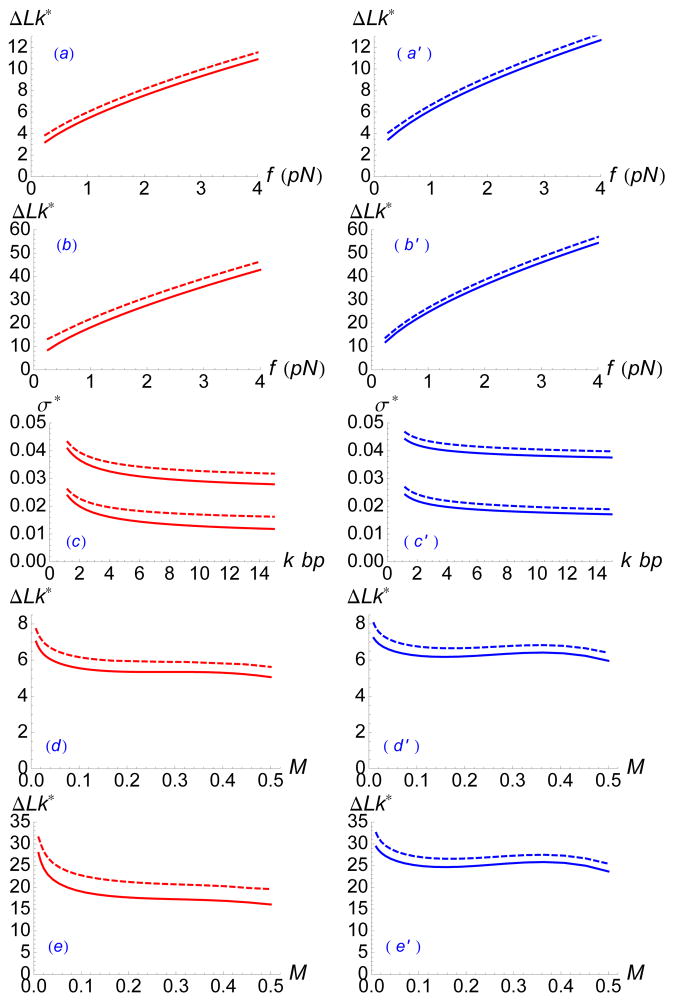
The variation of with DNA length, applied force, and salt concentration is shown in Fig. 7 (left column, red curves). In the same figure we compare (right column, blue curves). Solid curves show the approximate formulae for the single plectoneme and single curl transitions, while dashed curves give the exact numerical solutions to βF(0, 0, 0) = βF(0, 1, Lp) and βF (0, 0, 0) = βF(1, 0, 0) obtained by minimizing the complete free energy (12). The approximate formulae are close to the exact result in all cases, and slightly underestimate the critical linking number.
FIG. 7.
(previous page) (Color online) Dependence of one-plectoneme transition point (left column) and one-curl transition point (right column) with force, salt, and length. For each panel in left column, solid curves show approximate formula (22); in right column to (24). Dashed curves in left column are numerical solutions of βF(0, 0, 0) = βF(0, 1, Lp) obtained by minimizing the complete free energy (12); in right column corresponding solutions for βF(0, 0, 0) = βF(0, 1, Lp) are shown. The different panels show results for: (a) (a′) 2.2 kbp and 150 mM, as a function of force (pN); (b) (b′) 10 kbp and 150 mM, as a function of force (pN); (c) (c′) supercoiling density σ ≡ 10.5 ΔLk/(nbp) for 150 mM and 0.5 pN (lower curves), 2 pN (upper curves), as a function of DNA length (kbp); (d) (d′) 2.2 kbp and 1 pN, as a function of univalent salt concentration (M); (e) (e′) 10 kbp and 1 pN, as a function of univalent salt concentration (M).
IV. BINDING OF CURL-TRAPPING PROTEINS
Sec. III C showed that an increase of the free energy of plectoneme formation via reduced salt concentration can greatly enhance curl formation as the preferred mode of supercoiling. A second mechanism to achieve this is through the action of proteins which preferentially bind to the teardrop-shaped curl structure over the end-loop of a supercoil. Such discrimination could be accomplished by a protein that e.g., binds to the loop tail regions.
This effect can easily be added to the model of Sec. II by simply adding the free energy associated with summing over all occupations of the n curls by protein, including a binding free energy μ per protein bound (most simply this binding free energy is kBT ln(c/KD) where c is the solution protein concentration and KD is the equilibrium dissociation constant; more positive μ generates stronger binding). This supposes that the curl-binding proteins bind preferentially to one chirality (positive Wr). The curls provide distinguishable binding sites, so the term to be added to the total free energy (11) is]
| (25) |
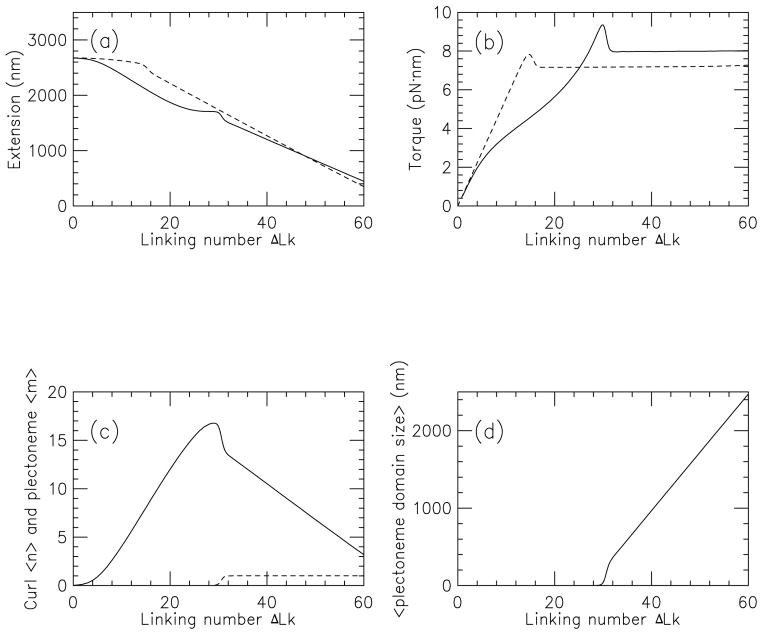
Results are shown in Fig. 8 for 150 mM salt, βμ = 10, and f = 1 pN (solid curves), and should be compared to the results for naked DNA for 1 pN and 150 mM salt (dashed curves, see also Fig. 5). When curl-binding proteins are present (solid curves), curls become favorable even for relatively low linking numbers, with the result is that the extension is reduced relative to naked DNA (Fig. 8(a)). The torque is dropped to lower levels than for naked DNA as linking number is increased (Fig. 8(b)). Although not apparent in the figure, the torque is driven to a slightly negative value at zero linking number by the positive-writhe-trapping proteins.
FIG. 8.
Behavior of supercoiled DNA in the presence of curl-binding proteins. Calculations are shown for f = 0.5 pN, 150 mM salt, and βμ = 10. The presence of the curl-binding proteins stabilizes the curls and drives formation of many curls at the buckling transition. Extension as a function of ΔLk is shown as the solid curve in (a); torque is shown as the solid curve in (b); dashed curves indicate results without curl-binding proteins from Fig. 5. Curl (〈n〉, solid) and plectoneme (〈m〉, dashed) numbers are shown in (c) for the curl-binding protein case; the corresponding interwound length per plectoneme (〈Lp/m〉) is shown in (d).
Fig. 8(c) shows the number of curls as a function of linking number, which increases steadily as linking number is increased. For large enough ΔLk (> 30 in this case), plectonemic domains become favorable, and the number of curls begins to decrease. For larger ΔLk, the torque reaches higher levels than for naked DNA. Notably, only one plectonemic domain forms in this case, so the length per plectoneme (Fig. 8(d)) is essentially the total length of interwound plectoneme.
It is straightforward to generalize this model to curls with both chiralities, which might be expected to be bound with different affinities by a curl-trapping protein complex. Furthermore, it is quite possible that a loop-binding protein might bind to both curls, and to plectoneme end-loops. To obtain a model where proteins bind with differing affinities to both plectoneme ends and curls, one could simply add a second copy of Eq. (25) with n replaced by m, and with a distinct value of binding free energy μsc. In this case, one would expect to observe a drop in the threshold for buckling, but with plectonemes competing with curls.
V. TORQUE OVERSHOOTS AND TORQUE MEASUREMENT
In Sec. III properties of molecules as a function of fixed force and ΔLk were presented. Experimentally, this corresponds to experiments where a constant force and fixed rotation angle of one end of the molecule are controlled, roughly the situation in magnetic tweezer experiments of the style developed by Strick, Allemand, Bensimon and Croquette [7]. For the short 2.2 kb molecules (and for 10 kb molecules at higher forces ≈ 3 pN) jump-like features are observed in extension as a function of ΔLk, corresponding to formation of the first plectonemic domain. The torque shows an “overshoot” feature at this point (Fig. 3 and 5). Overshoot features have been observed in analytical and simulation equilibrium torque calculations for DNA buckling by Brutzer et al. [10] and by Daniels et al. [13]. In experiments on short molecules this behavior is reasonably clear although quantifying the size of the torque jumps is challenging due to the high level of Brownian noise [8, 26].
A. Non-monotonic variation of torque with rotation in fixed-ΔLk ensemble
At first glance the torque overshoot is a bit surprising: one has a prejudice that torque should be a monotonically increasing function of rotation angle Θ = 2πΔLk for a mechanical system in equilibrium. But the torque curves of Fig. 3 and Fig. 5 are equilibrium curves, computed from a partition function based on a mechanical (free) energy that itself depends on rotation angle and force, Es(Θ, f), for some set of configurations indexed by s. Similar “backbending” behavior occurs in analogous magnetic systems, notably the Ising model with fixed magnetization [27].
The partition function at fixed angle (and force) is Z(Θ) = Σs exp[−βEs], and the free energy at fixed angle is F(Θ) = −kBT ln Z. The average torque is
| (26) |
Given that the mechanical torque for each state is τs = ∂Es/∂Θ, this amounts to 〈τ〉 = 〈βEs/∂Θ〉 = 〈τs〉. Note that this formulation of the problem is completely general, and includes the microscopic theory discussed in the previous Sections as a particular case.
We may then compute the change of 〈τ〉 with Θ (the slope of the torque versus angle curves) to obtain
| (27) |
Thus even if each state satisfies the stability requirement ∂τs/∂Θ > 0, it is still possible for ∂〈τ〉/∂Θ to be negative, if the torque fluctuations become sufficiently large. At a point where two states of different torques become equally probable, this can occur, and this is just what occurs at the buckling transition. Of course the fluctuations must be large enough to cancel off the most likely positive 〈∂τ/∂Θ〉, and this will depend on the external force and the molecule length.
B. Monotonic variation of Θ with torque in fixed-τ ensemble
In the alternate fixed-torque ensemble, where angle freely fluctuates, the partition function for fixed torque is Zτ = ∫dΘZ(Θ)eβτΘ. The average angle is
| (28) |
and the angle change with torque is
| (29) |
the expected angle fluctuation formula. So, in the fixed-torque ensemble, angle must be a monotonic function of torque. The two ensembles are inequivalent for finite-length molecules, but in the thermodynamic limit (long-molecule: L → ∞), one expects the two ensembles to yield converging results for ∂τ/∂(Θ/L). This can be seen by comparing Figs. 3(b) to 5(b); increasing L decreases the size of the torque overshoot at the transition.
C. Experimental torque measurements
In magnetic tweezer experiments, force is constant, and can be measured from fluctuations of the end position of the molecule. Actual measurements of torque using magnetic tweezers (or other methods) are more complex since there is no convenient way to apply absolutely constant torque; in practice one must use a calibrated angle-confining potential to measure torques [8, 19] (an alternate possibility is to use drag forces to infer torques from rotational motions [28]).
One way to angularly confine rotational fluctuations is with polarized laser tweezers and birefringent particles attached to the end of DNA molecules [8]. “Traditional” magnetic tweezers experiments [7] have such tight confinement of angular fluctuations that it is difficult to measure angular fluctuations. However, recent experiments have been able to design magnet arrangements where there is less strong confinement [19]. In any case, torques are measured by use of an angular potential with calibrated spring constant. The partition function for angular fluctuations in such an experiment is
| (30) |
Here Θ0 is the experimentalist-controlled angle (e.g., angle of rotation of a magnetic tweezer), and one measures the difference between rotation of the molecule (in practice, rotation of the bead attached to molecule) Θ and Θ0. Once the angular spring constant k is calibrated, the experimentally inferred torque is [19]
| (31) |
Recent experiments of Lipfert et al. measured torques using an angular spring constant of k ≈ 102 pN·nm/rad [19].
In the experimental torque-measuring ensemble, the mean angle is
| (32) |
which may be computed from the results of Sec. III. For sufficiently large k, one will see the “fixed-angle” torque as a function of Θ0. In the opposite k → 0 limit, the torque will become essentially constant over the range of angle fluctuation, and must become a monotonic function of linking number. For some intermediate value of k there will be partial suppression of the torque overshoots by the measurement apparatus.
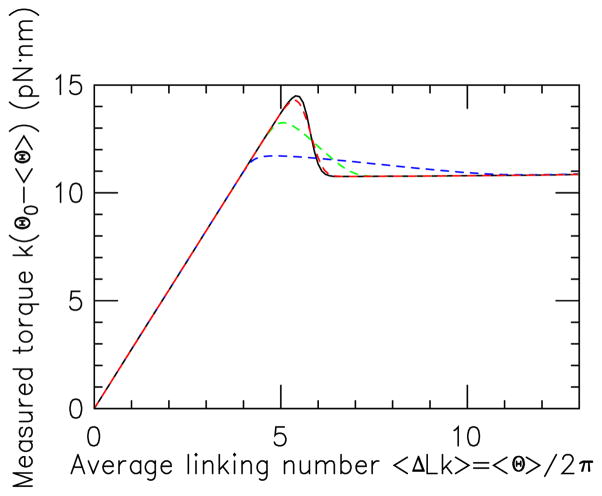
Fig. 9 shows a series of predictions for experimental torque measurement (values of k(Θ0 − 〈Θ〉) versus 〈Θ〉) for k = 1, 0.1 and 0.01 kBT/rad2 (successively lower-peak solid curves) for the 2.2 kb molecule in 150 mM salt and held at 1 pN force. Even for k = 1, the measured torque is nearly exactly coincident with the fixed-angle result (dashed curve).
FIG. 9.
(Color online) Measured torque for 2.2 kb DNA in 150 mM salt buffer under 1 pN force, for spring constants k = 1, 0.1 and 0.01 kBT/rad2 (dashed uppermost red, middle green and bottom blue curves, respectively). Torque overshoot is smoothed out as k is decreased, but small values of k are needed to completely eliminate it. The k = 1 curve is indistinguishable from the “true” torque (solid black, same as 1 pN curve in Fig. 3(b)).
For lower values of spring constant one starts to see some smearing of the overshoots, but one needs to reduce the measurement spring constant k to low values (k = 0.01kBT/rad2) to see near-complete erasure of the torque overshoots. This corresponds to the measurement device spring constant k becoming appreciably smaller than the torsional spring constant of the molecule itself (roughly kBTC/L ≈ 0.1kBT/(rad2) for the 2.2 kb molecules of Ref. [8] and Fig. 9). As k is reduced below this level, the torque becomes a nearly monotonic function of ΔLk as one approaches the constant-torque ensemble.
For the small values of k in Fig. 9, the measurement potential is so weak that Θ0 − 〈Θ〉 is much larger than 2π: such values of k are far below those that are in use experimentally in current torque-measurement experiments. In magnetic and optical angular potential experiments k will have to be at least ≈ 1, and in this range measurement of the torque overshoots should not be limited by the measurement spring constant.
VI. CONCLUSIONS
We have presented a theory of supercoiling of DNA under applied tension which is based on previously established properties of the double helix: bending and twisting elasticity and helix-helix electrostatic interaction. There are no fit parameters for our model for supercoiling of naked DNA. Our model goes beyond previous work [1, 2, 17, 21] in accounting for multiple and variable-length plectonemic domains, as well as small chiral curls, for finite-length molecules. We have discussed detailed results for extension and torque for the cases of ≈ 2 kb and ≈ 10 kb molecules in the fixed force and linking number ensemble appropriate to describe magnetic tweezer experiments [9, 10] or angle-constrained optical trap experiments [8]. We have also presented an analytical analysis of the supercoiling transition point, giving closed-form expressions for critical linking number at which single curls or plectonemes become state, as a function of force, molecule length and other physical quantities (Section III D).
A. Number of plectonemes and curls
Under most conditions relevant to experiment (2 to 10 kb molecules in physiological buffers with univalent salt in the 100 to 200 mM range, forces larger than 0.25 pN), we find that the buckling transition involves formation of a single plectonemic domain: the entropic gain of multiple domains does not fully cancel the energetic cost of additional plectoneme end loops. In the situations mentioned above we do not find a high level of chiral curls; near the buckling transition under most circumstances we find a mean curl number of less than one, again due to the fact that the increased entropy associated with curls does not counteract their energy cost. The plectonemic domains simply have too low a mechanical energy (through relaxation of twisting energy by their high level of writhe) and are further helped by the entropy of their length fluctuation (note the rather broad free energy dispersion of the plectonemic states near buckling in Fig. 2 which gives rise to the broader extension distribution of the plectoneme peak in Fig. 4). Curl fluctuations do occur near the buckling transition, and might be observable as ≈ 100 nm extension fluctuations in experiments with sufficiently fast time resolution.
The prediction of isolated plectonemic domains should be testable in single-molecule experiments which are able to observe the conformation of supercoiled molecules, e.g., by use of fluorescent dyes on the DNA: the plectonemic region should be observable along the stretched molecule as a bright region. Inhomogeneities along the molecule are likely to localize the plectonemic region(s) [10, 42], and to further reduce the number of plectonemic regions.
Our model also predicts that as force is reduced to low values (< 0.25 pN), as salt concentration is decreased (< 50 mM), or as molecule length is increased, multiple plectonemic domains and larger numbers of curls become favorable. Thes trends would also be straightforward to observe using fluorescence combined with micromanipulation.
The present theory does involve approximations, the improvement of which could change details of exactly at which forces and for what salt levels proliferation of curls and plectonemes will occur. For example, our model of the free energy cost of curls and plectoneme end-tails is based solely on bending energy, and fluctuation entropy may shift the free energy of those structures to somewhat lower levels: this will likely become important at low forces in the < 0.25 pN range. Since the free energies of curl and plectoneme states are rather close to one another (Fig. 2), shifts in curl and end-loop free energies of a few kBT may impact the predictions of the model (the effects of using proteins to shift this balance were discussed in Sec. IV). It is likely that both curl and end-loop structures would receive similar entropic corrections, lessening the effect of fluctuation entropy on curl-plectoneme competition, and the general trend of more curls appearing at low forces and low salt should continue to hold.
B. Extension distributions near the supercoiling transition
This paper presents the first microscopic theory of the distribution of extensions near the supercoiling transition (similar distributions could be computed for the torque as a function of angle). We have shown how the extension distribution evolves from a bimodal form at high force, to a broad, unimodal distribution at lower forces (see Fig. 4), which might be studied experimentally [8]. Our model also provides a microscopically-based prediction for the free energy barrier associated with the transition state between extended and supercoiled DNA [14]. Our distributions are equilibrium thermal distributions, and their accurate experimental measurement requires as little low-pass-filtering of extension signals as is practical.
C. Torque and overshoots
Our model provides microscopically-based calculations of the torque as one passes through the supercoiling transition. For relatively short molecules (2 kb, see Fig. 3(b)), the torque shows a quite pronounced “overshoot” behavior as a function of angle; similar overshoots have been observed in theoretical work of Brutzer et al. [10]. Thermodynamically, such overshoots are expected given the fact that one has an energy barrier between two “coexisting” extended and supercoiled states which should generate jumps in both extension and torque [13].
While the extension jumps are easily observed [8], there are not yet very precise measurements of torque overshoots or jumps [13, 26], due to the large amount of thermal noise inherent to torque measurements (note the large amount of fluctuation relative to signal in Fig. 2b. of Ref. [13]). However, it does appear that torque jumps observed experimentally are smaller than is theoretically expected (Fig. 3 and Ref. [10]). While the torque jumps could be smeared by the torsional potential used to do the measurements, current experiments appear to be using stiff enough torsional potentials that this should not be occurring (Sec. V). We cannot rule out an overestimate of the torque jumps in our model, possibly due to a systematic underestimate of the torque (i.e., free energy) of the plectonemic state, or perhaps due to our overestimating the bending energy cost at the plectoneme end, e.g., because of DNA kinking [43, 44].
D. DNA denaturation and other structural transitions
The present model does not include base-pair-separation effects, which play an important role for sufficiently large forces and linking numbers [2, 12, 29, 30]. In short, for positive supercoiling, DNA remains base-paired as long as torques stay below about 35 pN·nm, which for forces < 5 pN is not approached for linking numbers < 0.1 (see [12, 30] for predicted phase diagrams). However, for negative supercoiling, DNA is driven to strand separate by only about 10 pN·nm, which occurs for physiological supercoiling levels (σ = −0.05) at forces above about 0.5 pN [30]. The model of this paper, which assumes DNA to be in a well-defined base-paired B form, only applies within these torque and supercoiling limits. The effect of DNA denaturation could be added by adding additional states such as in Refs. [12, 30], with some increase in computational complexity.
The main effects will be similar to those described by “bulk-phase” models such as Refs. [12, 30], where for negative supercoiling, DNA denaturation will occur for forces beyond about 0.5 pN. The resulting extension vs. linking number slope will be greatly reduced relative to the positive supercoiling case, by the fact that each 10.5 bp that are denatured are able to absorb a whole unit of linking (and more if the denatured strands are tightly wound, see Refs. [29, 45]). Recently, the model of [12] has been used to provide a reasonable description of extension and torque at negative supercoiling during DNA denaturation [46], and the same general kind of model could be used for denatured states within the finite-phase-domain framework developed in this paper. A key ingredient is the inclusion of the effect that when denatured by torsional stress, DNA single strands appear to wrap into non-base-paired, or loosely paired helical structures that can be described reasonably well as semiflexible polymers [46].
E. Supercoiling transition at low forces
The presence of (not too large!) applied force simplifies many aspects of the present model. First, the description of extended DNA we have used [11] relies on the presence of high enough forces to make tangent vector fluctuations small. The practical limit for this is roughly 0.2 pN (recall that at zero linking number DNA reaches half-extension for about 0.08 pN force [24]. For lower forces curls play a major role at nonzero linking number [18]).
Second, in the model presented here, the sizes of the plectoneme end loops and the curls are assumed to be determined by a balance between bending energy and work done against applied force. This is appropriate for determining loop sizes for DNA under tensions that are large enough to extend the DNA between plectonemic regions. However, when force is below ≈ 0.2 pN, the loop sizes will be determined by balance of bending energy against the free energy of the supercoiled regions themselves [2]. A similar change in underlying physics determining loop size will come when the entire molecule is supercoiled, where force no longer plays a role in controlling plectoneme end loop size. To describe either case, a generalization of the model presented here would be required, where the size of loops would be determined by free energy minimization, and which would result in loops controlled by force for large forces, but loops controlled by their packing along the DNA for small or zero force. Including this effect would lessen the saturation of extension seen in Fig. 3a for ΔLk > 10.
A third effect that should be taken into account at low or zero force, and in the situation where molecules are entirely supercoiled, is the additional entropy of branching of the plectonemic regions. Given the relatively small number of plectonemic loops arising in the examples considered here, branching is not a crucial ingredient. However, for large plectonemic regions which are extensively supercoiled, roughly one branch point per 2 kb of DNA can be expected [2], and branching entropy should be taken into account. Development of a model applicable to zero force is important since this could be used to describe supercoiling of supercoiled circular DNA molecules or supercoiled domains of chromosomes as occur in vivo in bacteria.
Acknowledgments
Work at NU was supported by NSF Grants DMR-0715099 and MCB-1022117, and by NIH Grant 1U54CA143869-01 (NU-PS-OC).
Appendix
We carried out numerical calculations of equilibria of macroscopic elastic rods with self-contact, building on previously published material [15, 31–33]. The elastic rod of length L is uniform and has a circular cross-section of radius ρ. Furthermore it is inextensible, unshearable, and has bending rigidity K0 = AkBT, and twist rigidity K3 = CkBT. In previous papers on open supercoiled DNA [12, 16, 17, 34] the configuration of the molecule was described as a composite of two phases: (i) straight twisted tails, and (ii) a purely helical plectonemic region. In this setup end-loop, matching regions, non-uniformity were neglected. The goal here is to compute corrections for the energy and writhe of open supercoiled DNA configurations, as well as curl configurations.
1. Numerical computations of elastic equilibria
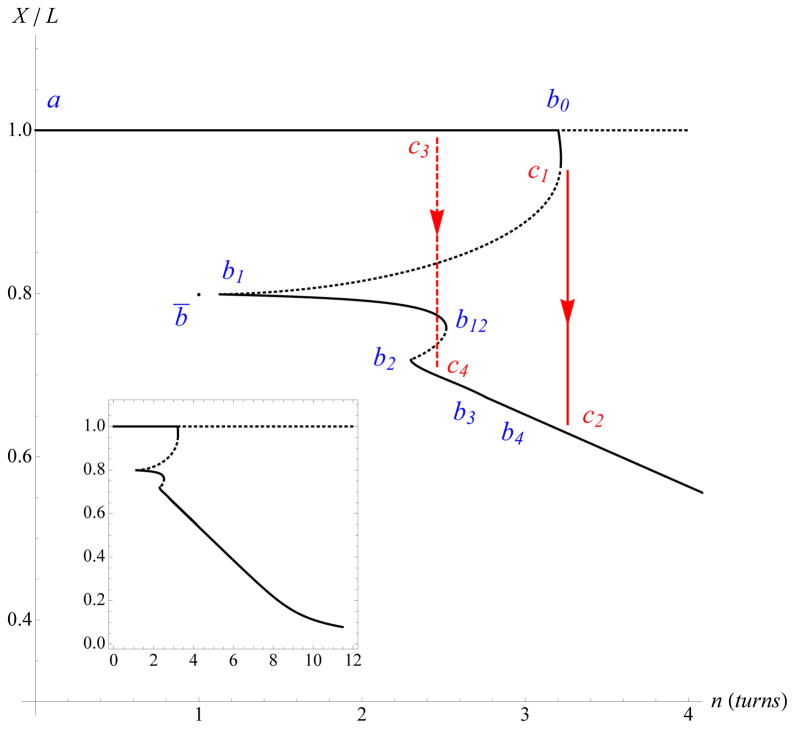
Fig. 10 shows a typical bifurcation diagram for a twisted elastic rod with self-contact, undergoing end-rotation (n turns; n = ΔLk) under constant tensile force f. The two ends of the rod are held aligned in clamps, see also [15, 35].
FIG. 10.
(Color online) Extension-rotation projection of the bifurcation diagram for (fL2)/[(2π)2 K0] = 10, L/(2ρ) = 170, and K3/K0 = 2. Plain (dotted) curves correspond to stable (unstable) configurations. Arrows show expected dynamic transitions between states as n is increased.
Each extension-rotation diagram is plotted for specific values of the three parameters (fL2)/[(2π)2 K0], L/(2ρ), and K3/K0. Due to the nonlinearity of the boundary value problem, several solutions of varying stability can coexist for the same end-rotation n. The line X/L = 1 corresponds to straight and twisted solutions. These solutions become unstable at point b0. From b0 to b1 we have 3D twisted configurations with no contact. Under the loading of interest here, where force instead of extension is prescribed, these solutions are stable from b0 up to c1 and unstable from c1 up to b1. From b1 to b2 one-point-of-contact solutions appear (curls) which are stable from b1 to b12 and unstable from b12 to b2.
From b2 to b3 stable solutions with two contact points arise. These solutions already look like plectonemic solutions. From b3 to b4 stable solutions with three contact points appear, and from b4 on the solutions have a continuous contact line flanked by two contact points. These last configurations correspond to fully developed plectonemic configurations (see e.g., Fig. 2 of [36] for more details and figures of these configurations).
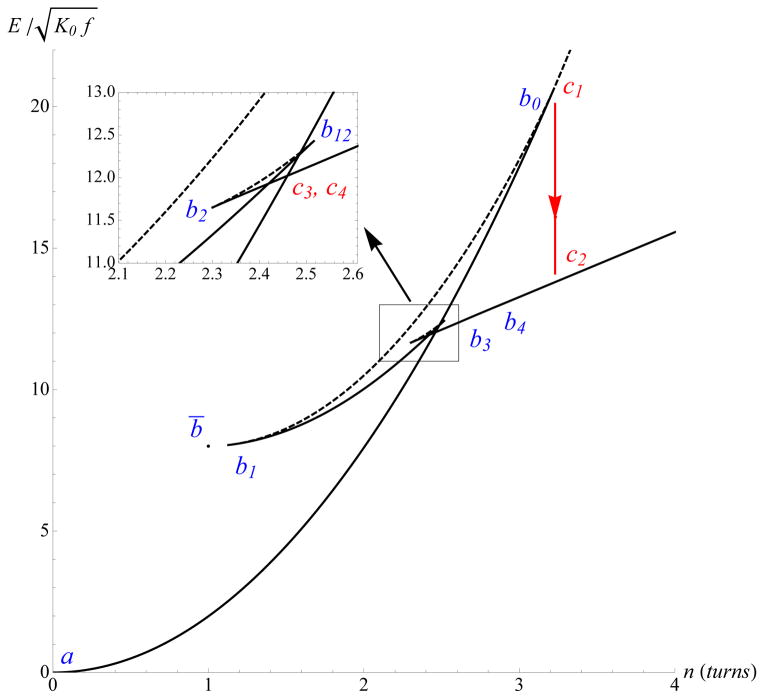
In a macroscopic experiment, increasing n from the unstressed configuration (point a in Fig. 10) eventually leads to instability at point c1. This instability leads to a fixed-rotation jump on the plectonemic branch, toward point c2 with n(c2) = n(c1). In a experiment on DNA, thermal fluctuations accelerate the transition which happens when the (free) energies (Fig. 11) of the twisted straight and plectonemic configurations become equal (point c3 to point c4).
FIG. 11.
(Color online) Energy-rotation projection of the bifurcation diagram for (fL2)/[(2π)2 K0] = 10, L/(2ρ) = 170, and K3/K0 = 2. Plain (dotted) curves correspond to stable (unstable) configurations. Arrows show expected dynamic transitions between states as n is increased.
2. Interpolation formulae for curls: writhe and energy
We now focus on the branch b1 to b12, where stable one-contact configurations occur, i.e. curls. For parameters corresponding to the range of forces encountered in single-molecule experiments (typically 0.5 to 4 pN) the extension X/L, writhe, and bending energy of a curl vary only slightly with imposed rotation n. Hence we consider only the b1 configuration. Numerical computations for several values of f and ρ show that the writhe of a curl is well approximated as:
| (A.1) |
with nondimensionalized force x = fρ2/K0.
The bending energy plus the mechanical work done by the external force for a curl configuration is similarly well approximated by , with
| (A.2) |
3. Interpolation formula for the end-loop+tails: writhe and energy
The writhe of an interwound plectonemic region of contour length Lp, ignoring the contribution of the end and tail, is
| (A.3) |
where ρ is the plectonemic radius [37]. The writhe of a finite supercoiled DNA domain extending from a stretched molecule, should account for (i) the end-loop of the plectonemic region, and (ii) the bending of the tails. To obtain an accurate end-tail correction to (A.3) we numerically compute the total writhe of an entire configuration for several forces and thicknesses, Wr(f, ρ), and we compute the difference wp(f, ρ) between the two. We numerically find that wp only depends on x = fρ2/K0 and can be interpolated as
| (A.4) |
The total writhe of a plectonemic domain is the sum of (A.3) and (A.4). The correction to bending energy and to the work of the external tension is interpolated in the same manner: several numerical simulations are performed and the total energy of the entire configuration is recorded. From this energy we subtract the total twist energy Et, the bending energy of a purely interwound region, , and the work done by the external force on the interwound region, Ef = −f (L −Lp). The remaining correction term is defined to be
| (A.5) |
Numerically we find that εp(f, ρ) only depends on x = fρ2/K0 and that it can be accurately interpolated as
| (A.6) |
This energy correction for the plectonemic phase accounts for the end-loop and the (bent) tails. The plectoneme correction has a similar form but a different value from the curl energy (A.2), reflecting its slightly different shape.
4. Relation between hard-core radius and supercoiling radius
a. Plectonemic end-loops
In the elastic rod simulations a hard-core radius ρ is used whereas in the free energy model for supercoiled DNA, long range electrostatic interactions and the entropic confinement potentials determine the supercoiling radius r. In order to use formula (A.1), (A.2), (A.4), and (A.6), one needs to know the value of ρ. Setting ρ = r leads to complications when m = 0 or when Lp is small. We therefore use for ρ the supercoiling radius formula given as Eq. (11) in [17]:
| (A.7) |
with , Bjerrum length ℓB = 0.7 nm, and Debye length . Under f = 1 pN with 150 mM salt at T = 296.5 K and for A = 45 nm, ρ = 2.935 nm.
b. Curls
For curls, we use the salt-dependent DNA effective diameter of Ref. [38]
| (A.8) |
5. Contour length of curls and end-loops
We here focus on the perfectly planar and twistless loop (Fig. 12) from which we estimate contour lengths for the curls and end-loop shapes. The branch for b0 to b1 (Fig. 10), which contains 3D twisted configurations, can be continued past b1 up to point b̄ where the rod is twistless, planar, and self-intersecting. This well-known solution is refered to as the homoclinic planar elastica (see [39] for a review), and has the following properties:
| (A.9) |
| (A.10) |
| (A.11) |
| (A.12) |
| (A.13) |
see also Refs. [40, 41]. This solution strictly has infinite span x(L/2)−x(−L/2) and contourlength L: one needs S → ±∞ for y(S) and y′(S) to vanish (clamped boundary conditions). Configuration b̄ and b1 are closely related, as can be seen when comparing (A.9) to (A.1) and (A.11) to (A.2). In Fig. 12, the contour length of the inner loop is with s1 ≃ 1.915, given by s1 = 2 tanh s1. For purposes of configuration counting, we consider that curls, and plectonemic end-loops and tails occupy a total contour length of .
FIG. 12.
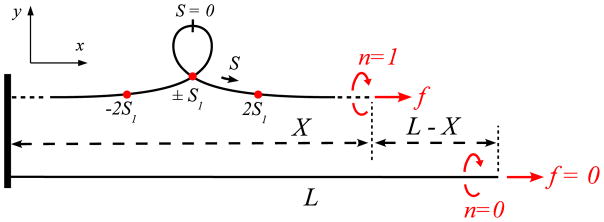
(Color online) Properties of the homoclinic planar elastica, configuration b̄ in Fig. 10.
References
- 1.Marko JF, Siggia ED. Science. 1994;265:506. doi: 10.1126/science.8036491. [DOI] [PubMed] [Google Scholar]
- 2.Marko JF, Siggia ED. Phys Rev E. 1995;52:2912. doi: 10.1103/physreve.52.2912. [DOI] [PubMed] [Google Scholar]
- 3.Postow L, Hardy CD, Arsuaga J, Cozzarelli NR. Genes Dev. 2004;18:1766. doi: 10.1101/gad.1207504. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Higgins NP, Yang X, Fu Q, Roth JR. J Bacteriol. 1996;178:2825. doi: 10.1128/jb.178.10.2825-2835.1996. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Hatfield GW, Benham CJ. Ann Rev Genet. 2002;36:175. doi: 10.1146/annurev.genet.36.032902.111815. [DOI] [PubMed] [Google Scholar]
- 6.Smith SB, Finzi L, Bustamante C. Science. 1992;258:1122. doi: 10.1126/science.1439819. [DOI] [PubMed] [Google Scholar]
- 7.Strick TR, Allemand JF, Bensimon D, Bensimon A, Croquette V. Science. 1996;271:1835. doi: 10.1126/science.271.5257.1835. [DOI] [PubMed] [Google Scholar]
- 8.Forth S, Deufel C, Sheinin MY, Daniels B, Sethna JP, Wang MD. Phys Rev Lett. 2008;100:148301. doi: 10.1103/PhysRevLett.100.148301. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Mosconi F, Allemand JF, Bensimon D, Croquette V. Phys Rev Lett. 2009;102:078301. doi: 10.1103/PhysRevLett.102.078301. [DOI] [PubMed] [Google Scholar]
- 10.Brutzer H, Luzzietti N, Klaue D, Seidel R. Biophys J. 2010;98:1267. doi: 10.1016/j.bpj.2009.12.4292. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Moroz JD, Nelson P. Proc Natl Acad Sci, USA. 1997;94:14418. doi: 10.1073/pnas.94.26.14418. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Marko JF. Phys Rev E. 2007;76:021926. doi: 10.1103/PhysRevE.76.021926. [DOI] [PubMed] [Google Scholar]
- 13.Daniels BC, Forth S, Sheinin MY, Wang MD, Sethna JP. Phys Rev E. 2009;80:040901. doi: 10.1103/PhysRevE.80.040901. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Daniels BC, Sethna JP. Phys Rev E. 2011;83:041924. doi: 10.1103/PhysRevE.83.041924. [DOI] [PubMed] [Google Scholar]
- 15.Neukirch S. Phys Rev Lett. 2004;93:198107. doi: 10.1103/PhysRevLett.93.198107. [DOI] [PubMed] [Google Scholar]
- 16.Clauvelin N, Audoly B, Neukirch S. Biophys J. 2009;96:3716. doi: 10.1016/j.bpj.2009.02.032. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Neukirch S, Marko JF. Phys Rev Lett. 2011;106:138104. doi: 10.1103/PhysRevLett.106.138104. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Rossetto V. Europhys Lett. 2005;69:142. [Google Scholar]
- 19.Lipfert J, Kerssemakers JW, Jager T, Dekker NH. Nature Methods. 2010;7:977. doi: 10.1038/nmeth.1520. [DOI] [PubMed] [Google Scholar]
- 20.Sankararaman S, Marko JF. Phys Rev E. 2005;71:021911. doi: 10.1103/PhysRevE.71.021911. [DOI] [PubMed] [Google Scholar]
- 21.Ubbink J, Odijk T. Biophys J. 1999;76:2502. doi: 10.1016/S0006-3495(99)77405-9. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Stigter D. J Colloid Interface Sci. 1975;296:296. [Google Scholar]
- 23.Schellman JA, Stigter D. Biopolymers. 1977;16:1415. doi: 10.1002/bip.1977.360160704. [DOI] [PubMed] [Google Scholar]
- 24.Marko JF, Siggia ED. Macromolecules. 1995;28:8759. [Google Scholar]
- 25.Wenner JR, Williams MC, Rouzina I, Bloomfield VA. Biophys J. 2002;82:3160. doi: 10.1016/S0006-3495(02)75658-0. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Sheinin MY, Wang MD. Phys Chem Chem Phys. 2009;11:4800. doi: 10.1039/b901646e. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Gulminelli F, Carmona JM, Chomaz P, Richert J, Jiménez S, Regnard V. Phys Rev E. 2003;68:026119. doi: 10.1103/PhysRevE.68.026119. [DOI] [PubMed] [Google Scholar]
- 28.Bryant Z, Stone MD, Gore J, Smith SB, Cozzarelli NR, Bustamante C. Nature. 2003;424:338. doi: 10.1038/nature01810. [DOI] [PubMed] [Google Scholar]
- 29.Sarkar A, Leger JF, Chatenay D, Marko JF. Phys Rev E. 2001;63:051903. doi: 10.1103/PhysRevE.63.051903. [DOI] [PubMed] [Google Scholar]
- 30.Marko JF. Mathematics of DNA Structure, Function and Interactions. In: Benham CJ, Harvey S, Olson WK, Sumners DWL, Swigon D, editors. The IMA Volumes in Mathematics and its Applications. Vol. 150. pp. 225–249. [Google Scholar]
- 31.Stump DM, Fraser WB, Gates KE. Proc R Soc Lond A. 1998;454:2123. [Google Scholar]
- 32.Coleman BD, Swigon D. J Elast. 2000;60:173. [Google Scholar]
- 33.van der Heijden GHM, Neukirch S, Goss VGA, Thompson JMT. Int J Mech Sci. 2003;45:161. [Google Scholar]
- 34.Clauvelin N, Audoly B, Neukirch S. Macromolecules. 2008;41:4479. [Google Scholar]
- 35.Swigon D. PhD thesis. Rutgers State University of New Jersey; U.S.A: 1999. [Google Scholar]
- 36.Neukirch S, Starostin EL. Phys Rev E. 2008;78:041912. doi: 10.1103/PhysRevE.78.041912. [DOI] [PubMed] [Google Scholar]
- 37.Fuller FB. Proc Natl Acad Sci, USA. 1971;68:815. doi: 10.1073/pnas.68.4.815. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 38.Rybenkov VV, Cozzarelli NR, Vologodskii AV. Proc Natl Acad Sci USA. 1993;90:5307. doi: 10.1073/pnas.90.11.5307. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 39.Goss VGA. Science & Education. 2009;18:1057. [Google Scholar]
- 40.Coyne J. IEEE J Ocean Eng. 1990;15:72. [Google Scholar]
- 41.Nizette M, Goriely A. J Math Phys. 1999;40:2830. [Google Scholar]
- 42.Klenin KV, Frank-Kamenetskii MD, Langowski J. Biophys J. 1995;68:81. doi: 10.1016/S0006-3495(95)80161-X. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 43.Yan J, Marko JF. Phys Rev Lett. 2004;93:108108. doi: 10.1103/PhysRevLett.93.108108. [DOI] [PubMed] [Google Scholar]
- 44.Wiggins PA, Phillips R, Nelson PC. Phys Rev E. 2005;71:021909. doi: 10.1103/PhysRevE.71.021909. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 45.Allemand JF, Bensimon D, Lavery R, Croquette V. Proc Natl Acad Sci USA. 1998;95:14152. doi: 10.1073/pnas.95.24.14152. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 46.Sheinin MY, Forth S, Marko JF, Wang MD. Phys Rev Lett. 2011;107:108102. doi: 10.1103/PhysRevLett.107.108102. [DOI] [PMC free article] [PubMed] [Google Scholar]