Abstract
Neural activation triggers a rapid, focal increase in blood flow and thus oxygen delivery. Local oxygen consumption also increases, although not to the same extent as oxygen delivery. This ‘uncoupling' enables a number of widely-used functional neuroimaging techniques; however, the physiologic mechanisms that govern oxygen transport under these conditions remain unclear. Here, we explore this dynamic process using a new mathematical model. Motivated by experimental observations and previous modeling, we hypothesized that functional recruitment of capillaries has an important role during neural activation. Using conventional mechanisms alone, the model predictions were inconsistent with in vivo measurements of oxygen partial pressure. However, dynamically increasing net capillary permeability, a simple description of functional recruitment, led to predictions consistent with the data. Increasing permeability in all vessel types had the same effect, but two alternative mechanisms were unable to produce predictions consistent with the data. These results are further evidence that conventional models of oxygen transport are not sufficient to predict dynamic experimental data. The data and modeling suggest that it is necessary to include a mechanism that dynamically increases net vascular permeability. While the model cannot distinguish between the different possibilities, we speculate that functional recruitment could have this effect in vivo.
Keywords: Cerebral blood flow, energy metabolism, mathematical modeling, microcirculation, neurovascular unit
Introduction
Increases in local neural activity lead to a rapid, focal increase in cerebral blood flow (CBF) and thus the amount of oxygen delivered to the region; this process is termed functional hyperemia. The cerebral metabolic rate of oxygen consumption (CMRO2) also increases, but not to the same extent as CBF.1 This dynamic mismatch between supply and demand is often referred to as ‘uncoupling' of CBF and CMRO2, and results in a decrease in the oxygen extraction fraction (OEF). While this phenomenon is critical for neurovascular imaging modalities such as functional magnetic resonance imaging and optical imaging of intrinsic signals, its physiologic purpose remains unclear.
The fact that CBF and glucose consumption remain closely coupled during functional hyperemia2 prompted suggestions that tissue demand for glucose—not oxygen—might drive the increases in CBF; however, the nature and compartmentalization of metabolism during neural activation remain hotly debated. Alternatively, recent measurements suggest that the increase in CBF may be necessary to prevent drops in oxygen partial pressure (PO2) at tissue locations with very low baseline PO2;3 however, it is not yet clear to what extent such regions of tissue require CBF increases to remain viable, if at all. Furthermore, it is also unclear whether the benefits for a small percentage of total brain tissue justify the energy costs associated with maintaining a large ‘safety factor' everywhere else.4
The physiologic mechanisms that govern oxygen transport during functional hyperemia also remain unclear, largely due to the difficulty in measuring CMRO2 directly.5 Unlike skeletal muscle, it is generally believed that classic capillary recruitment (binary switching from fully closed to fully open state) does not occur in the brain.6 However, while far from definitive, there is a range of experimental evidence consistent with functional recruitment (poorly perfused capillaries becoming better perfused) occurring in vivo.
For example, early analyses of vascular transit times using tracer kinetics implied the presence of heterogeneity in CBF velocities, and the amount was influenced by changes in CBF.7, 8 Subsequent measurements using microtransillumination,9 confocal,10 and two-photon microscopy11 also observed considerable heterogeneity in baseline blood cell velocity. In one of the few direct measurements, Villringer et al10 observed a significant decrease in heterogeneity in response to hypercapnia-induced hyperemia.
It is probable that any reduction in heterogeneity under these conditions would be dominated by poorly perfused capillaries becoming better perfused, rather than well perfused capillaries becoming poorly perfused. This being the case, a reduction in capillary perfusion heterogeneity would lead to an increase in the effective permeability of a population of capillaries. In this context, ‘effective permeability' includes the effect of effective surface area changes, as it represents the permeability-surface area product. As capillaries are not thought to dilate significantly during functional activation,12 surface area increases are likely to result from the recruitment of capillaries that are poorly perfused at baseline.
In addition to experimental observations, previous mathematical models have explored the presence or effect of functional recruitment. Using an approach we extend here, Vazquez et al13 observed that increases in capillary permeability improved the fit of model predictions to the data. However, this model considered oxygen flux from capillaries to tissue only, and more recent evidence suggests that descending arterioles supply non-negligible amounts of oxygen to tissue.14, 15 Using a steady-state model, Jespersen and Ostergaard16 recently predicted that increasing CBF normally leads to a reduction in heterogeneity and increases in OEF, with the underlying mechanism being an increase in the effective surface area available for oxygen diffusion.
In this study, we hypothesized that functional recruitment of capillaries has an important role during neural activation. Using a dynamic mathematical model based on fundamental biophysical principles, we explored whether conventional mechanisms alone would be sufficient to make predictions consistent with in vivo experimental measurements of tissue PO2. In addition, we tested a number of plausible but poorly-characterised physiologic mechanisms to determine whether they could improve the model's predictions. Finally, we validated the model's predictions against additional experimental data, including vascular PO2 measurements.
Materials and methods
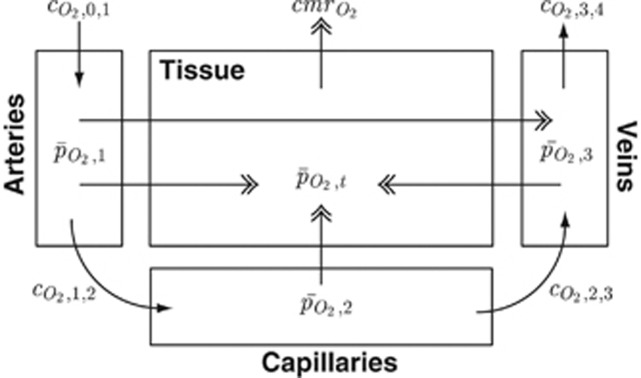
To focus on the bulk mechanisms while maintaining computational simplicity, here we represent the complex cerebrovascular network as four lumped compartments: arteries, capillaries, veins, and tissue (Figure 1). These are referred to by the subscripts 1, 2, 3, and t, respectively. The subscripts 0 and 4 refer to notional larger arterial and venous compartments.
Figure 1.
Schematic diagram of the oxygen transport model showing O2 concentrations (CO2), mean oxygen partial pressures (PO2), and cerebral metabolic rate of oxygen consumption (CMRO2). Subscripts 1, 2, 3 and t refer to arterial, capillary, venous, and tissue compartments, while subscripts 0 and 4 refer to notional larger arterial and venous compartments, respectively. Movement of O2 by convection (i.e., via blood flow) is shown with single arrowheads, while movement via diffusion is shown with double arrowheads. All mathematical notation is as per the equations in the Methods section.
The oxygen transport model builds on our model of CBF and cerebral blood volume, which has been described in detail previously.12 Briefly, the model predicts dynamic changes in CBF and cerebral blood volume in response to an increase in arterial compliance, which represents relaxation of arterial smooth muscle. The signaling pathways responsible for this process remain unclear (for a review, see Attwell et al17), so this change in compliance is driven by an empirical vasodilatory stimulus. The model produces predictions consistent with steady-state and dynamic measurements of CBF and cerebral blood volume, and dynamic measurements of vessel diameter and red blood cell velocity.
The governing equations of the oxygen delivery model are presented in the following sections, while Table 1 summarizes the dynamic variables used in the model, and Supplementary Table 1 lists the parameter values. Continuing a previous convention, variables in upper case are absolute quantities, while those in lower case are dimensionless.12, 18 The superscript * (e.g., 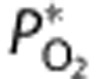 ) represents a baseline value.
) represents a baseline value.
Table 1. List of dynamic variables.
| Symbol | Description |
|---|---|
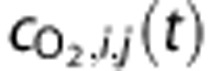 |
O2 concentration of 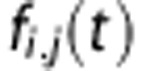
|
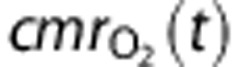 |
Cerebral metabolic rate of O2 consumption |
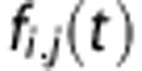 |
Blood flow from i to 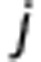
|
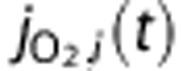 |
O2 flux to tissue |
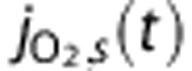 |
O2 flux through shunt |
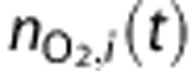 |
O2 amount |
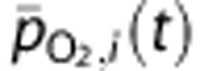 |
Average O2 partial pressure |
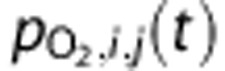 |
O2 partial pressure of 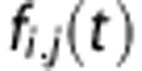
|
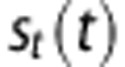 |
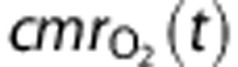 stimulus stimulus |
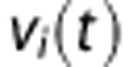 |
Blood volume |
Oxygen Transport Model
The amount of O2 in a vascular compartment, 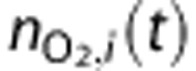 , is described by the ordinary differential equations
, is described by the ordinary differential equations
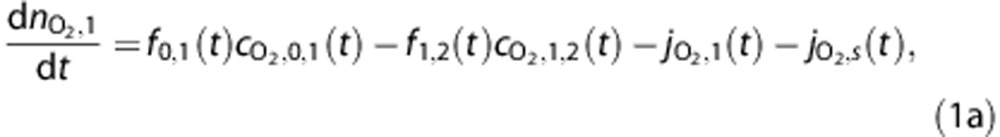 |
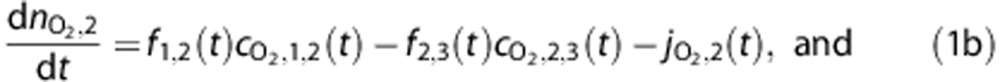 |
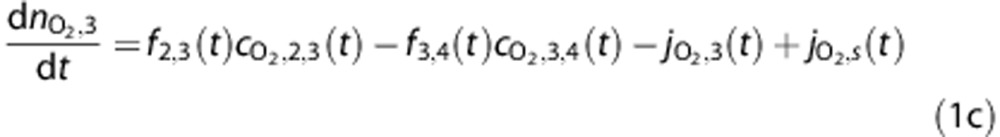 |
where fi,j(t) is the flow from i to j, while the amount in the tissue compartment is given by
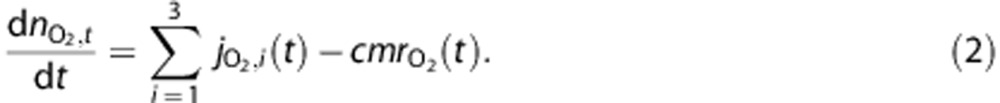 |
The concentration of O2 entering or leaving vascular compartments, 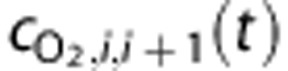 , is calculated by
, is calculated by
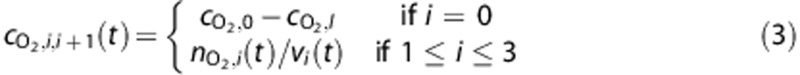 |
where the constants 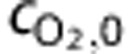 and
and 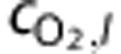 are the systemic arterial O2 concentration (typically measured in the femoral artery) and the oxygen concentration ‘leaked' from the blood before reaching the brain, respectively, and vi(t) is blood volume. In tissue, O2 concentration is calculated as
are the systemic arterial O2 concentration (typically measured in the femoral artery) and the oxygen concentration ‘leaked' from the blood before reaching the brain, respectively, and vi(t) is blood volume. In tissue, O2 concentration is calculated as
where the tissue volume, vt, is assumed constant.
Several groups have reported increases in venous PO2 with increasing diameter,19, 20 and Lecoq et al21 recently observed PO2 increases in venules crossing arterioles in the olfactory bulb. Therefore, we include an arteriovenous diffusional shunt in the model and describe the O2 flux from blood to tissue, 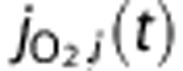 , and through the shunt,
, and through the shunt, 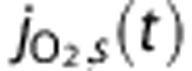 , using Fick's first law such that
, using Fick's first law such that
where 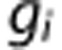 and
and 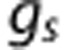 are coefficients describing the net ‘conductance' of O2 between compartments, and include the effects of surface area. The average PO2 in each vascular compartment,
are coefficients describing the net ‘conductance' of O2 between compartments, and include the effects of surface area. The average PO2 in each vascular compartment, 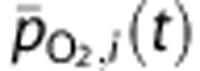 , is calculated from the input and output partial pressures so
, is calculated from the input and output partial pressures so
For simplicity, we ignore the small fraction of oxygen dissolved in plasma and calculate input and output partial pressures using a Hill equation formulation to describe the O2–hemoglobin saturation curve, such that
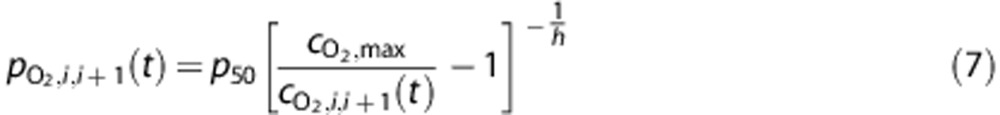 |
where the constant 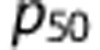 represents the PO2 at which hemoglobin is 50% saturated,
represents the PO2 at which hemoglobin is 50% saturated, 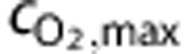 represents the maximum concentration of O2 in whole blood, and
represents the maximum concentration of O2 in whole blood, and 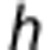 is the Hill exponent. In tissue, the average PO2,
is the Hill exponent. In tissue, the average PO2, 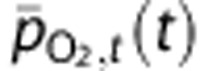 , is calculated from Henry's law so
, is calculated from Henry's law so
where the constant 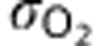 represents the solubility of oxygen in tissue.
represents the solubility of oxygen in tissue.
The cerebral metabolic rate of oxygen consumption, 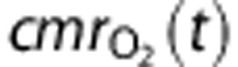 , is given by
, is given by
where the constant 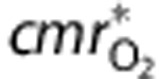 is the baseline rate of oxygen consumption, and
is the baseline rate of oxygen consumption, and  is an empirical stimulus described in more detail in the Supplementary Methods. This model does not consider the details of mitochondrial oxygen consumption, so
is an empirical stimulus described in more detail in the Supplementary Methods. This model does not consider the details of mitochondrial oxygen consumption, so 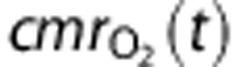 represents a simple tissue O2 ‘sink'.
represents a simple tissue O2 ‘sink'.
Additional Mechanisms
The equations in the previous section include only conventional (i.e., no additional) mechanisms; therefore, simulations under these conditions are abbreviated as ‘NoMech'. We also tested four modifications to these equations to determine whether including additional mechanisms would improve the predictive power of the model.
The first mechanism (‘CapPerm') described the effects of functional recruitment by dynamically increasing capillary permeability as a function of CBF, such that
where the constants 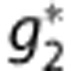 and f* represent values at baseline, and
and f* represent values at baseline, and 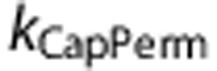 describes the magnitude of the change in capillary permeability for a given change in CBF. This increase in net permeability includes any effect from changes in surface area, although capillaries are not thought to dilate significantly.12
describes the magnitude of the change in capillary permeability for a given change in CBF. This increase in net permeability includes any effect from changes in surface area, although capillaries are not thought to dilate significantly.12
The second mechanism (‘AllPerm') imposed a global increase in vascular permeability to determine whether this would generate different predictions to a specific increase in capillaries. Mathematically,
where  describes the change in permeability in all compartments.
describes the change in permeability in all compartments.
The third mechanism (‘Leak') tested the effect of recruiting upstream oxygen, in this case reducing the amount of O2 ‘leaked' from the blood before reaching the brain such that
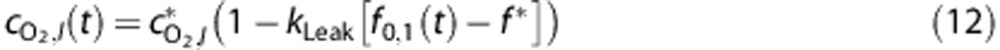 |
where kLeak describes the reduction in O2 leakage. We imposed the constraint 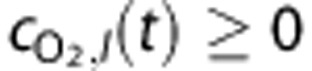 to ensure that blood entering the brain could not have a higher O2 concentration than systemic arteries.
to ensure that blood entering the brain could not have a higher O2 concentration than systemic arteries.
The increase in oxidative metabolism caused by neural activation is likely to lead to an increase in CO2 levels and thus blood acidity, although it is not clear how important this increase would be. The final mechanism (‘P50') tested the possibility that this increase would be sufficient to increase the P50 of oxygen–hemoglobin binding, a process commonly known as the Bohr effect. Mathematically,
where 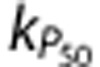 describes the extent of the Bohr shift for a given increase in metabolism.
describes the extent of the Bohr shift for a given increase in metabolism.
Adjusting Tissue Oxygen Partial Pressure Predictions
Detailed measurements of tissue PO2 using two-photon microscopy recently observed considerable variation over relatively short distances.3, 22 These reports cast doubt over the ability of oxygen sensitive microelectrodes to estimate the true mean PO2 of a region of tissue from a small number of measurements. For example, Vazquez et al19 reported a mean tissue PO2 of 38.0 mm Hg (n=9), which is higher than the mean venous PO2 of ∼37.8 mm Hg (n=21). While it is probable that there are tissue regions with PO2 higher than veins, we suggest that it is unlikely for the tissue PO2 to exceed that of the veins on average. Using values of this nature directly in a compartmental model would result in net oxygen transfer from tissue to venous blood and lead to physiologically implausible behavior.
Therefore, we chose not to fit model predictions of mean tissue PO2 at baseline, 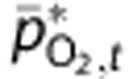 , to the reported values. Instead, we calculated
, to the reported values. Instead, we calculated 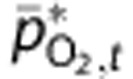 based on the detailed measurements of Vovenko20 and a steady-state *Krogh cylinder-type model (see Supplementary Methods for more detail and derivation). Then, we calculated adjusted predictions of tissue PO2,
based on the detailed measurements of Vovenko20 and a steady-state *Krogh cylinder-type model (see Supplementary Methods for more detail and derivation). Then, we calculated adjusted predictions of tissue PO2, 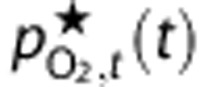 , to represent the experimental observations, and it is these predictions that are used in the fitting and shown in the figures. The Supplementary Methods contain full details of this calculation, but briefly,
, to represent the experimental observations, and it is these predictions that are used in the fitting and shown in the figures. The Supplementary Methods contain full details of this calculation, but briefly, 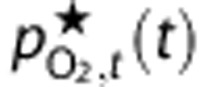 is a weighted average of the model predictions of arterial, capillary, venous, and mean tissue PO2. The weights are defined so the value of
is a weighted average of the model predictions of arterial, capillary, venous, and mean tissue PO2. The weights are defined so the value of 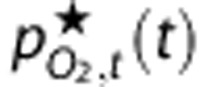 at baseline matches the reported ‘mean' PO2 value. However, the weights are only calculated once for each set of baseline conditions, and are not used as fitting parameters in the optimization of dynamic predictions.
at baseline matches the reported ‘mean' PO2 value. However, the weights are only calculated once for each set of baseline conditions, and are not used as fitting parameters in the optimization of dynamic predictions.
Experimental Design
This section gives an overview of the design of the numerical experiments, which were done in three stages. More information, including detail on parameter selection, can be found in the Supplementary Methods.
Baseline PO2
The first stage of simulations considered only baseline conditions, to confirm that the model was able to make predictions consistent with a range of experimental PO2 measurements at baseline. We used the detailed measurements of Vovenko20 as a reference state, and modified these where necessary to account for the different conditions of the other sets of measurements14, 19, 23 (see Table 2). For the reference state, 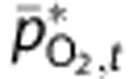 was determined from the experimental data, then measured values of vascular PO2 were used in the steady-state forms of equations (1) and (2) to determine the baseline CMRO2 and O2 conduction coefficients. However, the other data sets did not include all measurements necessary to determine model parameters uniquely. In these cases, we assumed the parameters (such as baseline CMRO2 and O2 conduction coefficients) would remain the same as the reference state, unless they conflicted with the experimental data. For example, the femoral artery and venous PO2 values reported by Yaseen et al14 and Vazquez et al19, 24 imply different values for baseline CMRO2 and oxygen conduction coefficients than Vovenko.20 Full details of the solution procedure are presented in the Supplementary Methods, and parameter values that changed as a result of these different baseline conditions are listed in Supplementary Table 2.
was determined from the experimental data, then measured values of vascular PO2 were used in the steady-state forms of equations (1) and (2) to determine the baseline CMRO2 and O2 conduction coefficients. However, the other data sets did not include all measurements necessary to determine model parameters uniquely. In these cases, we assumed the parameters (such as baseline CMRO2 and O2 conduction coefficients) would remain the same as the reference state, unless they conflicted with the experimental data. For example, the femoral artery and venous PO2 values reported by Yaseen et al14 and Vazquez et al19, 24 imply different values for baseline CMRO2 and oxygen conduction coefficients than Vovenko.20 Full details of the solution procedure are presented in the Supplementary Methods, and parameter values that changed as a result of these different baseline conditions are listed in Supplementary Table 2.
Table 2. List of baseline PO2 values specified when adjusting to different experimental conditions.
| Symbol | Description |
Value (mm Hg) for simulations of: |
||
|---|---|---|---|---|
| Yaseen et al14 | Masamoto et al23 | Vazquez et al19, 24 | ||
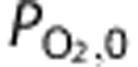 |
Femoral artery PO2 | 108.3 | 114.0 | 133.0 |
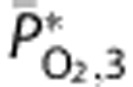 |
Mean venous PO2 | 52.3 | — | 37.8 |
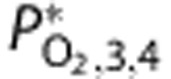 |
Output venous PO2 | 54.4 | — | 40.3 |
PO2, oxygen partial pressure. Parameter values that are adjusted as a result of these different baseline values are listed in Supplementary Table 2.
Tissue Oxygen Partial Pressure
The second stage of simulations considered dynamic measurements of tissue PO2 made by Masamoto et al23 in response to forepaw stimulation in rats. These simulations were performed to determine whether conventional oxygen transport was sufficient to produce predictions consistent with the data. In these experiments, the authors used sodium nitroprusside (SNP), a vasodilator, to ‘predilate' the vessels and thus minimize further vascular dilation in response to neural activation. This treatment reduces the confounding effect of changes in CBF on measurements of tissue PO2, so provides a clearer insight into the dynamics of CMRO2. (The SNP-induced vasodilation also induces hypotension, which is accounted for in the simulations by the CBF model.)
There was no difference in electrical activity (measured by local field potential) between the control and SNP conditions,23 so we assumed that CMRO2 was also the same. Furthermore, because there was also no significant difference in baseline arterial blood conditions between control and SNP measurements, we assumed that differences in tissue PO2 between the two cases were solely attributable to differences in CBF. First, we adjusted the vasodilatory stimulus to fit the model predictions of CBF to the observations, as in our previous work.12 Then, we adjusted the three time constants and two amplitudes of the CMRO2 stimulus (see Supplementary Methods) to minimize the error between the model predictions and experimental measurements of tissue PO2 (both conditions simultaneously).
Tissue and Vascular Oxygen Partial Pressure
The final stage of simulations considered dynamic measurements of PO2 in arteries, veins, and tissue made by the same group as in the previous stage, using a similar experimental protocol.19 (Some of the reported PO2 values had a minor correction applied in a subsequent publication,24 and these updated values are used here.) The simulations were performed to confirm that the previous results were repeatable, and to validate the predictions. First, we fit model predictions of CBF to the observations. Then, we adjusted the CMRO2 stimulus (as in the previous stage) to minimize the error between the model predictions and experimental measurements of tissue PO2. In this way, the measurements of PO2 in arteries and veins were not involved in the optimization, so act as an independent validation of the model's predictive power.
Optimization and Data Analysis
All optimization was implemented in MATLAB R2010a (The MathWorks, Natick, MA, USA) using a constrained Nelder-Mead simplex algorithm,25 with initial parameter values chosen from a uniform random distribution. We repeated each stage of optimization with different initial guesses, typically three or four times, to ensure that the values converged to a true optimal solution, and used the best of these repeats.
We also conducted analyses to determine whether the model predictions were sensitive to the choice of parameters. We independently perturbed each parameter by a representative amount, typically ±10% (see Supplementary Table 3), and repeated the appropriate optimization stage(s) in each case. Unless otherwise specified, model results are presented as the median±s.d. of this sensitivity analysis, where n=29 simulations (when comparing to Masamoto et al23) or 35 simulations (when comparing to Vazquez et al13). Unless otherwise specified, experimental data are presented as mean±s.e.m. (where available).
Raw experimental data were not available, so it was not possible to compare model predictions to the data directly using statistical methods. However, we used statistical tests to provide evidence of differences between the predictions from different model mechanisms, given some variation in the parameters. To test for statistically significant differences between mechanisms, we compared metrics (e.g., PO2 increases) from the simulations in the sensitivity analysis using either a t-test or a non-parametric Wilcoxon rank sum test, depending on the result of a Shapiro–Wilk normality test. In all analyses, two-tailed tests were used unless specified otherwise, and results were considered significant for P<0.05.
Results
Baseline Oxygen Partial Pressure
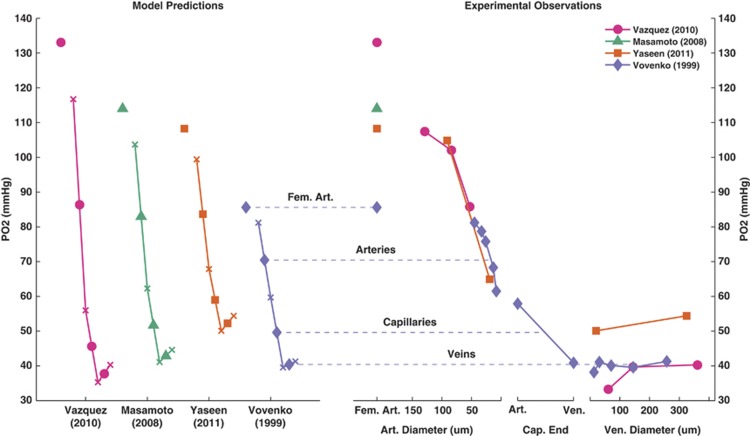
Figure 2 shows the model predictions and experimental measurements of PO2 at baseline for the different data sets considered here. Since the model does not account for variation in PO2 based on vessel size, it is more accurate to compare the model predictions to the mean observations for each vessel type; however, the PO2 values of the blood flowing into and out of a model compartment give an indication of the predicted range of values.
Figure 2.
Model predictions (left) and experimental observations (right) of oxygen partial pressure (PO2) at baseline. Model predictions are shown with the femoral artery (Fem. Art.) and mean compartmental PO2 values in solid shapes, and the PO2 values into or out of compartments as ‘x'.
Measurements made by Vovenko20 were used as a reference state in the model, and as such the model predictions are very similar to the data: the model predicted PO2 values of (70.5, 49.6, 40.4) mm Hg (corresponding to arteries, capillaries, veins) compared with mean values of (73.1, 49.4, 40.0) mm Hg from the data.
The model predictions were also consistent for the other two sets of data. Yaseen et al14 measured mean PO2 values of (84.9, –, 52.3) mm Hg, compared with model predictions of (83.7, 59.0, 52.3) mm Hg. For the measurements made by Vazquez et al19, 24 the model predicted values of (90.9, 51.2, 37.8) mm Hg compared with (85.0, –, 37.8) mm Hg from the data. While there were no vascular PO2 measurements to compare to, model predictions of vascular PO2 under the conditions reported by Masamoto et al23 (83.0, 51.7, 42.9 mm Hg) appeared to be reasonable in light of the other measurements.
Tissue Oxygen Partial Pressure
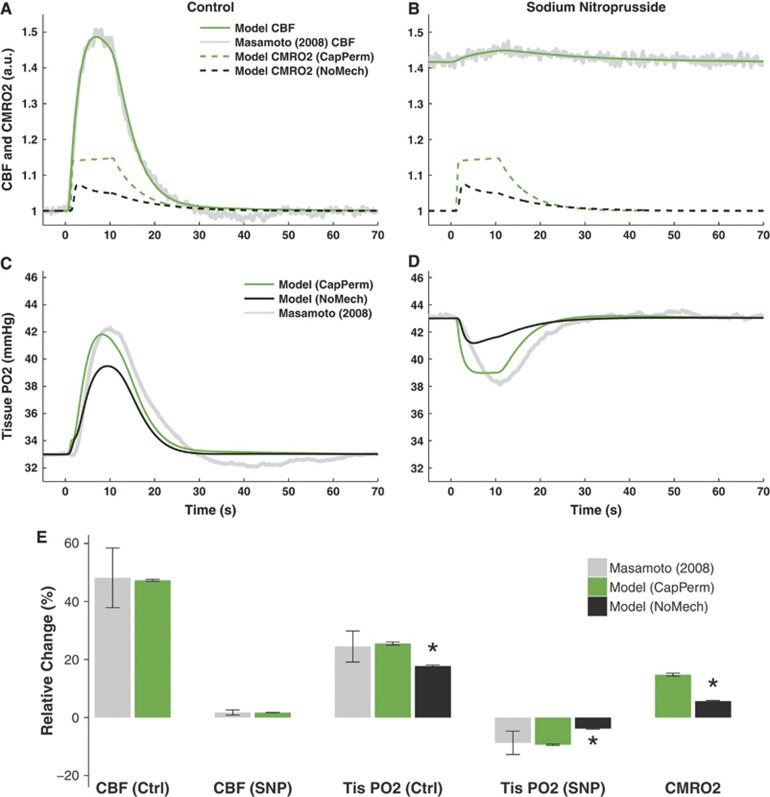
Figures 3A–D displays the optimal model predictions of CBF, CMRO2, and tissue PO2 for the set of experiments reported by Masamoto et al.23 The predictions of CBF under both control and vasodilated (SNP) conditions were a good fit to the data (Figures 3A–B), so would be unlikely to cause significant errors in predictions of PO2.
Figure 3.
Model predictions of data from Masamoto et al23 in response to 10-second electrical forepaw stimulation. (A–D) Optimal predictions of cerebral blood flow (CBF), cerebral metabolic rate of oxygen consumption (CMRO2), and tissue oxygen partial pressure (PO2) under control (Ctrl, panels A and C) and sodium nitroprusside (SNP) induced vasodilated conditions (panels B and D). (E) Changes from baseline CBF, tissue PO2, and CMRO2 induced by stimulation. Predictions show median±s.d. of n=29 simulations obtained by varying model parameters in the sensitivity analysis. Experiments show mean±s.e.m. of n=5 measurements. Predictions of CMRO2 and PO2 are shown with either increased capillary permeability (CapPerm, green) or without any additional mechanisms (NoMech, black). Asterisk (*) indicates P<0.05 versus CapPerm simulations. See Supplementary Figure 1 for results from remaining mechanisms.
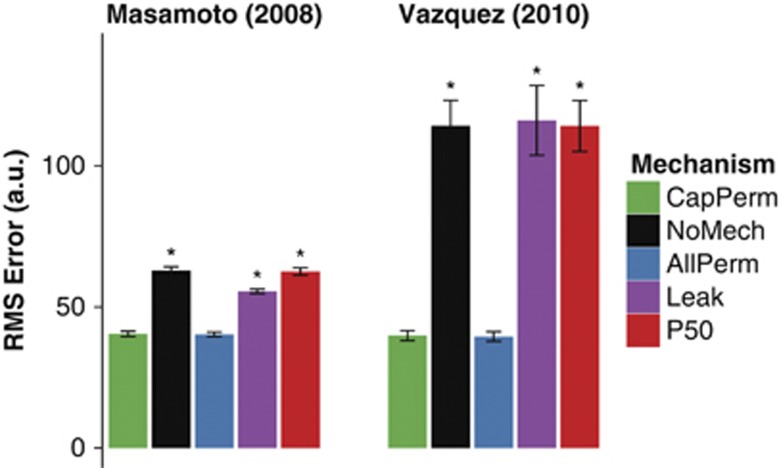
The model predictions of tissue PO2 using a mechanism that simulated functional recruitment (CapPerm) appeared consistent with the data; however, predictions without any additional mechanisms (NoMech) did not (Figures 3C–D). When compared with the CapPerm simulations, the NoMech simulations predicted significantly smaller increases in tissue PO2 under control conditions, smaller decreases in tissue PO2 under vasodilated conditions, and smaller increases in CMRO2 for both conditions (Figure 3E, all P<0.001). The root mean square (RMS) error associated with the optimization was also significantly higher for the NoMech simulations than the CapPerm, indicating a less accurate fit to the data (Figure 5, P<0.001). For the CapPerm simulations, the optimal value for 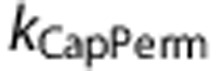 was determined to be 0.79±0.05, which is equivalent to an increase in capillary oxygen permeability of 37.5±2.3% above baseline.
was determined to be 0.79±0.05, which is equivalent to an increase in capillary oxygen permeability of 37.5±2.3% above baseline.
Of the other mechanisms tested, only the AllPerm simulations were able to produce predictions that appeared consistent with the data (Supplementary Figures 1A and 1B). There were no significant differences in predicted tissue PO2 increases (Control or SNP), CMRO2 increases, or RMS error between the CapPerm and AllPerm simulations (all P>0.3). The predicted metrics from the Leak and P50 simulations were all significantly different to the CapPerm simulations (Supplementary Figure 1G, all P<0.001). Both of these additional mechanisms resulted in a significantly poorer fit to the data (Figure 5 and Supplementary Figures 1C–F).
The optimal value for  was determined to be 0.63±0.04, which is equivalent to an increase in oxygen permeability of 29.6±1.8% above baseline in all vascular compartments; the optimal value for
was determined to be 0.63±0.04, which is equivalent to an increase in oxygen permeability of 29.6±1.8% above baseline in all vascular compartments; the optimal value for  was 3.81±0.40, which is equivalent to cerebral arterial oxygenation reaching the level of the femoral artery in response to a CBF increase of ∼25% above baseline; and the optimal value for
was 3.81±0.40, which is equivalent to cerebral arterial oxygenation reaching the level of the femoral artery in response to a CBF increase of ∼25% above baseline; and the optimal value for 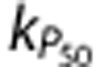 was 0.71±0.20, which is equivalent to an increase in P50 of 24.6±11.1% above baseline.
was 0.71±0.20, which is equivalent to an increase in P50 of 24.6±11.1% above baseline.
Tissue and Vascular Oxygen Partial Pressure
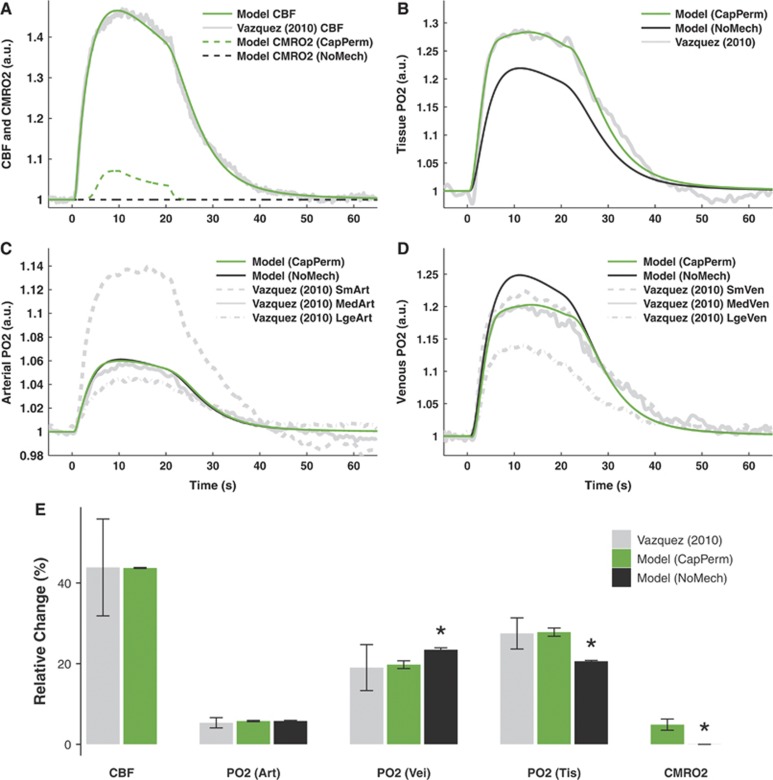
Figures 4A–D display the optimal model predictions of CBF, CMRO2, and PO2 for the set of experiments reported by Vazquez et al.19 The predictions of CBF were a good fit to the data here also (Figure 4A), so would be unlikely to confound subsequent predictions of PO2.
Figure 4.
Model predictions of data from Vazquez et al24 in response to 20-second electrical forepaw stimulation. (A–D) Optimal predictions of cerebral blood flow (CBF) and cerebral metabolic rate of oxygen consumption (CMRO2, panel A), tissue oxygen partial pressure (PO2, panel B), arterial PO2 (panel C), and venous PO2 (panel D). (E) Changes from baseline induced by stimulation. Predictions show median±s.d. of n=35 simulations obtained by varying model parameters in the sensitivity analysis. Experiments show mean±s.e.m. of n=6 or 9 measurements. Predictions of CMRO2 and PO2 are shown either with increased capillary permeability (CapPerm, green) or without any additional mechanisms (NoMech, black), although these mechanisms overlap in panel C. Asterisk (*) indicates P<0.05 versus CapPerm simulations. See Supplementary Figure 2 for results from remaining mechanisms.
For the CapPerm—but not the NoMech—simulations, predictions of tissue, and venous PO2 appeared consistent with the data (Figures 4B–D). When compared with the CapPerm simulations, the NoMech simulations predicted significantly smaller increases in tissue PO2, larger increases in arterial and venous PO2, smaller increases in CMRO2, and a larger RMS error (Figures 4E and 5, all P<0.001). For this set of data, the CapPerm mechanism predicted an increase in capillary permeability of 33.6±2.1% above baseline.
Figure 5.
Root mean square (RMS) error associated with fitting the model to data for all of the mechanisms considered. Data shown as mean±standard error of means (s.e.m.); asterisk (*) indicates P<0.05 versus CapPerm simulations; n=29 simulations for data from Masamoto et al23 and n=35 simulations for data from Vazquez et al.24
As with the previous stage, predictions from the AllPerm simulations appeared consistent with the data (Supplementary Figures 2A and 2B). There was no significant difference in predicted tissue PO2 increases (P>0.7), CMRO2 increases (P>0.05), or RMS error (Figure 5, P>0.6) between CapPerm and AllPerm simulations; however, the predicted increases in arterial and venous PO2—although small—were significantly different to those from the CapPerm simulations (Supplementary Figure 2J, all P<0.001). For these measurements, the AllPerm mechanism predicted an increase in vascular permeability in all compartments of 27.2±1.6% above baseline.
For the Leak and P50 simulations, all the predicted metrics were significantly different to those from the CapPerm simulations (Supplementary Figure 2J, all P<0.001), and both of these mechanisms resulted in a significantly poorer fit to the data compared with the CapPerm simulations (Figure 5 and Supplementary Figures 2D–I, all P<0.001). The effect of  was very similar to the previous simulations, as CBF increases above 25% in both cases. The value of
was very similar to the previous simulations, as CBF increases above 25% in both cases. The value of 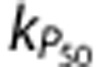 had virtually no effect on these simulations as the CMRO2 increase above baseline was negligible.
had virtually no effect on these simulations as the CMRO2 increase above baseline was negligible.
Discussion
In this study, we used a mathematical modeling approach to test whether functional recruitment—or another similar mechanism—was necessary and/or sufficient to produce predictions consistent with experimental data. We compared model predictions to measurements of PO2 at baseline, and to two sets of dynamic PO2 measurements in tissue. One set of data included measurements made under conditions with almost no CBF increase, so provided a more direct insight into the dynamics of CMRO2. The other set of data included measurements of PO2 in arteries and veins, which acted as an independent validation of the model predictions.
Baseline Predictions
The model predictions of baseline PO2 were consistent with the data (Figure 2). It was expected that the predictions would agree well with the measurements made by Vovenko20 since we used these values to define our ‘reference state'. However, despite changing only a small number of parameters to account for the different experimental conditions, the model predictions also agreed well with the other measurements.19, 23 Even when adjusting only for femoral artery PO2, the model predictions were reasonable, particularly to the capillary level (data not shown). However, specifying the venous PO2 also, which is equivalent to specifying the baseline CMRO2 or OEF, led to more accurate predictions. As discussed by Yaseen et al,14 it is not clear what caused the differences between the measurements of venous PO2, but it may be related to animal preparation (e.g., anesthesia, spontaneous breathing versus artificial ventilation) or measurement modality (e.g., electrode measurements from the surface of vessels versus intravascular measurements using optical methods).
Conventional Mechanisms
Using only conventional mechanisms (abbreviated as NoMech), the model could not produce predictions consistent with the PO2 measurements from Masamoto et al23 under both control and suppressed CBF conditions (Figure 3). While the predictions of arterial PO2 were consistent with the second set of data,19 the predicted changes in tissue and venous PO2 were not (Figure 4). These results are similar to those from an earlier model that considered capillaries only.13 The fact that we reach the same conclusion here, despite our model allowing flux from arteries to tissue, is further evidence that conventional mechanisms are not sufficient to describe dynamic measurements of PO2.
Importantly, the predicted increase in CMRO2 in the second set of simulations was negligible (Figure 4), which is not likely to represent the in vivo behavior. As the difference between arterial and venous PO2 is related to the CMRO2, and arterial PO2 was relatively insensitive to changes in CMRO2, it is likely that the model's overprediction of the increase in venous PO2 results from an underprediction of the increase in CMRO2. As would be expected, forcing the model to include a non-negligible increase in CMRO2 led to a smaller increase in tissue PO2 and thus a higher RMS error, but improved the prediction of venous PO2 (data not shown).
Combined, these results suggest that it is necessary to include an additional mechanism—one not captured by conventional lumped compartment models—to produce predictions consistent with dynamic experimental measurements of PO2.
Permeability Increases
The model produced predictions consistent with the data from Masamoto et al23 under both control and vasodilated conditions using the CapPerm mechanism, which dynamically increased capillary permeability to simulate functional recruitment (Figure 3). The model also produced predictions consistent with the second set of data,19 despite changing only a small number of parameters (Figure 4). This stage of simulations adjusted for the different experimental conditions and varied the CMRO2 stimulus, but all other parameters—including the constant governing the CapPerm mechanism (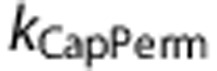 )—were identical to the previous stage.
)—were identical to the previous stage.
Vazquez et al13 considered a similar mechanism and also produced predictions consistent with the measurements, but ruled the mechanism out on the basis that ‘it is unlikely that the permeability would increase... with increases in blood flow within the compartment'. While the permeability of individual capillaries is not likely to change to a significant degree, we suggest that the net permeability of the capillary compartment, which represents the entire population of capillaries in a region, may indeed change due to a mechanism like functional recruitment.6 Our model predicted that a dynamic increase in capillary compartment permeability to around 35% above baseline was sufficient to describe the data, which is similar to the prediction in Vazquez et al.13 In addition, the fact that the model was able to make predictions consistent with a second set of data, including predictions of vascular PO2 measurements that were independent of the optimization process, suggests that the model can produce valid, repeatable predictions.
The AllPerm mechanism, which increased permeability by the same proportion in all vessel types, produced predictions that were very similar to those made using the CapPerm mechanism (Supplementary Figures 1 and 2). The difference in predicted increase of PO2 between the AllPerm and CapPerm simulations reached statistical significance in some cases; however, the differences were small and the predictions from both sets of simulations appeared to be within the uncertainty of the experimental data. In addition, there was no significant difference in the predicted CMRO2 increase between the two sets of predictions. The model predicted that a dynamic permeability increase in all compartments to around 28% above baseline was sufficient to describe the data.
Taken as a whole, these results suggest that a global increase in vascular permeability during functional hyperemia could lead to predictions consistent with the measurements, although it is not clear what mechanism might have this effect since arteries and veins are thought to be well perfused at baseline. However, the results suggest that a moderate increase in the effective permeability of a population of capillaries is also sufficient to produce predictions consistent with the observations. While there is no way to distinguish between these two—or other similar—possibilities using the model, we speculate that functional recruitment may be the mechanism that produces this effect in vivo.
Recruitment of Upstream Oxygen
The predictions from the Leak mechanism simulations, which reduced the amount of oxygen lost from the blood before the cerebral arteries, were not consistent with the experimental measurements (Supplementary Figures 1 and 2), and the RMS error for this mechanism was significantly higher than the simulations that increased permeability (Figure 5). In addition, it is likely that the optimized model predictions for this mechanism were based on a smaller increase in CMRO2 than occurred in vivo, as the model predictions of venous PO2 increased more than the data. Similar to the conventional mechanism simulations, forcing the model to use a larger increase in CMRO2 increased the RMS error associated with the predictions of tissue PO2, improved the prediction of venous PO2, and had little effect on arterial PO2 (data not shown).
In contrast to these results, Vazquez et al13 reported that an increase in input arterial oxygenation, which is equivalent to the Leak mechanism here, could produce predictions consistent with the measurements from Masamoto et al.23 This discrepancy is likely due to differences in the method used to calculate input arterial oxygenation, as different values for input arterial oxygenation imply different levels of upstream oxygen capacity. Since Masamoto et al23 did not report measurements of cerebral artery oxygenation, both models use data from Vovenko20 as a reference state. Here, we assumed that the concentration of oxygen lost between femoral and cerebral arteries was constant between the reference state and the data, and used a value of 103 mm Hg; Vazquez et al13 assumed a constant ratio of cerebral to femoral artery partial pressure and calculated a value of 87 mm Hg. As the relationship between PO2 and hemoglobin saturation is nonlinear over this range, we suggest that the method used here is more appropriate. In addition, the method we use produces baseline predictions consistent with a range of measurements (Figure 2), and our predictions were repeatable for a second set of dynamic measurements that included measurements of arterial PO2 (Figure 2), which suggests that the method and the findings are valid.
Therefore, our results suggest that increasing oxygen saturation even to the level of large systemic (femoral) arteries is not sufficient to produce predictions consistent with the data. Furthermore, the mean femoral artery oxygen tension at baseline was >110 mm Hg in Masamoto et al23 and >130 mm Hg in Vazquez et al,19 so any increase in femoral artery PO2 beyond these levels due to cardiac or respiratory changes would be unlikely to cause a significant additional increase in oxygen saturation.
Change in Oxygen–Hemoglobin Binding
The final mechanism (P50), which adjusted the oxygen–hemoglobin saturation relationship, was also unable to produce predictions consistent with the data (Supplementary Figures 1 and 2), and the RMS error was similar to the simulations without any additional mechanisms (Figure 5). Inspection of the raw values from the sensitivity analysis (data not shown) suggested that there may have been two classes of response for the predictions of data from Masamoto et al:23 (i) simulations with low values of 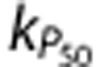 and small increases in CMRO2, which behaved similarly to the NoMech simulations (example in Supplementary Figures 1E and 1F); and (ii) simulations with higher values of
and small increases in CMRO2, which behaved similarly to the NoMech simulations (example in Supplementary Figures 1E and 1F); and (ii) simulations with higher values of 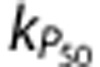 and larger increases in CMRO2. However, while there was a large amount of variation in these values, there was much less variation in the RMS error, which suggests that all of the parameter combinations produced similarly poor fits to the data.
and larger increases in CMRO2. However, while there was a large amount of variation in these values, there was much less variation in the RMS error, which suggests that all of the parameter combinations produced similarly poor fits to the data.
In addition, the model predicted that the value of P50 needed to increase by around 25%, on average, to minimize the RMS error. According to detailed biochemical modeling of hemoglobin binding,26 this change is equivalent to an increase in PCO2 of more than 50 mm Hg, an increase in temperature of more than 3° C, or a decrease in pH of more than 0.15. Changes as large as this do not seem physiologically plausible, especially during stimulation periods of less than 30 seconds. Finally, as per the NoMech and Leak mechanism simulations, the predicted increase in CMRO2 was negligible for the simulations of data from Vazquez et al.19 Forcing the model to use a larger increase in CMRO2 had the same effect as previously (data not shown).
Using a similar mechanism, Vazquez et al24 reported that dynamically increasing P50 was sufficient to produce predictions consistent with the data, but that the increases required were outside the expected physiologic limits. Combined, these results suggest that dynamic changes in the relationship between vascular oxygen tension and hemoglobin saturation are not sufficient to produce predictions consistent with dynamic measurements of PO2.
Methodological Considerations
There are some limitations of the model, which may affect interpretation of the results. Several models have examined oxygen or general scalar transport in more complex geometries;27, 28, 29 however, here we chose to focus in more detail on the bulk mechanisms and represented the network of cerebral blood vessels and tissue as four dimensionless compartments. These simplifications eliminate some of the more complicated effects of structure on function, and may not describe the in vivo dynamics exactly. In particular, our model assumes well-mixed compartments, and does not include any temporal delays in transport between compartments. This limitation may explain some of the temporal discrepancies between the model predictions and data from Masamoto et al23 under control and vasodilated conditions (Figure 3). However, this approach has been shown to produce results consistent with experimental measurements here and in a number of other cases,13, 30, 31 and it makes the model sufficiently tractable to consider transient mechanisms in detail.
Although we relied on measurements from the literature for many of the parameters in the model, the predictions from our simulations were not unduly sensitive to a reasonable level of uncertainty in these parameters. This suggests that the findings here should remain valid even if there was some error in the measurement or selection of parameters.
The model here also includes several improvements over previous models. On the basis of recent observations,21 we included a diffusional arteriovenous shunt in the model. This makes it possible for PO2 in the venous compartment to increase without forcing nonphysiologic high values for average tissue PO2.14, 19, 20 In addition, a new technique developed in this model makes it possible to simulate the dynamics of PO2 at tissue locations with a wide range of baseline values, rather than being restricted to predicting the average behavior of the tissue. Finally, the model predictions were subjected to an independent validation, since the predictions were consistent with experimental data (vascular PO2 measurements) not used in the optimization process.
While the model is a powerful predictive tool, it remains mathematically and computationally simple. Using the model, we were able to integrate observations from multiple experiments into a plausible framework based on fundamental biophysical mechanisms, and test whether hypotheses relating to these mechanisms were consistent with experimental measurements.
Acknowledgments
The authors thank Alberto Vazquez for assistance with the experimental data, Richard Buxton for useful comments on a preliminary version of the manuscript, and Merryn Tawhai for insightful suggestions during early stages of the research.
The authors declare no conflict of interest.
Footnotes
Supplementary Information accompanies the paper on the Journal of Cerebral Blood Flow & Metabolism website (http://www.nature.com/jcbfm)
Supplementary Material
References
- Fox PT, Raichle ME. Focal physiological uncoupling of cerebral blood flow and oxidative metabolism during somatosensory stimulation in human subjects. Proc Natl Acad Sci USA. 1986;83:1140–1144. doi: 10.1073/pnas.83.4.1140. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fox P, Raichle M, Mintun M, Dence C. Nonoxidative glucose consumption during focal physiologic neural activity. Science. 1988;241:462–464. doi: 10.1126/science.3260686. [DOI] [PubMed] [Google Scholar]
- Devor A, Sakadžić S, Saisan PA, Yaseen MA, Roussakis E, Srinivasan VJ, et al. ‘Overshoot' of O2 is required to maintain baseline tissue oxygenation at locations distal to blood vessels. J Neurosci. 2011;31:13676–13681. doi: 10.1523/JNEUROSCI.1968-11.2011. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Leithner C, Royl G, Offenhauser N, Fuchtemeier M, Kohl-Bareis M, Villringer A, et al. Pharmacological uncoupling of activation induced increases in CBF and CMRO2. J Cereb Blood Flow Metab. 2010;30:311–322. doi: 10.1038/jcbfm.2009.211. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Buxton R. Interpreting oxygenation-based neuroimaging signals: the importance and the challenge of understanding brain oxygen metabolism. Front Neuroenergetics. 2010;2:8. doi: 10.3389/fnene.2010.00008. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kuschinsky W, Paulson O. Capillary circulation in the brain. Cerebrovasc Brain Metab Rev. 1992;4:261–286. [PubMed] [Google Scholar]
- Hertz MM, Paulson OB. Heterogeneity of cerebral capillary flow in man and its consequences for estimation of blood-brain barrier permeability. J Clin Invest. 1980;65:1145–1151. doi: 10.1172/JCI109769. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Knudsen GM, Pettigrew KD, Paulson OB, Hertz MM, Patlak CS. Kinetic analysis of blood-brain barrier transport of d-glucose in man: quantitative evaluation in the presence of tracer backflux and capillary heterogeneity. Microvasc Res. 1990;39:28–49. doi: 10.1016/0026-2862(90)90057-x. [DOI] [PubMed] [Google Scholar]
- Pawlik G, Rackl A, Bing RJ. Quantitative capillary topography and blood flow in the cerebral cortex of cats: an in vivo microscopic study. Brain Res. 1981;208:35–58. doi: 10.1016/0006-8993(81)90619-3. [DOI] [PubMed] [Google Scholar]
- Villringer A, Them A, Lindauer U, Einhaupl K, Dirnagl U. Capillary perfusion of the rat brain cortex. An in vivo confocal microscopy study. Circ Res. 1994;75:55–62. doi: 10.1161/01.res.75.1.55. [DOI] [PubMed] [Google Scholar]
- Kleinfeld D, Mitra PP, Helmchen F, Denk W. Fluctuations and stimulus-induced changes in blood flow observed in individual capillaries in layers 2 through 4 of rat neocortex. Proc Natl Acad Sci USA. 1998;95:15741–15746. doi: 10.1073/pnas.95.26.15741. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Barrett MJP, Tawhai MH, Suresh V. Arteries dominate volume changes during brief functional hyperemia: evidence from mathematical modeling. Neuroimage. 2012;62:482–492. doi: 10.1016/j.neuroimage.2012.05.005. [DOI] [PubMed] [Google Scholar]
- Vazquez AL, Masamoto K, Kim S-G. Dynamics of oxygen delivery and consumption during evoked neural stimulation using a compartment model and CBF and tissue PO2 measurements. Neuroimage. 2008;42:49–59. doi: 10.1016/j.neuroimage.2008.04.024. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Yaseen MA, Srinivasan VJ, Sakadzic S, Radhakrishnan H, Gorczynska I, Wu W, et al. Microvascular oxygen tension and flow measurements in rodent cerebral cortex during baseline conditions and functional activation. J Cereb Blood Flow Metab. 2011;31:1051–1063. doi: 10.1038/jcbfm.2010.227. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kasischke KA, Lambert EM, Panepento B, Sun A, Gelbard HA, Burgess RW, et al. Two-photon NADH imaging exposes boundaries of oxygen diffusion in cortical vascular supply regions. J Cereb Blood Flow Metab. 2011;31:68–81. doi: 10.1038/jcbfm.2010.158. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Jespersen SN, Ostergaard L. The roles of cerebral blood flow, capillary transit time heterogeneity, and oxygen tension in brain oxygenation and metabolism. J Cereb Blood Flow Metab. 2012;32:264–277. doi: 10.1038/jcbfm.2011.153. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Attwell D, Buchan AM, Charpak S, Lauritzen M, MacVicar BA, Newman EA. Glial and neuronal control of brain blood flow. Nature. 2010;468:232–243. doi: 10.1038/nature09613. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Buxton RB, Uludag K, Dubowitz DJ, Liu TT. Modeling the hemodynamic response to brain activation. Neuroimage. 2004;23 (Suppl1:S220–S233. doi: 10.1016/j.neuroimage.2004.07.013. [DOI] [PubMed] [Google Scholar]
- Vazquez AL, Fukuda M, Tasker ML, Masamoto K, Kim S-G. Changes in cerebral arterial, tissue and venous oxygenation with evoked neural stimulation: implications for hemoglobin-based functional neuroimaging. J Cereb Blood Flow Metab. 2010;30:428–439. doi: 10.1038/jcbfm.2009.213. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Vovenko E. Distribution of oxygen tension on the surface of arterioles, capillaries and venules of brain cortex and in tissue in normoxia: an experimental study on rats. Pflugers Arch. 1999;437:617–623. doi: 10.1007/s004240050825. [DOI] [PubMed] [Google Scholar]
- Lecoq J, Parpaleix A, Roussakis E, Ducros M, Houssen YG, Vinogradov SA, et al. Simultaneous two-photon imaging of oxygen and blood flow in deep cerebral vessels. Nat Med. 2011;17:893–898. doi: 10.1038/nm.2394. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sakadžić S, Roussakis E, Yaseen MA, Mandeville ET, Srinivasan VJ, Arai K, et al. Two-photon high-resolution measurement of partial pressure of oxygen in cerebral vasculature and tissue. Nat Meth. 2010;7:755–759. doi: 10.1038/nmeth.1490. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Masamoto K, Vazquez A, Wang P, Kim S-G. Trial-by-trial relationship between neural activity, oxygen consumption, and blood flow responses. Neuroimage. 2008;40:442–450. doi: 10.1016/j.neuroimage.2007.12.011. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Vazquez AL, Masamoto K, Fukuda M, Kim S-G. Cerebral oxygen delivery and consumption during evoked neural activity. Front Neuroenerg. 2010;2:11. doi: 10.3389/fnene.2010.00011. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lagarias JC, Reeds JA, Wright MH, Wright PE. Convergence properties of the nelder–mead simplex method in low dimensions. SIAM J Optim. 1998;9:112–147. [Google Scholar]
- Dash R, Bassingthwaighte J. Blood HbO2 and HbCO2 dissociation curves at varied O2, CO2, pH, 2,3-DPG and temperature levels. Ann Biomed Eng. 2004;32:1676–1693. doi: 10.1007/s10439-004-7821-6. [DOI] [PubMed] [Google Scholar]
- Boas DA, Jones SR, Devor A, Huppert TJ, Dale AM. A vascular anatomical network model of the spatio-temporal response to brain activation. Neuroimage. 2008;40:1116–1129. doi: 10.1016/j.neuroimage.2007.12.061. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fang Q, Sakadzic S, Ruvinskaya L, Devor A, Dale AM, Boas DA. Oxygen advection and diffusion in a three-dimensional vascular anatomical network. Opt Express. 2008;16:17530–17541. doi: 10.1364/oe.16.17530. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Reichold J, Stampanoni M, Lena Keller A, Buck A, Jenny P, Weber B. Vascular graph model to simulate the cerebral blood flow in realistic vascular networks. J Cereb Blood Flow Metab. 2009;29:1429–1443. doi: 10.1038/jcbfm.2009.58. [DOI] [PubMed] [Google Scholar]
- Huppert TJ, Allen MS, Benav H, Jones PB, Boas DA. A multicompartment vascular model for inferring baseline and functional changes in cerebral oxygen metabolism and arterial dilation. J Cereb Blood Flow Metab. 2007;27:1262–1279. doi: 10.1038/sj.jcbfm.9600435. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zheng Y, Johnston D, Berwick J, Chen D, Billings S, Mayhew J. A three-compartment model of the hemodynamic response and oxygen delivery to brain. Neuroimage. 2005;28:925–939. doi: 10.1016/j.neuroimage.2005.06.042. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.