Multiphasic DNA Adsorption to Silica Surfaces under Varying Buffer, pH, and Ionic Strength Conditions

Abstract

Reversible interactions between DNA and silica are utilized in the solid phase extraction and purification of DNA from complex samples. Chaotropic salts commonly drive DNA binding to silica, but inhibit DNA polymerase amplification. We studied DNA adsorption to silica using conditions with or without chaotropic salts through bulk depletion and Quartz Crystal Microbalance (QCM) experiments. While more DNA adsorbed to silica using chaotropic salts, certain buffer conditions without chaotropic salts yielded a similar amount of eluted DNA. QCM results indicate that under stronger adsorbing conditions, the adsorbed DNA layer is initially rigid, but becomes viscoelastic within minutes. These results qualitatively agreed with a mathematical model for a multiphasic adsorption process. Buffer conditions that do not require chaotropic salts can simplify protocols for nucleic acid sample preparation. Understanding how DNA adsorbs to silica can help optimize nucleic acid sample preparation for clinical diagnostic and research applications.

INTRODUCTION

Nucleic acids must be isolated, purified and concentrated from complex samples for both research and clinical diagnostic applications.^1-3 Nucleic acid sample preparation is commonly accomplished through solid phase extraction (SPE), which relies on the reversible interactions between nucleic acids and a solid support, such as silica. The silica solid support required for these methods is implemented either in the form of a filter membrane³ or as silica-coated magnetic particles.¹ A better understanding of the fundamental processes involved in DNA adsorption to silica surfaces under different experimental conditions such as buffer composition, pH, and ionic strength will help optimize methods for preparing nucleic acid samples.

To drive adsorption of DNA to silica, typical SPE protocols require buffers with high concentrations of chaotropic salts, such as guanidinium thiocyanate, plus ethanol or other organic solvents.² After washing to remove impurities, DNA is eluted from the surface using a high pH, low ionic strength buffer that is compatible with subsequent polymerase based DNA amplification methods, such as the Polymerase Chain Reaction (PCR). A common problem arises when residual chaotropic salts and ethanol are carried over into the amplification reaction and inhibit polymerase amplification.⁴ Recently, several methods have been reported that do not require chaotropic salts and organic solvents, but utilize a pH dependent anion exchange approach.^5,6 Another report suggested that nucleic acids bind to silica, independent of chaotropic salts, under acidic conditions in the presence of kosmotropic salts.⁴ At low pH and high ionic strength, DNA can also bind to sand, which is similar to silica.^7,8

DNA adsorption to silica has been attributed to multiple and sometimes varying driving forces. In general, the DNA-silica interaction is electrostatically unfavorable, since under most experimental conditions DNA and the silica surface are both negatively charged,^9,10 with silica having a point of zero charge around 1.5 to 3.6.¹⁰ Silica surfaces can exist in a number of possible conformations and associated protonation states, giving rise to a range of accessible pK_a values.^10-12 These surfaces can display one or two OH groups per surface silica atom, called isolated or geminal hydroxyls, in addition to bridging ethereal oxygens between silica surface atoms.¹³ Perfect SiO₂ (Quartz) exists mainly in the bridging ethereal oxygen conformation, and has no free surface hydroxyl groups. Acid treatment of silica hydrolyzes the surface, increases the concentration of surface silanol groups,^14,15 and removes metal impurities at the surface.¹² Lowering the solution pH decreases the silica’s negative surface charge density, thereby reduces the electrostatic repulsion between DNA and silica.^9,16,17 Likewise, adding electrolytes shields electrostatic interaction, and compresses the electrostatic double layer surrounding the DNA and the silica surface, which facilitates DNA adsorption to silica.^7-9,17,18 Some investigators have proposed that DNA adsorption occurs via hydrogen bonding between unwound nucleotides and the silica surface.^16,19,20 Alternatively, DNA adsorption to silica has been attributed to an increase in entropy, whereby ordered water molecules that solvate the DNA and surface are released during the adsorption process.⁹ Entropy-driven adsorption of DNA to surfaces has also been explained by the hydrophobic effect.^21,22 The total amount of DNA that adsorbs to silica, and the conformation of DNA adsorbed at the silica surface depends on solution pH, ^{7-9,16,18,19,23,24} ionic strength, ^{7-9,17,18,20,24-26} electrolyte type and valency, ^7,8,17,18,25 and conformation of DNA (linear, plasmid, supercoiled). ^8,9,19,27

One can determine the total amount of DNA adsorbed to solid supports through equilibrium bulk depletion assays.^7-9,24,28 However, these experiments do not provide direct evidence of DNA conformational changes, nor do they allow for real-time monitoring of adsorption kinetics. The conformation of DNA adsorbed to surfaces has been studied directly or indirectly using other methods including evanescent wave-induced fluorescent spectroscopy,²⁰ atomic force microscopy (AFM),^23,29-31 voltammetry, ^32,33 microscopy using intercalating fluorescent dyes,^16,19,23 dual polarization interferometry,^26,34-38 and quartz crystal microbalance with dissipation monitoring (QCM-D).^{17,18,25,39,40}

QCM-D can measure the kinetics of DNA adsorption to a piezoelectric silica (quartz) crystal. For thin, rigid, and uniform films, the adsorbed mass can be calculated using the Sauerbrey equation:

$$\mathrm{\Delta }m=\frac{-C\Delta F_n}{n}$$ (1)

where Δm is the change in mass, ΔF_n is the change in the frequency of oscillation (Hz) at an overtone n, and C is a constant. However, for viscoelastic biomolecular films, ΔF_n/ n is not constant, and therefore the Sauerbrey equation is not valid. ^36,41-43 QCM-D also measures the change in dissipated energy, ΔD, of the oscillating crystal/adsorbed substrate film. Changes in dissipation are associated with changes in the viscoelastic nature of the adsorbed film. In a plot of ΔD_n vs ΔF_n, higher slopes (larger values of |ΔD_n/ΔF_n|) indicate a less rigidly adsorbed film.^17,18,44 For example, QCM-D experiments suggest that increasing the ionic strength of monovalent electrolytes results in DNA adsorbing to silica in a more rigid and compact conformation.^17,18

In this study, we experimentally characterized the binding kinetics, surface coverage, and viscoelastic properties of DNA adsorbed to silica surfaces using bulk DNA depletion experiments and QCM-D as complementary tools. We analyzed the effect of different buffers and varying pH and ionic strength conditions on the adsorption characteristics. We included a series of buffers that do not contain chaotropic salts, and are thereby more compatible with downstream polymerase amplification. Although QCM-D data cannot identify specific structural conformations, we hypothesized that the measured change in viscoelastic properties of the adsorbed DNA layer are correlated with relative conformational changes of adsorbed DNA. We developed a mathematical model for a multiphasic DNA adsorption process, which is consistent with this hypothesis. The knowledge gained from this study can contribute to future development and optimization of novel solid phase nucleic acid extraction protocols, and can further the understanding of the underlying fundamental processes.

MATERIALS AND METHODS

General Reagents

UltraPure™ salmon sperm DNA (15632-011) was purchased from Invitrogen (Carlsbad, Ca). TE buffer refers to 10 mM tris(hydroxymethyl) aminomethane containing 1 mM ethylenediaminetetraacetic acid, at pH 7.4. All buffers were prepared using volumetric flasks and were sterile filtered using 0.2 μm vacuum filter units. 1 M KOH and concentrated HCL were used to adjust the pH. When KOH was required to raise the pH, we accounted for the added potassium when reporting the final potassium concentration. The composition of buffers used was 50 mM Tris with 6 M sodium perchlorate salt (SP), 0.25 M acetic acid (AA), 0.25 M glycine (GL), and 0.2 M sodium citrate (SC). Sodium citrate buffer was prepared by combining sodium citrate monobasic and sodium citrate dihydrate solutions.

Bulk depletion experiments

Tubes for bulk depletion measurements were acquired from Value Plastics (VPB0850400N, Fort Collins, CO). Caps for the tubes (65803) were obtained from Qosina (Edgewood, New York). The FineMix30 oscillator was custom ordered from Claremont BioSolutions (Upland, CA). Sigma-Aldrich (St. Louis, MO) silicon dioxide particles (S5631) were washed with 2 M HCL, rinsed with copious amounts of NanoPure water, and then dried overnight at 225°C.^9,24 The surface area of these particles was 4.61 ± 0.23 m²/g, as measured via BET for triplicate samples (test T404, performed by Porous Materials Inc., Ithaca, New York). MagPrep Silica particles (70912) from Merck (Darmstadt, Germany) had a surface area of 18 m²/g based on material specifications provided by the distributor (EMD Chemicals, a subsidiary of Merck). The MagPrep particles were washed once with the test solution immediately prior to testing. For experiments using MagPrep beads, the tubes contained 250 μg beads and 100 ng/uL salmon sperm DNA in 150 μL of the buffer under investigation. For experiments using Sigma Aldrich SiO₂ particles, the tubes contained between 3 and 6 mg of the particles. The precise mass of particles in each tube was recorded and used for further calculations. The tubes further contained 150 μL of the buffer under investigation with either 200 ng/uL salmon sperm DNA for experiments using SP buffer, or 80 ng/uL for all other buffers and conditions. For each condition, we included 3-5 replicate sample tubes with particles, DNA and buffer, and 3 replicate control tubes containing the same concentration of DNA in buffer without particles. All tubes were vigorously agitated by the FineMix30 oscillator (Supporting Information, S1) at 10 ± 2 Hz for a fixed period of time at room temperature (~ 22 ± 2°C). We monitored the frequency of oscillation using the Extech (Waltham, Massachusetts) combination photo tachometer (461825). After this incubation period, particles were removed from the liquid suspension either magnetically for the MagPrep beads or by centrifugation (5 minutes at 17,200 rcf) for the Sigma-Aldrich silica particles. We determined the concentration of DNA remaining in solution in each sample and control tube spectrophotometrically at 260 nm using the NanoQuant or via the PicoGreen Assay, which uses an intercalating dye to quantify dsDNA. For the PicoGreen Assay, standards and blanks were prepared in the same test solution as the samples. The samples, controls, standards, and blanks were diluted 1:160 or 1:320 in TE buffer. We added 100 μL of the diluted samples to 100 μL of 2x Quant-iT™ PicoGreen® dye (Invitrogen, P7589m Carlsbad, Ca) in a 96 well Microtiter plate (7905, Waltham, MA). After mixing and 10 min incubation, we read the fluorescence intensity using the SpectraMax GeminiEM Fluorescence Microplate Reader with excitation and emission set to 485 and 525 nm, respectively. To calculate the amount of DNA adsorbed to the particles we used the difference of DNA concentrations between sample and control tubes, i.e. tubes with and without particles, and the known particle mass, DNA concentration, and sample volume initially added. For experiments that included wash and elution steps, the silica particles were briefly washed with 150 μL of the same buffer condition (without DNA) used during the adsorption step, and elution was performed by adding 150 μL of TE pH 8.8 and mixing for 30 minutes at 10 Hz. The DNA concentration in the wash and elution buffers was determined via UV absorbance as described above.

QCM-D

Liquid handling accessories (QLH401), the Q-Sense (E4) device, and silicon dioxide crystals (QSX-303) were acquired from Q-sense (Gothenburg, Sweden). Before and after each experiment, the QCM crystals were exposed to UV-ozonation for 30 minutes, followed by washing in 2% Hellmanex solution (Hellma GmbH & Co.) for 5 minutes, and several wash steps with ultrapure water. The cleaned crystals were then immersed for 10 minutes in 2 M HCL, followed by rinsing with ultrapure water and ethanol. The QCM crystals were then dried with nitrogen gas, followed by another UV-ozonation treatment. Additionally, before and after each experiment, the QCM-D chambers were cleaned with 2% Hellmanex solution followed by thorough rinsing with NanoPure water. All experiments were conducted using a flow rate of 300 μL/min and a stabilized temperature of 20°C. For each experiment, we established a baseline by passing the blank buffer under investigation (without DNA) through the chamber for 10 minutes. The respective buffer containing 10 ng/μL salmon sperm DNA was then passed over the crystal for 50 minutes, followed by 30 minutes of the blank buffer solution. After experiments using sodium perchlorate, the crystals and tubing/fittings were replaced.

RESULTS AND DISCUSSION

Bulk Depletion DNA Adsorption Experiments

We used bulk depletion experiments to determine the amount of DNA adsorbed by two different silica particle types, MagPrep silica particles and pure silica particles, under varying buffer conditions. The MagPrep silica particles are silica-coated magnetic nanoparticles commercialized specifically for use in nucleic acid purification.^1,4 However, the surface chemistry of these particles is proprietary, and might not represent a pure silica surface. Because of this, we also used finely ground pure silica as a second solid matrix for bulk depletion experiments. For the high chaotropic salt condition, we used 6 M sodium perchlorate in 50 mM Tris, analogous to the study reported by Melzak et al.⁹ Others have reported that nucleic acids bind to the MagPrep silica particles in an acetic acid buffer at low pH containing the kosmotropic salt ammonium sulfate.⁴ We found that in this low pH acetic acid buffer, ionic strength in general, rather than the presence of kosmotropic ions, seems to drive DNA adsorption. For equal concentrations of either KCl or ammonium sulfate, buffers containing KCl resulted in slightly higher amounts of adsorbed DNA (Supporting Information, S2). Therefore, we studied DNA adsorption to silica from an acetic acid buffer, in addition to glycine and citric acid as buffers, since these compounds are structural derivatives of acetic acid. Glycine contains a primary amine in addition to the carboxylate group, and exists mainly in the zwitterionic form under the pH conditions used in this study. Citrate (2-Hydroxy-1,2,3-propanetricarboxylate) contains three carboxylate groups joined via a carbon aliphatic backbone.

To enable comparisons across the different buffer types, we set all buffers at pH 5 with similar electrolyte conditions: Each buffer contained 400 mM potassium ions, in the form of KCl for the glycine and sodium citrate buffers, while the acetate buffer contained a combination of KCl and potassium acetated (KOAc). The sodium citrate contained an additional 420 mM of sodium ions. The cation electrolyte is involved in DNA charge screening, and therefore likely plays a more important role than the anion.⁸ In all experiments, the total DNA amount in solution was ≥1.7x of the amount of DNA adsorbed. Although the total bulk DNA concentration was not constant, DNA was present in excess. In all bulk DNA depletion experiments, DNA solutions were vigorously mixed with the different particles for 2 hours, which allowed the system to plateau (Supporting Information, S3). To determine the DNA concentration of the supernatant, we used UV absorption at 260 nm or a PicoGreen intercalating dye assay, which yielded similar results.

Our data indicates that the amount of DNA adsorbed depends on the particle type and buffer composition (Figure 1A). For all buffer conditions, the amount of DNA adsorbed per unit area to the MagPrep silica particles was significantly higher than the amount adsorbed to the Sigma-Aldrich silica particles, likely because the MagPrep particles have been optimized for DNA extraction, and may have additional surface modifications. However, both surfaces followed the same trends with regards to the effect of buffer on the amount of DNA adsorbed. The 6M sodium perchlorate solution shows the highest amount of DNA adsorbed, followed, in descending order, by the acetic acid, glycine, and sodium citrate buffers. Our results obtained for DNA adsorption to the Sigma-Aldrich silica particles from buffer containing sodium perchlorate were in good agreement with results obtained under almost identical conditions by another group (~ 800 μg DNA/m² silica).⁹

Figure 1.

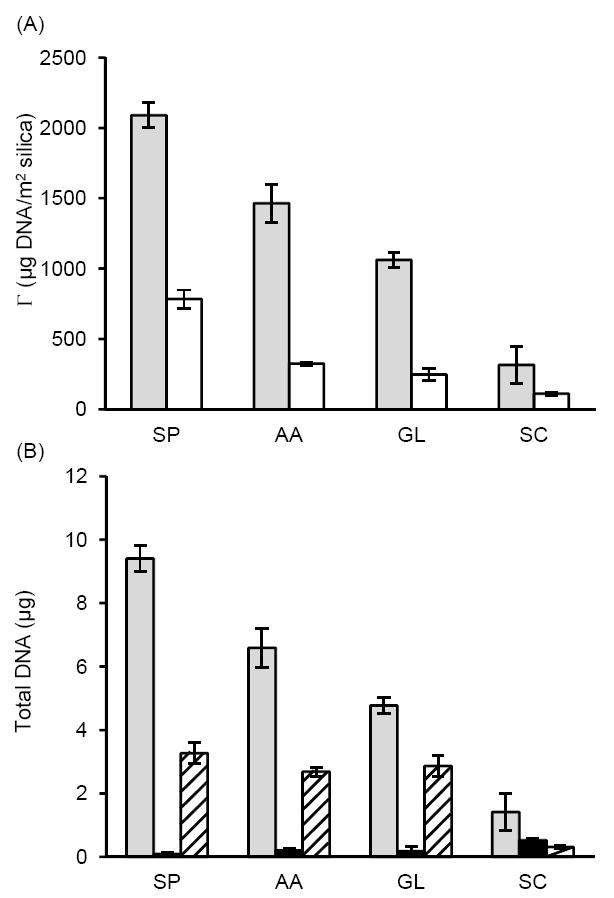
Bulk depletion experiments. (A) DNA adsorbed to silica (mass per unit area) at pH 5 in 6 M sodium perchlorate (SP), acetic acid containing 400 mM K⁺ (AA), glycine containing 400 mM KCl (GL), or sodium citrate containing 400 mM KCl (SC), using MagPrep (grey) or Sigma-Aldrich (white) silica particles. (B) Total DNA adsorbed to 250 μg MagPrep silica particles as function of buffer (grey); DNA recovered after a brief wash step using the same buffer without DNA (black); DNA eluted in TE buffer pH 8.8 (hashed).

The acetic acid, glycine, and sodium citrate buffers were at the same pH and contained comparable electrolyte conditions. This suggests that the buffer ions play a role in the DNA adsorption process beyond simply maintaining the pH. Glycine is known to adsorb to silica, possibly through the amine group,⁴⁵ but other conformations have been proposed.⁴⁶ Acetic acid adsorbs to silica, presumably through the carboxyl group.⁴⁷ Differences in the charge, structure, and adsorption conformation of glycine and acetic acid to silica may cause differences in the adsorption and elution profiles of DNA. Alternatively, the buffer ions may interact with DNA itself in a manner that influences the adsorption and elution characteristics. While citrate is known to bind to DNA in the presence of divalent cations,^48,49 our conditions included only monovalent salts.

DNA adsorption to a silica surface is just the first step required in solid phase DNA extraction. After washing to remove impurities, DNA is eluted from the surface using a higher pH, low ionic strength buffer that is compatible with downstream amplification and detection. With this in mind, we determined the amount of DNA that could be eluted from the MagPrep beads under the different buffer conditions (Figure 1B). Although sodium perchlorate led to the highest amount of DNA adsorbed, the amount of DNA eluted was comparable with acetic acid and glycine. These results suggest that it is more difficult to detach DNA that adsorbs to silica in the presence of high concentrations of chaotropic salts, which is likely the reason why many nucleic acid purification protocols require heating during the elution step to obtain better yield.^1,4 However, this heating step requires additional instrumentation and complicates the protocol. Additionally, residual chaotropic salts can inhibit DNA polymerases used in downstream nucleic acid amplification. Therefore, most industry-standard SPE protocols require extensive wash steps prior to elution.^4,9 SPE protocols that do not use chaotropic salts, including established methods^5,6 and the glycine conditions used herein, are more compatible with polymerase amplification and require fewer wash steps prior to elution.

For the glycine buffer, we investigated in more detail the influence of ionic strength and pH on DNA adsorption to silica particles. Our results (Figure 2) indicate that increasing the concentration of KCl increases the amount of DNA adsorbed, consistent with previous reports.^7,8 The amount of DNA adsorbed to silica particles decreased sharply between pH 6 and 8. These results are qualitatively similar to studies performed with sodium perchlorate, wherein a sharp decrease in the amount of DNA adsorbed to silica was observed at pH values greater than 6.5.⁹ Increasing the pH increases the electrostatic repulsion between DNA and silica, which is likely a major factor contributing to the decreasing quantity of adsorbed DNA.

Figure 2.

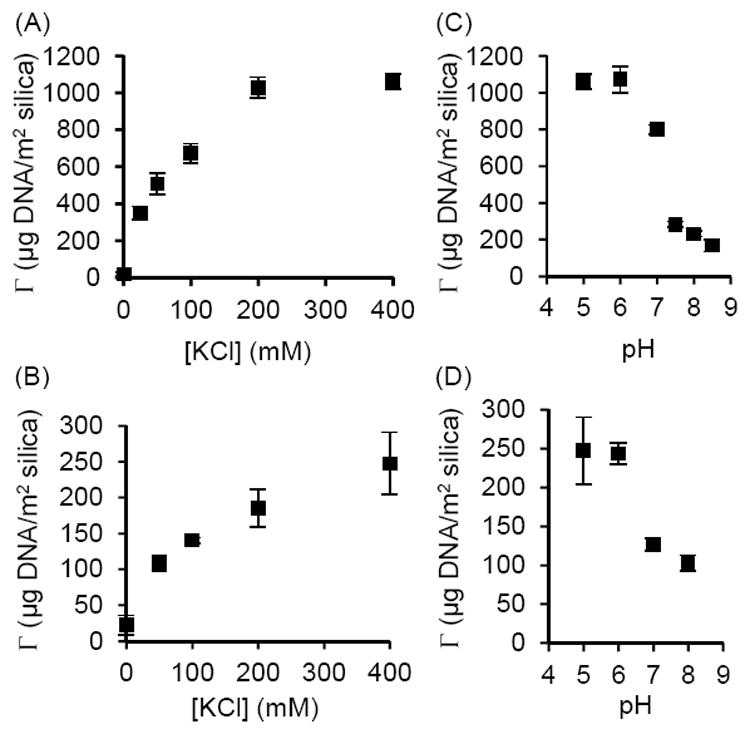
DNA adsorbed to (A) MagPrep silica beads and (B) Sigma-Aldrich silica particles as function of KCl concentration at pH 5 in glycine buffer. Increasing the concentration of KCl increased the amount of DNA adsorbed. DNA adsorbed to (C) MagPrep silica beads and (D) Sigma-Aldrich silica particles as function of pH in glycine buffer with 400 mM KCl. The amount of DNA adsorbed decreases sharply between pH 6 and 8.

QCM-D DNA Adsorption Experiments

To obtain information about the adsorption kinetics in real time, and to investigate the viscoelastic behavior of DNA adsorbed to the surface, we studied DNA adsorption to a quartz (SiO₂) surface using QCM-D. In these experiments, we found that surface pre-treatment affects the amount of DNA adsorbed, and the shape of the ΔF and ΔD response curves. Very little DNA adsorbs to the quartz surface unless the crystals were acid washed, and treated at low pH prior to the final water rinse. Acid treatment increases the concentration of surface silanol groups,^14,15 which likely facilitates DNA binding to silica. At low pH, the silica’s negative surface charge density decreases, this reduces the electrostatic repulsion between DNA and silica.^9,16,17 Acid washed silica particles are used in most bulk depletion experiments reported in the literature^2,7-9 and in this study. We therefore implemented this pre-treatment protocol to make bulk depletion and QCM-D results more comparable. However, related QCM-D studies of DNA adsorption to quartz crystals either did not clearly specify the surface cleaning and pre-treatment process,¹⁷ or used only a basic detergent (Hellmanex) rinse, but no acid treatment.¹⁸ This difference in surface pre-treatment may explain some of the differences observed between our experiments and previous reports. In our studies, we further used a relatively high flow-rate of 300 μL/min, compared to 100 μL/min in other studies,^17,18 to minimize any mass transport artifacts in the data.

Analogous to the bulk depletion experiments (Figure 1), our first set of QCM-D experiments was aimed at understanding the impact of different buffer compositions on DNA adsorption (Figure 3). The ΔF and ΔD data as function of time show that DNA adsorption out of the sodium perchlorate, acetic acid and glycine conditions is distinctly multi-phasic, but less so for the sodium citrate buffer. The mass of DNA adsorbed in these QCM-D studies cannot readily be determined, since the Sauerbrey equation relating ΔF to mass is not valid throughout the entire adsorption process (Supporting Information, S4 and S5). In addition, the measured ΔF includes contributions from co-adsorbed water.⁵⁰ However, the general trends are comparable for the bulk depletion and QCM-D results.

Figure 3.

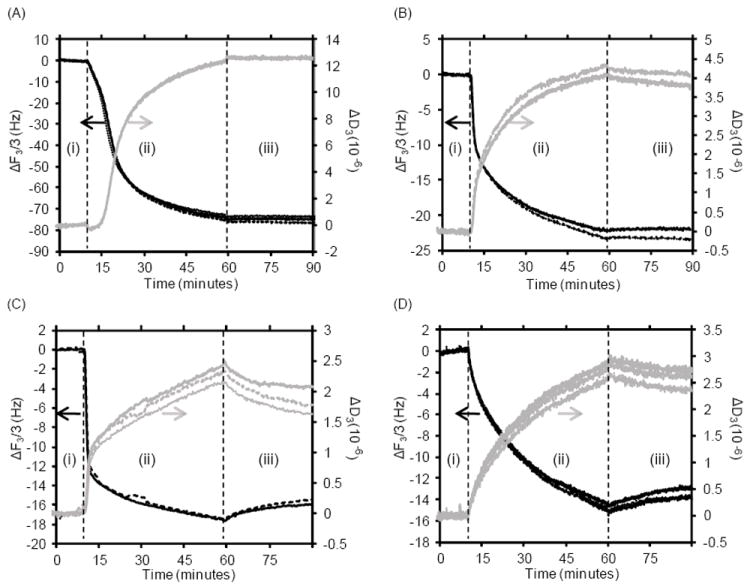
QCM-D results showing changes in resonance frequency (ΔF) and dissipation (ΔD) as function of time for replicates of DNA adsorption to quartz at pH 5 in: (A) 6 M sodium perchlorate (SP), (B) acetic acid containing 400 mM K⁺ (AA), (C) glycine containing 400 mM KCl (GL), (D) sodium citrate containing 400 mM KCl (SC). A baseline was established using the buffer solution (without DNA) for 10 minutes (i), followed by 50 minutes of the buffer solution with 10 ng/μL DNA (ii), then 30 minutes of the buffer solution as a rinse (iii).

During the initial phase of DNA adsorption to the quartz surface, the Sauerbrey equation is valid for the sodium perchlorate, acetic acid, and glycine conditions, since the calculated Sauerbrey masses overlap for the various overtones (Supporting Information, S4 and S5). This indicates that initially the DNA is adsorbed as a rigid film. Since the Sauerbrey equation is valid, it is possible to accurately determine the initial rates of mass adsorbed per unit time from the change in Sauerbrey mass. The sodium citrate buffer condition showed a rapid divergence of the calculated Sauerbrey masses for the various overtones, and was therefore not considered in this analysis.

The initial adsorption appears to be fastest out of glycine buffer (1.8 mg/(m² min)), followed by acetic acid buffer (1.5 mg/(m² min)). For the sodium perchlorate containing buffer, the initial adsorption rate is significantly lower (0.6 mg/(m² min)). It therefore appears that the rate of DNA adsorption to silica is modulated by the buffer composition. The linear regime, in which the Sauerbrey masses overlap, lasts much longer for the sodium perchlorate condition (~ 6 min), compared to the glycine and acetic acid buffers (< 1 min), which is consistent with the much stronger adsorption of DNA to silica out of the sodium perchlorate solutions. After the time point at which the Sauerbrey masses diverge, the curves start to decrease in slope and plateau for the glycine and acetic acid buffers, while the curves increase in slope for the sodium perchlorate containing buffer. A possible cause for this observation is discussed later under mathematical modeling.

The viscoleastic nature of the adsorbed film can be inferred from the graph of ΔD versus ΔF (Figure 4). The slope of this graph (|ΔD/ΔF|) is related to the energy dissipated per unit mass adsorbed.^17,18,44 Amongst the different buffers used in this experiment, only the sodium citrate condition resulted in a predominately linear response (Figure 4) with a relatively constant |ΔD/ΔF| except for a slight divergence at the very early time points (Supporting Information, S6). This indicates that the energy dissipated per unit mass adsorbed was relatively constant, and that the viscoelastic nature of the film did not change significantly during the adsorption process. Conversely, the slopes (|ΔD/ΔF|) for the sodium perchlorate, acetic acid, and glycine conditions significantly changed during the adsorption process, with an initially lower slope which indicates that the DNA film adsorbed is initially more rigid, followed by an increase in slope, which indicates that the DNA layer becomes viscoelastic in later stages of the adsorption process. A similar change in |ΔD/DF| was observed during the adsorption of cationic polyelectrolytes to silica,⁴⁴ which was interpreted in an analogous manner.

Figure 4.

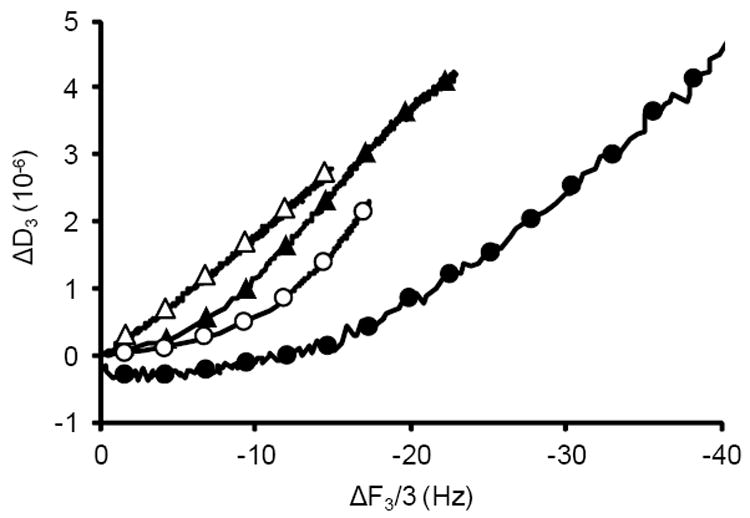
QCM-D results showing ΔD as a function of ΔF for DNA adsorption to quartz at pH 5 in (●) 6 M sodium perchlorate, (○) glycine containing 400 mM KCl, (▲) acetic acid containing 400 mM K⁺, or (Δ) sodium citrate containing 400 mM KCl. Only the sodium citrate condition showed a predominately linear relationship between ΔD and ΔF. The reported results represent the average of replicate runs shown in Figure 3, phase (ii) using the third overtone. Each replicate provided a graph similar to the average.

We have observed a positive correlation between the elution yield (i.e. the ratio of [DNA] eluted / [DNA] adsorbed) in the bulk depletion experiments and the maximum slope |ΔD/ΔF|_max found in the QCM-D experiments (Supporting Information, S7). This may indicate, as intuitively expected, that DNA which is more rigidly adsorbed to the surface is harder to elute. Adsorption out of glycine buffer resulted in the largest |ΔD/ΔF|_max, meaning that the DNA layer is more viscoelastic in later stages of the adsorption process than for the other conditions, and therefore is easier to elute.

We used QCM-D to further investigate the influence of ionic strength and pH on DNA adsorption to quartz out of the glycine buffer (Figure 5 and Supporting Information, S8). The total mass adsorbed was largest at lower pH and higher ionic strength (400 mM KCl pH 5, compared to 200 mK KCl, pH5 or 400 mM KCl, pH6), as inferred by a larger magnitude of ΔF. This observation is in agreement with the bulk depletion experiments (Figure 2). Additionally, we found that the pH and ionic strength of the solution affects the viscoelastic nature of the adsorbed DNA film. Lower ionic strength (200 vs 400 mM KCl) and higher pH conditions (pH 6 vs pH 5) result in a predominately linear relationship between ΔD and ΔF (R² > 0.99), in agreement with the constant |ΔD/ΔF| observed for DNA adsorption to quartz under similar conditions by another group.¹⁷ Binding of DNA to silica out of sodium citrate buffer resulted in similar QCM-D data. We have therefore categorized as “weaker binding” conditions the DNA adsorption to quartz out of glycine pH5 containing 200 mK KCl or pH6 containing 400 mM KCl, and out of the sodium citrate buffer. These “weaker binding” conditions all have a relatively constant |ΔD/ΔF| and the Sauerbrey mass rapidly diverges for different overtones, indicating that the adsorbed DNA films is predominantly viscoelastic throughout the adsorption process. Conversely, we have defined as “stronger binding” conditions the DNA adsorption to quartz out of glycine at pH 5 containing 400 mM KCl, acetic acid buffer with comparable pH and ionic strength, and the 6M sodium perchlorate solution. These “stronger binding” conditions all have a maximum |ΔF| which is much larger than for “weaker binding” conditions and clear non-linear behavior for ΔD vs. ΔF, which indicates a multi-phasic DNA adsorption process with a DNA layer that is initially more rigid but becomes viscoelastic.

Figure 5.

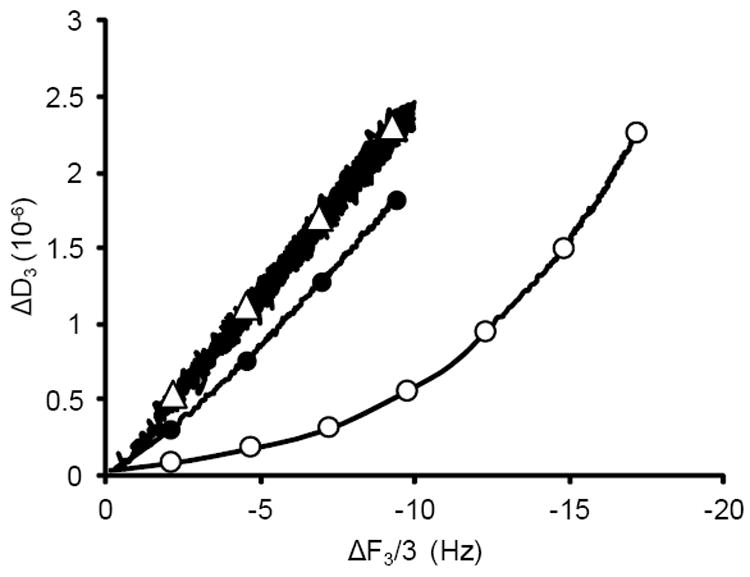
QCM-D results showing ΔD as a function of ΔF for DNA adsorption to quartz from glycine buffer (○) at pH 5 containing 400 mM KCl, (●) at pH 5 containing 200 mM KCl, and (Δ) at pH 6 containing 400 mM KCl. The reported results represent the average of triplicate runs using the third overtone.

Mathematical Model to Describe DNA Adsorption

We have developed a mathematical model to qualitatively describe our experimental observations under “weaker” and “stronger” binding conditions. In a simplified model, the DNA can exist in three states only: in solution, rigidly bound, and loosely bound to the surface (Figure 6). In reality, the transition from rigid to loosely bound DNA likely involves multiple intermediates, therefore we do not anticipate that the model perfectly agrees with the experimental data. The proposed model (Figure 6) can be captured by equations (2) to (4).

$$A+\mathit{nS}\underset{k_2}{\overset{k_1}{\rightleftarrows }}B$$ (2)

$$B\underset{k_4}{\overset{k_3}{\rightleftarrows }}C+(n-1)S$$ (3)

$$A+S\underset{k_6}{\overset{k_5}{\rightleftarrows }}C$$ (4)

Figure 6.

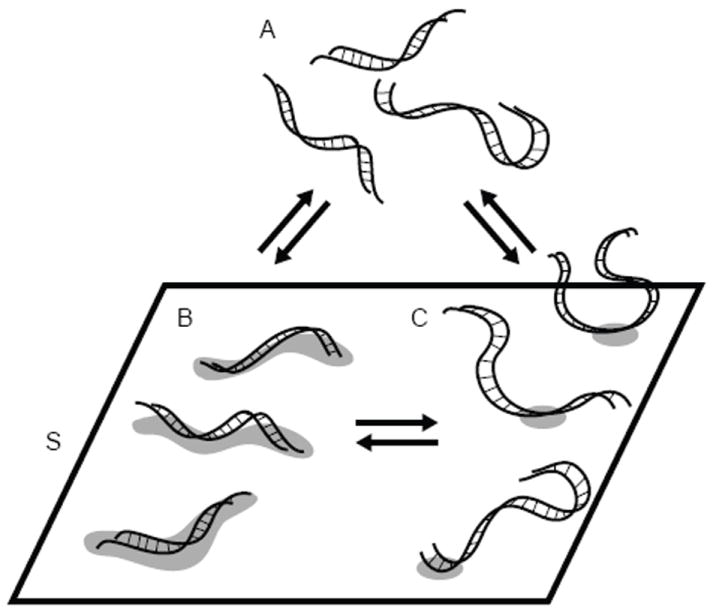
Model for DNA adsorption to silica. A represents bulk DNA in solution, S denotes the available surface binding sites. B and C represent DNA tightly and loosely bound to the surface through multiple binding sites or a singe binding site, respectively.

We used simple mass-action kinetics for the equilibrium reactions between these states to obtain a numerical mathematical model for the adsorption process, as a function of initial concentrations for the three states, concentration of surface binding sites, and the forward or reverse reaction rate constants k₁ through k₆. To further reduce the considerable number of degrees of freedom in this model, we implemented additional assumptions. We hypothesize that under “stronger binding” conditions, DNA initially adsorbs to the silica surface in a relatively compact and flat conformation through n “binding sites” S (Figure 6, transition from A to B). “Binding site” here represents the smallest required footprint for a stable interaction between the silica surface and a DNA molecule. We further hypothesize that as the surface coverage increases, some of the adsorbed DNA strands break contact with the silica surface and extend into the solution to allow room for additional DNA to adsorb (Figure 6, transition from B to C). This transition releases n-1 binding sites for the adsorption of additional DNA strands. If these are the predominant processes, then we can assume that the transitions from A to B, and from B to C, are irreversible, meaning k₂ and k₄ can be treated as zero, and that the transition from A to C does not occur, therefore k₅, and k₆ can be treated as zero. We have combined selected parameters into dimensionless groups (denoted by corresponding lower case letters), and have included the complete set of scaled differential equations that describe this simplified model under Supporting Information (Mathematical Model I). As additional boundary conditions, the initial dimensionless concentrations of b(0) and c(0) are set to zero, the initial dimensionless concentration of free surface binding (s(0)) sites is set to 1 (100%), and ε, which is equal to the ratio of the dimensional initial concentrations of DNA in solution and available surface binding sites, was set to 10^-2, meaning a 100 fold excess of DNA is present compared to surface binding sites. For the experimental data, we assume that |ΔF| is linearly proportional to the mass of DNA adsorbed. For comparison purposes, results for the mathematical model and experimental data were normalized to one in the x and y dimensions.

As an example data set for “stronger binding” conditions, we used DNA adsorption out of glycine buffer pH 5 containing 400 mM KCl. The general biphasic shape of the QCM-D data is well represented by the model. As shown in Figure 7A, initial rapid adsorption of tightly bound DNA (b(t), orange curve) is followed by a slower, almost linear increase in the loosely bound form (c(t), blue curve), resulting in a graph for total DNA adsorbed (red curve) which closely mimics the experimental data (black curve).

Figure 7.

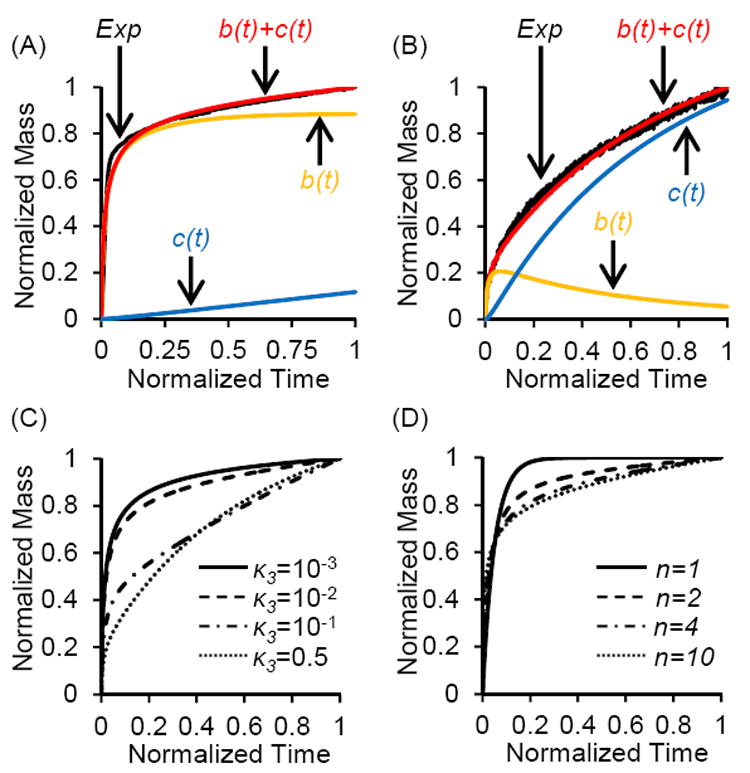
Mathematical modeling of a multiphasic DNA adsorption process, wherein DNA initially adsorbs to silica in a tightly bound conformation B, which converts to a loosely bound conformation C (Figure 6). (A) and (B) Experimental data (EXP) for DNA adsorption from (A) glycine, pH 5, 400 mM KCL (stronger binding), and (B) glycine, pH 6, 400 mM KCL (weaker binding), plus simulated data for time dependent concentration of tightly bound DNA (b(t)), loosely bound DNA (c(t)), and total bound DNA (b(t) + c(t)). Normalized dimmensioless data was simulated using (A) κ₃=7×10^-3, n=4, and (B) κ₃=0.4, n=4. We observed good agreement between experimental data (EXP) and simulated total bound DNA, with R² values of (A) 0.966 and (B) 0.993. (C) Effect of varying on κ₃ the simulated curve shape (n=4). (D) Effect of varying the number of binding sites n on the simulated curve shape (κ₃=10^-2). For all graphs, ε was 10^-2 and t’ was 20.

As an example data set for the “weaker binding” conditions, we used DNA adsorption out of glycine buffer pH 6 containing 400 mM KCl. For this condition, we originally tried to fit the data to a model that assumes direct reversible adsorption into the loosely bound form, i.e. transition from A to C (Supporting Information, Mathematical Model II). This alternate model is dictated by k₅ and k₆, with all other rate constants set to zero. However, we were unable to obtain good agreement between the experimental and simulated data for this alternate model (Supporting Information, Figure S9). For all three weaker binding conditions, the initial phase in the graph of ΔD vs. ΔF deviates from linear behavior (Supporting Information, Figure S6), and has a lower slope, indicating the brief presence of a more rigid layer. This observation supports fitting the weaker binding condition to the same bi-phasic model (initial tight binding, then conversion to loosely bound form) as the stronger binding condition. As shown in Figure 7B, there is a small initial accumulation of tightly bound DNA (orange curve) that subsequently decreases over time, with loosely bound DNA (blue curve) becoming the dominant conformation. Using this model, we obtained good agreement between simulated (red) and experimental data (black).

The bi-phasic model with transition from A to B, then B to C has three main variables. The first variable, κ₃, is a dimensionless group proportional to k₃ / k₁, i.e. the rates for conversion of tightly into loosely bound DNA (Figure 6, transition from B to C) versus initial adsorption from solution into the tightly bound DNA form (Figure 6, transition from A to B). Increasing κ₃ from 0.01 to 0.5 dramatically decreases the magnitude of the initial rapid rise of the curve (Figure 7C), while the curve does not change significantly when decreasing κ₃ below 0.01. “Weaker binding” conditions that favor loosely bound forms therefore have a larger value for κ₃ and a more gradual initial rise. For values of κ₃ below 0.01, meaning relatively slow conversion from B to C compared to initial adsorption of B, the difference in curve shape becomes less pronounced. In our example data sets, the “stronger binding” curve was best fit with a κ₃ of 0.007, while the “weaker binding” curve was best fit with a κ₃ of 0.4. This ~60 fold increase in κ₃ means that for the “weaker binding” example data set, the DNA initially adsorbed in a rigid conformation is rapidly converted to loosely bound DNA.

The second variable, n, represents the number of “binding sites” S occupied by the DNA strand in the rigidly adsorbed form B. Increasing n also influences the shape of the curve. For n=1, forms B and C are identical, therefore the curve represents a mono-phasic binding process that follows first order kinetics and can be modeled using a single exponential function. Our experimental data could not be modeled well using n=1. For n >1, B and C are two distinct states, therefore the curve for this multi-phasic binding process can no longer be represented by a single exponential (Supporting Information, Mathematical Model II). Increasing n from 1 to 4 significantly changes the shape of the curve, while increasing n beyond 4 has only a minor effect on the curve (Figure 7D). For very large n, the initial rise is almost vertical. In our case, we used n=4 for both the “stronger” and “weaker” binding conditions, since it resulted in the highest R² values.

The third variable, t’, is a dimensionless time constant that represents the time of the experiment scaled by the rate of initial adsorption, and the total concentrations of DNA and surface binding sites. We found that setting t’=20 resulted in reasonable R² values between our data and the model. Changing t’ to 15 or 25 did not substantially change the R² values of the fits.

Limitations and Alternative models

Our model makes several simplifying assumptions, therefore is only meant to provide qualitative information about likely processes occurring at the surface. This analysis is not meant to accurately quantify n and κ₃, but can shed light on general trends and the effects of these parameters on the curve shape. Our simple three-state model focuses on the limiting scenarios wherein DNA interacts with 1 or n binding sites, and neglects intermediate binding conformations, thus may not accurately capture the entire curve shape. Nevertheless, we found remarkably good agreement between the simulated and experimental data. Furthermore, our model assumes that |ΔF| is linearly proportional to the mass of DNA adsorbed, which strictly speaking is not the case. The Sauerbrey equation is not valid since the different overtone curves of |ΔF| versus time diverge. Although the proportionality constant between |ΔF| and adsorbed mass is not constant, all overtone curves closely follow the same general trend; therefore it is possible to obtain qualitative information from the data. In addition, the adsorbed mass measured in QCM-D includes DNA and co-adsorbed water.⁵⁰ The assumption that |ΔF| is linearly proportional to the mass of DNA adsorbed is therefore only valid if the ratio between DNA and water mass does not change significantly throughout the adsorption process, which may not be the case for all conditions. It has been proposed that DNA adsorption from solutions containing high concentrations of chaotropic salts (in our case sodium perchlorate) is entropically driven by the release of water molecules upon DNA binding to the surface.⁹ If the rigidly bound DNA form B has significantly less hydrating water molecules than the more extended, loosely bound DNA conformation C, then the increase in co-adsorbed water during the transition from B to C would cause an upward kink in the curve of |ΔF| versus time. Indeed, we have observed such a kink for the sodium perchlorate binding condition, but not for the other buffers.

One could argue that during initial stages of adsorption, DNA is first loosely bound, and then establishes additional surface interactions to transition into a tightly bound conformation. This scenario is believed to occur for the adsorption of neutral polymers to a solid support.⁵¹ However, such a process would lead to a decreasing |ΔD/ΔF| in the initial phases of the process, which we have not observed in our experiments. If a transition from loosely to tightly bound DNA occurs (Figure 6, transition from A to C), then it does so in a few seconds or less, on a time scale faster than observable by our QCM-D experiments.

An alternate hypothesis for this multiphasic binding process assumes that DNA initially adsorbed remains in a tightly bound conformation (Figure 6B), while DNA that reaches the surface during later stages binds in a more extended, loosely bound conformation (Figure 6C) in the remaining available surface binding sites. This alternate model assumes that form B cannot convert into form C, which leads to two distinct DNA conformations on the surface. We attempted to model this process by varying k₁ and k₅, assuming that both processes are irreversible, while setting all other rate constants to zero. However, we were unable to obtain good agreement between the simulated and experimental data using this alternate model.

The model proposed herein assumes that DNA which initially adsorbs to the surface in a flat and rigid form can convert into a loosely bound extended conformation. This transition from B to C gives rise to the biphasic curve shape in our simulated data. During later stages of the adsorption process, as the surface becomes more crowded, it is likely that DNA in solution can directly adsorb in the loosely bound conformation C. Our model cannot rule out such a process. It is possible to model this and other more complex processes by varying more than two of the six rate constants, but we decided not to do so since this would be over-fitting the data.

CONCLUSION

We studied DNA adsorption to silica under conditions that do not require the use of chaotropic salts. While more DNA was adsorbed to silica using buffers with the chaotropic salt sodium perchlorate, compared to acetic acid and glycine buffers without chaotropic salts, the amount of eluted DNA was similar for all three conditions. Glycine or acetic acid buffers without chaotropic salts may therefore enable implementation of simpler SPE protocols for nucleic acid purification compatible with downstream polymerase amplification. Comparing the results obtained using acetate, glycine, and citrate buffers, it appears that buffer ions influence the adsorption of DNA to silica surfaces beyond simple pH stabilization. The precise mechanism underlying this phenomenon is unclear. We are currently conducting further systematic studies to elucidate how DNA adsorption to and elution from silica surfaces is modulated by different buffer ions.

Our QCM-D results show that the viscoelastic properties of the surface DNA layer change throughout the adsorption process, which indicates that the conformation of DNA adsorbed to silica changes during the initial phases of the adsorption process. Under stronger binding conditions (low pH, high ionic strength), the adsorbed DNA layer is initially rigid, but becomes viscoelastic within minutes. Under weaker binding conditions, the adsorbed DNA film is viscoelastic throughout most of the adsorption process. We hypothesize that DNA initially adsorbs in a relatively flat conformation and interacts with the silica surface through many binding sites. As the DNA surface coverage increases, the adsorbed DNA rearranges, extending further into solution while interacting with the silica surface through fewer binding contacts. We qualitatively obtained agreement between our experimental results and a mathematical model for this multiphasic adsorption process. Improved understanding on the processes involved in DNA adsorption to silica can facilitate future optimization of nucleic acid sample preparation for clinical diagnostic and research applications.