Segmentation and Estimation for SNP Microarrays: a Bayesian Multiple Change Point Approach

Summary

High-density SNP microarrays provide a useful tool for the detection of copy number variants (CNVs). The analysis of such large amounts of data is complicated, especially with regard to determining where copy numbers change and their corresponding values. In this paper, we propose a Bayesian multiple change point model (BMCP) for segmentation and estimation of SNP microarray data. Segmentation concerns separating a chromosome into regions of equal copy number differences between the sample of interest and some reference, and involves the detection of locations of copy number difference changes. Estimation concerns determining true copy number for each segment. Our approach not only gives posterior estimates for the parameters of interest, namely locations for copy number difference changes and true copy number estimates, but also useful confidence measures. In addition, our algorithm can segment multiple samples simultaneously, and infer both common and rare CNVs across individuals. Finally, for studies of CNVs in tumors, we incorporate an adjustment factor for signal attenuation due to tumor heterogeneity or normal contamination that can improve copy number estimates.

1. Introduction

Much recent work in human genetics has focused on structural variants (SVs), a class of genomic alterations involving segments of DNA typically larger than 1 kilobase (kb). SVs with changes in DNA copy numbers are termed copy number variants (CNVs) or polymorphisms (CNPs) in the germline, or copy number aberrations (CNAs) in tumor cells. Here we refer to any of these as CNVs. One can estimate genome-wide copy numbers and characterize CNVs at high resolution with data from high-density SNP microarrays, which currently feature more than one million SNPs and non-polymorphic probes.

Calling CNVs requires segmentation and estimation. By segmentation, we mean delineating a chromosome into equal copy number difference regions. This definition is slightly broader than traditional definition for segmentation in that we are interested in the difference between the true copy number of the sample of interest and the reference copy number. The reference copy number does not have to equal two for all locations, though if it does our definition and the traditional definition are equivalent. Such a broad definition is useful since CNVs can exist in non-diseased reference samples. For example, studies of CNVs in tumors may search for chromosomal regions with different copy numbers between paired tumor and blood samples from the same subject. In this case, the paired blood sample may not have two copies across all locations on a chromosome. As in traditional segmentation, our approach involves accurate boundary detection. And by estimation, we mean the estimation of true copy number for each segment.

We consider three different scenarios for segmentation and estimation: one-sample, multi-sample, and familial-sample models. The one-sample model refers to the case when only the CNVs of a particular sample is of interest so segmentation is done on this sample only. In the multi-sample model, interest is in inferring shared CNVs across samples and segmentation is performed on these samples simultaneously. When one has data on related family members, a special type of the multi-sample model infers family-specific CNVs, where segmentation is performed on all family members simultaneously. By incorporating the potential familial correlation in copy numbers, the familial-sample model should improve copy number estimation, in comparison with ignoring this correlation (e.g. as is done by the multi-sample model).

Many techniques have been proposed for one-sample segmentation of array-based copy number data. The two most common approaches are the Hidden Markov Model (HMM) and change-point model. Fridlyand et al. (2004) presented one of the earliest approaches to segmenting array CGH data with an unsupervised HMM. Marioni et al. (2006) extended their model to incorporate additional biological covariates (e.g. distance between adjacent clones). Wang et al. (2007) adopted a six state HMM based on total copy number (for autosomes) and CNV genotypes: deletion of two copies, deletion of one copy, normal, copy-neutral with LOH, single copy duplication, and double copy duplication. However, they only defined CNV genotypes at single SNPs, even though CNVs occur on DNA segments with multiple SNPs and the definition for CNV genotypes should combine all the SNP genotypes within a CNV region. In addition, the fixed number of states in any HMM limits the CNV types it can model. For example, the ‘deletions and duplications’ class at the same locus (Redon et al., 2006) and multi-allelic copy number variation (Aitman et al., 2006; Redon et al., 2006; Conrad and Hurles, 2007) may not be captured by the six-state model in Wang et al. (2007). Rueda and Daz-Uriarte (2007) proposed a Bayesian nonhomogeneous HMM fitted by reversible-jump Markov Chain Monte Carlo. Their approach gave the posterior probability that a region is a CNV. In addition, it incorporated interprobe distances. Unlike most other HMM methods, it has the flexbility that the number of states does not have to be fixed in advance and can be determined by the model. Guha et al. (2008) proposed a four-state Bayesian HMM for the same problem. One feature of their approach is that they identified outliers using the states of interest.

Olshen et al. (2004) proposed a change-point based segmentation method called circular binary segmentation (CBS). This approach repeatedly splits each chromosome segment until no additional statistically significant splits are found using a maximal t statistic with a permutation reference distribution to obtain the corresponding p value. Venkatraman and Olshen (2007) extended this work to improve the computational speed with a hybrid approach to obtain the p value of the test statistic in linear time and an early stopping rule. Lai et al. (2008) proposed a Bayesian stochastic method for estimation. Their approach focused on estimation only and provided explicit formula for posterior estimates of true signals. However, they did not use actual chromosome locations and assumed that markers are spaced uniformly across the genome.

In addition to HMM and change-point model based methods, some authors used mixture model approaches. Engler et al. (2006) presented a Gaussian mixture model with a Hidden Markov dependence structure for this problem. They adopted a pseudolikelihood approach to reduce the compuational burden for genome-wide analysis. Broet and Richardson (2006) utilized a Bayesian three-state spatially correlated mixture model to detect genomic regions of gain or loss.

As noted above, above methods focus on segmenting one sample at a time, and thus are not meant for finding CNVs shared by multiple individuals. In this case, combining CNVs across multiple samples generally requires ad hoc approaches. However, it might be difficult to detect weak signals (e.g. for small CNVs) if segmenting each sample separately. Combining the signals across all individuals could potentially increase the power to detect these CNVs (Zhang et al., 2008). While Zhang et al. (2008) extended the one-sample method by Olshen et al. (2004) using a mixture model weighted sum of chisquare statistic for finding shared change points across multiple samples, their approach is focused on segmentation only. Existing methods focus on either segmentation or estimation, but not both. Consequently, some of them do not provide a direct estimate and confidence measures of the true copy number (e.g. Broet and Richardson (2006); Guha et al. (2008); Rueda and Daz-Uriarte (2007)). All these HMM based methods except Rueda and Daz-Uriarte (2007) assume a fixed number of states which may not capture all the CNV events, and none of the existing approaches address signal attenuation issues arising in studies of tumors. Another important issue in segmentation and estimation approaches is that copy numbers may not be integers. For example, in cancer studies, tumors are frequently heterogeneous or contaminated with varying proportions of normal cells. Here, using a continuous scale allows one to redefine copy number gain or loss by setting new thresholds that depend on this proportion. Moreover, heterogeneous samples may not have the same copy numbers throughout, so the average copy number should be continuous. Therefore, an ideal segmentation algorithm should provide the user continuous segment-specific copy number estimates and correct for signal attenuation due to tumor heterogeneity or normal contamination.

In this paper, we build a unified Bayesian multiple change point model for segmentation and estimation of SNP microarrays. Our method performs segmentation and estimation for one-, multi- and familial-samples. By allowing for multi- and familial-sample situations, we do not need to use an ad hoc approach to combine sample-level CNVs. The use of familial-sample approach for family data can improve copy number estimates, as we will show with an empirical example. In addition, our method not only gives posterior summaries (i.e. posterior mean and 95% CI) for the locations of copy number difference changes, but also gives those for the copy number of each segment. Our method also incorporates a component adjusting for signal attenuation in its model formulation. This extra component together with the ability for both segmentation and estimation preclude us from getting closed-form formula for inferences like Lai et al. (2008) and so we use Monte Carlo simulation to infer parameters of interest.

This paper is organized as follows. The next section presents our model. In section 3, results from a simulation study to assess the proposed approach are given. Section 4 provides applications of the one- and familial-sample approaches. Finally, we summarize and discuss our work in section 5.

2. Model

In this section, we construct a multiple change-point model for segmentation and estimation. Multiple change-point models have been proposed for different applications (e.g. Suchard et al. (2003); Tai et al. (2009b)). Our multiple change-point model consists of two fundamental elements: the locations along the sequence (chromosome) where copy number difference changes occur, and the copy number of each segment. For the one-sample approach, we are interested in dividing a chromosome of a sample into regions of equal copy number difference (i.e. between the sample of interest and reference). In the multi-sample case, there are two possible scenarios of interest. First, finding common CNVs of the same copy number difference (e.g. common deletions) based on all the samples available. In this case, all the individuals are assumed to have the same locations of copy number difference changes and the same copy number difference within each segment. Second, finding both common and rare CNVs whose copy number differences do not have to be identical across samples. The copy number difference within each segment is allowed to differ across samples, and are assumed independent. The same scenarios hold for the familial-sample approach, except that familial CNVs are inherited within family members and are correlated. These three approaches yield the same data model, which we outline below.

We describe the model based on SNP arrays with both SNP and non-polymorphic probes. It is straightforward to apply the model to arrays with SNP probes only. We borrow the notation from Tai et al. (2009b). For each chromosome, assume there are L nucleotide locations. We denote the observed log₂ copy number ratio of the sample of interest over some reference for a SNP in sample i at location l by s_il, and for a CNV probe in the same sample at l by c_il, l = 1, …, L.

2.1 Multiple Change Point Model

2.1.1 One-Sample Model

As Tai et al. (2009b), suppose that a chromosome is divided into K + 1 blocks by K change points τ₁, …, τ_K, where 1 = τ₀ < τ₁ < … < τ_K < τ_K+1 = L + 1 and 0 ≤ K ≤ L − 1. We denote the true copy number at location l for the sample of interest by α_l, and its difference with the reference at the same location by d_l = α_l − α_lR. The difference d_l is a step function staying constant within each segment. We further denote a particular partition by ρ = (τ₁, …, τ_K, K). The observed log₂ ratios s_l and c_l are assumed to be conditionally independent and normally distributed, i.e., $s_l\mid {\lambda }_l,{\sigma }_{sl}^2~N({\lambda }_l,{\sigma }_{sl}^2)$ and $c_l\mid {\lambda }_l,{\sigma }_{cl}^2~N({\lambda }_1,{\sigma }_{cl}^2)$. The mean parameter λ_l depends on d_l and the parameter β_l, a factor adjusting for d_l due to signal attenuation. It can be modeled by λ_l = log₂(β_ld_l+α_lR)− log₂α_lR, where β_l = 0.5 when d_l = 0, ∀l, and 0 < β_l < 1 otherwise. Note that α_lR is location-specific and does not have to equal 2 ∀l. Following Tai et al. (2009b), for identifiability purposes, we impose a constraint on ${\beta }_l:{\sum }_{k=1}^K{w}_k\mathit{logit}({\beta }_k)=0$, where w_k is the proportion of data points within segment k. The adjustment factor β_l is also location-specific because it equals any value between 0 and 1 when d_l = 0 such that the identifiability constraint is met. Note that incorporating β_l is motivated by the idea that copy number differences are reduced by a constant factor in a CNV region. For example, in cancer studies, β_l could represent the proportion of tumor cells. A factor of 1 indicates pure tumor cells, while 0.5 represents 50% tumors and 50% normals. In a non CNV region, the factor can be any number between 0 and 1 without loss of generality, since the reduced difference equals 0 whatever value the factor is. In other words, β_l in a CNV region represents the proportion of tumor cells, while in a non CNV region it is just a factor adjusted accordingly such that the constraint is met. Finally, by checking the real data, it is reasonable to assume that intensity variabilities ( ${\sigma }_{sl}^2,{\sigma }_{cl}^2$) are different between SNP and CNV probes.

2.1.2 Multi-Sample Model

If the segment-specific copy number difference is allowed to differ across samples, then d_l above becomes sample-specific d_il. It is also possible that the proportion of contamination differs across samples within a study. In that case, β_l becomes sample-specific β_il. Intensity variability could vary across samples or labs, so ${\sigma }_{sl}^2$ and ${\sigma }_{cl}^2$ become sample-specific ${\sigma }_{\mathit{isl}}^2$ and ${\sigma }_{\mathit{icl}}^2$.

2.1.3 Familial-Sample Model

Here, the offspring’s copy numbers should depend on those of the parents. The segment-specific copy number typically differs across family members, so we denote the true copy numbers of the father and mother at location l by α_fl and α_ml, and that of the offspring by α_ol. The observed log₂ ratios are s_fl, s_ml, s_ol, c_fl, c_ml, and c_ol, respectively. This notation can be easily extended to a family of larger size (Web Appendix A). The model for the SNP data becomes $s_{fl}\mid {\lambda }_{fl},{\sigma }_{\mathit{fsl}}^2~N({\lambda }_{fl},{\sigma }_{\mathit{fsl}}^2),s_{ml}\mid {\lambda }_{ml},{\sigma }_{\mathit{msl}}^2~N({\lambda }_{ml},{\sigma }_{\mathit{msl}}^2)$, and $s_{ol}\mid {\lambda }_{ol},{\sigma }_{\mathit{osl}}^2~N({\lambda }_{ol},{\sigma }_{\mathit{osl}}^2)$. Again, λ_il = log₂(β_ild_il+α_ilR) − log₂α_ilR, i = {f, m, o}. The model for the CNV probes are similar. The same notation applies when the segment-specific copy number is the same across family members, except that α_fl, α_ml, and α_ol all become α_l.

2.2 Priors and Posterior

We use a Bayesian framework to draw inferences on the parameters of interest. The number of change points K is difficult to determine before undertaking segmentation. Thus, we assign a uniform prior on K, i.e., P(K = k) = 1/(K_max + 1), k = 0, 1, …, K_max, 0 ≤ K_max ≤ L − 1 to let the data estimate K. Given K, the prior for change point locations τ₁, …, τ_K can be uniformaly or non-uniformaly distributed along the chromosome. The joint distribution for τ₁, …, τ_K and K is simply P(ρ) = P(τ₁, …, τ_K|K)P(K). Now we discuss the other priors under different situations.

2.2.1 One-Sample Model

We assume that d, the vector of copy number differences, is truncated multivariate normal with mean d₀, covariance matrix δ²I, and truncation lower bound −α_R, denoted by N_−αR(d₀, δ²I). The hyperparameter d₀ is assumed to be truncated multivariate normal N_−αR(0, I). The priors for the individual elements of ${\mathit{\sigma }}_s^2$ and ${\mathit{\sigma }}_c^2$ are assumed to be inverse gamma with parameters a and b. The prior for the individual elements of the adjustment factor β is assumed to be Uniform[0,1].

Given the above priors, the posterior can be expressed using the likelihood. The parameters to be estimated are ρ, d, β, ${\mathit{\sigma }}_s^2,{\mathit{\sigma }}_c^2$, and d₀. The hyperparameters δ², a and b are determined by the user or the data. The posterior can be written by

$$\begin{array}{l}P(\mathit{\rho },\mathit{d},\mathit{\beta },{\mathit{\sigma }}_s^2,{\mathit{\sigma }}_c^2,{\mathit{d}}_0\mid \mathit{data})\propto \\ P(\mathit{data}\mid \mathit{\rho },\mathit{d},\mathit{\beta },{\mathit{\sigma }}_s^2,{\mathit{\sigma }}_c^2)P(\mathit{\rho },\mathit{d},\mathit{\beta },{\mathit{\sigma }}_s^2,{\mathit{\sigma }}_c^2,{\mathit{d}}_0)\\ ={\prod }_{l=1}^{L}P(s_l\mid d_l,{\beta }_l,{\sigma }_{sl}^2){\prod }_{l=1}^{L}P(c_l\mid d_l,{\beta }_l,{\sigma }_{cl}^2)P(\mathit{\rho })P(\mathit{d}\mid {\mathit{d}}_0)P(\mathit{\beta })P({\mathit{d}}_0)P({\mathit{\sigma }}_s^2)P({\mathit{\sigma }}_c^2).\end{array}$$ (1)

2.2.2 Multi-Sample Model

The priors for the one-sample model also apply here, except that when the segment-specific copy number difference is allowed to vary across samples, d₁, …, d_I are assumed truncated multivariate normal N_−αR(d_i0, δ²I). The posterior becomes

$$\begin{array}{l}P(\mathit{\rho },{\mathit{d}}_1,\dots ,{\mathit{d}}_I,{\mathit{\beta }}_1,\dots ,{\mathit{\beta }}_I,{\mathit{\sigma }}_{1s}^2,\dots ,{\mathit{\sigma }}_{Is}^2,{\mathit{\sigma }}_{1c}^2,\dots ,{\mathit{\sigma }}_{Ic}^2,{\mathit{d}}_{10},\dots ,{\mathit{d}}_{I0}\mid \mathit{data})\propto \\ P(\mathit{data}\mid \mathit{\rho },{\mathit{d}}_1,\dots ,{\mathit{d}}_I,{\mathit{\beta }}_1,\dots ,{\mathit{\beta }}_I,{\mathit{\sigma }}_{1s}^2,\dots ,{\mathit{\sigma }}_{Is}^2,{\mathit{\sigma }}_{1c}^2,\dots ,{\mathit{\sigma }}_{Ic}^2)\times \\ P(\mathit{\rho },{\mathit{d}}_1,\dots ,{\mathit{d}}_I,{\mathit{\beta }}_1,\dots ,{\mathit{\beta }}_I,{\mathit{\sigma }}_{1s}^2,\dots ,{\mathit{\sigma }}_{Is}^2,{\mathit{\sigma }}_{1c}^2,\dots ,{\mathit{\sigma }}_{Ic}^2,{\mathit{d}}_{10},\dots ,{\mathit{d}}_{I0})\\ ={\prod }_{i=1}^I{\prod }_{l=1}^{L}P(s_{il}\mid d_{il},{\beta }_{il},{\sigma }_{\mathit{isl}}^2){\prod }_{i=1}^I{\prod }_{l=1}^{L}P(c_{il}\mid d_{il},{\beta }_{il},{\sigma }_{\mathit{icl}}^2)P(\mathit{\rho }){\prod }_{i=1}^{I}P({\mathit{d}}_i\mid {\mathit{d}}_{i0})\times \\ {\prod }_{i=1}^{I}P({\mathit{\beta }}_i){\prod }_{i=1}^{I}P({\mathit{d}}_{i0}){\prod }_{i=1}^{I}P({\mathit{\sigma }}_{is}^2){\prod }_{i=1}^{I}P({\mathit{\sigma }}_{ic}^2).\end{array}$$ (2)

If the segment-specific copy number difference is the same across samples, the posterior becomes

$$\begin{array}{l}P(\mathit{\rho },\mathit{d},\mathit{\beta },{\mathit{\sigma }}_{1s}^2,\dots ,{\mathit{\sigma }}_{Is}^2,{\mathit{\sigma }}_{1c}^2,\dots ,{\mathit{\sigma }}_{Ic}^2,{\mathit{d}}_0\mid \mathit{data})\propto \\ {\prod }_{i=1}^I{\prod }_{l=1}^{L}P(s_{il}\mid d_l,{\beta }_l,{\sigma }_{\mathit{isl}}^2){\prod }_{i=1}^I{\prod }_{l=1}^{L}P(c_{il}\mid d_l,{\beta }_l,{\sigma }_{\mathit{icl}}^2)P(\mathit{\rho })P(\mathit{d}\mid {\mathit{d}}_0)P(\mathit{\beta })P({\mathit{d}}_0)\times \\ {\prod }_{i=1}^{I}P({\mathit{\sigma }}_{is}^2){\prod }_{i=1}^{I}P({\mathit{\sigma }}_{ic}^2).\end{array}$$ (3)

2.2.3 Familial-Sample Model

The priors for the parents’ copy number differences d_f and d_m are assumed to be truncated multivariate normal N_−αR(d_f0, δ²I), N_−αR(d_m0, δ²I), respectively. We assume that any offspring’s copy number difference given the parents’ is truncated multivariate normal

$${\mathit{d}}_o\mid {\mathit{d}}_f,{\mathit{d}}_m~N_{-{\mathit{\alpha }}_R}\left(\frac{{\mathit{d}}_f+{\mathit{d}}_m}{2},{\delta }^2\mathbf{I}\right).$$ (4)

We describe the posterior for the case of a trio. The extension to other family structures is easily conceived (Web Appendix A).

$$\begin{array}{l}P(\mathit{\rho },{\mathit{d}}_f,{\mathit{d}}_m,{\mathit{d}}_o,{\mathit{\beta }}_f,{\mathit{\beta }}_m,{\mathit{\beta }}_o,{\mathit{\sigma }}_{fs}^2,{\mathit{\sigma }}_{ms}^2,{\mathit{\sigma }}_{os}^2,{\mathit{\sigma }}_{fc}^2,{\mathit{\sigma }}_{mc}^2,{\mathit{\sigma }}_{oc}^2,{\mathit{d}}_{f0},{\mathit{d}}_{m0}\mid \mathit{data})\propto \\ P(\mathit{data}\mid \mathit{\rho },{\mathit{d}}_f,{\mathit{d}}_m,{\mathit{d}}_o,{\mathit{\beta }}_f,{\mathit{\beta }}_m,{\mathit{\beta }}_o,{\mathit{\sigma }}_{fs}^2,{\mathit{\sigma }}_{ms}^2,{\mathit{\sigma }}_{os}^2,{\mathit{\sigma }}_{fc}^2,{\mathit{\sigma }}_{mc}^2,{\mathit{\sigma }}_{oc}^2)\times \\ P(\mathit{\rho },{\mathit{d}}_f,{\mathit{d}}_m,{\mathit{d}}_o,{\mathit{\beta }}_f,{\mathit{\beta }}_m,{\mathit{\beta }}_o,{\mathit{\sigma }}_{fs}^2,{\mathit{\sigma }}_{ms}^2,{\mathit{\sigma }}_{os}^2,{\mathit{\sigma }}_{fc}^2,{\mathit{\sigma }}_{mc}^2,{\mathit{\sigma }}_{oc}^2,{\mathit{d}}_{f0},{\mathit{d}}_{m0})\\ ={\prod }_{i=f,m,o}{\prod }_{l=1}^{L}P(s_{il}\mid d_{il},{\beta }_{il},{\sigma }_{\mathit{isl}}^2){\prod }_{i=f,m,o}{\prod }_{l=1}^{L}P(c_{il}\mid d_{il},{\beta }_{il},{\sigma }_{\mathit{icl}}^2)P(\mathit{\rho }){\prod }_{i=f,m}P({\mathit{d}}_i\mid {\mathit{d}}_{i0})\times \\ {\prod }_{i=f,m,o}P({\mathit{\beta }}_i)P({\mathit{d}}_o\mid {\mathit{d}}_f,{\mathit{d}}_m)P({\mathit{d}}_{f0})P({\mathit{d}}_{m0}){\prod }_{i=f,m,o}P({\mathit{\sigma }}_{is}^2){\prod }_{i=f,m,o}P({\mathit{\sigma }}_{ic}^2).\end{array}$$ (5)

2.3 Parameter Inference

To draw inferences on the parameters of interest, we use the reversible jump Markov Chain Monte Carlo algorithm (rjMCMC) (Green, 1995; Suchard et al., 2003; Tai et al., 2009b). The algorithm is comprised of four move types: add a change point, delete a change point, move a change point, and alter parameters. At each iteration a move type is proposed, and accepted or rejected based on a probability depending on ratios of posteriors and proposal of the new and old parameters. The details of the algorithm are described in Web Appendix B.

3. Simulation

3.1 Method

We performed a simulation study under different scenarios to evaluate the performance of our method, which we call BMCP (for Bayesian multiple change point) thereafter. The simulation data were generated based on Affymetrix SNP 6.0 chromosome 21 arrays from HapMap samples and from a study of skin cancer. Eight models (M₁–M₈) were used to simulate data under different scenarios with regard to marker density, region length, data variability, and with or without outliers (Table 1). We then compared the performance of BMCP with two commonly used algorithms: Circular Binary Segmentation (CBS) in the software DNAcopy (Olshen et al., 2004; Venkatraman and Olshen, 2007) and the Hidden Markov Model (HMM) implemented in aCGH (Fridlyand et al., 2004). More details of the simulation method are described in Web Appendix C.

Table 1.

Simulation Models. Theparametrs ${\sigma }_{sA}^2,{\sigma }_{cA}^2$ and β_A are ${\sigma }_s^2,{\sigma }_c^2$ and β for the CNV regions. Those for the normal regions are indexed by N. x stands for the top x% locations sampled for BMCP analysis. Mosaicism means whether or not CNVs have mosaic copy numbers. Type stands for the region type described in Web Appendix C. M₁: Typical data, moderate contamination. M₂: Same as M₁, but more contamination. M₃: Same as M₁, but higher variability. M₄: Perfect correlation among true copy number differences. M₅: Same as M₁, but fewer candidate locations searched. M₆: Same as M₁, but more candidate locations searched. M₇: Same as M₁, but copy numbers are mosaic. M₈: Same as M₁, but CNV regions are longer.

Model	${\sigma }_{sA}^2$	${\sigma }_{sN}^2$	${\sigma }_{cA}^2$	${\sigma }_{cN}^2$	βA	βN	δ2	r	x	Mosaicism	Type
M1	0.06	0.07	0.07	0.08	0.7	0	0.01	0.3	20	No	1
M2	0.06	0.07	0.07	0.08	0.5	0	0.01	0.3	20	No	1
M3	0.1	0.15	0.1	0.15	0.7	0	0.01	0.3	20	No	1
M4	0.06	0.07	0.07	0.08	0.7	0	0.01	1	20	No	1
M5	0.06	0.07	0.07	0.08	0.7	0	0.01	0.3	5	No	1
M6	0.06	0.07	0.07	0.08	0.7	0	0.01	0.3	95	No	1
M7	0.06	0.07	0.07	0.08	0.7	0	0.01	0.3	20	Yes	1
M8	0.06	0.07	0.07	0.08	0.7	0	0.01	0.3	20	No	4

3.2 Results

Before comparing different approaches, we consider BMCP for a single simulation. In particular, Web Table 1 lists the estimated parameters of interest with their corresponding 95% CIs for one simulation with outliers from model M₁. The true values were all covered by the 95% CIs. This shows that BMCP gives reasonable results even in the presence of outliers. The inclusion of an adjustment factor improved copy number estimates. The true copy numbers for the gain and loss regions of the simualtion presented in Web Table 1 were 2.82 and 1.08, respectively. The estimated copy numbers from BMCP were 2.66 and 1.28, which are closer to the true values than those estimated from observed log₂ ratios (2.57 and 1.36, respectively).

Table 2 gives the numbers of FP and FN when there are no outliers. The FPs for BMCP were close to or lower than those of CBS except for M₃ and M₄. This suggests that data variability has an impact on FPs for BMCP. When copy numbers are perfectly correlated (unlikely in reality), BMCP may detect more FPs. M₁ showed that ignoring potential correlations between copy numbers does not prevent us from getting reasonable results, while reducing the number of parameters to be estimated. This is important because the rjMCMC fitting procedure may get complicated when the number of parameters gets large. HMM achieved similar or lower FP than CBS except M₇. This agrees with our discussion earlier that HMM is not suitable when copy numbers are mosaic. In all cases, BMCP achieved higher FN than CBS and HMM. BMCP achieved lower FN in M₆ than M₁ and M₅, suggesting that the more candidate locations being searched, the lower the FN. The comparision between M₁ and M₂ indicates that the more signal attenuation, the higher the FN. Such an effect was not observed from CBS.

Table 2.

Mean and 95% CI for the numbers of false positives (FP) and false negatives (FN) of each method under 8 simulation models without outliers.

Model	CBS FP	HMM FP	BMCP FP	CBS FN	HMM FN	BMCP FN
M1	0.04 [0, 0]	0 [0, 0]	0.04 [0, 0.78]	0 [0, 0]	0 [0, 0]	0.44 [0, 1.78]
M2	0.04 [0, 0]	0.02 [0, 0]	0.02 [0, 0]	0 [0, 0]	0 [0, 0]	1 [0, 2]
M3	0.04 [0, 0]	0.04 [0, 0]	0.06 [0, 1]	0 [0, 0]	0 [0, 0]	0.14 [0, 1]
M4	0.04 [0, 0]	0 [0, 0]	0.14 [0, 1.78]	0 [0, 0]	0 [0, 0]	0.42 [0, 2]
M5	0.04 [0, 0]	0 [0, 0]	0 [0, 0]	0 [0, 0]	0 [0, 0]	0.26 [0, 1.78]
M6	0.08 [0, 0]	0 [0, 0]	0.04 [0, 0.78]	0 [0, 0]	0 [0, 0]	0.08 [0, 1]
M7	0 [0, 0]	0.34 [0, 0.78]	0 [0, 0]	0 [0, 0]	0 [0, 0]	1.26 [0, 2.78]
M8	0.16 [0, 2]	0.16 [0, 2]	0 [0, 0]	0 [0, 0]	0 [0, 0]	0.54 [0, 2]

The presence of outliers greatly increased the numbers of FP from CBS and HMM (Table 3). BMCP achieved the lowest FP compared to CBS and HMM. CBS achieved similar FN as HMM. Web Figures 1–3 show the log₂ ratio plot, posterior distribution of number of change points, trace plots of β for a simulated dataset from M₁, respectively.

Table 3.

Mean and 95% CI for the numbers of false positives (FP) and false negatives (FN) of each method under 8 simulation models with outliers.

Model	CBS FP	HMM FP	BMCP FP	CBS FN	HMM FN	BMCP FN
M1	1.36 [0, 4]	5.68 [2, 9.55]	0.10 [0, 1]	0 [0, 0]	0 [0, 0]	0.74 [0, 2]
M2	0.12 [0, 2]	0.88 [0, 12]	0 [0, 0]	0 [0, 0]	0 [0, 0]	0.96[0,2]
M3	1.02 [0, 4]	3.18 [0, 2]	0 [0, 0]	0 [0, 0]	0 [0, 0]	0.24 [0, 1]
M4	1.72 [0, 6]	4.80 [2, 6]	0 [0, 0]	0 [0, 0]	0 [0, 0]	0.64 [0, 2]
M5	0.94 [0, 3.78]	4.24 [2, 6]	0.10 [0, 1]	0 [0, 0]	0 [0, 0]	0.22 [0, 1]
M6	1.64 [0, 4]	4.40 [2, 6]	0.18 [0, 2]	0 [0, 0]	0 [0, 0]	0.32 [0, 1]
M7	0.20 [0, 2]	2.94 [0, 19.55]	0 [0, 0]	0 [0, 0]	0 [0, 0]	1.28 [0, 3]
M8	0.08 [0, 1.55]	3.52 [0, 17.10]	0 [0, 0]	0 [0, 0]	0 [0, 0]	0.96 [0, 2]

4. Applications

4.1 One-Sample Example

We evaluated the q-arm of chromosome 11 from a prostate tumor sample and its paired blood sample, both typed by the Illumina 1M Duo BeadArrays (Tai et al., 2009a). The reference for the tumor sample was the paired blood, such that the CNVs detected were somatic changes. We began with no change points, and the starting values are ${\sigma }_s^2=0.038,{\sigma }_c^2=0.057$, and β = 0.5. The upper bound for the number of change points was set to 30. BMCP searched through the top 20% of candidate locations to improve computational speed. The chain was run for 100,000 iterations. The first 50,000 iterations were thrown away as burn-ins, and we sampled every 10^th of the remaining iterations for our final analyses.

We also segmented the same tumor sample using DNAcopy and aCGH. As the analysis for the simulation models with outliers, we did outlier smoothing and undo split for segments that were less than 1.2 SD apart between means in DNAcopy analysis, and merged states whose predicted values are less than 0.21 apart in aCGH analysis. To see how outliers affect segmentation results by CBS and HMM, we repeated these two analysis without any smoothing, undo split, or merging.

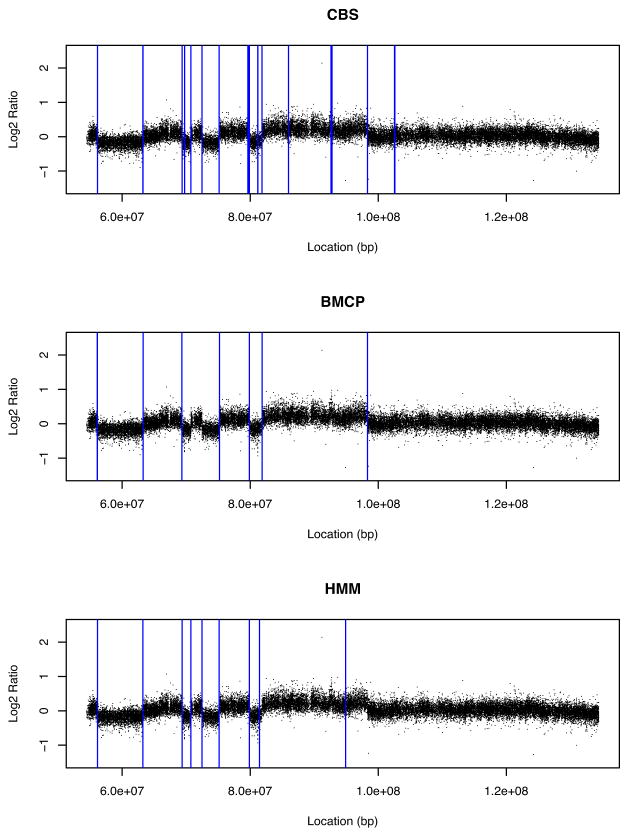
Figure 1 shows the estimated change points for the tumor sample found by these three algorithms with outlier handling for CBS and HMM. CBS gave 21 change points, while BMCP and HMM gave 8 and 10 change points, respectively. All of these three methods identified most breakpoints. However, none of them detected any change point around the right end of the chromosome arm where there seemed to be a slight downward trend in log₂ ratios. Even with outlier handling, CBS seemed to detect more change points between 80, 000, 000 and 100, 000, 000 bps, some of which did not appear to reflect changes. The results for BMCP and HMM looked more similar, except that BMCP missed two change points between 69, 333, 663 bp and 75, 212, 671 bp where a normal region existed between two deletion regions. HMM missed a change point around 98, 319, 393 bp where a large deletion seemed to occur.

Figure 1.

Estimated change point locations for the tumor sample by CBS, BMCP, and HMM with outlier handling.

Web Figure 4 plots the estimated change points from CBS (top) and HMM (bottom) without outlier handling, and the top 48 locations by BMCP (middle). In this case, CBS gave 48 change points, while HMM identified 130 change points. The use of a merging step for HMM had a great impact on the result. Both CBS and HMM produced many apparent FPs, even though they no longer missed the change point around the right end of the chromosome arm where there seemed to be a slight downward trend in log₂ ratios. In addition, HMM now detected the apparent change point around 98, 319, 393 bp when removing the merging step. The top 48 locations by BMCP indicated change points around the right end of the chromosome arm where there seemed to be a slight downward trend in log₂ ratios. It also now detected one of the previously missed change points between 69, 333, 663 bp and 75, 212, 671 bp.

This comparison showed two things. First, both CBS and HMM were very sensitive to outliers. Second, for BMCP analysis, one could use the posterior probabilities as a way to rank regions of interest for further experimental validation. Web Figure 5 plots the estimated log₂ ratio, posterior probability, copy number, and adjustment factor by BMCP. The copy number estimate indeed indicated a slight downward trend at the right end of the chromosome arm, even though the locations in that region were not within the top 8. Web Table 2 gives the posterior probabilities for the top 20 locations. Web Table 3 lists the estimated parameters of interest. The two missed change points between 69,333,663 bp and 75,212,671 bp were covered by the 95% CI for τ₃. This suggests that these might have been missed because the change points were not well separated, and that confidence measures could be another alternative for defining CNVs.

4.2 Familial-Sample Example

We also applied the familial-sample model with copy numbers are allowed to differ across family members to the q arm of chromosome 1 of a YRI trio from HapMap (NA18852, NA18853 and NA18854). The reference was the median across all samples in the YRI population. The starting values for this example were: ${\sigma }_{fs}^2={\sigma }_{ms}^2={\sigma }_{os}^2=0.06,{\sigma }_{fc}^2={\sigma }_{mc}^2={\sigma }_{oc}^2=0.07$, β_f = β_m = β₀ = 0.5. As above, we start with no change points, set the upper bound to 30, and searched through the top 20% of candidate locations. The chain was run for 100,000 iterations, and 50,000 iterations were discarded, and we sampled every 10^th observation from the remaining iterations for analysis.

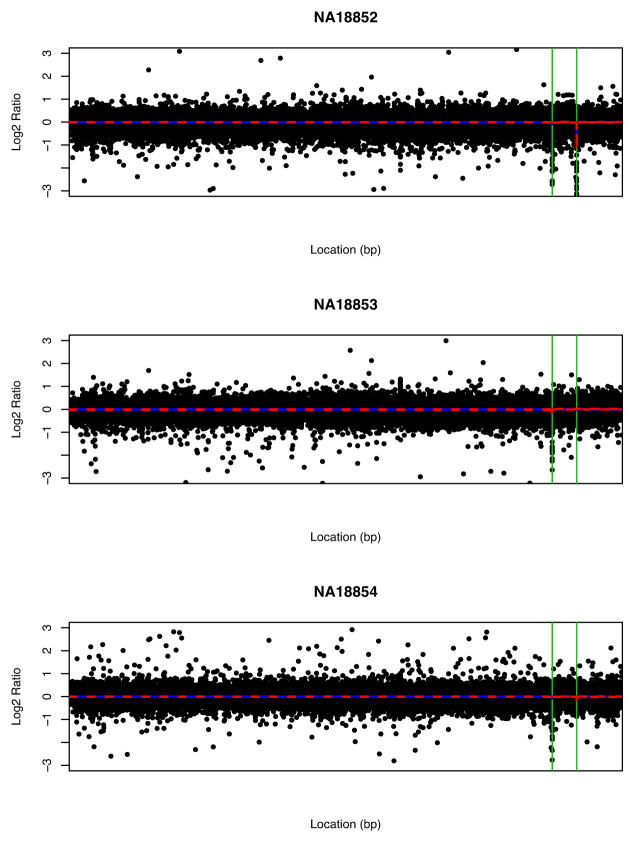
Figure 2 gives the segmentation results on the trio.

Figure 2.

Estimated common change points (green vertical lines) for the trio (NA18852, NA18853, NA18854) by BMCP familial-sample model. The blue solid and red dashed lines are the estimated log₂ ratios and the corresponding 95% CIs, respectively.

The familial-sample segmentation found a common deletion within this family (from 105, 803, 129 to 105, 841, 589 bps). The estimated copy numbers for this common CNV are 1.76, 1.78, 1.69 for samples NA18852, NA18853 and NA18854, respectively. In addition, the deletion from 111, 179, 089 to 111, 185, 496 bps in NA18852 was also detected. The estimated copy numbers for this region are 0.91, 1.53, 1.6 for NA18852, NA18853 and NA18854, respectively. This shows that the familial-sample BMCP approach can detect both familial and individual CNVs.

To see how the familial model compares to multi-sample or one-sample models, we fit these models to the YRI trio. The multi-sample approach also found the shared deletion within this family (from 105, 814, 900 to 105, 823, 899 bps). The estimated copy numbers for this common CNV are 1.68, 1.81, 1.84 for NA18852, NA18853 and NA18854, respectively. In addition, the deletion from 111, 179, 089 to 111, 213, 759 bps in NA18852 was also detected. The estimated copy numbers for this region are 1.62, 2.06, 1.91 for NA18852, NA18853 and NA18854, respectively. Note that the copy number estimates from the familial- and multi-sample approaches were somewhat different. Since these are HapMap samples, it is reasonable to assume that there is no signal attenuation and that the true copy number could be converted from log₂ ratios directly. Web Table 5 gives the log₂ ratio, estimated copy number, and the absolute difference between the estimated and true copy number for both CNVs in all these three individuals. We found that all of the absolute differences except one are smaller for familial-model analysis. The total absolute difference is larger for the multi-sample model (4.3) than for the familial-sample model (3.04). Thus, the familial-sample model gave improved copy number estimates compared to the multi-sample model. When fitting the one-sample model to each member of the YRI trio separately, BMCP was not able to detect any signal for NA18853 and NA18854. It detected both CNVs for NA18852, however, the boundaries for one CNV did not overlap with those observed for the familial-sample model. This may have been caused by the weak signal, and the one-sample analysis demonstrates the value of pooling information across samples when individual signals are weak.

5. Discussion

In this paper, we propose a Bayesian multiple change point framework for segmentation and estimation of SNP microarrays. Our approach provides the following advantages: being less sensitive to outliers; allowing for joint modeling of multiple and familial samples to help detect short CNV regions with weak signals; and improving copy number estimates. Nevertheless, BMCP may have lower power to detect short regions with low marker density. One future research direction is to modify BMCP such that it has a greater power to detect such regions.

Estimating the number of change points has been an active research area in the context of multiple change point models. Our algorithm provides a natural way to estimate this quantity, even in the presence of outliers, as demonstrated by the simulation study. The modified BIC procedure of Zhang and Siegmund (2007) may also provide useful guidance here. In our application, we found that CBS and HMM tended to detect more change points than BMCP even when outlier handling procedures are used. Since the distinction between outliers and true signals is not always clear, this disparity may lead to concerns that BMCP is under-powered in comparison to CBS and HMM. To address this issue, we provide an alternative approach to change point selection based on posterior probabilities. Here, one can prespecify a target number of change points and obtain corresponding locations using posterior probabilities. Another pertinent question is how to choose the upper bound on the number of change points, K_max. Based on the simulation study and real data analysis, we observe that BMCP is not sensitive to the choice of K_max, so one can set it to any large integer.

Our BMCP multi-sample model forces the breakpoints to be the same even if they are not perfectly aligned. This is useful for finding the overlapping regions of these common CNVs. To identify what portions of a structural variant overlap, one can simply fit any one-sample segmentation algorithm to each sample independently, and subtract out the overlapping region from each sample-specific region to locate those non-overlapping regions.

Although BMCP is more general than other approaches, it can have a higher computational burden. There is a tradeoff between chain length (convergence) and the accuracy of parameter estimates, especially for high density SNP arrays. Subsampling is one way to address this issue. Here, we have fixed chain lengths and burn-ins at 100, 000 and 50, 000 respectively which, combined with the proposed starting values and tuning parameters, produced reasonable estimates as demonstrated by our simulation study and real data application. In a straightforward implementation of our rjMCMC algorithm, evaluation of the likelihood dominates the computational time. This scales as O(ISM), with I = iterations, S = number of samples, and M = the number of markers. By caching parts of the likelihood that remain invariant across a step, we need only to calculate segments that change across a step. By rewriting the log likelihood expression in terms of sums over log ratios and squared log ratios, we can use precomputed look-up tables to reduce the calculation to a few table accesses and some arithmetic. The result of these optimizations change the scaling to O(ISG) + O(M), with G the number of change points. With this, for Illumina 1M SNP array data, it takes only 75 seconds for BMCP to run 100, 000 iterations genome-wide in C++ with a Core2 Duo system running the Linux 2.6 kernel.

Finally, in contrast to a HMM, we are not aware of any segmentation-based approaches (including BMCP) that can detect copy-neutral LOH regions. Given the advantage over a HMM of handling mosaicism, it would be useful to extend any segmentation-based method for detecting copy-neutral LOH regions, which is important in cancer studies