Abstract
We consider, in the modern setting of high-dimensional statistics, the classic problem of optimizing the objective function in regression using M-estimates when the error distribution is assumed to be known. We propose an algorithm to compute this optimal objective function that takes into account the dimensionality of the problem. Although optimality is achieved under assumptions on the design matrix that will not always be satisfied, our analysis reveals generally interesting families of dimension-dependent objective functions.
Keywords: robust regression, prox function
In this article, we study a classical statistical problem: how to pick optimally (among regression M-estimates) the objective to be minimized in a parametric regression when we know the error distribution. Our study is carried out in the modern setting where the number of predictors is proportional to the number of observations.
The classical answer to the problem we posed at the beginning, maximum likelihood, was given by Fisher (1) in the specific case of multinomial models and then at succeeding levels of generality by Cramér (2), Hájek (3), and, above all, Le Cam (4). For instance, for p fixed or  fast enough, least squares is optimal for Gaussian errors, whereas least absolute deviations (LAD) is optimal for double-exponential errors. We shall show that this is no longer true in the regime we consider with the answer depending, in general, on the limit of the ratio
fast enough, least squares is optimal for Gaussian errors, whereas least absolute deviations (LAD) is optimal for double-exponential errors. We shall show that this is no longer true in the regime we consider with the answer depending, in general, on the limit of the ratio 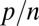 as well as the form of the error distribution. Our analysis in this paper is carried out in the setting of Gaussian predictors, although as we explain below, this assumption should be relaxable to a situation in which the distribution of the predictors satisfy certain concentration properties for quadratic forms.
as well as the form of the error distribution. Our analysis in this paper is carried out in the setting of Gaussian predictors, although as we explain below, this assumption should be relaxable to a situation in which the distribution of the predictors satisfy certain concentration properties for quadratic forms.
We carry out our analysis in a regime that has been essentially unexplored, namely 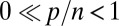 , where p is the number of predictor variables and n is the number of independent observations. Because in most fields of application, situations in which p as well as n are large have become paramount, there has been a huge amount of literature on the case where
, where p is the number of predictor variables and n is the number of independent observations. Because in most fields of application, situations in which p as well as n are large have become paramount, there has been a huge amount of literature on the case where 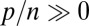 but the number of “relevant” predictors is small. In this case, the objective function, quadratic (least squares) or otherwise (
but the number of “relevant” predictors is small. In this case, the objective function, quadratic (least squares) or otherwise (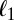 for LAD) has been modified to include a penalty (usually
for LAD) has been modified to include a penalty (usually 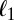 ) on the regression coefficients, which forces sparsity (5). The price paid for this modification is that estimates of individual coefficients are seriously biased and statistical inference, as opposed to prediction, often becomes problematic.
) on the regression coefficients, which forces sparsity (5). The price paid for this modification is that estimates of individual coefficients are seriously biased and statistical inference, as opposed to prediction, often becomes problematic.
In ref. 6, we showed† that this price need not be paid if 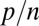 stays bounded away from 1, even if the regression does not have a sparse representation. We review the main theoretical results from this previous paper in Result 1 below. Some of our key findings were as follows: (i) Surprisingly, when
stays bounded away from 1, even if the regression does not have a sparse representation. We review the main theoretical results from this previous paper in Result 1 below. Some of our key findings were as follows: (i) Surprisingly, when 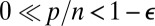 , it is no longer true that LAD is necessarily better than least squares for heavy-tailed errors. This behavior is unlike that in the classical regime p bounded or
, it is no longer true that LAD is necessarily better than least squares for heavy-tailed errors. This behavior is unlike that in the classical regime p bounded or 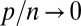 fast enough studied, for instance, in ref. 7. (ii) Linear combinations of regression coefficients are unbiased and still asymptotically Gaussian at rate‡
fast enough studied, for instance, in ref. 7. (ii) Linear combinations of regression coefficients are unbiased and still asymptotically Gaussian at rate‡
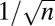 .
.
This article contains three main parts: Background and Main Results contains needed background and a description of our findings. In Computing the Optimal Objective, we give two examples of interest to statisticians: the case of Gaussian errors and the case of double-exponential errors. We present our derivations in the last section.
Background and Main Results
We consider a problem in which we observe n independent, identically distributed pairs 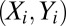 , where
, where 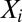 is a p-dimensional vector of predictors, and
is a p-dimensional vector of predictors, and 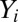 is a scalar response. We call the problem high-dimensional when the ratio
is a scalar response. We call the problem high-dimensional when the ratio 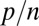 is not close to 0. In effect, we are considering an asymptotic setting where
is not close to 0. In effect, we are considering an asymptotic setting where 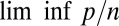 is not 0. We also limit ourselves to the case in which
is not 0. We also limit ourselves to the case in which 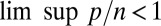 . As far as we know, all of the very large body of work developed in robust regression (following ref. 7) is concerned with situations in which
. As far as we know, all of the very large body of work developed in robust regression (following ref. 7) is concerned with situations in which 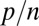 tends to 0, as n tends to infinity.
tends to 0, as n tends to infinity.
Let us briefly recall the details of the robust regression problem. We consider the estimator
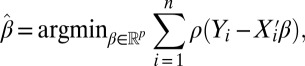 |
where ρ is a function from 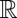 to
to 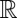 , which we will assume throughout is convex.§ Furthermore, we consider a linear regression model
, which we will assume throughout is convex.§ Furthermore, we consider a linear regression model
where  is unknown and
is unknown and 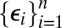 are random errors, independent of
are random errors, independent of 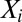 ’s. Naturally, our aim is to estimate
’s. Naturally, our aim is to estimate 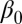 from our observations
from our observations 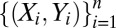 and the question is therefore, which ρ we should choose. We can separate this into the following two questions: (i) What choice of ρ minimizes the asymptotic error for estimating an individual regression coefficient (or a given linear form in
and the question is therefore, which ρ we should choose. We can separate this into the following two questions: (i) What choice of ρ minimizes the asymptotic error for estimating an individual regression coefficient (or a given linear form in 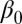 )? (ii) What choice of ρ minimizes the asymptotic prediction error for a new observation
)? (ii) What choice of ρ minimizes the asymptotic prediction error for a new observation 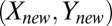 given the training data? The answers to (i) and (ii) turn out to be the same in the high-dimensional and Gaussian setting we are considering, just as in the low-dimensional case, but the extension is surprising.
given the training data? The answers to (i) and (ii) turn out to be the same in the high-dimensional and Gaussian setting we are considering, just as in the low-dimensional case, but the extension is surprising.
Some Recent High-Dimensional Results.
In a recent paper (6), we found heuristically the following.
Result 1.
[See El Karoui et al. (6).] Suppose
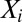 are independent identically distributed (i.i.d)
are independent identically distributed (i.i.d) 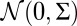 , with
, with
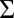 positive definite. Suppose
positive definite. Suppose
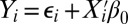 ,
, 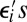 are i.i.d, independent of
are i.i.d, independent of
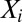 ,
, 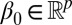 is deterministic, and
is deterministic, and
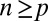 . Call
. Call
 |
Then we have the stochastic representation
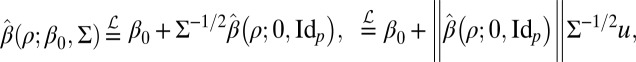 |
where u is uniform on
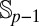 (the unit sphere in
(the unit sphere in
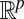 ) and independent of
) and independent of
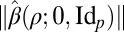 .
.
Let us call
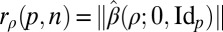 . As p and n tend to infinity, while
. As p and n tend to infinity, while
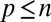 and
and
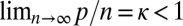 ,
, 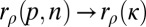 in probability (under regularity conditions on ρ and ε), where
in probability (under regularity conditions on ρ and ε), where
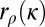 is deterministic. Define
is deterministic. Define
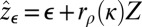 , where
, where
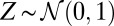 is independent of ε, and ε has the same distribution as
is independent of ε, and ε has the same distribution as
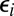 . We can determine
. We can determine
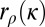 through
through
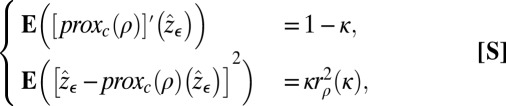 |
where c is a positive deterministic constant to be determined from the previous system.
The definition and details about the prox mapping are given in Appendix: Reminders. This formulation is important because it shows that what matters about an objective function in high dimension is not really the objective itself but rather its prox, in connection with the distribution of the errors. We also note that our analysis in ref. 6 highlights the fact that the result concerning 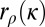 should hold when normality of the predictors is replaced by a concentration of quadratic form assumption. System S is the basis of our analysis.
should hold when normality of the predictors is replaced by a concentration of quadratic form assumption. System S is the basis of our analysis.
Consequences for estimation of 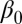 .
.
If v is a given deterministic vector, we see that 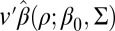 is unbiased for
is unbiased for 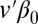 and
and
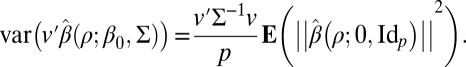 |
In other words, in high dimension, the simple estimator 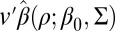 is
is 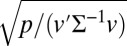 -consistent for
-consistent for 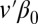 . We further note that
. We further note that 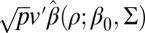 is asymptotically normal, and its variance can be estimated, so inference about
is asymptotically normal, and its variance can be estimated, so inference about 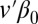 is easy. More details are in SI Text, including for instance explicit confidence intervals. Picking v to be the kth canonical basis vector,
is easy. More details are in SI Text, including for instance explicit confidence intervals. Picking v to be the kth canonical basis vector, 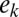 , we also see that we can consistently estimate the kth coordinate of
, we also see that we can consistently estimate the kth coordinate of 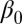 ,
, 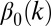 , at rate
, at rate 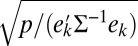 .
.
A similar analysis can be performed to obtain unbiased (and consistent) estimators of quadratic forms in 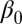 , i.e., quantities of the form
, i.e., quantities of the form 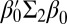 , where
, where 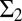 is a given covariance matrix.
is a given covariance matrix.
The situation in which the vector v is random (and for instance dependent on the design) is beyond the scope of this paper. We note that Huber (7) has early very partial results on this problem.
On expected prediction error.
In the case in which 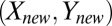 follows the model above and is independent of
follows the model above and is independent of 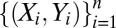 , we immediately see that
, we immediately see that
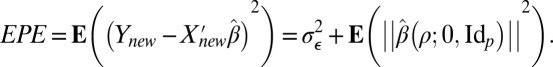 |
Picking ρ to minimize the quantity 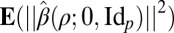 (viewed as a function of ρ) will allow us to get the best estimators (in the class we are considering) for both expected prediction error (EPE) and, as it turns out, linear forms in
(viewed as a function of ρ) will allow us to get the best estimators (in the class we are considering) for both expected prediction error (EPE) and, as it turns out, linear forms in 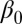 .
.
Potential Limitations of the Model.
Assumptions concerning the predictors.
The impact of changing the distributional assumptions of the predictors on Result 1 is explored and explained in details in our papers (6) and especially ref. 8. We present in ref. 8 design matrices for which Result 1 does not hold. For those designs, using the family of objective functions described in Theorem 1 below will not yield optimal results—however, using dimension-dependent objective functions may still yield improvement over using standard, dimension-independent objective functions. We also note that parts of Result 1 hold under less restrictive assumptions, but one key limitation is that our generalizations do not include categorical predictors.
The question of intercept.
The model and estimation problem described in Result 1 do not include an intercept. Furthermore, both 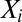 and
and 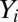 are assumed to have mean 0. However, if we recenter both the responses
are assumed to have mean 0. However, if we recenter both the responses 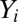 ’s and the predictors
’s and the predictors 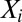 ’s and fit a linear model (without intercept) on this recentered dataset, we have a solution to these problems that essentially fits into the framework of our analysis. The corresponding
’s and fit a linear model (without intercept) on this recentered dataset, we have a solution to these problems that essentially fits into the framework of our analysis. The corresponding 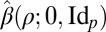 has the same stochastic representation properties as the ones described in Result 1, and hence inference about
has the same stochastic representation properties as the ones described in Result 1, and hence inference about 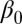 is possible in this case, too. More details and justifications are provided in SI Text. We note that, as presented in this paper, our results do not allow us to address inferential questions involving the intercept. However, in separate and ongoing work, we have obtained results that suggest that we will be able to answer some of these inferential questions as well as issues pertaining to the fitted values [see Huber (7), remarks 2 and 3, pp. 803–804, for early comments about the difficulty they pose in the high-dimensional setting].
is possible in this case, too. More details and justifications are provided in SI Text. We note that, as presented in this paper, our results do not allow us to address inferential questions involving the intercept. However, in separate and ongoing work, we have obtained results that suggest that we will be able to answer some of these inferential questions as well as issues pertaining to the fitted values [see Huber (7), remarks 2 and 3, pp. 803–804, for early comments about the difficulty they pose in the high-dimensional setting].
The rest of the paper is focused on the model and statistical problem discussed in Result 1.
Main Result.
We propose an algorithm to determine the asymptotically optimal objective function to use in robust regression. As explained in SI Text, under the assumptions of Result 1, this optimal objective function is the same regardless of the norm chosen to assess the performance of our regression estimator. Just as in the classical case, determining the optimal objective function requires knowledge of the distribution of the errors, which we call ε. We call the density of the errors 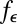 and assume that
and assume that 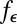 is log-concave.
is log-concave.
If 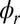 is the normal density with variance
is the normal density with variance 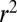 and
and 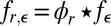 , where
, where  is the usual convolution operation,
is the usual convolution operation, 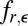 is log-concave. As a matter of fact, it is well known (9, 10) that the convolution of two log-concave densities is log-concave.
is log-concave. As a matter of fact, it is well known (9, 10) that the convolution of two log-concave densities is log-concave.
We call 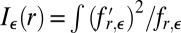 the information of
the information of 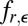 , which we assume exists for all
, which we assume exists for all 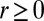 . It is known that, when ε has a density,
. It is known that, when ε has a density, 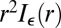 is continuous in r (11), where it is explained that
is continuous in r (11), where it is explained that 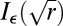 is differentiable or see ref. 12.
is differentiable or see ref. 12.
Throughout the paper, we denote by 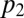 the function taking value
the function taking value
Here is our theorem.
Theorem 1.
If
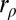 is a solution of system
S, we have
is a solution of system
S, we have
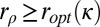 , where
, where
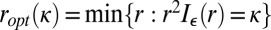 .
.
Furthermore, 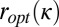 is the solution of system
S
when
is the solution of system
S
when
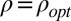 , and
, and
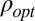 is the convex function
is the convex function
[For a function g, 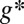 is its (Fenchel–Legendre) conjugate, i.e.,
is its (Fenchel–Legendre) conjugate, i.e., 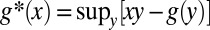 .]
.]
We give an alternative representation of 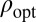 in Appendix: Reminders.
in Appendix: Reminders.
We propose the following algorithm for computing the optimal objective function under the assumptions of the theorem.
1. Solve for r the equation
Define 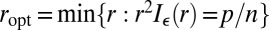 .
.
2. Use the objective function¶
The theorem and the algorithm raise a few questions: Is there a solution to the equation in step 1? Is the min well defined? Is the objective function in step 2 convex? We address all these questions in the course of the paper.
The significance of the algorithm lies in the fact that we are now able to incorporate dimensionality in our optimal choice of ρ. In other words, different objectives turn out to be optimal as the ratio of dimensions varies. Naturally, the optimality of the objective function is restricted to situations in which our assumptions on the design matrix are satisfied. However, more generally, our results provide practitioners with a “natural” family of objective functions that could be tried if one would like to use a dimension-dependent objective function in a high-dimensional regression problem. This family of functions is also qualitatively different from the ones that appear naturally in the small p setting, as our derivation (see below) shows.
Because our estimators are M-estimators, they are not immune to inadmissibility problems, as has been understood, in an even simpler context, since the appearance of James–Stein estimators. Picking 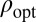 instead of another ρ, although improving performance when our assumptions are satisfied, does not remove this potential problem.
instead of another ρ, although improving performance when our assumptions are satisfied, does not remove this potential problem.
It should also be noted that at least numerically, computing 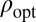 is not very hard. Similarly, solving Eq. 1 is not hard numerically. Hence, the algorithm is effective as soon as we have information about the distribution of ε.
is not very hard. Similarly, solving Eq. 1 is not hard numerically. Hence, the algorithm is effective as soon as we have information about the distribution of ε.
As the reader will have noticed, a crucial role is played by 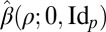 . In the rest of the paper, we use the lighter notation
. In the rest of the paper, we use the lighter notation
The dependence of 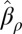 on p and n is left implicit in general, but will be brought back when there are any risks of confusion.
on p and n is left implicit in general, but will be brought back when there are any risks of confusion.
Next, we illustrate our algorithm in a few special cases.
Computing the Optimal Objective
The Case of Gaussian Errors.
Corollary 1.
In the setting of i.i.d Gaussian predictors, among all convex objective functions, 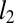 is optimal in regression when the errors are Gaussian.
is optimal in regression when the errors are Gaussian.
In the case of Gaussian ε, it is clear that  is a Gaussian density. Hence,
is a Gaussian density. Hence, 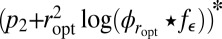 is a multiple of
is a multiple of 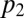 (up to centering) and so is
(up to centering) and so is 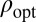 . General arguments given later guarantee that this latter multiple is strictly positive. Therefore,
. General arguments given later guarantee that this latter multiple is strictly positive. Therefore, 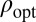 is
is 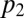 , up to positive scaling and centering. Carrying out the computations detailed in the algorithm, we actually arrive at
, up to positive scaling and centering. Carrying out the computations detailed in the algorithm, we actually arrive at 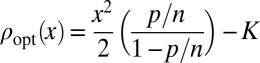 . Details are in SI Text.
. Details are in SI Text.
The Case of Double-Exponential Errors.
We recall that in low dimension (e.g., p fixed, n goes to infinity), classic results show that the optimal objective is 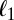 . As we will see, it is not at all of the case when p and n grow in such a way that
. As we will see, it is not at all of the case when p and n grow in such a way that 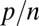 has a finite limit in
has a finite limit in 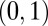 . We recall that, in ref. 6, we observed that when
. We recall that, in ref. 6, we observed that when 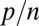 was greater than 0.3 or so,
was greater than 0.3 or so, 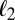 actually performed better than
actually performed better than 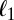 for double-exponential errors.
for double-exponential errors.
Although there is no analytic form for the optimal objective, it can be computed numerically. We discuss how and present a picture to get a better understanding of the solution of our problem.
The Optimal Objective.
For 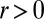 ,
, 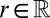 , and
, and 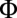 , the Gaussian cumulative distribution function, let us define
, the Gaussian cumulative distribution function, let us define
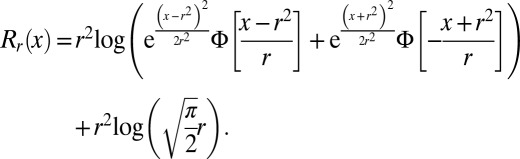 |
It is easy to verify that, when the errors are double exponential, 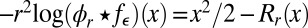 . Hence, effectively the optimal objective is the function taking values
. Hence, effectively the optimal objective is the function taking values
It is of course important to be able to compute this function and the estimate 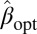 based on it. We show below that
based on it. We show below that 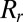 is a smooth convex function for all r. Hence, in the case we are considering,
is a smooth convex function for all r. Hence, in the case we are considering, 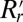 is increasing and therefore invertible. If we call
is increasing and therefore invertible. If we call 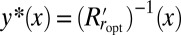 , we see that
, we see that 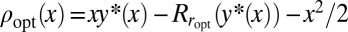 . We also need to be able to compute the derivative of
. We also need to be able to compute the derivative of 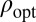 (denoted
(denoted 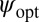 ) to implement a gradient descent algorithm to compute
) to implement a gradient descent algorithm to compute 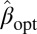 . For this, we can use a well-known result in convex analysis, which says that for a convex function h (under regularity conditions)
. For this, we can use a well-known result in convex analysis, which says that for a convex function h (under regularity conditions) 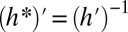 (see ref. 13, corollary 23.5.1).
(see ref. 13, corollary 23.5.1).
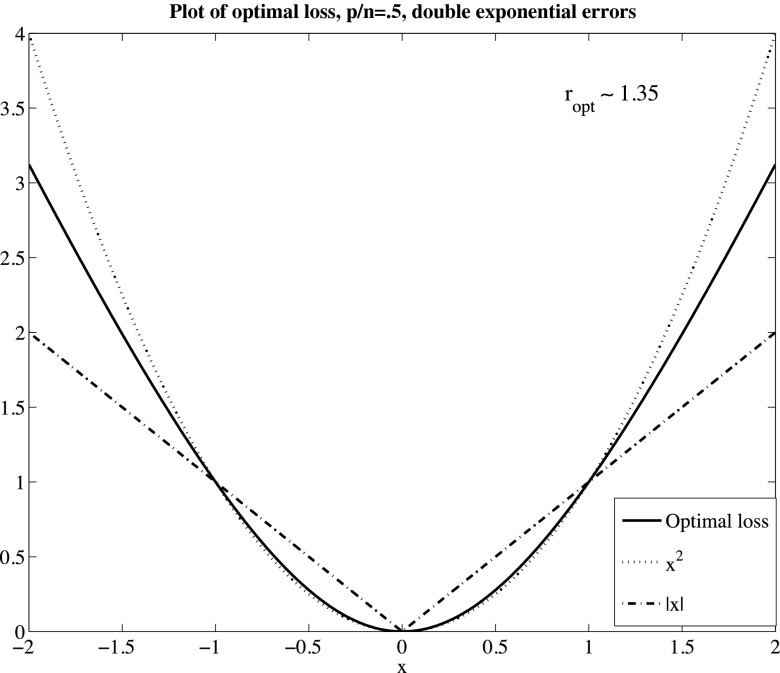
We present a plot to get an intuitive feeling for how this function 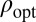 behaves (more can be found in SI Text). Fig. 1 compares
behaves (more can be found in SI Text). Fig. 1 compares 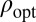 to other objective functions of potential interest in the case of
to other objective functions of potential interest in the case of 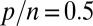 . All of the functions we compare are normalized so that they take value 0 at 0 and 1 at 1.
. All of the functions we compare are normalized so that they take value 0 at 0 and 1 at 1.
Fig. 1.
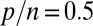 : comparison of
: comparison of 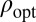 (optimal objective) to
(optimal objective) to 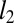 and
and 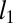 .
. 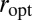 is the solution of
is the solution of 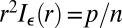 ; for
; for 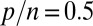 ,
, 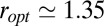 .
.
Comparison of Asymptotic Performance of 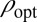 Against Other Objective Functions.
Against Other Objective Functions.
We compare 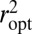 to the results we would get using other objective functions ρ in the case of double-exponential errors. Recall that our system S allows us to compute the asymptotic value of
to the results we would get using other objective functions ρ in the case of double-exponential errors. Recall that our system S allows us to compute the asymptotic value of 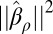 ,
, 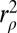 , as n and p go to infinity for any convex (and sufficiently regular) ρ.
, as n and p go to infinity for any convex (and sufficiently regular) ρ.
Comparison of 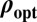 to
to 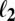 .
.
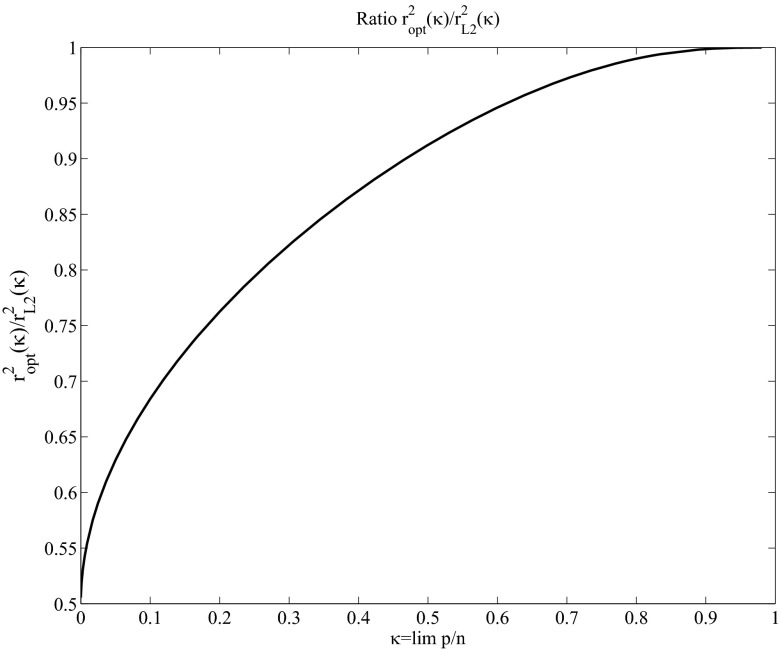
We compare 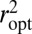 to
to 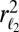 in Fig. 2. Interestingly,
in Fig. 2. Interestingly, 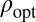 yields a
yields a 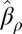 that is twice as efficient as
that is twice as efficient as 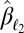 as
as 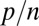 goes to 0. From classical results in robust regression (p bounded), we know that this is optimal because
goes to 0. From classical results in robust regression (p bounded), we know that this is optimal because 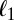 objective is optimal in that setting, and also yields estimators that are twice as efficient as
objective is optimal in that setting, and also yields estimators that are twice as efficient as 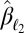 .
.
Fig. 2.
Ratio 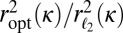 for double-exponential errors: the ratio is always less than 1, showing the superiority of the objective we propose over
for double-exponential errors: the ratio is always less than 1, showing the superiority of the objective we propose over 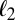 .
.
Comparison of 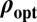 to
to 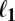 .
.
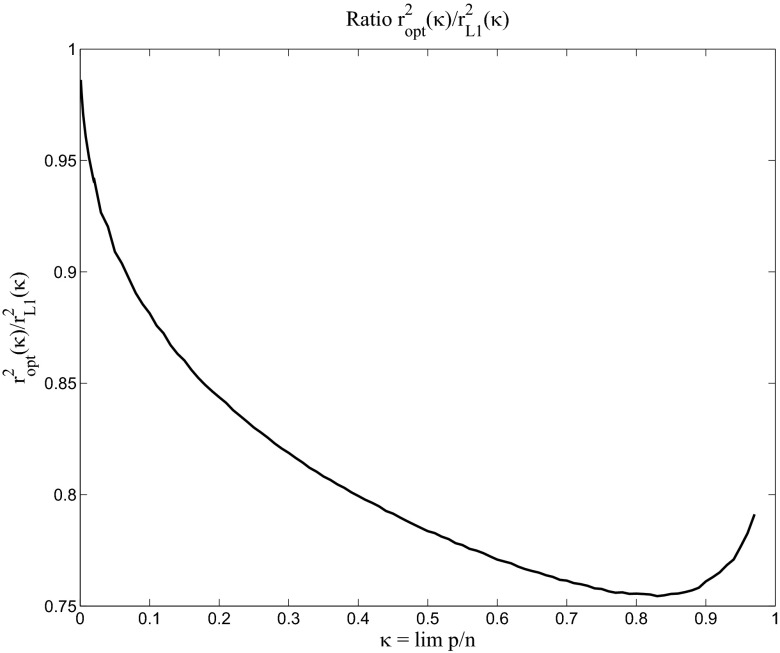
We compare 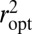 to
to 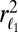 in Fig. 3. Naturally, the ratio goes to 1 when
in Fig. 3. Naturally, the ratio goes to 1 when 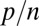 goes to 0, because
goes to 0, because 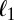 , as we just mentioned, is known to be the optimal objective function for
, as we just mentioned, is known to be the optimal objective function for 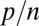 tending to 0.
tending to 0.
Fig. 3.
Ratio 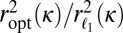 : the ratio is always less than 1, showing the superiority of the objective we propose over
: the ratio is always less than 1, showing the superiority of the objective we propose over 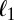 . Naturally, the ratio goes to 1 at 0, because we know that
. Naturally, the ratio goes to 1 at 0, because we know that 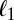 is the optimal objective when
is the optimal objective when 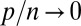 for double-exponential errors.
for double-exponential errors.
Simulations.
We investigate the empirical behavior of estimators computed under our proposed objective function. We call those estimators 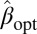 . Table 1 shows
. Table 1 shows 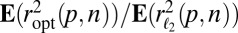 over 1,000 simulations when
over 1,000 simulations when 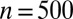 for different ratios of dimensions and compares the empirical results to
for different ratios of dimensions and compares the empirical results to 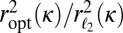 , the theoretical values. We used
, the theoretical values. We used 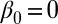 ,
, 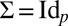 and double-exponential errors in our simulations.
and double-exponential errors in our simulations.
Table 1.
n = 500:  over 1,000 independent simulations
over 1,000 independent simulations
| p/n | 0.1 | 0.2 | 0.3 | 0.4 | 0.5 | 0.6 | 0.7 | 0.8 | 0.9 |
| Observed mean ratio | 0.6924 | 0.7732 | 0.8296 | 0.8862 | 0.9264 | 0.9614 | 0.9840 | 0.9959 | 0.9997 |
| Predicted mean ratio | 0.6842 | 0.7626 | 0.8224 | 0.8715 | 0.9124 | 0.9460 | 0.9721 | 0.9898 | 0.9986 |
| |Relative error|, % | 1.2 | 1.4 | 0.8 | 1.7 | 1.5 | 1.6 | 1.2 | 0.6 | 0.1 |
In SI Text, we also provide statistics concerning  computed over 1,000 simulations. We note that our predictions concerning
computed over 1,000 simulations. We note that our predictions concerning  work very well in expectation when p and n are a few 100’s, even though in these dimensions,
work very well in expectation when p and n are a few 100’s, even though in these dimensions,  is not yet close to being deterministic (see SI Text for details—these remarks also apply to
is not yet close to being deterministic (see SI Text for details—these remarks also apply to 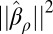 for more general ρ).
for more general ρ).
Derivations
We prove Theorem 1 assuming the validity of Result 1.
Phrasing the Problem as a Convex Feasibility Problem.
Let us call 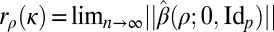 , where
, where 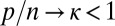 . We now assume throughout that
. We now assume throughout that 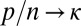 and call
and call 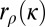 simply
simply 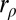 for notational simplicity. We recall that for
for notational simplicity. We recall that for 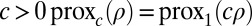 (Appendix: Reminders). From now on, we call
(Appendix: Reminders). From now on, we call 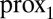 just prox. If
just prox. If 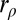 is feasible for our problem, there is a ρ that realizes it and the system S is therefore, with
is feasible for our problem, there is a ρ that realizes it and the system S is therefore, with 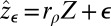 ,
,
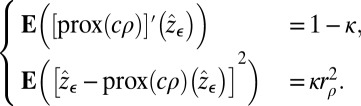 |
Now it is clear that if we replace ρ by 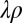 ,
, 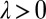 , we do not change
, we do not change 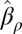 . In particular, if we call
. In particular, if we call 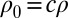 , where c is the real appearing in the system above, we have, if
, where c is the real appearing in the system above, we have, if 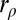 is feasible: there exists
is feasible: there exists 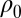 such that
such that
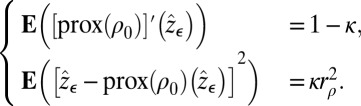 |
We can now rephrase this system using the fundamental equality (see ref. 14 and Appendix: Reminders) 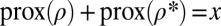 , where
, where 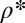 is the (Fenchel–Legendre) conjugate of ρ. It becomes
is the (Fenchel–Legendre) conjugate of ρ. It becomes
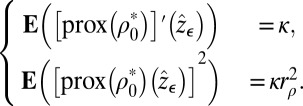 |
Prox mappings are known to belong to subdifferentials of convex functions and to be contractive (see ref. 14, p. 292, corollaire 10.c). Let us call 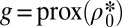 and recall that
and recall that 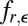 denotes the density of
denotes the density of 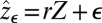 . Because g is contractive,
. Because g is contractive, 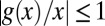 as
as 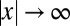 . Because
. Because 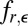 is a log-concave density (as a convolution of two log-concave densities—see refs. 9 and 10) with support
is a log-concave density (as a convolution of two log-concave densities—see refs. 9 and 10) with support 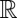 , it goes to zero at infinity exponentially fast (see ref. 15, p. 332). We can therefore use integration by parts in the first equation to rewrite the previous system as (we now use r instead of
, it goes to zero at infinity exponentially fast (see ref. 15, p. 332). We can therefore use integration by parts in the first equation to rewrite the previous system as (we now use r instead of 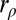 for simplicity)
for simplicity)
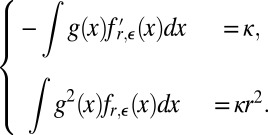 |
Because 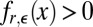 , for all x, we can multiply and divide by
, for all x, we can multiply and divide by 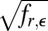 inside the integral of the first equation and use the Cauchy–Schwarz inequality to get
inside the integral of the first equation and use the Cauchy–Schwarz inequality to get
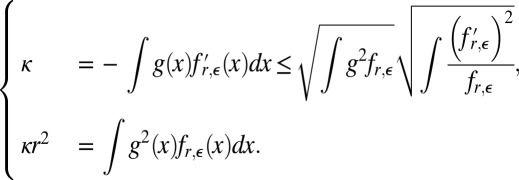 |
It follows that
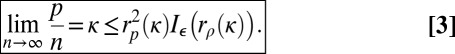 |
We now seek a ρ to achieve this lower bound on 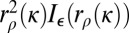 .
.
Achieving the Lower Bound.
It is clear that a good g [which is 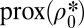 ] should saturate the Cauchy–Schwarz inequality above. Let
] should saturate the Cauchy–Schwarz inequality above. Let 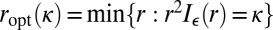 . A natural candidate is
. A natural candidate is
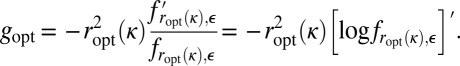 |
It is easy to see that for this function 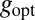 , the two equations of the system are satisfied (the way we have chosen
, the two equations of the system are satisfied (the way we have chosen 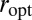 is of course key here). However, we need to make sure that
is of course key here). However, we need to make sure that 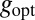 is a valid choice; in other words, it needs to be the prox of a certain (convex) function.
is a valid choice; in other words, it needs to be the prox of a certain (convex) function.
We can do so by using ref. 14. By proposition 9.b on p. 289 in ref. 14, it suffices to establish that, for all 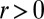 ,
,
is convex and less convex than 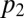 . That is, there exists a convex function γ such that
. That is, there exists a convex function γ such that 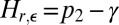 .
.
When ε has a log-concave density, it is well known that 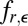 is log-concave.
is log-concave. 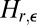 is therefore convex.
is therefore convex.
Furthermore, for a constant K,
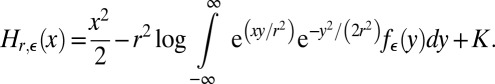 |
It is clear that 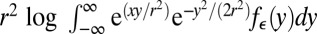 is convex in x. Hence,
is convex in x. Hence, 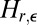 is less convex than
is less convex than 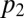 . Thus,
. Thus, 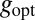 is a prox function and a valid choice for our problem.
is a prox function and a valid choice for our problem.
Determining 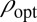 from
from 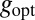 .
.
Let us now recall another result of ref. 14. We denote the inf-convolution operation by 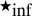 . More details about
. More details about 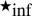 are given in SI Text and Appendix: Reminders. If γ is a (proper, closed) convex function, and
are given in SI Text and Appendix: Reminders. If γ is a (proper, closed) convex function, and 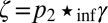 , we have (see ref. 14, p. 286)
, we have (see ref. 14, p. 286)
Recall that 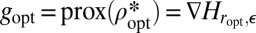 . So up to constants that do not matter, we have
. So up to constants that do not matter, we have
It is easy to see (SI Text) that, for any function f,
So we have 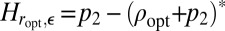 . Now, for a proper, closed, convex function γ, we know that
. Now, for a proper, closed, convex function γ, we know that 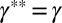 . Hence,
. Hence,
Convexity of 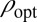 .
.
We still need to make sure that the function 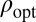 we have obtained is convex. We once again appeal to ref. 14, proposition 9.b. Because
we have obtained is convex. We once again appeal to ref. 14, proposition 9.b. Because 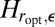 is less convex than
is less convex than 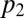 ,
, 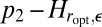 is convex. However, because
is convex. However, because 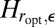 is convex,
is convex, 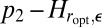 is less convex than
is less convex than 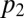 . Therefore,
. Therefore, 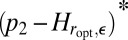 is more convex than
is more convex than 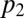 , which implies that
, which implies that 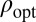 is convex.
is convex.
Minimality of 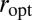 .
.
The fundamental inequality we have obtained is Eq. 3, which says that, for any feasible 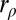 , when
, when 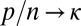 ,
, 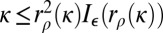 . Our theorem requires solving the equation
. Our theorem requires solving the equation 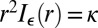 . Let us study the properties of the solutions of this equation.
. Let us study the properties of the solutions of this equation.
Let us call ξ the function such that 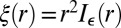 . We note that
. We note that 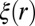 is the information of
is the information of 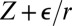 , where
, where 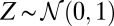 and independent of ε. Hence
and independent of ε. Hence 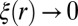 as
as 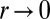 and
and 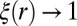 as
as 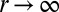 . This is easily established using the information inequality
. This is easily established using the information inequality 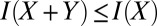 when X and Y are independent (I is the Fisher information; see, e.g., ref. 16). As a matter of fact,
when X and Y are independent (I is the Fisher information; see, e.g., ref. 16). As a matter of fact, 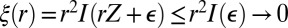 as
as 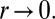 However,
However, 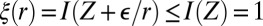 . Finally, as
. Finally, as 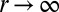 , it is clear that
, it is clear that 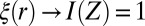 (see SI Text for details). Using the fact that ξ is continuous (see, e.g., ref. 11), we see that the equation
(see SI Text for details). Using the fact that ξ is continuous (see, e.g., ref. 11), we see that the equation  has at least one solution for all
has at least one solution for all 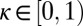 .
.
Let us recall that we defined our solution as 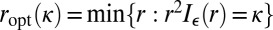 . Denote
. Denote 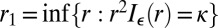 . We need to show two facts to guarantee optimality of
. We need to show two facts to guarantee optimality of 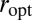 : (i) the inf is really a min; (ii)
: (i) the inf is really a min; (ii) 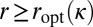 , for all feasible r’s (i.e., r’s such that
, for all feasible r’s (i.e., r’s such that 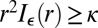 ). (i) follows easily from the continuity of ξ and lower bounds on
). (i) follows easily from the continuity of ξ and lower bounds on 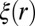 detailed in SI Text.
detailed in SI Text.
We now show that, for all feasible r’s, 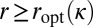 . Suppose it is not the case. Then, there exists
. Suppose it is not the case. Then, there exists 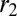 , which is asymptotically feasible and
, which is asymptotically feasible and 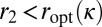 . Because
. Because 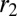 is asymptotically feasible,
is asymptotically feasible, 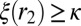 . Clearly,
. Clearly, 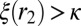 , for otherwise we would have
, for otherwise we would have 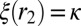 with
with 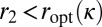 , which would violate the definition of
, which would violate the definition of 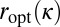 . Now recall that
. Now recall that 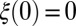 . By continuity of ξ, because
. By continuity of ξ, because 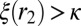 , there exists
, there exists 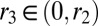 such that
such that 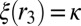 . However,
. However, 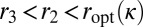 , which violates the definition of
, which violates the definition of 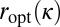 .
.
Appendix: Reminders
Convex Analysis Reminders.
Inf-convolution and conjugation.
Recall the definition of the inf-convolution (see, e.g., ref. 13, p. 34). If f and g are two functions,
Recall also that the (Fenchel–Legendre) conjugate of a function f is
A standard result says that, when f is closed, proper, and convex, 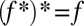 (ref. 13, theorem 12.2).
(ref. 13, theorem 12.2).
We also need a simple remark about relation between inf-convolution and conjugation. Recall that 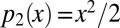 . Then (we give details in SI Text),
. Then (we give details in SI Text),
The prox function.
The prox function seems to have been introduced in convex analysis by Moreau (refs. 13, pp. 339–340, and 14). The definition follows. We assume that f is a proper, closed, convex function. Then, when f: 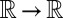 , and
, and 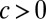 is a scalar,
is a scalar,
 |
In the last equation, 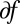 is in general a subdifferential of f. Although this could be a multivalued mapping when f is not differentiable, the prox is indeed well defined as a (single-valued) function.
is in general a subdifferential of f. Although this could be a multivalued mapping when f is not differentiable, the prox is indeed well defined as a (single-valued) function.
A fundamental result connecting prox mapping and conjugation is the equality
An Alternative Representation for 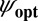 .
.
We give an alternative representation for 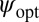 . Recall that we had
. Recall that we had 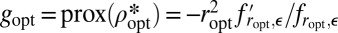 . Using
. Using 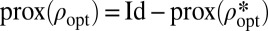 , we see that
, we see that 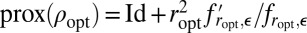 . In the case in which
. In the case in which 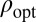 is differentiable, this gives immediately
is differentiable, this gives immediately
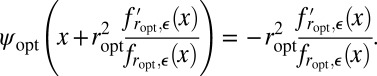 |
Because 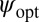 is defined up to a positive scaling factor,
is defined up to a positive scaling factor,
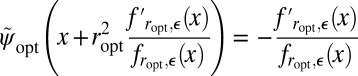 |
is an equally valid choice.
Interestingly, for 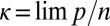 near 0,
near 0, 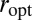 will be near zero too, and the previous equation shows that
will be near zero too, and the previous equation shows that 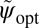 will be essentially
will be essentially 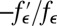 , corresponding to the objective derived from maximum-likelihood theory.
, corresponding to the objective derived from maximum-likelihood theory.
Supplementary Material
Acknowledgments
We thank the referees for their interesting and constructive comments. We thank Prof. Steven Portnoy for several thought-provoking remarks and discussions. D.B. gratefully acknowledges support from National Science Foundation (NSF) Grant DMS-0636667 (Vertical Integration of Research and Education in the Mathematical Sciences). P.J.B. gratefully acknowledges support from NSF Grant DMS-0907362. N.E.K. gratefully acknowledges support from an Alfred P. Sloan Research Fellowship and NSF Grant DMS-0847647 (Faculty Early Career Development). B.Y. gratefully acknowledges support from NSF Grants SES-0835531 (Cyber-Enabled Discovery and Innovation), DMS-1107000, and CCF-0939370.
Footnotes
The authors declare no conflict of interest.
†Heuristically.
‡Under conditions depending on the model and the linear combination; see details below.
§The properties of 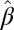 naturally depend on ρ—this dependence will be made clear later.
naturally depend on ρ—this dependence will be made clear later.
¶Note that any 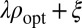 , where λ and ξ are real valued with
, where λ and ξ are real valued with 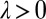 , yields the same solution for
, yields the same solution for 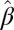 .
.
This article contains supporting information online at www.pnas.org/lookup/suppl/doi:10.1073/pnas.1307845110/-/DCSupplemental.
References
- 1. Fisher RA (1922) On the mathematical foundations of theoretical statistics. Philos Trans R Soc Lond A 222:309–368.
- 2. Cramér H (1946) Mathematical Methods of Statistics. Princeton Mathematical Series (Princeton Univ Press, Princeton), Vol 9.
- 3. Hájek J (1972) Local asymptotic minimax and admissibility in estimation. Proceedings of the Sixth Berkeley Symposium on Mathematical Statistics and Probability (University of California, Berkeley, California, 1970/1971) (Univ of California Press, Berkeley, CA), Vol I: Theory of Statistics, pp 175–194.
- 4.Le Cam L. On the assumptions used to prove asymptotic normality of maximum likelihood estimates. Ann Math Stat. 1970;41:802–828. [Google Scholar]
- 5. Bühlmann P, van de Geer S (2011) Statistics for High-Dimensional Data. Methods, Theory and Applications. Springer Series in Statistics (Springer, Heidelberg)
- 6.El Karoui N, Bean D, Bickel P, Lim C, Yu B. On robust regression with high-dimensional predictors. Proc Natl Acad Sci USA. 2012;110:14557–14562. doi: 10.1073/pnas.1307842110. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Huber PJ. Robust regression: Asymptotics, conjectures and Monte Carlo. Ann Stat. 1973;1:799–821. [Google Scholar]
- 8. El Karoui N, Bean D, Bickel P, Lim C, Yu B (2012) On robust regression with high-dimensional predictors (Department of Statistics, Univ of California, Berkeley, CA), Technical Report 811.
- 9.Ibragimov IA. On the composition of unimodal distributions. Teor Veroyatnost i Primenen. 1956;1:283–288. [Google Scholar]
- 10.Prékopa A. On logarithmic concave measures and functions. Acta Sci Math (Szeged) 1973;34:335–343. [Google Scholar]
- 11.Costa MHM. A new entropy power inequality. IEEE Trans Inf Theory. 1985;31:751–760. [Google Scholar]
- 12.Guo D, Wu Y, Shamai S, Verdú S. Estimation in Gaussian noise: Properties of the minimum mean-square error. IEEE Trans Inf Theory. 2011;57:2371–2385. [Google Scholar]
- 13. Rockafellar RT (1997) Convex analysis. Princeton Landmarks in Mathematics (Princeton Univ Press, Princeton), Reprint of the 1970 original, Princeton Paperbacks.
- 14.Moreau J-J. Proximité et dualité dans un espace hilbertien. Bull Soc Math France. 1965;93:273–299. French. [Google Scholar]
- 15.Karlin S. Total positivity. Vol I. Stanford, CA: Stanford Univ Press; 1968. [Google Scholar]
- 16.Stam AJ. Some inequalities satisfied by the quantities of information of Fisher and Shannon. Inf Control. 1959;2:101–112. [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.