Testing the Ability of Non-Methylamine Osmolytes Present in Kidney Cells to Counteract the Deleterious Effects of Urea on Structure, Stability and Function of Proteins

Abstract

Human kidney cells are under constant urea stress due to its urine concentrating mechanism. It is believed that the deleterious effect of urea is counteracted by methylamine osmolytes (glycine betaine and glycerophosphocholine) present in kidney cells. A question arises: Do the stabilizing osmolytes, non-methylamines (myo-inositol, sorbitol and taurine) present in the kidney cells also counteract the deleterious effects of urea? To answer this question, we have measured structure, thermodynamic stability (ΔG _D ^o) and functional activity parameters (K _m and k _cat) of different model proteins in the presence of various concentrations of urea and each non-methylamine osmolyte alone and in combination. We observed that (i) for each protein myo-inositol provides perfect counteraction at 1∶2 ([myo-inositol]:[urea]) ratio, (ii) any concentration of sorbitol fails to refold urea denatured proteins if it is six times less than that of urea, and (iii) taurine regulates perfect counteraction in a protein specific manner; 1.5∶2.0, 1.2∶2.0 and 1.0∶2.0 ([taurine]:[urea]) ratios for RNase-A, lysozyme and α-lactalbumin, respectively.

Introduction

The waste product, urea plays a key role in the osmoregulation of reno-medullary cells in diuretic and antidiuretic conditions. As part of the urinary concentrating mechanism, renal inner medullary cells are normally exposed to variable and often very high interstitial levels of urea, yet they survive and function. The urea concentration under diuretic condition is 400–600 mM in the mammalian kidneys including human [1] and reaches up to 3–4 M under antidiuretic conditions [2]. High urea is harmful to cells, altering many enzymatic functions or even killing them by apoptosis [3], [4]. Urea is a chaotropic agent that disrupts non-covalent interactions responsible for the globular structure of proteins [5], [6], [7], [8] and also influences enzyme kinetic properties such as maximal velocity (V _max) and K _m [6], [7]. In addition to the chaotropic nature, high urea concentration can also bring about post-translational modification of large number of proteins either by carbamoylation or carbonylation near physiological pH and temperature [9], [10].

It is generally believed that the deleterious effect of urea on macromolecules (in kidney cells) is offset by the accumulation of small organic compounds in the osmoticum (called osmolytes). In fact, the principal osmolytic compounds present in the urea-rich kidney cells consists of methylamines (glycerophosphocholine (GPC) and glycine betaine (GB)) and non-methylamines (myo-inositol, sorbitol and taurine). The physiological concentration of each non-methylamine is different in cells of different species [11]–[22]. In mammalian kidney cells concentrations of myo-inositol, sorbitol and taurine are 10–21, 5–16 and less than 10–20 mosmol/L, respectively. It has been observed that concentration of non-methylamines does not change during urea stress [23], [24]. On the contrary, methylamine concentration increases with an increase in urea concentration [25]. The effect of methylamine osmolytes in offsetting the effects of urea on proteins (in terms of thermodynamic stability, structure and activity) has earlier been investigated. It is known that when the concentration ratio of methylamines to urea is 1∶2, their opposing effects are independently additive, preserving macromolecular structure and function [7], [26].

Earlier studies have shown that concentrations of non-methylamines in kidney cells increases with an increase in NaCl concentration, but it remains unchanged with an increase in urea concentration [23], [24]. A question arises: Do non-methylamines have the ability to offset the deleterious effect of urea on protein structure and function? In this communication we have investigated the counteractive ability of all the non-methylamine osmolytes present in the osmoticum of the reno-medullary cells in terms of structure, stability and function of three proteins namely, RNase-A, lysozyme and α-lactalbumin (α-LA). To our surprise we discovered that the non-methylamine osmolytes, myo-inositol and taurine have the counteracting ability on the three proteins investigated. Myo-inositol brings about perfect counteraction at 1∶2 ratio (myo-inositol: urea) on all the proteins; while taurine shows protein-specific counteraction ratios. This study shows that in addition to methylamines, myo-inositol and taurine might be counteracting osmolytes (osmolytes that can reverse the denaturing effect of urea on macromolecules) in vivo.

Methods

Reagents

Commercial lyophilized preparations of ribonuclease-A (type III-A) from bovine pancreas (RNase-A), chicken egg-white lysozyme and α-lactalbumin (type I) from bovine milk were purchased from Sigma Chemical Co. Urea was procured from ICN Biomedicals Inc. Sorbitol, myo-inositol, and taurine were also obtained from Sigma Chemical Co. Guanidinium chloride (GdmCl) was ultrapure sample from Schwarz/Mann. These and other chemicals, which were of analytical grade, were used without further purification.

Stock solution of each protein was dialyzed extensively against 0.1 M KCl pH 7.0 at 4°C. Apo-α-lactalbumin (α-LA) was prepared by adding 4.0 mM EGTA to the dialyzed solution of holoprotein (with Ca²⁺ bound). Protein stock solutions were filtered using 0.22 µm Millipore filter paper. All three proteins gave single band during polyacrylamide gel electrophoresis. Protein concentration was determined experimentally using molar absorption coefficient, ε (M⁻¹cm⁻¹) value of 9800 at 277.5 nm for RNase-A [27], 39000 at 280 nm for lysozyme [28] and 29210 at 280 nm for α-LA [29]. Urea stock solution was prepared fresh for each day. Concentrations of the stock solutions of urea and GdmCl were determined by refractive index measurements [30]. All solutions for optical measurements were prepared in degassed 50 mM buffers containing 0.1 M KCl. For various pH ranges, the buffers used were KCl-HCl buffer (pH 2.0), citrate buffer (pH 3.0), acetate buffer (pH 4.0) and cacodylic acid buffer (pH range 5.0–7.0). Since, the change in pH may also occur on heating, or on addition of urea, the pH of the solution was, therefore, measured after the denaturation experiment; the variation in the pH was found to be insignificant.

Thermal Denaturation Studies

Thermal denaturation studies were carried out in Jasco V-560 UV/Vis spectrophotometer equipped with a peltier type temperature controller (ETC-505T), with a heating rate of 1°C/min. This scan rate was found to provide adequate time for equilibration. Each sample was heated from 20 to 85°C. Change in the absorbance with increasing temperature was followed at 287 nm for RNase-A, 300 nm for lysozyme and 295 nm for α-LA. About 650 data points of each transition curve were collected. After denaturation, the sample was immediately cooled down to measure reversibility. All solution blanks showed negligible change in absorbance with temperature and were, therefore, neglected during the data analysis. The raw absorbance data were converted into Δε _λ, the difference molar absorption coefficient (M⁻¹ cm⁻¹) at a given wavelength, λ (ε _λ at any temperature T – ε _λ at 20°C). Each heat-induced transition curve (plot of Δε versus temperature) was analyzed for T _m (the midpoint of heat denaturation) and ΔH _m (the enthalpy change of denaturation at T _m) using a non-linear least-squares analysis according to the relation [31],

(1)

where y(T) is the optical property at temperature T (Kelvin); y _N(T) and y _D(T) are the optical properties of the native and denatured protein molecules, respectively; and R is the gas constant. In the analysis of the transition curve, it was assumed that a parabolic function describes the dependence of the optical properties of the native and denatured protein molecules (i.e., y _N(T) = a _N+b _N T+c _N T ², and y _D(T) = a _D+b _D T+c _D T ², where a _N, b _N, c _N, a _D, b _D, and c _D are temperature-independent coefficients). The reason for using cubic dependencies of baselines is an observation that there exists and excellent agreement between a thermodynamic parameters obtained from such an analysis of the thermal transition curve and from DSC measurements [31], [32]. ΔG _D (T), the value of ΔG _D at any temperature T was estimated using the known values of T _m, ΔH _m and ΔC _p (constant-pressure heat capacity change on denaturation) in the Gibbs-Helmholtz equation,

(2)

CD Measurements

The far- and near-UV circular dichroism (CD) spectra of RNase A, lysozyme, and α-LA in the presence and absence of the co-solvents were measured in J-715 (Jasco spectropolarimeter) equipped with a Peltier-type temperature controller (PTC-348-WI) at least three times at 25 and 85°C. At least six scans were accumulated to average out a spectrum to improve upon the signal-to-noise ratio in each case, including the base line. Each spectrum of a protein was corrected for the contribution of its blank in the entire wavelength range. The CD signal at each wavelength was converted into mean residue ellipticity (deg cm² dmol^–1) using the relation,

(3)

where θ _λ is the observed ellipticity (millidegrees) at the wavelength λ, M _o is the mean residue weight of the protein, c is the protein concentration (mg/cm³), and l is the path length (centimeters). The protein concentration for the CD measurements was in the range 0.2–0.3 mg/cm³. A 0.1 cm path length cell was used for the far-UV CD measurements, and a 1.0 cm path length cell was used for the near-UV CD measurements. It should be noted that the CD instrument was routinely calibrated with D-10-camphorsulfonic acid.

Measurements of Enzymatic Activity Parameters

The effect of different concentrations of urea and each stabilizing osmolyte alone, and different urea-osmolyte mixtures on the kinetic parameters (K _m and k _cat) for the lytic activity of lysozyme towards M. luteus cell walls was measured at pH 7.0 and 25°C by the method of Maurel & Douzou [33]. The substrate and the enzyme were pre-incubated in a given concentration of urea, each stabilizing osmolyte (myo-inositol, sorbitol and taurine) alone and in combined osmolyte-urea mixtures. The decrease in absorbance of a turbid aqueous suspension of M. luteus on the addition of lysozyme was recorded at 450 nm in Jasco V-660 UV/Visible spectrophotometer with constant stirring. The rate of lysis was deduced from the slope of the linear part of the recordings, usually over the first 30 sec, wherein 10 to 20% of the substrate was lysed. At 450 nm the apparent specific absorbance of an aqueous suspension of M. luteus cell walls was ε ₄₅₀ = 0.65×10⁻² mg l⁻¹. The rate of lysis was defined as the weight of cells lysed (in mg ml⁻¹) per sec and per mol of lysozyme. The assay media were directly prepared in 1 cm path length glass cell. In a typical experiment, different concentrations, ranging from 10 to 200 µl, of a stock aqueous suspension of M. luteus cells (3 mg m1⁻¹), were added, and the final volume was adjusted to 3 ml with 50 mM cacodylate buffer, pH 7.0. The cell was then placed into the spectrophotometer cell holder maintained at 25±0.1°C. The reaction was initiated by the addition of 20 µl of a lysozyme stock solution (1 mg/ml, in 50 mM cacodylate buffer, pH 7.0). The kinetic parameters K _m (µg m1⁻¹) and V _max (s⁻¹ M⁻¹) were determined from Michaelis-Menten plots using equation,

(4)

where ν is the initial velocity, and [S] is the substrate concentration. In these experiments M. luteus concentration was varied from 10 to 200 µg m1⁻¹ and the lysozyme concentration was kept constant at 0.45 µM. The value of k _cat (mg ml⁻¹ s⁻¹ M⁻¹) is the product of V _max and enzyme concentration.

RNase-A activity was assayed to see the effect of different concentrations of urea and each osmolyte alone, and different concentrations of each osmolyte-urea mixture on its kinetic parameters (K _m and k _cat) as described previously [34]. For this, the substrate (2′–3′ cyclic monophosphate) and enzyme solutions were pre-incubated in a given concentration of urea and each osmolyte alone and in each osmolyte-urea mixture. RNase-A mediated hydrolysis of the substrate in the concentration range 0.05–0.50 mg ml⁻¹ was followed by measuring the change in absorbance at 292 nm at 25.0±0.1°C for 20 min in Jasco V-660 UV/Vis spectrophotometer. From each progress curve at a given substrate concentration, initial velocity (ν) was determined from the linear portion of the progress curve, usually first 30 sec. The plot of ν versus [S] (in mM) at each co-solvent concentration was analyzed for K _m and V _max using equation (4). From this analysis the values of k _cat were determined.

Results

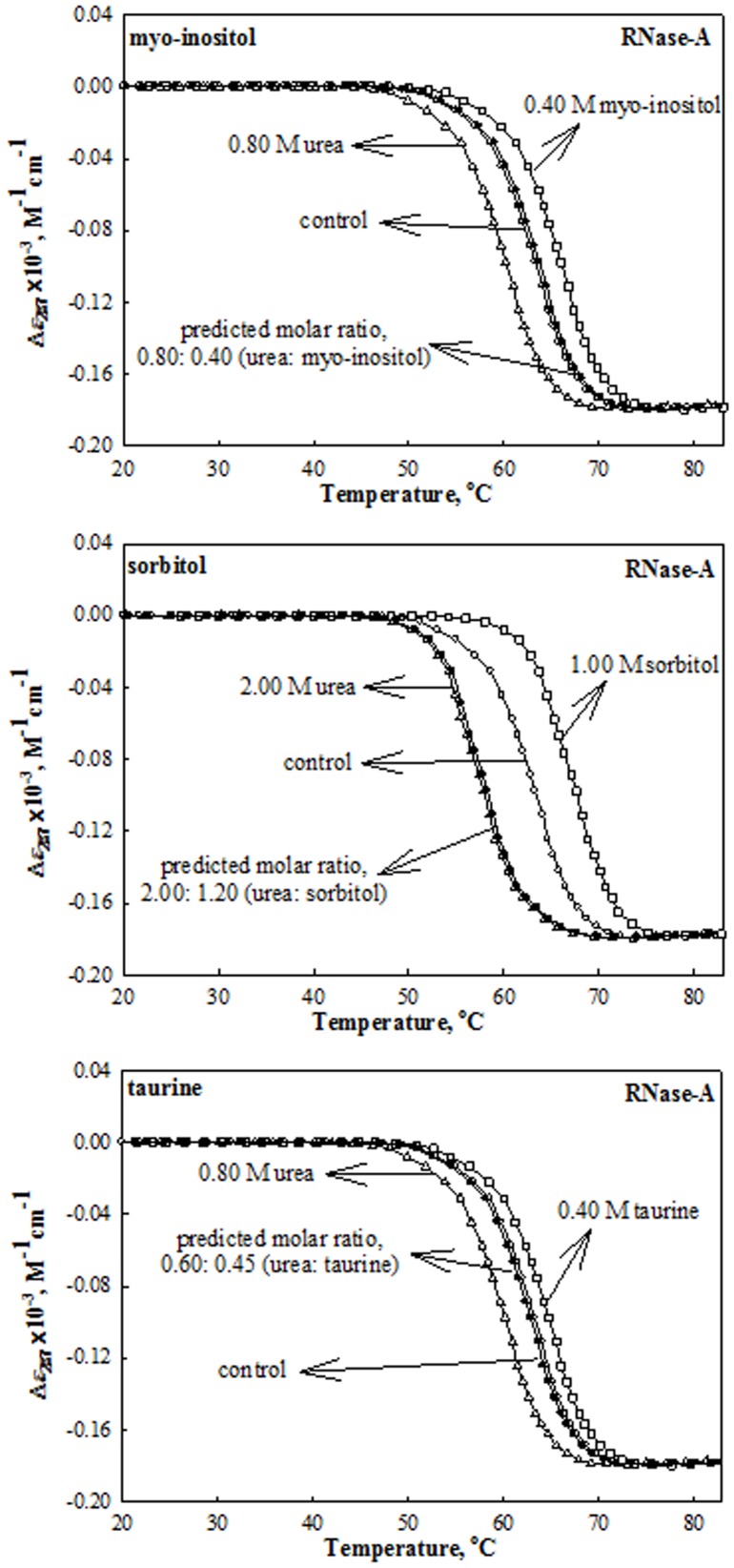
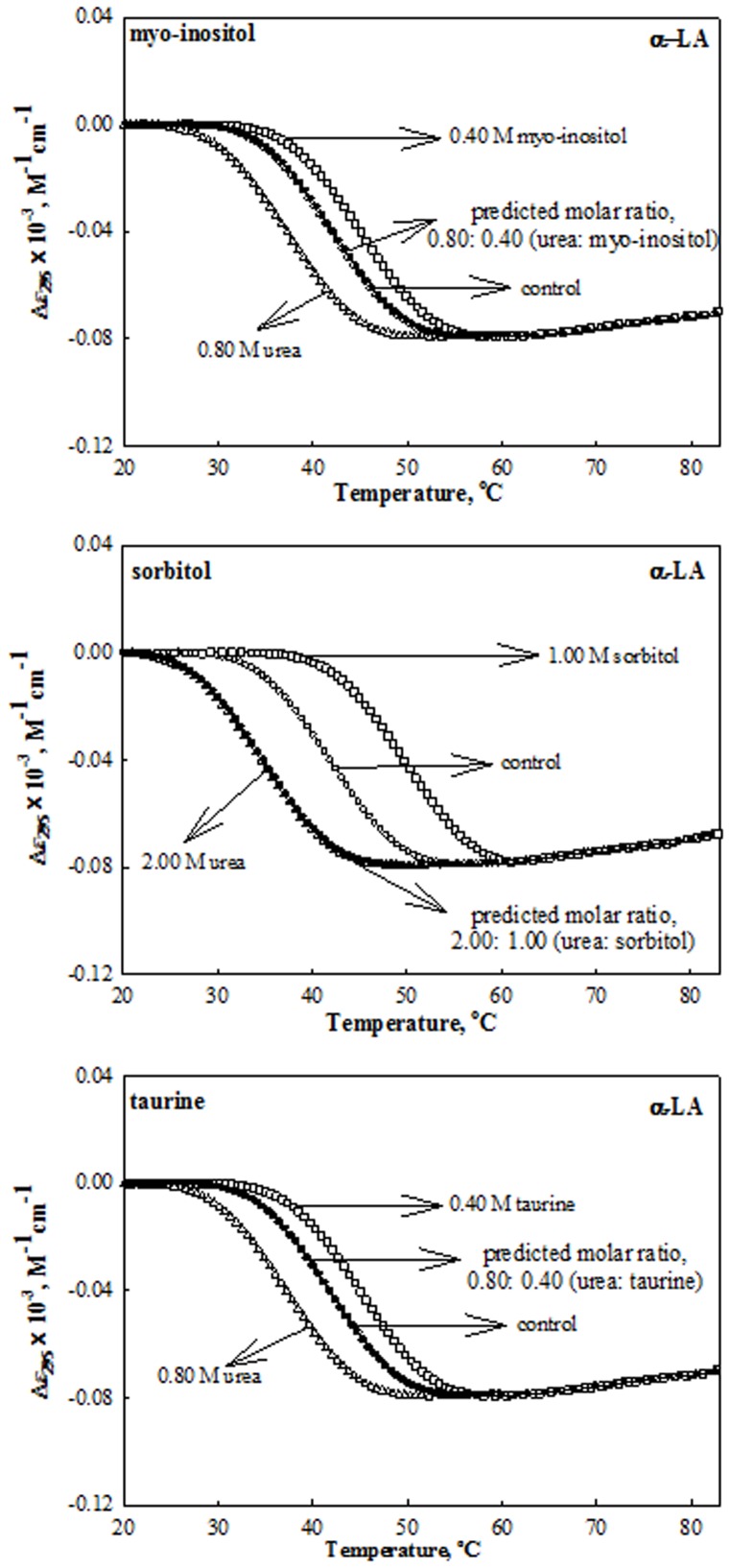
The role of non-methylamine osmolytes (myo-inositol, sorbitol and taurine) in counteracting the effects of urea on protein stability was investigated by measuring the heat-induced denaturation curves of the proteins (RNase-A, lysozyme and α-LA) at different pH values in the presence of each of the osmolytes and urea at various concentrations (0.1–1.0 M for stabilizing osmolytes and 0.2–2.0 M in case of urea). We have intentionally chosen these urea concentrations as all the three proteins exist in native state in the presence of these urea concentrations. To investigate the effect of these co-solutes on the protein stability, heat-induced denaturation curves were monitored by following changes in Δε_λ, the difference in molar absorption co-efficient at the wavelength, λ; Δε ₂₈₇ for RNase-A, Δε ₃₀₀ for lysozyme and Δε ₂₉₅ for α-LA. Figures 1 to 3 show the representative heat-induced denaturation curves of RNase-A, lysozyme and α-LA in the absence and presence of the highest concentration of these co-solutes at pH 7.0. It should be noted that we could not measure the effects of myo-inositol and taurine beyond 0.4 M due to their limited solubility. Denaturation of each protein was reversible in the presence and absence of urea and each stabilizing osmolyte making it amenable for the thermodynamic analysis. All heat-induced denaturation curves were analyzed for T _m and ΔH _m (enthalpy change at T _m) using equation (1). This analysis involves fitting the entire (Δε, T) data of a transition curve to equation (1) with all eight free parameters (a _N, b _N, c _N, a _D, b _D, c _D, ΔH _m and T _m). Table 1 shows values of ΔH _m and T _m of each protein at the given co-solute concentrations. In the case of lysozyme we could not get a complete transition curve in the measurable temperature range in the presence and absence of osmolytes at pH 7.0. To bring down the thermal denaturation curves in the measurable temperature range, measurements were carried out in the presence of 2.0 M GdmCl. The contribution of the 2.0 M GdmCl to the observed thermodynamic parameters was corrected using the method published earlier [35]. Therefore, the values of T _m and ΔH _m shown in Table 1 (at pH 7.0) are the corrected values for the contribution of GdmCl.

Figure 1. Effect of urea, stabilizing osmolytes and their mixtures (at predicted ratio for perfect counteraction) on RNase-A at pH 7.0 and 25°C.

Representative thermal denaturation curves of RNase-A in the presence of the indicated concentrations of urea, osmolytes and their mixtures at predicted ratios given in Table 2. To maintain clarity all data points and all transition curves are not shown.

Figure 3. Effect of urea, stabilizing osmolytes and their mixtures (at predicted ratio for perfect counteraction) on α-LA at pH 7.0 and 25°C.

Representative thermal denaturation curves of α-LA in the presence of the indicated concentrations of urea, osmolytes and their mixtures at predicted ratios given in Table 2. To maintain clarity all data points and all transition curves are not shown.

Table 1. Thermodynamic parameters associated with the thermal unfolding of RNase-A, Lysozyme and α-LA at pH 7.0.^{a, b, c.}

	RNase-A			Lysozyme			α-LA
[Osmolyte]	ΔG D o	T m	ΔH m	ΔG D o	T m	ΔH m	ΔG D o	T m	ΔH m
M	kcal mol−1	°C	kcal mol−1	kcal mol−1	°C	kcal mol−1	kcal mol−1	°C	kcal mol−1
Urea
0.00	10.41	63.0	116	13.00	86.0	129	2.01	42.3	50
0.50	9.93	61.6	114	12.67	84.4	127	1.54	40.1	44
1.00	9.28	60.0	111	12.31	83.2	125	1.47	38.0	42
1.50	8.72	57.9	109	12.06	82.4	123	1.21	36.2	39
2.00	8.34	56.3	108	11.69	80.9	121	0.91	35.0	35
		(56.0)	(109)		(80.7)	(121)		(34.8)	(34)
Myo-inositol
0.10	10.67	63.7	117	13.17	86.4	129	2.12	43.2	51
0.20	10.93	64.3	118	13.31	86.9	130	2.21	43.8	52
0.30	11.05	65.0	118	13.43	87.3	130	2.36	44.6	53
0.40	11.29	65.7	119	13.56	87.8	131	2.43	45.3	54
		(66.0)	(118)		(88.0)	(130)		(45.5)	(56)
Urea+myo-inositol
0.20+0.10	10.36	63.1	115	13.00	86.1	129	2.00	42.1	50
0.40+0.20	10.37	63.3	115	12.95	86.6	128	1.93	42.4	49
0.60+0.30	10.33	63.5	114	13.06	86.5	128	2.02	42.2	50
0.80+0.40	10.36	63.8	114	12.84	86.7	127	1.90	42.1	48
		(63.7)	(114)		(86.6)	(126)		(42.1)	(50)
Sorbitol
0.25	10.93	64.3	118	13.30	86.7	131	2.24	44.1	52
0.50	11.36	65.4	120	13.49	87.6	131	2.55	45.9	55
0.75	11.73	66.9	121	13.80	88.5	132	2.79	47.7	57
1.00	12.27	68.5	123	13.83	89.7	132	3.07	50.1	59
		(68.1)	(122)		(89.9)	(131)		(50.3)	(58)
Urea+sorbitol c	9.80	61.5	113	12.79	84.4	128	1.67	40.3	45
0.50+ v	9.46	60.1	112	12.26	83.2	125	1.43	38.2	42
1.00+ w	8.87	57.9	110	11.74	82.0	122	1.21	36.2	39
1.50+ x	8.22	56.2	107	11.53	80.5	121	0.92	35.1	36
2.00+ y		(55.8)	(107)		(80.3)	(121)		(34.8)	(35)
Taurine
0.10	10.48	63.4	116	13.02	86.8	129	2.09	42.8	51
0.20	10.64	63.7	117	13.14	87.3	130	2.19	44.0	51
0.30	10.83	64.1	118	13.15	87.8	130	2.29	44.4	52
0.40	10.94	64.5	118	13.33	88.3	131	2.40	45.4	53
		(64.0)	(120)		(88.5)	(131)		(45.1)	(53)
Urea+taurine c
0.20+ v	10.30	62.8	116	13.00	85.8	129	2.05	42.1	51
0.40+ w	10.11	62.4	115	12.82	85.7	128	1.91	42.4	48
0.60+ x	10.11	62.4	115		(85.5)	(129)	2.01	42.2	50
		(62.5)	(114)				1.94	42.1	49
								(42.0)	(50)

^aErrors in ΔG _D ^o, ΔH _m and T _m from triplicate measurements are 5–9%, 2–5% and 0.1–0.6%, respectively.

^bValues in the parentheses are from [θ]₂₂₂ measurements.

^cv, w, x and y represent concentrations of the osmolyte predicted from results given in Table 2 (see text). For instance, values of y for sorbitol are 1.20, 1.60 and 1.00 for RNase-A, lysozyme and α-LA, respectively.

Figure 2. Effect of urea, stabilizing osmolytes and their mixtures (at predicted ratio for perfect counteraction) on Lysozyme at pH 7.0 and 25°C.

Representative thermal denaturation curves of Lysozyme in the presence of the indicated concentrations of urea, osmolytes and their mixtures at predicted ratios given in Table 2. To maintain clarity all data point and all transition curves are not shown.

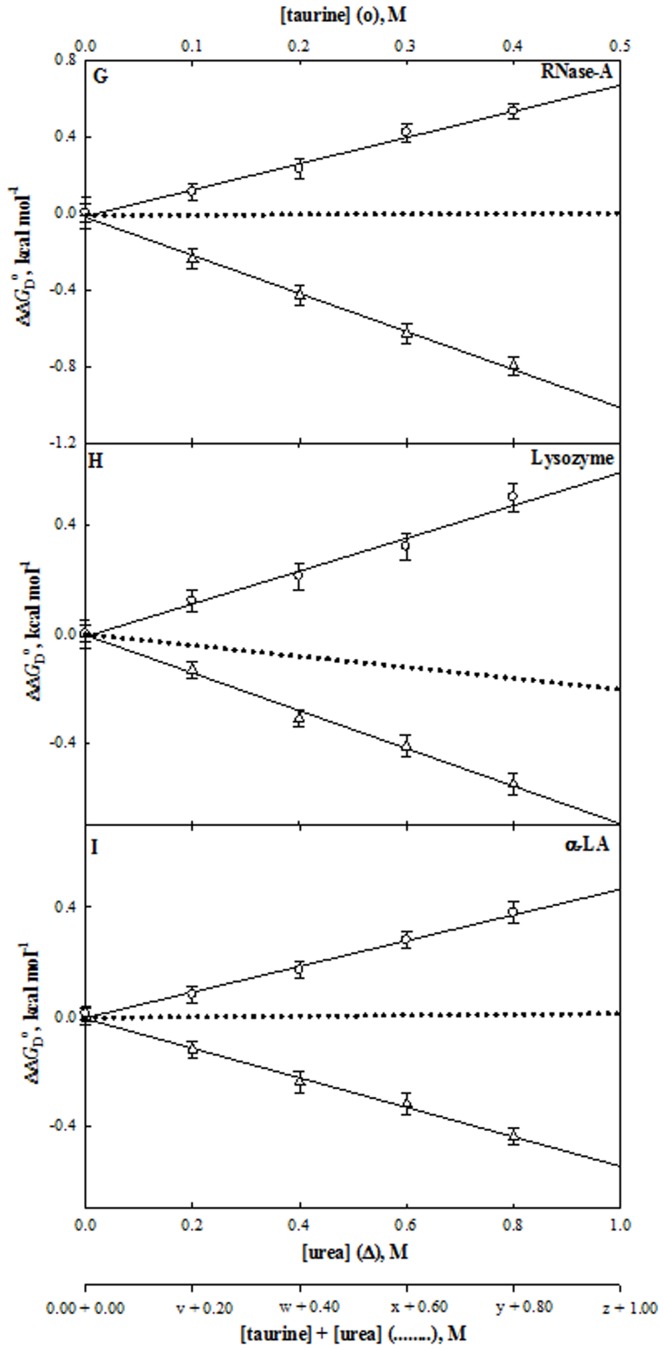
Values of ΔC _p (constant-pressure heat capacity change) of the protein were determined by plotting ΔH _m and T _m values in the absence and presence of each co-solute, generated at five different pH values (see Tables S1–S12 in Appendix S1), for ΔC _p is independent of pH [36]. Values of ΔG _D ^o, (value of ΔG _D at 25°C) estimated at pH 7.0 using equation (2), are given in Table 1. Figures 4 to 6 show representative plots of ΔΔG _D ^o (ΔG _D ^o in the presence of co-solute - ΔG _D ^o in the absence of co-solute) versus [co-solute], the molar concentration of the co-solute. It is seen in these figures that ΔΔG _D ^o of the proteins increases in the presence of the stabilizing osmolytes, whereas it decreases in the presence of urea. Values of m (for detail see Discussion) for all co-solutes obtained from the linear analysis of ΔΔG _D ^o versus [co-solute] are given in Table 2. Following Mello and Barrick [37], the predicted ratio for non-methylamine-induced counteraction of urea’s effect on protein stability (for each of the protein) obtained by using the m-values of urea (m _u) and non-methylamine osmolyte (counteracting osmolyte (m _CO)) are also presented in Table 2. This table also shows the ratio of m _u: m _CO required for thermodynamic counteraction. It is seen in Table 2 that myo-inositol exhibits counteraction at 2∶1 (urea: osmolyte) ratio for all the three proteins while ratio of urea-sorbitol and urea-taurine mixture varies depending on the protein chosen. We have further checked if the prediction ratio for the counteraction is indeed true by measuring heat-induced denaturation of each of the protein in the presence of the several concentrations of urea-non-methylamine mixtures at the ratio obtained from the predictions. Such heat-induced transition curves in the presence of the urea-non-methylamine mixtures are also presented in Figures 1 to 3, and the evaluated thermodynamic parameters are also given in Table 1. Figures 4 to 6 also show the plot of ΔΔG _D ^o versus [urea-non-methylamine mixture], the molar concentrations of urea-non-methylamine mixtures. It is seen in these figures that the predicted ratio turns true for thermodynamic counteraction for urea-myo-inositol and urea-taurine mixtures. Interestingly, for all the proteins investigated, sorbitol shows no counteraction at the predicted ratio. The results indicate that, in addition to the methylamine, non-methylamine osmolytes, myo-inositol and taurine exhibit thermodynamic counteraction.

Figure 4. Effect of myo-inositol, urea and their mixtures on stability of proteins at pH 7.0 and 25°C.

Plots of ΔΔG _D ^o versus [myo-inositol] (○) and [urea] (Δ). The dotted line represents the ΔΔG _D ^o values measured at the predicted ratios (see Table 2). The values of v, w, x, y and z of each protein are those predicted from results given in Table 2. For instance, value of y for myo-inositol is 0.40 M for RNase-A, lysozyme and α-LA.

Figure 6. Effect of taurine, urea and their mixtures on stability of proteins at pH°C.

Plots of ΔΔG _D ^o versus [taurine] (○) and [urea] (Δ). The dotted line represents the ΔΔG _D ^o values measured at the predicted ratios (see Table 2). The values of v, w, x, y and z of each protein are those predicted from results given in Table 2. For instance, values of y for taurine are 0.60, 0.48 and 0.40 M for RNase-A, lysozyme and α-LA, respectively.

Table 2. m-values (dependence of ΔG _D ^o on concentrations of different co-solutes) and the ratios, [urea]: [CO] predicted for perfect counteraction using equation 5 for RNase-A, lysozyme and α-LA at pH 7.0 and 25°C.

	RNase-A		Lysozyme		α-LA
Co-solute	m kcal mol−1 M−1	Predicted Ratio [urea]:[CO]	m kcal mol−1 M−1	Predicted Ratio [urea]:[CO]	m kcal mol−1 M−1	Predicted Ratio [urea]: [CO]
Urea	−1.07	–	−0.70	–	−0.54	–
Myo-inositol	2.15	2.0∶1.0	1.38	2.0∶1.0	1.09	2.0∶1.0
Sorbitol	1.81	2.0∶1.2	0.90	2.0∶1.6	1.08	2.0∶1.0
Taurine	1.41	2.0∶1.5	1.13	2.0∶1.2	1.08	2.0∶1.0
Betainea	0.98	2.0∶2.2	2.33	2.0∶0.6	1.39	2.0∶0.8
GPCb	–	2.0∶2.7	–	–	–	–

^aThe values are taken from Singh et al. [69].

^bValues taken from Burg et al. [70].

To validate our observations from thermodynamic measurements, we have carried out measurements of enzymatic parameters (K _m and k _cat) of RNase-A and lysozyme in the absence and presence of urea, stabilizing osmolytes and their mixtures at pH 7.0 and 25°C. These results are shown in Table 3. Values of K _m and k _cat of both the enzymes in the absence of co-solutes are in agreement with the earlier reports [34], [38], [39] suggesting that the values obtained in this study are authentic and accurate. It is seen in Table 3 that (a) urea increases K _m and decreases k _cat of both enzymes, and (b) myo-inositol, sorbitol and taurine do not perturb K _m and k _cat, i.e., they are compatible osmolytes. This table also shows values of kinetic parameters in the presence of non-methylamine-urea mixtures (at the predicted molar ratio of non-methylamine and urea). It is observed that (a) myo-inositol and taurine reverses the effect urea on K _m and k _cat of enzymes, (b) sorbitol does not show any counterbalancing effects on both the kinetic parameters of both enzymes.

Table 3. Activity parameters of RNase-A and lysozyme in the presence and absence of co-solutes at pH 7.0 and 25°C.^a .

	RNase-A			Lysozyme
[Co-solute]	K m	k cat	[Co-solute]	K m	k cat
M	mM	s−1	M	µg ml−1	mg ml−1 s−1 M−1
Urea			Urea
0.00	0.99±0.02	3.44±0.08	0.00	77.8±2	484.1±29
0.50	1.16±0.02	3.22±0.10	0.50	87.3±3	451.6±30
1.00	1.36±0.04	3.02±0.06	1.00	93.4±4	417.7±20
1.50	1.49±0.02	2.75±0.07	1.50	97.6±3	380.6±15
2.00	1.69±0.03	2.48±0.09	2.00	107.7±4	349.6±20
Myo-inositol			Myo-inositol
0.10	1.00±0.04	3.50±0.18	0.10	77.9±2	483.5±35
0.20	0.99±0.04	3.45±0.14	0.20	77.1±3	482.9±30
0.30	1.01±0.09	3.44±0.23	0.30	76.5±2	484.5±15
0.40	1.02±0.06	3.47±0.13	0.40	77.8±1	484.9±20
Sorbitol			Sorbitol
0.25	1.01±0.09	3.44±0.23	0.25	77.7±3	483.0±15
0.50	1.00±0.07	3.50±0.18	0.50	76.8±4	483.8±16
0.75	1.01±0.05	3.47±0.30	0.75	77.1±2	484.6±11
1.00	0.99±0.10	3.45±0.14	1.00	76.1±2	485.1±10
Taurine			Taurine
0.10	1.00±0.05	3.47±0.08	0.10	78.3±3	484.9±18
0.20	0.99±0.02	3.46±0.09	0.20	77.8±3	483.1±20
0.30	0.97±0.05	3.43±0.10	0.30	77.4±1	484.5±16
0.40	0.95±0.02	3.41±0.06	0.40	77.1±1	483.6±09
Myo-inositol+urea			Myo-inositol+urea
0.10+0.20	1.05±0.03	3.44±0.08	0.10+0.20	78.0±3	483.2±12
0.20+0.40	1.03±0.06	3.40±0.08	0.20+0.40	78.3±3	481.1±15
0.30+0.60	1.00±0.06	3.40±0.07	0.30+0.60	77.4±4	480.2±07
0.40+0.80	1.06±0.04	3.35±0.09	0.40+0.80	77.1±3	481.6±11
Sorbitol+urea			Sorbitol+urea
0.30+0.50	1.17±0.02	3.20±0.10	0.40+0.50	87.5±2	448.2±12
0.60+1.00	1.33±0.04	3.05±0.06	0.80+1.00	93.1±3	435.6±14
0.90+1.50	1.45±0.02	2.70±0.07	1.20+1.50	96.3±2	378.0±07
1.20+2.00	1.70±0.03	2.50±0.09	1.60+2.00	107.2±4	345.9±15
Taurine+urea			Taurine+urea
0.15+0.20	1.02±0.03	3.44±0.08	0.12+0.20	79.9±3	477.1±18
0.30+0.40	1.03±0.06	3.39±0.08	0.24+0.40	81.7±4	462.1±30
0.45+0.60	1.00±0.06	3.36±0.07

^aA ± with K _m and k _cat is the mean error obtained from the triplicate measurements.

Discussion

The preceding section presents results of our measurements of the effects of non-methylamines (myo-inositol, sorbitol and taurine) and urea alone and in combination on structure, stability and function of three model proteins (RNase-A, lysozyme and α-LA). A question arises: Do these results have any relevance to kidney proteins? It has been shown that stabilizing osmolytes including non-methylamines are preferentially excluded from the protein domain [40], [41]. This property of stabilizing osmolytes has two important consequences. (a) There is no binding between osmolyles and proteins. (b) Stabilization by osmolytes is protein non-specific due to osmophobic effect originating from the overwhelming unfavourable interaction between osmolytes and the peptide backbone [41]. Hence, findings of this study will have relevance to kidney proteins as well.

Analysis of a thermal denaturation curve according to equation (1) assumes that denaturation follows a two-state mechanism. Differential scanning calorimetric (DSC) measurements suggest that this is, indeed, true for these proteins in the absence of osmolytes [42], [43]. Furthermore, DSC measurements suggest that the heat-induced denaturation of RNase-A, and lysozyme in the presence of methylamines [38], [44] and urea [45] is a two-state process. To check whether the two-state assumption is valid in the presence of kidney osmolytes, non-methylamines (myo-inositol, sorbitol and taurine) and urea-osmolyte mixtures, the heat-induced denaturation of RNase-A, lysozyme, and α-LA in the presence of 2.0 M urea, 0.4 M myo-inositol, 1.0 M sorbitol, 0.4 M taurine and their combined mixtures were measured by two different optical techniques, namely, mean residue ellipticity at 222 nm ([θ]₂₂₂) which measures the change in the peptide backbone conformation (see Figures S1 to S3 in Appendix S1) and Δε in the near- UVregion (see Figures 1 to 3), which measures the change in the tyrosine/tryptophan environment. All denaturation curves were analyzed for ΔH _m and T _m using a non-linear analysis according to equation (1). We compared ΔH _m and T _m values thus obtained from Δε measurements with those from [θ]₂₂₂ measurements. It is seen in Table 1 that both measurements gave, within experimental errors, identical values of these thermodynamic parameters. Thus, a two-state assumption for thermal denaturation of RNase-A, lysozyme, and α-LA in the presence of urea, stabilizing osmolytes and their predicted ratio combined mixtures seems to be valid.

It is necessary to show that values of ΔC _p, ΔH _m and T _m obtained from the analysis of thermal transition curves such as shown in Figures 1 to 3, are in good agreement with those obtained from DSC measurements. Makhatadze and Privalov [45] have reported calorimetric values of these parameters for RNase-A and lysozyme in the absence and presence of 1 and 2 M urea at pH 5.5 and 4.6, respectively. Since these pH values are different from those used in this study, a comparison of ΔH _m and T _m are not possible. However, a direct comparison of ΔC _p values is possible, for ΔC _p is independent of pH [36]. It has been observed that there exists, within experimental errors, an excellent agreement between calorimetric ΔC _p values [45] and those observed in this study (see Tables S1 and S5 in Appendix S1).

To compare a thermodynamic quantity of a protein in the absence and presence of urea (0.2–2.0 M), stabilizing osmolytes (0.1–1.0 M) and their mixture, it is necessary to show that the structural characteristics of the two end states, i.e, N and D states of denaturations of RNase A, lysozyme and α-LA, are not affected due to the presence of urea, stabilizing osmolytes and their combined mixtures. We observed that the far- and near-UV CD spectra of both native and denatured proteins in the absence and presence of the osmolytes were, within the experimental errors, identical (see Figures S4 to S6 in Appendix S1). These observations on the native proteins are consistent with the x-ray results showing that the native structure of proteins is unperturbed by osmolyte [46] and with the size exclusion chromatography results suggesting that an osmolyte has no effect on the dimensions of the native proteins [47], [48], [49]. Our observation on denatured proteins is also in agreement with the report that methylamines are non-perturbing in its effects on fully solvent-exposed amide protons [50]. Hence, a comparison of a thermodynamic property of denaturation in the presence and absence of the urea, non-methylamine osmolytes and their mixtures is valid.

The thermodynamic basis of urea-osmolyte compensation on protein stability has been explained in terms of preferential binding and preferential exclusion of these co-solutes, respectively [51], which is supported by observations on the transfer-free energy of the protein groups from the solvent water to the co-solute solutions [52] . Based on this model, osmolytes stabilize proteins by shifting the denaturation equilibrium, N state ↔ D state toward the left, while urea destabilizes proteins by shifting the denaturation equilibrium toward the right, and urea-osmolyte mixture brings about compensatory effect. Thus, what effects co-solutes will have on the denaturation equilibrium, N state ↔ D state under the native condition will be known only by measuring ΔG _D ^o (value of Gibbs energy change, ΔG _D at 25°C) in different solvent conditions. Values of ΔG _D ^o of all proteins at different concentrations of urea and each stabilizing osmolyte are given in Table 1. These observations are also shown in Figures 4 to 6 which show the plots of ΔΔG _D ^o versus [urea] and ΔΔG _D ^o versus each [non-methylamine] (ΔΔG _D ^o is defined as the difference between ΔG _D ^o in the presence of co-solute and ΔG _D ^o in the absence of co-solute). It is seen in Table 1 and Figures 4 to 6 that myo-inositol, sorbitol and taurine increase ΔG _D ^o of each protein while urea decreases ΔG _D ^o in a concentration dependent manner.

The main reason for the thermodynamic counteraction is that urea and its counteracting osmolytes act independently on the proteins, i.e., none of the co-solutes alters the efficacy of the other in forcing proteins to fold or unfold [52]. This means that the sensitivity of ΔG _D ^o of proteins on [urea] (the m _u-value) is independent of [CO], the counteracting osmolyte (CO) concentration, and vice-versa. Following Mello and Barrick [37], the combined effects of urea and CO on denaturation free energies can be modeled as being linear in both co-solutes:

(5)

where ΔG _D ^o _{(urea, CO)} and ΔG _D ^o _(0,0) are values of ΔG _D ^o measured in the presence and absence of urea- CO mixture, respectively, and m _co gives the dependence of ΔG _D ^o _(CO) on [CO]. It then follows from equation (5) that the ratio [urea]: [CO] for a perfect compensation can be predicted if one knows values of m _u and m _co. For a protein-co-solute system a linear analysis of ΔΔG _D ^o (co-solute) versus [co-solute] plots (Figures 4 to 6) yielded the m-values (m _u and m _co). These values are shown in Table 2. Values given in this table, suggest that for urea-myo-inositol interaction with proteins, the ratio m _co: m _u is 2.0∶1.0 for all the proteins. This implies that a perfect counteraction is expected at 2∶1 ([urea]: [CO]) ratio. It is seen in Figure 4 that this is indeed true experimentally. We, therefore, conclude that urea-myo-inositol exhibits perfect counteraction at 2.0∶1.0, and these two co-solutes act on proteins independent of each other. Interestingly, the ratio of myo-inositol-induced counteraction of urea’s effect observed here on the three proteins is the same ratio found for methylamine-induced counteraction.

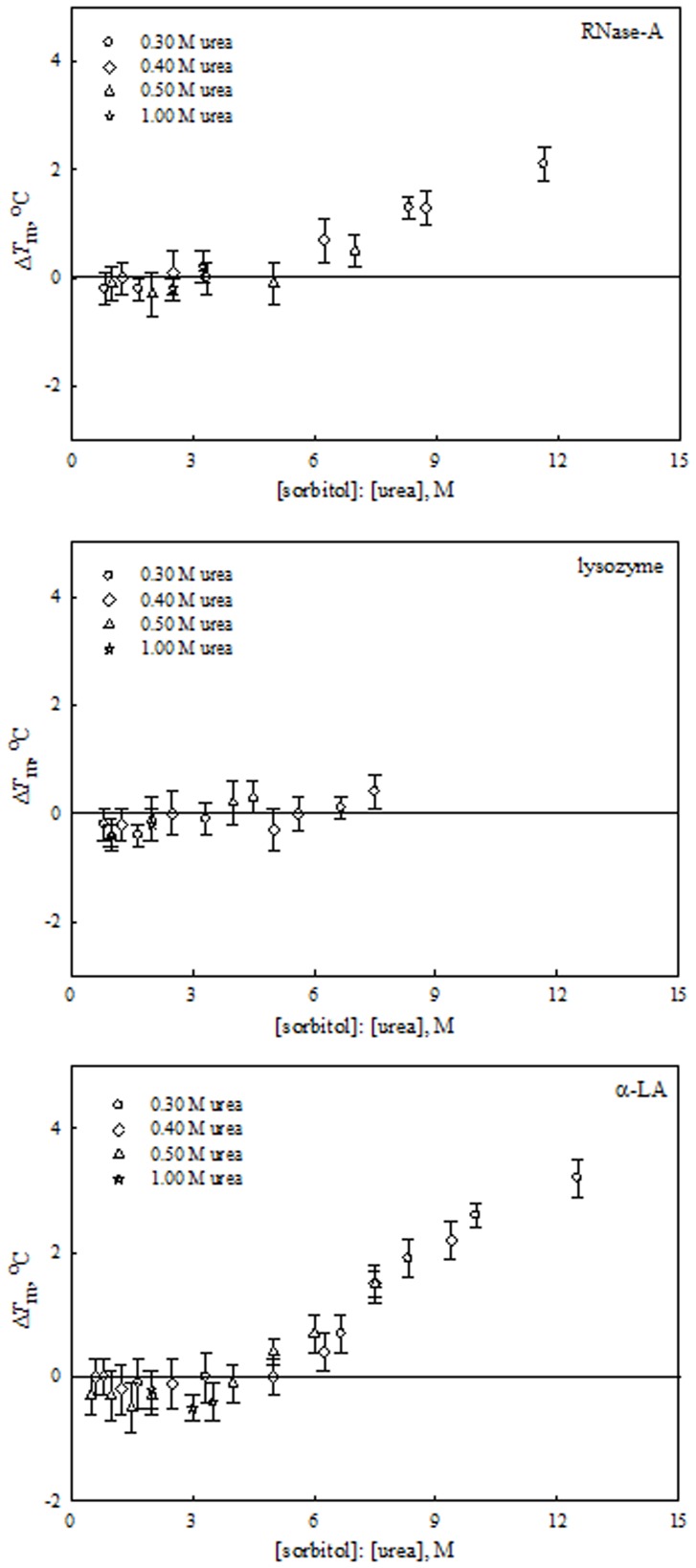
Similarly, from the measured m-values of urea and sorbitol (and taurine) for all proteins we predicted the [urea]: [sorbitol] (and [urea]: [taurine]) ratios for counteraction (see Table 2). Table 2 indicates that the predicted ratio for thermodynamic counteraction is apparently protein dependent for urea-sorbitol and urea-taurine mixtures. Figures 4 to 6 show plots of experimentally measured values of ΔΔG _D ^o of urea, non-methylamines and the urea-non-methylamine mixtures at the given predicted molar ratios. To our surprise, the highly stabilizing osmolyte, sorbitol completely lost its ability to offset the effects of urea on all proteins studied (Figure 5). This observation on sorbitol led us to conclude that in spite of being a good protein folder in various stress conditions [34], [53], [54], it does not refold the urea-denatured proteins. To check whether it is, indeed, true at all sorbitol to urea ratios, we have measured heat-induced denaturation curves of each protein as function of [sorbitol] at 0.25 M and above in the presence of a fixed urea concentration in the range 0.3, 0.4, 0.5, and 1.0 M (e.g. see Figure S7 in Appendix S1). These results were analyzed for T _m, and its values under different solvent conditions are shown in Table S13 in Appendix S1. For each protein effect of sorbitol-urea mixture on ΔT _m is shown in Figure 7, where ΔT _m = T _m in the presence of sorbitol-urea mixture – T _m in the presence of urea alone. It is seen in this figure that sorbitol has lost its ability to counteract the effect of urea on thermal stability of proteins if its concentration is six times less than that of urea. However, if [sorbitol]: [urea] ratio is ≥6, ΔT _m of RNase-A and α-LA increases with an increase in [sorbitol]: [urea] ratio, suggesting that sorbitol can refold urea-denatured proteins; about 2.1 and 3.2°C increase in T _m of RNase-A and α-LA at a ratio of 12, respectively. Due to experimental constraints, we could not measure ΔT _m values above 7.5 ([sorbitol]: [urea]) ratio.

Figure 5. Effect of sorbitol, urea and their mixtures on stability of proteins at pH°C.

Plots of ΔΔG _D ^o versus [sorbitol] (○) and [urea] (Δ). The dotted line represents the ΔΔG _D ^o values measured at the predicted ratios (see Table 2). The values of v, w, x, y and z of each protein are those predicted from results given in Table 2. For instance, values of y for sorbitol are 1.20, 1.60 and 1.00 M for RNase-A, lysozyme and α-LA, respectively.

Figure 7. Effect of [sorbitol]: [urea] mixtures at different ratios on the stability of proteins at pH 7.0 and 25°C.

Plots of ΔT _m versus different combined ratios of [sorbitol]: [urea] mixtures.

We have seen above that myo-inositol has the ability to counteract the deleterious effect of urea on protein stability at a ratio of 0.5 for [myo-inositol]: [urea] (see Figure 4) whereas sorbitol completely fails to do so (see Figure 7). Is this difference in the counteraction of urea’s effects by sorbitol (linear 6-carbon polyol) and myo-inositol (cyclic 6-carbon polyol) due to difference in their structure? Our research is underway to answer this question.

Contrary to myo-inositol and sorbitol, taurine was found to have protein specific effect on counteracting the urea’s effect. At the predicted ratio (2.0∶1.5 for RNase-A and 2.0∶1.0 for α-LA) [urea]: [taurine] there exists a perfect counteraction of the urea’s effect on proteins. However, only a partial compensation is observed in the case of lysozyme at the predicted ratio of 2.0∶1.2 (see Figure 6). These observations on taurine clearly indicate that it exhibits protein specific counteraction. It is worth noting that, as observed in the case of taurine, methylamine osmolytes found in human kidney or in marine invertebrates, with a few exceptions, always yield partial counteraction [7], [55], [56], [57], [58], [59].

It may be noted that thermodynamic quantities obtained here are merely physical parameters and hence needs to be validated against the biological function. We have therefore, validated our observations on the thermodynamic parameters of the proteins by measuring functional activity parameters (K _m and k _cat) of RNase-A and lysozyme. If the observed urea-osmolyte counteraction phenomenon is due to the shift in the thermodynamic equilibrium, N (functional) state ↔ D (non-functional) state (as indicated by ΔG _D ^o values), then it must be reflected in activity parameters of the enzymes. Because urea is known to push this thermodynamic equilibrium toward the right [51], [60] and consequently affects the number of enzymatically active fractions. As a result, K _m of the enzyme-catalyzed reaction is increased and k _cat is decreased in the presence of urea [7]. In agreement with this, results given in Table 3 show that K _m of both RNase-A and lysozyme increases while k _cat is decreased in urea’s presence. Furthermore, if the osmolytes myo-inositol, sorbitol and taurine have the same efficacy to fold urea-denatured proteins, then the number of active fractions is expected to be similar and consequently will have the same ability to counter the inactivation caused by urea on the enzymes. Our results given in Table 3 suggest that at predicted ratios myo-inositol and taurine can nullify the effect of urea inactivation of the enzymes in terms of K _m and k _cat, while sorbitol has no ability to counterbalance the effects of urea on K _m and k _cat of both the enzymes. Thus, the observed effects on the activity parameters are in good agreement with those of the thermodynamic measurements. The data therefore, suggest that the effectiveness of refolding urea-denatured protein is different for all the three osmolytes. Myo-inositol is able to generate all of the urea-denatured protein fractions to functionally active ones while taurine shows ratio dependent counteraction. Sorbitol cannot refold urea-denatured proteins and hence it cannot convert the urea-inactivated protein fractions to functionally active molecules. Therefore, among the non-methylamines used in this study myo-inositol but not sorbitol or taurine stands as the best urea’s counteractant on protein stability and function.

Taken together, our results suggest that similar to the methylamine osmolytes, some non-methylamine osmolytes (especially myo-inositol and taurine) are good counteractants of urea’s effect on protein stability and function. Sorbitol is a key component of the renal cell osmotic system, but it may not be part of the urea-counteraction system as high concentrations of sorbitol have many clinical complications including, diabetes, cataract, neuropathy [61], [62].

As observed in our study, although myo-inositol is a better counteractant of urea’s effect on protein stability and function than methylamines, the major response of renal cells in cultures to high urea is the increase of GPC, not myo-inositol [63]. It is very likely that evolution might have favored GPC over myo-inositol to counteract the deleterious effects of urea in the renal cells. However, we do not rule out the possibility that myo-inositol (or taurine) might be acting as a counteracting osmolyte in other organisms wherein GPC or other methylamines are absent.

Inside the cells the urea-counteraction system is not confined to only one. There exist multiple urea-counteracting systems. The most efficient one (based on this study) is the urea-myo-inositol system and other includes urea-taurine and urea-methylamine systems that work in a protein specific manner. Speculatively, the urea-myo-inositol may act as a house keeping counteracting system while the other two may invoke only on cellular demands (e.g., extreme stresses) because the existing levels of myo-inositol may not be sufficient enough to take care of the whole proteome stability under high hypertonic conditions (e.g., anti-diuretic condition) in the kidney. Interestingly, almost all reports on the osmotic content of the kidney cells were derived from the measurements under high hypertonic conditions [64], [65], [66], [67], [68]. It is, therefore, important to estimate osmotically active solute in the kidney cells under hypotonic conditions or diuresis.

Supporting Information

Appendix S1

Supplementary data. The following supplementary data is available: FIGURE S1. Effect of urea, osmolyte and their predicted ratio mixtures on RNase-A; FIGURE S2. Effect of urea, osmolyte and their predicted ratio mixtures on Lysozyme; FIGURE S3. Effect of urea, osmolyte and their predicted ratio mixtures on α-LA; FIGURE S4. Effect of urea, myo-inositol and their predicted ratio mixtures on secondary and tertiary structures of proteins; FIGURE S5. Effect of urea, sorbitol and their predicted ratio mixtures on secondary and tertiary structures of proteins; FIGURE S6. Effect of urea, taurine and their predicted ratio mixtures on secondary and tertiary structures of proteins; FIGURE S7. Effect of urea, sorbitol and their mixtures (at different ratios) on the proteins at pH 7.0; Table S1. Thermodynamic parameters associated with the thermal unfolding of RNase-A at different pH values in the presence and absence of urea; Table S2. Thermodynamic parameters associated with the thermal unfolding of RNase-A at different pH values in the presence and absence of myo-inositol; Table S3. Thermodynamic parameters associated with the thermal unfolding of RNase-A at different pH values in the presence and absence of sorbitol; Table S4. Thermodynamic parameters associated with the thermal unfolding of RNase-A at different pH values in the presence and absence of taurine; Table S5. Thermodynamic parameters associated with the thermal unfolding of lysozyme at different pH values in the presence and absence of urea; Table S6. Thermodynamic parameters associated with the thermal unfolding of lysozyme at different pH values in the presence and absence of myo-inositol; Table S7. Thermodynamic parameters associated with the thermal unfolding of lysozyme at different pH values in the presence and absence of sorbitol; Table S8. Thermodynamic parameters associated with the thermal unfolding of lysozyme at different pH values in the presence and absence of taurine; Table S9. Thermodynamic parameters associated with the thermal unfolding of α-LA at different pH values in the presence and absence of urea; Table S10. Thermodynamic parameters associated with the thermal unfolding of α-LA at different pH values in the presence and absence of myo-inositol; Table S11. Thermodynamic parameters associated with the thermal unfolding of α-LA at different pH values in the presence and absence of sorbitol; Table S12. Thermodynamic parameters associated with the thermal unfolding of α-LA at different pH values in the presence and absence of taurine; Table S13. Thermal denaturation studies on proteins to see the counteracting effect of sorbitol with increasing urea concentration at pH 7.0.

(DOC)

Funding Statement

The authors are grateful to CSIR, the Council of Scientific and Industrial Research (India), for the financial support. The funders had no role in study design, data collection and analysis, decision to publish, or preparation of the manuscript.